Keywords

1 Introduction

Data clustering aims at deciphering the inherent relationship of data points and obtaining reasonable clusters  [1, 2]. Also, as an unsupervised learning problem, data clustering has been explored through deep generative models  [3,4,5] and the two most prominent models are Variational Autoencoder (VAE)  [6] and Generative Adversarial Network (GAN)  [7]. Owing to the belief that the ability to synthesize, or “create” the observed data entails some form of understanding, generative models are popular for the potential to automatically learn disentangled representations  [8]. A WGAN-GP framework with an encoder for clustering is proposed in  [9]. It makes the latent space of GAN feasible for clustering by carefully designing input vectors of the generator. Specifically, Mukherjee et al. proposed to sample from a prior that consists of normal random variables cascaded with one-hot encoded vectors with the constraint that each mode only generates samples from a corresponding class in the original data (i.e., clusters in the latent space are separated). This insight is key to clustering in GAN’s latent space. During the training process, the noise input vector of the generator is recovered by optimizing the following loss function:

$$\begin{aligned} J=||E(G(z_{n}))-z_{n}||_{2}^{2}+L(E(G(z_{c})), z_{c}) \end{aligned}$$
(1)

where \(z_{n}\) and \(z_{c}\) are Gaussian and one-hot categorical components of the input vector of the generator respectively and \(L(\cdot )\) denotes the cross-entropy loss function.

However, as pointed in  [10], one can not take it for granted that pretty small recovery loss means pretty good features. So we propose a CD2GAN method for latent space clustering via dual discriminator GAN. The problem of mode collapse can be largely eliminated by introducing the dual discriminators. Then by focusing on recovering the one-hot vector we can obtain the final clustering result by the cross-entropy minimization operation rather than by applying the traditional clustering techniques like K-means.

2 The Proposed Method

First of all, we will give key definitions and notational conventions. In what follows, K represents the number of clusters. \(D_{1}\) and \(D_{2}\) denote two discriminators respectively, where \(D_{1}\) favors real samples while \(D_{2}\) prefers fake samples. G denotes the generator that generates fake samples and E stands for the encoder or the inverse network that serves to reduce dimensionality and get the latent code of the input sample. Let \(z\in \mathbb {R}^{1\times \tilde{d}}\) denote the input of the generator, which consists of two components, i.e., \(z = (z_{n}, z_{c})\). \(z_{n}\) is sampled from a Gaussian distribution, i.e., \(z_{n}\sim \mathcal {N}(\mu ,\sigma ^{2}I_{d_{n}})\). In particular, we set \(\mu =0\), \(\sigma =0.1\) in our experiments and it is typical to set \(\sigma \) to be a small value to ensure that clusters in the latent space are separated. And \(z_{c}\in \mathbb {R}^{1\times K}\) is a one-hot categorical vector. Specifically, \(z_{c} = e_{k}, k\sim \mathcal {U}\{1,2,\cdots , K\}\), \(e_{k}\) is the k-th elementary vector.

2.1 Latent Space Clustering via Dual Discriminator GAN

From Eq. (1) we know that in  [9], in order to get the latent code corresponding to the real sample, it recovers the vector \(z_{n}\) which is sampled from a Gaussian distribution and offers no useful information for clustering. In addition, as pointed in  [10], small recovery loss does not necessarily mean good features. So here comes the question, what are good features? Intuitively, they should contain the unique information of the latent vector. The above two aspects show that the latent vector corresponding to the real sample should not contain the impurity (i.e., \(z_{n}\)). In other words, the degree of dimension reduction is not enough. Motivated by this observation, our method only needs to perfectly recover the most unique information (i.e., \(z_{c}\)) of the latent vector corresponding to the real sample, and utilizes only this part for clustering.

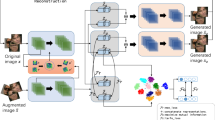
Motivated by all above facts, we propose a dual discriminator GAN framework  [11] with an inverse network architecture for latent space clustering, which is shown in Fig. 1. From  [11], the Kullback-Leibler (KL) and reverse KL divergences are integrated into a unified objective function for the D2GAN framework as follows:

$$\begin{aligned} \mathop {\min }_{G} \mathop {\max }_{D1, D2} L_{1}(G, D_{1}, D_{2})=\,&\alpha E_{x\sim P_{data}}[log(D_{1}(x))]+E_{z\sim P_{noise}}[-D_{1}(G(z))] \\ \nonumber&+E_{x\sim P_{data}}[-D_{2}(x)]+\beta E_{z\sim P_{noise}}[log(D_{2}(G(z))] \end{aligned}$$
(2)

where \(P_{data}\) and \(P_{noise}\) denote the unknown real data distribution and the prior noise distribution respectively. \(\alpha \) and \(\beta \) are two hyperparameters, which control the effect of KL and reverse KL divergences on the optimization problem. It is worth mentioning that the problem of mode collapse encountered in GAN can be largely eliminated since the complementary statistical properties from KL and reverse KL divergences can be exploited to effectively diversify the estimated density in capturing multi-modes.

Fig. 1.
figure 1

The CD2GAN framework.

Full size image

In addition, the input noise vector (i.e., z) of the generator is \(z_{n}\) (sampled from a Gaussian distribution without any cluster information) concatenated with a one-hot vector \(z_{c}\in \mathbb {R}^{1\times K}\) (K is the number of clusters). To be more precise, \(z = (z_{n}, z_{c})\). It is worth noting that each one-hot vector \(z_{c}\) corresponds to one type of mode provided \(z_{n}\) is well recovered  [9]. The inverse network, i.e., the encoder, has exactly opposite structure to the generator and serves to map data into the separable latent space. The overall loss function is:

$$\begin{aligned} \mathop {\min }_{E, G} \mathop {\max }_{D1, D2} L_{1}(G, D_{1}, D_{2})+L_{2}(E, G)+L_{3}(E, G) \end{aligned}$$
(3)

where

$$\begin{aligned} L_{2}(E, G)=\lambda ||E(G(z_{c}))-z_{c}||_{2}^{2} \end{aligned}$$
(4)
$$\begin{aligned} L_{3}(E, G)=\epsilon \mathcal {L}_{CE}(z_{c}, E(G(z_{c}))) \end{aligned}$$
(5)

and \(E(G(z_{c}))\) denotes the last K dimensions of E(G(z)), \(\mathcal {L}_{CE}(\cdot )\) is the cross-entropy loss. Similar to GAN  [7], the D2GAN with an inverse network model can be trained by alternatively updating \(D_{1}\), \(D_{2}\), G and E, where Adam  [12] is adopted for optimization. It is worth noting that the one-hot vector, i.e., \(z_{c}\in \mathbb {R}^{1\times K}\) can be regarded as the cluster label indicator of the fake sample generated from G since each one-hot vector corresponds to one mode. In addition, through adequate training, data distribution of samples generated from G will become much more identical to the real data distribution \(P_{data}\). From this perspective, the inverse network (i.e., the encoder E) can be regarded as a muti-class classifier, which is the key reason why we introduce the cross-entropy loss \(L_{3}(E, G)\) to the overall loss function.

When it comes to clustering, we can utilize the well trained encoder E. Formally, given a real sample x, the corresponding cluster label \(\tilde{y}\) can be calculated as follows:

$$\begin{aligned} \begin{aligned} \tilde{y}=\mathop {\arg \min }_{t}\epsilon \mathcal {L}_{CE}(one\_hot(t), E(x)[\tilde{d}-K:])+&\lambda ||one\_hot(t)-E(x)[\tilde{d}-K:]||_{2}^{2} \\ \end{aligned} \end{aligned}$$
(6)

where \(t = 0,1,\cdots , K-1\), \(one\_hot(t)\in \mathbb {R}^{1\times K}\) is the t-th elementary vector and \(E(x)[\tilde{d}-K:]\) returns a slice of E(x) consisting of the last K elements. \(\lambda \) and \(\epsilon \) remain the same as in the model training phase. For clarity, the proposed CD2GAN method is summarized in Algorithm 1.

figure a

2.2 Semi-supervised Strategy

In this section, we propose a semi-supervised strategy to accelerate and stabilize the training process of our model.

From  [9] we know that the one-hot component can be viewed as the label indicator of the fake samples. With the training going on, we get lots of real samples with their labels, and the encoder can be seen as a multi-class classifier. Like semi-supervised classification problem. Specifically, given a dataset with ground-truth cluster labels, a small portion (1%–2% or so) of it will be sampled along with the corresponding ground-truth cluster labels. Let \(\tilde{x} = (x,y)\) denote one of the real samples for semi-supervised training, where \(x \in \mathbb {R}^{1\times d}\) represents the observation while y is the corresponding cluster label. During the training process, y is encoded to a one-hot vector just like \(z_{c}\), which will then be concatenated with one noise vector \(z_{n}\) to serve as the input of the generator G. Afterwards, the latent code of G(z), i.e. E(G(z)), can be obtained through the encoder. Subsequently, the corresponding x will be fed into the encoder E to get another latent code E(x). As mentioned above, the last K dimensions of the latent code offer the clustering information, and intuitively, one could expect better clustering performance if the the last K dimensions of E(G(z)) and E(x) are more consistent. In light of this, a loss function can be designed accordingly:

$$\begin{aligned} \begin{aligned}&L_{4}(E, G)= \gamma ||(E(x_{r})-E(G(z_{n}, one\_hot(x_{l}))))[\tilde{d}-K:]||_{2}^{2}) \end{aligned} \end{aligned}$$
(7)

where \(\gamma \) is a hyperparameter. In essence, we compute the Euclidean distance between the last K dimensions of E(G(z)) and E(x), which is easy to be optimized. In this way, the overall objective function for the semi-supervised training can be defined as follows:

$$\begin{aligned} \mathop {\min }_{E, G} \mathop {\max }_{D_{1}, D_{2}} L_{1}(G, D_{1}, D_{2})+L_{2}(E, G)+L_{3}(E, G)+L_{4}(E, G) \end{aligned}$$
(8)

From the perspective of semi-supervised learning, we should sample a fixed small number of real samples when updating the parameters of E and G. In practice, faster convergence and less bad-training can be achieved when the semi-supervised training strategy is adopted.

Table 1. Summary of the five datasets in the experiments.
Full size table
Table 2. Comparison results for unsupervised clustering. The best result in each measure is highlighted in bold.
Full size table

3 Experiments

3.1 Experimental Setting

Datasets and Evaluation Measures. We adopt five well-known datasets (i.e. MNIST  [13], Fashion  [14], Pendigit  [15], 10_x73k  [9] and Pubmed  [16]) in the experiments and the basic information are listed in Table 1. Two commonly used evaluation measures, i.e., normalized mutual information (NMI) and adjusted Rand index (ARI) are utilized to evaluate the clustering performance  [17].

Baseline Methods and Parameter Setting. We adopt 8 clustering methods as our baseline methods including both GAN-based methods and traditional clustering methods. They are ClusterGAN  [9], GAN with bp  [9], adversarial autoencoder (AAE)  [18], GAN-EM  [19], InfoGAN  [8], spectral clustering (SC)  [20], Agglomerative Clustering (AGGLO)  [21] and Non-negative Matrix Factorization (NMF)  [22].

We set \(\alpha = 0.1\), \(\beta = 0.1\), \(\epsilon = 1\), \(\gamma = 1\) for all the datasets. As for \(\lambda \), we set \(\lambda = 0\) for 10_x73k and MNIST and set \(\lambda =0.1\) for the other datasets. When it comes to the network architecture, we adopt some techniques as recommended in  [23] for image datasets, and for the other datasets we use the full connected networks. The learning rate of Pubmed is set to be 0.0001 while 0.0002 for the other datasets.

Table 3. Comparison results with adopting the semi-supervised strategy for model training. The best result in each measure is highlighted in bold.
Full size table

3.2 Comparison Results

Comparison results are reported in Table 2 for unsupervised clustering, where the values are averaged over 5 normal training (GAN-based methods typically suffer from bad-training). As can be seen, the proposed CD2GAN method beats all the baseline methods on all the datasets in terms of the two measures. Particularly, CD2GAN is endowed with the powerful ability of representation learning, which accounts for the superiority over traditional clustering methods, i.e., SC, AGGLO and NMF. What’s more, we also conduct experiments to validate the effectiveness of the semi-supervised training strategy and the results are reported in Table 3. As shown in the table, the proposed CD2GAN-Semi (CD2GAN with semi-supervised training strategy) beats AAE-Semi (AAE with semi-supervised training strategy) and GAN-EM-Semi (GAN-EM with semi-supervised training strategy) on almost all the datasets except MNIST.

4 Conclusion

In this paper, we propose a method termed CD2GAN for latent space clustering via D2GAN with an inverse network. Specifically, to make sure that the continuity in latent space can be preserved while different clusters in latent space can be separated, the input of the generator is carefully designed by sampling from a prior that consists of normal random variables cascaded with one-hot encoded vectors. In addition, the mode collapse problem is largely eliminated by introducing the dual discriminators and the final cluster labels can be obtained by the cross-entropy minimization operation rather than by applying traditional clustering method like K-means. What’s more, a novel semi-supervised strategy is proposed to accelerate and stabilize the training process. Extensive experiments are conducted to confirm the effectiveness of the proposed methods.