Quality of Service Optimization in Mobile Edge Computing Networks via Deep Reinforcement Learning

Abstract

Mobile edge computing (MEC) is an emerging paradigm that integrates computing resources in wireless access networks to process computational tasks in close proximity to mobile users with low latency. In this paper, we propose an online double deep Q networks (DDQN) based learning scheme for task assignment in dynamic MEC networks, which enables multiple distributed edge nodes and a cloud data center to jointly process user tasks to achieve optimal long-term quality of service (QoS). The proposed scheme captures a wide range of dynamic network parameters including non-stationary node computing capabilities, network delay statistics, and task arrivals. It learns the optimal task assignment policy with no assumption on the knowledge of the underlying dynamics. In addition, the proposed algorithm accounts for both performance and complexity, and addresses the state and action space explosion problem in conventional Q learning. The evaluation results show that the proposed DDQN-based task assignment scheme significantly improves the QoS performance, compared to the existing schemes that do not consider the effects of network dynamics on the expected long-term rewards, while scaling reasonably well as the network size increases.

This work is partially supported by the National Science Foundation under Grants CNS-1910348 and CNS-1822087, and InterDigital Communications, Inc.

1 Introduction

The rapid development of Internet of Things (IoT) has generated a huge volume of data at the edge of the network. This requires a large amount of computing resources for big data analysis and processing, the capability of real-time remote control over both real and virtual objects, as well as physical haptic experiences. Cloud computing has been proposed as a promising solution to meet the fast-growing demand for IoT applications and services. However, centralized cloud data centers are often far from the IoT devices and users. How to provide high quality of service (QoS) to the interactive IoT applications, especially at the edge of the network, is still an open problem. This motivates a new paradigm referred to as mobile edge commuting (MEC), also called multi-access edge computing or fog computing, which extends cloud computing to the network edge [1, 2]. Edge nodes or edge devices provide computing services and carry out computationally intensive application and data processing tasks at the edge of the network between end users and cloud data centers. They can be computing servers or micro data centers deployed with routers, gateways, and access points in wireless access networks, and can also correspond to portable devices such as mobile phones, drones, robots, and vehicles with excessive computing resources that can be utilized to offer services to others. MEC can reduce transmission latency and alleviate network congestion. It also allows network operators to provide value-added real-time services and enhance QoS to end users.

A resource demand estimation and provisioning scheme for an edge micro data center is presented in [3] to maximize resource utilization. In [4], the authors proposed a hierarchical game framework to model the interactions where the edge nodes help the cloud data center operators process delay-sensitive tasks from mobile users and to determine the edge node resource allocation, service price, and pairing of edge nodes and data center operators with Stackelberg game and matching theory. These works focus on the interaction between edge nodes and cloud data centers to better serve the users, but they either abstract the MEC layer as a single edge server or assume that the edge nodes are independent of each other without consideration of their cooperation in processing tasks. The authors in [5] proposed an offloading scheme that allows a MEC edge node to forward its tasks to its neighboring edge nodes for execution to balance the workload fluctuations on different nodes and reduce the service delay. However, the paper made many idealized assumptions in assigning the tasks to the edge nodes, such as a fixed task arrival rate at each edge node as well as pre-known queuing delay of each node and transmission delay between the nodes. Their task assignment algorithm utilizes the classical model-based techniques that relies on these idealized assumptions to minimize service delay for one-shot optimization under a given deterministic MEC network state. Such an approach fails to capture the broad range of network parameters and ignores the impacts of dynamic network situations and heterogeneous nodes to the network performance.

On the other hand, reinforcement learning techniques can capture a wide range of control parameters and learn the optimal action, i.e. the policy for task assignments, with no or minimal assumptions on the underlying network dynamics. The conventional Q-learning algorithm is based on a tabular setting with high memory usage and computation requirements and is known to overestimate action values under certain conditions [6]. Recently, double deep Q networks (double DQN or DDQN) were introduced to address the problems of conventional Q-learning, which combines double Q-learning with two deep neural networks [7]. DDQN can provide large-scale function approximation with a low error and reduces the overestimations.

In this paper, we propose an online DDQN-based algorithm for task assignment in dynamic MEC networks, which accounts for both performance and complexity. The proposed algorithm takes into consideration the cooperation among the edge nodes as well as the cooperation between the edge nodes and a cloud data center. It performs sequential task assignment decisions in a series of control epochs to enable the nodes to help each other process user tasks and optimize a long-term expected QoS reward in terms of the service delay and task drop rate. The algorithm is designed to operate under stochastic and time-varying task arrivals, node processing capabilities, and network communication delays without a prior knowledge of these underlying dynamics. A decomposition technique is also introduced to reduce computational complexity in DDQN learning.

The remainder of the paper is organized as follows: Sect. 2 describes the problem formulation. In Sect. 3, we derive the online DDQN-learning based cooperative MEC task assignment algorithm in detail. In Sect. 4, we provide the numerical experimental results. Finally, the conclusions are given in Sect. 5.

2 Problem Formulation

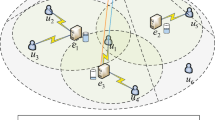
Figure 1 illustrates an example MEC system model for consideration in this paper. A set of N edge nodes, ${\mathcal{N}} = \left\{ { 1, \ldots ,N} \right\}$, with computing, storage, and communication resources are co-located or integrated with cellular base stations (BSs) or WiFi access points (APs) in a wireless access network. IoT devices or mobile users connect to nearby edge nodes through their cellular or WiFi radios and send their computation-intensive tasks to the edge nodes to be processed. When an edge node receives tasks from its associated users, it either processes them locally, or forwards part or all of its unprocessed tasks to other edge nodes or to a remote cloud data center for processing if the node does not have sufficient resources to complete all the tasks. The remote cloud data center, $n_{c}$ is modeled as a special node that is equipped with powerful computing capability but incurs a high network delay due to the distant location.

Fig. 1.

An example MEC system model.

We assume that the system operates over discrete scheduling slots of equal time duration. At the beginning of a time slot t, a controller in the MEC network collects the network conditions and determines a task assignment matrix, ${\varvec{\Phi}}^{t} = [\phi_{n,j}^{t} :n, j \in {\mathcal{N}} \cup n_{c} \}$. It informs the edge nodes to offload or receive computing tasks to/from the other nodes depending on the task assignment, where $\varvec{\phi}_{n}^{t} = [\phi_{n,j}^{t} , \phi_{j,n}^{t} : j \in {\mathcal{N}} \cup n_{c} \}$ represents the task assignment vector regarding edge node n. $\phi_{n,j}^{t}$ specifies the number of tasks that edge node n will send to node j for processing in the time slot t, and $\phi_{n, n}^{t}$ is the number of tasks that are processed locally by edge node n. We assume that the data center $n_{c}$ will process all the received tasks by itself without offloading them to the edge nodes, i.e. $\phi_{{n_{c} ,j}}^{t} = 0, j \in {\mathcal{N}}$.

We first formulate the problem of stochastic task assignment optimization and then explore the methods to solve the optimization problem. Each edge node maintains a queue buffering the tasks received from its users, and $q_{n}^{t}$ represents the queue length of node n at the beginning of time slot t. The queue size is bounded as $q_{n}^{{\left( {max} \right)}}$. It is assumed that the number of computational tasks arrived at edge node n in time slot t, $A_{n}^{t}$, is random and its distribution is unknown in advance. We denote $\varvec{A}^{\varvec{t}} = \{ A_{n}^{t} :n \in {\mathcal{N}}\}$. The task processing capability of node n in time slot t, denoted as $s_{n}^{t}$, which is the maximal number of tasks that node n can serve in the slot t, is also time-varying and unknown in advance due to the variable task complexity and adaptation of CPU cycles based on the power status and heat. The queue evolution of node n can then be written as $q_{n}^{t + 1} = { \hbox{max} }\{ 0, \hbox{min} \left[ {q_{n}^{t} + {\text{A}}_{n}^{t} + \sum\nolimits_{{i \in e_{n} }} {\phi_{i, n}^{t} } - \phi_{n, i}^{t} - s_{n,}^{t} , q_{n}^{{\left( {max} \right)}} } \right]\} ,$ where $\sum\nolimits_{{i \in e_{n} }} {\phi_{n, i}^{t} }$ with $e_{n} = \left\{ {{\mathcal{N}} \cup n_{c} } \right\}\backslash \left\{ n \right\}$ represents the number of tasks that edge node n offloads to other nodes, and $\sum\nolimits_{{i \in e_{n} }} {\phi_{i, n}^{t} }$ is the number of tasks that edge node n receives from other nodes in slot t.

When an edge node n, $n \in {\mathcal{N}}$ offloads a task to another node j, $j \in {\mathcal{N}} \cup n_{c}$ for execution at time slot t, it incurs an network delay cost, denoted as $c_{n,j}^{t}$. Let $\varvec{c}_{n}^{t} = (c_{n,j}^{t} ,c_{j,n}^{t} : j \in {\mathcal{N}} \cup n_{c} )$ represent the network delay vector for offloading the tasks from node n to any other node j, or vice versa, and $c_{n,n}^{t} = 0$. The network delay between two nodes is also time-varying and unknown in advance due to dynamic network conditions, traffic load, and many other uncertain factors. For a node n, $n \in {\mathcal{N}} \cup n_{c} ,$ at the beginning of time slot t, we characterize its state by its queue size $q_{n}^{t}$, its task processing capability $s_{n,}^{t}$, and the delay cost to offload a task to other nodes $\varvec{c}_{n}^{t}$, thus $\varvec{\chi}_{n}^{t} = \left( {q_{n}^{t} ,s_{n,}^{t} \varvec{c}_{n}^{t} } \right)$. The global state of the MEC network at the beginning of scheduling slot t can be expressed as $\varvec{\chi}^{\varvec{t}} = (\varvec{\chi}_{n}^{t} : n \in {\mathcal{N}} \cup n_{c} ) = (\varvec{q}^{\varvec{t}} ,\varvec{ s}^{\varvec{t}} ,\varvec{ c}^{\varvec{t}} ) \in X$, where $\varvec{q}^{\varvec{t}} = \{ q_{n}^{t} :n \in {\mathcal{N}} \cup n_{c} \}$, $\varvec{s}^{\varvec{t}} = \varvec{ }\left\{ {s_{n}^{t} :n \in {\mathcal{N}} \cup n_{c} } \right\}$, $\varvec{c}^{\varvec{t}} = \varvec{ }\left\{ {\varvec{c}_{n}^{t} :n \in {\mathcal{N}} \cup n_{c} } \right\}$, and $X$ represents the whole MEC system state space.

We consider real-time interactive IoT applications and employ the task service delay and task drop rate to measure the system QoS. The task service delay, $d_{n}^{t} ,$ is defined as the duration from the time a task arrives at an edge node to the time it is served, and the task drop rate, $o_{n}^{t}$, is defined as the number of dropped tasks per unit of time. Given the MEC network state, $\varvec{\chi}^{\varvec{t}} = (\varvec{q}^{\varvec{t}} ,\varvec{ s}^{\varvec{t}} ,\varvec{ c}^{\varvec{t}} )$ at the beginning of a time slot t, a task assignment ${\varvec{\Phi}}^{t} = {\varvec{\Phi}}\left( {\varvec{\chi}^{\varvec{t}} } \right) = [\phi_{n,j} \left( {\varvec{\chi}^{\varvec{t}} } \right):n, j \in {\mathcal{N}} \cup n_{c} \}$ is performed, which results in an instantaneous QoS reward. We define the instantaneous QoS reward at time slot t as

$$ U\left( {\varvec{\chi}^{\varvec{t}} , {\varvec{\Phi}}\left( {\varvec{\chi}^{\varvec{t}} } \right)} \right) = \sum\nolimits_{{n \in {\mathcal{N}}}} {[w_{d} U_{n}^{\left( d \right)} (\varvec{\chi}^{\varvec{t}} , {\varvec{\Phi}}\left( {\varvec{\chi}^{\varvec{t}} } \right)) + w_{o} U_{n}^{\left( o \right)} \left( {\varvec{\chi}^{\varvec{t}} , {\varvec{\Phi}}\left( {\varvec{\chi}^{\varvec{t}} } \right)} \right)]} , $$

(1)

where $U_{n}^{\left( d \right)} \left( . \right)$ and $U_{n}^{\left( o \right)} \left( . \right)$ measure the satisfaction of the service delay and task drop rate, respectively. $w_{d}$ and $w_{o}$ are the weight factors indicating the importance of delay and task drop in the reward function of the MEC system, respectively.

As mentioned before, the task arrivals and network states are non-deterministic and vary over time. We therefore want to cast the task assignment as a dynamic stochastic optimization problem, which maximizes the expected long-term QoS reward of an MEC network while ensuring the service delay and task drop rate are within their respective acceptable thresholds. More specifically, we define $V\left( {\varvec{\chi},\varvec{ }{\varvec{\Phi}}} \right) = {\text{E}}\left[ {\left( {1 - \gamma } \right)\sum\nolimits_{t = 1}^{\infty } {\upgamma^{t - 1} U\left( {\varvec{\chi}^{\varvec{t}} ,{\varvec{\Phi}}\left( {\varvec{\chi}^{\varvec{t}} } \right)} \right)|\varvec{ \chi }^{\mathbf{1}} } } \right]$ as the discounted expected value of the long-term QoS reward of an MEC network, where $\upgamma \in \left[ {0, 1} \right)$ is a discount factor that discounts the QoS rewards received in the future, and (γ)^t−1 denotes the discount to the (t − 1)-th power. $\varvec{ \chi }^{\mathbf{1}}$ is the initial network state. $V\left( {\varvec{\chi},\varvec{ }{\varvec{\Phi}}} \right)$ is also termed as the state value function of the MEC network in state $\varvec{\chi}$ under task assignment policy ${\varvec{\Phi}}$. Therefore, the objective is to design an optimal task assignment control policy ${\varvec{\Phi}}^{*}$ that maximizes the expected discounted long-term QoS reward, that is,

$$ \begin{array}{*{20}c} {{\varvec{\Phi}}^{*} = { \arg }\mathop {max}\limits_{{\varvec{\Phi}}} \left( {V\left( {\varvec{\chi},\varvec{ }{\varvec{\Phi}}} \right)} \right)} \\ {{\text{subject}}\,{\text{to}}\,d_{n}^{t} \le d^{{\left( { \hbox{max} } \right)}} ,\,o_{n}^{t} \le o^{{\left( { \hbox{max} } \right)}} ,\,\forall :n \in {\mathcal{N}} \cup n_{c} } \\ \end{array} $$

(2)

where $d^{{\left( { \hbox{max} } \right)}}$ and $o^{{\left( { \hbox{max} } \right)}}$ are the maximal tolerance thresholds for the service delay and the task drop rate, respectively. $V^{*} \left(\varvec{\chi}\right) = V\left( {\varvec{\chi},\varvec{ }{\varvec{\Phi}}^{*} } \right)$ is the optimal state value function. We assume that the probability of a network state in the subsequent slot depends only on the state attained in the present slot and the control policy, i.e. the MEC network state $\varvec{\chi}^{\varvec{t}}$ follows a controlled Markov process across the time slots. The task assignment problem can then be formulated as a Markov decision process (MDP) with the discounted reward criterion, and the optimal task assignment control policy can be obtained by solving the following Bellman’s optimality equation [8],

$$ V^{*} \left(\varvec{\chi}\right) = \mathop {\hbox{max} }\limits_{{\varvec{\Phi}}} \left\{ {\left( {1 -\upgamma} \right) U\left( {\varvec{\chi},\varvec{ }{\varvec{\Phi}}\left(\varvec{\chi}\right)} \right) +\upgamma\sum\nolimits_{{\varvec{\chi^{\prime}}}} {{ \Pr }\left\{ {\varvec{\chi^{\prime}} |\varvec{\chi},\varvec{ }{\varvec{\Phi}}\left(\varvec{\chi}\right)} \right\}V^{*} \left( {\varvec{\chi^{\prime}}} \right)} } \right\} , $$

(3)

where $\varvec{\chi^{\prime}} = \left\{ {\varvec{q^{\prime}},\varvec{s^{\prime}},\varvec{c^{\prime}}} \right\}$ is the subsequent MEC network state, and $\Pr \left\{ {\varvec{\chi^{\prime}}|\varvec{\chi},\varvec{ }{\varvec{\Phi}}\left(\varvec{\chi}\right)} \right\}$ represents the state transition probability to the next state $\varvec{\chi^{\prime}}$ if the task assignment ${\varvec{\Phi}}\left(\varvec{\chi}\right)$ is performed in state $\varvec{\chi}$. $\varvec{q^{\prime}} = \left\{ {q'_{n } :n \in {\mathcal{N}} \cup n_{c} } \right\}$, $\varvec{s^{\prime}} = \left\{ {s'_{n } :n \in {\mathcal{N}} \cup n_{c} } \right\}$, and $\varvec{c^{\prime}} = \left\{ {\varvec{c}'_{n } :n \in {\mathcal{N}} \cup n_{c} } \right\}$ are the queue, task processing capability, and network delay states in the subsequent time slot.

The traditional solutions to (3) are based on value iteration, policy iteration, and dynamic programming [9, 10], but these methods require a full knowledge of the network state transition probabilities and task arrival statistics that are unknown beforehand in our dynamic network case. Thus, we seek the online reinforcement learning approach which does not have such a requirement. In previous research, we introduced an algorithm based on conventional Q-learning [6], which defines an evaluation function, called Q function, $Q\left( {\varvec{\chi},\varvec{ }{\varvec{\Phi}}} \right) = \left( {1 -\upgamma} \right) U\left( {\varvec{\chi},\varvec{ }{\varvec{\Phi}}} \right) +\upgamma\sum\nolimits_{{\varvec{\chi^{\prime}}}} {{ \Pr }\left\{ {\varvec{\chi^{\prime}} |\varvec{\chi},\varvec{ }{\varvec{\Phi}}} \right\}Q\left( {\varvec{\chi^{\prime}},{\varvec{\Phi}}} \right)}$ and learns an optimal state-action value table in a recursive way to decide the optimal task assignment control policy for each time slot. However, for the cooperative MEC network, the task assignment decision-making for a node depends on not only its own resource availability and queue state, but also is affected by the resource availabilities and queue states of other nodes. The system state space and control action space grows rapidly as the number of involved nodes increases. The conventional tabular-based Q-learning process will search and update a large state-action value table, which incurs high memory usage and computation complexity.

3 Optimal Task Assignment Scheme Based on DDQN

In this section, we focus on developing an efficient algorithm to approach the optimal task assignment policy based on recent advances in deep reinforcement learning, which combines Q-learning and deep neural networks to address the state and action space explosion issue of the conventional Q learning with no requirement for a prior statistical knowledge of network state transitions and user task arrivals. Specifically, we design a DDQN-based algorithm to approximate the optimal state value function. In addition, it can be observed that the QoS reward function is of an additive structure, which motivates us to linearly decompose the state value function, and incorporate the decomposition technique into the deep reinforcement learning algorithm to lower its complexity.

Figure 2 illustrates the DDQN-based reinforcement learning scheme for the collaborative MEC task assignment. DDQN replaces the tabular setting of conventional Q-learning with two neural networks, Q evaluation network and Q target network, to learn and approach the optimal state value function and decide the optimal action [7]. The Q evaluation network (Q-eval) is used to select the task assignment matrix ${\varvec{\Phi}}^{\varvec{t}} \left( {\varvec{\chi}^{\varvec{t}} ;\theta } \right)\varvec{ }$ based on the collected network states $\varvec{\chi}^{\varvec{t}}$ at the time slot t, and the Q target network (Q-tar) is used to select the task assignment matrix ${\varvec{\Phi}}^{{\varvec{t} + {\mathbf{1}}}} \left( {\varvec{\chi}^{{\varvec{t} + {\mathbf{1}}}} ;\overline{\uptheta} } \right)$ at the following time slot t + 1. The parameters $\uptheta$ and $\overline{\uptheta}$ can be learned and updated iteratively. The standard DDQN algorithm outputs the state-action values and select the action with the maximum Q value. Unfortunately, the traditional DDQN approach in [7] cannot be directly applied to solve our problem because we do not know the number of the new task arrivals in a time slot at the beginning of that time slot. To solve the problem, we modified the Q-eval and Q-tar networks in the standard DDQN to output a probability matrix, which indicates the probability to forward a task from one edge node to another edge node in the slot.

Fig. 2.

DDQN-based cooperative MEC task assignment.

The modified DDQN is used to approximate the optimal state value function in (3) and select the best action. We redefine the state value function (3) as

$$ \begin{array}{*{20}c} {V^{t} \left( {\varvec{\chi}^{\varvec{t}} } \right) = \mathop {\hbox{max} }\limits_{{\varvec{\Phi}}} \{ \left( {1 -\upgamma^{t} } \right)U\left( {\varvec{\chi}^{\varvec{t}} ,\varvec{ }{\varvec{\Phi}}^{\varvec{t}} \left( {\varvec{\chi}^{\varvec{t}} ,\varvec{ }{\mathcal{P}}\left( {\varvec{\chi}^{\varvec{t}} ;\uptheta^{t} } \right)} \right)} \right) } \\ { +\,\upgamma^{t} \left[ {{ \Pr }\left\{ {\varvec{\chi}^{{\varvec{t} + {\mathbf{1}}}} |\varvec{\chi}^{\varvec{t}} ,\varvec{ }{\varvec{\Phi}}^{\varvec{t}} \left( {\varvec{\chi}^{\varvec{t}} ,\varvec{ }{\mathcal{P}}\left( {\varvec{\chi}^{\varvec{t}} ;\uptheta^{t} } \right)} \right)} \right\}U\left( {\varvec{\chi}^{{\varvec{t} + {\mathbf{1}}}} ,\varvec{ }{\varvec{\Phi}}^{{\varvec{t} + {\mathbf{1}}}} \left( {\varvec{\chi}^{{\varvec{t} + {\mathbf{1}}}} ,\varvec{ }{\mathcal{P}^{\prime}}\left( {\varvec{\chi}^{{\varvec{t} + {\mathbf{1}}}} ;\overline{\uptheta}^{t} } \right)} \right)} \right)} \right]\} } \\ \end{array} , $$

(4)

where $\varvec{ }{\mathcal{P}}\left( {\varvec{\chi}^{\varvec{t}} ;\uptheta^{t} } \right)$ and ${\mathcal{P}^{\prime}}\left( {\varvec{\chi}^{{\varvec{t} + {\mathbf{1}}}} ;\overline{\uptheta}^{t} } \right)$ are the probability matrices calculated by Q evaluation and Q target networks, respectively. In the standard DDQN algorithm, the state value will be updated in each time slot and used to determine the optimal action. To simplify the updates, in our implementation, the state value obtained from (4) is stored in a replay memory for training and updating $\uptheta$ and $\overline{\uptheta}$ in the learning process so that the Q-eval and Q-tar can select the optimal task assignment matrices directly and accurately. The loss function for updating the parameters $\uptheta$ of Q-eval can be defined as

$$ {\mathbb{L}}\left( {\uptheta } \right) = E\left[ {\left( {\left( {1 - {\upgamma }} \right)U\left( {\varvec{\chi},\varvec{ }{\varvec{\Phi}}\left( {\varvec{\chi},\varvec{ }{\mathcal{P}}\left( {\varvec{\chi};{\uptheta }} \right)} \right)} \right) + {\upgamma }U\left( {\varvec{\chi^{\prime}},\varvec{ }{\varvec{\Phi}}^{\prime}\left( {\varvec{\chi^{\prime}},\varvec{ }{\mathcal{P}^{\prime}}\left( {\varvec{\chi^{\prime}};\overline{\uptheta } } \right)} \right)} \right) - V\left(\varvec{\chi}\right)} \right)^{2} } \right] , $$

(5)

and the parameters $\overline{\uptheta}$ will be updated by copying $\uptheta$ after a predefined number of steps.

At the beginning of each time slot t, the MEC controller determines the task assignment matrix ${\varvec{\Phi}}^{\varvec{t}} \left( {\varvec{\chi}^{\varvec{t}} } \right)\varvec{ }$ based on the collected network states and informs the edge nodes of the task assignment decision. The task assignment matrix ${\varvec{\Phi}}^{t} = [\phi_{n,j}^{t} :n, j \in {\mathcal{N}} \cup n_{c} \}$ at the beginning of scheduling slot t is determined as,

$$ {\varvec{\Phi}}^{t} = {\mathcal{P}}^{t} \left( {\varvec{\chi}^{\varvec{t}} ;\uptheta^{t} } \right) $$

(6)

An edge node then offloads the tasks to other nodes or receives tasks from other nodes and processes these tasks based on the task assignment decision. The new task arrivals $\varvec{\rm A}^{\varvec{t}}$ will be counted at the end of the time slot t and the new network state is collected and updated to $\varvec{\chi}^{{\varvec{t} + {\mathbf{1}}}}$ by the controller. The MEC network receives a QoS reward $\varvec{U}^{t} = \varvec{ }U\left( {\varvec{\chi}^{\varvec{t}} ,\varvec{ }{\varvec{\Phi}}^{\varvec{t}} \left( {\varvec{\chi}^{\varvec{t}} ,\varvec{ }{\mathcal{P}}\left( {\varvec{\chi}^{\varvec{t}} ;\uptheta^{t} } \right)} \right)} \right)$ by performing the task processing. The Q-tar network is used to calculate ${\varvec{\Phi}}^{{\varvec{t} + {\mathbf{1}}}}$. As mentioned before, the DDQN includes a replay memory that is used to store a pool of the most recent M transition experiences, , where each experience is occurred at the transition of two consecutive slots t and t + 1 during the learning process. At each slot t, the k previous experiences are randomly sampled as a batch from the memory pool $\Omega ^{t}$ to train the DDQN online. The learning process will calculate the approximated overall state value for each experience in the batch and update the parameters $\uptheta$ with an goal to minimize the loss function (5). Once the state value function is converged, we can obtain the optimal parameters $\uptheta^{*}$ for Q-eval. The optimal policy will be

$$ {\varvec{\Phi}}^{*} = {\mathcal{P}}^{*} \left( {\varvec{\chi};\uptheta^{*} } \right) $$

(7)

The MEC network QoS reward in (1) is the summation of the service delay and task drop rate satisfactions of the edge nodes, and the task arrival statistics and task processing capabilities of the edge nodes are independent each other. We can then decompose (4) into per node QoS reward and separate the satisfactions regarding the service delay and the task drops [11]. We first rewrite (6) as

$$ {\varvec{\Phi}}^{t} = {\varvec{\Phi}}^{t} \left( {\varvec{\chi}^{\varvec{t}} } \right) = \left\{ {\phi_{n}^{t} \left( {\chi_{n}^{t} } \right):n \in {\mathcal{N}}} \right\} . $$

(8)

$n$ agents $n \in {\mathcal{N}}$ can be employed and each agent learns the respective optimal state value function through a per node sub-DDQN. An optimal joint task assignment control decision is thus made to maximize the aggregated state value function from all the agents. The task assignment related to node n can be expressed as

$$ \phi_{n}^{t} \left( {\chi_{n}^{t} } \right) = {\mathcal{P}}_{n}^{t} \left( {\chi_{\varvec{n}}^{\varvec{t}} ;\uptheta_{n}^{t} } \right) , $$

(9)

where ${\mathcal{P}}_{n} \left( . \right)$ is the task assignment probability obtained through DDQN $n$. The state value function in (4) can be decomposed and expressed as in (10) and (11)

$$ V^{t} \left( {\varvec{\chi}^{\varvec{t}} } \right) = \mathop \sum \nolimits_{{n \in {\mathcal{N}} }} V_{n}^{t} \left( {q_{n}^{t} ,s_{n}^{t} ,c_{n}^{t} } \right), $$

(10)

$$ \begin{array}{*{20}c} {V_{n}^{t} \left( {\chi_{n}^{t} } \right) = \left( {1 -\upgamma^{t} } \right)U\left( {\chi_{n}^{t} ,\Phi ^{t} \left( {\chi_{n}^{t} , {\mathcal{P}}_{n} \left( {\chi_{n}^{t} ;\uptheta_{n}^{t} } \right)} \right)} \right) + } \\ {\upgamma^{t} \left[ {{ \Pr }\left\{ {\chi_{n}^{t + 1} |\chi_{n}^{t} ,\Phi ^{t} \left( {\chi_{n}^{t} , {\mathcal{P}}_{n} \left( {\chi_{n}^{t} ;\uptheta_{n}^{t} } \right)} \right)} \right\}U\left( {\chi_{n}^{t + 1} ,\Phi ^{t + 1} \left( {\chi_{n}^{t + 1} , {\mathcal{P}}_{n}^{'} \left( {\chi_{n}^{t + 1} ;\overline{\uptheta}_{n}^{t} } \right)} \right)} \right)} \right]} \\ \end{array} $$

(11)

With the linear decomposition, the problem to solve a complex Bellman’s optimality Eq. (4) is broken into simpler MDPs and the computation complexity is lowered. In order to derive a task assignment policy based on the global MEC network state, $\varvec{\chi}= \left( {\chi_{n} :n \in {\mathcal{N}} \cup n_{c} } \right)$ with $\chi_{n} = \left( {q_{n} ,s_{n} ,c_{n} } \right)$ and $c_{n} = \left( {c_{n,j} , c_{j,n } : j \in {\mathcal{N}} \cup n_{c} } \right),$ at least $\prod\nolimits_{{n \in {\mathcal{N}} \cup n_{c} }} {\prod\nolimits_{{j \in {\mathcal{N}} \cup n_{c} }} {(\left| {q_{n} } \right|\left| {s_{n} } \right|\left| {c_{n,j} } \right|\left| {c_{j,n} } \right|)} }$ states should be trained. Using linear decomposition, only $\left( {N + 1} \right) \left| {q_{n} } \right|\left| {s_{n} } \right| \prod\nolimits_{{j \in {\mathcal{N}} \cup n_{c} }} {\left( {\left| {c_{n,j} } \right|\left| {c_{j,n} } \right|} \right)}$ states need to be trained, resulting in much simplified task assignment decision makings and significantly reducing training time. The online DDQN-based algorithm to estimate the optimal state value function and determine the optimal task assignment policy is summarized in Algorithm 1.

4 Numerical Experiments

In this section, we evaluate the cooperative MEC task assignment performance achieved by our derived online DDQN-based algorithm. Throughout the simulation experiments, we assume that the processing capability $s_{n}^{t}$, $\forall n \in {\mathcal{N}}$ of different edge nodes are independent of each other and evolve according to a Markov chain model, each modeled with three states characterizing the high, medium, and low with {4, 2, 1} tasks per slot. We simulated multiple MEC network scenarios with different system parameters. Due to the page limit, we present the results for several typical settings. The slot duration is set to be 30 ms. The network delay between two edge nodes, $c_{nj}^{t}$, $\forall n,j \in {\mathcal{N}}$, is also modeled as a Markov chain with three states, {1, 0.5, 0.2} slots. Edge nodes communicate with a cloud data center through the Internet. The network delay between the edge node and the cloud data center $c_{{nn_{c} }}^{t}$, $\forall n \in {\mathcal{N}}$ is assumed to be 10 slots. $U_{n}^{\left( d \right)}$ and $U_{n}^{\left( o \right)}$ in the QoS reward function are chosen to be the exponential functions [12] with $U_{n}^{\left( d \right)} = { \exp }\left( { - d_{n}^{t} /d^{{\left( { \hbox{max} } \right)}} } \right)$ and $U_{n}^{\left( o \right)} = { \exp }\left( { - o_{n}^{t} /o^{{\left( { \hbox{max} } \right)}} } \right)$.

The neural networks used for Q-tar and Q-eval have a single hidden layer with 15 neurons. We use ELU (Exponential Linear Unit) as the activation function for the hidden layer and Softmax for the output layer to output the probability matrices for the action selection. The optimizer is based on RMSProp [7]. The number of iterations for updating parameters of Q-tar is set to be 30, and the memory replay size and the batch size are also set to be 30. The training process will be triggered when the system collects enough samples and it will pull out all samples to train. There are other sampling optimization techniques, e.g. prioritized experience replay, which will be included in our future work.

We first investigate the convergence performance of the proposed online DDQN-based cooperative MEC task assignment algorithm under dynamic stochastic MEC network environments with different number of MEC edge nodes. As shown in Fig. 3, we can observe that the proposed algorithm spends a short time period to learn and then converges to the global optimal solution at a reasonable time period which is less than 150 slots. In addition, the network size does not have noticeable effects on the convergence time of the algorithm.

Fig. 3.

Convergence of the proposed DDQN-based learning process.

Next, we evaluate the QoS performance of the proposed online DDQN-based cooperative task assignment scheme. For the purpose of comparison, we simulate four baselines as well, namely,

• 1) No Cooperation: An edge node processes all the tasks it receives from its associated users by itself. There is no task offloading.

• 2) Cloud Execution: An edge node offloads all its received tasks to the cloud data center for execution.

• 3) One-shot Optimization: Like the scheme in [5], at each scheduling slot, the task assignment is performed with the aim of minimizing the immediate task service delay. Note that the power efficiency constraint is not considered here because we assume the edge nodes have sufficient power supply.

• 4) Q-Learning: Task assignment optimization based on conventional Q-learning.

Figures 4 (a) and (b) show the average task service delay and the average number of dropped tasks per slot, respectively, for the proposed scheme and baselines, with three edge nodes and one cloud data center as the task arrivals per slot at the edge nodes follow independent Poisson arrival process. The delay is measured in the unit of the time slot duration. We can observe that the DDQN-based and conventional Q-learning based task assignment schemes perform better than the other baselines such as No Cooperation, Cloud Execution, and One-shot Optimization schemes. This is because they not only consider the current task processing performance but also take into account the QoS performance in the future when determining the optimal task assignment matrix under time-varying stochastic task arrivals and network states. Their task drops are zero because the algorithms tend to minimize the task drops, and the edge nodes will forward the tasks to the cloud data center when their buffers are full. For the No Cooperation scheme, an edge node does not send the unprocessed tasks to the cloud and other edge nodes, so that there are tasks drops when the node’s buffer becomes overflow. For the Cloud Execution scheme, a large network delay is always incurred to ship the tasks to the cloud data center for processing over the Internet. The One-Shot Optimization scheme performs relatively well. However, it makes task assignment decisions to minimize the immediate task service delay in a slot and may cause shipping many tasks to the cloud data center for processing under fluctuating task arrivals and non-stationary node process capabilities, with such tasks incurring a large network delay.

Fig. 4.

(a) the average task service delay and (b) the average number of dropped tasks per slot versus the average task arrivals per slot for different algorithms.

Figure 5 shows the memory usage of DDQN- and Q-learning task assignment schemes. The traditional tabular Q-learning consumes much higher system resources than the DDQN scheme and cannot scale well due to the explosion in state and action spaces, making the solution unviable. On the other hand, the memory usage by the DDQN-based task assignment scheme scales well as the number of edge nodes in the network increases.

Fig. 5.

The memory usage of DDQN and Q-learning task assignment schemes.

5 Conclusions

In this paper, we have investigated the task assignment problem for cooperative MEC networks, which enables horizontal cooperation between geographically distributed heterogeneous edge nodes and vertical cooperation between MEC edge nodes and remote cloud data centers to jointly process user computational tasks. We have formulated the optimal task assignment problem as a dynamic Markov decision process (MDP), and then proposed an online double deep Q-network based algorithm to obtain the optimal task assignment matrix. A function decomposition technique is also proposed to simplify the problem in DDQN learning. The proposed online DDQN algorithm does not require for a statistical knowledge of task arrivals and network state transitions. The evaluation results validate the convergence of the proposed algorithm and demonstrate that it outperforms the traditional schemes that optimize the immediate task service delay with no consideration of the impacts of network dynamics to the expected long-term QoS rewards. In addition, the proposed DDQN scheme can scale reasonably well, and requires much less memory than the conventional Q-learning based algorithm.