3PointTM: Faster Measurement of High-Dimensional Transmission Matrices

Abstract

A transmission matrix (TM) describes the linear relationship between input and output phasor fields when a coherent wave passes through a scattering medium. Measurement of the TM enables numerous applications, but is challenging and time-intensive for an arbitrary medium. State-of-the-art methods, including phase-shifting holography and double phase retrieval, require significant amounts of measurements, and post-capture reconstruction that is often computationally intensive. In this paper, we propose 3PointTM, an approach for sensing TMs that uses a minimal number of measurements per pixel—reducing the measurement budget by a factor of two as compared to state of the art in phase-shifting holography for measuring TMs—and has a low computational complexity as compared to phase retrieval. We validate our approach on real and simulated data, and show successful focusing of light and image reconstruction on dense scattering media.

1 Introduction

When coherent light passes through a highly scattering medium, the photons encounter multiple scattering events, and the resultant interference gives rise to a random speckle pattern. This random input-to-output mapping makes imaging and focusing light through multiple-scattering media a challenging task.

The most general method for imaging through an arbitrarily thick scattering medium is by measuring the transmission matrix (TM) [1, 6, 30, 33, 34], which characterizes the relationship between the input and output complex wavefronts. Specifically, the mesoscopic TM of an optical system at a specific wavelength can be represented as a matrix T with complex-valued elements $t_{kn}$ connecting the field in the $k-$th camera pixel (also, commonly referred to as an “output mode”) to the field in the $n-$th spatial light modulator (SLM) pixel (or, an “input mode”):

$$\begin{aligned} u_k^{out} = \sum _{n}t_{kn}u_n^{in}, \end{aligned}$$

(1)

where $u_k^{out}$ and $u_n^{in}$ are the complex phasor at the $k-$th camera pixel and $n-$th SLM pixel, respectively. However, while we can control the phase and intensity of the input phasor $u_n^{in}$, we can only measure the intensity of the output phasor $| u_k^{out}|^2$ and hence, we do not have a direct measurement of its phase. This makes the measurement of TMs a hard and nonlinear inverse problem.

There are two well known methods to measure the TM of an arbitrary medium: phase-shifting holography [34] and phase retrieval [12, 27, 35, 37]. Phase-shifting holography measures the TM by acquiring four images per SLM pixel; it relies on using a portion of the SLM or its surrounding region as a static reference wave and learning the TM against this reference. Phase retrieval methods, on the other hand, acquire multiple intensity measurements by varying the phase pattern on the SLM; the TM is estimated by solving a phase retrieval problem. While phase retrieval methods require a minimum of four measurements per SLM pixel [38], in practice, robustness to measurement noise requires eight to twelve measurements per pixel. Finally, the algorithm to reconstruct the final TM is computationally intensive; for example, [27] reports requiring tens of CPU hours for estimating a TM of size of $128^2\times 60^2$.

Given a TM of size $M \times N$, corresponding to an SLM with N pixels and an image sensor with M pixels, prior approaches require at least 4N intensity images. In contrast, the number of degrees of freedom in a TM is only $M(2N-1)$ since its elements are complex numbers; further, since we can only measure intensities, each row of the TM has a constant phase ambiguity that we cannot resolve. This leads us to pose and subsequently answer the following question: how do we measure a TM with a minimal number of intensity measurements?

Contributions. This paper proposes an efficient approach for measuring TMs associated with arbitrary scattering media. We make the following contributions.

• Our main contribution is a near-optimal measurement strategy that measures an $M \times N$ TM from $2N+1$ intensity measurements.

• Our approach provides an analytical expression for estimating the TM from the acquired measurements and is computationally efficient.

• We present detailed empirical analysis of the stability of our method under different operating conditions, including the number of SLM pixels and the signal-to-noise ratio of the measurements, as well as comparisons to prior art.

• We validate our approach using a lab prototype, using which we scan several optical media and demonstrate applications in the form of inverse scattering and focusing through the media.

Limitations. There are three principal limitations of our work, some of which we share with existing approaches. First, since our technique acquires fewer measurements than prior work, our performance is often worse than them in low SNR settings. We characterize this gap in performance with simulations. Second, similar to prior work, our approach requires access to both sides of the scattering medium, something that is unrealistic when the imaging target is biological tissue in-vivo. Third, even with the reduction in the number of measurements, the acquisition of the TM with our approach can take several minutes for high-resolution TMs.

2 Prior Work

The study of light transport in a scene has a long history in the optics and vision community. For incoherent illumination, the propagation of light from the illuminant(s) to the camera is modelled via the light transport matrix, which has found immense applications for image-based relighting [10, 36]. In contrast, for coherent light, the propagation also needs to consider the interference between illuminants, which is better modelled via the complex-valued TM. We are particularly interested in propagation of coherent light through or off random scattering media, following the work of Freund [13].

Imaging Based on the Strong Memory Effect. A scatterer is said to possess a strong memory effect if the translation of an input point light source results in a translation of the speckle pattern at the output. This property has been used to enable single shot imaging through a thin multiple-scattering media [19]. However, this method critically relies on the assumption that the medium is thin enough to exhibit the memory effect.

Exploring Time-of-Flight Information. Time-of-flight imaging systems use the photon travel time to differentiate between the scattered and ballistic photons [18, 29, 31, 32, 40]. Since these systems only measure ballistic photons, they require high-intensity pulsed lasers as well as time-resolved cameras, with time-resolutions in nano/pico-seconds, which is expensive.

Multi-slice Light Propagation. Multi-slice light-propagation models a scattering media as a sequence of 2D slices [25], thereby modeling the transmission matrix as a composition of linear transformations. However, this method has not been evaluated for thick scatterers that have no memory effect.

2.1 Measurement of Transmission Matrices

Holographic Interferometry. One of the most common methods to measure a TM is holographic interferometry [34]. Here, part of the SLM is held constant and used as a reference and the remainder is modulated, in a Hadamard basis, one input channel at a time using four-step holography. The use of Hadamard basis allows the use of a phase-only SLM. In contrast, we show that it is possible to measure the TM without resorting to probing in Hadamard basis while using a phase-only SLM; crucially, this choice allows to reduce the number of measurements from 4N per camera pixel to $2N+1$. Finally, an interesting difference in our approach is that we do not have any area on the SLM plane allocated as a reference.

Quadrature Phase-Shifting Holography. A recent result recovers the phase of a wavefront from two measurements [3, 22]. Quadrature phase-shifting holography takes samples at phase 0 and $\frac{\pi }{2}$ for each SLM pixel, and estimates the complex measurement at the camera  [22]. However, the method has very stringent requirements on the capture setup; specifically, it requires uniform illumination on the camera from the reference signal, such that a separate reference arm is necessary and cannot be estimated as done in four-step holography  [34]. It also assumes that reference intensity is larger than the object wave intensity, which is a stringent condition to fulfill at bright speckle positions  [23]. Comparisons between two-step, three-step, and four-step holography methods have shown that the two-step method is less accurate compared with the four-step method because of the above mentioned reasons  [23]. It should be noted that quadrature phase-shifting holography has not been applied to TM estimation and its performance in this task is not yet understood.

2.2 Focusing Light Through a Scattering Media

Focusing light through a scattering media [8, 9, 17, 20, 24, 39, 42, 43] is one of the intriguing applications for measurement of TMs. We provide a brief overview of the methods most relevant to the ideas of this paper.

Assume that the beam incident on the SLM is collimated with spatially constant intensity. Then, when the $n-$th SLM pixel has the phase shift of $\phi _n$, the output on the $k-$th camera pixel can be written as

$$\begin{aligned} y_k = \left| \sum _{n=1}^{N}t_{kn}e^{i{\phi _n}} \right| ^2+{\epsilon }, \end{aligned}$$

(2)

where ${\epsilon }$ is the measurement noise. Suppose that we seek to focus light on this $k-$th camera pixel. From (2), we observe that the intensity at $y_k$ is largest when all the terms in the summation are in-phase, which is achieved by choosing $\phi _{n}^*= c - \angle t_{kn}$ where c is a constant; this choice of SLM phase aligns the phasors in the $k-$th row of the TM to form constructive interference at the target pixel.

We can define the effect of focusing using the ratio between the focused intensity and the average intensity prior to it. Assuming the individual TM components $t_{mn}$ are statistically independent and follows the circular Gaussian distribution, the expected maximal enhancement, $\gamma$, is defined as

$$\begin{aligned} \gamma = \frac{\pi }{4}(N-1)+1, \end{aligned}$$

(3)

where N is the number of SLM pixels  [4, 14, 15, 39].

Vellekoop and Mosk  [39] present a method that uses a feedback-based phase modulation technique to focus light through scattering media. This approach works by individually manipulating the phase at each SLM pixel from 0 to $2\pi$ in small steps, while fixing the phase on the rest of the pixels. The phase value that produces maximum intensity $y_k$ is chosen as the estimate of the optimal value $\angle \phi _{n}^*$. This procedure is repeated for all SLM pixels, updating them one at a time. After multiple such iterations over the whole SLM, we can expect to achieve a near-optimal focusing at the desired camera pixel(s).

The work of Vellekoop and Mosk  [39] is closely related to our proposed ideas. Specifically, we advance this technique to make only a single pass over the SLM pixel and further, restrict the number of phase patterns to three values at each pixel, of which one is shared across all pixels. In addition to focusing, we also show how to estimate the TM of the system from the measurements.

Genetic Algorithms (GAs). Genetic algorithm interprets the intensity at a chosen point on the camera as the objective function, and optimizes the SLM pixels by randomly selecting patterns and breeding between them  [7]. Empirically, we observe that GAs provide steady state solution after 10N measurements, and its performance is robust to noise. However, this algorithm requires both amplitude and phase modulation to estimate TMs. Further, the number of measurements required to recover TMs is 10MN, such that GA is even more computationally intensive than phase retrieval algorithms.

3 Minimal Measurement of Transmission Matrices

We now present an approach for measurement of TMs, that we call 3PointTM. 3PointTM requires only $2N+1$ images to measure the TM, given an SLM with N pixels, and hence, is nearly minimal.

The core idea underlying 3PointTM relies on an observation that we make about the focusing approach of Vellekoop and Mosk  [39]. As before let’s consider the intensity at the $k-$th pixel on the sensor, $y_k$, while optimizing the phase value $\phi _n$ on the $n-$th SLM pixel. As a small, but important deviation, we set the phase value at the other SLM pixels at zero. Given these, we can write the intensity $y_k$ as a function of $\phi _n$ as follows:

$$\begin{aligned} \small y_k(\phi _n) = \left| t_{kn} e^{i \phi _n} + \sum _{\ell \ne n} t_{k\ell } \right| ^2 + {\epsilon }. \end{aligned}$$

(4)

Denoting $u_{kn} = \sum _{\ell \ne n} t_{k\ell },$ and dropping the noise term, we get

$$\begin{aligned} \small y_k(\phi _n) = | t_{kn} |^2 + |u_{kn} |^2 + 2 | t_{kn} ||u_{kn} | \cos \left( \phi _n + \angle t_{kn} - \angle u_{kn} \right) . \end{aligned}$$

(5)

This suggests that, as we vary the phase $\phi _n$, the intensity at the target pixel varies on a sinusoidal curve with unknown offset $|t_{kn }|^2+|u_{kn}|^2$, amplitude $2|t_{kn}||u_{kn}|$, and phase offset $\angle t_{kn}-\angle u_{kn}$.

Instead of sweeping a dense set of phase values, as in [39], we propose to sample this sinusoid at three distinct phase values to recover its parameters. As we will show subsequently, recovering the sinusoidal parameters allows us to estimate the TM and subsequently focus light at any desired sensor pixel (Fig. 1).

Fig. 1.

Graphical Illustration of 3PointTM. We vary the phase at each SLM pixel to three values, of which one is shared across all pixels, and measure the resulting intensity image on the camera. The TM matrix is estimated from these intensity images and enables us to perform focusing and imaging operations.

Step 1—Sinusoidal Parameter Fitting. We acquire three sensor measurements for each SLM pixel. Specifically, for the $n-$th SLM pixel, we take three measurements with $\phi _n \in \left\{ 0, \frac{2\pi }{3}, \frac{4\pi }{3} \right\}$, with the phase values at other pixels set to zero. For each of the three phase values, we make full sensor measurements and computationally recover the column of the TM corresponding to the $n-$th SLM pixel, i.e., the elements $\{ t_{kn}, \forall k \}$.

Our technique recovers the TM elements for each sensor pixel in isolation, and so we focus on an arbitrary sensor pixel, say the $k-$th pixel on the sensor. Given the three intensities measured at this pixel, $y_{k_1}$, $y_{k_2}$, and $y_{k_3}$, corresponding to the $\phi _n$ set to $0, \frac{2\pi }{3}$, and $\frac{4\pi }{3}$, respectively, we compute the parameters of the sinusoid. The three measured intensities can be described as

$$\begin{aligned} y_{k_1} = c_0+A\cos (\theta ), \quad y_{k_2} = c_0+A\cos (\theta +\frac{2\pi }{3}), \quad y_{k_3} = c_0+A\cos (\theta +\frac{4\pi }{3}), \end{aligned}$$

(6)

where

$$\begin{aligned} c_0 = |t_{kn}|^2+|u_{kn}|^2, \quad A = 2|t_{kn}||u_{kn}|, \quad \theta = \angle t_{kn} - \angle u_{kn}. \end{aligned}$$

(7)

We use the technique described in  [41] to estimate the three parameters $c_0, A$ and $\theta$ from the three measured intensities. It is also worth noting that sinusoidal fitting of this form has found numerous applications in imaging and vision, including polarimetry, and correlation-based time-of-flight sensing.

Step 2—TM Estimation. We now describe the procedure for estimating the TM elements from the sinusoidal parameters, $c_0$, A and $\theta$. Given $c_0$ and A defined as in (7), the first step is to solve for $|t_{kn}|$ and $|u_{kn}|$. However, we can immediately observe that the symmetry in the occurrence of $|t_{kn}|$ and $|u_{kn}|$ in both $c_0$ and A implies that we cannot uniquely recover them. Specifically, while we can estimate the set $\{ |t_{kn}|, |u_{kn}| \}$, we cannot associate them without any additional information. One approach is to look beyond a single SLM pixel and jointly estimate $\{ t_{k\ell }, \forall \ell \}$ since $u_{kn}$ is dependent on TM elements corresponding to other SLM pixels. This can however be quite cumbersome. In practice, we observe that the magnitude of $u_{kn}$ is almost always greater than that of $t_{kn}$. This can be attributed to the fact that while $t_{kn}$ is a single element of the TM matrix, $u_{kn}$ is the magnitude of sum of $N-1$ random phasors and hence its magnitude is expected to be larger. We also validated this assumption on three previously measured TMs  [27]. When no noise is added to the measurements in simulation, $0.0341\%$ of all the TM elements do not satisfy this assumption. When Poisson noise is added at an SNR of 10 dB into the intensity measurements, $0.007\%$ of TM elements do not satisfy this assumption, presumably because the term $|u_{kn}|$ is amplified more as noise is added.

Once we have estimates of $|t_{kn}|$ and $|u_{kn}|$, we define a new variable $z_{kn}$ as

$$\begin{aligned} z_{kn} =&| u_{kn} | e^{-i \theta }+|t_{kn}| = |u_{kn}| e^{i\angle u_{kn}-i\angle t_{kn}}+|t_{kn}|\nonumber \\ =&\left( |u_{kn}|e^{i\angle u_{kn}}+|t_{kn}|e^{i\angle t_{kn}} \right) e^{-i\angle t_{kn}} = e^{-i\angle t_{kn}} \sum _\ell t_{k\ell }. \end{aligned}$$

(8)

Hence, if we take the angle of the phasor $z_{kn}$, we get

$$\begin{aligned} \angle z_{kn} = -\angle t_{kn} + \angle \sum _\ell t_{k\ell } = -\angle t_{kn} + \psi _k, \end{aligned}$$

(9)

where $\psi _k$ is a constant that is dependent only the sensor pixel but constant for all the SLM pixels. We can now provide an estimate for the TM element as

$$\begin{aligned} \widehat{t}_{kn} = | t_{kn} | e^{-i\angle z_{kn}} = t_{kn} e^{-\psi _k}. \end{aligned}$$

The unknown phase shift does not affect any subsequent processing tasks like focusing as it is independent of the SLM pixels.

Table 1. Number of measurements and computation time required for reconstructing a TM of size $256^2\times 16^2$.

Advantages of 3PointTM. Our core contribution is reformulating the problem of TM estimation to this sinusoidal fitting approach, even in the absence of a reference wave. The proposed method has many advantages over its competitors because of the sinusoidal fitting step.

First, given N SLM pixels, we only need to display $2N+1$ SLM patterns (and capture an equal number of images) since we can share the all-zero phase measurements across pixels. Without the assumption of sparsity, this is not just minimal in the sense of the number of unknowns, but also a $2\times$ improvement over holography-based competitors. We highlight these advantages in Table 1, and in the next section provide simulation results that support these claims. Another approach for reducing measurements is the use of compressive sensing where we take advantage of sparsity [28]; however, this imposes priors on the nature of the TM. In contrast, we make no assumption on the unknown medium.

Second, we provide closed-form analytical expressions for estimates of the TM elements. Further, we can do so for each TM element in parallel which can be exploited by parallel processing architectures. This is in sharp contrast to phase retrieval-based methods that require complex optimization.

Third, we do not make any assumptions about the image formation except perhaps for the validity of the TM model. Hence, our method is widely applicable to many different kinds of scattering media—a key improvement over memory-effect based approaches.

Fig. 2.

Normalized angle bias of the ground truth and TM estimated by 3PointTM. By comparing the computed TM with the ground truth, it is evident that the bias is low at high SNRs, and the performance of 3PointTM degrades quadratically pass 30 dB.

Fig. 3.

Performance characterization of 3PointTM. The theoretical maximum intensity enhancement that can be obtained using illumination modulation is directly dependent on the number of SLM pixels, N. Plotted above is the actual performance in intensity enhancement obtained by 3PointTM as a function of measurement SNR, each computed over 50 independent trials for $N=100, 400, 900,$ and 1600. 3PointTM asymptotically achieves theoretical maximum intensity enhancement at high SNR regimes, and degrades at lower SNR.

Fig. 4.

Performance comparisons. (left) We compare the focusing efficiency of 3PointTM, four-step holography, a genetic algorithm (GA) and prVAMP on randomly generated TMs of size $256^2\times 16^2$. Both GA and prVAMP are robust against noise, in part due to the larger number of measurements, while the focusing ability of both four-step holography and 3PointTM degrades as noise increases. (right) We compare the focusing efficiencies of the aforementioned four methods under the same settings, but at 4N image measurements for all of them.

4 Simulation Results

We perform simulations by generating random transmission matrices from i.i.d. circularly symmetric complex Gaussian distributions of size $256^2\times 16^2$. For the noise simulations, we mimicked a sensor with a full well-capacity of 10k electrons and a read noise standard deviation of 4.7 electrons—these numbers are indicative of the sensor used in our real experiments. Given a noise-free measurement $y_0$, the simulated noisy measurement is given as

$$\begin{aligned} \text {poisson}(y_0) + 4.7\mathcal {N}(0,1), \end{aligned}$$

(10)

which accounts for both photon and read noise. To operate at different SNRs, we adjust the global scene light level by scaling $y_0$ across all pixels.

Evaluation of Estimated TMs. To characterize how 3PointTM performs against noise, we compute the TM under different levels of noise. Figure 2 plots the relationship between average SNR and the measurement error, which is defined as normalized angle bias,

$$\begin{aligned} \text {error} = \sqrt{\frac{\sum _n(e^{i\text {diag}(\angle \overline{T^*\widehat{T}})}T-\widehat{T})^2}{\sum _n T^2}}. \end{aligned}$$

(11)

The estimation error, or angle bias measured in percentage, is small at low noise region, and increases quadratically as the SNR decreases from 32 dB to 12 dB.

Focusing Enhancement with Respect to Number of Input Channels. To understand the relationship between enhancement and number of input channels, TMs of different sizes are generated and their estimations are used to focus energy at an arbitrarily chosen position, and the ensuing intensity enhancement is computed. We compare this value to the theoretical maximum, described in Eq. (3). From Fig. 3, we observe two distinct trends. First, as expected, a larger number of SLM pixels does lead to a higher intensity enhancement. Second, once the SNR of the measurements are greater than 35dB, the achieved enhancement starts to approach the theoretical maxima indicating that the phase of the TM elements have been accurately estimated. For SNRs smaller than 30dB, errors in estimates lead to a wide gap between the two. The enhancement decays follow a similar pattern across different numbers of SLM pixels.

Comparisons with prior art. To quantitatively compare 3PointTM with the existing methods to recover TMs, we implemented prVAMP from  [27] with 12N measurements, the GA from [7] with 10NM measurements, and the four-step holography from  [34] with 4N measurements, and compared their respective focusing enhancement abilities.

As shown in Fig. 4 (left), phase retrieval is robust against noise, as its focusing efficiency remains high at different measurement SNRs. 3PointTM is comparative to four-step holography in all cases. It performs worse comparing with phase retrieval in high noise scenarios, but the advantage of phase retrieval diminishes when noise is low. On the Grasshopper camera we simulated, a 10 dB operating point would correspond to 33 photoelectrons. In a typical operating point, our measurements have speckle intensity peaks at nearly 9k e-, which would correspond to a measurement SNR of 39 dB. Thus our experiments operate in the regime that 3PointTM could generate reliable estimations. Since 3PointTM requires 6$\times$ fewer measurements and is 13640$\times$ faster computationally, it could be used with slowly-decorrelating mediums, for which there is not enough time to perform phase retrieval.

Besides running each method until it reaches the optimal solution, we also compared the performances of the methods performed with the same number of measurements. Since four-step holography only works 4 N measurements, all four methods are simulated 4 N measurements. As shown in Fig. 4(right), the performances of prVAMP and GA significantly compromise when no sufficient samples are taken.

Fig. 5.

Performance comparisons of different measurements. We show the performance of our approach when we acquire more measurements and fit sinusoids on them.

Comparisons with 6-point and 52-point Sinusoidal Estimates. In 3Point TM, the accuracy of TM estimation is dependent on the ability to correctly fit sinusoid parameters from the three measurements made at each SLM pixel. To check the benefits to be derived by taking additional measurements, we compare against methods where we obtain more measurements at each SLM and, in particular, 6 and 52 measurements, by uniformly sampling between 0 and $2\pi$ and solving the best fitting cosines with the Levenberg algorithm  [21, 26]. The performances of the methods on focusing is shown in Fig. 5, and we observe the expected improvement in performance with increased measurements. Although the proposed method 52 N measurements takes substantially more measurements compared to prVAMP, prVAMP still outperforms because it uses a richer measurement matrix, where all the phase SLM pixels are changed randomly at each measurement.

Fig. 6.

Experimental setup of 3PointTM. SF: Spatial filter, L1: collimator, L2: Focusing lens, SLM: Spatial light modulator, P1 and P2: Polarizers, A1 and A2: Apertures, CCD: Sensor. The laser beam passes through SF and is collimated by L1, and hits the reflection mode SLM, on which an input mode pattern is displayed. The modulated beam is then directed onto the diffuser D. Finally, the modulated wave is focused onto the CCD sensor.

5 Experimental Results

Setup and Data Collection. The optical system that we use is shown in Fig. 6. It consists of a spatially filtered and collimated laser beam, generated using a laser diode (ZM18GF024) with wavelength $\lambda$ = 540 nm. The SLM (Holoeye Leto) used is a phase only modulator with $1920\times 1080$ pixels and $6.4 \mu m$ pixel pitch. The modulated light is focused on a strongly scattering sample by the lens L2. We have used holographic diffusers from Edmund optics and PDMS tissue phantoms developed in our lab for the experiments; the phantoms are made with polystyrene beads (0.6mL) and isopropyl alcohol (0.6mL). The scattered light is then collected by a microscope objective (Newport 10X, 0.25 NA), and imaged using a CCD camera (Point Grey Grasshopper3 GS3-U3-14S5M).

Fig. 7.

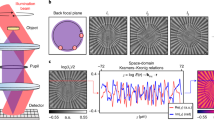
Verification of 3PointTM principle: sinusoidal curve fitting on experimental data. The phase of each SLM pixel is sampled from 0 to $2\pi$ in 52 steps, which forms the ground truth measurements (blue curves). The optimal $\theta$ is extracted from the 52 samples. 3PointTM is then run on 3 samples to get the estimation (red curves), and thus produces the estimated optimal phase $\hat{\theta }$. The plots show that the estimation could accurately predict the ground truth measurements.

Sinusoidal Fitting on Real Data. We evaluate the accuracy of sinusoidal parameters estimated from intensity measurements made at three phase values ($0, \frac{2\pi }{3}, \frac{4\pi }{3}$) to find the sinusoidal parameters. For comparison, we also measure the actual intensity profile at 52 phase values from 0 to $2\pi$, and visualize this dense measurements along with the sinusoidal fitted using 3PointTM in Fig. 7. The estimated sinusoidal parameters match the dense measurements accurately. Since the TM is computed directly from the estimated cosine, the accuracy of curve fitting in turn suggests that our computed TM have high accuracy.

Fig. 8.

Reconstruction results for imaging through a 20 degree diffuser and tissue phantom. The TM is computed with $60^2$ SLM pixels and $625^2$ camera pixels. For imaging through the diffuser, the SSIM index of the smiley is 0.678, and the PSNR is 20.20. For the tissue phantom, the SSIM index of the smiley is 0.683, and the PSNR is 20.60.

Fig. 9.

Reconstruction results for imaging through a 20 degree diffuser at higher resolution. The setup is the same to that in Fig. 8, but the TM has $120^2$ SLM pixels, which increases the degrees of freedom by 4 folds. The SSIM index of the reconstructed smiley is 0.447, and that of the rupee is 0.308. The PSNR of the smiley reconstruction is 13.68 dB, and it is 12.89 dB for the rupee reconstruction.

Image Reconstruction with the Computed TM. With the computed TMs, it is possible to invert the scattering effects and reconstruct images from the captured noisy speckles. To do this, we capture images by displaying an object on the center part of the SLM, and the remaining outer region of the SLM is used as a reference. We compute the complex wavefront on the camera using 3-step phase shifting holography  [2], i.e., the phase of the reference is set to 0, $\frac{\pi }{2}$, and $\pi$, and the complex wavefront y at the sensor is recovered as:

$$\begin{aligned} y = \frac{1}{4}[I_0-I_\pi +i(2I_{\pi /2} - I_0 -I_\pi )], \end{aligned}$$

(12)

where $I_\theta$ is the intensity image at the sensor when the reference phase is $\theta$.

To construct amplitude objects from the phase SLM, two complex measurements $y_{obj}^{(1)}$ and $y_{obj}^{(2)}$ are made, following the steps in [34]. $y_{obj}^{(1)}$ is obtained with zero phase at the object, and $y_{obj}^{(2)}$ is obtained by flipping the phase of the object from 0 to $\pi$. The reconstruction is computed with the least squares solution:

$$\begin{aligned} \widehat{x} = (T^\top T)^{-1}T^\top (y_{obj}^{(2)}-y_{obj}^{(1)}). \end{aligned}$$

(13)

To characterize the reconstruction quality, the structural similarity (SSIM) indices and the peak signal-to-noise ratios (PSNR) are computed for each pair of reconstruction $\widehat{x}$ and ground truth x [16, 44]. We have computed the TM for a $60^2$ input size for a 20$^\circ$ diffuser and for a 270$\mu m$ thick tissue phantom (mean free path about 90 $\upmu$m), and the reconstruction results are shown in Fig. 8. Since we are able to compute a good quality transmission matrix with only $2N+1$ measurements, it is possible for us to compute a large size TM. We could compute the TM for a $120^2$ SLM for a 20$^\circ$ diffuser, and the image reconstructions are shown in Fig. 9.

Focusing Light Through Scattering Media. To focus at a single spot p on the camera, its corresponding row $t_p$ in the computed TM is selected, and its conjugate phase $e^{-i\angle t_p}$ is displayed onto the SLM. To focus at multiple spots, the optimal SLM phase pattern is determined by maximizing the sum of intensities observed at those multiple locations. Specifically, the sinusoidal curves for the spots are first computed individually, and then added up. The optimal SLM pattern is then determined to be the phasor which produces maximum intensity at the sum of the curves. As shown in Fig. 10, focus spots can be created at any point on the camera, and at multiple positions. At the single focusing spot through the 20$^\circ$ diffuser, the enhancement is 2059, which is around 75$\%$ of the theoretical maximum, which is consistent with our simulation findings.

Fig. 10.

Focusing results through scattering materials. Laser light is focused through a 20$^\circ$ diffuser (top row) and a tissue phantom (bottom row) by displaying different combinations of rows of the computed TM onto the SLM. Without input modulation, only speckle patterns are recorded on the camera.

6 Conclusions

Our proposed system provides a significant speed up to the measurement of TM, and so it can be applied to many scenarios. In our current experiment, the speed of the data capture is limited by the SLM, which operates at 16ms. If the currently used SLM could be substituted by a faster device, such as a nano-mechanical phase modulator, which operates at $1\mu$s  [11], then the data capture process could be faster by $1.6\times 10^4$ times. The system would then be able to successfully compute the TM with a $70\times 70$ SLM for a perfused tissue, which decorrelates on the scale of 10 ms [5]. With such a large TM, focusing at a single point through the tissue can be enhanced by over 3,800 times, and a high resolution image could be reconstructed through the medium.