Abstract
We construct a general purpose secure multiparty computation protocol which remains secure under (a-priori) bounded-concurrent composition and makes only black-box use of cryptographic primitives. Prior to our work, constructions of such protocols required non-black-box usage of cryptographic primitives; alternatively, black-box constructions could only be achieved for super-polynomial simulation based notions of security which offer incomparable security guarantees.
Our protocol has a constant number of rounds and relies on standard polynomial-hardness assumptions, namely, the existence of semi-honest oblivious transfers and collision-resistant hash functions. Previously, such protocols were not known even under sub-exponential assumptions.
S. Garg—Supported in part from DARPA SIEVE Award, AFOSR Award FA9550-15-1-0274, AFOSR Award FA9550-19-1-0200, AFOSR YIP Award, NSF CNS Award 1936826, DARPA and SPAWAR under contract N66001-15-C-4065, a Hellman Award, a Sloan Research Fellowship and research grants by the Okawa Foundation, Visa Inc., and Center for Long-Term Cybersecurity (CLTC, UC Berkeley). The views expressed are those of the author and do not reflect the official policy or position of the funding agencies.
X. Liang and O. Pandey—Supported in part by DARPA SIEVE Award HR00112020026, NSF grant 1907908, and a Cisco Research Award. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the United States Government, DARPA, NSF, or Cisco.
I. Visconti—This research has been supported in part by the European Union’s Horizon 2020 research and innovation programme under grant agreement No 780477 (project PRIViLEDGE.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Secure multiparty computation (MPC) allows n players to jointly compute a functionality, while no group of (malicious parties) learn anything beyond their inputs and prescribed outputs. Introduced in the seminal works of [25, 58], this model has since been studied extensively. General constructions for computing any functionality even when a majority of players are adversarial have been long known. The focus of this work are MPC protocols that only make a black-box use of cryptographic primitives and maintain security in the concurrent setting where several instances of the protocol may execute simultaneously.
Black-Box Constructions. General purpose MPC protocols are often non-black-box in nature, i.e., they use the code of the underlying cryptographic primitives at some stage of the computation. For example, a common step in such protocols is to use general-purpose zero-knowledge proofs which perform NP reductions. Non-black use of primitives is usually undesirable since not only is it computationally expensive, it also renders the protocol useless in situations where such code is not available (e.g., primitives based on hardware-tokens). One therefore seeks black-box constructions of such protocols which use the underlying primitives only in black-box way (i.e., only through their input/output interfaces).
Black-box constructions of general MPC protocols have received considerable attention recently. In the standalone setting, Ishai et al. [35] (together with Haitner [32]) presented the first black-box construction of general purpose MPC under the minimal assumption of semi-honest oblivious Transfer (OT). Subsequently, Wee [57] reduced the round complexity of these constructions to \(O(\log ^*n)\), and Goyal [26] to only constant rounds. Very recently, Applebaum et al. [1] showed that 2-round MPC is unachievable by making only black-box use of 2-round OT. In the two-party setting, black-box construction were obtained by Pass and Wee [53] in constant-rounds and Ostrovsky et al. [47] in 5 rounds, which is optimal w.r.t. black-box proof techniques [37]. We discuss the concurrent setting next.
Concurrent Security. The standard notion of security for MPC, also called stand-alone security considers only a single execution of this protocol. While this is sufficient for many applications, other situations (such as protocol executions over the Internet) require stronger notions of security. This setting, where there may be many protocols executions at the same time, is called the concurrent setting. Unfortunately, it is known that stand-alone security does not necessarily imply security in the concurrent setting [19].
To address the above issue, Canetti [10] proposed the notion of universally composable (UC) security where protocols maintain their strong simulation based security guarantees even in the presence of other arbitrary protocols. Achieving such strong notion of UC-security turned out to be impossible in the plain model [10, 11]. Moreover, Lindell [43, 44] proved that even in the special case where only instantiations of the same protocol are allowed, standard notion of polynomial-time simulation is impossible to achieve. (This is called “self composition” and also corresponds to the setting in this work.)
These strong negative results motivated the study of alternative notions of security. Our focus is the plain model where no trusted setup is available. Two directions that are relevant to us in this model are:
-
Bounded-Concurrent Composition: in this model, a bound m is fixed a-priori, and the protocol design may depend on m. The adversary is allowed to participate in at most m simultaneous executions of the protocol. We consider security against dishonest majority with interchangeable roles, i.e., the adversary can choose an arbitrary subset of (all but one) parties to corrupt in each session. As in the original (unbounded) setting, the ideal-world simulator is required to run in (expected) polynomial time. Due to the a-priori bound, it is feasible to bypass the aforementioned negative results. Lindell presented a m-bounded concurrent two-party protocol in O(m)-rounds using black-box simulation [43]. Subsequently Pass and Rosen [52] presented a constant round two-party protocol and Pass [50] a constant round MPC protocol (under improved assumptions), using non-black-box simulation. All general-purpose secure-computation protocols in this setting make non-black-box use of the underlying cryptographic primitives.
-
Super-Polynomial Simulation: while it is not directly relevant to this work, we build upon techniques developed in the context of super-polynomial simulation where the simulator is allowed to run in super-polynomial time. This relaxation provides somewhat weaker security guarantees (which are, nonetheless, meaningful for many functionalities), and allows (unbounded) concurrent composition. Three different ways to formulate this notion are super-polynomial simulation (SPS) [49], angel-based security [12, 55], and security with shielded oracles [9].
Prabhakaran and Sahai [55] provided the initial positive result for SPS security. Although, these early results [6, 42, 45, 55] relied on non-standard/sub-exponential assumptions, Canetti, Lin and Pass achieved this notion under standard polynomial-time assumptions [12] in polynomially many rounds, and soon after, Garg et al. [21] in constant rounds. The works in [12, 45, 55] actually achieve angel-based security, though only [12] relies on standard polynomial hardness. Subsequently, Goyal et al. [30] presented a \(\widetilde{O}(\log n)\) round construction under the same assumptions.
Black-box constructions of angel-based secure computation were first presented by Lin and Pass [41] assuming the existence of semi-honest OT, in
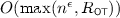 rounds, where \(\epsilon >0\) is an arbitrary constant and
rounds, where \(\epsilon >0\) is an arbitrary constant and 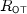 is the round complexity of the underlying OT protocol. (Hence, if the underlying OT protocol has only constant round, the round complexity is \(O(n^{\epsilon })\).) Subsequently, Kiyoshima
[38] provided a \(\tilde{O}(\log ^2n)\)-round construction under the same assumption. To achieve constant round constructions, Broadnax et al.
[9] proposed security with shielded oracles, a notion that lies strictly between SPS and angel-based security, along with a constant-round black-box construction under polynomial hardness assumptions. Recently, Garg, Kiyoshima, and Pandey
[22] presented a constant-round black-box MPC protocol which achieves SPS security under polynomial hardness assumptions (which are weaker than those in
[9] at the cost of (weaker) SPS security).
is the round complexity of the underlying OT protocol. (Hence, if the underlying OT protocol has only constant round, the round complexity is \(O(n^{\epsilon })\).) Subsequently, Kiyoshima
[38] provided a \(\tilde{O}(\log ^2n)\)-round construction under the same assumption. To achieve constant round constructions, Broadnax et al.
[9] proposed security with shielded oracles, a notion that lies strictly between SPS and angel-based security, along with a constant-round black-box construction under polynomial hardness assumptions. Recently, Garg, Kiyoshima, and Pandey
[22] presented a constant-round black-box MPC protocol which achieves SPS security under polynomial hardness assumptions (which are weaker than those in
[9] at the cost of (weaker) SPS security).
State of the Art. The notion of bounded-concurrent composition requires standard polynomial-time simulation. It does not follow from security notions that rely on super-polynomial simulation (which are known to have black-box constructions). Consequently, all known constructions of bounded-concurrent secure MPC rely on non-black-box usage of underlying cryptographic primitives.
1.1 Our Contribution
In this work, we seek to construct general-purpose MPC protocols that make only black-box use of cryptographic primitives and remain secure under bounded-concurrent self composition. Furthermore, we seek constructions whose security can be proven under standard polynomial hardness assumptions (although, to the best of our knowledge, such protocols are not known even under, say, sub-exponential assumptions since the simulator must still run in polynomial time).
Towards this goal, we first aim to construct a black-box bounded-concurrent oblivious transfer (OT) protocol. At a high level, this construction relies on non-black-box simulation to handle simulation in the bounded-concurrent setting (along the lines of [3, 50]); to ensure that this does not result in non-black-box use of cryptographic primitives, we implement this idea using the “black-box non-black-box” protocol of Goyal et al. [31]. Once we have control over bounded-concurrent simulation, we rely on the OT protocol of Garg et al. [22] to achieve the full oblivious transfer functionality. Unfortunately, implementing this idea is somewhat complex, perhaps in part because abstractions such as “straight-line simulation/extraction” are not straightforward to formalize despite their intuitive appeal. We mitigate this situation by defining a new abstraction which we call (bounded) robust zero-knowledge; this notion asks for simulators to work even in the presence of (bounded) external communication which cannot be “rewound” (and therefore, looks very close to UC zero-knowledge [10]). Similar notion has been defined by [40] in the context of non-malleable commitment w.r.t. an external party. Zero-knowledge (\(\mathcal {ZK}\)) with this robust property allows us to combine the non-black-box simulation techniques with the SPS based proof techniques of [22] to achieve black-box bounded-concurrent OT. An additional feature of our protocol is that it has constant rounds.
Along the way, we also present the first “straight-line”Footnote 1 extractable commitment scheme that only makes black-box use of semi-honest OTs. This primitive may be useful for other applications, especially for black-box constructions of MPC protocols from minimal assumption.
Having obtained bounded-concurrent security for OT, we proceed to construct bounded-concurrent MPC protocols for all functionalities. This step is executed almost identically to a similar step in [22] and does not require any additional assumptions. It also maintains the black-box and constant round properties of the original OT protocol. Consequently, we obtain the first general-purpose bounded-concurrent secure MPC protocol that makes only black-box use of cryptographic primitives; furthermore, the protocol has constant rounds and relies only on standard polynomial hardness assumptions.
Theorem 1 (Informal)
Assume the existence of constant-round semi-honest oblivious transfer protocols and collision-resistant hash functions. Then, there exists a constant-round black-box construction of general-purpose MPC that achieves bounded-concurrent security.
The formal statement is given as Theorem 4 in Sect. 7. This result is essentially a black-box version of Pass’s result [50].
1.2 Other Related Works
In addition to the works mentioned in the introduction, there are several works that study security in the concurrent setting. For SPS-security, Pass et al. [51] present a constant-round non-black-box construction of MPC from constant-round semi-honest OT. Dachman-Soled et al. and Venkitasubramaniam [17, 56] present a non-black-box construction that satisfies adaptive security. And very recently, Badrinarayanan et al. [2] present a non-black-box 3-round construction assuming sub-exponential hardness assumptions. For angel-based security, Kiyoshima et al. [39] present a constant-round black-box construction albeit under a sub-exponential hardness assumption, and Hazay and Venkitasubramaniam [34] present a black-box construction that achieves adaptive security.
We have not discussed works that focus on other security notions, e.g., input-indistinguishable computation and multiple ideal-query model [28, 46, 50].
Black-box constructions have been extensively explored for several other primitives such as non-malleable or CCA-secure encryption, non-malleable commitments, zero-knowledge proofs and so on (e.g., [14, 16, 29, 31, 48, 54]). For concurrent OT, Garay and MacKenzie [20] presented a protocol for independent inputs under the DDH assumption, and Garg et al. [23] proved the impossibility of this task for general input distributions.
2 Overview of Our Techniques
Before describing our approach, we first make some observations. We start by noting that in the context of concurrent secure computation, it is not possible to use rewinding-based simulation techniques since the simulator will have to provide additional outputs during rewinding but the ideal functionality does not deliver more than one output. This is in sharp contrast to concurrent zero-knowledge where the output is simply “yes” since the statement is in the language. While this can be salvaged for certain functionalities as shown by Goyal [27], it is essential to move to straight-line simulators for general functionalities. In particular, in the bounded-concurrent setting we must move to non-black-box simulation techniques [4].
Let us also note that in some situations, particularly in the setting of resettable zero-knowledge, a long line of work shows that it is possible to perform non-black-box simulation under one-way functions [7, 8, 15]. Furthermore, a black-box version of these simulation techniques under one-way functions was obtained by Ostrovsky, Scafuro, and Venkitasubramaniam [48]. It therefore seems possible to construct bounded-concurrent MPC under the minimal assumption of semi-honest OT in a black-box manner.Footnote 2 Unfortunately, this approach is flawed since all known non-black-box simulation techniques are based on rewinding and therefore cannot be applied to the concurrent MPC setting. It is also not at all clear if “straight-line” simulatable zero-knowledge based only on one-way functions can be constructed from known approaches. Therefore, we stress that even without the requirement of black-box usage of primitives, constructing bounded-concurrent MPC under semi-honest OT only remains as a fascinating open problem.
We therefore attempt to obtain a construction that exploits collision-resistant hash functions, in addition to the minimal assumption of semi-honest OTs. Toward this goal, we build upon techniques developed in the following two works:
-
1.
Garg, Kiyoshima, and Pandey [22] construct a constant-round black-box MPC protocol with SPS-security under polynomial hardness assumptions. The simulator works by extracting crucial information from adversary’s messages via brute-force. The simulator is straight-line and such extraction steps are the only non-polynomial work in its execution.
-
2.
Goyal et al. [31] present a black-box implementation of the non-black-box simulation techniques that rely on adversary’s code [3]. Such techniques often (and certainly those of [3, 31]) extend to situations where the adversary may receive arbitrary but a-priori bounded amount of external communication.
At a high level, our main idea is to use the simulation technique of [31] to replace the brute-force extraction steps in [22] with polynomial-time extraction using adversary’s code. The corresponding commitment scheme will be interactive. Since this simulator is polynomial time, we can hope to get bounded-concurrent MPC (in contrast to SPS MPC). Implementing this idea turns out to be rather involved. The fact that the commitment protocol is interactive brings its own issues of non-malleability and also interferes with some key proof steps in [22] which rely on rewinding. It is also not enough that the underlying commitment protocol be extractable in a “bounded-concurrent” setting; instead we need a more flexible notion (that, roughly speaking, mirrors straight-line simulation).
Although we have non-black-box simulation techniques at our disposal, we do not rely on the multiple slots approach of Pass [50] to build simulation soundness directly into our protocols. Instead, by relying on the techniques in the aforementioned two works, we obtain a more modular approach where non-malleability and simulation soundness are obtained with the help of an underlying non-malleable commitment. In this sense, the structure of our bounded-concurrent protocol is fundamentally different from that of [50] to achieve bounded-concurrent MPC. We now provide more details.
The high-level structure of our protocol is similar to that of [22] where the MPC protocol is obtained in two steps. First, we obtain a (constant-round) black-box construction of a bounded-concurrent OT protocol. Next, we compose this OT protocol with an existing constant-round OT-hybrid UC-secure MPC protocol. We elaborate on each step below. We remark that we consider concurrent security in the interchangeable-roles setting. So, in the case of OT, the adversary can participate in a session as the sender while concurrently participating in another session as the receiver.
2.1 Black-Box (Constant-Round) Bounded-Concurrent OT
Our OT protocol is very similar to the OT protocol of [22] (which in turn is based on the high-level cut-and-choose structure of [41] inspired from [13, 33, 57]) except that we will implement the basic commitment scheme using a “straight-line extractable” commitment (with some other properties that we will discussion soon). At a high level, the OT protocol of [22] proceeds as follows:
-
1.
The protocol is based on cut-and-choose techniques. Therefore, as the first step of the protocol, the sender S and the receiver R commit to their challenges for future stages in advance. This step uses a two-round statistically binding commitment scheme \(\mathsf {Com}\). This step avoids selective opening attacks. The ideal-world simulator can extract these challenges by brute-force to perform the simulation. This is the only non-polynomial time step of this simulator (and the one we wish to replace).
-
2.
Next, S and R execute many instances of a semi-honest OT protocol in parallel, where in each instance S and R use the inputs and the randomness that are generated by a coin-tossing protocol.
-
3.
Next, S and R use a non-malleable commitment scheme \(\mathsf {NMCom}\) to set up a “trapdoor statement” which, roughly speaking, commits a witness to the fact that the trapdoor statement is false. This step, following [21], makes it possible to commit to a false witness in the security proof while ensuring (due to non-malleability of \(\mathsf {NMCom}\)) that the adversary still continues to commit to a correct witness (so that his statement is still false). The step is performed by modifying different stages of one session at a time. This ensures that changes in one interactive part of the protocol are not affected by what happens in later stages of that same session.
-
4.
Finally, S and R use OT combiner which allows them to execute an OT with their real inputs securely when most of the OT instances in the previous steps are correctly executed. To check that most of the OT instances in the previous steps were indeed correctly executed, S and R do use cut-and-choose where S (resp., R) chooses a constant fraction of the OT instances randomly and R (resp., S) reveals the input and randomness that it used in those instances so that S (resp., R) can verify whether R executed those instances correctly.
Replacing \(\mathsf {Com}\) with Straight-Line Extractable Commitments. Our goal is to eliminate brute-force extraction using code of the adversary. In doing so, we have to ensure that (1) the interactive nature of the commitment protocol so obtained does not result into new malleability issues in the proof; and (2) the extraction step can be done in a modular fashion (especially in straight-line) so that we can keep the overall proof structure of [22] where one session is modified at a time.
As a starting point, let us consider the Barak-Lindell extractable commitment scheme [5]. In their construction, the committer C first sends an enhanced trapdoor permutation f.Footnote 3 Then the two parties involve in the following 3-step coin tossing: (1) R sends a commitment \(\mathsf {Com}(r_1)\) to a random string \(r_1\); (2) C replies with a random string \(r_2\); (3) R then sends \(r_1\) with a \(\mathcal {ZK}\) argument on the fact that this \(r_1\) is indeed the random string he committed in step (1). Both parties learn the value \(r = r_1 \oplus r_2\) as the output of the coin tossing. To commit to a (single-bit) message \(\sigma \), C sends \(\sigma \) masked by the hard-core bit of \(f^{-1}(r)\). An extractor can use the \(\mathcal {ZK}\) simulator to bias the coin-tossing result to some value \(r'\), for which it knows the preimage of \(f^{-1}(r')\). Thus, it can extract the committed value.
Straight-Line Extraction. To adapt the above scheme for our purpose, we need to ensure that the construction is black-box and that the committed value can be extracted in a straight-line fashion. Toward this goal, we replace R’s commitment and \(\mathcal {ZK}\) argument with the protocol of Goyal et al. [31]. More specifically, [31] provides a “commit-and-prove” primitive \(\varPi _{ZK}\) where:
-
they provide a (non-interactive statistically-binding) commitment schemeFootnote 4 called \(\mathsf {VSSCom}\) using which one can send a commitment y to a string x;
-
and later, prove to a verifier, that “y is a commitment to string x such that \(\phi (x)=1\)” where \(\phi \) is an arbitrary function.
In particular, \(\phi \) is chosen to be the \(\mathcal {NP}\)-relation for an \(\mathcal {NP}\)-complete language in [31] to get a black-box version of Barak’s result [3].
In our case, we will choose \(\phi \) to be the identity function \(I_x(\cdot )\).Footnote 5 Therefore, the Barak-Lindell commitment protocol mentioned above can be implemented in a black-box manner by ensuring that: (1) R uses \(\mathsf {VSSCom}\) to prepare the commitment to \(r_1\), and (2) protocol \(\varPi _{ZK}\) is the aforementioned proof protocol with \(\phi :=I_{r_1}(\cdot )\).
At a high level, this approach meets our needs for a black-box construction that supports straight-line extraction. But more caution is needed to handle the actually simulation as we are in the (bounded) concurrent setting. We will address this concern soon (see the discussion in the Robust-\(\mathcal {ZK}\) for Bounded Concurrency part below).
Removing TDPs. Since we aim to have a construction assuming only semi-honest OTs (and CRHFs), we also want to remove the reliance on the (enhanced) TDPs. As the first attempt, we ask C to secret-share the message \(\sigma \) to \(n\) random shares using exclusive-or. Then let the receiver learn through a special OT (e.g. an n/2-out-of-n OT) half of these shares. Next, we invoke the above (black-box) version of coin-tossing in Barak-Lindell protocol to determine another n/2 shares that C will decommit to. Due to the pseudo-randomness of the coin-tossing result, R will learn the the shares that “complement” what he learned through OT with only negligible probability. Thus, we can hope to achieve (computational) hiding. Meanwhile, an extractor could always bias the coin-tossing result to the complement shares, thus allowing it to extract the value \(\sigma \).
However, there are several issues with this approach. First, the sender’s (committer’s) input to the OT must be the decommitment information to the secret shares. Otherwise, a malicious sender can use arbitrary values in the OT execution, which will disable our extraction strategy.Footnote 6 Also, this construction suffers from selective opening attacks (SOAs) as the values in the commitments are correlated. It is not clear how we can use standard techniques (e.g. asking R to commit to his challenges in advance, or using another coin-tossing to determine his challenges) to get rid of SOAs. This is because we need to keep R’s challenges in this stage hidden from C (to ensure extractability).
To solve this problem, we let C commit to \(2n\) secret shares of \(\sigma \), denoted as \(\{\mathsf {Com}(s_{i,b})\}_{i \in [n], b \in \{0,1\}}\). Then \(n\) 1-out-of-2 OT instances are executed in parallel, where R learns (the decommitment to) one share out of \((s_{i,0}, s_{i,1})\) in the i-th OT. Next, we can use the Barak-Lindell coin tossing to determine an \(n\)-bit string \(r = r_1 \Vert \ldots \Vert r_n\). Finally, C decommits to \(\{\mathsf {Com}(s_{i,r_i})\}_{i\in [n]}\). In this construction, R’s input to (a single) OT can be guessed correctly with probability 1/2. By a careful design of hybrids, we show this is sufficient to get rid of SOAs, thus allowing us to prove hiding property (See Sect. 5). Moreover, the extractor can still learn all the shares by biasing \(r_i\) to the complement to its input in the i-th OT instance (for all \(i \in [n]\)).
Merging with [22]. Finally, to ensure that the interactive nature does not create non-malleability issues, we will ask each party to commit to a long-enough random string, using the above extractable commitment. This step is done as the foremost step in our OT protocol (called “Step 0”). Then each party will use the long random string as one-time pad to “mask” the values that they want to commit to during the execution of our OT protocol. Now, we can rely on the structure of the hybrid proof of [22], which first deals with all stages of a given session and then moves on to the next session in a specific order (determined by the transcript). The key observation here is that since Step 0 is performed ahead of all other steps for a fixed session s, changes in later stages of s cannot affect what happens in Step 0 (for example, issues of malleability and simulation-soundness do not arise). Furthermore, since any rewinding-based proofs of [22] are only relevant to later stages, they do not rewind Step 0 of sessions s.
Remark 1
Ostrovsky et al. [48] showed how to achieve the same as [31] while relaxing the assumption from CRHFs to one-way functions (OWFs). But we cannot use their approach (or any of the prior approaches that perform non-black-box simulation under OWFs) since simulators in these approaches are not straight-line. It uses both the adversary’s code and rewinding to get a OWF-based construction.
Robust-\(\mathcal {ZK}\) for Bounded Concurrency. The final issue that we need to address is how the non-black-box simulation will actually be performed corresponding to protocol \(\varPi _{ZK}\) (in Step 0) mentioned above. The main issue is that there are concurrently many sessions of \(\varPi _{ZK}\) executing simultaneously. In particular, if there are m sessions of OT protocol, then there will be \(\ell = 2m\) sessions of \(\varPi _{ZK}\). Simply replacing the prover with the non-black-box simulator may not result in polynomial-time simulation.
An immediate idea is that if \(\varPi _{ZK}\) is bounded-concurrent \(\mathcal {ZK}\) for up to \(\ell \) sessions, then we can use the concurrent non-black-box simulator to simulate Step 0 of all m sessions of the OT protocol at once. This allows us to bias coin-tossing for all m sessions and then we can design hybrids exactly as in [22].
Unfortunately, bounded-concurrent \(\mathcal {ZK}\) only guarantees self composition; i.e., it can only deal with messages of protocol \(\varPi _{ZK}\). In our case, \(\varPi _{ZK}\) is part of a larger protocol execution and the adversary receives messages from different stages of all sessions. We thus need a more robust notion of non-black-box simulation which, roughly speaking, (a) is straight-line, and (b) enables bounded-concurrent composition of \(\mathcal {ZK}\) protocols even in the presence of external messages as long as the total communication outside the \(\mathcal {ZK}\) protocol is a-priori bounded.
We formulate this notion explicitly in Sect. 4 and call it robust zero-knowledge. The notion requires that the view of a (standalone) verifier \(V^*\) who interacts with an external party B can be simulated by a simulator S only on input the code of \(V^*\). The simulator is not allowed to rewind \(V^*\) or B. However, both B and S are allowed to see each others messages (which is essential to make sure that many concurrent instances of the simulators compose seamlessly). This yields a notion that is similar in spirit to UC zero-knowledge [10] and implies bounded-concurrent \(\mathcal {ZK}\).
We remark that most \(\mathcal {ZK}\) protocols based on non-black-box simulation, with suitable adjustment of parameters, can actually handle arbitrary external messages (and not just the messages of the same protocol) without any modification. This observation was first used in Barak’s original work [3], and finds applications in other places [5, 50, 52]. In particular, it also holds for the protocol of Goyal et al. [31] and is implicit in their security proof. Thus, these protocols already achieve the (bounded) robust-\(\mathcal {ZK}\) notion. Robust-\(\mathcal {ZK}\) is just a convenient tool to help in the hybrid proofs.
By setting the parameters of \(\varPi _{ZK}\) so that it is \(\ell \)-robust-\(\mathcal {ZK}\) allows us to replace the provers of \(\varPi _{ZK}\) with simulator instances in Step 0 of any given session s while maintaining the overall structure and sequence of hybrids in [22] where stages of one session are handled at any given time. This gives us m-bounded concurrent OT.
2.2 Composition of OT with OT-hybrid MPC
The final step of our construction is the same as in [22]. Namely, we compose our bounded-concurrent OT protocol with a OT-hybrid UC-secure MPC protocol (i.e., replace each invocation of the ideal OT functionality in the latter with an execution of the former), thereby obtaining a MPC protocol in the plain model. While selecting the parameters, we have to ensure we adjust the parameters of \(\varPi _{ZK}\) to allow long enough messages so that simulation can be performed for the MPC protocol instead of the OT protocol. Since we only proved bounded-concurrent self composition for OT (not full UC-security), we do not get a proof for the MPC protocol right away. Hence, we prove the security by analyzing the MPC protocol directly. In essence, what we do is to observe that the security proof for our OT protocol (which consists of a hybrid argument from the real world to the ideal world) still works even after the OT protocol is composed with a OT-hybrid MPC protocol.
3 Preliminaries
We denote the security parameter by \(n\). We use \({\mathop {\approx }\limits ^{\text {c}}} \) to denote computational indistinguishability between two probability ensembles. For a set \(\mathsf {S}\), we use \(x \xleftarrow {\$} \mathsf {S}\) to mean that x is sampled uniformly at random from \(\mathsf {S}\). \(\textsc {ppt} \) denotes probabilistic polynomial time and \(\mathsf {negl}(\cdot )\) denotes negligible functions. Other relevant concepts include verifiable secret sharing schemes, extractable commitments, (robust) non-malleable commitments, and bounded-concurrent MPC (with interchangeable roles). Due to space constraints, we provide formal descriptions for these definitions in the full version of this paper [24].
4 Robust Zero-Knowledge and Commit-and-Prove
Goyal et al. [31] present a new \(\mathcal {ZK}\) argument for \(\mathcal {NP}\), assuming only back-box access to CRHFs. Their protocol (with a slight modification) can be interpreted as a “commit-and-prove” ZK. The prove stage relies on Barak’s non-black-box simulation [3], thus inheriting the following property: the protocol has a “preamble” phase where the verifier sends a random string r; the simulator is “straight-line” even in the presence of arbitrary (external) incoming communication of a-priori bounded length \(\ell (n)\) once |r| is sufficiently bigger than \(\ell (n)\).
We capture this property by defining the notion of robust zero-knowledge in Definition 1. Roughly, it considers the interaction between a prover P and a (dishonest) verifier \(V^*\), where \(V^*\) may also interact with an external ppt machine B. A protocol is \(\ell \)-robust ZK if there is a straight-line simulator whose output (\(\mathsf {Sview}\)) is indistinguishable from the view of \(V^*\) in the aforementioned real interaction (\(\mathsf {Rview}\)), where the size of all the messages that \(V^*\) receives from B is bounded by \(\ell \).Footnote 7
Definition 1 (Robust Zero-Knowledge (Informal))
An interactive argument system \(\mathrm {\Pi }\) for a language \(L\in \mathcal {NP}\) is robust \(\mathcal {ZK}\) w.r.t. a \(\textsc {ppt}\ \textsc {itm}\) B if for all \(\textsc {ppt}\ \textsc {itm}\) \(V^*\) there exists a \(\textsc {ppt}\ \textsc {itm}\) S (called the robust simulator), such that:
where \(n\in \mathbb {N}, x\in L, w\in R_L(x), z\in \{0,1\}^*, y\in \{0,1\}^*\).
For a polynomial \(\ell :\mathbb {N}\rightarrow \mathbb {N}\), \(\mathrm {\Pi }\) is \(\ell \)-robust zero-knowledge if it is robust w.r.t. every \(\textsc {ppt}\ \textsc {itm}\) B that sends at most \(\ell (n)\) bits. \(\mathrm {\Pi }\) is robust zero-knowledge if it is \(\ell \)-robust zero-knowledge for every polynomial \(\ell \).
It can be shown that the zero-knowledge protocol in [31, Section 4.2] is a black-box \(\ell \)-robust commit-and-prove zero knowledge protocol. That protocol (with slight modifications) consists of two phase: (1) in VSS Commit Phase, the prover commits to a witness w; (2) in a Proof Phase that may happen alter, the prover proves that the value committed in previous phase is indeed the witness to the common theorem x. We denote this protocol as \(\mathrm {\Pi }_\textsc {gosv}\). It will play an important role in next section (in Protocol 1). Due to page limits, we refer the reader to the full version [24], where we provide more details about \(\mathrm {\Pi }_\textsc {gosv}\), a formal treatment of robust ZK and a lemma that robust ZK implies bounded-concurrent ZK.
5 Straight-Line Extractable Commitments
In this section, we construct an extractable commitment scheme, assuming black-box access to any semi-honest oblivious transfer. The construction (shown in Protocol 1) makes black-box use of a statistically-binding commitment \(\mathsf {Com}\) and a maliciously-secure oblivious transfer \(\mathsf {OT}\). For the \(\mathsf {OT}\), we require (computational) indistinguishability-based security against malicious senders, and simulation-based security (ideal/real paradigm) against malicious receivers. Such OTs can be constructed in a black-box manner from any semi-honest OT [32]. To ease the presentation, we show in Protocol 1 a single-bit commitment. It can be easily extend to committing to multi-bit strings by standard techniques (see [24]).

Theorem 2
Protocol 1 is a straight-line extractable statistically-binding commitment scheme, which accesses the underlying primitives in a black-box manner.
Proof
The construction is black-box as we use the black-box commit-and-prove of [31] in the coin-tossing step. Statistically-binding property follows directly from that of the Step-2 commitment scheme \(\mathsf {Com}\). But the proofs for hiding property and extractability are more involved. In the following, we describe the ideas behind them. The complete proof can be found in [24].
Computationally-Hiding Property. We want to build a sequence of hybrids, where we switch from the honest commitment to a bit \(\sigma \) to the commitments to  , without being distinguished by any \(\textsc {ppt} \) malicious receiver \(R^*\). To do that, we first substitute the \(\mathsf {OT}\) instance in Step 4 with the ideal OT functionality
, without being distinguished by any \(\textsc {ppt} \) malicious receiver \(R^*\). To do that, we first substitute the \(\mathsf {OT}\) instance in Step 4 with the ideal OT functionality  (thanks to its simulation-based security against malicious receivers). Now the hybrid will learn in Step 4 the (ideal-world) \(R^*\)’s input b to this OT instance, while \(R^*\) has (information-theoretically) no information about \(s_{n,1-b}\). Recall that \(\{s_{i,b}\}\) are random secret shares of \(\sigma \). Thus, the hybrid can switch to a commitment to \(\overline{\sigma }\) by simply changing \(s_{n,1-b}\) to
(thanks to its simulation-based security against malicious receivers). Now the hybrid will learn in Step 4 the (ideal-world) \(R^*\)’s input b to this OT instance, while \(R^*\) has (information-theoretically) no information about \(s_{n,1-b}\). Recall that \(\{s_{i,b}\}\) are random secret shares of \(\sigma \). Thus, the hybrid can switch to a commitment to \(\overline{\sigma }\) by simply changing \(s_{n,1-b}\) to  , in the Step-2 commitment. The computational indistinguishability can essentially be reduced to that of \(\mathsf {Com}\). Note that the hybrid will not learn b until Step 4, so it has to make a random guess when it prepares \(\{s_{i,b}\}\) in Step 1 and 2. This will result in a loss of 1/2 adversarial advantage in our reduction to the hiding of \(\mathsf {Com}\). Also, there is another 1/2 factor due to the possibility that the last bit of Step-5 coin tossing hits \((1-b)\)Footnote 9 (recall that we cannot open \(c_{n,1-b}\) as the hybrid lies about it). Therefore, the adversarial advantage will be reduced by a (multiplicative) factor of 1/4 in total. But this is still enough for us to finish the reduction.
, in the Step-2 commitment. The computational indistinguishability can essentially be reduced to that of \(\mathsf {Com}\). Note that the hybrid will not learn b until Step 4, so it has to make a random guess when it prepares \(\{s_{i,b}\}\) in Step 1 and 2. This will result in a loss of 1/2 adversarial advantage in our reduction to the hiding of \(\mathsf {Com}\). Also, there is another 1/2 factor due to the possibility that the last bit of Step-5 coin tossing hits \((1-b)\)Footnote 9 (recall that we cannot open \(c_{n,1-b}\) as the hybrid lies about it). Therefore, the adversarial advantage will be reduced by a (multiplicative) factor of 1/4 in total. But this is still enough for us to finish the reduction.
Extractability. First, note that there exists a simulator for Step-5 coin tossing which can bias the result to any target value. This can be done relying on the ZK simulator for Step 5d (same as in Barak-Lindell extractable commitment [5]) plus the sender’s security of \(\mathsf {OT}\). Therefore, the extractor can work in the following way: it first uses a random \(\tau \) as the honest receiver in the \(\mathsf {OT}\) instances, which allows him to learn \(\{s_{i,\tau _i}\}_{i \in [n]}\); then it biases the coin-tossing result to \(\overline{\tau }\), which will let him learn \(\{s_{i,\overline{\tau }_i}\}_{i \in [n]}\) from the committer’s decommitments. With all shares \(\{s_{i,b}\}\), the extractor can compute \(\sigma \).
6 Our Bounded Concurrent OT Protocol
In this section, we prove the following theorem.
Theorem 3
Assume the existence of constant-round semi-honest oblivious transfer protocols and collision-resistant hash functions. Then, for every polynomial m, there exists a constant-round protocol that securely computes the ideal OT functionality \(\mathcal {F}_{\mathrm OT}\) under m-bounded concurrent composition, and it uses the underlying primitives in the black-box way.
At a high-level, we obtain the OT claimed in Theorem 3 by replacing the statistically-binding commitment \(\mathsf {Com}\) in the OT of [22] (denoted as GKP-OT) with a new commitment based on Protocol 1. Due to space constraints, we give only a high-level description of our construction, highlighting the modifications we made to the GKP-OT, and then talk about the security proof. The formal description of our protocol and security proof are given in the full version [24].
As mentioned in the technical overview (Sect. 2.1), we want to rely on the same simulation technique for GKP-OT, but with an (efficient) alternative way in which the simulator can “extract” the value committed in \(\mathsf {Com}\). Let us first recall the (only) two places where \(\mathsf {Com}\) is used in GKP-OT:
-
1.
In the very beginning (Stage 1), S (resp. R) uses \(\mathsf {Com}\) to commit to a random set \(\varGamma _S\) (resp. \(\varGamma _R\)), which is used later for cut-and-chose.
-
2.
Next, S (resp. R) uses \(\mathsf {Com}\) to commit to a random string \(\textit{\textbf{a}}^S\) (resp. \(\textit{\textbf{a}}^R\)) in the (Stage-2) coin tossing, which will later be used as inputs to the parallel execution of several random OT instances (which are in turned used for an OT-combiner stage later).
Since we now have the straight-line extractable commitment (Protocol 1) at our disposal, we may replace \(\mathsf {Com}\) with Protocol 1. We notice that the GKP simulator \(\mathcal {S}im_{\mathrm {OT}}\) can be extended to our setting by substituting the brute-forcing with the Protocol-1 extractor. However, this method requires us to insert many intermediate hybrids in carefully-chosen places as we need to ensure that the extractions happen in time, while not disturbing the adjacent hybrids. We thus take the following alternative approach.
Our Approach. We add a new step (called Stage 0) in the beginning of GKP-OT, where S (resp. R) commits using Protocol 1 to two random strings \(\phi ^S\) and \(\psi ^S\) (resp. \(\phi ^R\) and \(\psi ^R\)) of proper length. We then continue identically as in GKP-OT with the following modifications:
-
In Stage 1, when S (resp. R) needs to commit to \(\varGamma _S\) (resp. \(\varGamma _R\)), he simply sends \(\phi ^S \oplus \varGamma _S\) (resp. \(\phi ^R \oplus \varGamma _R\));
-
In Stage 2, when S (resp. R) needs to commit to \(\textit{\textbf{a}}^S\) (resp. \(\textit{\textbf{a}}^R\)), he simply sends \(\psi ^S \oplus \textit{\textbf{a}}^S\) (resp. \(\psi ^R \oplus \textit{\textbf{a}}^R\)).
Intuitively, we ask both parties commit to random strings which will later be used as one-time pads to “mask” the values they committed to by \(\mathsf {Com}\) in the original GKP-OT. The hiding of \(\varGamma _S\) and \(\textit{\textbf{a}}^S\) follows straightforwardly. To allow the simulator to extract them efficiently, it is sufficient to let \(\mathcal {S}im_{\mathrm {OT}}\) use the extractor of Protocol 1 to extract \(\phi ^S\) and \(\psi ^S\). This can be done based on two important properties of the extractor for Protocol 1:
-
1.
Straight-line: this guarantees that \(\mathcal {S}im_{\mathrm {OT}}\) can finish the extraction efficiently, free of the exponential-time problem due to recursive rewinding (similar as that for concurrent zero-knowledges [18]).
-
2.
Robustness: since Protocol 1 is based on the \(\ell \)-robust ZK (Sect. 4), its extractor inherits the \(\ell \)-robustness. By setting the parameter \(\ell \) carefully, we make sure that the simulator can switch from honest receiver’s strategy to the extractor’s strategy session by session, even in the presence of (bounded-ly) many other sessions.
Since we put the commitments to those masks in the very beginning, all the extractions can be done before further hybrids are defined. Similar arguments also apply when the receiver is corrupted. Therefore, we can make use of the GKP technique in a modular way to finish the proof of Theorem 3. We refer the reader to [24] for more details.
7 Our Bounded-Concurrent MPC Protocol
In this section, we prove the following theorem.
Theorem 4
Assume the existence of constant-round semi-honest oblivious transfer protocols and collision-resistant hash functions. Let \(\mathcal {F}\) be any well-formed functionality. Then, for every polynomial m, there exists a constant-round protocol that securely computes \(\mathcal {F}\) under m-bounded concurrent composition; furthermore, it uses the underlying primitives in the black-box way.
The protocol and the proofs are identical to those in [22] except that we use the bounded-concurrent secure OT protocol described in previous section. We now provide more details. We focus on the two-party case below (the MPC case is analogous).
Protocol Description. Roughly speaking, we obtain our bounded-concurrent 2PC protocol by composing our bounded-concurrent OT protocol in Sect. 6 with a UC-secure OT-hybrid 2PC protocol. Concretely, let \(\varPi _{\mathrm {OT}}\) be our \(\ell \)-bounded-concurrent OT protocol in Sect. 6, and \(\varPi _{\mathrm {2PC}}^{\mathcal {F}_{\mathrm {OT}}}\) be a UC-secure OT-hybrid 2PC protocol with the following property: The two parties use the OT functionality \(\mathcal {F}_{\mathrm OT}\) only at the beginning of the protocol, and they send only randomly chosen inputs to \(\mathcal {F}_{\mathrm OT}\). Then, we obtain our bounded-concurrent 2PC protocol \(\varPi _{\mathrm {2PC}}\) by replacing each invocation of \(\mathcal {F}_{\mathrm OT}\) in \(\varPi _{\mathrm {2PC}}^{\mathcal {F}_{\mathrm {OT}}}\) with an execution of \(\varPi _{\mathrm {OT}}\) (i.e., the two parties execute \(\varPi _{\mathrm {OT}}\) instead of calling to \(\mathcal {F}_{\mathrm OT}\)), where all the executions of \(\varPi _{\mathrm {OT}}\) are carried out in a synchronous manner, i.e., in a manner that the first message of all the executions are sent before the second message of any execution is sent etc.; furthermore, the bounded-concurrency parameter for \(\varPi _{\mathrm {OT}}\) is set to be \(m'\) defined as follows: let \(\nu _{_\mathrm {{2PC}}}\) denote the length of all messages of the hybrid 2PC protocol \(\varPi _{\mathrm {2PC}}^{\mathcal {F}_{\mathrm {OT}}}\) protocol (which does not include the length of messages corresponding to OT calls since we are in the hybrid model). Then, we set \(m'\) so that the length \(\ell \) of long messages of \(\varPi _{\mathrm {OT}}\) would be n bits longer than \(\nu _{_\mathrm {{OT}}} + \nu _{_\mathrm {{2PC}}}\). This can be ensured by setting \(m' = a\cdot m\) where a is the smallest integer that is bigger than \(\max ({\nu _{_\mathrm {{OT}}}}/{\nu _{_\mathrm {{2PC}}}}, {\nu _{_\mathrm {{2PC}}}}/{\nu _{_\mathrm {{OT}}}})\).
As the UC-secure OT-hybrid 2PC protocol, we use the constant-round 2PC (actually, MPC) protocol of Ishai et al. [36]Footnote 10, which makes only black-box use of pseudorandom generators (which in turn can be obtained in the black-box way from any semi-honest OT protocol).
Since the OT-hybrid protocol of Ishai et al. [36] (as well as its modification in [22]) is a black-box construction and has only constant number of rounds, our protocol \(\varPi _{\mathrm {2PC}}\) is also a black-box construction and has only constant number of rounds.
The security of this protocol can be proved in a similar way as our OT protocol. The formal proof is provided in the full version [24].
Notes
- 1.
It means the extraction strategy does not involve rewinding techniques.
- 2.
In some works, when the construction is black-box but the proof of security uses non-black-box techniques (as in this paper), this is referred to as a semi-black-box protocol.
- 3.
In their original construction, C sends a trapdoor permutation (TDP) f and then proves in zero-knowledge that f is indeed a valid TDP. To make this step black-box, C can send an enhanced TDP instead (without the need of \(\mathcal {ZK}\) proof).
- 4.
- 5.
Note \(I_x(y) = 1\) if and only if \(y=x\) is well defined and the “code” of \(I_x\) requires only the knowledge of x.
- 6.
Note that we cannot ask the committer to prove in zero-knowledge that he uses the committed shares as sender’s input in the OT execution, because such proof will make non-black-box use of both the commitment and OT.
- 7.
- 8.
We remark that this step can actually happen in parallel with the \(\mathsf {OT}\) instances in Step 3. It is put here (only) to ease the presentation of the security proof. In [24], we talk about how the proof can be modified to accommodate the case where the Step-4 \(\mathsf {OT}\) happens in parallel with Step 3.
- 9.
Note that the security of Step-5 coin tossing ensures that \(R^*\) can learn both (decommitments to) \(s_{n,0}\) and \(s_{n,1}\) with only negligible probability.
- 10.
References
Applebaum, B., Brakerski, Z., Garg, S., Ishai, Y., Srinivasan, A.: Separating two-round secure computation from oblivious transfer. In: 11th Innovations in Theoretical Computer Science Conference (ITCS 2020). Schloss Dagstuhl-Leibniz-Zentrum für Informatik (2020)
Badrinarayanan, S., Goyal, V., Jain, A., Khurana, D., Sahai, A.: Round optimal concurrent MPC via strong simulation. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 743–775. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_25
Barak, B.: How to go beyond the black-box simulation barrier. In: 42nd FOCS, pp. 106–115. IEEE Computer Society Press (2001). https://doi.org/10.1109/SFCS.2001.959885
Barak, B.: Constant-round coin-tossing with a man in the middle or realizing the shared random string model. In: 43rd FOCS, pp. 345–355. IEEE Computer Society Press (2002). https://doi.org/10.1109/SFCS.2002.1181957
Barak, B., Lindell, Y.: Strict polynomial-time in simulation and extraction. In: 34th ACM STOC, pp. 484–493. ACM Press (2002). https://doi.org/10.1145/509907.509979
Barak, B., Sahai, A.: How to play almost any mental game over the net - concurrent composition via super-polynomial simulation. In: 46th FOCS, pp. 543–552. IEEE Computer Society Press (2005). https://doi.org/10.1109/SFCS.2005.43
Bitansky, N., Paneth, O.: From the impossibility of obfuscation to a new non-black-box simulation technique. In: 53rd FOCS, pp. 223–232. IEEE Computer Society Press (2012). https://doi.org/10.1109/FOCS.2012.40
Bitansky, N., Paneth, O.: On the impossibility of approximate obfuscation and applications to resettable cryptography. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 241–250. ACM Press (2013). https://doi.org/10.1145/2488608.2488639
Broadnax, B., Döttling, N., Hartung, G., Müller-Quade, J., Nagel, M.: Concurrently composable security with shielded super-polynomial simulators. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 351–381. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_13
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd FOCS, pp. 136–145. IEEE Computer Society Press (2001). https://doi.org/10.1109/SFCS.2001.959888
Canetti, R., Kushilevitz, E., Lindell, Y.: On the limitations of universally composable two-party computation without set-up assumptions. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 68–86. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_5
Canetti, R., Lin, H., Pass, R.: Adaptive hardness and composable security in the plain model from standard assumptions. In: 51st FOCS, pp. 541–550. IEEE Computer Society Press (2010). https://doi.org/10.1109/FOCS.2010.86
Choi, S.G., Dachman-Soled, D., Malkin, T., Wee, H.: Simple, black-box constructions of adaptively secure protocols. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 387–402. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_23
Choi, S.G., Dachman-Soled, D., Malkin, T., Wee, H.: A black-box construction of non-malleable encryption from semantically secure encryption. J. Cryptol. 31(1), 172–201 (2017)
Chung, K.M., Pass, R., Seth, K.: Non-black-box simulation from one-way functions and applications to resettable security. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 231–240. ACM Press (2013). https://doi.org/10.1145/2488608.2488638
Cramer, R., et al.: Bounded CCA2-secure encryption. In: Kurosawa, K. (ed.) ASIACRYPT 2007. LNCS, vol. 4833, pp. 502–518. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-76900-2_31
Dachman-Soled, D., Malkin, T., Raykova, M., Venkitasubramaniam, M.: Adaptive and concurrent secure computation from new adaptive, non-malleable commitments. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 316–336. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_17
Dwork, C., Naor, M., Sahai, A.: Concurrent zero-knowledge. In: 30th ACM STOC, pp. 409–418. ACM Press (1998). https://doi.org/10.1145/276698.276853
Feige, U., Shamir, A.: Witness indistinguishable and witness hiding protocols. In: 22nd ACM STOC, pp. 416–426. ACM Press (1990). https://doi.org/10.1145/100216.100272
Garay, J.A., MacKenzie, P.D.: Concurrent oblivious transfer. In: 41st FOCS, pp. 314–324. IEEE Computer Society Press (2000). https://doi.org/10.1109/SFCS.2000.892120
Garg, S., Goyal, V., Jain, A., Sahai, A.: Concurrently secure computation in constant rounds. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 99–116. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_8
Garg, S., Kiyoshima, S., Pandey, O.: A new approach to black-box concurrent secure computation. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 566–599. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_19
Garg, S., Kumarasubramanian, A., Ostrovsky, R., Visconti, I.: Impossibility results for static input secure computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 424–442. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_25
Garg, S., Liang, X., Pandey, O., Visconti, I.: Black-box constructions of bounded-concurrent secure computation. Cryptology ePrint Archive, Report 2020/216 (2020). https://eprint.iacr.org/2020/216
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or A completeness theorem for protocols with honest majority. In: Aho, A. (ed.) 19th ACM STOC, pp. 218–229. ACM Press (May 1987). https://doi.org/10.1145/28395.28420
Goyal, V.: Constant round non-malleable protocols using one way functions. In: Fortnow, L., Vadhan, S.P. (eds.) 43rd ACM STOC, pp. 695–704. ACM Press (2011). https://doi.org/10.1145/1993636.1993729
Goyal, V.: Positive results for concurrently secure computation in the plain model. In: 53rd FOCS, pp. 41–50. IEEE Computer Society Press (2012). https://doi.org/10.1109/FOCS.2012.13
Goyal, V., Jain, A.: On concurrently secure computation in the multiple ideal query model. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 684–701. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_40
Goyal, V., Lee, C.K., Ostrovsky, R., Visconti, I.: Constructing non-malleable commitments: a black-box approach. In: 53rd FOCS, pp. 51–60. IEEE Computer Society Press (2012). https://doi.org/10.1109/FOCS.2012.47
Goyal, V., Lin, H., Pandey, O., Pass, R., Sahai, A.: Round-efficient concurrently composable secure computation via a robust extraction lemma. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 260–289. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_12
Goyal, V., Ostrovsky, R., Scafuro, A., Visconti, I.: Black-box non-black-box zero knowledge. In: Shmoys, D.B. (ed.) 46th ACM STOC, pp. 515–524. ACM Press (2014). https://doi.org/10.1145/2591796.2591879
Haitner, I.: Semi-honest to malicious oblivious transfer—the black-box way. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 412–426. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_23
Haitner, I., Ishai, Y., Kushilevitz, E., Lindell, Y., Petrank, E.: Black-box constructions of protocols for secure computation. SIAM J. Comput. 40(2), 225–266 (2011)
Hazay, C., Venkitasubramaniam, M.: Composable adaptive secure protocols without setup under polytime assumptions. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9985, pp. 400–432. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_16
Ishai, Y., Kushilevitz, E., Lindell, Y., Petrank, E.: Black-box constructions for secure computation. In: Kleinberg, J.M. (ed.) 38th ACM STOC, pp. 99–108. ACM Press (2006). https://doi.org/10.1145/1132516.1132531
Ishai, Y., Prabhakaran, M., Sahai, A.: Founding cryptography on oblivious transfer – efficiently. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 572–591. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_32
Katz, J., Ostrovsky, R.: Round-optimal secure two-party computation. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 335–354. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_21
Kiyoshima, S.: Round-efficient black-box construction of composable multi-party computation. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 351–368. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_20
Kiyoshima, S., Manabe, Y., Okamoto, T.: Constant-round black-box construction of composable multi-party computation protocol. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 343–367. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_15
Lin, H., Pass, R.: Non-malleability amplification. In: Mitzenmacher, M. (ed.) 41st ACM STOC, pp. 189–198. ACM Press (2009). https://doi.org/10.1145/1536414.1536442
Lin, H., Pass, R.: Black-box constructions of composable protocols without set-up. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 461–478. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_27
Lin, H., Pass, R., Venkitasubramaniam, M.: A unified framework for concurrent security: universal composability from stand-alone non-malleability. In: Mitzenmacher, M. (ed.) 41st ACM STOC, pp. 179–188. ACM Press (2009). https://doi.org/10.1145/1536414.1536441
Lindell, Y.: Bounded-concurrent secure two-party computation without setup assumptions. In: 35th ACM STOC, pp. 683–692. ACM Press (2003). https://doi.org/10.1145/780542.780641
Lindell, Y.: Lower bounds for concurrent self composition. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 203–222. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_12
Malkin, T., Moriarty, R., Yakovenko, N.: Generalized environmental security from number theoretic assumptions. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 343–359. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_18
Micali, S., Pass, R., Rosen, A.: Input-indistinguishable computation. In: 47th FOCS, pp. 367–378. IEEE Computer Society Press (2006). https://doi.org/10.1109/FOCS.2006.43
Ostrovsky, R., Richelson, S., Scafuro, A.: Round-optimal black-box two-party computation. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 339–358. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_17
Ostrovsky, R., Scafuro, A., Venkitasubramanian, M.: Resettably sound zero-knowledge arguments from OWFs - the (semi) black-box way. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 345–374. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_15
Pass, R.: Simulation in quasi-polynomial time, and its application to protocol composition. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 160–176. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_10
Pass, R.: Bounded-concurrent secure multi-party computation with a dishonest majority. In: Babai, L. (ed.) 36th ACM STOC, pp. 232–241. ACM Press (2004). https://doi.org/10.1145/1007352.1007393
Pass, R., Lin, H., Venkitasubramaniam, M.: A unified framework for UC from only OT. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 699–717. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_42
Pass, R., Rosen, A.: Bounded-concurrent secure two-party computation in a constant number of rounds. In: 44th FOCS, pp. 404–415. IEEE Computer Society Press (2003). https://doi.org/10.1109/SFCS.2003.1238214
Pass, R., Wee, H.: Black-box constructions of two-party protocols from one-way Functions. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 403–418. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_24
Peikert, C., Waters, B.: Lossy trapdoor functions and their applications. SIAM J. Comput. 40(6), 1803–1844 (2011)
Prabhakaran, M., Sahai, A.: New notions of security: achieving universal composability without trusted setup. In: Babai, L. (ed.) 36th ACM STOC, pp. 242–251. ACM Press (2004). https://doi.org/10.1145/1007352.1007394
Venkitasubramaniam, M.: On adaptively secure protocols. In: Abdalla, M., De Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 455–475. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10879-7_26
Wee, H.: Black-box, round-efficient secure computation via non-malleability amplification. In: 51st FOCS, pp. 531–540. IEEE Computer Society Press (2010). https://doi.org/10.1109/FOCS.2010.87
Yao, A.C.C.: How to generate and exchange secrets (extended abstract). In: 27th FOCS, pp. 162–167. IEEE Computer Society Press (1986). https://doi.org/10.1109/SFCS.1986.25
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Garg, S., Liang, X., Pandey, O., Visconti, I. (2020). Black-Box Constructions of Bounded-Concurrent Secure Computation. In: Galdi, C., Kolesnikov, V. (eds) Security and Cryptography for Networks. SCN 2020. Lecture Notes in Computer Science(), vol 12238. Springer, Cham. https://doi.org/10.1007/978-3-030-57990-6_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-57990-6_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-57989-0
Online ISBN: 978-3-030-57990-6
eBook Packages: Computer ScienceComputer Science (R0)





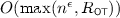 rounds, where
rounds, where 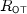 is the round complexity of the underlying OT protocol. (Hence, if the underlying OT protocol has only constant round, the round complexity is
is the round complexity of the underlying OT protocol. (Hence, if the underlying OT protocol has only constant round, the round complexity is