Abstract
We study anonymity of probabilistic encryption (pE) and probabilistic authenticated encryption (pAE). We start by providing concise game-based security definitions capturing anonymity for both pE and pAE, and then show that the commonly used notion of indistinguishability from random ciphertexts (IND$) indeed implies the anonymity notions for both pE and pAE. This is in contrast to a recent work of Chan and Rogaway (Asiacrypt 2019), where it is shown that IND$-secure nonce-based authenticated encryption can only achieve anonymity if a sophisticated transformation is applied. Moreover, we also show that the Encrypt-then-MAC paradigm is anonymity-preserving, in the sense that if both the underlying probabilistic MAC (pMAC) and pE schemes are anonymous, then also the resulting pAE scheme is. Finally, we provide a composable treatment of anonymity using the constructive cryptography framework of Maurer and Renner (ICS 2011). We introduce adequate abstractions modeling various kinds of anonymous communication channels for many senders and one receiver in the presence of an active man-in-the-middle adversary. Then we show that the game-based notions indeed are anonymity-preserving, in the sense that they imply constructions between such anonymous channels, thus generating authenticity and/or confidentiality as expected, but crucially retaining anonymity if present.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
When transmitting messages in the symmetric-key setting, where communicating parties share secret keys a priori, traditionally confidentiality and authenticity are the security properties that are mostly considered. Confidentiality guarantees exclusivity of the receiving party (no one but the receiver should be able to gain any partial information about the transmitted message, possibly other than its length), while authenticity guarantees exclusivity of the sending party (no one except the sender should be able to convince the receiver that it indeed originated the message). But in a scenario where there are more than just two communicating parties using the same protocol, e.g., many senders and one receiver (as considered in this work), another important security property must be taken into account, namely anonymity.
For the mentioned setting, we are more specifically interested in external sender anonymity, that is, the property that guarantees that no one but the receiver can learn from which sender a message originated. The main focus of our work is on security definitions which capture exactly this guarantee.
1.1 Background
Anonymity, as opposed to confidentiality and authenticity, in most settings (as is the case for the one considered here) cannot be “created out of the blue”; rather, an intrinsic property of anonymity is that it can be preserved. In the game-based spirit of security definitions, this is reflected by the fact that conventional anonymity notions are captured by the concept of key-indistinguishability of a scheme originally intended to provide other forms of security, as confidentiality or authenticity. More specifically, in the symmetric-key setting this means that anonymity is a property that needs to be provided in conjunction with confidentiality for encryption schemes and with authenticity for MAC schemes.
But when considered from a composable standpoint, the fact that anonymity can merely be preserved becomes even more evident: consider for example a protocol employing a MAC scheme and shared secret keys between the senders and the receiver, which is executed on top of an insecure channel to obtain an authenticated channel; if one wishes for the constructed channel to additionally be also anonymous, it must be the case that the insecure channel is anonymous as well, and this construction is still possible precisely if the employed MAC scheme not only is unforgeable, but is also key-indistinguishable.
The latter considerations were made explicit by Alwen, Hirt, Maurer, Patra, and Raykov in [4], and our work can be seen as a continuation and refinement of this line of research: Here we consider the construction of an anonymous secure (confidential and authenticated) channel from an anonymous authenticated one, and show that this is possible precisely if the employed encryption scheme not only has indistinguishable ciphertexts, but also indistinguishable keys. Moreover, we show that only if a secure authenticated encryption scheme which is key-indistinguishable is employed, one can construct the anonymous secure channel directly from the anonymous insecure one.
1.2 Contributions
We consider the following setting: n parties, the senders, wish to securely and anonymously transmit messages to the same party, the receiver, and we assume that the receiver a priori shares a (different) secret key with each of the n senders. Since all of our treatment is in the symmetric-key setting, and the considered protocols employ probabilistic (as opposed to nonce-based) schemes, we often tacitly assume these two facts throughout the paper. Moreover, since the meaning of security usually depends on the context, we adopt the convention that for a cryptographic scheme by anonymous security we mean anonymity (in form of key-indistinguishability) in conjunction with its conventionally associated security notion, that is, confidentiality for encryption, authenticity for MAC, and confidentiality plus authenticity (usually simply referred to as just security) for authenticated encryption.
Game-Based Security Definitions. We start by providing game-based security definitions capturing anonymity for both probabilistic encryption (pE) and probabilistic authenticated encryption (pAE). For the former, we revisit the notion of key-indistinguishability, originally put forth by Fischlin [13], and subsequently treated in [12] by Desai and in [1] by Abadi and Rogaway. In all three works this notion has been expressed for \(n=2\) senders; here we generalize it to an arbitrary number of senders. For nonce-based authenticated encryption (nAE), the analogous notion of key-indistinguishability has been recently put forth by Chan and Rogaway [11]. Here we propose a concise definition for the case of pAE instead.
For both pE and pAE, we show the relevant implications among the introduced security definitions, exposing the concrete security losses surfacing from the reductions (in the full version [5]). Furthermore, we formally show that indeed the strong security notion of indistinguishability from random ciphertexts (dubbed IND$, and valid for both schemes) implies key-indistinguishability. Finally, we prove that the Encrypt-then-MAC (EtM) paradigm, applied on secure and anonymous pE and probabilistic MAC (pMAC), yields pAE which is not only secure, but crucially also anonymous, thus confirming that EtM is anonymity-preserving.
Composable Security Definitions. We next move to the focal point of our work, the composable treatment of anonymity. Here we introduce alternative security definitions within the constructive cryptography (CC) framework of Maurer and Renner [17, 19], which enjoy composability and allow to make explicit security goals from an application point of view.
First we phrase the desired security properties of (symmetric-key) protocols as specific constructions of cryptographic communication channels. More concretely, we start by defining the following resources which expose n interfaces to send messages and one to receive them: the insecure anonymous channel (\(\mathsf {A\text {-}\mathsf{INS}}\)), the authenticated anonymous channel (\(\mathsf {A\text {-}\mathsf{AUT}}\)), and the secure anonymous channel (\(\mathsf {A\text {-}\mathsf{SEC}}\)). Then we state that a protocol (executed by the senders and the receiver, which share secret keys a priori) provides authenticity in conjunction with anonymity if it constructs \(\mathsf {A\text {-}\mathsf{AUT}}\) from \(\mathsf {A\text {-}\mathsf{INS}}\), provides confidentiality in conjunction with anonymity if it constructs \(\mathsf {A\text {-}\mathsf{SEC}}\) from \(\mathsf {A\text {-}\mathsf{AUT}}\), and provides security (i.e., confidentiality and authenticity) in conjunction with anonymity if it constructs \(\mathsf {A\text {-}\mathsf{SEC}}\) directly from \(\mathsf {A\text {-}\mathsf{INS}}\).
Secondly, we establish relations between the previously introduced game-based security definitions and their composable counterparts, that is, we show sufficiency conditions in terms of game-based definitions for the above mentioned constructions. As already mentioned earlier, in [4] it was shown that key-indistinguishable pMAC schemes enable the construction of \(\mathsf {A\text {-}\mathsf{AUT}}\) from \(\mathsf {A\text {-}\mathsf{INS}}\). Here we show that anonymous secure pE enables the next logical step, namely the construction of \(\mathsf {A\text {-}\mathsf{SEC}}\) from \(\mathsf {A\text {-}\mathsf{AUT}}\). In terms of time-complexity, this significantly improves upon the MAC-based solution proposed in [4] for the same construction. Furthermore, we show that these two steps can be performed in one shot using authenticated encryption instead, that is, we show that anonymous secure pAE constructs a \(\mathsf {A\text {-}\mathsf{SEC}}\) directly from \(\mathsf {A\text {-}\mathsf{INS}}\). Again, this significantly improves upon the MAC-based solution proposed in [4] for the same construction. Moreover, this provides further evidence of the anonymity preservation of EtM.
Preferring Probabilistic Schemes for Anonymity. We observe that our constructive treatment strengthens the role of probabilistic authenticated encryption in contrast to its nonce-based counterpart when it comes to anonymity. According to Rogaway [20], a main advantage provided by nonces is that
“encryption schemes constructed to be secure under nonce-based security notions may be less prone to misuse”.
Nevertheless, this raises concerns about attacks in the multi-user (mu) setting, where crucially anonymity lives. For this reason in TLS 1.3 a randomized nonces mechanism has been proposed for the employed nAE scheme, AES with GCM (Galois/Counter Mode). This recently spawned work by Bellare and Tackmann [9] and Hoang, Tessaro, and Thiruvengadam [14], which initiated and refined the study of mu security of nAE in order to rigorously formalize security under such randomized nonces mechanism (but they did not address anonymity, in the form of key-indistinguishability).
But quoting again Rogaway [21, I.8 (page 22)],
“[if] an IV-based encryption scheme [...] is good in the nonce-based framework [...] then it is also good in the probabilistic setting”,
which implies that an IND$-secure nAE scheme is an IND$-secure pAE scheme, when the nonce is randomized (if one ignores the concept of associated data). Therefore, in view of our previously mentioned result attesting that IND$-secure pAE implies anonymity, our work can be considered as a confirmation that the random nonce mechanism, if used with an IND$-secure nAE scheme and under the assumption that the nonces are indeed truly uniformly random, also provides anonymity. Note that our consideration here is rather informal, and a more thorough study should be carried out to also incorporate the issue of nonce repetition and related birthday paradox security bounds (in our discussion, we are assuming a setting where not too many messages are exchanged).
This is to be compared to a recent work by Chan and Rogaway [11], which studies the anonymity of nAE: the authors observe that because of the session-related nature of the nonces, nAE actually fails to generally provide anonymity. For this reason, they introduce a transformation (dubbed NonceWrap) which converts an nAE scheme into a (syntactically different) new scheme, anonymous nAE (anAE), which they show does achieve anonymity (i.e., key-indistinguishability).
A Framework for Security Definitions and Proofs. We formulate all of the above mentioned security definitions in a systematic and concise language. We see the framework we put forth as an independent contribution, since it allows for compact formulations of security definitions, and enables easy and short (reduction-based) proofs of security, which in principle could be formally verified in a rather direct way (we leave this task open). Our proposed framework is based on the earlier work on cryptographic systems of Maurer, Pietrzak, and Renner [16, 18], can be seen as a specialization of the recent work of Brzuska, Delignat-Lavaud, Fournet, Kohbrok, and Kohlweiss [10], and is inspired by the approach taken by Rosulek in [24].
1.3 Outline
We begin by providing the necessary background in Sect. 2, where we introduce our notation and the framework we use to state and prove security notions. As motivating examples, we revisit the classical security definitions for pE and pAE by capturing them within our framework. We proceed in Sect. 3 by providing game-based security definitions of anonymity, in terms of key-indistinguishability, for both pE and pAE. We introduce different notions, some capturing single security goals while others capturing more together, and then we show the relevant relations among them. Moreover, we show that for both pE and pAE, their respective stronger IND$ security notions imply anonymity. As a last result within the realm of game-based security notions, we show that the Encrypt-then-MAC paradigm, used to build secure pAE from secure pE and secure pMAC, not only preserves security, but anonymity as well. Finally, in Sect. 4 we provide composable security definitions capturing anonymity for both pE and pAE, and show that these notions are implied by the previously introduced game-based definitions. This is our main contribution, and it should be seen as shedding light into what anonymity (in the sense of key-indistinguishability) of symmetric cryptographic primitives really achieves from an application point of view. Our analysis makes it explicit that in this setting, key-indistinguishability must be understood as a tool that preserves anonymity, rather than creating it. The proofs of all of our results are deferred to the full version [5].
2 Preliminaries
2.1 Notation
We write \(x,\ldots \leftarrow y\) to assign the value y to variables \(x,\ldots \), and \(w,\ldots \overset{\text {iid}}{\leftarrow }\mathcal D\) to assign independently and identically distributed values to variables \(w,\ldots \) according to distribution \(\mathcal D\). \(\varnothing \) denotes the empty set, \(\mathbb {N}\doteq \{0,1,2,\ldots \}\) denotes the set of natural numbers, and for \(n\in \mathbb {N}\), we use the convention \([n]\doteq \{1,\ldots ,n\}\). For \(n\in \mathbb {N}\), \(\{0,1\}^n\) denotes the set of bitstrings of length n, \(\{0,1\}^*\doteq \bigcup _{i\ge 0}\{0,1\}^i\) denotes the set of all finite length bitstrings, for \(s\in \{0,1\}^*\), \(\left| s\right| \) denotes the length of s (in bits), and \(\$^n\) represent a uniformly sampled random bitstring of length n. Finally, for a random variable X over a set \(\mathcal {X}\), \(\mathrm {supp}\,X\doteq \{x\in \mathcal {X}\,|\,\mathrm {Pr}^{}\left[ X=x\right] >0\}\).
2.2 Cryptographic Systems
We model cryptographic objects as discrete reactive systems with interfaces, that is, systems that can be queried with labeled inputs in a sequential fashion, where each distinct label corresponds to a distinct interface, and for each such input generate (possibly probabilistically) an equally labeled output depending on the input and the current state (formally defined by the sequence of all previous inputs and the associated outputs). Such systems can be formally described by conditional distributions of output values given input values, that is, by their input-output behavior (often described with pseudocode), as they formally correspond to random systems originally introduced in [16], and later refined in [18]. For two such systems \(\mathbf {S}\) and \(\mathbf {T}\) having the same input-output behavior (but possibly different implementation), we write \(\mathbf {S}\equiv \mathbf {T}\).
In cryptography we are also interested in other objects (which can be formally modeled as special kinds of random systems). The first type we consider are distinguishers, which are just like the systems mentioned above, but enhanced with a special initial output which does not require an input, and a special final binary output. Formally, we usually consider a random experiment involving a distinguisher \(\mathbf {D}\) and a system \(\mathbf {S}\) which interact as follows: first \(\mathbf {D}\) starts by (possibly probabilistically) generating the first output \(X_1\) with some label (corresponding to a specific interface of \(\mathbf {S}\)), which will be used as the first input for \(\mathbf {S}\) at that interface, which in turn will generate its first output \(Y_1\) at the same interface, to be used as first input for \(\mathbf {D}\). From \(Y_1\) and the current state (\(X_1\)), \(\mathbf {D}\) will then generate its second output \(X_2\), with some (possibly different) label, and \(\mathbf {S}\) will respond with \(Y_2\) (depending on \(X_1\), \(Y_1\), and \(X_2\)), and so on, until \(\mathbf {D}\) stops and outputs a bit Z. We call the operation of connecting \(\mathbf {D}\) and \(\mathbf {S}\) in the described way sequential composition and we syntactically represent it by the expression \(\mathbf {D}\mathbf {S}\), which is only valid if the number and types of labels (interfaces) match. We use the expression \(\mathbf {D}\mathbf {S}\) to also denote the random variable Z representing \(\mathbf {D}\)’s final binary output.
The second type of special objects are converters, which are similar to systems but defining two disjoint sets of labels, and which can be used to extend either distinguishers (with labels matching the one in the first set) or systems (with labels matching the ones in the second set). We refrain from defining this concept on a formal level, and limit ourselves to give an intuitive description: a converter \(\mathbf {C}\) is an object such that \(\mathbf {D}\mathbf {C}\) (the sequential composition restricted to the first set of labels of distinguisher \(\mathbf {D}\) with \(\mathbf {C}\)) is again a distinguisher, and \(\mathbf {C}\mathbf {S}\) (the sequential composition restricted to the second set of labels of \(\mathbf {C}\) with system \(\mathbf {S}\)) is again a system.
As for example also done in [10] and [24], it is then possible to formalize an (associative) algebra of systems. Let \(\mathbf {D}\) be a distinguisher, \(\mathbf {C}\) a converter, and \(\mathbf {S}\) a (regular) system. Then the experiment where \(\mathbf {D}\mathbf {C}\) interacts with \(\mathbf {S}\) is the same experiment where \(\mathbf {D}\) interacts with \(\mathbf {C}\mathbf {S}\), and we just denote this by \(\mathbf {D}\mathbf {C}\mathbf {S}\) (again with the understanding that this expression also represents the final binary output of \(\mathbf {D}\)). Syntactically, this could be expressed as \((\mathbf {D}\mathbf {C})\mathbf {S}=\mathbf {D}(\mathbf {C}\mathbf {S})=\mathbf {D}\mathbf {C}\mathbf {S}\).
We next define another way to compose systems, parallel composition: given two (or more) systems \(\mathbf {S}\) and \(\mathbf {T}\), a new system \(\mathbf {V}\) is the (independent) parallel composition of \(\mathbf {S}\) and \(\mathbf {T}\), denoted \(\mathbf {V}=[\mathbf {S},\mathbf {T}]\), if a system \(\mathbf {D}\) interacting with \(\mathbf {V}\) can (independently) access system \(\mathbf {S}\) and system \(\mathbf {T}\). We remark that \(\mathbf {V}\) is merely a “wrapper” for two independent instances of systems \(\mathbf {S}\) and \(\mathbf {T}\). On the other hand, it is often also the case that two systems composed in parallel need some correlation, that is, need to lose their independence (usually trough a shared random variable or, more in general, some shared state); two such systems \(\mathbf {S}\) and \(\mathbf {T}\) might be used to create what is called a correlated parallel composition, which we formalize as a new system \(\mathbf {V}\) such that \(\mathbf {V}=\mathbf {C}[\mathbf {S},\mathbf {T}]\), for some system \(\mathbf {C}\) accessing the independent systems \(\mathbf {S}\) and \(\mathbf {T}\), and emulating two (correlated) systems towards a system \(\mathbf {D}\) interacting with \(\mathbf {V}\). We introduce the notation \(\mathbf {V}=\langle \mathbf {S},\mathbf {T}\rangle \), which makes the correlating system \(\mathbf {C}\) implicit in the following sense: a system \(\mathbf {D}\) interacting with \(\mathbf {V}\) can access the system \(\mathbf {S}\) and system \(\mathbf {T}\), but only through \(\mathbf {C}\), and \(\mathbf {S}\) and \(\mathbf {T}\) become “labels” for the correlated systems emulated by \(\mathbf {C}\). Figure 1 illustrates the two different concepts. Note that we can naturally extend both definitions to the case of n systems.
Definition 1
(Systems Parallel Composition). Given the sequence of systems \(\mathbf {S}_1,\ldots ,\mathbf {S}_n\), for \(n\in \mathbb {N}\), define:
-
Their (independent) parallel composition, denoted \([\mathbf {S}_1,\ldots ,\mathbf {S}_n]\), as the system that exports n interfaces labeled \(\mathbf {S}_1,\ldots ,\mathbf {S}_n\), where label \(\mathbf {S}_i\) is directly connected to system \(\mathbf {S}_i\), for \(i\in [n]\).
-
Their correlated parallel composition, denoted \(\langle \mathbf {S}_1,\ldots ,\mathbf {S}_n\rangle \), as the system \(\mathbf {C}[\mathbf {S}_1,\ldots ,\mathbf {S}_n]\), where \(\mathbf {C}\) is some (implicit) system which exports n interfaces labeled \(\mathbf {S}_1,\ldots ,\mathbf {S}_n\).Footnote 1
2.3 Indistinguishability of Cryptographic Systems
In cryptography, we are usually interested in how similarly two systems \(\mathbf {S}\) and \(\mathbf {T}\) (with matching interfaces) behave. Intuitively, the more indistinguishable their behavior is, the closer \(\mathbf {S}\) and \(\mathbf {T}\) are. We can measure such closeness by means of the indistinguishability between systems \(\mathbf {S}\) and \(\mathbf {T}\) from the perspective of a distinguisher \(\mathbf {D}\) which interacts with either of them, and outputs the bit denoted by \(\mathbf {D}\mathbf {V}\), for \(\mathbf {V}\in \{\mathbf {S},\mathbf {T}\}\), indicating its guess as to which system it is interacting with, where the understanding is that 0 indicates \(\mathbf {S}\) and 1 indicates \(\mathbf {T}\).
Definition 2
For distinguisher \(\mathbf {D}\) and systems \(\mathbf {S}\) and \(\mathbf {T}\), \(\mathbf {D}\)’s advantage in distinguishing between \(\mathbf {S}\) and \(\mathbf {T}\) is
Moreover, in cryptography security statements are often conditional, as is the case for the present work. This means that, given two systems \(\mathbf {S}\) and \(\mathbf {T}\), we do not give a concrete value for the distinguishing advantage depending on a distinguisher \(\mathbf {D}\), but rather relate this quantity to the distinguishing advantage of another distinguisher \(\mathbf {D}'\) for two different systems \(\mathbf {S}'\) and \(\mathbf {T}'\). Such a relation should entail that if \(\mathbf {S}'\) and \(\mathbf {T}'\) are close (which usually can be either in turn related to the distinction between two further systems, or just crystallized as an hardness assumption), then so are \(\mathbf {S}\) and \(\mathbf {T}\). Such a relation can be carried out by using the same distinguisher for the two different distinction problems, but more in general usually requires a reduction system \(\mathbf {C}\) which translates \(\mathbf {S}'\) and \(\mathbf {T}'\) into two systems \(\mathbf {C}\mathbf {S}'\) and \(\mathbf {C}\mathbf {T}'\) that, towards \(\mathbf {D}\), behave similarly to \(\mathbf {S}\) and \(\mathbf {T}\), respectively. Turned around, this also means that \(\mathbf {C}\) translates the distinguisher \(\mathbf {D}\) for \(\mathbf {S}\) and \(\mathbf {T}\) into the (similarly good) distinguisher \(\mathbf {D}'=\mathbf {D}\mathbf {C}\) for \(\mathbf {S}'\) and \(\mathbf {T}'\).Footnote 2 Therefore, if we assume that no (efficient) distinguisher can have a good advantage in distinguishing \(\mathbf {S}'\) and \(\mathbf {T}'\), then so does \(\mathbf {D}'\), and in turn also \(\mathbf {D}\) in distinguishing \(\mathbf {S}\) and \(\mathbf {T}\). By Definition 2 and associativity of sequential systems composition this in particular implies \(\Delta ^\mathbf {D}(\mathbf {S},\mathbf {T})=\Delta ^\mathbf {D}(\mathbf {C}\mathbf {S}',\mathbf {C}\mathbf {T}')=\Delta ^{\mathbf {D}\mathbf {C}}(\mathbf {S}',\mathbf {T}')=\Delta ^{\mathbf {D}'}(\mathbf {S}',\mathbf {T}')\).
2.4 Probabilistic (Authenticated) Encryption (pE/pAE)
Syntactically, probabilistic encryption (pE) and probabilistic authenticated encryption (pAE) are the same object, which we generally call an encryption scheme. The distinction is merely on the level of security: if an encryption scheme provides confidentiality (or is
 ), we consider it secure pE, whereas if it provides both confidentiality and authenticity (or is
), we consider it secure pE, whereas if it provides both confidentiality and authenticity (or is
 ), we consider it secure pAE.
), we consider it secure pAE.
Definition 3
(Encryption Scheme). A (probabilistic) encryption scheme \(\Pi \doteq (\mathtt {Gen},\mathtt {Enc},\mathtt {Dec})\) over key-space \(\mathcal K\), message-space \(\mathcal M\), and ciphertext-space \(\mathcal C\) (with \(\bot \notin \mathcal K\cup \mathcal M\cup \mathcal C\)), is such that
-
\(\mathtt {Gen}\) is an (efficiently samplable) distribution over \(\mathcal K\);
-
\(\mathtt {Enc}:\mathcal K\times \mathcal M\rightarrow \mathcal C\) is a (efficiently computable) probabilistic function;
-
\(\mathtt {Dec}:\mathcal K\times \mathcal C\rightarrow \mathcal M\cup \{\bot \}\) is an (efficiently computable) deterministic function.
As customary, for \(k\in \mathcal K\) we use the short-hand notation \(\mathtt {Enc}_k(\cdot )\) for \(\mathtt {Enc}(k,\cdot )\) and \(\mathtt {Dec}_k(\cdot )\) for \(\mathtt {Dec}(k,\cdot )\), and we also assume that \(\mathcal M\subseteq \{0,1\}^*\) and for any \(m\in \mathcal M\), \(\{0,1\}^{\left| m\right| }\subseteq \mathcal M\), whereas \(\mathcal C=\{0,1\}^*\), but for any \(m\in \mathcal M\) and \(k\in \mathcal K\), \(\left| \mathtt {Enc}_k(m)\right| =\left| m\right| +\tau \) for some fixed expansion factor \(\tau \in \mathbb {N}\). Moreover, we assume correctness of \(\Pi \), that is, for all keys k distributed according to \(\mathtt {Gen}\), and all ciphertexts \(c\in \mathcal C\), \(\mathtt {Dec}_k(c)=m\) if \(c\in \mathrm {supp}\,(\mathtt {Enc}_k(m))\) and \(\mathtt {Dec}_k(c)=\bot \) otherwise.
In order to define the security (and later also anonymity) of a fixed scheme \(\Pi \), we define the following single and double interface systems (where the dependency on \(\Pi \) is implicit), parameterized by a fixed key \(k\in \mathcal K\):
-
\(\mathbf {E}_k\): On input a message \(m\in \mathcal M\), return \(\mathtt {Enc}_k(m)\in \mathcal C\).
-
\(\mathbf {E}_k^\$\): On input a message \(m\in \mathcal M\), return \(\mathtt {Enc}_k(\tilde{m})\in \mathcal C\) for freshly and uniformly sampled \(\tilde{m}\in \mathcal M\) with \(\left| \tilde{m}\right| =\left| m\right| \).
-
\(\langle \mathbf {E}_k,\mathbf {D}_k\rangle \):
-
On input a message \(m\in \mathcal M\), return \(\mathtt {Enc}_k(m)\in \mathcal C\).
-
On input a ciphertext \(c\in \mathcal C\), return \(\mathtt {Dec}_k(c)\in \mathcal M\cup \{\bot \}\).
-
-
\(\langle \mathbf {E}_k,\mathbf {D}^\bot \rangle \): Initially set \(\mathcal Q\subseteq \mathcal M\times \mathcal C\) to \(\varnothing \) and then:
-
On input a message \(m\in \mathcal M\), return \(c\doteq \mathtt {Enc}_k(m)\in \mathcal C\) and set \(\mathcal Q\) to \(\mathcal Q\cup \{(m,c)\}\).
-
On input a ciphertext \(c\in \mathcal C\), if there is an \(m\in \mathcal M\) such that \((m,c)\in \mathcal Q\), then return m, otherwise return \(\bot \).
-
-
\(\langle \mathbf {E}_k^\$,\mathbf {D}^\bot \rangle \): Initially set \(\mathcal Q\subseteq \mathcal M\times \mathcal C\) to \(\varnothing \) and then:
-
On input a message \(m\in \mathcal M\), return \(c\doteq \mathtt {Enc}_k(\tilde{m})\in \mathcal C\) for freshly and uniformly sampled \(\tilde{m}\in \mathcal M\) with \(\left| \tilde{m}\right| =\left| m\right| \), and set \(\mathcal Q\) to \(\mathcal Q\cup \{(m,c)\}\).
-
On input a ciphertext \(c\in \mathcal C\), if there is an \(m\in \mathcal M\) such that \((m,c)\in \mathcal Q\), then return m, otherwise return \(\bot \).
-
In our definitions, the key k will always be replaced by a random variable (usually denoted K or \(K_i\), for some \(i\in \mathbb {N}\)) distributed according to \(\Pi \)’s \(\mathtt {Gen}\).
We remark that in our security definitions below we will slightly abuse notation and informally refer to efficient distinguishers and negligible advantages; both concepts should be properly defined asymptotically, which we do not explicitly do, since we do not define any security parameter. Nevertheless, correct asymptotic security statements may be easily recovered by considering sequences of our security statements, and taking the limit. Still, when relating such definitions, we will not (need to) use such asymptotic concepts, since we will employ a concrete approach, as done for example by Bellare, Desai, Jokipii, and Rogaway [6].
2.5 Game-Based Security of pE/pAE
Following
[6], we first define the game-based security of pE in the real-or-random fashion, where the adversary must distinguish between a true encryption oracle and one which ignores inputs and encrypts random messages of the same length instead. For this reason we interchangeably talk about adversary and distinguisher. The following definition captures well-known
 security notions commonly found in the literature.
security notions commonly found in the literature.
Definition 4
(Game-Based Security of pE). An encryption scheme \(\Pi \) is secure pE (or
 ) if
) if
is negligible for any efficient distinguisher \(\mathbf {D}\).
For pAE we closely follow the all-in-one security definition style originally introduced by Shrimpton in
[25] and dubbed
 , where an adversary must distinguish between two sets of oracles: the first set consists of true encryption and decryption oracles, whereas the second set consists of a fake encryption oracle which ignores inputs and encrypts random messages of the same length instead, and a fake decryption oracle which always return \(\bot \), except if the provided ciphertext was previously output upon (fake) encryption, in which case the original message is returned. Note that this is actually a slightly different version than Shrimpton’s original definition, and was put forth in
[2] by Alagic, Gagliardoni, and Majenz, where the equivalence with the former is shown.
, where an adversary must distinguish between two sets of oracles: the first set consists of true encryption and decryption oracles, whereas the second set consists of a fake encryption oracle which ignores inputs and encrypts random messages of the same length instead, and a fake decryption oracle which always return \(\bot \), except if the provided ciphertext was previously output upon (fake) encryption, in which case the original message is returned. Note that this is actually a slightly different version than Shrimpton’s original definition, and was put forth in
[2] by Alagic, Gagliardoni, and Majenz, where the equivalence with the former is shown.
Definition 5
(Game-Based Security of pAE). An encryption scheme \(\Pi \) is secure pAE (or
 ) if
) if
is negligible for any efficient distinguisher \(\mathbf {D}\).
3 Game-Based Anonymous Security of pE/pAE
We define game-based anonymity of pE and pAE in terms of what in the literature is usually termed key-indistinguishability. For this, recall from our discussion above (see Fig. 1) that the system \([\mathbf {S}_{K_1},\ldots ,\mathbf {S}_{K_n}]\) provides the distinguisher with n interfaces to n distinct and independent copies of system \(\mathbf {S}_k\), each of which is parameterized by a different, freshly and independently sampled key \(K_i\). On the other hand, the system \(\langle \mathbf {S}_K,\ldots ,\mathbf {S}_K\rangle \) provides the distinguisher with n interfaces to essentially the same copy of system \(\mathbf {S}_k\), each of which is parameterized by the same key K (previously freshly sampled).
While here we only provide definitions, in the full version [5] we also show the relevant relations among them. We begin by providing a game-based security definition capturing exclusively the notion of anonymity (in terms of key-indistinguishability) of pE and pAE. In the following, when dropping the term [n-] we mean “for any integer \(n\ge 2\)”.
Definition 6
(Game-Based Anonymity of pE). An encryption scheme \(\Pi \) is [n-]anonymous pE (or [n-]
 ) if
) if
is negligible for any efficient distinguisher \(\mathbf {D}\).
Definition 7
Game-Based Anonymity of pAE). An encryption scheme \(\Pi \) is [n-]anonymous pAE (or [n-]
 ) if
) if
is negligible for any efficient distinguisher \(\mathbf {D}\).
Next, we define the coupling of the traditional security goal of pE/pAE with anonymity. For both notions, we use the term anonymous security; specifically, by anonymous and secure pE we mean key-indistinguishable and confidential encryption, whereas by anonymous and secure pAE we mean key-indistinguishable, confidential, and authenticated encryption.
Definition 8
(Game-Based Anonymous Security of pE). An encryption scheme \(\Pi \) is [n-]anonymous secure pE (or [n-]
 ) if
) if
is negligible for any efficient distinguisher \(\mathbf {D}\).
Definition 9
(Game-Based Anonymous Security of pAE). An encryption scheme \(\Pi \) is [n-]anonymous secure pAE (or [n-]
 ) if
) if
is negligible for any efficient distinguisher \(\mathbf {D}\).
Remark
The concept of key-indistinguishability has been first introduced under the name of “key-hiding private-key encryption” by Fischlin in
[13] as 2-
 according to Definition 6. Subsequently, in
[12], Desai also studied the problem introducing the concept of “non-separability of keys”, but specifically for encryption schemes based on block ciphers. Later, in
[1], Abadi and Rogaway presented a security notion called “which-key concealing”, that is basically identical to Fischlin’s, but they defined security as a combination of key-indistinguishability and ciphertext-indistinguishability, that is, as 2-
according to Definition 6. Subsequently, in
[12], Desai also studied the problem introducing the concept of “non-separability of keys”, but specifically for encryption schemes based on block ciphers. Later, in
[1], Abadi and Rogaway presented a security notion called “which-key concealing”, that is basically identical to Fischlin’s, but they defined security as a combination of key-indistinguishability and ciphertext-indistinguishability, that is, as 2-
 according to Definition 8. They also claimed that popular modes of operation for symmetric encryption yield key-private encryption schemes. We will prove this formally in Sect. 3.1. Interestingly, the concept of key-indistinguishability was successfully translated to the public-key setting by Bellare, Boldyreva, Desai, and Pointcheval in
[7], where the terms key-privacy and indistinguishability of keys were originally suggested.
according to Definition 8. They also claimed that popular modes of operation for symmetric encryption yield key-private encryption schemes. We will prove this formally in Sect. 3.1. Interestingly, the concept of key-indistinguishability was successfully translated to the public-key setting by Bellare, Boldyreva, Desai, and Pointcheval in
[7], where the terms key-privacy and indistinguishability of keys were originally suggested.
As previously mentioned, regarding key-indistinguishability of AE, in a very recent work Chan and Rogaway [11] introduce the nonce-based counterpart of our notion for pAE, Definition 9, which is crucially not directly applicable to nAE, but rather to anAE, a syntactically different scheme which can be obtained from nAE through the transformation NonceWrap that they introduce.
3.1 Computationally Uniform Ciphertexts Imply Anonymity
In this section we revisit a stronger security notion for symmetric encryption, which we call indistinguishability from uniform ciphertexts, strong security, or
 , and show a simple folklore result that was stated in
[1] (of which, to the best of our knowledge, there is no formal proof yet). This definition intuitively should capture indistinguishability of ciphertexts, but it actually overshoots this goal, and it is stronger in the sense that it also implies indistinguishability of keys. Recall that
, and show a simple folklore result that was stated in
[1] (of which, to the best of our knowledge, there is no formal proof yet). This definition intuitively should capture indistinguishability of ciphertexts, but it actually overshoots this goal, and it is stronger in the sense that it also implies indistinguishability of keys. Recall that
 does not imply indistinguishability of keys, but it turns out to be easier to prove that schemes meet the stronger notion, which is also conceptually simpler. Essentially, instead of choosing a random message to be encrypted in the ideal world, a random ciphertext is output (thus neglecting encryption altogether).
does not imply indistinguishability of keys, but it turns out to be easier to prove that schemes meet the stronger notion, which is also conceptually simpler. Essentially, instead of choosing a random message to be encrypted in the ideal world, a random ciphertext is output (thus neglecting encryption altogether).
In order to formalize this notion, we need to introduce the system \(\mathbf \$ \) (with implicit dependency on a fixed encryption scheme \(\Pi \)) which on input any message \(m\in \mathcal M\) simply outputs a uniformly sampled ciphertext of appropriate length, that is, according to our Definition 3, a uniform random bitstring of length \(\left| m\right| +\tau \), where \(\tau \in \mathbb {N}\) is the expansion factor defined by \(\Pi \) (thus, in particular, \(\mathbf \$ \) does not make use of the underlying encryption function defined by \(\Pi \)). Then for the case of pE we can increase the security requirement as follows.
Definition 10
(Game-Based Strong Security of pE). An encryption scheme \(\Pi \) is strongly secure pE (or
 ) if
) if
is negligible for any efficient distinguisher \(\mathbf {D}\).
The analogous notion for pAE was introduced by Rogaway and Shrimpton in [23], and is adapted within our framework as follows.
Definition 11
(Game-Based Strong Security of pAE). An encryption scheme \(\Pi \) is secure pE (or
 ) if
) if
is negligible for any efficient distinguisher \(\mathbf {D}\).
Next, starting with the case of pE, we show that the stronger notion of
 indeed implies
indeed implies
 (and thus also both
(and thus also both
 and
and
 ), as originally pointed out in
[1]. This is captured formally by the following statement, shown for 2 users for cleaner presentation, but easily generalized to n users.
), as originally pointed out in
[1]. This is captured formally by the following statement, shown for 2 users for cleaner presentation, but easily generalized to n users.
Theorem 1
For every distinguisher \(\mathbf {D}\), there exists a reduction \(\mathbf {C}\) such that
In particular, this implies that if an encryption scheme is
 , then it is also
, then it is also

Finally, the analogous statement for the case of pAE just follows as a natural lifting of Theorem 1, but since we consider this result rather important, instead of only providing a corollary we actually state it as a theorem, that is, we show that the stronger notion of
 indeed implies
indeed implies
 (and thus also both
(and thus also both
 and
and
 ). We remark that this fact was informally pointed out by Rogaway
[22].
). We remark that this fact was informally pointed out by Rogaway
[22].
Theorem 2
For every distinguisher \(\mathbf {D}\), there exists a reduction \(\mathbf {C}\) such that
In particular, this implies that if an encryption scheme is
 , then it is also
, then it is also
 .
.
3.2 Anonymity Preservation of Encrypt-then-MAC
After having related the various game-based notions for pE and for pAE separately, we finally show how the anonymity enhanced security definitions for pE relate with those of pAE. For this, we need to introduce the concept of message authentication code (MAC) and its security and anonymity notions, which we only introduce in an intuitive and informal way here (see the full version
[5] for more details). Recall that Bellare and Namprempre
[8] and Krawczyk
[15] have shown that the combination of an unforgeable (
 ) MAC and a secure (
) MAC and a secure (
 ) encryption scheme, performed according to the Encrypt-then-MAC (EtM) paradigm, yields an encryption scheme which is both secure (
) encryption scheme, performed according to the Encrypt-then-MAC (EtM) paradigm, yields an encryption scheme which is both secure (
 ) and unforgeable (
) and unforgeable (
 , the equivalent notion of
, the equivalent notion of
 for encryption). Later, Shrimpton
[25] showed that a nice all-in-one security definition for secure authenticated encryption,
for encryption). Later, Shrimpton
[25] showed that a nice all-in-one security definition for secure authenticated encryption,
 , is equivalent to the combination
, is equivalent to the combination
 and
and
 , thus attesting that EtM performed on a
, thus attesting that EtM performed on a
 MAC scheme and an
MAC scheme and an
 encryption scheme, yields a
encryption scheme, yields a
 authenticated encryption scheme. The encryption scheme \(\mathtt {EtM}(\Pi ,\Sigma )\doteq (\widehat{\mathtt {Gen}},\widehat{\mathtt {Tag}},\widehat{\mathtt {Vrf}})\), resulting from this specific composition of an encryption scheme \(\Pi \doteq (\mathtt {Gen}_\Pi ,\mathtt {Enc},\mathtt {Dec})\) (with key-space \(\mathcal K_\Pi \)) and a MAC scheme \(\Sigma \doteq (\mathtt {Gen}_\Sigma ,\mathtt {Tag},\mathtt {Vrf})\) (with key-space \(\mathcal K_\Sigma \), \(\mathtt {Tag}:\mathcal K\times \mathcal C\rightarrow \mathcal C\times \mathcal T\), and \(\mathtt {Vrf}:\mathcal K\times \mathcal C\times \mathcal T\rightarrow \mathcal C\cup \{\bot \}\)) is defined as follows:
authenticated encryption scheme. The encryption scheme \(\mathtt {EtM}(\Pi ,\Sigma )\doteq (\widehat{\mathtt {Gen}},\widehat{\mathtt {Tag}},\widehat{\mathtt {Vrf}})\), resulting from this specific composition of an encryption scheme \(\Pi \doteq (\mathtt {Gen}_\Pi ,\mathtt {Enc},\mathtt {Dec})\) (with key-space \(\mathcal K_\Pi \)) and a MAC scheme \(\Sigma \doteq (\mathtt {Gen}_\Sigma ,\mathtt {Tag},\mathtt {Vrf})\) (with key-space \(\mathcal K_\Sigma \), \(\mathtt {Tag}:\mathcal K\times \mathcal C\rightarrow \mathcal C\times \mathcal T\), and \(\mathtt {Vrf}:\mathcal K\times \mathcal C\times \mathcal T\rightarrow \mathcal C\cup \{\bot \}\)) is defined as follows:
-
\(\widehat{\mathtt {Gen}}\) is the product distribution of \(\mathtt {Gen}_\Pi \) and \(\mathtt {Gen}_\Sigma \) over \(\mathcal K_\Pi \times \mathcal K_\Sigma \);
-
\(\widehat{\mathtt {Enc}}_{({k_{\text{ e }}},{k_{\text{ a }}})}\doteq \mathtt {Tag}_{k_{\text{ a }}}\circ \mathtt {Enc}_{k_{\text{ e }}}\);
-
\(\widehat{\mathtt {Vrf}}_{({k_{\text{ e }}},{k_{\text{ a }}})}\doteq \mathtt {Dec}_{k_{\text{ e }}}\circ \mathtt {Vrf}_{k_{\text{ a }}}\).
If we now want to define security of the composed scheme \(\widehat{\Pi }\doteq \mathtt {EtM}(\Pi ,\Sigma )\), we need to introduce a simple operator between (single-interface) systems, namely cascading: Informally, given systems \(\mathbf {S}\) and \(\mathbf {T}\), we define the new system \(\mathbf {S}{\vartriangleright }\mathbf {T}\) as the system that on input x computes \(y\doteq \mathbf {S}(x)\), and returns \(z\doteq \mathbf {T}(y)\) (where we are assuming matching domains). As we did for \(\Pi \), we can define systems \(\mathbf {T}_k\), \(\mathbf {V}_k\), \(\langle \mathbf {T}_k,\mathbf {V}_k\rangle \) and \(\langle \mathbf {T}_k,\mathbf {V}^\bot \rangle \) relative to \(\Sigma \). Then \(\widehat{\mathtt {Enc}}_{({k_{\text{ e }}},{k_{\text{ a }}})}\) is modeled by \(\widehat{\mathbf {E}}_{({k_{\text{ e }}},{k_{\text{ a }}})}\doteq \mathbf {E}_{k_{\text{ e }}}{\vartriangleright }\mathbf {T}_{k_{\text{ a }}}\), and \(\widehat{\mathtt {Dec}}_{({k_{\text{ e }}},{k_{\text{ a }}})}\) by \(\widehat{\mathbf {D}}_{({k_{\text{ e }}},{k_{\text{ a }}})}\doteq \mathbf {V}_{k_{\text{ a }}}{\vartriangleright }\mathbf {D}_{k_{\text{ e }}}\).
We can now show that EtM is anonymity-preserving, in the sense that if an encryption scheme \(\Pi \) is both
 and
and
 (that is,
(that is,
 ) and a MAC scheme \(\Sigma \) is both
) and a MAC scheme \(\Sigma \) is both
 and
and
 (the analogous anonymity property of pMAC introduced in
[3], which combined with that
(the analogous anonymity property of pMAC introduced in
[3], which combined with that
 results in
results in
 , as we show in the full version
[5]), then \(\mathtt {EtM}(\Pi ,\Sigma )\) not only is
, as we show in the full version
[5]), then \(\mathtt {EtM}(\Pi ,\Sigma )\) not only is
 , but also
, but also
 (that is,
(that is,
 ). This is captured formally by the following statement, shown for 2 users for cleaner presentation, but easily generalized to n users.
). This is captured formally by the following statement, shown for 2 users for cleaner presentation, but easily generalized to n users.
Theorem 3
For every distinguisher \(\mathbf {D}\), there exist reductions \(\mathbf {C}\) and \(\mathbf {C}'\) such that
In particular, this implies that if \(\Pi \) is
 and \(\Sigma \) is
and \(\Sigma \) is
 ,Footnote 3 then \(\mathtt {EtM}(\Pi ,\Sigma )\) is
,Footnote 3 then \(\mathtt {EtM}(\Pi ,\Sigma )\) is
 .
.
4 Composable Security of Anonymous Communication
In this section we turn our attention to composable security, as opposed to game-based security. For this, we make use of the constructive cryptography (CC) framework by Maurer [17], which is a specialization of the abstract cryptography theory by Maurer and Renner [19].
4.1 Constructive Cryptography
In essence, CC allows to define security of cryptographic protocols as statements about constructions of resources from other resources, which we model as cryptographic systems from Sect. 2.2. For such systems, we might at times use suggestive words typed in sans-serif rather than bold-faced letters. The various interfaces of a resource should be thought of as being assigned to parties. In this work, all resources are parameterized by an integer \(n\ge 2\) (the case \(n=1\) would be pointless for anonymity), and each defines \(n+2\) interfaces: n for the senders, denoted \(S_i\), for \(i\in [n]\), one for the adversary, denoted \(E\), and one for the receiver, denoted \(R\). Therefore, in the following we use the expression n-resource to make explicit such parameter. Another crucial ingredient of CC are converters, also formally modeled as systems (labeled by lower-case sans-serif suggestive words), which when applied to interfaces of n-resources, give raise to a new n-resource. Within our formalization of cryptographic systems, CC converters thus correspond to converters of systems as defined in Sect. 2.2, but where we extend the sequential composition notion by allowing a (single-interface) converter system to be attached to just one of the interfaces of another n-resource system. Given a converter \(\mathsf {cnv}\) and an n-resource \({\mathbf {R}}\), for \(i\in [n]\) we denote the new n-resource system resulting from attaching converter \(\mathsf {cnv}\) to interface \(S_i\) of n-resource \({\mathbf {R}}\) as \(\mathsf {cnv}^{S_i}\,{\mathbf {R}}\). Note that this automatically implies commutativity of converters attached to different interfaces, that is, considering a second converter \(\widehat{\mathsf {cnv}}\) and letting \(j\in [n]\) such that \(j\ne i\), then \(\mathsf {cnv}^{S_i}\,\widehat{\mathsf {cnv}{}}^{S_j}\,{\mathbf {R}}\equiv \widehat{\mathsf {cnv}{}}^{S_j}\,\mathsf {cnv}^{S_i}\,{\mathbf {R}}\).
To make security statements within CC, we model protocols as lists of converters. For n-resources, this means that a protocol \(\pi \) executed by n senders and one receiver (an n-protocol) is a list of \(n+1\) converters \((\mathsf {cnv}_1,\ldots ,\mathsf {cnv}_{n+1})\), where the adopted convention is that \(\mathsf {cnv}_i\) is attached to sender interface \(S_i\), for \(i\in [n]\), while \(\mathsf {cnv}_{n+1}\) is attached to the receiver interface \(R\). In the following, we use the short-hand notation \(\pi {\mathbf {R}}\) for the n-resource \(\mathsf {cnv}_1^{S_1}\cdots \,\mathsf {cnv}_n^{S_n}\,\mathsf {cnv}_{n+1}^R\,{\mathbf {R}}\). Moreover, for a second n-protocol \(\hat{\pi }\doteq (\widehat{\mathsf {cnv}}_1,\ldots ,\widehat{\mathsf {cnv}}_{n+1})\), we define the composition of \(\hat{\pi }\) and \(\pi \) as \(\hat{\pi }\pi \doteq (\widehat{\mathsf {cnv}}_1\mathsf {cnv}_1,\ldots ,\widehat{\mathsf {cnv}}_{n+1}\mathsf {cnv}_{n+1})\), and therefore \(\hat{\pi }\pi {\mathbf {R}}\) is the n-resource \((\widehat{\mathsf {cnv}}_1\mathsf {cnv}_1)^{S_1}\cdots \,(\widehat{\mathsf {cnv}}_n\mathsf {cnv}_n)^{S_n}\,(\widehat{\mathsf {cnv}}_{n+1}\mathsf {cnv}_{n+1})^R\,{\mathbf {R}}\). The last ingredient we need is that of a simulator, which can be simply understood as a converter to be attached to the adversarial interface \(E\). With this, we can now express composable security of an n-protocol \(\pi \) in terms of indistinguishability as follows.
Definition 12
(Construction). For n-resources \({\mathbf {R}}\) and \(\mathbf {S}\), and function \(\varepsilon \) mapping distinguishers to real values, we say that an n-protocol \(\pi \) constructs \(\mathbf {S}\) from \({\mathbf {R}}\) within \(\varepsilon \), denoted \({\mathbf {R}}\xrightarrow {\pi ,\varepsilon }\mathbf {S},\) if there exists a simulator \(\mathsf {sim}\) such that for all distinguishers \(\mathbf {D}\), \(\Delta ^\mathbf {D}(\pi {\mathbf {R}},\mathsf {sim}^E\,\mathbf {S})\le \varepsilon (\mathbf {D}).\)
The intuition is that, if lifted to the asymptotic setting, Definition 12 implies that if \(\varepsilon (\mathbf {D})\) is negligible for every efficient distinguisher \(\mathbf {D}\), then the real n-resource \({\mathbf {R}}\) looks indistinguishable from the ideal n-resource \(\mathbf {S}\). This naturally hints to the intuition that in any context where \(\mathbf {S}\) is needed, \(\pi {\mathbf {R}}\) can be safely used instead. This is the central point of composable security definitions, and is formalized by the following theorem, following directly from [19].
Theorem 4
(Composition). Let \({\mathbf {R}},\mathbf {S},\mathbf {T}\) be n-resources, and \(\pi _1,\pi _2\) n-protocols. If \({\mathbf {R}}\xrightarrow {\pi _1,\varepsilon _1}\mathbf {S}\) and \(\mathbf {S}\xrightarrow {\pi _2,\varepsilon _2}\mathbf {T}\), then \({\mathbf {R}}\xrightarrow {\pi _2\pi _1,\hat{\varepsilon }_1\oplus \hat{\varepsilon }_2}\mathbf {T}\), where \(\hat{\varepsilon }_1(\mathbf {D})\doteq \varepsilon _1(\mathbf {D}\pi _2)\), \(\hat{\varepsilon }_2(\mathbf {D})\doteq \varepsilon _2(\mathbf {D}\,\mathsf {sim}_2^E)\), \(\mathsf {sim}_2\) is any simulator whose existence justifies \(\mathbf {S}\xrightarrow {\pi _2,\varepsilon _2}\mathbf {T}\), and \((\hat{\varepsilon }_1\oplus \hat{\varepsilon }_2)(\mathbf {D})\doteq \hat{\varepsilon }_1(\mathbf {D})+\hat{\varepsilon }_2(\mathbf {D})\).
Anonymous Channels. There are four n-resources that we consider in this work. The first, \(\mathsf {KEY}_\mathcal K^n\), models the initial symmetric-key setup: it generates n independent keys \(K_1,\ldots ,K_n\in \mathcal K\) according to an implicitly defined distribution \(\mathtt {Gen}\) over \(\mathcal K\), and for \(i\in [n]\) it outputs \(K_i\) at interface \(S_i\); at interface \(R\) it outputs the list \((K_1,\ldots ,K_n)\) of all generated keys, while it outputs nothing at interface \(E\). The remaining three n-resources model the anonymous channels for n senders and one receiver mentioned above (for messages over some set \(\mathcal {X}\)), where we assume a central adversary that is in full control of the physical communication between the senders and the receiver, that is, an adversary that can delete, repeat, and reorder messages.Footnote 4 \(\mathsf {A\text {-}\mathsf{INS}}_\mathcal {X}^n\) models the channel which leaks every message input by any sender (but not their identities) directly to the adversary. Note that in particular this means that the receiver does not directly receive the messages sent by the senders. Moreover, \(\mathsf {A\text {-}\mathsf{INS}}_\mathcal {X}^n\) allows the adversary to inject any message to the receiver (thus, in particular, also the ones originally sent by the senders). Note that this channel, while providing anonymity, is per se pretty useless, since the receiver has also no information about the identity of the sender of any message. Instead, \(\mathsf {A\text {-}\mathsf{AUT}}_\mathcal {X}^n\), while still leaking all the messages sent by the senders directly to the adversary, does not allow the latter to inject any message; instead, the adversary can now select messages that it wants to be forwarded to the receiver. Moreover, the forwarded messages also carry the identity of the original sender, still hidden to the adversary. Finally, \(\mathsf {A\text {-}\mathsf{SEC}}_\mathcal {X}^n\) essentially works as \(\mathsf {A\text {-}\mathsf{AUT}}_\mathcal {X}^n\), except that now only the lengths of the messages sent by the senders are leaked directly to the adversary. We sketch the three anonymous channels in Fig. 2 and provide a formal description of the behavior of the systems implementing such n-resources in Fig. 3.
4.2 Composable Anonymous Security of pE
In this section we first introduce a composable definition of anonymous security for pE, and then we show that the previously introduced game-based notion of
 implies the former. The composable definition can be interpreted as providing composable semantics to
implies the former. The composable definition can be interpreted as providing composable semantics to
 for pE, in the sense that the result we show here attests that if an encryption scheme is
for pE, in the sense that the result we show here attests that if an encryption scheme is
 , then it can be safely used to construct a secure channel from an authenticated one, while preserving anonymity.
, then it can be safely used to construct a secure channel from an authenticated one, while preserving anonymity.
In the following, for a fixed encryption scheme \(\Pi \) let the converter \(\mathsf {enc}\) behave as follows when connected to interface \(S_i\) of \(\mathsf {KEY}_\mathcal K\) and interface \(S_i\) of \(\mathsf {A\text {-}\mathsf{AUT}}_\mathcal C\), for \(i\in [n]\): on input a message \(m\in \mathcal M\) from the outside, if not already done so before, output \(\diamond \) to \(\mathsf {KEY}_\mathcal K\) in order to fetch key \(K_i\), then compute \(c\leftarrow \mathtt {Enc}_{K_i}(m)\in \mathcal C\) and output c to \(\mathsf {A\text {-}\mathsf{AUT}}_\mathcal C\). Also let the converter \(\mathsf {dec}\) (where again the dependency on \(\Pi \) is implicit) behave as follows when connected to interface \(R\) of \(\mathsf {KEY}_\mathcal K\) and interface \(R\) of \(\mathsf {A\text {-}\mathsf{AUT}}_\mathcal C\): on input \(\diamond \) from the outside, if not already done so before, output \(\diamond \) to \(\mathsf {KEY}_\mathcal K\) in order to fetch keys \(K_1,\ldots ,K_n\), and then output \(\diamond \) to \(\mathsf {A\text {-}\mathsf{AUT}}_\mathcal C\); for each obtained tuple (j, c, i), compute \(m\leftarrow \mathtt {Dec}_{K_i}(c)\), and output the collection of all such resulting tuples (j, m, i) to the outside. Finally, we define the n-protocol \(\pi _\mathsf {enc}\doteq (\mathsf {enc},\ldots ,\mathsf {enc},\mathsf {dec})\).
Definition 13
(Composable Anonymous Security of pE). An encryption scheme \(\Pi \) achieves composable anonymous confidentiality if
that is, if there exists a simulator \(\mathsf {sim}\) such that for all distinguishers \(\mathbf {D}\),
We next relate our game-based notion from Definition 8 to the above, and defer an in-depth discussion of the result to the full version [5].
Theorem 5
If an encryption scheme \(\Pi \) is
 , then it achieves composable anonymous confidentiality, that is,
, then it achieves composable anonymous confidentiality, that is,
with \(\varepsilon (\mathbf {D})\doteq \Delta ^{\mathbf {D}\mathbf {C}}([\mathbf {E}_{K_1},\ldots ,\mathbf {E}_{K_n}],\langle \mathbf {E}_K^\$,\ldots ,\mathbf {E}_K^\$\rangle )\) and appropriate reduction system \(\mathbf {C}\).
4.3 Composable Anonymous Security of pAE
In this section we first introduce a composable definition of anonymous security for pAE, and then we show that the previously introduced game-based notion of
 implies the former. The composable definition can be interpreted as providing composable semantics to
implies the former. The composable definition can be interpreted as providing composable semantics to
 for pAE, in the sense that the result we show here attests that if an (authenticated) encryption scheme is
for pAE, in the sense that the result we show here attests that if an (authenticated) encryption scheme is
 , then it can be safely used to construct a secure channel from an insecure one, while preserving anonymity.
, then it can be safely used to construct a secure channel from an insecure one, while preserving anonymity.
In the following, for a fixed (authenticated) encryption scheme \(\Pi \) let the converter \(\mathsf {ae}\) (where the dependency on \(\Pi \) is implicit) behave as follows when connected to interface \(S_i\) of \(\mathsf {KEY}_\mathcal K\) and interface \(S_i\) of \(\mathsf {A\text {-}\mathsf{INS}}_\mathcal C\), for \(i\in [n]\): on input a message \(m\in \mathcal M\) from the outside, if not already done so before, output \(\diamond \) to \(\mathsf {KEY}_\mathcal K\) in order to fetch key \(K_i\), then compute \(c\leftarrow \mathtt {Enc}_{K_i}(m)\in \mathcal C\) and output c to \(\mathsf {A\text {-}\mathsf{INS}}_\mathcal C\). Also let the converter \(\mathsf {ad}\) (where again the dependency on \(\Pi \) is implicit) behave as follows when connected to interface \(R\) of \(\mathsf {KEY}_\mathcal K\) and interface \(R\) of \(\mathsf {A\text {-}\mathsf{INS}}_\mathcal C\): on input \(\diamond \) from the outside, if not already done so before, output \(\diamond \) to \(\mathsf {KEY}_\mathcal K\) in order to fetch keys \(K_1,\ldots ,K_n\), and then output \(\diamond \) to \(\mathsf {A\text {-}\mathsf{INS}}_\mathcal C\); for each obtained tuple (j, c), find the index \(i\in [n]\) such that \(m\ne \bot \), for \(m\leftarrow \mathtt {Dec}_{K_i}(c)\), and output the collection of all such resulting tuples (j, m, i) to the outside. Finally, we define the n-protocol \(\pi _\mathsf {ae}\doteq (\mathsf {ae},\ldots ,\mathsf {ae},\mathsf {ad})\).
Definition 14
(Composable Anonymous Security of pAE). An (authenticated) encryption scheme \(\Pi \) achieves composable anonymous security if
that is, if there exists a simulator \(\mathsf {sim}\) such that for all distinguishers \(\mathbf {D}\),
We next relate our game-based notion from Definition 9 to the above, and defer an in-depth discussion of the result to the full version [5].
Theorem 6
If an (authenticated) encryption scheme \(\Pi \) is
 , then it achieves composable anonymous security, that is,
, then it achieves composable anonymous security, that is,
with \(\varepsilon (\mathbf {D})\doteq \Delta ^{\mathbf {D}\mathbf {C}}([\langle \mathbf {E}_{K_1},\mathbf {D}_{K_1}\rangle ,\ldots ,\langle \mathbf {E}_{K_n},\mathbf {D}_{K_n}\rangle ],\langle \langle \mathbf {E}_K^\$,\mathbf {D}^\bot \rangle ,\ldots ,\langle \mathbf {E}_K^\$,\mathbf {D}^\bot \rangle \rangle )\)and appropriate reduction system \(\mathbf {C}\).
Notes
- 1.
Note that correlated parallel composition is merely syntactic construct, and we only use this notation throughout our paper for easier (and nicer) statements.
- 2.
In this work, we assume that such translations (reductions) are black-box, that is, \(\mathbf {C}\) only has access to the outputs of \(\mathbf {D}\), not to its internal behavior.
- 3.
In the full version [5] we show that indeed the last term captures
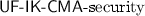 .
. - 4.
Note that while deletion is a physical phenomenon, and can thus not be prevented using cryptography, it is in principle possible to prevent repetition and reordering, concretely by means of sequence numbers. But we do not cover this aspect of security in this work.
References
Abadi, M., Rogaway, P.: Reconciling two views of cryptography. In: van Leeuwen, J., Watanabe, O., Hagiya, M., Mosses, P.D., Ito, T. (eds.) TCS 2000. LNCS, vol. 1872, pp. 3–22. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44929-9_1
Alagic, G., Gagliardoni, T., Majenz, C.: Unforgeable quantum encryption. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10822, pp. 489–519. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_16
Alwen, J., Hirt, M., Maurer, U., Patra, A., Raykov, P.: Key-indistinguishable message authentication codes. In: Abdalla, M., De Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 476–493. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10879-7_27
Alwen, J., Hirt, M., Maurer, U., Patra, A., Raykov, P.: Anonymous authentication with shared secrets. In: Aranha, D.F., Menezes, A. (eds.) LATINCRYPT 2014. LNCS, vol. 8895, pp. 219–236. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16295-9_12
Banfi, F., Maurer, U.: Anonymous symmetric-key communication. Cryptology ePrint Archive, Report 2020/073 (2020). https://eprint.iacr.org/2020/073
Bellare, M., Desai, A., Jokipii, E., Rogaway, P.: A concrete security treatment of symmetric encryption. In: Proceedings 38th Annual Symposium on Foundations of Computer Science – FOCS 1997, pp. 394–403, October 1997
Bellare, M., Boldyreva, A., Desai, A., Pointcheval, D.: Key-privacy in public-key encryption. In: Boyd, C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 566–582. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45682-1_33
Bellare, M., Namprempre, C.: Authenticated encryption: relations among notions and analysis of the generic composition paradigm. In: Okamoto, T. (ed.) ASIACRYPT 2000. LNCS, vol. 1976, pp. 531–545. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44448-3_41
Bellare, M., Tackmann, B.: The multi-user security of authenticated encryption: AES-GCM in TLS 1.3. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 247–276. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_10
Brzuska, C., Delignat-Lavaud, A., Fournet, C., Kohbrok, K., Kohlweiss, M.: State separation for code-based game-playing proofs. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018. LNCS, vol. 11274, pp. 222–249. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03332-3_9
Chan, J., Rogaway, P.: Anonymous AE. In: Galbraith, S.D., Moriai, S. (eds.) ASIACRYPT 2019. LNCS, vol. 11922, pp. 183–208. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34621-8_7
Desai, A.: The security of all-or-nothing encryption: protecting against exhaustive key search. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 359–375. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44598-6_23
Fischlin, M.: Pseudorandom function tribe ensembles based on one-way permutations: improvements and applications. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 432–445. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_30
Hoang, V.T., Tessaro, S., Thiruvengadam, A.: The multi-user security of GCM, revisited: tight bounds for nonce randomization. In: Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security – CCS 2018, pp. 1429–1440. Association for Computing Machinery, New York (2018)
Krawczyk, H.: The order of encryption and authentication for protecting communications (or: How secure is SSL?). In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 310–331. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_19
Maurer, U.: Indistinguishability of random systems. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 110–132. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_8
Maurer, U.: Constructive cryptography – a new paradigm for security definitions and proofs. In: Mödersheim, S., Palamidessi, C. (eds.) TOSCA 2011. LNCS, vol. 6993, pp. 33–56. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-27375-9_3
Maurer, U., Pietrzak, K., Renner, R.: Indistinguishability amplification. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 130–149. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_8
Maurer, U., Renner, R.: Abstract cryptography. In: Innovations in Theoretical Computer Science – ICS 2011, pp. 1–21. Tsinghua University Press (2011)
Rogaway, P.: Nonce-based symmetric encryption. In: Roy, B., Meier, W. (eds.) FSE 2004. LNCS, vol. 3017, pp. 348–358. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-25937-4_22
Rogaway, P.: Evaluation of some blockcipher modes of operation. Cryptography Research and Evaluation Committees (CRYPTREC) for the Government of Japan (2011). https://web.cs.ucdavis.edu/~rogaway/papers/modes.pdf
Rogaway, P.: The evolution of authenticated encryption. In: Workshop on Real-World Cryptography (2013). https://crypto.stanford.edu/RealWorldCrypto/slides/phil.pdf
Rogaway, P., Shrimpton, T.: A provable-security treatment of the key-wrap problem. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 373–390. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_23
Rosulek, M.: The joy of cryptography. Oregon State University EOR (2018). http://web.engr.oregonstate.edu/~rosulekm/crypto/
Shrimpton, T.: A characterization of authenticated-encryption as a form of chosen-ciphertext security. Cryptology ePrint Archive, Report 2004/272 (2004). https://eprint.iacr.org/2004/272
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Banfi, F., Maurer, U. (2020). Anonymous Symmetric-Key Communication. In: Galdi, C., Kolesnikov, V. (eds) Security and Cryptography for Networks. SCN 2020. Lecture Notes in Computer Science(), vol 12238. Springer, Cham. https://doi.org/10.1007/978-3-030-57990-6_23
Download citation
DOI: https://doi.org/10.1007/978-3-030-57990-6_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-57989-0
Online ISBN: 978-3-030-57990-6
eBook Packages: Computer ScienceComputer Science (R0)







 : interfaces;
: interfaces;
 : inputs;
: inputs;
 : outputs). (Color figure online)
: outputs). (Color figure online)
 .
.