Modelling of Spur Gear Dynamic Behaviours with Tooth Surface Wear

Abstract

In gear transmission systems, the gear tooth surface will get inevitable worn due to various abnormal working conditions. The wear on gear tooth surface will cause deformation of the gear tooth profile. Furthermore, the wear will cause changes in gear tooth mesh stiffness, then deteriorate the gear dynamics. In the past decades, a number of studies had been carried out to investigate the process of gear tooth wear and its monitoring techniques. However, the interactions between the gear dynamics and gear tooth wear are still not got fully investigated. Therefore, this study proposed an eight-degree of freedom dynamic model to study the dynamic behaviours of the gear system with gear wear. When modelling the dynamic behaviours, a modified time-varying mesh stiffness (TVMS) model was derived by employing the potential energy method. The numerical results show that with the increase of the wear depth, the amplitudes at 1 × f_m1 and 2 × f_m2 increase gradually which can reflect the progressive wear process. Furthermore, an experimental study was conducted based on a run-to-fatigue test and the gear vibration responses were studied using the well-known de-noising method Time synchronous averaging (TSA). The experimental validation has a good consistency with the numerical analysis.

117.1 Introduction

The gear transmission system is widely used for transmitting power and motion in mechanical equipment. However, with the development of technology, the requirements to the gears are becoming much stricter. From the condition monitoring point of view, early detection of faults which occur in a gear transmission system can prevent catastrophic failure of the whole system and reduce the economic loss. Among all the gear fault types, progressive gear wear is the most challenging one to study as it involves multi-discipline such as material, mechanical, chemical, and so on. Normally, gear tooth wear is regarded as a process of progressive material removal on the mating surfaces which generally arises from the inadequate lubrication and extreme working conditions. The progressive wear can lead to non-uniform gear rate, poor dynamic behaviour, and potential severe gear failures. Additionally, for high precision machining, the gear tooth wear can cause low machining accuracy and poor products quality and then lead to vast economic loss.

Gear tooth wear can lead to the deterioration of the gear tooth profile and worsen the gear contact state, further will affect the gear dynamic behaviours. Researchers have been studying the wear mechanism for decades and a number of papers related were published. Flodin and Andersson [1, 2] studied different wear severities of a spur gear using a Winkler surface model. After that, they simulated the helical gear wear by equivalising the helical gear as a combination of numbers of slices of spur gear [3, 4]. K. Mao analysed the gear contact state using the finite element method by taking the effect induced by shaft misalignment, deflection, and assembly deflection into consideration. Kahraman [5] investigated the wear process by considering the tooth profile deviation and found that the wear is generated due to the combined modification parameters rather than signal gear parameter. Mert [6] studied the influence of operating conditions like speed and load on the wear process using Archard’s wear model. Valentin [7] explored the gear wear from scuffing of heavy-duty machine spur gears considering the instant contact temperature. Other studies [8,9,10,11] also was conducted to determine the process of gear tooth wear, however, most of the studies were carried out either numerically or experimentally. Besides, the influences of tooth wear on gear dynamic behaviours are not investigated comprehensively.

This study proposed an eight-degree of freedom dynamic model to study the dynamic behaviours of the gear system with gear wear. The gear wear depth was obtained through the Archard’s wear model taking the Hertzian contact into account. In addition, a run-to-fatigue test was carried out to study the vibration response induced by gear wear. The following sections will illustrate the detailed modelling process and experimental study.

117.2 Modelling of Gear Mesh Stiffness with Tooth Wear

117.2.1 Gear Tooth Wear Modelling

The Archard’s wear equation is widely used to predict the wear depth in mechanical equipment. The normalised Archard’s equation can be written as:

$$ \frac{V}{s} = K\frac{W}{H} $$

(117.1)

where, V stands for the worn volume, s stands for the relative sliding distance between mating surfaces, K stands for the dimensionless wear coefficient, W stands for the normal load on the mating surfaces, H stands for the material hardness.

Due to the change in the meshing position along the line of action, the relative sliding distance will be different at every instant. So, taking into account the wear on each local point is very important rather than during the whole contact period. For any point ‘p’ on the gear tooth surface, the wear depth can be obtained via the Archard’s wear equation:

$$ h_{p} = \int_{0}^{s} {kpds} $$

(117.2)

where, h_p denotes the wear depth of point ‘p’; k denotes the dimensional wear coefficient; p denotes the local contact pressure.

The contact between two mating gears can be regarded as the contact of two parallel cylinders. According to the Hertzian contact theory, the semi-Hertzian contact width is:

$$ a_{h} = \sqrt {\frac{{4F_{t} \rho }}{\pi bE}} $$

(117.3)

where, F_t is the tangential force, b is the gear width, ρ and E are the equivalent curvature radius of the contacting surfaces and the equivalent elasticity modulus of materials respectively.

The maximum contact pressure between the mating surfaces:

$$ P_{max} = \frac{{2F_{t} }}{{\pi a_{h} b}} $$

(117.4)

117.2.2 Sliding Distance

Figure 117.1 shows the relative positions of the meshing points on the gear and pinion respectively. Due to the difference in peripheral velocities. The sliding distances corresponding to the gear and pinion can be calculated respectively as:

Fig. 117.1

The relative sliding distance between the meshing points on gear and pinion

$$ S_{p1} = 2a_{h} \frac{{U_{p} - U_{g} }}{{U_{p} }} $$

(117.5)

$$ S_{p2} = 2a_{h} \frac{{U_{g} - U_{p} }}{{U_{g} }} $$

(117.6)

where α_h is the semi-Hertzian contact width, U_g and U_p are the peripheral velocities of gear and pinion which can be obtained as respectively:

$$ U_{g} = \omega_{g} \left( {\frac{{d_{g} }}{2}\sin \alpha + y} \right) $$

(117.7)

$$ U_{p} = \omega_{p} \left( {\frac{{d_{p} }}{2}\sin \alpha + y} \right) $$

(117.8)

where, ω denotes for the rotational speed; d_g,p denotes for the diameter of pitch circle; α denotes for the pressure angle; y denotes for the distance from the pitch point to the instant meshing point.

As detailed above, the relative sliding distance can be obtained from Eq. (117.5) and (117.6), then substitute it into Eq. (117.2), the accumulated gear tooth wear after n revolution can be estimated as:

$$ h_{p,\left( n \right)} = h_{{p,\left( {n - 1} \right)}} + kP_{{p,\left( {n - 1} \right)}} S_{p} $$

(117.9)

where, h_p,(n) stands for the wear depth at the meshing point ‘p’ on the tooth surface after n revolution, h_p,(n−1) stands for the wear depth after n-1 revolution, P_p,(n−1) stands for the corresponding pressure at meshing point ‘p’.

117.2.3 Time-Varying Gear Mesh Stiffness

117.2.3.1 Modified Involute Gear Profile

For involute spur gear, the tooth profile can be expressed as:

$$ \left\{ {\begin{array}{*{20}l} {x_{d} = r_{b} \left( {\sin \alpha - \alpha \,\cos \alpha } \right)} \hfill \\ {y_{d} = r_{b} \left( {\cos \alpha + \alpha \,\sin \alpha } \right)} \hfill \\ \end{array} } \right. $$

(117.10)

By introducing the wear depth into the gear profile equation, the modified gear profile can be estimated:

$$ \left\{ {\begin{array}{*{20}l} {x_{d1} = r_{b} \left( {\sin \alpha - \alpha \,\cos \alpha } \right) - h_{p,n} \sin \alpha_{1} } \hfill \\ {y_{d1} = r_{b} \left( {\cos \alpha + \alpha \,\sin \alpha } \right) - h_{p,n} \cos \alpha_{1} } \hfill \\ \end{array} } \right. $$

(117.11)

117.2.3.2 Gear Mesh Stiffness

Consider the structure of the gear, the gear tooth can be treated as a non-uniform cantilever beam. The gear tooth can be divided into n segments as depicted in Fig. 117.2. Thus, the bending deflection can be obtained as:

Fig. 117.2

Modelling spur gear tooth as a non-uniform cantilever beam with tooth wear

$$ \delta_{b} = F\cos^{2} \alpha_{m} \sum\limits_{i = 1}^{n} {e_{i} } \left\{ {\frac{{\left( {d_{i} - e_{i} d_{i} + \frac{1}{3}e_{i}^{2} } \right)}}{{E^{\prime}\bar{I}_{i} }} + \frac{1}{{s_{n} G\bar{A}_{i} }} + \frac{{\tan^{2} \alpha_{m} }}{{\bar{A}_{i} E^{\prime}}}} \right\} $$

(117.12)

where, F stands for the contact force, α_m stands for the operating pressure angle, G stands for the shear modulus, S_n stands for a shear factor, e_i and d_i are depicted in Fig. 117.2. E’, I_i and A_i can be calculated as illustrated in [12].

The corresponding bending stiffness of the tooth can be obtained as:

$$ k_{b} = \frac{F}{{\delta_{b} }} $$

(117.13)

The fillet-foundation deflection can be calculated as:

$$ \delta_{f} = \frac{{F\cos^{2} \alpha_{m} }}{WE}\left\{ {L^{*} \left( {\frac{{u_{f} }}{{S_{f} }}} \right)^{2} + M^{*} \left( {\frac{{u_{f} }}{{S_{f} }}} \right) + P^{*} \left( {1 + Q^{*} \tan^{2} \alpha_{m} } \right)} \right\} $$

(117.14)

where, W stands for the tooth width, u_f and S_f are specified in Fig. 117.2. The coefficients L*, M*, P*, Q* can be approached by referencing the polynomial function put forward by Sainsot [13].

Correspondingly, the fillet-foundation stiffness can be calculated as:

$$ k_{f} = \frac{F}{{\delta_{f} }} $$

(117.15)

As stated in [14], the stiffness of the Hertzian contact of two meshing teeth is a constant along the line of action. k_h can be given by:

$$ k_{h} = \frac{\pi EW}{{4\left( {1 - v} \right)}} $$

(117.16)

The local deformation is then expressed by:

$$ \delta_{h} = \frac{F}{{k_{h} }} $$

(117.17)

Considering the three stiffness into account, the total mesh stiffness K₁₂ can be estimated by the following equation:

$$ K_{12} = \frac{1}{{k_{bg} + k_{fg} + k_{bg} + k_{bp} + k_{h} }} $$

(117.18)

Figure 117.3 shows the modelling results of the TVMS, as can be observed in the figure, with the movement of the meshing position, the wear depth decrease first then increase. The mesh stiffness reduces gradually with the increase of wear depth, and the reduction in gear mesh stiffness on the double-tooth-mesh area is more severe than on the single-tooth-pair mesh area.

Fig. 117.3

Modelling results of gear wear depth and mesh stiffness

117.3 Dynamic Modelling Analysis

117.3.1 Eight-Degree of Freedom Dynamic Model

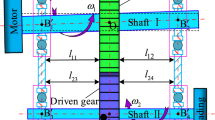
In order to simulate the influence of gear tooth wear on gear dynamics, an eight-degree of freedom dynamic model was developed based on the real gearbox test rig. As depicted in Fig. 117.4, the model is comprised of four inertias, namely driving motor, gear, pinion, load generator. Both the torsional motion of shafts and the translational motion of bearings are considered into this model. Besides, the damping and stiffness are also taken into consideration. The model has four torsional motions, two translational motions along the line of action, and two transversal motions associated with mating gears.

Fig. 117.4

Dynamic model of one stage gear system

The governing equations of the eight-degree of freedom numerical model can be represented by:

$$ \begin{array}{*{20}c} {I_{m} \ddot{\theta }_{m} + c_{1} \left( {\dot{\theta }_{m} - \dot{\theta }_{g} } \right) + k_{1} \left( {\theta_{m} - \theta_{g} } \right) = T_{d} } \\ {I_{g} \ddot{\theta }_{g} + c_{1} \left( {\dot{\theta }_{g} - \dot{\theta }_{m} } \right) + k_{1} \left( {\theta_{g} - \theta_{m} } \right) = - F_{m} r_{bg} - F_{f} l_{g} } \\ {I_{p} \ddot{\theta }_{p} + c_{2} \left( {\dot{\theta }_{p} - \dot{\theta }_{L} } \right) + k_{2} \left( {\theta_{p} - \theta_{L} } \right) = - F_{m} r_{bp} + F_{f} l_{p} } \\ {I_{L} \ddot{\theta }_{L} + c_{2} \left( {\dot{\theta }_{L} - \dot{\theta }_{p} } \right) + k_{2} \left( {\theta_{L} - \theta_{p} } \right) = - T_{L} } \\ {m_{g} \ddot{x}_{g} + c_{b} \dot{x}_{g} + k_{b} x_{g} = - F_{f} } \\ {m_{g} \ddot{y}_{g} + c_{b} \dot{y}_{g} + k_{b} y_{g} = - F_{m} } \\ {m_{p} \ddot{x}_{p} + c_{b} \dot{x}_{p} + k_{b} x_{p} = F_{f} } \\ {m_{p} \ddot{y}_{p} + c_{b} \dot{y}_{p} + k_{b} y_{p} = F_{m} } \\ \end{array} $$

(117.19)

where I_i is the moment of inertia, the subscript i = m, p, g, L denotes motor, pinion, gear, load generator respectively; m_i denotes the mass of the gear, $\theta_{i}$/$\dot{\theta }_{i}$/$\ddot{\theta }_{i}$ represents the angle/velocity/acceleration of rotation; x_i, y_i denotes the translational displacement; c_j and k_j respectively denotes the damping constant and stiffness constant, the subscript j = 1, 2, b are for first coupling, second coupling and bearing. T_d, T_L are the loads applied on the driving motor and load generator; α is the pressure angle; r_bg, r_bp are the radius of the base circle of gear and pinion; F_m, F_f is the meshing force and friction force which can be obtained respectively as:

$$ F_{m} = c_{m} \dot{\delta } + k_{m} \delta $$

(117.20)

$$ F_{f} = \mu \left( t \right)F_{m} $$

(117.21)

where $\delta$ is the relative displacement which can be calculated as

$$ \Delta {\text{s}} = \left( {{\text{y}}_{g} + r_{bg} \theta_{g} } \right) - \left( {y_{p} - r_{bp} \theta_{p} } \right) + e $$

(117.22)

The time-varying friction coefficient $\mu \left( t \right)$ was derived based on the non-Newtonian, thermal EHL theory:

$$ \mu \left( t \right) = e^{{f\left( {SR\left( t \right), P_{h} \left( t \right), \upsilon_{0} , S} \right)}} P_{h} \left( t \right)^{{b_{2} }} \left| {SR\left( t \right)} \right|^{{b_{3} }} V_{e} \left( t \right)^{{b_{6} }} \upsilon_{0}^{{b_{7} }} R\left( t \right)^{{b_{8} }} $$

The derivation process of the equation and the meaning of the variables used in the equation are detailed in Xu’s study [15].

By substituting the gear mesh stiffness, which was obtained from the modified TVMS model depicted in Sect. 117.2, into the governing equations, the dynamic response relating to gear tooth wear can be simulated. The following section will illustrate the modelling results under different operating revolutions. The modelling gear parameters are the same as depicted in Table 117.1.

Table 117.1 Main parameters of the modelled gear set

117.3.2 Modelling Results

117.3.2.1 Contact Parameters

Figure 117.5(a) shows the change of gear relative displacement. As can be seen in the figure, with the increase in gear tooth wear, the gear relative displacement increases to some extent. Figure 117.5(b) shows the time-varying friction coefficient, actually, no obvious change can be observed in the figure.

Fig. 117.5

Changes in gear contact parameters under different operating revolutions

Figure 117.6(a) shows the time-varying mesh stiffness under different operating revolutions. With the increase in the accumulated wear depth, the magnitude of the mesh stiffness increases to some extent. Figure 117.6(b) illustrates the change in time-varying friction force. The negative value represents the direction of the friction force change to the opposite. Moreover, the friction force decreases slightly when the wear depth increases.

Fig. 117.6

Time-varying gear mesh stiffness and friction force

117.3.2.2 Translational Acceleration

Figure 117.7 respectively present the translational acceleration in a frequency band ranging from 0–7000 Hz. From both the two figures, the gear mesh frequency and its harmonics can be noticeably observed, with the increase of the harmonic order, the magnitude of the mesh frequency reduces gradually.

Fig. 117.7

Translational acceleration of the gear and pinion in Y-direction

117.3.2.3 Changes in Amplitudes of Gear Mesh Frequency and Its Harmonics

In order to have a more distinctive indication about how the wear depth influence the gear dynamics, the amplitudes of the mesh frequency and its first three harmonics were extracted from the spectra shown in Fig. 117.7. The variations of the amplitudes at each harmonic were illustrated in Fig. 117.8(a), (b), and (c). The amplitudes at 1 × f_m1 and 2 × f_m1 increase gradually with the increase of the operating revolutions. This variation can be able to reflect the deterioration of the gear wear. The amplitude at 3 × f_m1 firstly increases then decrease gradually which is mainly caused by the nonlinear effect of the gear dynamics.

Fig. 117.8

Changes in amplitude of the mesh frequency and its harmonics

117.4 Experimental Validation

In order to verify the results obtained from the numerical analysis, a run-to-fatigue test was carried out to investigate the vibration responses with the progressive gear tooth wear. Figure 117.9 illustrates the test rig used in this study. Time-Synchronous Averaging (TSA) analysis was employed to process the vibration data due to its abilities in noise reduction and feature enhancement. Figure 117.10 shows the magnitudes at the first three harmonics of the gear meshing frequency at four different operating hours. With the increase of the operating time, the magnitude increases gradually which has a good consistency with the numerical result.

Fig. 117.9

Gear Run-to-fatigue Test rig

Fig. 117.10

TSA Magnitude at the first three harmonics of the meshing frequency

117.5 Conclusion

This study investigated the influence of gear tooth wear on gear dynamic behaviours. Firstly, a modified numerical model was put forward to determine the time-varying mesh stiffness considering gear wear, furthermore, the TVMS was introduced into the gear dynamic model to study the dynamic behaviour.

The modified TVMS model shows that the gear tooth wear will cause changes on gear mesh stiffness in both amplitude and phase. Besides, the reduction in mesh stiffness on the double-tooth meshing area is much obvious than that on the single-tooth-meshing area as the load changes when the mesh tooth pair varies.

The gear dynamic responses illustrate that the dynamic gear mesh stiffness increase slightly when the gear tooth wear occurred, however, the friction force decreased slightly due to the reduction in time-varying friction coefficient. Besides, with the increase of the wear depth, the amplitudes at 1 × fm1 and 2 × fm2 increase gradually which can reflect the progressive wear process. The experimental results agree with the numerical results, which can verify the reliability of the numerical study.