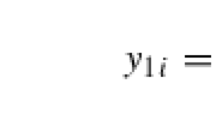Introduction to Independent Counterfactuals

Abstract

The aim of this contribution is to introduce the idea of independent counterfactuals. The technique allows to construct a counterfactual random variable which is independent from a set of given covariates, but it follows the same distribution as the original outcome. The framework is fully nonparametric, and under error exogeneity condition the counterfactuals have causal interpretation. On an example of a stylized linear process, I demonstrate the main mechanisms behind the method. The finite-sample properties are further tested in a simulation experiment.

1 Introduction

Estimation of counterfactual designs has become a focal point for policymakers and practitioners in the fields of policy evaluation and impact assessment. Counterfactual distributions are an important landmark in the methodology, as they allow to measure not only average effects but, under some regularity conditions, they also capture the relationship for any point across the distribution of interest [1].

In the context of a counterfactual analysis, one is interested in approximating the dynamics of an outcome variable Y under a new, possibly unobserved, scenario. Typically, the construction of such a scenario assumes a shift of a set of covariates from X to, say, $X'$. For instance, a policymaker may want to investigate the effects of a tariff change on local food prices where the relevant covariates (taxes, fees or other policy instruments) increase or decrease by some amount.

The vast majority of counterfactual scenarios are user-designed, suffering from an over-simplification and potential model misspecification biases. Nevertheless, the recent advances in counterfactual distributions aim at providing possibly assumption-free inference techniques. [1] offers a complete toolbox to study counterfactual distributions through a prism of regression methods. [5] extends the approach to a fully nonparametric setup and demonstrates that nonparametric estimation has superior Mean Squared Error (MSE) performance in the case of (functional) model misspecification. [6] further extends the nonparametric approach to cover partial distributional effects.

Capitalizing on [8], I propose an alternative identification strategy which defines the counterfactual scenario as independent from a given set of covariates. Using an example from above, a policymaker may be interested in approximating the behaviour of food prices under no policy intervention, exemplifying the overall distortions created by relevant taxes or fees. In this simple case, one would consider independent counterfactuals as dropping the entire policy instrument rather than estimating a counterfactual distribution of food prices at a zero tax rate. Setting a covariate to zero does not have to uniquely identify the independence criterion. If the taxation becomes effective only above some minimum threshold, there may be multiple choices for the counterfactual designs. Similarly, the true relation between the outcome and the covariates may be actually undefined, or not directly interpretable, for zero-valued arguments. In such cases, independent counterfactuals offer an attractive alternative to a standard toolkit.

The framework requires to take a somehow broader perspective on the interpretation of counterfactuals. More specifically, it asks what would be the realization of an outcome variable for which there would be no evidence against the independence condition given the realizations of the covariates. As such, the distribution of the counterfactual coincides with the distribution of the observed variable, spanning over the same information set, but the dependence link versus the covariates is removed.

The framework has desired asymptotic properties, allowing to apply standard statistical inference techniques. It also advertises the use of nonparametric methods, utilizing a smooth version of kernel density/distribution estimates. This, in fact, turns out to generate substantial efficiency gains over the step-wise estimators [8].

The purpose of this contribution is to offer the basic concepts behind independent counterfactual random variables. The extended description of the framework, covering also an idea of conditionally independent counterfactuals, together with an extensive numerical exercise and empirical study, is offered by [8]. Section 2 introduces the methodology, which is further illustrated numerically and compared against the standard linear framework in Sect. 3. A brief numerical study is described in Sect. 4. Finally, Sect. 5 concludes.

2 Framework

Assume two random variables $Y \in \mathbb {R}$ and $X \in \mathbb {R}^{d_X}$, where $d_X\ge 1$, with a joint Cumulative Distribution Function (CDF) denoted by $F_{Y,X}(y,x)$, which is r-times differentiable and strictly monotonic.

Filtering out the effects between X and Y means constructing a counterfactual random variable $Y' =^D Y$ that is independent of X. (Clearly, in case, Y and X are independent, $Y'$ would be simply equal to Y.)

In terms of CDFs, one can write the independence condition as

$$\begin{aligned} F_{Y'|X}(y|x) = F_Y(y) \end{aligned}$$

(1)

for all y and x.

The random variable $Y'$ can be obtained directly from Eq. (1) by assuming that, for any point along the X marginal, there is an increasing functional $\phi$, such that $Y'=\phi (Y,X)$, which is invertible in Y for all x in the support of X, for which Eq. (1) holds. The realizations of the counterfactual random variable $Y'$ are given by $y'=\phi (y,x)$. [8] shows that Eq. (1) is satisfied by

$$\begin{aligned} Y' = F^{-1}_Y(F_{Y|X}(Y|x)), \end{aligned}$$

(2)

where $F^{-1}_{Y}( q ) = \inf \{y: F_{Y}(y) \ge q \}$ is the quantile function of Y, under the assumption that $F_Y$ is invertible around the argument. The invertability assumption is satisfied by the monotonicity of $F_Y(y)$, which also guarantees that the relation is uniquely identified for any y and x.¹

The relation between Eqs. (2) and (1) follows from

$$ F_{Y'|X}(y|x) = P( \phi (Y,X) \le y | X=x) = P( Y \le \phi ^{-1}(y,X) | X=x) = F_{Y|X}(\phi ^{-1}(y,x)|x), $$

which makes $\phi ^{-1}(y,x) = F^{-1}_{Y|X}(F_Y(y)|x)$, or equivalently $\phi (y,x) {=} F^{-1}_Y(F_{Y|X}(y|x))$, under the assumptions outlined above.

For the moment, the setup is designed for real-valued Y. In principle, the framework may be extended to multivariate outcome variables, under additional regularity conditions on the corresponding CDF and conditional CDF. This topic is, however, beyond the scope of this manuscript.

2.1 Estimation

A major challenge in estimating the function in Eq. (2) results from its nested structure. [8] provides a set of necessary conditions under which the kernel-based estimator of Eq. (2) is asymptotically tight. In fact, the crucial condition is the Donsker property of the quantile and conditional CDF estimators, respectively.

In the setup below I take that Y is univariate and X is potentially multivariate with $d_X \ge 1$. The kernel CDF and conditional CDF estimators are given by²

$$\begin{aligned} \hat{F}_{Y}(y) = n^{-1} \sum _{i=1}^n \bar{K}_{\mathbf {H}^Y_0}\left( y-Y_i\right) , \end{aligned}$$

(3)

and

$$\begin{aligned} \hat{F}_{Y|X}(y|x) = \frac{\sum _{i=1}^n\bar{K}_{\mathbf {H}^{Y|X}_0} (y - Y_i) K_{\mathbf {H}^{Y|X}}\left( x-X_i\right) }{ \sum _{i=1}^n K_{\mathbf {H}^{Y|X}}\left( x-X_i\right) }, \end{aligned}$$

(4)

where $\bar{K}_{\mathbf {H}_0}(w) = \int _{-\infty }^{w} K(\mathbf {H}_0^{-1/2} u)\mathrm{d}u$ is an integrated kernel function. Matrices ${\mathbf {H}}$ contain smoothing parameters, dubbed as bandwidths, with subscript 0 marking the CDF marginal and superscripts determining the corresponding distribution of interest. To simplify the presentation, I take $\mathbf {H}^{Y}_0 = h^2_{0Y}$, $\mathbf {H}^{Y|X}_0 = h^2_{0YX}$ and $\mathbf {H}^{Y|X} = \mathrm{diag}(h^2_{1YX},..., h_{d_XYX}^2)$. Expression

$$\begin{aligned} K_\mathbf {H}(\textit{\textbf{w}}) = ( \det \mathbf {H} )^{-1/2} K(\mathbf {H}^{-1/2}\textit{\textbf{w}}) \end{aligned}$$

(5)

is the scaled kernel with ‘$\det$’ denoting the determinant and K being a generic multiplicative $d_W$-variate kernel function

$$\begin{aligned} K(w_1,...,w_{d_W}) = \prod _{j=1}^{d_W}k(w_j), \end{aligned}$$

(6)

satisfying for each marginal j

$$\begin{aligned} \begin{aligned} \int k(w_j) \mathrm{d} w_j&= 1, \\ \int w_j^c k(w_j) \mathrm{d} w_j&= 0 \quad \mathrm{for} \quad c=1,...,r-1, \quad \\ \int w_j^c k(w_j) \mathrm{d} w_j&= \kappa _r < \infty \quad \mathrm{for} \quad c=r, \end{aligned} \end{aligned}$$

(7)

and k(w) being symmetric and r-times differentiable [4].

The convergence properties of estimators in Eqs. (3) and (4) can be tuned by the rates of convergence of the smoothing parameters, i.e. $h_{0Y}$ and $h_{jYX}$ for $j=0,...,d_X$. Following [3], to guarantee that Eqs. (3) and (4) are uniformly tight, the sequences of bandwidths $h \equiv h(n)$ need to satisfy

$$\begin{aligned} \begin{aligned} \lim _{n\rightarrow \infty } n^{1/2} h_{0Y}^r = 0,&\quad \lim _{n\rightarrow \infty } n^{\alpha _1} h_{0Y} = \infty , \\ \lim _{n\rightarrow \infty } n^{1/2} h_{0YX}^r = 0,&\quad \lim _{n\rightarrow \infty } n^{\alpha _2} h_{0YX} = \infty , \end{aligned} \end{aligned}$$

(8)

for some $\alpha _1,\alpha _2>0$ and

$$\begin{aligned} \lim _{n\rightarrow \infty } n^{1/2}\max _{j\in {1,...,d_X}}(h_{jXY})^r = 0, \quad \lim _{n\rightarrow \infty } \frac{\log (n)}{n^{1/2}\Pi _{j=1}^{d_X}h_{jXY}} = 0. \end{aligned}$$

(9)

If the support of Y is a compact set on $\mathbb {R}$, the functionals in Eqs. (3) and (4) are Donsker, and under an additional assumption that $F_Y^{-1}$ is Hadamard differentiable, the fitted values of $y' \equiv \hat{y}'$ are asymptotically tight [7].

If one represents the sequence of bandwidth as $h = C n^{-\beta }$, for some constant $C>0$, Eq. (8) implies that $\beta >1/(2r)$ for $h_{0Y}$ and $h_{0YX}$, and from Eq. (9) it follows that $\beta \in (1/(2r),1/(2d_X))$ for $h_{jYX}$ where $j=1,...,d_X$. These conditions are satisfied for the basic setup with the second-order kernels and $d_X=1$. In fact, if one extends dimensionality of X to $d_X>1$, condition Eq. (9) requires a higher order kernel.

A plug-in estimator of Eq. (2) becomes

$$\begin{aligned} \hat{y}' = \hat{F}^{-1}_Y(\hat{F}_{Y|X}(y|x)), \end{aligned}$$

(10)

for fixed realizations $(Y,X)=(y,x)$. By rearranging the terms and substituting the kernel estimators from Eqs. (3) and (4), one may obtain $\hat{y}'$ by solving

$$\begin{aligned} n^{-1} \sum _{i=1}^n \bar{K}_{\mathbf {H}^Y_0}\left( \hat{y}' - Y_i\right) = \frac{\sum _{i=1}^n\bar{K}_{\mathbf {H}^{Y|X}_0} (y - Y_i) K_{\mathbf {H}^{Y|X}}\left( x - X_i\right) }{ \sum _{i=1}^n K_{\mathbf {H}^{Y|X}}\left( x - X_i\right) }. \end{aligned}$$

(11)

[8] shows that under the data assumptions outlined above and if $\hat{F}_Y$ and $\hat{F}_{Y|X}$ are Donsker then

$$\begin{aligned} \sqrt{n} \left( \hat{y}' - y'\right) \mathop {\longrightarrow } \limits ^{d} N(0,\sigma ^2), \end{aligned}$$

(12)

where $\sigma ^2$ is given by

$$\begin{aligned} \sigma ^2 = \frac{F_{Y|X}(y|x)(1 - F_{Y|X}(y|x))}{f_Y\left( F^{-1}_Y(F_{Y|X}(y|x))\right) } + \frac{\int K(u)^2 \mathrm{d}u / f_X(x)}{\Pi _{j=1}^{d_X}h_{jXY}}\frac{F_{Y|X}(y|x)(1 - F_{Y|X}(y|x))}{f_Y\left( F^{-1}_Y(F_{Y|X}(y|x))\right) }. \end{aligned}$$

(13)

The first term in $\sigma ^2$ is the variance of the standard quantile estimator evaluated at the known quantity $F_{Y|X}(y|x)$. The second term results from the fact that the quantity $F_{Y|X}(y|x)$ is, in fact, estimated.

3 Interpretation

Removing the dependence between X and Y cannot be directly interpreted as a causal relation from X to Y. Reverse causality effects are also present in the joint distribution of (Y, X), and so are in the conditional distribution of $Y|X=x$. Nevertheless, the effects of X onto Y have causal interpretation under the so-called exogeneity assumption, or selection on observables. The assumption requires that there is no dependence between the covariates and the unobserved error component, $X \perp \!\!\! \perp \varepsilon$.

To introduce the concept formally, imagine that $\varepsilon$ describes a (possibly discrete) policy option assigned between different groups of individuals. With the aim to study the causal effects of a policy e on the outcome Y, denote the set of potential outcomes by $(Y^*_{e}: \varepsilon \sim F_\varepsilon (e))$. The identification problems arise as Y is observed only conditional on $\varepsilon =e$. If the error term e is not randomly assigned (for instance, a policymaker discriminates between groups what policy e they receive), the observed Y conditional on $\varepsilon =e$ may not be equal to the true variable $Y^*_{e}$. On the other hand, if e is assigned randomly, variables $Y^*_{e}$ and $Y|\varepsilon =e$ coincide. The exogeneity assumption may be extended by a set of conditioning covariates X. Under conditional exogeneity, the independent counterfactuals have also causal interpretation such that if conditional on X, the error component e is randomly assigned to Y, variables $Y^*_e|X$ and $Y|X,\varepsilon =e$ agree. Since the observed conditional random variable has causal interpretation, so has the independent counterfactual for which the X conditional effects have been integrated out (for more discussion see [1]).

Exogeneity assumption allows also to relate independent counterfactuals to the distribution of the error term. Consider a general nonseparable model

$$\begin{aligned} Y = m(X,\varepsilon ), \end{aligned}$$

(14)

where m is the general functional model and $\varepsilon$ is an unobserved continuous error term. For identification purposes, let us assume that m(x, .) is strictly increasing in e and continuous for all $x\in \mathrm {supp} (X)$, so that its inverse exists and is strictly increasing and continuous.

Under exogeneity, one finds that after removing the effects of X onto Y, the counterfactual random variable $Y'$ is identified at the $F_\varepsilon (\varepsilon )$ quantiles of Y. Note that

$$\begin{aligned} \begin{aligned} Y'&= F_{Y}^{-1}(P(m(X,\varepsilon )\le Y|X=x)) \\&=F_{Y}^{-1}(P(\varepsilon \le m^{-1}(X,Y)|X=x)) \\&=F_{Y}^{-1}(F_{\varepsilon |X}(\varepsilon |x)) \\&=F_{Y}^{-1} (F_\varepsilon (\varepsilon )). \end{aligned} \end{aligned}$$

(15)

By the inverse transformation method, one can also readily observe that the distribution of $Y'$ coincides with the distribution of Y, i.e. $F_{Y'}(y) = F_Y(y)$ for all y. This is not surprising as a sample from a null hypothesis of independence can be often constructed by permutation methods [2].³ Permutations are, however, not uniquely defined, as for a sample $\{Y_i,X_i\}_{i=1}^n$, for any fixed point $X=X_i$ any outcome $Y_i$ may be assigned in the permutation process. Therefore, although permutations are a powerful tool in hypothesis testing, they cannot be applied as an identification strategy. Independent counterfactuals offer an alternative in this respect, for which the counterfactual realization is identified at the quantiles determined by the realization of the error term. It follows that

$$\begin{aligned} \begin{aligned} F_{Y'}(y')&= F_Y(y') = F_{Y|X}(y|x) = F_Y(y) \delta (y,x), \end{aligned} \end{aligned}$$

(16)

where I substituted $\delta (y,x)\equiv F_{Y,X}(y,x)/(F_Y(y)F_{X}(x))$.

With endogenous error terms, the counterfactual $Y'$ is still identified by the data but the dependence filtering is contaminated by the relation between X and $\varepsilon$. In such a case, the independent counterfactual removes the causal relation from X onto Y, but also from Y onto X, such that the random variables $Y'$ and $F_Y^{-1}(F_\varepsilon (\varepsilon ))$ do not necessarily agree. To illustrate it analytically, let us consider a simple linear framework.

3.1 Exogenous Linear Model

Consider a stylized process with the first-moment dependence between X and Y

$$\begin{aligned} \begin{aligned} x&= e_X, \\ y&= a x + \sqrt{1-a^2} e_Y, \end{aligned} \end{aligned}$$

(17)

where $a\in (0,1)$ is a tuning parameter. Error terms $\varepsilon _{X}$ and $\varepsilon _{Y}$ follow standard normal distributions and are mutually independent. (Note that the setup ensures that the marginal of Y follows also a standard normal distribution.) The closed form expression for transformation in Eq. (2) can be derived as

$$\begin{aligned} \begin{aligned} F^{-1}_Y(q)&= \mathrm {\Phi }^{-1}(q) \quad q\in (0,1),\\ F_{Y|X}(y|x)&= \mathrm {\Phi }\left( \frac{y - ax}{\sqrt{1-a^2}}\right) , \end{aligned} \end{aligned}$$

(18)

where $\mathrm {\Phi }$ is the standard normal CDF. Putting the expressions together, for the linear mean-dependent process in Eq. (17) I arrive at

$$\begin{aligned} \begin{aligned} y'&\equiv \phi (y,x) = F^{-1}_Y(F_{Y|X}(y|x)) \\&= \mathrm {\Phi }^{-1}\left( \mathrm {\Phi } \left( \frac{y - a x}{\sqrt{1-a^2}}\right) \right) = \frac{y - a x}{\sqrt{1-a^2}} = e_Y. \end{aligned} \end{aligned}$$

(19)

Equation (19) confirms Eq. (15). In the proposed stylized setup, the distribution of $Y'$ corresponds to the distribution of errors so that the independent counterfactuals are asymptotically equal to the residuals from the standard Ordinary Least Squares (OLS) regression applied to the process from Eq. (17). In more general nonseparable models, the distribution of the error component would be scaled, by the inverse transformation method, to match the scale of the dependent variable.

3.2 Endogenous Linear Model

Consider now a similar process as in Eq. (17) but with inverse causality structure

$$\begin{aligned} \begin{aligned} y&= e_{Y}, \\ x&= a y + \sqrt{1-a^2} e_{X}, \end{aligned} \end{aligned}$$

(20)

with similar stationarity conditions as before. Clearly, the exogeneity condition is violated as $X|\varepsilon _Y=e_{Y} \sim N(a e_{Y},1-a^2)$. Having pointed this out, the identification in independent counterfactuals removes the entire dependence structure between the variables, which is exactly the same as in Eq. (17), such that

$$\begin{aligned} \begin{aligned} y' = \frac{y - a x}{\sqrt{1-a^2}} = \sqrt{1-a^2} e_{Y} - a e_{X}. \end{aligned} \end{aligned}$$

(21)

In this extreme example, because of reverse causality, the counterfactual variable $Y'$ does not correspond to the potential outcome variable, which in this case is given by $\varepsilon _Y$. Nevertheless, the independence condition between $Y'$ and X is satisfied as both variables are transformations of independent random variables and, since the distributions of $Y'$ and Y coincide, $F_{Y'|X}(y|x)=F_{Y'}(y)=F_Y(y)$.

4 Illustration

To present the setup graphically, I choose the linear model given in Eq. (17), with additive and exogenous errors. For transparency, I fix the X marginal at $x=1$, and I set the dependence parameter at $a=0.75$, such that $Y|X=1\sim N(0.75,1-0.75^2)$. The unconditional distribution of Y and the distribution of $\varepsilon$ follow standard normal distributions.

The strategy is as follows. I randomly draw samples from the joint distribution (Y, X) and from the conditional distribution $Y|X=1$ for different sample lengths n. Each realization from the conditional distribution sample is then transformed by Eq. (10), estimated over the joint distribution. The bandwidth parameters are set by the rule of thumb at $h_{0Y} = 1.59 \hat{\sigma }_Y n^{-1/3}$, $h_{0XY}=1.59 \hat{\sigma }_Y n^{-1/3}$ and $h_{1XY} = 1.06 \hat{\sigma }_X n^{-1/3}$, where $\hat{\sigma }_Y$ and $\hat{\sigma }_X$ correspond to standard deviation of samples $\{Y_i\}$ and $\{X_i\}$, respectively. Quantiles of Y are evaluated over the support $[-3.7,3.7]$ to meet the compactness condition. If the value falls beyond that interval, I record it as a fail, and set $\hat{Y}'_i=Y_i$.

The results are presented in two ways. Firstly, for different sample sizes, I plot the histograms of random realizations of independent counterfactuals against the true densities of Y and $Y|X=1$. The outcomes are depicted in Fig. 1.

Fig. 1

Independent counterfactuals. The plots show the true densities of random variables Y and $Y|X=1$ under process from Eq. (17), together with a histogram of a counterfactual sample $\{Y_i'\}$ of an independent counterfactual random variable $Y'$. Vertical lines correspond to the expectations of Y and $Y|X=1$

Secondly, I calculate the MSE of the fitted independent counterfactuals as

$$\begin{aligned} \mathrm{MSE}(\phi (Y,1)) = n^{-1} \sum _{i=1}^n \left( \hat{F}_Y^{-1}(\hat{F}^{-i}_{Y|X}(Y_i|X=1)) - F^{-1}_Y(F_{Y|X}(Y_i|X=1)) \right) ^2, \end{aligned}$$

(22)

where the superscript $-i$ stands for the leave-one-out kernel aggregate. The numbers are aggregated over 1000 runs of process in Eq. (17). The MSE results, together with the average estimation fails, are given in Table 1.

Table 1 Average MSE and number of fails of fitted independent counterfactuals from Eq. (17). The numbers are aggregated over 1000 runs

The simulation results suggest that as the sample size increases the independent counterfactuals converge to the true unconditional realizations of $\varepsilon$. The number of estimation fails appears to be contained at negligible levels, and clearly would be even lower for wider quantile support.

5 Conclusions

The purpose of this study is to familiarize the Reader with a novel dependence filtering framework. Under mild regularity conditions, and without assuming any specific parametric structure, the method allows to construct a counterfactual random variable which is independent from the effects of given covariates. Under error exogeneity assumption such a counterfactual has causal interpretation, and moreover, one can directly relate the counterfactuals with the distribution of the error component through the probability integral transform.

In settings where a no-dependence scenario can be expressed by specific values of the covariates, for instance, $X=0$, independent counterfactuals can be related to the literature on counterfactual distributions [1, 5, 6]. Whenever $X=0$ is not directly interpretable as independence, the proposed framework offers an attractive alternative to a standard toolkit.

I demonstrate how independent counterfactuals perform in a simple linear model with exogenous and endogenous error terms. In a simulation study, I also show the finite-sample consistency of the method.

The framework offers an easy extension to conditionally independent counterfactuals, along the lines proposed by [8]. It can be also applied to support identification in nonseparable models, statistical tests of independence between the variables or tests of error exogeneity.