Keywords

1 Introduction

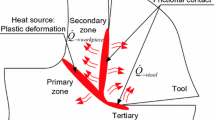
The manufacture of deep holes machining is a rather laborious and demanding technological cutting operation. The complexity of this process is due to the presence of a long mechanical line (metal stem, drilling pipe), perceiving axial, torsional, and bending loads, Fig. 1 [1].

Fig. 1.
figure 1

Deep hole machining scheme: 1—cutting part with cutting and support plates, 2—drilling pipe, 3—work spindle, 4—aligning bushing, 5—machine support stand, 6—machined part.

Full size image

This leads to the problem of the functioning of the cutting tool, remote from the machine spindle at a considerable distance. Due to the uneven rotation of the tool, due to the elasticity of the line and variable moment and axial cutting force, various dynamic phenomena occur in the “machine-cutting tool-part” system, which lead to a loss in the accuracy of the dimensions and location of the surfaces, as well as to a decrease in the quality of the machined surface of the part. In addition, when developing a deep-drilling machining technological operation, specialists have to solve issues related to the formation and removal of chips from the hole, supply of cutting fluid (coolant) to the cutting zone, reduction of torsional longitudinal vibrations of the cutting tool, deformation of the drill bit, etc.

In this regard, two characteristic causes of the emerging dynamic phenomena in the operation of deep-drilling machining should be distinguished. For the first reason, we attribute the dynamic processes due to the mechanical interaction of the cutting part of the tool (Fig. 1, position 1) with the workpiece surface in the technological system “machine-cutting tool-part.” The second reason should be associated with thermal processes caused by internal and outer heats sources during the interaction of the cutting part of the tool with the part and forced cooling of the cutting zone.

At present, a sufficient number of works are devoted to the optimization of the technology for manufacturing deep holes machining and to improve the quality indicators of the finished part. For example, works [2,3,4,5] are devoted to the analysis of dynamic processes when drilling deep holes machining. However, there are still unanswered questions related to the study of the dynamics of a mechanical system.

The study of thermal processes due to the mechanical interaction of the tool with the part and the resulting frictional forces and the fluxes of heat in the technological system is associated with great mathematical difficulties. Whereas the Mathematical Theory of Conductivity and Mass Transfer is quite well developed.

This is due, first of all, to the difficulty of setting up an adequate experiment and obtaining experimental data that make it possible to compare the results of analytical calculations with experimental data.

This article sets out an approach to the study of thermal processes in the technological subsystem “tool-part” as applied to the process of deep hole drilling machining and related dynamic processes.

Hereinafter, following the work of Professor A. Reznikov, we will operate with the concept of “technological subsystem,” which is one of the components of the overall technological system that ensures the performance of specified technological processes or operations [6].

2 Statement of the Problem

It is known that in any technological subsystem heat sources can be internal or external. Internal sources arise in the subsystem itself as a result of the working process, for example, during the operation of equipment and the directly proceeding cutting process. In the latter case, heat is generated due to the forces of friction between the material and the tool, as well as the deformation of the processed material. External sources (or heat sinks) are supplied to the subsystem independently of internal sources. In the process of drilling, forced cooling of the material and tool is carried out, i.e., drains of heat occur.

As a result of this, in the technological subsystem “tool-part” under consideration, heat exchange between components is carried out by at least two existing methods: thermal conductivity and convection. We believe that there is no thermal radiation here.

Heat sources during metal cutting occur on the front surface of the tool, on the surface of the workpiece immediately proximate to the tip point and in the chips removed [6, 7].

For a detailed discussion of heat transfer methods, we distinguish the following heat chains: “heat source-workpiece”; “heat source-chips”; heat source-tool”; “heat source-cooling liquid.” Each of them is enumerated as follows—1, 2, 3, 4 correspondingly.

In the first three heat chains, heat sources are internal sources. Heat exchange between the components is carried out by thermal conductivity. In the last heat chain, heat energy is transferred from the cooling medium to the tool and vice versa by convective heat transfer. It is external to the heat source.

Thus, in the study of thermal processes, one should consider the differential equation of conduction of heat for a solid and the system of differential equations describing convective heat transfer in an incompressible fluid (i.e., heat propagation in forced convection).

Since the cutting edges of the tool rotate when drilling along the radius of the hole, it is advisable to consider the one-dimensional problem conduction of heat. The main relations are taken in the following form.

The differential equation of conduction of heat is given by [8, 9]

$$\frac{{\partial^{2} T\left( {\xi ,\tau } \right)}}{{\partial \xi^{2} }} - \frac{1}{a}\frac{{\partial T\left( {\xi ,\tau } \right)}}{\partial \tau } = 0 .$$
(1)

Here T is the temperature; ξ is coordinate in the direction of the cutting edge of the drill, Fig. 1; a is the coefficient of thermal diffusivity; τ is time.

Convective of heat transfer is described by a system of equations [6]

$$\frac{{\partial ^{2} T\left( {x,\tau } \right)}}{{\partial x^{2} }} - \frac{1}{a}\left( {\frac{{\partial T\left( {x,\tau } \right)}}{{\partial \tau }} + u\frac{{\partial T\left( {x,\tau } \right)}}{{\partial x}}} \right)\, = 0;\,\rho \frac{{du}}{{d\tau }} = \rho g_{x} - \frac{{\partial p}}{{\partial x}} + \mu \frac{{\partial ^{2} u}}{{\partial x^{2} }} .$$
(2)

Here u is the fluid velocity in the x-axis direction; ρ is the density of the liquid; p is the pressure at a given point in the flow; μ is dynamic coefficient of viscosity of a fluid.

On solving Eqs. (1) and (2) the initial and boundary conditions are stated.

Differential Eq. (1) is satisfied by several types of solutions. These are the source solution, the error function solution, the solutions in exponentions, etc. [8].

An analytical solution to the system of differential Eq. (2) is associated with mathematical difficulties and can be obtained for simple cases that are far from real heat transfer conditions in technological systems [6]. However, this problem can be considered using the theory of regular thermal regime developed by Kondratyev [10]. In this theory, the assumption is made that the temperature of any point on the body changes exponentially for the period of the regular cooling regime

$$T\left( {x,\tau } \right) = T\left( x \right)\exp \left( { - m_{0} \tau } \right)\,m_{0} = \psi \lambda \frac{S}{V}$$
(3)

Here T (x) is the temperature of the point along the x-coordinate at the moment corresponding to the beginning of the regular mode process (τ = 0), m0 is the cooling rate, 1/s; ψ is coefficient of non-uniformity of the temperature field; λ is the coefficient of thermal conductivity of the medium; S and V are the surface area and volume of the cooled body, respectively.

3 Description of the Approach and Derivation of the Basic Equations

The considered relations (1)–(3) cannot be applied to the study of thermal processes in the operation of deep holes machining drilling. They do not take into account the features of the technology for manufacturing such holes, which include the following fundamental differences.

  • The power spent on heat transfer should be determined taking into account the assessment of the dynamics of the mechanical drive of the machine in the subsystem “cutting part-machine spindle.” This is explained by the presence of a long force line (from the machine spindle to the interaction surface of the cutting part of the tool with the part) and the oscillations arising in the system as a result of variable actions [4, 5].

  • In the system under consideration, frictional forces of various nature and values arise, which include hydraulic friction, boundary friction, dry friction, etc. Therefore, friction losses will be different [11].

  • The influence of foreign particles (chips, metal particles, abrasive particles, etc.) that fall between the support elements and the wall of the hole and affect the friction process should be taken into account. The friction process will be variable.

  • Coolant enters the radial clearance between the cylindrical surfaces of the tool head and the hole. Thus, lubrication and heat removal from the contacting surfaces of the tool and the metal layer, which is removed in the form of chips, are carried out.

Taking into account that in the process of mechanical interaction of the cutting part of the tool with the metal of the part, the prevailing force factor is the friction force, which is converted into heat flux; the heat flux can be estimated by the friction coefficient taking into account the dynamics of the deep-drilling process. The methodology for studying the dynamic phenomena of this process is described in [1, 4, 5, 12, 13].

We write the equation of the total resistance moment acting on the cutting part of the drill as the sum of functions depending on all the characteristic cutting parameters and the forces acting on the cutting part, in the form [4]

$$M_{r} \left( \varPhi \right) = \varPhi^{'} + \varPhi_{0}^{'} + \varPhi_{0}^{''} + \varPhi_{0}^{'''} .$$
(4)

Here Mr is the moment of resistance; Ф′, Ф′0, Ф′′0, Ф′′′0 are functions depending on all specific cutting parameters and forces acting on the cutting part.

In the process of drilling, power is consumed N, which can be determined by the formula [4]

$$N = M_{r} \varOmega ,$$
(5)

where Ω is angular speed of the head rotation.

In addition, the power in the cutting zone (NT) is spent on heat transfer in different directions. We write the ratio of the power in the cutting zone spent on heat transfer in these directions

$$N_{T} = \sum\limits_{i = 1}^{k} {\frac{{\Delta T_{i} }}{{R_{i} }}} ,$$
(6)

Here ΔTi is a temperature drop in each heat transfer channel; Ri is thermal resistance in each i-th channel.

It means that any channel absorbs as much heat as its heat transfer resistance allows for.

According to [4, 11, 14], the heat resistance during the heat transfer without formation of any protective films can be found by

$$R_{i} = \frac{{\Delta_{i} }}{{f_{i} \cdot \lambda_{i} }} ,$$
(7)

where Δi is a distance of the heat wave or depth of the layer in question; fi is area of the contact; λi is coefficient of heat conductivity of the channel.

The depth of the layer can be evaluated by comparing it with the depth of the heat wave penetration [4], which variation can be accepted exponentially

$$\Delta_{i} = \sqrt {\frac{{a_{{}} \tau }}{\pi }} \exp \left( \nu \right) .$$
(8)

Here ν is a share of the heat fluctuations amplitude at the depth Δi; a is thermal diffusivity, which is definable by a standard equation a = λ/(cp ρ) via heat conductivity λ, specific heat capacity c and metal density ρ; and τ is time of propagation of the heat front.

The Eq. (8) allows to define the border of the heat effect propagation during τ, s. Supposingν = 0, and inserting the thermal and physical parameters of the steel into the Eq. (8)

$$\Delta_{i} = 0,02\sqrt \tau ,{\text{m}}.$$
(9)

Supposing that they are arranged radially, the contact time of blades with each radial line of contact in the heat chain of “heat source-workpiece” shall be evaluated as follows:

$$\tau_{1} = \frac{h}{{\varOmega^{{}} r}} ,$$
(10)

where h is blade thickness; r is radius of the actual point of the cutting edge.

In accordance with this, the thermal resistance of the heat transfer channel to the part can be rewritten in the form

$$R_{1} = 0,002\frac{{\sqrt {hr_{{}} \varOmega } }}{\lambda } .$$
(11)

The heat resistance of the channel “heat source-cooling liquid” can be defined on the assumption that the liquid, cooling the heat source, absorbs energy as [9]

$$Q = \rho_{cool} c_{cool} q_{cool} \Delta T ,$$
(12)

Here ρcool, ccool, and qcool are density, heat capacity, and flow of the cooling liquid correspondingly.

Taking into account, that Q = ΔT/R, and equalizing these relations, the required value can be found

$$R_{4} = \frac{1}{{\rho_{cool} c_{cool} q_{cool} }} .$$
(13)

The Eq. (13) is true in case of absence of any films on the cooled surfaces and for the liquid without air or gaseous bubbles, which change density and heat capacity of the medium. In real conditions, the cooling liquid in the cutting zone interacts with the heated surface and forms oxides films. The gaseous phase appears in the cooling liquid at the very moment of the contact. Jointly, these factors can significantly change the heat resistance of the heat transfer channel.

For the heat chains “heat source-chips” and “heat source-tool,” the relation between the contact time τ2,3 and contact area f2,3 for the chips and tool can be written as follows with their equality evident:

$$\tau_{2} = \tau_{3} = \frac{\eta }{{\varOmega^{{}} r}},\,f_{2} = f_{3} = b_{{}} \zeta$$
(14)

Here η is the coefficient of the chips thickness shrinkage; ζ is the length of the contact line of the chips with the lead surface of the cutting part; b is the width of the contact or total length of the cutting edges. These quantities are known and are determined from the geometrical parameters of the drill.

It is known that a necessary condition for the distribution of heat is the presence of a temperature gradient [9]. Since during the cutting process the heat in the part spreads over the volume surrounding the contact point with the cutting edge, it is advisable to describe the heat transfe,r in this case, using the Fourier’s law of thermal conductivity: q = −λ grad T. Here q is density of the heat flux; i.e., the quantity of heat through in unit area per unit time. Then for a unidirectional flow of the heat and one-dimensional temperature field, we can write the following equality [4, 14]:

$$\frac{c}{f}\frac{dT}{d\tau } = - \lambda \frac{dT}{d\xi } .$$
(15)

Here f is an area of contact of the cutting edge with the workpiece; ξ is a coordinate of actual point of the heat propagation line.

After integration (5) in reference to the coordinate ζ and appropriate transformations taking into account (7), (8), (11), the dependence between the heat propagation velocity and rotation speed of the drill (spindle). The final formula is of the form

$$\frac{dT}{d\tau } = - \frac{\lambda \sqrt \pi }{c}\Delta T\sqrt {\frac{h}{{a^{{}} \varOmega^{{}} r}}} .$$
(16)

Here, ΔT is a temperature drop along the line of propagation of the heat front; h is the thickness of the blade; τis the contact time of the blade with a point on the surface to be treated.

Variable effects cause mechanical oscillations in the system “cutting part-spindle.” After stronger oscillations, assessment of the dynamic aspects of the mechanical drive of the machine is a must. A summary of this issue is provided in the articles [11, 14].

4 Conclusions

It is obvious that upon contact of the cutting edge of the tool with the surface of the hole at each point, an unsteady temperature field occurs, i.e., there is a heat flow variable in time. If we consider its value to be maximum when the cutting edge passes at a strictly fixed point, then attenuation will occur with distance from it in any direction along the generatrix of the curved surface.

Comparing the foregoing with the arguments of Reznikov [7] that in a cutting process the initial temperature is assumed to be constant at each point on the surface of the hole, the following can be said. This approach is not entirely correct in conditions of drilling deep holes machining, although we explain the sufficiency of cooling.

However, even with small dimensions of the part, and even more so when drilling, cooling may not be enough. In these cases, there will be a constant increase in the temperature of the part, which should be aggravated by the friction of the guide elements of the drill having a large contact area.

Due to the fact that the blade movements are not uniform, dynamic phenomena lead to pulsation of the heat flux, which affects the friction coefficients, and hence the cutting forces.

The study of the dependence of the coefficient of friction and heat fluxes during deep hole drilling is outlined briefly in [11]. The authors are ready to present a more detailed presentation of this issue in a full-length article.