Keywords

1 Introduction

About 30% of finishing operations for tempered steel parts in contemporary machine engineering is plane grinding with wheel periphery (PGWP). This operation is done by computerized numerical control (CNC) machine tools. The performance management for plane grinding operations is done by incremental changing of programmatic feed rates using controlling software during each part’s grinding cycle. However, contemporary machine production establishments still face problems associated with the lack of AWCS systems and regulatory references for the selection of optimized cutting modes for PGWP operations performed by CNC machine tools. Therefore, the actual production lacks full automation of controlling software for plane grinding CNC tools, and the incremental feed change cycles are defined manually, thus reducing the grinding rates in order to keep the set quality of surface processing. This problem occurs due to the absence of a set of mathematical models that would allow automated planning for optimized feed cycles and other cutting modes maintaining the quality of surface finish when processing part batches under unstable grinding conditions and taking into consideration various processing requirements and restrictions associated with machines, grinding tools, workpieces, and processing organization conditions. One of the key tasks to solve the problem is the development of a mathematical model that would establish the relationship of the cutting force and the processing mode (axial and radial feed, wheel and workpiece movement rates), as well as basic processing parameters (wheel specifications and its bluntness index, the geometrical parameters of the contact area of the wheel and the workpiece, physical and mechanical characteristics of the processed metal, etc.) [1,2,3], and take into consideration the following features of the processes taking place during PGWP operations done by CNC tools:

  1. 1.

    The processing is controlled simultaneously by incremental axial and radial feed cycles and workpiece plate feed;

  2. 2.

    A standard PGWP cycle consists of the direct and the reverse stroke; each stroke includes the cutting-in stage to the value of radial feed (cutting-in only takes place in the initial cross-section of the processed surface, thus leading to selecting another processing modes for other cross-sections);

  3. 3.

    Instable grinding conditions due to various grinding scenarios and the alternating contact area between the wheel and the workpiece;

  4. 4.

    Varying conditions during the grinding of the surfaces increase the instability of grinding conditions and lead to various processing inaccuracies in certain cross-sections.

2 Analytical Simulation of the Relations Between the Cutting Force and the Elastic Distortion of a Process System During Plane Grinding

Due to the presence of elastic movements in the processing system and the inertance of displaced masses (the plane and the workpiece), the actual feed ∆tf with the incremental shift of programmatic feed ∆tp, changes smoothly and is not equal to the programmatic feed increments values. Thus, the programmatic feed ∆tp, cannot be used to calculate the basic time TO [4,5,6].

The actual feed ∆tf by the end of a cycle stage is conditionally equal to the programmatic feed ∆tp, though it is possible that in some cycles the actual feed cannot reach the programmatic value [7,8,9,10,11]. Figure 1 shows the graphs of programmatic and actual feeds for a two-stage automated cycle. The programmatic feed for the first stage is shown in the bold line and ∆tp = 0.02 mm. The graph chart shows that the actual feed ∆tf per each stage stroke approaches the programmatic value, but it is only reached at stroke 40. Then the second stage begins where ∆tp = 0.005 mm and ∆tf continues approaching the programmatic value until the end of the second stage of the cycle. The presence of clearances in the drive train of the machine tool and the elastic flexibility of processing system units leads to the discrepancies between the actual radial feed and programmatic values.

Fig. 1.
figure 1

Feed graphs for two-stage PGWP cycle with double stroke.

Full size image

Therefore, the removal of metal during the grinding operation in a processing system (PS) shall be done while taking into consideration the flexibility γ and elastic distortion y of the PS that bind the actual feed ∆tf, the programmatic feed ∆tp, and various processing parameters (physical and mechanical properties of the processed material, workpiece diameter, etc.).

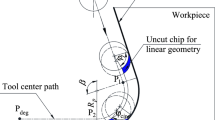
Let us look at a schematic representation of programmatic ∆tp and average actual ∆tf feeds in an automated two-stage grinding cycle for a hypothetical, fully flattened workpiece.

In order to create a mathematical model for the relationships between elastic distortions and technological parameters, we will use the known empirical interrelations [12,13,14,15,16,17], while considering the specific features of PGWP. To this end, we shall draw a graph of accumulated feeds (Fig. 2), and mark the dimension chain on it, where \(\sum t_{{p_{z,i} }}\) is the accumulated programmatic feed, \(\Delta t_{{p_{z,i} }}\) isthe programmatic feed per 1 stroke, \(t_{{t_{z,i} }}\) isthe processing tension, \(\sum t_{{f_{z,i - 1} }}\) is the accumulated actual feed, \(\Delta t_{{f_{z,i} }}\) is the actual feed per 1 stroke, z is the stage, i is the stroke.

Fig. 2.
figure 2

Standard feed graph for two-stage PGWP cycle with double stroke.

Full size image

In order to establish the regularities in actual feed changes within the processing cycle, we shall look at the design diagram of the relationships between the programmatic and actual feeds with elastic distortions of the PS. The graph shows the values of accumulated programmatic and actual feeds for the i-th stroke of the z-th stage along the reference axes, calculated as sums of the corresponding feeds for every wheel stroke. Let us find the actual feed for the i-th stroke of the z-th stage using a restricted dimension contour. The restricted dimension contour for a cycle with direct stroke (DS) and reverse stroke (RS) when both are operational looks the following way (Fig. 3a and 3b, bold line):

Fig. 3.
figure 3

Feed accumulation bar graph for two-stage PGWP cycle with double stroke and dimension chain.

Full size image
$$\Delta t_{{p_{z,i} }}^{{{\text{DS}}}} + y_{z,i - 1}^{{{\text{RS}}}} = \Delta t_{{f_{z,i} }}^{{{\text{DS}}}} + y_{z,i}^{{{\text{DS}}}}$$
(1)
$$\Delta t_{{p_{z,i} }}^{{{\text{RS}}}} + y_{z,i - 1}^{{{\text{DS}}}} = \Delta t_{{f_{z,i} }}^{{{\text{RS}}}} + y_{z,i}^{{{\text{RS}}}}$$
(2)

The analysis of Eqs. (1–2) and works [1, 7, 18], shows that the current value of the actual radial feed is in direct relationship to the elastic distortion delta between the current and the previous stroke. Thus, we can produce the following universal mathematical notation:

$$\Delta t_{{p_{z,i} }} + y_{z,i - 1} = \Delta t_{{f_{z,i} }} + y_{z,i}$$
(3)

One stroke makes evident the relationship between the programmatic and actual feeds via the elastic movements (elastic releases of the machine-device-tool-part system) \(y_{{f_{z,i} }}\), i.e., it is basically the difference between the programmatic and actual feeds at the current operational stroke:

$$y_{{f_{z,i} }} = \gamma Py_{{f_{z,i} }}$$
(4)

The accumulated programmatic feed is the sum of processing tension and the accumulated actual feed for i-th stroke of z-th cycle stage. The equation looks as follows:

$$t_{{p_{z,i} }} = t_{{t_{z,i} }} + t_{{f_{z,i - 1} }}$$
(5)

The processing tension \(t_{{t_{z,i} }}\), in its turn, is the sum of elastic movements per stroke and the accumulated programmatic feed. The equation looks as follows:

$$t_{{t_{z,i} }} = y_{z,i} + \vartriangle t_{{f_{z,i} }}$$
(6)

where \(\Delta t_{{p_{z,i} }}^{{{\text{DS}}({\text{RS}})}}\) is the programmatic value of the radial feed for the direct (reverse) stroke in mm/dx.str.; \(y_{z,i}^{{{\text{DS}}({\text{RS}})}}\) is the elastic distortion of the wheel axis for the direct (reverse) stroke; \(\Delta t_{{f_{z,i} }}^{{{\text{DS}}({\text{RS}})}}\) is the actual radial feed for the direct (reverse) stroke in mm.

Equations (4–6) above lead us to the following pars:

$$t_{{t_{z,i} }} = y_{z,i} + \Delta t_{{f_{z,i} }} = t_{{p_{z,i} }} - t_{{f_{z,i - 1} }}$$
(7)
$$t_{{t_{z,i} }} = \gamma P_{{y_{z,i} }} + \Delta t_{{f_{z,i} }} = t_{{p_{z,i} }} - t_{{f_{z,i - 1} }}$$
(8)

From [1], we know how to calculate Py using the average actual feed per stroke

$$P_{y} = \kappa_{1} \Delta t_{{f_{z,i} }}^{{{\text{me}}}} + \kappa_{2} \sqrt {t_{{f_{z,i} }}^{{{\text{me}}}} }$$
(9)

where K1 and K2 are the constituents of Eq. 9. They used for the simpler and more apparent representation of the equation from [19], and they look, respectively, as follows:

$$\begin{aligned} \kappa_{1} = V_{p} B\frac{{\sigma_{i} \varepsilon_{i} tg_{\beta } }}{{V_{\kappa } }} \\ \kappa_{2} & = B\frac{{\sigma_{i} }}{3}\sqrt D \\ \end{aligned}$$

In order to establish the correlation, it is necessary to use this equation because the average actual feed, in this case, equals the actual feed per stroke.

Thus, by introducing expression Eq. 8, into Eq. 9, we can get this

$$K_{1} \cdot \Delta t_{{f_{z,i} }}^{{{\text{me}}}} + K_{2} \cdot \sqrt {\Delta t_{{f_{z,i} }}^{{{\text{me}}}} } + \Delta t_{{f_{z,i} }}^{{{\text{me}}}} = t_{{p_{z,i} }} - t_{{f_{z,i - 1} }}$$
(10)

Then it is necessary to group the variables using mathematic transformations for the further expression of the average actual feed taking into consideration the elastic movements of the processing system during the processing. For the sake of convenience, let us move all the components to one side and make them equal to zero. Then let us group and factor out Eq. 10, to get Eq. 11

$$\sqrt {\Delta t_{{f_{z,i} }}^{{{\text{me}}}} } = \frac{{ - \gamma K_{2} }}{{2(\gamma K_{1} + 1)}} + \sqrt {\left( {\frac{{\gamma K_{2} }}{{2(\gamma K_{1} + 1)}}} \right)^{2} - \frac{{4(\gamma K_{1} + 1)\left( {t_{{f_{z,i - 1} }} - t_{{p_{z,i} }} } \right)}}{{4(\gamma K_{1} + 1)^{2} }}}$$
(11)

Having solved the equation relative to \(\sqrt {\Delta t_{{f_{z,i} }}^{{{\text{me}}}} }\), we receive the following equation of the relationship between the feeds, elastic distortions, and processing parameters:

$$\Delta t_{{f_{z,i} }}^{{{\text{me}}}} = \left( {\frac{{ - \gamma K_{2} }}{{2(\gamma K_{1} + 1)}} + \sqrt {\left( {\frac{{\gamma K_{2} }}{{2(\gamma K_{1} + 1)}}} \right)^{2} - \frac{{t_{{f_{z,i - 1} }} - t_{{p_{z,i} }} }}{{\gamma K_{1} + 1}}} } \right)^{2}$$
(12)

The calculation using Eq. 12, starts with the first stroke of the cycle. For the first stroke it is \(t_{{f_{z,i - 1} }} = 0\), for the second, it is \(t_{{f_{z,i - 1} }} = \Delta t_{{f_{1,1} }}^{{{\text{me}}}}\), etc.

Thus, we have established the correlation between the actual feed, elastic distortions, and technological parameters of Plane grinding with wheel periphery for double operating stroke.

3 Practical Significance, Proposals and Implementation Results, Experimental Results

The comparison and adequacy analysis was performed using experimental data [20], received during plane grinding. During the workpiece processing, the following parameters were used: wheel: 500 × 20 × 203 25A BM1 12К5; material: 1045 steel; cutting mode: Vw = 35 mps; B = 20 mm; t = 1 mm; Vp = 400 mm/min. In order to compare the calculated and experimental data, we built a graph shown in Fig. 4, where experimental data are marked as open circles and calculated data are filled circles and a line.

Fig. 4.
figure 4

Comparison graph for calculated and experimental data: a dependence of Py on the graininess of the wheel; b dependence of Py on thehardness of the wheel; c dependence of Py on the structure of the wheel.

Full size image

The comparison of the received and experimental data shows that the difference between them is no greater than 10% which confirms the adequacy of the developed analytical model of relations between cutting forces and technological parameters during the Plane grinding with wheel periphery.

4 Conclusions

Based on work performed, we may draw the following conclusions:

  1. 1.

    The relevance of metal removal modeling in automated cycles of Plane grinding with wheel periphery performed by CNC machine tools is stipulated by the absence of automated planning systems, regulatory references and cycle planning methods satisfying the requirements of modern automated production.

  2. 2.

    The analytical model presented solves the problem of automated PGWP cycle planning and calculation by calculating the actual feeds and cutting forces for the cycle and grinding conditions giving.

  3. 3.

    The proposed calculation methods for automated cycles is based on the establishment of correlations between fundamental regularities of metal flow mechanics in the cutting area, cutting force model, PGWP kinematics, cutting modes, elastic distortions of the processing system associated with the programmatic and actual feeds, which allows the calculation of cycle parameters in a wide variation range of processing factors.