Keywords

1 Defining Dissipative Model Parameters

Considerable damage in modern machines and apparatus for chemical production occurs due to high stresses arising in their components during vibrations. The vibrations are caused by periodic or suddenly applied forces acting both independently and in combination with thermal, static, and other factors [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18].

In practice, the dissipative parameters of model elements are determined experimentally based on the values of damping decrements of the vibrations of individual masses. At the design stage of the chemical production apparatus it is often difficult, and sometimes impossible to obtain experimental data of this type. Therefore, many engineers use data obtained previously by other researchers on similar plants. For power trains and drive systems, the experimental values of the logarithmic decrements of vibrations are given in Tables 1 and 2.

Table 1 Power train damping parameters
Full size table
Table 2 Generalized logarithmic decrements of vibrations
Full size table

The damping coefficient values k of the masses of the given model calculated by Eq. 1 are shown in Table 3.

Table 3 Logarithmic damping decrements of vibrations and model damping coefficients
Full size table
$$k = 2I\omega \lambda ,$$
(1)

where I is the moment of inertia, ω is the partial frequency of mass vibrations, for which k is found.

The damping coefficient of the mixers depends on the physical properties of the mixed media (reaction products).

In Table 3, the partial frequencies ωp of each inertial mass of the model were calculated by the equation:

$$\omega_{pi} = \frac{1}{2\pi }\sqrt {\frac{{C_{\varSigma } }}{{I{}_{i}}}} ,$$
(2)

where Ii is the moment of inertia of the i-th mass; CΣ is the total rigidity of the sections attached to the mass Ii.

2 Construction of Differential Equations of the System

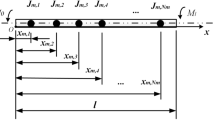
Based on the D’Alembert principle, using the Lagrange equations of the second kind, the motion of a torsionally vibrating nine-mass system under forced vibrations is described by the following system of differential equations:

$$\left\{ {\begin{array}{*{20}c} {I_{1} \ddot{\varphi }_{1} + C_{1,2} (\varphi_{1} - \varphi_{2} ) = M_{\text{mot}} } \\ {I_{2} \ddot{\varphi }_{2} - C_{1,2} (\varphi_{1} - \varphi_{2} ) + C_{2,3} (\varphi_{2} - \varphi_{3} ) = 0} \\ {I_{3} \ddot{\varphi }_{3} - C_{2,3} (\varphi_{2} - \varphi_{3} ) + C_{3,4} (\varphi_{3} - \varphi_{4} ) = 0} \\ {I_{4} \ddot{\varphi }_{4} - C_{3,4} (\varphi_{3} - \varphi_{4} ) + C_{4,5} (\varphi_{4} - \varphi_{5} ) = 0} \\ {I_{5} \ddot{\varphi }_{5} - C_{4,5} (\varphi_{4} - \varphi_{5} ) + C_{5,6} (\varphi_{5} - \varphi_{6} ) = 0} \\ {I_{6} \ddot{\varphi }_{6} - C_{5,6} (\varphi_{5} - \varphi_{6} ) + C_{6,7} (\varphi_{6} - \varphi_{7} ) = 0} \\ {I_{7} \ddot{\varphi }_{7} - C_{6,7} (\varphi_{6} - \varphi_{7} ) + C_{7,8} (\varphi_{7} - \varphi_{8} ) = 0} \\ {I_{8} \ddot{\varphi }_{8} - C_{7,8} (\varphi_{7} - \varphi_{8} ) + C_{8,9} (\varphi_{8} - \varphi_{9} ) = M_{r1} } \\ {I_{9} \ddot{\varphi }_{9} - C_{8,9} (\varphi_{8} - \varphi_{9} ) = M_{r2} } \\ \end{array} } \right.$$
(3)

where I1, I2, … I9 are the inertia moments of the masses; C1,2, C2,3, … C8,9 are the rigidity of their linkages; φ1, φ2, φ9 are the rotation angles of the masses; \(\ddot{\phi }_{1} ,\ddot{\phi }_{2} , \ldots \ddot{\phi }_{9}\) are mass accelerations in oscillatory motion; Mmot is the torque of the electric motor; Mr1, Mr2 are the resistance moments of the first and second mixers.

To solve this system of equations we use the Matlab software package for scientific and engineering calculations [1, 19,20,21]. The description of blocks and algorithms for constructing dynamic models in the Simulink visual modeling environment are discussed in detail in the reference and specialized literature [19, 22]. Based on the system of differential Eq. (3), the dynamic model of the mixer drive in the Simulink visual simulation system is shown in Fig. 1.

Fig. 1
figure 1

Implementation of a system of differential equations in a Simulink environment

Full size image

The above calculation algorithm linearizes the Simulink model, creates a transfer function from the form of the state-space model, searches for the roots of the characteristic equation in the complex plane, constructs the Bode diagrams (amplitude-frequency response, phase response, Fig. 2a) and Nyquist diagrams (amplitude-phase frequency response, Fig. 2b) [1]. The calculation algorithm provides checking the sign of the imaginary part of the obtained roots of the characteristic equation, based on which the own frequencies are sampled (the imaginary part of the root must be greater than 0).

Fig. 2
figure 2

a The resulting amplitude-frequency response and phase-frequency response; b amplitude-phase frequency response of the system

Full size image

Based on the analysis of the Bode (see Fig. 2a) and Nyquist diagrams (see Fig. 2b), the vibration forms for the first four frequencies of the system are found (see Figs. 3 and 4).

Fig. 3
figure 3

a Single-node waveform for a frequency of 52.71 Hz; b two-node waveform for a frequency of 106.38 Hz

Full size image
Fig. 4
figure 4

a Three-node waveform for a frequency of 152.45 Hz; b four-node waveform for a frequency of 496.18 Hz

Full size image

The obtained values of the natural frequencies of the system are shown in Table 4.

Table 4 The calculated values of the natural frequencies of the system
Full size table

3 Conclusion

As we see in the system under consideration, the number of natural frequencies and modes of vibration is one less than the number of masses, that is, the number of forms is 8. Waveforms are referred to by the number of nodes: with one node is a single-node form, with two nodes is a two-node form, etc. The zero form has no nodes and corresponds to the free rotation of the shaft. Each form has its own frequency of natural vibrations. The single-node form corresponds to the natural frequency of the first degree or first order, the two-node form corresponds to the second degree or second order, etc.

Based on the analysis of the Bode and Nyquist diagrams, the vibration forms for the first four frequencies of the system are found (see Figs. 3 and 4). The frequencies from 5th to 8th have high values lying in the range of sound waves. In practice, vibrations with such frequencies have small amplitudes and do not significantly affect the overall dynamic vibrational load of the transmission. Therefore, further analysis is impractical.

Of the total number of frequencies and modes of natural vibrations, of practical interest are only those frequencies whose resonance can cause dangerous stresses in the shaft line of the calculated system. The main source of external uneven load is the electric motor and mixers.

The analysis is given in Figs. 3 and 4 forms showed that the vibration nodes with a significant difference in the amplitudes of the neighboring masses are observed in sections 4–5, 7–8 and 9–10. Moreover, section 4–5 is heavily loaded at all frequencies under consideration.

All found natural frequencies are much higher than the rotational speeds of the motor shaft, which eliminates the occurrence of resonant phenomena in steady-state operating modes. However, transient resonances are possible, as well as resonances with frequencies caused by uneven re-gearing of gear teeth in gears, gear couplings, cardan gears, etc. It is possible to generate high-frequency perturbations caused by the uneven distribution of mixed reaction products on the blades of the mixers, which can also cause resonance phenomena in the drive.

The analysis of the modes of vibration allows one tuning the natural frequencies of the system from the frequencies of external disturbing influences, identify hazardous areas with high dynamic load, and develop a set of measures to reduce this load in order to ensure the reliability and durability of the drive units and assemblies of a chemical reactor.