Detecting Tranquil and Bubble Periods in Housing Markets: A Review and Application of Statistical Methods

Abstract

We provide a brief review of recent developments in research on price movements of real estate, especially bubbles, and highlight the gap between theoretical and statistical approaches to bubble detection. We also propose applying a top-down strategy to a bounds testing method (Pesaran et al. in J. Appl. Econom. 16(3):289–326, 2001) to investigate rational price bubbles. Furthermore, by introducing nonlinearity into the autoregressive distributed lag model, we modify the bounds test to be more suitable for bubble analyses.

The earlier version of this paper was presented at the annual meeting of the Nippon Finance Association. I modified and extended the paper, “A top-down method for rational bubbles: Application of the threshold bounds testing approach” (2016) substantially. I would like to thank Naoya Katayama, Masayuki Susai, and the conference participants for constructive comments. However, all remaining errors are mine. This paper has been prepared for Recent Econometric Techniques for Macroeconomic and Financial Data (Springer).

1 Introduction

Financial bubbles, that is abnormally high asset and real estate prices, are generally believed to be temporary and recurrent and closely associated with investors’ expectations.¹ Because their collapse has catastrophic effects on the standard of living of most people, both policymakers and investors show interest in their identification. However, despite numerous studies,² it is difficult to reach an academic consensus on not only the timing and duration of financial bubbles, but also the definition of bubbles. Indeed, there are many common terms in financial research, such as rational/speculative bubbles, irrational bubbles, intrinsic bubbles, and periodically collapsing bubbles. Further, because financial bubbles and investors’ expectations are unobservable, previous empirical findings are almost always under scrutiny.

Researchers long recognized the significant role of investors’ expectations in asset price determination, and its importance increases during bubble periods. Fama (1970), a Nobel Prize winner in Economic Sciences in 2013, discussed investors’ expectations formation using the information in the context of stock price behaviors, known as the efficient market hypothesis, and provided a statistical framework to test investor rationality. Fama proposed three types of expectations: weak, semi-strong, and strong forms of rational expectations. Investors form weak expectations based solely on historical price data, semi-strong expectations using any relevant publicly available information, and strong expectations based on private information that can be exclusive to a limited number of investors. Since then, much theoretical and empirical research utilized these concepts of expectations, particularly the weak form. However, more recent research tends to consider the market microstructure as an explanation of how private information transmits to investors and affects financial asset prices over time (Easley et al. 2002).

Today, much research provides evidence against investor rationality. One example is noise traders, who possess limited information and behave irrationally, creating significant noise in the market (De Long et al. 1990). Because institutional investors have more time and financial resources to analyze the market, noise traders are often considered private traders. However, there is no clear empirical evidence to conclude whether private or institutional traders are the main driver of noise and financial bubbles. Nagayasu (2018) showed that the transactions of private traders in real estate markets can explain historically high price movements. Choi and Skiba (2015) concluded that institutional herding helped stabilize securities prices in 41 global markets. In contrast, Choi et al. (2015) showed that private traders tend to engage in contrarian trades in Korea, and Zeng (2016) concluded that institutional traders also create noise in the US market.

Traditionally, financial studies referred to irrational behaviors as a market anomaly, akin to the January effect (Rozeff and Kinney 1976) and the Monday effect (Gibbons and Hess 1981). The January effect refers to the phenomenon of asset price increases in January and the Monday effect to price behaviors on Monday that are similar to those on Friday. Conventional economic theory based on profit maximization behaviors cannot explain these price movements. Similarly, other factors such as weather conditions (Hirshleifer and Shumway 2003) also influence market participants, who react more to bad news than to good news (De Bondt and Thaler 1985). Abreu and Brunnermeier (2003) showed that even rational behaviors create persistent deviations of financial prices from economic fundamentals if investors’ coordination fails in selling strategies.

Despite evidence of investor irrationality, most empirical investigations and statistical approaches were proposed within a framework of rational expectations. One popular method is based on the statistical concept of integration. For example, integration studies characterize a weak form of market efficiency as a random walk. Given that asset prices and their determinants (i.e., economic fundamentals) are non-stationary, the lack of cointegration is a traditionally considered evidence of financial bubbles. Typically, unit root and cointegration tests are left-tailed tests designed to detect periods of economic equilibriums, which is reflected in their alternative hypotheses, $\rho <1$, where $y_t=\rho y_{t-1}+\epsilon _t$ and $\epsilon _t$ is a white noise error, as a simple example.

Recently, Phillips et al. (2011) and Phillips et al. (2015) proposed recursive and rolling explosive unit root tests, where they examined the null hypothesis of the unit root $(\rho =1)$ against the alternative of an explosive case $(\rho >1)$. The authors developed these tests to deal with potential statistical problems related to unique price movements characterized as periodically collapsing bubbles (Evans 1991). Since then, explosive tests became a popular analytical tool. However, the advantage of explosive tests may become a potential problem in financial research. Because both the null and alternative hypotheses of explosive tests consider persistent deviations from economic fundamentals, these tests preclude the possibility of tranquil moments that the economy is expected to maintain and in which economists show the most interest.

Against this background, we will critically review recent developments in the statistical methods to investigate financial bubbles. Furthermore, as an extension to traditional approaches, we propose applying a top-down method to a threshold autoregressive distributed lag (T-ARDL) model to study housing markets. This statistical method is not an answer to all questions and criticisms in studies of financial bubbles, but it has interesting features that other popular methods do not share.

2 The Theoretical Concept of Rational Bubbles

The main objective of this study is to review statistical methods, but it is still important to understand the underlying economic theory of financial bubbles in order to specify a composition of statistical models. As discussed, recent research casts doubt on the rationality of investors, but many economic analyses maintain this assumption and it is often explained using the present value model (PVM). The rationality assumption prevails in academic research largely for convenience; it is easier to model rational behaviors than irrational ones. Survey data on investors’ expectations are the best source of information about investors’ expectations, but in the absence of survey data for a comprehensive number of countries and infrequent dissemination of survey data, we also maintain the rationality assumption.

According to the PVM, rational bubbles are defined as sizable and persistent deviations from economic fundamentals and follow a non-stationary process in a statistical sense. Based on the definition of asset returns or returns on real estate ($r_{t+1}=(P_{t+1}+D_{t+1})/P_t - 1$), the PVM suggests that the contemporaneous prices ($P_t$) will be determined by the expected value of future economic fundamentals (D) and prices:

$$\begin{aligned} P_t = E_t \left[ \frac{P_{t+1}+D_{t+1}}{1+r_{t+1}} \right] \end{aligned}$$

(1)

where t denotes time ($t=1,\ldots ,T$) and E is an expectation operator. D is an economic fundamental, such as dividend payments in equity analyses or rental costs in housing analyses. Solving Eq. (1) forwardly and using the law of iterated expectations, we can obtain Eq. (2):

$$\begin{aligned} P_t = E_t \left[ \sum _{h=0}^\infty \left( \prod _{k=0}^h \left( \frac{1}{1+r_{t+k}}\right) \right) D_{t+h}+ \underset{h\rightarrow \infty }{\text {lim}} \prod _{k=0}^h \left( \frac{1}{1+r_{t+k}} \right) P_{t+h} \right] \end{aligned}$$

(2)

When P and D are cointegrated, and when the transversality condition holds (i.e., $E_t [\text {lim}_{h\rightarrow \infty } \prod _{k=0}^h ( \frac{1}{1+r_{t+k}} ) P_{t+h} ]\rightarrow 0$), then the result shows no evidence of bubbles. Therefore, in this case, asset prices tend to move along with the economic fundamentals. On the other hand, when these conditions do not hold, then the results indicate evidence of bubbles. For this reason, prior studies frequently investigated rational bubbles using integration methods.

In the standard setting, r is often assumed to be constant over time. Then, we can simplify Eq. (2):

$$\begin{aligned} P_t = E_t \left[ \sum _{h=0}^\infty \left( \frac{1}{1+r}\right) ^h D_{t+h}\right] + E_t \left[ \left( \frac{1}{1+r}\right) ^h P_{t+h} \right] \end{aligned}$$

(3)

It follows that the current price comprises the present value of the market fundamentals ($P^*_t=E_t [ \sum _{h=0}^\infty ( \frac{1}{1+r} )^h D_{t+h} ]$) and bubbles ($B_t=E_t [ ( \frac{1}{1+r} )^h P_{t+h} ]$). In short,

$$\begin{aligned} P_t=P^*_t+B_t \end{aligned}$$

(4)

Furthermore, subtracting a multiple of D from both sides of Eq. (3) and assuming that the transversality condition ($B_t\rightarrow 0$) holds,

$$\begin{aligned} rP_t-D_t = E_t \left[ \sum _{h=0}^\infty \left( \frac{1}{1+r}\right) ^h \Delta D_{t+h}\right] \end{aligned}$$

(5)

This is probably the most popular theoretical explanation of a financial bubble and has been applied to the analysis of not only housing markets, but also the financial markets of equities and foreign exchange rates. Additionally, this model has been extended in many ways, such as by accommodating a time-varying r. Furthermore, as an extension to this model, Froot and Obstfeld (1991) proposed a concept of intrinsic bubbles that can be born out of rational behaviors and the fundamental determinants of asset prices. Intrinsic bubbles are created by a nonlinear function of the fundamentals. They proposed the following intrinsic bubble equation, which replaces $B_t$ with $P^{*\gamma }_t$ in Eq. (4):

$$\begin{aligned} P_t=P^*_t+ aP^{*\gamma }_t \end{aligned}$$

(6)

When $a\ne 0$, then a bubble exists in the market. Using dividends as the economic fundamental in the analysis of the UK stock prices, they argued that a nonlinear solution to asset prices was consistent with investors’ overreaction to news and showed that this concept offers a better explanation of stock prices than does the standard PVM.

While intrinsic bubbles are an alternative formation of bubbles and provide additional information about sources of rejecting the relationship between asset prices and economic fundamentals, we do not focus on this concept because the most recent statistical models are based on a linear PVM, as in Eq. (5). Furthermore, intrinsic bubbles are sensitive to the specification of the evolution of bubbles using economic fundamentals; moreover, an intrinsic bubble component is very small compared with the regime-switching components in the standard stock price model (Driffill and Sola 1998).

Another drawback of the standard PVM is that it is not possible to distinguish between positive and negative bubbles. Negative bubbles occur during periods of low asset prices and positive bubbles at times of high prices. There is a conceptual problem for negative bubbles because very low prices are not regarded as financial bubbles conventionally.³ Therefore, it is price levels rather than the level of inflation that should serve as a criterion to determine bubble periods. In fact, distinguishing between negative and positive bubbles was discussed before. Blanchard and Watson (1982) proposed several evolution processes of bubbles, and similarly, Diba and Grossman (1998) described the evolution of bubbles as follows:

$$\begin{aligned} E(B_t)=(1+r)B_t \end{aligned}$$

which states that bubbles are independent of asset prices and generated by themselves. Then, we can state the expected value of bubbles following Blanchard and Watson (1982) as

$$\begin{aligned} \lim _{i \rightarrow \infty } E(B_{t+i})= & {} +\infty \quad \text {if}\ B_t>0 \\= & {} -\infty \quad \text {if}\ B_t<0 \end{aligned}$$

It follows that when $B_t>0$, there is a chance of a bubble. On the other hand, when $B_t<0$, $E(B_{t+i})$ may become large and negative in the future, which will make $P_t$ negative. Negative prices are not realistic for most financial assets and real estate because in these cases, the solution to the model should be a case of no bubbles (Blanchard and Watson 1982).

3 Econometric Methods

Econometricians proposed many statistical methods, with statistical hypotheses that seem designed to be suitable from their perspectives. Consequently, some approaches were developed to look for tranquil periods, while others investigate financial bubbles. Unlike previous studies, we make a clear distinction between statistical approaches to determine tranquil and bubble periods. This distinction is important since differences in the statistical hypotheses can explain the different results from these two approaches. In this section, we will clarify these two approaches using popular statistical specifications in studies of bubbles.

To investigate the theoretical model and predictions in Eq. (2) quantitatively, previous studies often focused on a single market utilizing time series methods. These statistical methods are one-tailed tests, but can be broadly categorized into left- and right-tailed approaches according to their alternative hypotheses. The left-tailed test is classical and is designed to look for cointegration between prices and economic fundamentals, and thus revealing tranquil periods. As an extension, we also propose a nonlinear approach that can be classified into a group of left-tailed tests. On the other hand, the right-tailed test, which has become popular, is an approach to identify explosive bubbles.

3.1 Classical Approaches

Left-tailed integration tests are classical approaches. Indeed, the majority of previous analyses used this conventional approach; in particular, the relationship between housing prices and their economic fundamentals was investigated by a cointegration method (Engle and Granger 1987). The concept of cointegration is widely accepted by economists who established a theoretical framework to identify economic equilibrium conditions and led to Prof. Granger receiving a Nobel Prize (2003). Today, many applied studies used this concept to analyze housing markets worldwide (Hendry 1984; Meese and Wallace 2003; McGibany and Nourzad 2004; Gallin 2006; Adams and Fuss 2010; Oikarinen 2012; De Wit et al. 2013). Because most economic and financial data, including real estate prices and their economic fundamentals, follow a non-stationary process (e.g., Nelson and Plosser (1982), cointegration was considered appropriate to test their long-run relationship and bubbles.

The concept of cointegration can be summarized by rewriting it as a dynamic bivariate relationship. More specifically, to derive the long-run relationship between housing prices $(y)$ and covariates $(x)$, for the period (${t} = 1, \ldots , {T}$), consider the following dynamic equation:

$$\begin{aligned} y_t=\alpha _0+\rho _1 y_{t-1}+\beta _0 x_t+\beta _1 x_{t-1}+u_t \end{aligned}$$

(7)

where the residual u is normally distributed $(u_t \sim \textit{N}(0,\sigma ^{2}))$. Both $x$ and $y$ are in natural the logarithmic form and are assumed to exhibit persistence, in line with many economic and financial variables. Then, we can transform Eq. (7) as follows:

$$\begin{aligned} \Delta y_t=\alpha _0+\beta _0 \Delta x_t+(\rho _1 - 1)\left( y_{t-1}+\frac{\beta _0+\beta _1}{\alpha _1 -1}x_{t-1}\right) +u_t \end{aligned}$$

(8)

or simply

$$\begin{aligned} \Delta y_t=a+b\Delta x_t+c_1(y_{t-1}+f x_{t-1})+u_t \end{aligned}$$

(9)

where $\Delta$ is the difference parameter and $c_1=\rho _{1}-1$. When y is a housing price, $\Delta y_t=y_t-y_{t-1}$ represents housing price inflation. Parameters $a, b, c_1$, and f need to be estimated. The parameter b measures the short-term sensitivity of y to x, and $c_1$ measures the speed of the return to the long-run path. The parameter f is a vector of cointegrating parameters that summarize the long-run relationship between x and y, and $y_{t-1}+fx_{t-1}$ is the error correction mechanism (ECM). It is stationary, I(0), in the presence of cointegration; in this case, the adjustment parameter $c_1$ will be $-1< c_1 < 0$ according to the Granger representation theorem (Engle and Granger 1987). A value of parameter $c_1$ close to −1 indicates a quick return to the long-run path, and a value close to 0 indicates a slow adjustment. In contrast, when there is no cointegration, $c_1$ will not lie within this theoretical range, which implies that there are significant deviations of prices from economic fundamentals, which provides evidence of a bubble. Because financial bubbles are unobservable and are considered leftover (i.e., residuals) in Eq. (9), bubble analyses are sensitive to what comprises economic fundamentals.

Despite the importance of defining economic fundamentals, the selection of economic fundamentals remains controversial. The simplest approach used in many studies considers only one economic variable as a proxy for the economic fundamental, such as housing rental costs (Meese and Wallace 1994; Phillips and Yu 2011), mortgage interest rates (McGibany and Nourzad 2004), the price of residential land (Ooi and Lee 2006), or household income (Gallin 2006). The first two are often used to create the price-to-rent ratio and price-to-income ratio. While the former compares financial burdens between different choices of residential type, the latter measures the difficulty of purchasing houses, also known as the affordability ratio. Such investigations become univariate analyses by dropping x from Eq. (9). For y as the price-to-rent ratio, finding stationarity implies that housing prices and rent are cointegrated with a cointegrating parameter equal to unity, and the market is said to be tranquil. Thus, researchers can use unit root tests rather than cointegration tests.

$$\begin{aligned} \Delta y_t=a+c_{1} y_{t-1}+u_t \end{aligned}$$

(10)

The parameter of interest is $c_1$, and the interpretation of the parameters remains unchanged. Equation (10) is a specification of the Dicky–Fuller (DF) unit root test and can be extended to include past differenced ratios to create a more general form [i.e., the augmented DF unit root test (ADF)].

$$\begin{aligned} \Delta y_{t}=\alpha +c_2 y_{t-1}+\sum _{i=1}^p\theta _{i}\Delta y_{t-i}+\epsilon _t \end{aligned}$$

(11)

where the residual $\epsilon _{t}\sim N(0,\sigma _{\epsilon }^{2})$. For the classical unit root tests, the null hypothesis of a unit root ($c_2=0$) is tested against the alternative of stationarity ($c_2<0$), and thus, can be regarded as a statistical approach to determine a tranquil period. The non-stationary process of y is traditionally regarded as evidence of housing market bubbles (without distinguishing between negative and positive bubbles). The methods described thus far are conventional statistical models for analyzing housing markets and bubbles and are consistent with the traditional definition of bubbles in economics. That is, financial bubbles are phenomena in which housing prices do not move along with economic fundamentals in the long run.

3.2 Explosive Unit Root Tests

Financial bubbles are expected to occur occasionally and be recurrent (Blanchard and Watson 1982); furthermore, housing prices may be more chaotic and integrated of an order higher than one. In these cases, the classical unit root and cointegration tests possess only a weak statistical power for detecting bubbles (Evans 1991). To address these shortcomings, Phillips and Yu (2011) proposed conceptually different statistical methods based on Bhargava (1986) and Diba and Grossman (1998). Their tests are right-tailed and aim to examine a high level of a non-stationary process based on Eq. (11). They are designed to trace the orientation and collapse of bubbles, and thus to find chaotic moments (i.e., explosive bubbles) in financial markets. These statistical tests do not aim to determine tranquil periods.

Phillips et al. (2011) is based on the right-tailed test. Their motivation is (Phillips et al. 2011, p. 206), who state that “In the presence of bubbles, $p_t$ is always explosive and hence cannot comove or be integrated with $d_t$ if $d_t$ is itself not explosive.” Here, $p_t$ is the log price, and $d_t$ represents the log economic fundamentals. This is a subtle difference from the view of economists who pay most attention to cointegration between prices and economic fundamentals. Whether or not prices and economic fundamentals follow a unit root or explosive process is not their major interest. Economists claim evidence of tranquility as long as prices and economic fundamentals are cointegrated, regardless of the order of integration for each variable.

This can be seen in the alternative hypotheses of statistical tests. With the same null hypothesis as that of the classical ADF ($c_2=0)$, Phillips and Yu (2011) suggested evaluating the right-tailed alternative of an explosive unit ($c_2>0)$. Therefore, compared with the classical unit root tests that define bubbles as I(1) under the null hypothesis, this alternative hypothesis has an implication for stronger bubbles. Thus, the explosive unit root test is conceptually different from the traditional test that looks for cointegration, that is, tranquil periods, and assumes the prevalence of financial bubbles in the market.

Phillips et al. (2011) and Phillips et al. (2015) proposed four types of explosive unit root tests: the right-tailed version of the conventional ADF (ADF), the rolling ADF (RADF), the supremum ADF (SADF), and the generalized SADF (GSADF) tests. The first test is the right-tailed version of the conventional ADF, with its statistic following a nonstandard distribution. Unlike the ADF, which utilizes all observations, the RADF shifts the starting and ending sample data points forward. The SADF is based on the recursive method, and thus the statistic is obtained by fixing the initial point ($r_0$) equal to the first observation in the data set, but extending the ending point ($r_2$) one by one for each successive run. The largest statistic obtained from the recursive method is used to evaluate the null hypothesis. Thus, for the period from 0 to $r_2$, in which r is a fraction of the total time period, the SADF statistic can be expressed as follows:

$$\begin{aligned} \text {SADF}(r_{0})= \text {sup} \ \underset{r_2\in [r_0,1]}{{\text {ADF}}_0^{r_2}} \end{aligned}$$

The SADF statistic is consistent if there exists only one bubble, but is problematic if multiple bubbles exist. For this reason, Phillips et al. (2011) proposed the GSADF. It relaxes the SADF such that the initial observation ($r_1$) in the analysis does not need to be identical to the first observation in the data set. Therefore, the GSADF is considered the most reliable among the right-tailed integration tests. Further, Phillips et al. (2015) proposed a statistical method to identify a period of multiple bubbles, which has reasonable power (Homm and Breitung 2012). The GSADF statistic can be expressed as follows:

$$\begin{aligned} \text {GSADF}(r_{0})=\text {sup} \underset{r_{1}\in [0,r_{2}-r_{1}]}{\underset{r_{2}\in [r_{0},1]}{\text {ADF}_{r_1}^{ r_2}}} \end{aligned}$$

Recent studies used these unit root tests. Phillips et al. (2011) applied them to the US markets for housing, crude oil, and bonds, and Phillips and Yu (2011) and Phillips et al. (2015) applied them to the US stock markets (the NASDAQ stock exchange and the S&P500 Index). Kraussl et al. (2016) used these tests to examine bubbles in art markets. In addition to the application of the right-sided tests to different economic areas, researchers made further developments for real-time monitoring of financial bubbles. Phillips and Shi (2018) proposed what they call a recursive reverse-sample regression approach to reduce the delay bias in Phillips et al. (2011).

In short, it is important to note that while explosive tests are suitable for detecting explosive behaviors in data, they are not designed to investigate tranquil periods. Thus, within their framework, we cannot consider normality, a state in which the economy is believed to stay most of the time. This contradicts the choice of economic fundamentals by economists. For example, housing prices in theory are equal to the present value of housing services (or rents) in a steady state of a competitive economy (Blanchard and Watson 1982). There is no scope for the explosive unit root tests to accommodate this possibility.

We therefore examine two types of bubbles and refer to the case in which $c_2>0$ as an explosive bubble and the case in which $c_2=0$ (unit root) as a mild bubble. We can confirm the existence of a tranquil period when $c_2<0$ in Eq. (11). Thus, we can evaluate both conventional (mild) and explosive bubbles and summarize the interpretation of the statistical hypotheses of the classical and explosive ADF tests as follows.

Proposition 1

Based on classical approaches, there is evidence of mild bubbles if $c_2 = 0$ in Eq. (11) and tranquility if $c_2 < 0$ in the housing market.

Proposition 2

Based on explosive tests, there is evidence of explosive bubbles if $c_2 > 0$ and mild bubbles if $c_2 = 0$ in the housing market.

Below, we summarize the statistical hypotheses of the classical and explosive tests. The findings from these two tests do not necessarily need to be consistent, as they consider different data processes under statistical hypotheses.

Test type	Null hypothesis	Alternative hypothesis
Classical test	Mild bubbles ($d=1$, $c_2=0$)	No bubbles ($d<1$, $c_2<0$)
Explosive test	Mild bubbles ($d=1$, $c_2=0$)	Explosive bubbles ($d>1$, $c_2>0$)

3.3 Panel Approach

A single-country analysis can be extended to a study of financial bubbles in a multivariate context. Panel data estimation approaches often exploit cross-sectional information and increase statistical power. A multi-country analysis may be more appropriate because housing prices are highly correlated, particularly among advanced countries (see next section).

Pavlidis et al. (2016) extended the GADF statistics originally developed for single-country analyses by following Im et al. (2003), who proposed a left-tailed panel unit root test by extending the conventional univariate ADF test. In their approach, test statistics calculated for each country are pooled to create a single statistic that can be used to assess the statistical hypotheses in a panel context. For country k ($k=1,\ldots ,K$), we can express the panel data version of Eq. (11) as follows:

$$\begin{aligned} \Delta y_{k,t}=\alpha _k+c_k y_{k,t-1}+\sum _{i=1}^p\theta _{k,i}\Delta y_{k,t-i}+\epsilon _{k,t} \end{aligned}$$

(12)

where $\epsilon _{k,t}\sim N(0,\sigma _{\epsilon _k}^{2})$. The null hypothesis is $c_k=0, \forall k$ against the alternative of explosive behaviors, $c_k>0$ for some k. The noble feature of this approach is that it allows heterogeneity (i.e., c). However, a conclusion from this test becomes somewhat unclear, as the alternative hypothesis states. In other words, a rejection of the null does not necessarily mean that financial bubbles existed in all countries under investigation, but did in at least one country. To obtain a country-specific conclusion, country-wise analyses are required, as we summarized in the previous subsections.

For example, the panel GSADF can be constructed as the supremum of the panel backward SADF (BSADF). The panel BSADF is in turn obtained as the average of the SADF calculated backwardly for individual countries.

$$\begin{aligned} \text {Panel GSADF}(\text {r}_0) =&\,\,\,\,\, \text {sub}\quad \quad \quad \text{Panel BSADF}_{\text {r}_2} (\text {r}_0)\\ \nonumber&\text {r}{_2} \in [\text {r}_0,1] \end{aligned}$$

(13)

Given the possible cross-country dependence, we follow the calculation method in Pavlidis et al. (2016) closely and use a sieve bootstrap approach. The panel approach using cross-sectional information may be useful to understand a general trend in real estate prices in global markets.

3.4 T-ARDL Model

Finally, as an extension to the classical approach, we propose the T-ARDL model.⁴ The linear ARDL is a classical method used to capture persistence in time series data, and Pesaran et al. (2001) proposed a bounds test to detect cointegration based on the ARDL. An advantage of this method is its ability to determine the presence of cointegration without prior knowledge of the explanatory variables being stationary (I(0)) or non-stationary (I(1)). This is a useful feature in studies of bubbles, as economies often experience periods of tranquility and mild bubbles.

Pesaran et al. (2001) proposed five specifications of the ARDL with a different combination of deterministic terms. Here, we use the most popular model in financial research, with an unrestricted constant and no trend. For asset prices (y), we can express this as

$$\begin{aligned} \Delta y_t = a + cy_{t-1}+ {\varvec{bx}} _{t-1}+\sum _{i=1}^{p-1}{\varvec{d}}_{i}^{'} \Delta {\varvec{z}}_{t-i} + {\varvec{f}}^{'}\Delta {\varvec{x}}_{t}+u_{t} \end{aligned}$$

(14)

where a, c, b, d, and f are the parameters to estimate by the ordinary least squares (OLS) for time (${t} = 1,\ldots , {T}$), and $u_t$ is the residual ($u_t \sim N(0, \sigma ^2$)). $\textit{\textbf{x}}$ is a matrix of explanatory variables and $\textit{\textbf{z}} = [y, \textit{\textbf{x}}]$. The appropriate lag length (p) is determined such that it captures the data generating process of y. We can study the cointegrated relationship between y and $\textit{\textbf{x}}$ by analyzing the time series properties of $cy_{t-1}+\textit{\textbf{bx}}_{t-1}$, known as the ECM. We can test the null hypothesis of no ECM ($c=0$ and $\textit{\textbf{b}}= \textit{\textbf{0}}$) by the F test or $c=0$ the t test.

As the conventional asymptotic distribution is invalid here, Pesaran et al. (2001) provided critical values based on Monte Carlo simulations for a different dimension of $\textit{\textbf{x}}$. Because economic variables may be I(0) or I(1), the critical values for these tests have both lower and upper bounds. For the F tests, the lower bound is determined when the data are I(0), and the latter when they are I(1). Test statistics above the upper bound imply evidence of cointegration, and those below the lower bound suggest the absence of cointegration. Test statistics between these bounds are inconclusive. For the t tests, the lower bound is determined when the data are I(1), as the test statistics are expected to be negative. The upper bound is designed for I(0) data.

However, this bounds testing approach is inappropriate for a study of bubbles because it investigates the possibilities of both negative and positive bubbles. That is, like the standard unit root tests, it considers bubbles even when housing prices are low. To treat bubbles as high price phenomena, we introduce nonlinearity into the ARDL as follows:

$$\begin{aligned} \Delta y_t&= \alpha _{1}g+\alpha _{2}\widetilde{g}+c_{1}gy_{t-1}+c_{2}\widetilde{g}y_{t-1}+b_{1}g\textit{\textbf{x}}_{t-1}+b_{2}\widetilde{g}\textit{\textbf{x}}_{t-1}+\sum _{i=1}^{p-1}\textit{\textbf{d}}_{i}^{'} \Delta \textit{\textbf{z}}_{t-i}\nonumber \\&\quad \textit{\textbf{f}}^{'} \Delta \textit{\textbf{x}}_{t}+u_{t} \end{aligned}$$

(15)

where g and $\widetilde{g}$ are dummy variables that distinguish the regimes, and Eq. (15) has two (upper (g) and lower $(\widetilde{g})$) regimes. When these regimes are determined by a certain threshold point (w), the dummies are defined as follows:

$$\begin{aligned} g={\left\{ \begin{array}{ll} 1 &{} \text{ if }\ y > w \\ 0 &{} \text{ otherwise } \end{array}\right. } \quad \text {and}\quad \widetilde{g}={\left\{ \begin{array}{ll} 1 &{} \text{ if }\ y \le w \\ 0 &{} \text{ otherwise }\end{array}\right. } \end{aligned}$$

(16)

To analyze the price-to-rent ratio when y already includes the economic fundamental variables, it becomes a univariate analysis by dropping $\textit{\textbf{x}}$ from (15). Furthermore, in the next section, we propose a top-down strategy for the T-ARDL model in order to determine the threshold point endogenously. To summarize, we can state the conditions of mild bubbles for this test in Proposition 3.

Proposition 3

For housing prices that follow an I(1) process, evidence of mild bubbles exists if prices are higher than the historical average (or predictions from economic fundamentals) and if there is no cointegration relationship between prices and economic fundamentals (i.e., the F test statistic < ucv, where ucv is an upper bound critical value, and/or the t test statistic > lcv, where lcv is a lower bound critical value).

4 Empirics

Using housing market data from advanced countries and the abovementioned statistical methods, we analyze the presence of tranquility and bubbles in real estate markets. We focus on advanced countries because the economic theory, for example, the link between housing prices and rents, assumes perfect and competitive markets, for which advanced countries provide a better proxy than do developing countries. Furthermore, longer sample period observations are available from advanced countries only.

4.1 Data

We obtain quarterly data on housing price-to-rent ratios from the OECD for the Euro area, Japan, the UK, and the USA (Table 1). The maximum sample period is from 1968 to 2018 (nearly 200 observations for each country), and the base year of the data is 2015. Here, the Euro area consists of 15 countries: Greece, France, the Slovak Republic, Italy, Spain, Belgium, Luxembourg, Germany, Portugal, the Netherlands, Finland, Ireland, Austria, Slovenia, and Estonia. (Hereafter, we refer to the Euro area as a country for convenience.) Because financial bubbles are traditionally considered infrequent phenomena, we chose countries with more than 195 observations. In terms of the standard deviations of this ratio, the US housing market is most stable, and the Japanese market is most volatile.

Table 1 Descriptive statistics: price-to-rent ratios

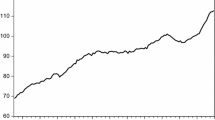
We also obtain housing price indices from the OECD. Housing prices appear to have a positive relationship with the price-to-rent ratios for all countries and exhibit more stable movements compared to prices (Fig. 1). Furthermore, while there are some similarities in the ratios across four countries, they have a declining trend in Japan during the “Lost Decades” (i.e., after 1990). This trend indicates relatively higher inflation in rental properties than houses in Japan and is indeed attributable to the deflation in housing prices according to this figure. This result indicates a weak demand for house purchases during the weak economic conditions of this period. In contrast, there is an increasing trend in the UK ratio from the late 1990s, indicating a housing market boom.

Fig. 1

Housing prices and the price-to-rent ratios

Table 2, which summarizes the correlation coefficients of the price-to-rent ratios and housing prices, also indicates the uniqueness of the Japanese market. On the one hand, housing prices are highly and positively correlated among countries. High correlation coefficients indicate that individual housing markets are highly integrated into global housing markets and are in similar stages of the business cycle, so housing markets are expected to respond similarly to global economic shocks. On the other hand, although the price-to-rent ratios are also highly correlated among countries in general, there is a peculiarity in the Japanese market, in that it is negatively associated with the other markets. This result makes the Japanese market very unique among global housing markets.

Table 2 Correlations among the price-to-rent ratios

We conduct a more formal analysis of the spillover effects between global housing markets using advanced statistical methods. Among the many statistical methods to measure spillovers, Diebold and Yilmaz (2009) proposed a method based on the vector autoregression (VAR) model to decompose aggregate spillovers into disaggregate and directional spillovers. Barunik and Krehlik (2018) extended their method to decompose spillovers using different frequencies of data (see the Appendix for a discussion of their method). Given that there may be time lag in spillovers, frequency analyses are interesting and give us a means to identify sources of spillovers. The short-term spillover is often believed to be influenced more by investors’ expectations and the long-term spillovers by changes in the real economy (i.e., business cycles).

Here, we study spillovers across housing markets using the volatility of the price-to-rent ratios. Volatility is often measured by the squared or absolute value of returns (i.e., $x^2$ or |x|, where x is the price) in the finance literature. Using the latter proxy of volatility and VAR(2), we estimate the overall and frequency spillovers using OLS. We plot the results in Fig. 2. Furthermore, we decompose the overall spillovers over the short (within three months), middle (four months to one year), and long (over one year) time ranges. This frequency division is somewhat arbitrary, but shows that spillovers are sensitive to the frequency range, and spillovers seem to increase in the second half of our sample period (i.e., from this century). Furthermore, spillovers are more prominent over the medium to long term. In contrast, we observe no significant spillovers in housing markets at a high frequency. The differing connectedness by data frequency appears to be related to the characteristics of housing markets; residences are traded much less frequently than financial assets are. In this regard, we infer that business cycle channels may be more relevant to explain the size of spillovers in housing markets.

Fig. 2

Spillover

4.2 Classical Test Approaches

We use three left-tailed unit root tests (the ADF, Phillips–Perron, and DF-GLS) that are popular univariate tests in economic and financial research. These tests investigate the null hypothesis that the price-to-rent ratio in levels follows the unit root process (I(1)), and a rejection of this null provides evidence of stationarity in this ratio, and thus cointegration between housing prices and rents. Therefore, a failure to reject this null hypothesis indicates that rents cannot explain the long-term housing price movements, thereby suggesting the presence of mild bubbles. We conduct these tests for the ratios in levels and first differences in order to check the order of integration.

Table 3 summarizes the test statistics for the Euro area, Japan, the UK, and the USA. The results suggest that these ratios follow the unit root process. Using the 5% critical values, we often fail to reject the null hypothesis for the data in levels, but can do so for the differenced data. Therefore, we conclude that mild bubbles existed in all countries, suggesting that rental increases are not always associated with housing price inflation, and there must be some periods when housing prices deviate substantially from the trend in rentals. Obviously, these tests preclude a possibility of explosive bubbles, and moreover, we need to pay attention to the composition of economic fundamentals. However, these outcomes are consistent with our expectations that all housing markets experienced chaotic moments during our sample period.

Table 3 Standard unit root tests for the price-to-rent ratios

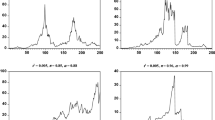
The potential non-stationary periods identified by the classical method are shaded in Fig. 3. We present two graphs for each country, and the upper figures (denoted as OLS estimates) are obtained from the classical method. As explained earlier, a drawback of this approach is the lack of statistical power to differentiate between hypotheses and that it allows for negative bubbles. For consistency with the standard phenomenon of financial bubbles, we should consider only the positive bubbles (above the horizontal line) as relevant to financial bubbles. Thus, only positive bubble periods are highlighted in gray in this figure and are potential bubble periods because these classical tests are not designed to identify the exact periods of bubbles while they give us evidence of mild bubbles during the sample period.⁵

Fig. 3

OLS and threshold estimation results

Table 4 Explosive unit root tests for the price-to-rent ratios

4.3 Explosive Test Approaches

Next, we conduct explosive unit root tests for each country and for a group of countries. From the classical tests, we already know that the price-to-rent ratio is non-stationary and, in fact, implies the presence of mild bubbles. However, when it is not known, we propose the following general steps to reach a conclusion. In short, explosive unit root tests should be conducted if and only if the classical approaches show the data (y) to be a non-stationary process.

Fig. 4

GSADF results

Failing to reject the null hypothesis that price-to-rent ratios are I(1) by the classical tests, we eliminated the possibility of market tranquility and thus conduct explosive unit root tests for each market. Table 4 summarizes the results from the right-tailed tests (RADF, SADF, and GSADF) for each country. The null hypothesis of these tests is consistent with our finding of a random walk price-to-rent ratio from the classical tests. The explosive test results differ somewhat by test type, but the null hypothesis is rejected frequently using the p-values obtained from 1000 replications, which is evidence in favor of explosive bubbles in all markets. The results from the GSADF are also depicted in Fig. 4. GSADF statistics greater than 95% critical values suggest the presence of explosive bubbles, which are also shaded in this figure, and generally identify explosive bubble periods when housing prices are high. The timing and duration of explosive bubbles differ among countries, but many countries seemed to experience explosive bubbles before the Lehman Brothers collapse in September 2018. The presence of real estate markets is consistent with the results from the classical approaches, but here we have evidence of explosive bubbles, which the classical approach cannot capture.

Given the cross-sectional dependence in international housing markets, we also conduct a multi-country analysis using two methods. First, we calculate panel GSADF statistics using the data of 12 countries: Canada, Denmark, Finland, France, Germany, Ireland, Italy, Japan, the Netherlands, Switzerland, the UK, and the USA. Second, in order to check the robustness of the findings from the panel explosive tests, we conduct the explosive unit root tests for a price-to-rent index that covers OECD countries.⁶ These analyses help us identify explosive bubbles in the global housing market.

The country coverage differs slightly in these analyses; however, we find many similarities in the results obtained from these groups of advanced countries. In particular, we observe that explosive bubbles existed just before the Lehman Brothers collapse in 2008, recently (2018), and at the end of the 1980s. The panel GSADF and GSADF statistics for the group of OECD countries are 1.882 and 3.157, respectively, which are greater than the 95% critical values of 0.349 and 2.169. This result confirms that explosive bubbles prevailed in the global housing market in the past decades. It follows that, despite some peculiarities of the Japanese market based on the correlation coefficients, there are similarities in terms of the timing of the evolution of explosive bubbles across countries.

These results are also depicted in Fig. 5. The GSADF statistics greater than critical values (cv, shaded) indicate the presence of explosive bubbles. In this figure, panel indicates the results using data from individual OECD countries (the upper graph) and OECD those using the OECD index. The figure indicates that all countries experienced several explosive bubbles since 1970. While the duration of the estimated bubbles differs by market, in some instances (e.g., around 1990 and 2005), many countries faced bubbles. Therefore, we confirm the spillovers in global real estate markets, and the global spillovers resemble regional spillovers in domestic housing markets (Montagnoli and Nagayasu 2015). Our frequency analysis in the previous section suggests that global market spillovers may result from similar business cycles, and common shocks occurred in the group of countries.

Fig. 5

Multi-country analyses

4.4 T-ARDL Approach

As an extension of the classical approaches that focused on individual markets, we apply a top-down strategy to the threshold ARDL (T-ARDL) method to distinguish between positive and negative bubbles. Choosing a threshold point requires careful consideration because mild bubbles exist only when housing prices are much higher than the historical average (or predictions from economic fundamentals). Moreover, like the explosive approaches, we estimate this method by changing the sample.

To choose the timing of mild bubbles endogenously, we suggest a theoretical threshold range within which we calculate the test statistics for each percentile of housing prices in a top-down approach (i.e., moving down on the y-axis). We use the theoretical range between the 95th percentile and the historical average. The latter allows us to differentiate between positive and negative bubbles. Importantly, Eq. (15) regards even deflationary periods $(\Delta y<0)$ as potential bubbles if prices are higher than the historical average. This is a more realistic assumption of bubbles than excluding all deflationary periods because real estate markets are volatile, even when prices are high. In the top-down approach, we estimate the T-ARDL from high to low prices and continue until we find evidence against the null in the upper regime. Finding a significant ECM points to tranquil periods, during which economic fundamentals can explain the trend in real estate prices.

This top-down approach has several advantages over the conventional approach, which relies on rolling or recursive methods (i.e., moving sideways on the x-axis), and is often used to detect structural shifts. First, the top-down approach does not require that we trim the beginning or end of the sample periods, which we need for the initial estimation. Researchers are often interested in an extreme sample periods. Second, like a rolling estimation method, we need not fix an unknown rolling window period to calculate the test statistics over time. Third, unlike rolling and recursive methods that require calculations of the test statistics at each point in time, further analyses to determine bubble periods are unnecessary once we find evidence of no bubble from the top-down approach. A y greater than the estimated threshold point $(\bar{y})$ indicates mild bubble periods. Therefore, this approach is more efficient than the conventional approaches in terms of computational time. In this way, mild bubbles can be detected endogenously.

To summarize our procedure, we propose the following top-down approach to study the presence and duration of bubbles based on the t statistics. Initially, we conduct the bounds test at the threshold point of the 95th percentile of the data. Failing to reject the null of no ECM, we implement this test again, this time decreasing the threshold by 1%. We continue this process until we find evidence against the null hypothesis (i.e., the t statistics become smaller than lcv) in the upper regime where $i=0$–45 (see Fig. 6).

Fig. 6

Image of the top-down approach

Figure 7 plots the sequence of test statistics, along with the 5% critical value, and shows that we can reject the null hypothesis after 2, 1, 27, and 5 iterations of the test for the Euro area, Japan, the UK, and the USA, respectively. As we start with at the 95th percentile of the data, we can regard the 93rd, 94th, 68th, and 90th percentile points as the thresholds for these countries. We report the estimation results in Table 5, though do not show the results for the parameters ds in Eq. (15) as they are insignificant and were removed from the model.

Table 5 T-ARDL estimation results

Fig. 7

Sequence of t-statistics from the threshold estimation

Figure 3 plots mild bubbles (shaded areas) predicted from the T-ARDL. As expected, possible periods of mild bubbles are sharpened now; there is evidence of shorter bubble periods from the T-ARDL compared with the standard classical test. This is noticeable for all countries. Compared with the OLS estimates, the evidence of bubbles immediately after the Lehman Shock (September 2008) disappears when we use the T-ARDL, and this T-ARDL result is consistent with an underling method that allows us to focus only on the upper regime.

4.5 Discussion

In this study, we considered three states of an economy; none, mild, and explosive bubble periods, and classified statistical approaches into two groups by their research objectives. In classical methods, non-tranquil periods can be considered mild bubble periods, and non-explosive bubble periods are equivalent to mild bubble periods in the explosive bubble analyses. Therefore, identifying explosive bubbles is of primary interest in the recent development in statistical approaches, while economists and policymakers are probably more interested in tranquil periods that may be identified by economic fundamentals (i.e., economic theories) and the classical approaches. The results are naturally sensitive to the test types; therefore, researchers need to decide the research objectives first and adopt an appropriate research framework accordingly.

Table 6 summarizes the possible mild and explosive bubble periods identified by the classical and explosive statistical approaches, which we explained using figures in the previous section. We determined the mild bubble periods from the classical approaches, which we denote as the OLS and the T-ARDL results in the table. These periods are equivalent to ones in which the price-to-rent ratio deviates substantially from the economic fundamental, suggesting no long-run relationship between housing and rental prices. The results from the OLS and T-ARDL differ slightly, and the latter tends to identify shorter periods for mild bubbles. This outcome shows that the threshold approach focuses on only housing prices that are historically expensive, while the OLS considers both expensive and inexpensive periods as potential bubble periods. The explosive bubbles obtained from the GSASF suggest a greater number of shorter periods for bubbles overall. As expected, the three tests predict different bubble periods, but the predictions show a lot of overlap. These overlapping periods are also reported as common periods in this table and are the mostly strongly supported bubble periods. In short, we reported several results from different statistical approaches and objectives in financial bubble studies.

Table 6 Periods of mild and explosive bubbles

5 Conclusion

Housing prices, especially abnormally high prices, are of interest to many people and policymakers because the residence is necessary, but can be very expensive. Consequently, property prices are a long-standing, popular research area. However, recent research appears to be diversified in terms of objectives with respect to detecting financial bubbles and tranquil periods. The methodological approach using statistics to identify explosive bubbles gives only limited economic implications from the data analysis. Given that such research does not give any scope for markets being in equilibrium, it is of less interest to economists and policymakers, who are concerned more with tranquil periods and are interested in providing economic explanations of how the economy changes over time.

Furthermore, we proposed applying a top-down method to the T-ARDL to analyze rational bubbles. While we presented a very simple example and further research is necessary to define the economic fundamentals, this top-down strategy is more efficient than the traditional one is and can be applied to other statistical tests (e.g., unit root and cointegration tests) that attempt to analyze rational bubbles.

Finally, future developments in statistics will be useful, particularly if the null and alternative hypotheses could be better designed to make both economic and statistical sense. An example of such a research direction may be to develop statistical tests evaluating the null hypothesis of no bubbles against the alternative of bubbles of any type. Another example, which is more radical and the most useful direction of statistical development, may be described as two-sided tests. Research along this line would be quite challenging, but useful in synthesizing economic and statistical methodologies.

Appendix

In deregulated markets, both domestic and foreign shocks are expected to influence economic development. Therefore, it is important to understand co-movements in global markets, even in an analysis of housing markets, which represent non-tradable goods. Among others, Diebold and Yilmaz (2009, 2012) and Barunik and Krehlik (2018) contributed recent methodological developments. The former authors proposed measurements for the total and directional spillovers, and the latter incorporated a frequency domain in these spillovers. These techniques were developed based on the decomposition method known as generalized impulse response functions, which are invariant to the order of variables in the VAR (Pesaran and Shin 1998).

Consider a stationary N-variate VAR(p) with the errors $\epsilon \sim (0, \sigma ).$

$$\begin{aligned} x_t=\sum _{i=1}^p\Phi _ix_{t-i}+\epsilon _t \end{aligned}$$

The moving average representation of this VAR is

$$\begin{aligned} x_t=\sum _{i=0}^\infty A_i\epsilon _{t-i} \end{aligned}$$

where $A_i=\Phi _1A_{i-1}-\Phi _2A_{i-2}+\cdots +\Phi _pA_{i-p}$. The proportion of the kth variable to the variance of the forecast errors of element j, for the h time horizon, is

$$\begin{aligned} (\theta _H)_{j,k}=\frac{\sigma _{k,k}^{-1} \sum _{h=0}^H((A_h\sigma )_{j,k})^2}{\sum _{h=0}^H(A_h \sigma A'_h)_{j,j}} \end{aligned}$$

The row of $\theta _H$ does not need to be equal to one, and it can be normalized by the row sum.

$$\begin{aligned} (\tilde{\theta }_H)_{j,k}=\frac{(\theta _H)_{j,k}}{\sum _{k=1}^N (\theta _H)_{j,k}} \end{aligned}$$

$(\tilde{\theta }_H)_{j,k}$ measures a pairwise spillover from k to j, and by construction, $\sum _{k=1}^{N}(\tilde{\theta }_H)_{j,k}=1$ and $\sum _{j,k=1}^{N}(\tilde{\theta }_H)_{j,k}=N$. We can obtain a total spillover index by aggregating each pair. That is,

$$\begin{aligned} C_H= \frac{\sum _{j \ne k}(\tilde{\theta }_H)_{j,k}}{\sum \tilde{\theta _H}} \times 100 \end{aligned}$$

Barunik and Krehlik (2018) defined a scaled generalized variance decomposition on a specific frequency band, $d=(a,b)$, where $a<b$ and $a,b \in (-\pi , \pi )$, which is from a set of intervals D.

$$\begin{aligned} (\tilde{\theta _d})_{j,k}=\frac{ (\theta _d)_{j,k}}{\sum _k(\theta _\infty )_{j,k}} \end{aligned}$$

Then, we can define the frequency spillover on the frequency band d as follows:

$$\begin{aligned} C_d=\left( \frac{\sum \ \tilde{\theta }_d }{\sum \tilde{\theta }_d}-\frac{\text {Tr}\{ \tilde{\theta }_d \}}{\sum \tilde{\theta }_d} \right) \times 100 \end{aligned}$$

Each component of $C_d$ can be obtained by defining the generalized caution spectrum over frequencies $\omega \in (-\pi , \pi )$ as (Barunik and Krehlik 2018):

$$\begin{aligned} (f(\omega ))_{j,k}\equiv \frac{\sigma ^{-1}_{kk}\left| (\Psi (\mathrm {e}^{-\mathrm {i}\omega })\Sigma )_{j,k}\right| ^2}{(\Psi (\mathrm {e}^{-\mathrm {i}\omega })\Sigma \Psi '(\mathrm {e}^{+\mathrm {i}\omega }))_{j,j}} \end{aligned}$$

where $\Psi (\mathrm {e}^{-\mathrm {i}})$ is the Fourier transform of the impulse response. It is a proportion of the spectrum of variable j in response to shocks in variable k. Then, we can specify the components of $C_d$ as follows:

$$\begin{aligned} (\theta _\infty )_{j,k}=\frac{1}{2\pi }\int \limits ^{\pi }_{-\pi }\Gamma _j(\omega )(f(\omega ))_{j,k}\text {d}\omega \end{aligned}$$

and

$$\begin{aligned} (\theta _d)_{j,k}=\frac{1}{2\pi }\int \limits _d\Gamma _j(\omega )(f(\omega ))_{j,k}\text {d}\omega \end{aligned}$$

where

$$\begin{aligned} \Gamma _j(\omega )=\frac{(\Psi (\mathrm {e}^{-\mathrm {i}\omega })\Sigma \Psi '(\mathrm {e}^{+\mathrm {i}\omega }))_{j,j}}{\frac{1}{2\pi }\int ^\pi _{-\pi }(\Psi (\mathrm {e}^{-\mathrm {i}\lambda })\Sigma \Psi '(\mathrm {e}^{+\mathrm {i}\lambda }))_{j,j}\mathrm {d}\lambda } \end{aligned}$$