Aeroelastic Instabilities of Wings with Active High-Lift Devices—A Reduced-Order Model

Abstract

A reduced-order model is developed to study the parameter-dependent aeroelastic behaviour of two wing configurations with high-lift devices. One is the wing of a conventional turboprop aircraft, the other a wing with over-the-wing mounted ultra high bypass ratio engine. Characteristic aerodynamic loads are investigated with steady and unsteady flow simulations of a 2D profile section. 3D effects are taken into account using an adapted lifting line theory according to Prandtl. Structure and aerodynamic loads are coupled in modal space to predict aeroelastic instabilities. Bending and bending-torsion instabilities due to the high-lift systems become visible.

1 Introduction

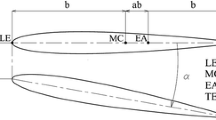
Aeroelastic investigations often area limiting factor in the design process of a new aircraft, as aeroelasticity can lead to structural failure. It is therefore desirable to develop a highly adaptable model to work with during the whole process. Furthermore, parameter variations must be taken into account to cover multiple flight situations. Two wing configurations are under investigation. In order to use existing, short runways, the wings are equipped with active and passive high-lift systems. The active system, Coandă flap, combines a trailing edge flap with a thin jet [1]. It is described by its momentum coefficient

$$\begin{aligned} c_{\mu } = \dfrac{\dot{m}_\text {jet}v_\text {jet}}{q_\infty A_\text {ref}} \end{aligned}$$

(1)

by setting the ratio of introduced jet momentum per time $\dot{m}_\text {jet}v_\text {jet}$ in proportion to the freestream dynamic pressure $q_\infty$ and the reference area $A_\text {ref}$. However, a heave flutter phenomenon can be observed for circulation-controlled wings [2]. As a passive system, a leading edge flap, called droop nose, is designed [3]. In contrast to conventional flaps, the developed droop nose is deformed without generating a gap.

Because of the high-lift systems, high-quality flow simulations would be necessary for a conventional investigation of aeroelasticity. This requires a lot of time and computing capacity. To provide a fast initial assessment, a reduced-order model (ROM), based on a substructure technique and two-dimensional (2D) aerodynamics, is developed. Using strip theory to calculate the three-dimensional (3D) wing aerodynamics, the heave flutter phenomenon is confirmed [4, 5]. However, adding Prandtl’s lifting line theory to the 3D aerodynamic calculations, the behaviour changes significantly [6].

2 Reduced-Order Model Setup

The developed ROM was first presented in [7] and continuously updated [4,5,6, 8]. Parameterisation of the wing structure concerning mass and stiffness on one hand and a substructure technique on the other ensures high adaptability of the reduced structure model. The aerodynamics of two-dimensional (2D) profile sections are investigated for both profile shapes with different momentum coefficients over a large range of angles of attack. Using strip theory and Prandtls lifting line theory three-dimensional (3D) aerodynamics are derived for different wing geometries.

2.1 Structure Parameterisation

Based on 3D finite element (FE) models, the equation of motion

$$\begin{aligned} \mathbf {M}_S\varvec{\ddot{x}}_S + \mathbf {K}_S \mathbf{x} _S = \mathbf{g} _S \end{aligned}$$

(2)

with $\mathbf {M}_S$ being the mass and $\mathbf {K}_S$ the stiffness matrix, is used to evaluate the dynamic properties of the structure. Thereby $\mathbf{x} _S$ describes the displacement degrees of freedom and $\mathbf {g}_S$ the net weight. The modal approach

$$\begin{aligned} \mathbf{x} _S= \mathbf {X}{} \mathbf{q} , \end{aligned}$$

(3)

with $\mathbf{q}$ being the vector of generalised coordinates and $\mathbf {X}$ the modal matrix, leads to the decoupled system of equations

$$\begin{aligned} \ddot{q}_j + \omega _{0j}^2q_j = \gamma _j g. \end{aligned}$$

(4)

In modal space the structure may be approximately described by selected eigenfrequencies $\omega _{0j}$, natural modes $\varvec{\hat{x}}_j$ and associated participation factors $\gamma _j$.

A deviating stiffness or mass distribution

$$\begin{aligned} \left( \mathbf {M}_S + \varDelta \mathbf {M} \right) \varvec{\ddot{x}}_S + \left( \mathbf {K}_S + \varDelta \mathbf {K} \right) \mathbf{x} _S = \mathbf{g} _S + \varDelta \mathbf{g} \end{aligned}$$

(5)

therefore leads to deviating natural modes $\varvec{\hat{v}}_{j}$ and eigenfrequencies $\tau _{0j}$ [5]. Transforming Eq. 5 into modal space by using the original approach in Eq. 3 leads to

$$\begin{aligned} (1 + \underbrace{\varvec{\hat{x}}_j^T \varDelta \mathbf {M}\, \varvec{\hat{x}}_j}_{\eta _m \varDelta m_j}) \, \ddot{q}_j + (\omega _{0j}^2 + \underbrace{\varvec{\hat{x}}_j^T \varDelta \mathbf {K}\, \varvec{\hat{x}}_j}_{\eta _k \varDelta \omega ^2_{0j}}) \, q_j = \gamma _j g + \varvec{\hat{x}}_j^T \varDelta \mathbf{g} \, \varvec{\hat{x}}_j \, . \end{aligned}$$

(6)

The differing generalised mass $\varDelta m_j$ and generalised natural frequencies $\varDelta \omega _{0j}$ are parameterised by $\eta _m$ and $\eta _k$. The natural frequencies of the deviating distribution result to

$$\begin{aligned} \tau _{0j}^2 = \dfrac{\omega ^2_{0j} + \eta _k \varDelta \omega ^2_{0j}}{1 + \eta _m \varDelta m_j} \, . \end{aligned}$$

(7)

A distinction of cases with $\eta _m = 1$ and $\eta _k = 0$ leads to

$$\begin{aligned} \varDelta m_j = \dfrac{\omega _{0j}^2}{\tau _{0j}^2} - 1 \, , \end{aligned}$$

(8)

whereas $\eta _k = 1$ and $\eta _m = 0$ yields

$$\begin{aligned} \varDelta \omega _{0j}^2 = \tau _{0j}^2 - \omega _{0j}^2 \, . \end{aligned}$$

(9)

Thus, the transition from one distribution to another is linearly approximated.

2.2 Substructure Technique

The structure to be examined is devided into substructures, e.g. wing, pylon and engine structures. Each substructure is transformed into modal space according to Eq. 3 and reduced by selecting the relevant natural modes and frequencies. Subsequently, the independently reduced and potentially parameterised substructures are merged using Lagrange multipliers $\varvec{\sigma }$. By introducing coupling matrices $\mathbf {C}$, the necessary physical degrees of freedom of two structures n and m are set equal

$$\begin{aligned} \begin{bmatrix} \mathbf {I} &{} \mathbf {0} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {I} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {0} &{} \mathbf {0} \end{bmatrix} \begin{bmatrix} \varvec{\ddot{q}}_n \\ \varvec{\ddot{q}}_m \\ \varvec{\sigma } \end{bmatrix} + \begin{bmatrix} \varvec{\omega}_{{\mathbf{0}}n}^2 &{} \mathbf {0} &{} (\mathbf {C}_n\mathbf {X}_{\mathbf {r}n})^T \\ \mathbf {0} &{} \varvec{\omega}_{{\mathbf{0}}m}^2 &{} -(\mathbf {C}_{m}\mathbf {X}_{\mathbf {r}m})^T \\ \mathbf {C}_n\mathbf {X}_{\mathbf {r}n} &{} -\mathbf {C}_{m}\mathbf {X}_{\mathbf {r}m} &{}\mathbf {0} \end{bmatrix} \begin{bmatrix} \mathbf{q} _n \\ \mathbf{q} _{m} \\ \varvec{\sigma } \end{bmatrix} = \begin{bmatrix} \mathbf{g} _{\mathbf{q} n}\\ \mathbf{g} _{\mathbf{q} m} \\ \mathbf {0} \end{bmatrix} \end{aligned}$$

(10)

using their reduced modal matrices $\mathbf {X_r}$. Here, $\mathbf {I}$ is the unit matrix, equivalent to the reduced mass matrix, $\varvec{\omega _0}^2$ is the reduced stiffness matrix and $\varvec{g_q}$ is the generalised net weight of the respective structure.

2.3 Coupling of Aerodynamics

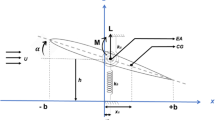
Next to structural properties, the dynamic behaviour strongly depends on the imposed aerodynamic loads. Lift and pitching moment are considered, described by their dimensionless coefficients

$$\begin{aligned} \begin{bmatrix} c_L\\ c_M \end{bmatrix} = \begin{bmatrix} c_{L0}\\ c_{M0} \end{bmatrix} + \begin{bmatrix} 0 &{} c_{L,\alpha }\\ 0 &{} c_{M,\alpha } \end{bmatrix} \begin{bmatrix} h\\ \alpha \end{bmatrix} \qquad + \dfrac{1}{v_\infty } \begin{bmatrix} c_{L,\dot{h}} &{} l\,c_{L,\dot{\alpha }}\\ c_{M,\dot{h}} &{} l\,c_{M,\dot{\alpha }} \end{bmatrix} \begin{bmatrix} \dot{h}\\ \dot{\alpha } \end{bmatrix} \end{aligned}$$

(11)

with the mass inertia being neglected. The pitching moment is related to the quarter chord and the terms are made dimensionless by chord length l and freestream velocity $v_\infty$. Using strip theory the aerodynamic loads are calculated along the span. This leads to

$$\begin{aligned} \mathbf{L} = \varvec{L_0} + \mathbf {A_0} \, \mathbf{x} _A + \mathbf {A_1} \, \varvec{\dot{x}}_A \end{aligned}$$

(12)

with a constant load vector $\varvec{L_0}$, the aerodynamic stiffness matrix $\mathbf {A_0}$ and aerodynamic damping matrix $\mathbf {A_1}$.

The aerodynamic degrees of freedom $\mathbf{x} _A$ according to Eq. 11 are the vertical displacement h and torsional rotation $\alpha$. These are different from the discretisation of the FE model, wherefore the natural modes are transformed to aerodynamic discretisation $\varvec{\hat{x}}_{Aj}$. The modal approach in Eq. 3 with the modal matrix in aerodynamic coordinates $\mathbf {X}_A$ leads to

$$\begin{aligned} \ddot{q}_j + \omega _{0j}^2q_j = \gamma _j g + \varvec{\hat{x}}_{Aj}^T \, \mathbf{L} (q,\dot{q}). \end{aligned}$$

(13)

For consideration of 3D aerodynamics, an approach based on the lifting-line theory [9] is described in [8]. Accordingly, downwash angles $\alpha _i$ are added as additional degrees of freedom. This leads to the schematical system of equation

$$\begin{aligned} \begin{aligned} \begin{bmatrix} \mathbf {I} &{} \mathbf {0} \\ \mathbf {0} &{} \mathbf {0} \end{bmatrix} \begin{bmatrix} \varvec{\ddot{q}} \\ \varvec{\ddot{\alpha }_i} \end{bmatrix} + \begin{bmatrix} -\mathbf {A_{1q}} &{} -\mathbf {D_{q\alpha _i}} \\ \mathbf {D_{\alpha _iq}} &{} \mathbf {0} \end{bmatrix} \begin{bmatrix} \varvec{\dot{q}} \\ \varvec{\dot{\alpha }_i} \end{bmatrix} \qquad \qquad \qquad \qquad \,\,\,\\ + \begin{bmatrix} \varvec{\omega _0}^2 - \mathbf {A_{0q}} &{} -\mathbf {K_{q\alpha _i}} \\ \mathbf {K_{\alpha _iq}} &{} \mathbf {K_{\alpha _i}} \end{bmatrix} \begin{bmatrix} \mathbf{q} \\ \varvec{\alpha _i} \end{bmatrix} = \begin{bmatrix} \varvec{g_q} + \varvec{L_{0q}} \\ \mathbf {0} \end{bmatrix} . \end{aligned} \end{aligned}$$

(14)

with $\varvec{L_{0q}}$, $\mathbf {A_{0q}}$ and $\mathbf {A_{1q}}$ being the aerodynamic matrices according to Eq. 12 transformed to generalised coordinates. The first line of Eq. 14 equals Eq. 13 plus the additional matrices $\mathbf {D_{q\alpha _i}}$ and $\mathbf {K_{q\alpha _i}}$ referring to the downwash angle $\alpha _i$. The second line contains the 3D-correction terms from lifting-line theory.

Accordingly, the system of equation used for the evaluation of aeroelastic stability results to

$$\begin{aligned} \begin{aligned} \begin{bmatrix} \mathbf {I} &{}\quad \mathbf {0} &{}\quad \mathbf {0} &{}\quad \mathbf {0}\\ \mathbf {0} &{}\quad \mathbf {I} &{}\quad \mathbf {0} &{}\quad \mathbf {0}\\ \mathbf {0} &{}\quad \mathbf {0} &{}\quad \mathbf {0} &{}\quad \mathbf {0}\\ \mathbf {0} &{}\quad \mathbf {0} &{}\quad \mathbf {0} &{}\quad \mathbf {0} \end{bmatrix} \begin{bmatrix} \varvec{\ddot{q}}_n \\ \varvec{\ddot{q}}_m \\ \varvec{\ddot{\sigma }} \\ \varvec{\ddot{\alpha }_i} \end{bmatrix} + \begin{bmatrix} -\mathbf {A_{1q}} &{}\quad \mathbf {0} &{}\quad \mathbf {0} &{}\quad -\mathbf {D_{q\alpha _i}} \\ \mathbf {0} &{}\quad \mathbf {0} &{}\quad \mathbf {0} &{}\quad \mathbf {0}\\ \mathbf {0} &{}\quad \mathbf {0} &{}\quad \mathbf {0} &{}\quad \mathbf {0}\\ \mathbf {D_{\alpha _iq}} &{}\quad \mathbf {0} &{}\quad \mathbf {0} &{}\quad \mathbf {0} \end{bmatrix} \begin{bmatrix} \varvec{\dot{q}}_n \\ \varvec{\dot{q}}_m \\ \varvec{\dot{\sigma }} \\ \varvec{\dot{\alpha }_i} \end{bmatrix} \qquad \qquad \qquad \qquad \\ + \begin{bmatrix} \varvec{\omega}_{{\mathbf{0}}n}^2 - \mathbf {A_{0q}} &{} \mathbf {0} &{} (\mathbf {C}_n\mathbf {X}_{\mathbf {r}n})^T &{} -\mathbf {K_{q\alpha _i}} \\ \mathbf {0} &{} \varvec{\omega}_{{\mathbf{0}}m}^2 &{} -(\mathbf {C}_{m}\mathbf {X}_{\mathbf {r}m})^T &{} \mathbf {0}\\ \mathbf {C}_n\mathbf {X}_{\mathbf {r}n} &{} -\mathbf {C}_{m}\mathbf {X}_{\mathbf {r}m} &{}\mathbf {0} &{}\mathbf {0}\\ \mathbf {K_{\alpha _iq}} &{} \mathbf {0} &{}\mathbf {0} &{} \mathbf {K_{\alpha _i}} \end{bmatrix} \begin{bmatrix} \mathbf{q} _n \\ \mathbf{q} _m \\ \varvec{\sigma } \\ \varvec{\alpha _i} \end{bmatrix} = \begin{bmatrix} \mathbf{0} \\ \mathbf{0} \\ \mathbf{0} \\ \mathbf{0} \end{bmatrix} . \end{aligned} \end{aligned}$$

(15)

The general eigen value problem of the complete system of equations

$$\begin{aligned} \left[ \lambda ^2\mathbf {M}_c + \lambda \mathbf {D}_c + \mathbf {K}_c\right] \hat{\mathbf{x }}_ce^{\lambda t} = \mathbf{0} \end{aligned}$$

(16)

with

$$\begin{aligned} \lambda _{j1,2} = \delta _j \pm i\omega _j \end{aligned}$$

(17)

leads to the damping coefficient $\delta _j$ and operating natural frequency $\omega _j$. Since the aerodynamic damping matrix is frequency-dependent, an iterative solution is required.

3 Wing Structures

Two wing configurations are being investigated. The REF2 configuration is a conventional turboprop aircraft, whereas the REF3 configuration is designed for higher speeds with an efficient ultra high bypass ratio (UHBR) engine. For acoustic reasons, among others, the UHBR engine is located behind and above the wing [10]. Design and development of the FE wing models is done by the Institute of Aircraft Design and Lightweight Structures, TU Braunschweig and the UHBR engine is modelled by the Institute of Aeroelasticity, DLR Göttingen.

3.1 REF2

The REF2 configuration has a high wing arrangement with a halfspan of 14.39 m and a dihedral angle of −2$^\circ$. The wing has a taper ratio of 0.38 and a leading edge sweep of 10$^\circ$. The structure model is devided into a parameterised wing structure and the nacelle body. Since the nacelle is modelled as a mass point, it is represented by six rigid body modes in modal space. Figure 1 shows a bending and torsion mode of the coupled structure with no tank fillig. However, as the tank mass increases, the torsion mode becomes a coupled bending-torsion mode.

Fig. 1

Bending and torsion mode of coupled wing and engine structure with droop nose, $\delta _{fl} = 65^\circ$ and $\eta _m = 0$

3.2 REF3

The REF3 is a low wing configuration with a halfspan of 14.37 m, a leading edge sweep angle of 26$^\circ$, a taper ratio of 0.32, and a dihedral angle of 3$^\circ$. The structure model is devided into 4 seperate structures—wing, pylon, nacelle and UHBR engine. To include gyroscopic effects in the ROM, the UHBR engine model is investigated for several rotation speeds. Pylon and nacelle are considered as rigid bodies, however an interface to couple the optimal sized pylon structure based on isogeometric analysis is already included. The wing structure is, again, parameterised. Figure 2 shows a mainly bending and torsion mode of the coupled structure with no tank fillig. However, both modes include bending and torsion components.

Fig. 2

Bending and torsion mode of coupled wing and engine structure with droop nose, $\delta _{fl} = 65^\circ$ and $\eta _m = 0$

4 Aerodynamics

According to the Coandă effect [11], blowing out the jet increases the velocity gradient and decreases the pressure near the surface, causing not only the jet but also the surrounding airflow to follow the curved surface of the flap. This leads to a suction peak at the Coandă slot and also at the leading edge and thus strongly influences the aerodynamic properties. Lift is increased [1, 12,13,14,15,16,17], but the suction peak at the leading edge causes premature stall behaviour [18].

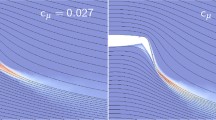
The droop nose is designed to counteract the weaknesses of the active system [3]. The profile shapes and according pressure distributions for an angle of attack of 0$^\circ$, a freestream velocity of 51 m/s, a flap deflection angle of $65^\circ$ and a momentum coefficient of 0.039 is shown in Fig. 3. As a result of the significantly reduced suction peak at the leading edge, the stall angle of attack is increased and the power needed for an efficient flow control is reduced.

Fig. 3

Profile shapes and pressure coefficient distribution for $\alpha = 0^\circ$, $\delta _{fl} = 65^\circ$, $c_\mu = 0.039$ and $v_\infty = 51\,$m/s

All results of numerical flow simulations presented for the 2D profile section are computed with the DLR TAU code of the German Aerospace Center [19], an unstructured finite volume code solving the Reynolds-averaged Navier-Stoke (RANS) equations. The original Spalart-Allmaras model is used for turbulence modelling [20]. Additionally, a 3D-correction based on Prandtl’s lifting line theory [9] is extended by empirical correction for fuselage and engine effects to approximate 3D aerodynamics.

4.1 3D-correction

In contrast to strip theory, Prandtl’s lifting line theory considers the effect of the finite ending of a wing. Along the span, a downwash velocity $v_w$ and a vortex is induced due to the circulation $\varGamma$. Depending on the considered wing span b, the downwash velocity at spanwise coordinate $y_0$ results to

$$\begin{aligned} v_w(y_0) = \dfrac{1}{4\pi } \int ^\frac{b}{2}_{-\frac{b}{2}} \dfrac{d\varGamma /dy}{y_0 - y} dy, \end{aligned}$$

(18)

inducing the downwash angle

$$\begin{aligned} \alpha _i(y_0) = \arctan \left( \dfrac{v_w(y_0)}{v_\infty }\right) \end{aligned}$$

(19)

leading to the effective angle of attack

$$\begin{aligned} \alpha _e (y_0) = \alpha (y_0) - \alpha _i (y_0). \end{aligned}$$

(20)

Along a continuous wing section, the vortices of right- and left-hand side cancel each other out. At the wing tip $y = l_S$ however, the circulation results in a free vortex. Discontinuities in the wing geometry, such as the fuselage, engine or variations in the flap angle, also cause sudden changes in circulation. Therefore the system of equations is enhanced with corresponding vortices at these discontinuities.

In Fig. 4 the comparison of lift coefficient distributions calculated with 3D CFD simulations, strip theory and the Prandtl-based 3D-correction is displayed for both wing configurations with deflected droop nose and trailing edge flap. Vortices are placed at fuselage-wing interference, wing tip and aileron in both cases. The left handside shows the REF2 configuration, whose 3D-correction includes multiple vortices and a correction of the angle of attack due to propeller slipstream. The UHBR-engine of the REF3 configuration, however, is placed behind the wing, wherefore the 3D-correction on the right handside contains no additional terms except vortices at the pylon disruption. Here, lift coefficients inbetween a dimensionless wing span of 0.4 and 0.8 are underestimated due to the neglection of sweep.

The effective angles of attack $\alpha _e$ resulting in the lift distribution approximated by the 3D-correction are pictured in Fig. 5. Whereas the aircraft angle of attack is 6$^\circ$, 2D aerodynamics inbetween −32$^\circ$ and 10$^\circ$ are used for the approximation.

Fig. 4

Comparison of 3D-CFD lift coefficient results with strip theory and the adapted lifting line theory for REF2 and REF3 configuration at $\alpha _{AC} = 6^\circ$, $c_\mu = 0.03$

Fig. 5

Effective angles of attack according to the adapted lifting line theory for REF2 and REF3 configuration at $\alpha _{AC} = 6^\circ$, $c_\mu = 0.03$

Prandtl’s lifting line theory does not apply to pitching moment coefficients. Here, the relationship between pitching moment coefficient, lift coefficient and the chordwise position of the neutral point can be used to calculate an induced pitching moment coefficient $c_{Mi}$

$$\begin{aligned} c_{Mi} = c_{M0,3D} + \dfrac{x_{n,3D}}{l} c_{Li} \end{aligned}$$

(21)

with the induced lift coefficient $c_{Li}$ being the difference of 3D-correction results and 2D strip theory

$$\begin{aligned} c_{Li} = c_{L,3D} - c_{L,2D}. \end{aligned}$$

(22)

Accordingly the 3D pitching moment coefficient results in

$$\begin{aligned} c_{M,3D} = c_{M,2D} + c_{Mi}. \end{aligned}$$

(23)

However, the 3D base pitching moment coefficient $c_{M0,3D}$ and the 3D chordwise position of the neutral point $x_{n,3D}$ are unknown and therefore empirically determined to fit the 3D-CFD results. Results of the 3D-CFD simulations and the ROM approaches are compared in Fig. 6. Strip theory coefficients are either to high or to low for both configurations. For the REF2 on the left-hand side, the neutral point position is separately defined in the section of the engine to capture the break-in. The visible differences result from the propeller slipstream effect on the pitching moment coefficient, which is not sufficiently described. The correction for the REF3 configuration on the right-hand side is, again, solely based on the additional vortices and leads to a good approximation.

Fig. 6

Comparison of 3D-CFD pitching moment coefficient results with strip theory and the adapted 3D-correction for REF2 and REF3 configuration at $\alpha _{AC} = 6^\circ$, $c_\mu = 0.03$

4.2 Steady Aerodynamics

According to the effective angles of attack needed (see Fig. 5), the dimensionless coefficients are calculated in a range of −30$^\circ$ to the respective stall angle for both profile shapes. Lift and pitching moment coefficients from steady CFD simulations and their derivatives are pictured for three jet momentum coefficients in Figs. 7 and 8. The derivatives are needed for the aerodynamic stiffness matrix according to Eq. 11. Two areas of angles of attack are of greater interest, since the aerodynamics differ from conventional profile shapes. One is the range of angles of attack close to maximum lift. Due to the influence of the jet effect on the boundary layer, lift coefficients reduce before stalling occurs [3]. This leads to a heave-flutter phenomenon, which can be observed for the profile and wing without 3D-correction [4, 5]. And secondly, the respective angles of attack below minimum pitching moment coefficient. Here, the seperation of flow on the upper side of the profile reaches the Coandă slot. Since the suction peak at the slot is responsible for the downwards pitching moment, a flow seperation in this regime leads to decreasing downwards pitching moment. The low pitching moment derivatives of the droop nose profile in Fig. 8 speak for a more rapid progress than for the clean nose profile.

Fig. 7

Lift and pitching moment coefficient from steady CFD

Fig. 8

Lift and pitching moment derivatives from steady CFD

4.3 Unsteady Aerodynamics

The investigation of the unsteady aerodynamics is based on an impulse method according to [21, 22]. It is performed for trimm angles of attack $\alpha _T$ in a range of -30$^\circ$ to the respective stall angle. The time-dependent system response is tranformed into frequency range using a Fourier transform. An immediate estimation of the damping behaviour can be made with the help of the values on the main diagonal from Eq. 11 – $c_{L,\dot{h}}$ and $c_{M,\dot{\alpha }}$. Figure 9 therefore shows lift derivatives due to heave motion on the left handside and pitching moment derivatives due to pitching motion on the right handside at a natural frequency of $\omega = 35$ rad/s. This frequency is close to the displayed bending mode of the REF2 configuration in Fig. 1. If the corresponding values in Fig. 9 are positive, they enter the damping matrix negatively according to Eq. 14 and potentially cause instability. For the lift derivative of the droop nose profile this concerns the range from −10$^\circ$ to −15$^\circ$, especially for a low momentum coefficient. The moment derivative of the droop nose profile is positive in between 0$^\circ$ and −20$^\circ$ and for the clean nose it is positive below −6$^\circ$.

Fig. 9

Lift derivatives due to heave and pitching moment derivatives due to pitching motion at $\omega = 35$ rad/s from unsteady CFD

5 Aeroelastic Instabilities

The aeroelastic stability is investigated for the bending modes of both wing configurations displayed in Figs. 1 and 2 respectively. Results for the REF2 configuration, evaluated with 3D-aerodynamics based on strip theory and the additional lifting line correction are displayed in Fig. 10. These stabilitymaps show the resulting damping coefficient of evaluated angle of attack and momentum coefficient combinations. A positive damping coefficient indicates an initially instable state. In accordance with the lift derivatives in Fig. 9, the evaluation based on strip theory implies instabilities of the bending mode below −6$^\circ$. With increasing momentum coefficient the respective angle of attack and damping coefficients decrease. Since the effective angle of attack is lowered by the lifting line correction, the evaluation with 3D-correction shows instabilities for angles of attack from 3$^\circ$ to 8$^\circ$. Here, momentum coefficients above 0.042 are stable. The modes that occur under the respective loads, called operation modes, are displayed in Fig. 11. For strip theory as well as with 3D-correction, the mode is mainly a bending mode.

Fig. 10

Stabilitymaps for REF2 configuration with engine and without thrust

Fig. 11

Operation modes of stability evaluation for REF2

For a better understanding, Fig. 12 shows the harmonic heave motion of the droop nose profile at −12$^\circ$, which leads to the positive lift derivatives in Fig. 9. At steady conditions, a movement downwards would result in better flow conditions and therefore greater lift. However, unsteady conditions cause a time delay in the propagation of the flow field, wherefore the best flow field in Fig. 12 occurs at the lowest position. This time delay and appearing turbulences result in negative work during the downturn (blue bar), but even more positive work during the upswing (red bar), leading to the observed droop nose bending flutter phenomenon.

Fig. 12

Harmonic heave motion of droop nose profile at $\alpha = -12^\circ$, $c_\mu = 0.033$ with implied flow field, resulting forces and work

For the REF3, the results are not based on the derivatives presented in Fig. 9, but on a natural frequency of 48 rad/s. However, based on strip theory on the left handside in Fig. 13, a compareable area indicates instabilities. Including 3D-correction, many of the investigated combinations result in positive damping coefficients. For some combinations the 3D-correction does not converge, wherefore these are left blank. The operation modes for two combinations are displayed in Fig. 14. In contrast to Fig. 11, coupled bending-torsion modes result for the REF3 configuration. This explains the large areas of instabilities, even for high momentum coefficients. According to Fig. 9, the pitching moment derivatives are less dependent on the momentum coefficient and unstable over a wider range.

Fig. 13

Stabilitymaps for REF3 configuration with engine and without thrust

Fig. 14

Operation modes of stability evaluation for REF3

6 Conclusion

A reduced-order model for efficient and adaptable aeroelastic investigation of different wing configurations was presented. The wing structures are seperated into substructures, which are individually transformed and reduced in modal space. A parameterisation and substructure technique provide high adaptability. Steady and unsteady aerodynamics are investigated with 2D-CFD-calculations for different profiles over a range of parameters. Using strip theory and an adapted lifting line theory based on Prandtl, 3D-aerodynamics are approximated. The results, using only strip theory, show aeroelastic instabilities at low angles of attack for both wing configurations. These are directly based on the derivatives from unsteady CFD-simulations. Using the adapted 3D-correction, however, shifts the unstable areas to higher angles of attack. While the bending instability of the REF2 configuration is limited and might be remedied with selected means if necessary, the bending-torsion instability of the REF3 configuration concerns large areas.

It is shown that the reduced-order model takes into account both the frequency dependence and different modes. However, since the 3D-correction adresses extremly negative angles of attack, especially low aircraft angles of attack show no convergence. A full 3D-CFD aeroelastic investigation is therefore necessary at points of interest to validate the presented results.