Octopus-Inspired Arm Movements

Abstract

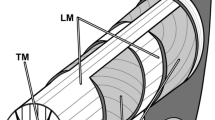
The octopus offers an enticing paradigm for the control of distributed, high-dimensional, underwater systems. Octopus arms are composed almost entirely of muscles, arranged in highly organized patterns, allowing active control of bending, twisting, and stretching. In particular, the octopus can form pointed joints along an arm to quickly fetch objects from a distance, and can use its arms to crawl bipedally on the seafloor. Here, we analyze image data of fetch and crawl motions, then reproduce these behaviors in a three-dimensional elastic filament model of the octopus arm. We first constrain the tip of the arm to follow prescribed trajectories consistent with experimental observations. We then reverse engineer the active internal forces and moments that produce compatible full arm movements, thus developing blueprints for basic motion primitives. We conclude by analyzing the effect of compliance on robustness of these motions to environmental variations and by commenting on the implications of our results to the motor control of cephalopods and to the development of control strategies for soft robotic systems.

Appendix: Numerical Implementation

To solve for the filament dynamics in three dimensions, we numerically integrate the governing equations (11.1), together with the corresponding boundary conditions. To this end, we discretize the filament’s centerline into n + 1 vertices r ₁, …, r _n+1 and n straight edges ℓ _i = r _i+1 −r _i, where i = 1, …, n, in the spirit of [7, 9]. The unit tangent to edge i is defined as t _i = ℓ _i∕ℓ _i, where ℓ _i = ∥ℓ _i∥. The translational velocities v ₁, …v _n+1 are assigned to vertices. The body frames {d _1,i, d _2,i, d _3,i = t _i} and the rotation matrices Q _i are naturally assigned to edges.

To obtain a discrete representation of the generalized curvature vector κ, we start from the definition of the associated skew-symmetric matrix κ ^× = Q(Q′)^T. The solution to this first-order differential equation is of the form $\mathbf {Q}(s+\Delta s) = \exp (-\boldsymbol {\kappa }^\times \Delta s)\mathbf {Q}(s)$, where Δs is a segment of constant curvature. Thus, writing ${\mathbf {Q}}_i = \exp (-\boldsymbol {\kappa }_{i}^\times \overline {\ell }_i){\mathbf {Q}}_{i-1}$, we define the discrete curvature matrix as $\boldsymbol {\kappa }_{i}^\times =-{\log \big ({\mathbf {Q}}_{i}{\mathbf {Q}}^{\mathsf {T}}_{i-1}\big )}/{\overline {\ell }_i}$, where $\overline {\ell }_i=\frac {1}{2} (\ell _{i-1}+\ell _{i})$ is a Voronoi integration domain from the midpoint of the previous edge to that of the next edge. Given $\boldsymbol {\kappa }_{i}^\times$, we can readily evaluate κ _i and the discrete elastic moments M _i in the filament material frame.

When computing derivatives of quantities expressed in the body frame (i.e., on edges), we need to consider appropriate frame transport. For example, the derivative of the internal moment is computed as follows:

$$\displaystyle \begin{aligned} \left(\frac{\partial \mathbf{M}}{\partial s} \right)_i=\mathcal{D}\big[{\mathbf{B}}_{i}\boldsymbol{{\kappa}}_{i}\big] + \mathcal{A}\big[\underbrace{(\boldsymbol{{\kappa}}_{i}\overline{\ell}_i)\times({\mathbf{B}}_{i}\boldsymbol{{\kappa}}_{i})}_{\text{frame}\ \text{transport}}\big], \end{aligned} $$

(11.7)

where $\mathcal {D}$ is a forward difference operator and $\mathcal {A}$ an averaging operator that maps quantities from adjacent vertices to the in-between edge. Specifically, when expressed in matrix form, the operators $\mathcal {D}$ and $\mathcal {A}$ have entries $\mathcal {D}_{ij} = \delta _{i,j+1} - \delta _{ij}$ and $\mathcal {A}_{ij} = \left (\delta _{i,j+1} + \delta _{ij}\right )/2$.

We solve the force and moment quantities in the strain-free reference configuration. Therefore, we need to adjust all quantities expressed in the current geometric configuration to the strain-free reference configuration denoted by $\hat {(\cdot )}$. Provided that cross-sections retain their circular shapes at all times, we need only to account for a local dilation scalar $e_i =\ell _i/\hat {\ell }_i$ at appropriate places in the discretized equations to ensure consistency. Specifically, due to the conservation of volume of an infinitesimal volume element, a dilation in edge length translates to a shrinkage of cross-sectional area; namely, we have $\ell _iA_i= \hat {\ell }_i\hat {A}_i$ which implies that ${A}_i = \hat {A}_i/e_i$. Consequently, the discrete bending/twisting rigidity tensor $\hat {\mathbf {B}}_i$ and tensile stiffness $\hat {K}_i$ in the stain-free reference configuration are related to B _i and K _i in the current configuration via ${\mathbf {B}}_i=\hat {\mathbf {B}}_i/{e_i^2}$ and $K_i=\hat {K}_i/{e_i}$. All length quantities need to scaled by a factor of e _i when converted to the strain-free reference configuration. In addition, because we use the integration domain $\overline {\ell }_i$, all quantities that vary with arc-length over the Voronoi region need to be properly averaged. For example, the dilation factor e is averaged over $\overline {\ell }_i$ using $\langle {e}_i \rangle =\left ({e_{i}\hat {\ell }_{i}+e_{i-1}\hat {\ell }_{i-1}}\right )/{2\hat {\overline {\ell }}_i}$. To adjust the generalized curvature with respect to the dilation factor, we write $\boldsymbol {{\kappa }}_i=\hat {\boldsymbol {{\kappa }}}_i/\langle {e}_i \rangle$.

The inextensibility condition is enforced weakly by setting K ≈ 10⁵B, requiring the use of standard time integrators for stiff equations (MATLAB’s ode15s) to propagate the filament position r _i forward in time. We enforce boundary conditions strongly by fixing r and t at the appropriate end vertices. Results of this numerical method have been validated against standard analytical results (e.g., Euler buckling and Mitchell’s instability thresholds, deflection curve of nonshearable cantilever beam). For more details, see the supplemental material accompanying [35].