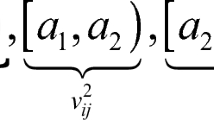Keywords

1 Introduction

Companies that sell goods to customers at multiple locations have to come up with a dedicated plan how to distribute their products over the different locations to perfectly fit the customers demands. Detailed vehicle routing problems arise naturally when planning these deliveries. The Vehicle Routing Problem and its variants are very well studied in the literature. We refer to [5] for a review. These problems become even more complex by adding constraints modeling characteristics of goods, vehicles, or strategic decisions. The authors of [2] call these problems rich vehicle routing problems. This paper focuses on a special case of these problems where perishable goods are considered, i.e. each product has a due date. Deliveries have to be performed before this date and it is prohibited to store the products for a long time at the individual locations. Since late deliveries have a direct impact on the revenues for these products, a precise demand prediction is even more important. Moreover, the demands and vehicle driving times required to transport the goods are dependent on the actual weather conditions. The problem we are dealing with was defined for the AIMMS-MOPTA Optimization Modeling Competition 2018 [3]. It came with a detailed problem description and a set of historical weather features, which have an influence on the product demands and the vehicle driving times to deliver the products. The data should be used to predict the demands and weather conditions on a fixed date and to create an optimal plan to deliver the perishable products to a set of customers. In this paper we present the definition and a solution approach to the Vehicle Routing Problem with Perishable Goods (VRPPG). This includes a procedure how historical weather data is used to predict the demands and driving times. The VRPPG can be seen as a mixture of the Capacitated Vehicle Routing Problem, first defined by Dantzig and Ramser [1] and the Vehicle Routing Problem with Time Windows presented in [4]. We test the approach which let our team finish second place in the MOPTA Competition 2018, on different data sets given by the competition. Finally, we discuss the quality of the approach in terms of run time and quality of the computed solutions.

2 The Vehicle Routing Problem with Perishable Goods

We consider a set of locations \(I \subset \mathbb {N}\) including warehouse 0 and set of retailers J ⊂ I. Each retailer j ∈ J has a demand of \(d_{j}\in \mathbb {N}\) of perishable goods. Deliveries of goods are in time if they arrive before a fixed due date h ∈ [0, H[. Each good delivered later is penalized by c m independently of the actual duration of the delay. A maximum number of \(A\in \mathbb {N}\) vehicles are available to perform deliveries. Each vehicle has a capacity of \(C\in \mathbb {N}\) items.

If a vehicle is used it induces the fixed cost \(M_{F}\in \mathbb {R}\) and, additionally, the variable costs of \(m_{t}, m_{v}\in \mathbb {R}\) for each hour and mile it is operated, respectively.

The possible trips between locations are given by the set E ⊆ I × I. The resulting graph G := (I, E) is used to compute feasible tours beginning and ending at the warehouse. It is assumed that unloading goods at a retailer takes no time. The duration of a trip between two locations and its length is given by \(\tau ,l: E \mapsto \mathbb {R}^{+}\), respectively.

Definition 1

The Vehicle Routing Problem with Perishable Goods is the task to find the following items: a set of cycles R in G, for each cycle r ∈ R an assignment of amounts of goods to retailers j, and an assignment of each cycle r ∈ R to a vehicle in {1, ..., A}. These assignments have to minimize penalties caused by late deliveries and the costs for operating the vehicles while satisfying the following conditions: each cycle visits 0; the sum of the goods assigned to a retailer of a cycle does not exceed C; the sum of all goods assigned to a fixed retailer j over all cycles satisfies d j.

For the MOPTA Competition 2018 the duration of a trip between two locations was only given by historical data including the following three weather features: temperature \(f\in \mathbb {R}^{+}\) in degrees Fahrenheit, precipitation \(p\in \mathbb {R}^{+}\) in cubic centimeters per hour, and wind \(w\in \mathbb {R}^{+}\) in kilometers per hour. Based on the historical data, the map \(\tau : E \times \mathbb {R}^{3} \mapsto \mathbb {R}^{+}\) for travel times between two locations in dependence of the features had to be generated.

3 A Solution Approach to the VRPPG

We present an approach to tackle the problem in this section. It is based on a mixed integer linear programming (MILP) model and optimizes the sequences of tours that have to be performed by the vehicles. We define a tour as a single vehicle movement along a cycle beginning at the warehouse, visiting one or more retailers j ∈ J, before returning to the warehouse. Let T denote the set of tours. The approach uses minimum and maximum numbers of tours given by \( m:= \lceil \frac {\sum _{j \in J} d_{j}}{C}\rceil \) and \(M:=\sum _{j\in J} \lceil \frac {d_{j}}{C}\rceil \), respectively.

Our solution approach can be summarized as follows. We assume that all travel times τ(e, f, p, w) are given for a fixed tuple of weather features. We connect all retailers in G to the warehouse 0. For those retailers originally not directly connected to 0, the length of the edges is set to the length of the shortest path with respect to travel time. We compute the set P of all possible cycles that visit at most n + 1 retailers with minimal travel time with respect to cycles that visit precisely the same retailers. Here, n is defined as \(n:=\max \{|S|| \sum _{j\in S}d_{j} \leq C, S \subseteq J\}\) and for a cycle p, let c p and τ p denote its length and duration. Further, let P j denote the set of cycles that visit j and let τ p,j denote the time to reach retailer j from the warehouse along some p ∈ P j. The model given in Sect. 3.1 is then solved by an commercial state of the art MILP solver.

3.1 MILP Model for the VRPPG

The MILP model formulation contains binary decision variables x t,p for all t ∈ T, p ∈ P that indicate if tour t performs cycle p, p t,j for all t ∈ T, j ∈ J that indicate if retailer j is delivered late on tour t, v t for all t ∈ T that indicate if tour t is operated by an additional vehicle, and r t for all t ∈ T that indicate if tour t is operated by the same vehicle as tour t − 1. Let l t,j be continuous variables that define the load of goods delivered in time for retailer j on tour t and s t,j the respective load delivered late. The continuous variables d t, a t define the departure and arrival time of a tour t at the warehouse. Finally, let H denote the time horizon. To shorten notation \(\tilde {d}_{j}\) defines \(\tilde {d}_{j} := \min \{C,d_{j}\}\).

Reloading a vehicle for a tour requires that the preceding tour has already arrived at the warehouse, which is controlled by constraints (3) and (4). The set of equalities (5) decides which cycle is assigned to an operated tour. The correct arrival and departure times are set by the constraints (6) with respect to the cycle operated on a tour. To satisfy the demand of each retailer and to prevent exceeding the vehicle capacity, the amount of transported goods for each retailer and each tour are summed up in (7) and (8), respectively. The next two sets of inequalities restrict the individual loads of each retailer on each tour. In set (9) the upper bound of the (in time) load variable for a retailer is set to the minimum of the vehicle capacity and the retailer’s demand, if a cycle containing the retailer is selected. It is set to zero if the retailer is visited late on the selected cycle. The upper bounds for the (late) load variables are enforced by (10). The set of constraints (11) takes care that the decision variable p t,j becomes 1 if retailer j will be handled late, i.e., tour t starts too late.

$$\displaystyle \begin{aligned} \min\, \sum_{t \in T}\, {c_{p}x_{t,p}} + \sum_{t \in T}\, {M_{F}v_{t}}&+\sum_{t \in T}\sum_{j \in J}\, {c_{m}s_{t,j}},&& \notag \\ \text{s.t.:}\quad \quad \sum_{t \in T} v_{t} & \leq A, & {} \end{aligned} $$
(1)
$$\displaystyle \begin{aligned} v_{t} + r_{t} & \leq 1, & \forall t \in T {} \end{aligned} $$
(2)
$$\displaystyle \begin{aligned} d_{t+1} + H (1 -r_{t}) & \geq a_{t} & \forall t \in T,{} \end{aligned} $$
(3)
$$\displaystyle \begin{aligned} \sum_{p \in P} x_{t,p} & \geq r_{t+1} & \forall t \in T,{} \end{aligned} $$
(4)
$$\displaystyle \begin{aligned} \sum_{p \in P} x_{t,p} & = v_{t} + r_{t} & \forall t \in T,{} \end{aligned} $$
(5)
$$\displaystyle \begin{aligned} d_{t} + \sum_{p \in P} \tau_{p} x_{t,p} & \leq a_{t} & \forall t \in T,{} \end{aligned} $$
(6)
$$\displaystyle \begin{aligned} \sum_{t \in T} l_{t,j} + s_{t,j} & \geq d_{j} & \forall j \in J,{} \end{aligned} $$
(7)
$$\displaystyle \begin{aligned} \sum_{j \in J} l_{t,j} + s_{t,j} & \leq C ( v_t + r_t ) & \forall t \in T,{} \end{aligned} $$
(8)
$$\displaystyle \begin{aligned} \tilde{d}_{j} \sum_{p \in P_{j}} x_{t,p} - \tilde{d}_{j} p_{t,j} & \geq l_{t,j}& \forall t \in T, j \in J,{} \end{aligned} $$
(9)
$$\displaystyle \begin{aligned} \tilde{d}_{j} \sum_{p \in P_{j}} x_{t,p} & \geq s_{t,j} & \forall t \in T, j \in J,{} \end{aligned} $$
(10)
$$\displaystyle \begin{aligned} \sum_{p \in P_{j}} \tau_{p,j} x_{t,p} + d_{t} & \leq h + H p_{t,j} & \forall t \in T, j \in J,{} \end{aligned} $$
(11)
$$\displaystyle \begin{aligned} x_{t,p} & \in \{0 , 1\} & \forall t \in T, p \in P,{} \end{aligned} $$
(12)
$$\displaystyle \begin{aligned} \hspace{-9pt} p_{t,j} \in \{0 , 1\},\; s_{t,l},l_{t,l}\in \{0 , \tilde{d}_{j}\},\; a_{t},d_{t} & \in \{0 , H\} & \forall t \in T, j \in J,{} \end{aligned} $$
(13)
$$\displaystyle \begin{aligned} v_{t}, r_{t} & \in \{0,1\} & \forall t \in T. {} \end{aligned} $$
(14)

3.2 Weather Features

So far we assumed that the travel times for each edge are given. As mentioned before this was not the case for the MOPTA Competition 2018. Instead a set of historical travel time data linked to weather features was given. To compute travel times for the edges of G for a fixed tuple of weather features we implemented two different methods.

The first method, which we call Closest Candidate Method (CCM), simply searches for the ‘closest’ weather feature tuple in the historical data set and applies these travel times to the edges of G. In this sense closest refers to the distance according to the following metric d. Let w 1 := (f 1, p 1, w 1) and w 2 := (f 2, p 2, w 2) be two weather tuples. The distance d(w 1, w 2) is a normalized Euclidean distance given by \(d(w_1,w_2):= \sqrt {\Big ( \frac {f_1 - f_2}{f_{\varDelta }} \Big )^{2}+ \Big ( \frac {p_1 - p_2}{p_{\varDelta }} \Big )^{2}+\Big ( \frac {w_1 - w_2}{w_{\varDelta }} \Big )^{2}}\).

Where f Δ, p Δ, w Δ are the ranges between minimum and maximum value of the respective weather feature included in the historical data set.

The second method, which we call Closest Pair Method (CPM), looks for two points w 1 := (f 1, p 1, w 1) and w 2 := (f 2, p 2, w 2) that enclose a given weather feature w := (f, p, w), i.e., f ∈ \([\min \{f_1, f_2\}\), \(\max \{f_1,f_2\}]\), p ∈ \([\min \{p_1, p_2\}\),\( \max \{p_1,p_2\}]\), w ∈ \([\min \{w_1, w_2\}\),\( \max \{f_1,f_2\}]\). CPM iterates through all pairs of historical weather w 1 and w 2 that enclose w to find the pair with a minimum cumulative distance d(w, w 1) + d(w, w 2). The found pair is then used to interpolate the searched point as follows. Each edge e ∈ E is assigned a travel time according to the weighted sum \(\tau (e):= \Big (\frac {\tau _1(e)}{d(w, w_1)} + \frac {\tau _2(e)}{d(w, w_2)}\Big )/\big (d(w,w_1)+d(w,w_2)\big )\) where τ i(e) is the travel time on edge e and weather feature i. If no suitable pair of features is found, CCM is used to assign travel times.

4 Computational Results

In this section we present the characteristics of the solution approach both for the CCM and CPM method to estimate the driving times. Table 1 contains an individual row for two data sets containing 50 respectively 100 VRPPG instances as shown in Column #. The “dependent” data set contains instances where the retailers’ demands are dependent from the weather conditions. Therefore, the demands were determined from a historical data set in a similar way like it was done for the driving times. The next two blocks of four columns show the characteristics of the CCM and CPM approach, respectively. The column ∅(s) marks the arithmetic average of the run times for the instances of each set. The columns 2m and 5m give the number of instances that were solved to optimality within 2 and 15 min, respectively, whereas the column 1h shows the number of instances that hit the time limit before proven to be optimal. The two columns headlined with gap mark the maximum gap between the upper and lower bound of instances that were not proven to be solved to optimality. Finally, the columns # and % in the Diff block compare the solutions found by each of the approaches. The column # gives the number of instances where a different number of vehicles is used in the solutions of CCM and CPM while Column % shows |c(CCM) − c(CPM)|∕c(CCM), i.e., the absolute value between the two objective function values divided by the CCM objective function value. All computations were done with AIMMS 4.53.5.7 with CPLEX 12.7.1 as internal MILP solver on a Intel(R) Core(TM) i7-4600U CPU with 2.10 GHz, four cores, 8 GB RAM and a maximum run time limit of 1 h.

Table 1 Computational results for CCM and CPM
Full size table

Table 1 shows that the presented approaches generate high quality solutions for all instances of both test sets in a short time, about 24 s on average per instance, in case of the instances with weather independent demands. None of these instances takes more than 4 min to solve, which is a promising result. The Diff block shows that both approaches lead to very similar solutions for most of all instances.

5 Conclusion

We presented two approaches for the VRPPG based on a MILP problem formulation with path variables. The chosen approach leads to high quality solutions combined with fast running times for the instances subject to the competition, which justifies the presented approach. To further improve the model and solve larger instances a dynamic cycle construction, i.e., variable generation should be used.