Abstract
DNA data provide us a considerable amount of information regarding our biological data, necessary to study ourselves and learn about variant characteristics. Even being able to extract the DNA from cells and sequence it, there is a long way to process it in one step.
Over past years, biologists evolved attempting to “decipher” the DNA code. Keyword search and string matching algorithms play a vital role in computational biology. Relationships between sequences define the biological functional and structural of the biological sequences. Finding such similarities is a challenging research area, comprehending BigData, that can bring a better understanding of the evolutionary and genetic relationships among the genes. This paper studied and analyzed different kinds of string matching algorithms used for biological sequencing, and their complexity and performance are assessed.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- DNA
- Patterns
- Genome assembly
- Graph
- BigData
- Assemblers
- Algorithms
- Matching algorithms
- Keyword search
- DNA sequence
- Distance measurements
1 Introduction
Keyword search and matching are techniques to discover patterns inside specific strings. Algorithms for matching, are used to discover matches between patterns and input strings. For instance, V represents an alphabet; in V there are characters or symbols. Assuming, \(V=\left\{ A, G \right\} \), then AAGAG is a string. Patterns are labeled by \(P\left( 1...M \right) \), while the string is labeled as \(T\left( 1...N \right) \). Pattern can occur inside a string by using a shifting operation.
Text-editing applications can also benefit from the aid of string matching algorithms, aiding and improving responsiveness while writing. There are two main approaches for string matching, first is exact matching, for instance: Smith-Waterman (SW); Needleman Wunsch (NW); Boyer Moore Horspool (BMH); Dynamic Programming; Knuth Morris Pratt (KMP). Second approach, is approximate matching, also known by Fuzzy string searching, for instance: Rabin Karp; Brute Force.
Many algorithms try to give solutions for the string matching problems like, pattern matching using wide window, approximate matching, polymorphic matching, minimize mismatches, prefix/suffix matching, similarity measure, longest commons sub-sequence (using dynamic programming algorithms), BHM, Brute Force, KMP, Quick search, Rabin Karp (Singla and Garg 2012).
In this paper is analyzed the similarity measures on Protein, DNA and RNA, using for that effect, different types of string matching algorithms, like: NW algorithm, Boyer Moore (BM), SW algorithm, Hamming Distance, Levenshtein Distance, AhoCorasick (AC), KMP, Rabin Karp, and CommentZwalter (CZW).
This paper is organized as follows, Sect. 2, reviews the related work in the field, Sect. 3 compares selected algorithms in therms of complexity. Section 4, presents experimental results comparing the different algorithms. Finally, Sect. 5, concludes the study and presents some future research lines.
2 Related Work
In pattern recognition problems it is essential to measure distance or similarity. Given the following example:

Pattern P can be matched in String T by adding four empty spaces before the pattern and two after.
Authors in (Yeh and Cheng 2008), use Levenshtein distance applied to images and videos to determine feature vectors. For instance:

The objective is to find the maximum matches between Input A and B. By removing the last triangle in Input A the maximum match is reached.
In (Amir et al. 2004), the authors propose a new distance for string matching, similar to Levenshtein distance, with K-Mismatches on the given string. This proposed approach was implemented with Message Passing Interface (MPI), and proved to be useful to establish similarity between strings.
Authors in (Knuth et al. 1977), proposed an algorithm for pattern matching in strings, with running time proportional to the sum of the length of the strings. This traditional algorithm is now known as KMP string matching algorithm.
Other classical string pattern matching algorithm was proposed in (Hussain et al. 2013), named Bidirectional Exact Pattern Matching (BDEPM). This algorithm introduces the idea to compare strings using pointers in simultaneous, one from the left other from the right. For example:

In (Alsmadi and Nuser 2012), they evaluated two algorithms for DNA string comparison in terms of accuracy and performance. The Longest Common Substring (LCS) algorithm, and Longest Common Sub-Sequence (LCSS) algorithms. In the following example, the highlighted letters, CTCT, in the sequences is LCSS of the specified sequences.

Different types of string matching algorithms are explored in (Singla and Garg 2012), concluding that for string matching, Boyer Moore algorithm is the best.
In (Pandey), authors test many algorithms for string pattern match. These algorithms are tested and compared based on multiple parameters, such as execution time, matching order, the number of comparisons, shift factor, and accuracy. Conclusions show that Boyer Moore algorithm is the more efficient when applied to a heterogeneous system for pattern matching.
Aho-Corasick and CommentZ-Walter algorithms (Vidanagamachchi et al. 2012) are two types of multiple patterns matching algorithms, authors in (Vidanagamachchi et al. 2012) implemented these two algorithms and worked with peptide sequences to study their accuracy and execution time. Results show that Aho-Corasick performs better than the CommentZ-Walter algorithm.
3 Algorithms Analysis
In this section, we analyze the proposed matching algorithms mentioned in Sect. 2 (Related work).
3.1 Hamming Distance
Hamming distance was introducing to measure, detect and correct codes in 1950. This distance can be applied to biological sequences. This algorithm measures the minimum number of substitutions required to transform one sequence into another.
Definition 1
(Hamming Distance). Consider two sequences \(A = (a_{1},\ldots ,a_{n})\) and \( B = (b_{1},\ldots ,b_{n})\) with sizes n over an alphabet \(\varSigma \). The Hamming distance between two sequences A and B is denoted by \(\delta _{ham} (A,B)\).
where \(\varphi _i\) is the pairing variable and \(s(\varphi _i)\) is equal to 1 when \(a_i \ne b_i\).
From Eq. 1, it is possible to calculate the minimum number of substitutions required to transform one sequence into another. Hamming distance fundamentally assumes that the input sequence have the same length. We can generalize the hamming distance to allow for insertions and deletions and calculate the Levenshtein distance.
3.2 Levenshtein Distance
Levenshtein distance between two sequences is defined as the minimum number of substitutions required to transform one sequence into another. It allowed to compare sequences with different lengths, by considering the operations insertion, deletion and substituting characters.
Definition 2
(Levenshtein Distance). Consider two sequences \(A = (a_{1},\ldots , a_{n_1})\) and \( B = (b_{1},\ldots ,\ b_{n_2})\) over the alphabet \(\varSigma \). The Levenshtein distance between two sequences A and B of length \(n_1\) and \(n_2\), respectively, is given by \(\delta _{lev}(n_1,n_2)\) where
where
and \(s(a_i,b_j) = 1\) when \(a_i \ne b_j\) and 0 otherwise. The first element in the minimum function corresponds to deletion from A to B, the second to insertion and the third to match or mismatch (substitution).
For instance, assuming that the Levenshtein distance between “CCGTCG” and “CGGTTGA” is three, then it is not possible to transform one into the other with less than three edits:
-
1.
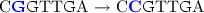 (replace ‘C’ for ‘G’);
(replace ‘C’ for ‘G’); -
2.
 (replace ‘T’ for ‘C’);
(replace ‘T’ for ‘C’); -
3.
 (remove ‘A’ from the end).
(remove ‘A’ from the end).
3.3 Damerau–Levenshtein
Damerau–Levenshtein distance includes transpositions among operations, additionally to the three classical single-character operations (insertions, deletions and substitutions) (Levenshtein 1966; Bard 2007). Damerau–Levenshtein distance is also applied in biology to measure the variation between protein sequences (Majorek et al. 2014).
To express the Damerau–Levenshtein distance between two strings a and b a function \(d_{a,b}(i,j)\) is defined, where the result is the distance between an i-symbol prefix (initial sub-string) of string a and a j–symbol prefix of b.
The restricted distance function is defined as follows in the equation:
* \(i,j > 1 \text{ and } a\left[ i \right] = b\left[ j-1 \right] \text{ and } a\left[ i-1 \right] = b\left[ j \right] \)
Where \(1_{(a_{i}\ne b_{j})}\) is the indicator function equal to 0 when \(a_i = b_j\) and equal to 1 otherwise.
Each recursive call matches one of the cases covered by the Damerau–Levenshtein distance:
-
\(d_{a,b}(i-1, j)+1\), corresponds to a deletion (from a to b);
-
\(d_{a,b}(i, j-1)+1\), corresponds to an insertion (from a to b);
-
\(d_{a,b}(i-1, j-1)+1_{(a_{i}\ne b_{j})}\), corresponds to a match or mismatch, depending on whether the respective symbols are the same;
-
\(d_{a,b}(i-2, j-2)+1\), corresponds to a transposition between two successive symbols;
The Damerau–Levenshtein distance between a and b is then given by the function value for the full strings \(d_{a,b}\left( \left| a \right| , \left| b \right| \right) \), where \(i = \left| a \right| \) is the length of string a and \(j = \left| b \right| \) is the length of b.
3.4 Needleman Wunsch Algorithm
The Needleman-Wunsch (NW) algorithm (Needleman and Wunsch 1970) is a Dynamic Programming (DP) algorithm that solves the problem of sequence alignment. It was one of the first applications of DP to compare biological sequences. To determine the degree of similarity (distance) between two sequences, an score function as given in Definition 3 is required.
Definition 3
(Score of a pairwise alignment). Let \(A = (a_{1},\ldots ,a_{n_1})\) and \( B = (b_{1},\ldots ,b_{n_2})\) be two sequences over an alphabet \(\varSigma \) and “−” indicate the indel (insertion or deletion) character. Let \( \varphi =(\varphi _{1},\ldots ,\varphi _{\ell }) \) be an alignment with length \(\ell \). For \(a,b \in \varSigma \), let \(s(\varphi _j)\) indicate the score of a pair such as \(((a,-)\), \((-,b)\) or (a, b) ) in the alignment, \(1\le j \le \ell \). let M be a substitution matrix for aligning two characters and d be the score for a pair that contains \((a,-)\) or \((-,b)\). The score function \( \delta (\varphi ) \) of the alignment \(\varphi \) is given by:
where,
Therefore, for finding the optimal alignment between two sequences, the maximum score of this function is needed to compute and the alignment that yields it. The working principle for solving the sequence alignment problem with DP is to compute the optimal alignment for all pairs of prefixes of the given sequences. The DP algorithm consists of four parts: (i) a recursive definition of the score; (ii) a dynamic programming matrix for storing the optimal scores of sub-problems; (iii) a bottom-up approach to complete the matrix starting from the smallest subproblems, and (iv) a traceback method to recover the optimal alignment (Kleinberg and Tardos 2006). The recursive definition of the score is as follows:
where
M is the substitution matrix and d is the score of an indel.
The recurrence is applied repeatedly to fill a score matrix and once it is filled, the last element of the matrix, \( (n_1,n_2) \), holds the score of the optimal alignment. Figure 1 shows the score matrix for the nucleotide sequences AGTA and ATA with match reward 1 \((a = b)\), mismatch penalty \(-1\) \((a \ne b)\) and indel penalty \((d = -2)\). From the bottom-right cell, a route is traced back to the top-left cell, which gives the alignment. By following the path in the matrix, an optimal alignment, with score 1, is:

3.5 Smith Waterman Algorithm
Global alignment methods force alignments to span the entire length of the sequences by attempting to align every character of each sequence. They are useful when two sequences are similar and have roughly equal length. Local alignments are more useful to identify discrete regions of similarity between otherwise divergent sequences. The algorithm for finding an optimal local alignment is called the Smith-Waterman algorithm (Smith and Waterman 1981). It is closely related to the algorithm for global alignment as described in the previous section. The two main differences are:
-
(i)
In each cell in the score matrix can take the value zero if all the three options have negative values. This option allows the algorithm to start a new alignment, which might result in a better score of the prefixes’ alignment than continuing an existing one. This translates into resetting the current score of the prefixes’ alignment to zero.
-
(ii)
In order to reconstruct the alignment, the trace back must start from the highest value in score matrix. The trace-back ends when a cell with value zero is found.
The recurrence equation for local alignment is given as follows:
with \(1\le i \le n_1\), \(1 \le j \le n_2\). A bottom-up DP algorithm can also be derived from the above recursions, analogously to the Needleman-Wunsch algorithm.
3.6 Knuth Morris Pratt Algorithm
Knuth Morris Pratt (KMP) algorithm is a linear time algorithm for string matching, where the longest prefix or suffix called core is represented by, \(u = t \left[ l'...r \right] \), \(v = t \left[ l...r \right] \), where, u represents to longest prefix and suffix of v (Knuth et al. 1977). KMP works left to right processing the pattern P, important to note that it uses a failure function. The KMP algorithm prepossess the pattern P by computing a failure function f that indicates the largest possible shift s using previously performed comparisons. Specifically, the failure function f(j) is defined as the length of the longest prefix of P that is a suffix of P[i . . j]. When a match is found the current index is increased, if not the failure function determines the new index, and P is again checked again against T. This process is repeated until a match P in text T or index for T reached n (the size of T). The main part of KMP algorithm is a loop which compares a character in T and P for each iteration. In KMP there is no backtrack and the shifting is only one position. The algorithm in Listing 1.1 exemplifies how the algorithm works in practice, as input there is the text T with size n and pattern P of size m, as output, the index of the string of T matching P.

For better understanding the algorithm, lets assume the following example, where, W = “APCDAPD” and S = “APC APCDAP APCDAPCDAPDE”. The state of the algorithm can be identified, at any given time, by two integer values:
-
1.
m, representing the position in S, which is the start of a match for W.
-
2.
i, the position in W, identifying the character being matched.
For each step of the algorithm, \(S \left[ m+i \right] \) is compared with \(W \left[ i \right] \), and moved forward if there is a match.

3.7 Boyer Moore Algorithm
Boyer Moore algorithm (BM) for string search and match is a standard benchmark algorithm, considered one of the most efficient when the alphabet comprises a small size of characters, used on standard editors to perform string search. SO this algorithm is often used in bioinformatics for disease detection. This algorithm works right to left by matching two sequences, thins method consists on a backward approach. When there is any mismatch it means that the patter was found, otherwise the sequence is moved to right (shifted) and a new match attempt is performed (Martin et al. 2005). The pseudo code in Listing 1.2 illustrates how the Boyer Moore algorithm works. Where as input, the text T of size n and pattern P of size m, and as output, the first index of the string T equal to P or −1 if no match is found.

Lets consider pattern P in the text T, with mismatches in text character \(T \left[ i \right] = c\), then, the corresponding text pattern search \(P \left[ j \right] \) is performed as follows; If c is within P, then completely shift the pattern P past i, else, shift P until c is in P and aligned with \(T \left[ i \right] \). For example:

3.8 Brute Force
This algorithm is the simplest method, it checks all patterns with the text, position by position, until matching characters are found. The algorithm works from left to right without the need for prepossessing. There are two steps in this algorithm, which consist on two nested loops (Rajesh et al. 2010; Dudas 2006). An example of implementation is as follows in Listing 1.3, where the input consists on the text T of size n and pattern P of size m, and the output is the index start of the string T equal to P or −1 if no match found.

The algorithm can be set to find the entire pattern or stop with just part of it. Example:

3.9 Rabin Karp Algorithm
Rabin Karp (RK) algorithm is used to look for similarities in two sequences, proteins, i.e. a high sequence similarity means significant structural or functional similarity. RK utilizes a hash function to make the string searching faster. The hash value for the pattern is calculated, used then to compare with sub-sequences of the text. When the hash values are different, RK algorithm estimates the hash for the next matching sequence of characters. If hash values are equal, RK algorithm uses brute-force to compare sequence pattern with the text. RK algorithm efficiency is based on the computation of hash values of text sub-strings.
Rolling hash functions analyze sub-strings as a number, the base of this functions, usually is a large prime number. For instance, considering the sub-string “AC” and the base 1011, the hash would be \(65 \times 10111 + 67 \times 10110 = 65782\), where “A” is 65 and “C” is 67 in the ASCII table.
Lets consider a M-character sequence with M-digit number, base b, where b is the number of letters in the alphabet, the text mapped into sub-sequence \(t \left[ 1 ... i + M -1 \right] \).
Equation 8 is used to compute sub-sequences of specific sequences.
Given \(x \left( i \right) \) it is possible to compute \(x \left( i + 1 \right) \) for the next sub-sequence \(t \left[ i + 1 ... i + M \right] \) as in Eq. 9
Equation 9 shows how to discover the next sub-sequence for the predecessor.
Equation 10 is used to calculate hash values for the sub sequences. Where:
-
\(x \left( i \right) \) represents the text sub-sequence \(t \left[ i \right] \);
-
\(h \left( i \right) \) represents the hash function;
-
b represents the base of the string;
-
q is the prime number;
3.10 Aho-Corasick Algorithm
Aho-Corasick (AC) algorithm is widely used for multi-pattern matching, and for exact string matching (Vidanagamachchi et al. 2012). This algorithm is divided into two stages. First, finite machine construction stage used to backtrack failures and remove them to the root node where there is presence of failure. Second, matching step is used to find patterns in the given string.
3.11 CommentZ Walter Algorithm
CommentZ-Walter (CZW) algorithm, used for multi-pattern matching, combines shifting techniques of BM with AC algorithm. CZW has three stages: finite state machine construction; shift calculation; and machining stage Note that, in this algorithm, the finite state machine is built in reverse order to use the shifting methods of BM algorithm.
After the result of CZW algorithm first stage, then the shift is calculated using BM. Finally, it is compared with string sequences.
3.12 Jaro and Jaro–Winkler
The Jaro distance between two sequences consists on the minimum number of single-character transpositions required to change one word into the other.
This approach gives more relevance to words with similar prefixes. Starting from the beginning with the Jaro distance formula, the Jaro distance between two sequences s1 and s2 is defined by Eq. 11 (Jaro distance formula):
Where in Eq. 11:
-
dj is the Jaro distance;
-
m is the number of matching characters (characters that appear in s1 and in s2);
-
t is half the number of transpositions (compare the i-th character of s1 and the i-th character of s2 divided by 2)
-
|s1| is the length of the first string;
-
|s2| is the length of the second string;
Considering the following example: the word “martha” and the word “marhta”. Then we have:

Jaro-Winkler similarity distance algorithm, Eq. 12, uses a prefix scale p which gives a better rating to strings which start matching from the beginning, for a set prefix length l.
p is a constant scaling factor for how much the score is adjusted upwards for having common prefixes. The standard value for this constant in Winkler’s work is p = 0.1, while l is a prefix, up to a maximum of 4 characters, at the start of the string.
Using again the example of “martha” and “marhta”, the prefix length of l is equal 3 (refers to “mar”).

Thus applying the Jaro-Winkler formula, the Jaro distance of 94% similarity increases to 96%.
4 Comparison Study
In this section all string matching algorithms are compared regarding complexity, accuracy and execution time until pattern matching.
First test consists on comparing only the three main matching algorithms for sequence matching, Knuth Morris Pratt, Brute Force, and Boyer Moore. The data-set used was two DNA sequences, a normal one, and the other with a disease to be checked. The three algorithms were implemented and tested in JAVA. Moreover, pattern matching techniques is used to optimize the time and to analyze the vast amount of data in a short span of time. Table 2 shows the result of the algorithms execution, where N and M are two strings. Where, Boyer Mores algorithm was the best, with 91% accuracy and 61 s of processing time. On the other hand, Brute Force algorithm was the worst, with 40% accuracy and 147 s of processing time.
Second, the complexity of each algorithm is studied and compared. Table 1, shows resumes study results. Results show the different string matching algorithms regarding accuracy and execution time until pattern matching, using online tools such as EMBOSS, GENE Wise, and manually implemented. For this comparison study the Genbank Accession No. JN222368 was used, which belongs to Marine Sponge. Sequence size was 1321 characters.
5 Conclusions and Future Work
In this survey are analyzed different string matching algorithms in the context of biological sequence, DNA and Proteins.
Algorithms like Knuth Morris Pratt are easier to implement, because they never need to back-reanalyze in the sequence, however, requires more space. Rabin Karp algorithm requires extra space for matching. Brute Force, has the advantage of not needing any pre-processing. However, it is slow. AhoCorasick algorithm is commonly used for a multi-pattern string match. CommentZ-Walter is slower to reach a result, Boyer More is faster when using large sequences, avoiding many comparisons. Boyer More in best case scenario complexity is sub-linear. As future work, it is proposed a parallel algorithm for fuzzy string matching, using artificial intelligence neural networks for better performance and accuracy.
References
Alsmadi, I., Nuser, M.: String matching evaluation methods for DNA comparison. Int. J. Adv. Sci. Technol. 47(1), 13–32 (2012)
Amir, A., Lewenstein, M., Porat, E.: Faster algorithms for string matching with k mismatches. J. Algorithms 50(2), 257–275 (2004)
Bard, G.V.: Spelling-error tolerant, order-independent pass-phrases via the Damerau-Levenshtein string-edit distance metric. In: Proceedings of the Fifth Australasian Symposium on ACSW Frontiers, vol. 68, pp. 117–124. Citeseer (2007)
Dudas, L.: Improved pattern matching to find DNA patterns. In: IEEE International Conference on Automation, Quality and Testing, Robotics, vol. 2, pp. 345–349. IEEE (2006)
Hussain, I., Kausar, S., Hussain, L., Khan, M.A.: Improved approach for exact pattern matching. Int. J. Comput. Sci. Issues 10, 59–65 (2013)
Kleinberg, J., Tardos, É.: Algorithm Design. Pearson Education India, Bangalore (2006)
Knuth, D.E., Morris Jr., J.H., Pratt, V.R.: Fast pattern matching in strings. SIAM J. Comput. 6(2), 323–350 (1977)
Levenshtein, V.I.: Binary codes capable of correcting deletions, insertions, and reversals. Sov. Phys. Dokl. 10, 707–710 (1966)
Majorek, K.A., et al.: The RNase H-like superfamily: new members, comparative structural analysis and evolutionary classification. Nucleic Acids Res. 42(7), 4160–4179 (2014)
Martin, D.P., Posada, D., Crandall, K.A., Williamson, C.: A modified bootscan algorithm for automated identification of recombinant sequences and recombination breakpoints. AIDS Res. Hum. Retroviruses 21(1), 98–102 (2005)
Needleman, S.B., Wunsch, C.D.: A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 48, 443–453 (1970)
Jain, P., Pandey, S.: Comparative study on text pattern matching for heterogeneous system. Citeseer (2008)
Rajesh, S., Prathima, S., Reddy, L.S.S.: Unusual pattern detection in DNA database using KMP algorithm. Int. J. Comput. Appl. 1(22), 1–5 (2010)
Singla, N., Garg, D.: String matching algorithms and their applicability in various applications. Int. J. Soft Comput. Eng. 1(6), 218–222 (2012)
Smith, T.F., Waterman, M.S.: Identification of common molecular subsequences. J. Mol. Biol. 147(1), 195–197 (1981)
Vidanagamachchi, S.M., Dewasurendra, S.D., Ragel, R.G., Niranjan, M.: CommentZ-Walter: any better than Aho-Corasick for peptide identification? Int. J. Res. Comput. Sci. 2(6), 33 (2012)
Yeh, M.-C., Cheng, K.-T.: A string matching approach for visual retrieval and classification. In: Proceedings of the 1st ACM international conference on Multimedia information retrieval, pp. 52–58. ACM (2008)
Acknowledgements
“This work is funded by National Funds through the FCT - Foundation for Science and Technology, I.P., within the scope of the project Refa UIDB/05583/2020. Furthermore, we would like to thank the Research Centre in Digital Services (CISeD) and the Polytechnic of Viseu for their support.”
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Abbasi, M., Martins, P. (2020). An Overview of Search and Match Algorithms Complexity and Performance. In: Rojas, I., Valenzuela, O., Rojas, F., Herrera, L., Ortuño, F. (eds) Bioinformatics and Biomedical Engineering. IWBBIO 2020. Lecture Notes in Computer Science(), vol 12108. Springer, Cham. https://doi.org/10.1007/978-3-030-45385-5_41
Download citation
DOI: https://doi.org/10.1007/978-3-030-45385-5_41
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-45384-8
Online ISBN: 978-3-030-45385-5
eBook Packages: Computer ScienceComputer Science (R0)





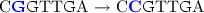 (replace ‘C’ for ‘G’);
(replace ‘C’ for ‘G’); (replace ‘T’ for ‘C’);
(replace ‘T’ for ‘C’); (remove ‘A’ from the end).
(remove ‘A’ from the end).