Keywords

1 Introduction

In current wireless communication networks, based stations are usually built and fixed on the ground, which can be costly and lack of flexibility. For this reason, the communication network assisted by unmanned aerial vehicle, which is cheaper and can adjust its position flexibly, becomes an attractive research direction. Compared with conventional static networks, the UAV-assisted network offers new opportunities for performance improvement through the adjustment of the UAV’s locations or trajectories [1,2,3].

According to the features of UAV, the existing works can be roughly divided into two categories: UAV-enabled base station (BS) [4,5,6] and UAV-enabled mobile relay [7, 8]. The authors of [4] use a UAV-BS to provide public information to a group of users. For this multicast channel, the achievable rate maximization problem is studied by jointly design the transmit power allocation and UAV trajectory, subject to UAV speed and power constraints. In [5], TDMA technology is applied on the UAV for user access control, and then a minimum throughput maximization problem is considered. In [6], the UAV is used to serve multiple ground nodes simultaneously, under the framework of downlink orthogonal frequency division multiple. And the minimum average throughput of users is maximized by transmit power and trajectory optimization. In the UAV-enabled relay network, the authors in [7] study the throughput maximization problem, where UAV trajectory and both source and relay transmit power are optimized jointly, subject to the constraints of UAV mobility and information causality. A multi-hop relay system containing multiple UAVs is considered in [8].

Another key difference between a ground based system and the UAV-enabled one is that the total energy budget of a UAV is strictly limited by its battery capacity, which is the reason for a power-efficient UAV-enabled communication system. Some early results consider only the transmission power of drones, but ignore the flight power consumption. However, in practice, flight power consumption may be higher than that of data transmission, and is thus not negligible. Therefore, the trade-off between network throughput and total energy consumption is studied in [9], based on which, a comprehensive energy consumption model for UAV was established. Based on this model, an energy-efficient drone is also studied in the wireless sensor network [10].

To the best of our knowledge, the power-efficient communication for a UAV-enabled relay has not been studied until now. In this paper, the UAV power consumption minimization problem is considered, where the UAV trajectory and transmit power of both UAV and source node are optimized, subject to the constraints of link transmission rate, UAV mobility, power budget, and information causality. Since the flight power consumption and information causality constraints are non-convex, the optimization problem is non-convex in general. We thus propose a successive convex approximation (SCA) based method to solve it approximately.

2 System Model and Problem Formulation

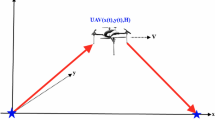
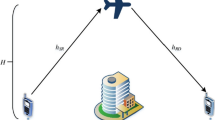
Consider a wireless communication network, which is composed of a source node S, a destination node D, and a UAV-enabled aerial relay. The UAV need to fly from a starting point to a terminal point in a given time duration T. During this time, it receives signal from S and then forwards it to D, where the locations of S and D are fixed. For ease of expression, we divide the period T into N equal time slots, which are indexed by \(n = 1,...,N\). Here, N is chosen such that the duration \(\delta =T/N\) is small enough and thus the UAV’s location in each time slot can be approximated by \([\varvec{q}^T[n],H]^T\), \(n = 1,\cdots ,N\), where \(\varvec{q}[n]=(x[n],y[n])^T\) denotes a point in Cartesian coordinate system.

Let us first consider the channel between UAV and the destination node D, which is assumed to be dominated by the line-of-sight (LoS) link. Then, the channel power gain at time slot n is given by

$$\begin{aligned} h_{ud}[n]=\frac{\beta _{0}}{d[n]^{2}}=\frac{\beta _{0}}{\Vert \varvec{q}[n]-\varvec{w}_D\Vert ^2+H^2} \end{aligned}$$
(1)

where \(\beta _{0}\) represents the reference channel gain at \(d = 1\) m and \(\varvec{w}_D\) denotes the horizontal coordinate of node D. Obviously, the achievable rate from the UAV to node D is

$$\begin{aligned} R_{ud}[n]&=\log _{2}\left( 1+\frac{p_u[n]h_{ud}[n]}{\sigma ^2}\right) \end{aligned}$$
(2)
$$\begin{aligned}&=\log _{2}\left( 1+\frac{p_u[n]\gamma _0}{\Vert \varvec{q}[n]-\varvec{w}_D\Vert ^2+H^2}\right) . \end{aligned}$$
(3)

where \(p_u[n]\) denotes the transmission power of UAV relay, \(\gamma _0=\beta _{0}/\sigma ^2\), and \(\sigma ^2\) denotes the noise power spectrum density.

Similarly, one can obtain the channel power gain from the node S to the UAV in the n-th time slot and the corresponding achievable rate, which are given by

$$\begin{aligned} \qquad h_{su}[n]&=\frac{\beta _{0}}{\Vert \varvec{q}[n]-\varvec{w}_S\Vert ^2+H^2},\end{aligned}$$
(4)
$$\begin{aligned} R_{su}[n]&=\log _{2}\left( 1+\frac{p_s[n]h_{su}[n]}{\sigma ^2}\right) \end{aligned}$$
(5)
$$\begin{aligned}&=\log _{2}\left( 1+\frac{p_s[n]\gamma _0}{\Vert \varvec{q}[n]-\varvec{w}_S\Vert ^2+H^2}\right) \end{aligned}$$
(6)

where \(\varvec{w}_S\) denotes the horizontal coordinate of node S, \(p_s[n]\) denotes the transmission power of node S at time slot n.

Note that in the n-th time slot, the UAV can only forward the data that has already been received from node S, which is referred to as information-causality constraint [6]. By assuming that the processing delay at UAV is one slot, this constraint can be expressed by

$$\begin{aligned} R_{ud}[1]=0, ~\sum _{i=2}^nR_{ud}[i]\le \sum _{i=1}^{n-1}R_{su}[i],~n=2,...,N \end{aligned}$$
(7)

The flight power consumption of UAV is given by [9]

$$\begin{aligned} P_p=\sum _{n=1}^N\left( k_1\Vert \varvec{v}[n]\Vert ^3+\frac{k_2}{\Vert \varvec{v}[n]\Vert }\left( 1+\frac{\Vert \varvec{a}[n]\Vert ^2}{g^2}\right) \right) , \end{aligned}$$
(8)

where \(k_1\) and \(k_2\) are constant numbers depend on the UAV’s structure and flight environment, \(\varvec{a}[n]\) and \(\varvec{v}[n]\) denote acceleration and speed of the UAV in the n-th time slot, and g the gravity acceleration.

Further define the transmit power of UAV in the n-th time slot by \(p_{u}[n]\), then the total transmit power consumption is \(P_{t}=\sum _{i=1}^Np_{u}[i]\). Finally, we can obtain the power-efficient communication (PEC) problem

$$\begin{aligned} (P) \min _{\{\varvec{q}[n],p_s[n],p_u[n],\varvec{v}[n],\varvec{a}[n]\}} ~~&P_t+P_p\end{aligned}$$
(9a)
$$\begin{aligned} s{.}t. ~~&\eta \le \frac{1}{N}\sum _{n=2}^{N}R_{ud}[n],\end{aligned}$$
(9b)
$$\begin{aligned}&\sum _{n=2}^{k}R_{ud}[n]\le \sum _{n=1}^{k-1}R_{su}[n], k=2,...,N,\end{aligned}$$
(9c)
$$\begin{aligned}&0\le \ p_s[n]\le \ p_{smax},\end{aligned}$$
(9d)
$$\begin{aligned}&0\le \ p_u[n]\le \ p_{umax},\end{aligned}$$
(9e)
$$\begin{aligned}&\varvec{q}[1]=\varvec{q}_0, \varvec{q}[N+1]=\varvec{q}_f,\end{aligned}$$
(9f)
$$\begin{aligned}&\varvec{v}[1]=\varvec{v}_0, \varvec{v}[N+1]=\varvec{v}_f,\end{aligned}$$
(9g)
$$\begin{aligned}&\varvec{q}[n+1]=\varvec{q}[n]+\varvec{v}[n]\delta +\frac{1}{2}\varvec{a}[n]\delta ^2, n=1,...,N,\end{aligned}$$
(9h)
$$\begin{aligned}&\varvec{v}[n+1]=\varvec{v}[n]+\varvec{a}[n]\delta , n=1,...,N,\end{aligned}$$
(9i)
$$\begin{aligned}&\Vert \varvec{v}[n]\Vert \le \ V_{max}, n=1,...,N,\end{aligned}$$
(9j)
$$\begin{aligned}&\Vert \varvec{a}[n]\Vert \le \ a_{max}, n=1,...,N, \end{aligned}$$
(9k)

where (9b) is the rate requirement at destination, (9c) is the information-causality constraint, (9d) and (9d) are the transmission power constraints for node S and UAV, respectively, (9f)–(9k) are constraints related to UAV’s flight trajectory.

Note that the objective function and constraints (9b) and (9c) are nonconvex, so is problem (9). Therefore, solving it directly is computationally inefficient. Next, we will propose a SCA based method [11] to solve it approximately.

3 Proposed Solution

To deal with the objective function, we first introduce slack variables \(\{\tau _n\}\), and modify (9) into

$$\begin{aligned} (P1)&\min _{\{\varvec{q}[n],p_s[n],p_u[n],\varvec{v}[n],\varvec{a}[n],\tau _n\}}P_t+P_p', \end{aligned}$$
(10a)
$$\begin{aligned}&s{.}t\quad (9b),(9c),(9d),(9e),(9f),(9g),(9h),(9i),(9j),(9k),\end{aligned}$$
(10b)
$$\begin{aligned}&\Vert \varvec{v}[n]\Vert ^2\ge \ \tau _n^2, n=1,...,N,\end{aligned}$$
(10c)
$$\begin{aligned}&\tau _n\ge 0, n=1,...,N, \end{aligned}$$
(10d)

where

$$\begin{aligned} P_p'=\sum _{n=1}^N(k_1\Vert \varvec{v}[n]\Vert ^3+\frac{k_2}{\tau _n}+\frac{k_2\Vert \varvec{a}[n]\Vert ^2}{g^2\tau _n}) \end{aligned}$$
(11)

Obviously, problem (9) and (10) are equivalent in the sense that optimal solution of the latter must satisfy \(\Vert \varvec{v}[n]\Vert =\tau _n\).

To deal with the nonconvex constraint (10c), we apply the first-order Taylor expansion to \(\Vert \varvec{v}[n]\Vert ^2\) and obtain

$$\begin{aligned} \Vert \varvec{v}[n]\Vert ^2&\ge \Vert \bar{\varvec{v}}^r[n]\Vert ^2+2\bar{\varvec{v}}^r[n]^\mathrm { T }(\varvec{v}[n]-\bar{\varvec{v}}^r[n])\triangleq f^{lb}(\varvec{v}[n]) \end{aligned}$$
(12)

where \(\bar{\varvec{v}}^r[n]\) is the solution of the previous iteration. Note that \(f^{lb}(\varvec{v}[n])\) is a concave lower bound of \(\Vert \varvec{v}[n]\Vert ^2\), therefore one can safely replace (10c) by the convex constraint

$$\begin{aligned} f^{lb}(\varvec{v}[n])\ge \tau _n^2. \end{aligned}$$
(13)

To deal with the non-convex constraint (9b), we define

$$\begin{aligned}&\bar{a}_u^r[n]=\sqrt{\bar{p}_{u}^r[n]}, \ \bar{d}_u^r[n]=H^2+\Vert \bar{\varvec{q}}^r[n]-\varvec{w}_D\Vert ^2,\end{aligned}$$
(14)
$$\begin{aligned}&a_u[n]=\sqrt{p_{u}[n]}, \ d_u[n]=H^2+\Vert \varvec{q}[n]-\varvec{w}_D\Vert ^2, \end{aligned}$$
(15)

where \(\bar{p}_{u}^r[n]\) and \(\bar{\varvec{q}}^r[n]\) denote some feasible transmit power and location of the UAV in n-th slot. Then, \(R_{ud}[n]\) can be written as

$$\begin{aligned} R_{ud}[n]=\log _{2}\left( 1+\frac{a_u^2[n]\gamma _0}{d_u[n]}\right) . \end{aligned}$$
(16)

Note that \(x^2/y\) is convex whenever \(x\in \mathbb {R}\) and \(y>0\), and \(\frac{x^2}{y}\ge \frac{2x'}{y'}x-\frac{x'^2}{y'^2}y\) is always satisfied for any \(x'\), \(y'\) in the function domain. Thus, \(R_{ud}[n]\) can be lower bounded by a concave function

$$\begin{aligned} R_{ud}^{lb,r}[n]=\log _2\left( 1+ \gamma _0\frac{2\bar{a}_u^r[n]}{\bar{d}_u^r[n]}a_u[n]-\gamma _0\frac{(\bar{a}_u^r[n])^2}{(\bar{d}_u^r[n])^2}d_u[n]\right) , \end{aligned}$$
(17)

where \(R_{ud}^{lb,r}[n]\) is a concave in \((a_u[n], \varvec{q}[n])\) [12].

Then, the constraint (9b) can safely replaced by

$$\begin{aligned} \eta \le \frac{1}{N}\sum _{n=2}^{N}R_{ud}^{lb,r}[n]. \end{aligned}$$
(18)

Next, we tackle the non-convex constraint (9c). First, for the left hand side, \(R_{ud}[n]\) can be written as

$$\begin{aligned} R_{ud}[n]&=\log _2(1+\frac{p_u[n]\gamma _0}{\Vert \varvec{q}[n]-\varvec{w}_D\Vert ^2+H^2})\end{aligned}$$
(19)
$$\begin{aligned}&=R_{lud}[n]-R_{rud}[n], \end{aligned}$$
(20)

where

$$\begin{aligned}&R_{lud}[n]=\log _2(H^2+\Vert \varvec{q}[n]-\varvec{w}_D\Vert ^2+p_u[n]\gamma _0),\end{aligned}$$
(21)
$$\begin{aligned}&R_{rud}[n]=\log _2(H^2+\Vert \varvec{q}[n]-\varvec{w}_D\Vert ^2). \end{aligned}$$
(22)

Given a feasible point \((\bar{p}_u^r[n], \bar{\varvec{q}}^r[n])\), a global upper bound of \(R_{lud}[n]\) and lower bound of \(R_{rud}[n]\) can be obtained by

$$\begin{aligned} \begin{aligned} R_{lud}^{ub,r}[n]&=\log _2(\bar{d}_u^r[n]+(\bar{a}_u^r[n])^2\gamma _0) \\&+\frac{(d_u[n]+(a_u[n])^2\gamma _0-\bar{d}_u^r[n]-(\bar{a}_u^r[n])^2\gamma _0)\log _2e}{\bar{d}_u^r[n][n]+(\bar{a}_u^r[n])^2\gamma _0}, \end{aligned} \end{aligned}$$
(23)
$$\begin{aligned} R_{rud}^{ub,r}[n]=\log _2(\bar{d}_u^r[n]+2(\varvec{q}[n]-\varvec{w}_D)^\mathrm { T }(\bar{\varvec{q}}^r[n]-\varvec{w}_D)). \end{aligned}$$
(24)

Hence, the global upper bound of \(R_{ud}[n]\) is given by

$$\begin{aligned} R_{lud}[n]=R_{lud}^{ub,r}[n]-R_{rud}^{ub,r}[n], \end{aligned}$$
(25)

Second, the right-hand-side of (9c) can be transformed similar to that of (9b). Denote

$$\begin{aligned}&\bar{a}_s^r[n]=\sqrt{\bar{p}_{s}^r[n]}, \ \bar{d}_s^r[n]=H^2+\Vert \bar{\varvec{q}}^r[n]-\varvec{w}_S\Vert ^2, \end{aligned}$$
(26)
$$\begin{aligned}&a_s[n]=\sqrt{p_{s}[n]}, \ d_s[n]=H^2+\Vert \varvec{q}[n]-\varvec{w}_S\Vert ^2, \end{aligned}$$
(27)

where \((\bar{p}_s^r[n], \bar{\varvec{q}}^r[n])\) is given feasible point. Then a global lower bound of \(R_{su}[n]\) can be obtained by

$$\begin{aligned} R_{su}^{lb,r}[n]=\log _2\left( 1+\gamma _0\left( \frac{2\bar{a}_s^r[n]}{\bar{d}_s^r[n]}a_s[n]-\frac{(\bar{a}_s^r[n])^2}{(\bar{d}_s^r[n])^2}d_s[n]\right) \right) , \end{aligned}$$
(28)

where \(R_{su}^{lb,r}[n]\) is concave in \((a_s[n], \varvec{q}[n])\) [12]. Then, the constraint (9c) can be safely replaced by

$$\begin{aligned} \sum _{n=2}^k(R_{lud}^{ub,r}[n]-R_{rud}^{ub,r}[n])\le \sum _{n=1}^{k-1}R_{su}^{lb,r}[n], k=2,...,N, \end{aligned}$$
(29)

which is convex [11].

Based on all the above approximations, an SCA sub-problem of (10) can be obtained by

$$\begin{aligned} (P2)&\min _{\{\varvec{q}[n],a_s[n],a_u[n],\varvec{v}[n],\varvec{a}[n],\tau _n\}}\sum _{n=2}^N(a_u[n])^2+P_p^{'}\end{aligned}$$
(30a)
$$\begin{aligned}&s{.}t\quad (9f),(9g),(9h),(9i),(9j),(9k),\end{aligned}$$
(30b)
$$\begin{aligned}&\eta \le \frac{1}{N}\sum _{n=2}^{N}R_{ud}^{lb,r}[n],\end{aligned}$$
(30c)
$$\begin{aligned}&\sum _{n=2}^k(R_{lud}^{ub,r}[n]-R_{rud}^{ub,r}[n])\le \sum _{n=1}^{k-1}R_{su}^{lb,r}[n], k=2,...,N,\end{aligned}$$
(30d)
$$\begin{aligned}&0\le \ a_s[n]\le \ \sqrt{p_{smax}},\end{aligned}$$
(30e)
$$\begin{aligned}&0\le \ a_u[n]\le \ \sqrt{p_{umax}}, \end{aligned}$$
(30f)

which is convex and can be efficiently solved by using optimization tools such as CVX [5].

Finally, the proposed SCA-based method for the PEC problem is summarized in Algorithm 1.

figure a

4 Numerical Results

In this section, experiments are performed to evaluate the proposed algorithm. The simulation settings are similar to those in [7], which are UAV parameters \(H=100\) m, \(a_{max}=30\,\mathrm{m/s}^2\), \(V_{max}=30\,\mathrm{m/s}^2\), \(k_1=0.002\), \(k_2=70.698\), \(p_{umax}=0.1\) W, \(\varvec{v}_0=(1,0.4)\), \(\varvec{v}_f=(0,0)\), and \(\delta =1\) s, channel power gain \(\beta _0=-50\) dB, source transmit power \(p_{smax}=0.2\,\mathrm{W}\), noise power spectrum density \(\sigma ^2=-110\,\mathrm{dBm}\), data rate requirement \(\eta =5\,\)bps/Hz.

The Algorithm 1 is initialized as follows: the initial trajectory is a straight line between the starting and terminal points, the accelerations of the first and last four time slots are \(\varvec{a}_1\) and \(\varvec{a}_2\), which are related to total duration T, respectively, and those of the other time slots are \(\varvec{0}\). The tolerance for convergence is \(\varepsilon =0.1\).

Fig. 1.
figure 1

UAV trajectories for different periods T, starting point is (0, 0), ending point is (1500, 600). The sampling interval of the path is 5 s and is marked as a ‘\(\square \)’.

Full size image
Fig. 2.
figure 2

Transmission power of the UAV

Full size image
Fig. 3.
figure 3

UAV speed and acceleration

Full size image

In Fig. 1, the UAV’s trajectories varying with total duration T is plotted, where the marker “o” denotes the locations of nodes S and D and the marker “\(\square \)” denotes the location of UAV with a sampling interval 5 s. In the figure, we see that when \(T=90\), the trajectory is a straight line. And it curves to node D, when T becomes large. The reason is that when T is large enough, the rate constraints can be satisfied easily and the UAV tries to fly at the speed with lowest propulsion power.

The corresponding transmission power of UAV is shown in Fig. 2. It is seen that the transmission power of UAV decreases with the increase of T. In Fig. 3, the speed and acceleration are also given out. We see that the UAV’s acceleration is large at the first and last several time slots, and is zero in the other slots. When the time T is large enough, the speed of UAV is stable.

Fig. 4.
figure 4

The power consumption

Full size image

In Fig. 4, the total power consumption varying with time for \(T=270\) s is illustrated, where “initial” denotes power consumption of UAV with its flight path as a straight line, while “Algorithm 1” denotes those given by Algorithm 1. We see that the proposed method is more energy efficient, which is remarkable when \(T>200\) s.

5 Conclusion

This paper considers power-efficient communication for a UAV-enabled mobile relay system. A rate constrained power-efficient relay-UAV trajectory and transmit power joint design problem is considered, which is non-convex and difficult to deal with. Hence, an SCA-based optimization method is proposed to solve the problem approximately. Numerical experiments are performed to show the effectiveness of the proposed method.