A High-Performance Implementation of a Robust Preconditioner for Heterogeneous Problems

Abstract

We present an efficient implementation of the highly robust and scalable GenEO (Generalized Eigenproblems in the Overlap) preconditioner [16] in the high-performance PDE framework DUNE [6]. The GenEO coarse space is constructed by combining low energy solutions of a local generalised eigenproblem using a partition of unity. The main contribution of this paper is documenting the technical details that are crucial to the efficiency of a high-performance implementation of the GenEO preconditioner. We demonstrate both weak and strong scaling for the GenEO solver on over 15, 000 cores by solving an industrially motivated problem in aerospace engineering. Further, we show that for highly complex parameter distributions arising in certain real-world applications, established methods become intractable while GenEO remains fully effective.

1 Introduction

Computer simulations have become a vital tool in science and engineering. The demand for solving PDEs on ever larger domains and increasing accuracy necessitates the use of high performance computers and the implementation of efficient parallel algorithms. When designing parallel algorithms two issues are crucial: Robustness and scalability.

• (i) Robustness: The parameters involved in the PDE affect the performance of the algorithm to a large extent. A frequent issue is a distribution of parameters with large contrast jumps at different length scales, which may lead to slow or no solver convergence.

• (ii) Scalability: The immediate scalability of the finite element method is limited as each degree of freedom is coupled with all others.

One approach to achieve scalability in solving partial differential equations are domain decomposition methods (see e.g. [14, 17]), splitting the given domain into multiple subdomains. The solution of the original problem restricted to each subdomain is computed in parallel and the results are combined to form an approximate solution. This is repeated until convergence is reached. The number of these iterations, however, still depends strongly on the number of subdomains involved as well as coefficient variations. Introducing an additional coarse space that covers all subdomains can restore performance for large numbers of subdomains.

This global space can be tailored to specific problem, as in the generalized finite element method [3]. While these methods are applicable to an entire class of parameter distributions, each of these approaches is based on certain assumptions on the parameters, e.g. the parameters vary strongly only in one direction. Over recent years, more generic approaches have been developed, e.g. [8, 11]. The GenEO coarse space chosen in this work is a related approach, originally introduced in [16]. It does not require a-priori knowledge of the parameter distribution and is applicable to a wide range of problems making it suitable as a ‘black-box’ solver.

In this paper we focus on two different elliptic problems; the Darcy equation describing incompressible flow in a porous medium and the anisotropic linear elasticity equations. For both equations the case of heterogeneous coefficients is of great interest.

Composite materials, which make up over 50% of recent aircraft constructions, are manufactured from carbon fibres and soft resin layers. The large jump in material properties between the layers makes the simulation of these materials challenging. Commercial solvers such as ABAQUS often rely on direct solvers to deal with these jumps [12]. However, the scalability of direct solvers is limited. We demonstrate that the GenEO approach converges independently of the contrast in material properties and the number of subdomains.

After introducing our PDE models in Sect. 2, we sketch the construction of the GenEO preconditioner in Sect. 3. In Sect. 4, we then discuss how to efficiently implement the solver in the high-performance finite element framework DUNE [4, 5]. Finally, in Sect. 5, we provide several numerical experiments demonstrating both robustness and scalability of the solver, including a large-scale industrially motivated example.

2 Problem Formulation and Variational Setting

Let V be a Hilbert space, $a\,:\,V\times V \rightarrow \mathbb {R}$ a symmetric and coercive bilinear form and $f\in V'$. We consider the following abstract variational problem. Find $v\in V$ such that

$$\begin{aligned} a(v,w) =\langle f, w \rangle ,~~~~\forall w \in V, \end{aligned}$$

(1)

where $\langle \cdot ,\cdot \rangle$ denotes the duality pairing.

This variational problem is associated with an elliptic boundary value problem on a domain $\varOmega \subset \mathbb {R}^d,$ $d= 2,3$ with Dirichlet boundary $\partial \varOmega _D$. In particular, we focus on the following two examples.

• (i) Darcy problem: Given material properties $\kappa \in L^\infty (\varOmega )$, find $v\in V = \{v\in H^1(\varOmega )\,:\, v|_{\varOmega _D} = 0\}$ such that

  $$\begin{aligned} a(v,w) = \int _{\varOmega } \kappa ( x) \nabla v ( x) \cdot \nabla w ( x) \, d x = \int _{\varOmega } f( x) w ( x) \, d x , ~~~~~ \forall w \in V. \end{aligned}$$

• (ii) Linear Elasticity: Given material properties C, find $v\in V = \{ v \in H^1(\varOmega )^d \, : \, v|_{\varOmega _D} = 0\}$ such that

  $$\begin{aligned} a(v,w) = \int _{\varOmega } C( x)\varepsilon ( v) : \varepsilon (w) d x = \int _\varOmega f \cdot w \, d x + \int _{\partial \varOmega } (\sigma \cdot { n}) \cdot { v}\,d x,~~~~~ \forall w \in V, \end{aligned}$$

  where $\varepsilon _{ij}(v)=\frac{1}{2}(\partial _i v_j + \partial _j v_i)$ is the strain, and $\sigma _{ij}(v)=\sum _{k,l=1}^dC_{ijkl}\varepsilon _{kl}$ is the stress.

Consider a discretization of the variational problem (1) using finite elements on a mesh $T_h$ of $\varOmega$ such that $\overline{\varOmega } = \cup _{\tau \in T_h}\tau .$ Let $V_h \subset V$ be a conforming space of finite element functions. Then the discrete form of (1) is: Find $v_h\in V_h$ such that

$$\begin{aligned} a(v_h,w_h) =\langle f, w_h \rangle ,~~~~\forall w_h \in V_h. \end{aligned}$$

(2)

3 The GenEO Preconditioner

In order to construct a parallel and scalable preconditioner, we employ a two-level Additive Schwarz preconditioner as comprehensively analyzed in [17]. Our specific choice of coarse space is the GenEO (Generalized Eigenproblems in the Overlap) space as introduced in [16] and proven to be robust in [15]. For brevity, we only give a brief review of the main results and otherwise refer to [15] for full details and notation.

Definition 1 (Two-level Additive Schwarz)

We denote the finite element matrix originating from (2) by $\mathbf {A}$. Using appropriate restrictions, we denote the problem restricted to subdomains by $\mathbf {A}_j:=\varvec{R}_j \varvec{A}\varvec{R}_j^T$ and to the coarse space by $\mathbf {A}_H:=\varvec{R}_H \varvec{A}\varvec{R}_H^T$. Then the two-level Additive Schwarz preconditioner is given by

$$ \varvec{M}_{{\text {AS}}, 2}^{- 1} :=\varvec{R}_H^T \varvec{A}_H^{- 1} \varvec{R}_H + \sum _{j = 1}^N \varvec{R}_j^T \varvec{A}_j^{- 1} \varvec{R}_j . $$

Definition 2 (GenEO eigenproblem)

For each subdomain $j = 1, \ldots , N$, we define the generalized eigenproblem: Find $p\in V_h(\varOmega _j)$ such that

$$\begin{aligned} a_{\varOmega _j} ( p, v) = \lambda a_{\varOmega _j^o} ( \varXi _j ( p), \varXi _j ( v)),~~ \forall v \in V_h ( \varOmega _j). \end{aligned}$$

Note that the eigenproblems are local to their respective subdomain $\varOmega _j$, i.e. they can be computed in parallel. To use them as a global basis they need to be extended to the entire domain using the partition of unity operators.

Definition 3 (GenEO coarse space)

For each subdomain $j = 1, \ldots , N$, let $( p_k^j)^{m_j}_{k = 1}$ be the eigenfunctions from the eigenproblem in Definition 2 corresponding to the $m_j$ smallest eigenvalues. Further, denote the partition of unity by $\varXi _j$. Then the GenEO coarse space is defined as

$$ V_H :={\text {span}} \{ R_j^T \varXi _j ( p_k^j) : k = 1, \ldots , m_j ; j = 1, \ldots , N \} . $$

In [15], the following condition bound proves robustness with respect to parameter contrast and number of subdomains.

Theorem 1

For all $1 \leqslant j \leqslant N$, let the number of eigenvectors chosen in each subdomain be

$$ m_j :=\min \left\{ m : \lambda _{m + 1}^j > \frac{\delta _j}{H_j} \right\} , $$

where $\delta _j$ is a measure of the width of the overlap $\varOmega _j^o$ and $H_j = {\text {diam}} ( \varOmega _j)$. Then,

$$ \kappa ( \varvec{M}^{- 1}_{{\text {AS}}, 2} \varvec{A}) \leqslant ( 1 + k_0) \left[ 2 + k_0 ( 2 k_0 + 1) \max _{1 \leqslant j \leqslant N} \left( 1 + \frac{H_j}{\delta _j} \right) \right] . $$

4 HPC Implementation of GenEO in Modern PDE Frameworks

When implementing the GenEO preconditioner in a PDE framework, the primary goal is to preserve the beneficial properties offered by its theoretical construction, namely:

• (i) High parallel scalability: Since the condition bound in Theorem 1 is independent of the number of subdomains we expect the implementation to yield high parallel scalability. The solution of the eigenproblems parallelizes trivially. However, care has to be taken when it comes to the communication necessary to set up and solve the coarse matrix.

• (ii) Robustness with respect to problem parameters: While this is an inherent property of the preconditioner, some care is required in implementing the Dirichlet boundary conditions.

• (iii) Applicability to various types of PDEs: The theoretical framework only requires a symmetric positive definite bilinear form as in (1). This flexibility can be preserved in any numerical framework that is based on abstract bilinear forms. This is the case for many modern PDE frameworks, e.g. FEniCS [1], DUNE [4], or deal.ii [2].

In this section, we present a new implementation of the GenEO coarse space and preconditioner within DUNE (Distributed and Unified Numerics Environment), which fulfills these properties. This section serves as a reference for the implementation, which is freely available as part of the dune-pdelab module [6] since version 2.6, as well as a general guideline for future implementations in other software packages. DUNE is a generic package that provides the user with key ingredients for solving any FEM problem. As an open source framework written using modern C++ programming techniques, it allows for modularity and reusability while providing HPC grade performance. Note that an alternative GenEO implementation is available in FreeFEM++ [9].

4.1 Prerequisites

Many of the components required to implement a two-level Schwarz method already exist within DUNE. In particular, we use the PDELab discretization module’s functionality to assemble stiffness matrices based on bilinear forms and for efficient communication across overlapping subdomains. The GenEO basis functions have support not restricted to individual elements, which makes the existing high-level components of PDELab unsuited for storing the coarse space. As part of this project, components facilitating such coarse spaces were fully integrated within the framework. Further, an efficient sequential solver for generalized eigenproblems is needed. Here, we choose ARPACK [10].

4.2 General Structure

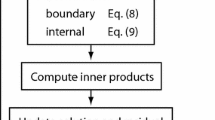
The implementation in PDELab closely follows the structure of the previous section. All mathematical objects are represented as individual classes (see Fig. 1). This separation of concerns leads to an easy to understand and well-structured code. Further, components are easily interchangeable when constructing related methods. In particular, the intricate process of constructing a global coarse space from per-subdomain basis functions is entirely contained in the class SubdomainProjectedCoarseSpace. Thus, the GenEO basis can easily be replaced by a different local basis.

The following subsections describe the steps of setting up the local eigenproblems, solving them, combining them to a coarse space and finally employing that space as a two-level Schwarz preconditioner.

Fig. 1.

Class hierarchy of GenEO implementation in DUNE PDELab

4.3 Discrete Basis

To calculate GenEO basis functions we solve the discrete form of the eigenproblem in Definition 2, i.e.

$$\begin{aligned} \varvec{\tilde{A}}_j p_k^j = \lambda _k^j \varvec{X}_j \varvec{\tilde{A}}_j^o \varvec{X}_j p_k^j, \end{aligned}$$

where $\varvec{X}_j$ is the discrete form of the partition of unity.

The matrix $\varvec{\tilde{A}}_j$ has to be assembled with Dirichlet constraints on the domain boundary as prescribed by the given PDE problem. However, in contrast to the matrices $\varvec{A}_j$ needed for the one-level component of the two-level additive Schwarz method, no Dirichlet constraints are imposed on subdomain boundaries.

For assembling $\varvec{\tilde{A}}_j^o$, the same boundary conditions can be applied. However, additionally, the matrix should only be assembled on the overlap region. Internally overlap elements are identified by adding a vector of ones across subdomains and checking for results greater than one.

The matrices $\varvec{X}_j$ representing the partition of unity operator are diagonal and can be stored as vectors. Entries of $\varvec{X}_j$ corresponding to Dirichlet domain boundaries or processor boundaries should be zero, and in sum they should add up to one across subdomains. Such a partition of unity is generated by adding vectors of ones with a single communication between subdomains.

4.4 Solving the Eigenproblem

As the eigenproblems are defined per-subdomain, the eigensolver itself does not need to run in parallel. However, solving larger problems requires an efficient iterative solver. A suitable choice is ARPACK [10].

In order to stabilize the method, the Shift and Invert Spectral Transformation Mode supported by ARPACK is used. Instead of the generalized eigenproblem $\varvec{A}x = \varvec{M}x \lambda$, ARPACK solves the transformed problem $( A - \sigma M)^{- 1} M x = x \nu$. The eigenvalues of the transformed problem are related to those of the original problem by $\nu = \frac{1}{\lambda - \sigma }$ and the eigenvectors are identical. In the transformed problem, the eigenvalues of the original problem whose absolute values are closest to $\sigma$ are now the eigenvalues of largest magnitude, and can therefore be efficiently solved by the Krylov method. Choosing $\sigma$ near zero, the method delivers the eigenvalues of smallest magnitude at good performance. Finally, in order to form the actual basis vectors, the eigenvectors are multiplied by $\varvec{X}_j$ and then normalized in the $l^2$ norm, as ARPACK delivers vectors of strongly varying norms.

4.5 Scalable Coarse Setup

Assembling the coarse matrix $\varvec{A_H}$ requires particular care, as it is a non-localized, not trivially scalable operation. Due to domain decomposition, the global matrix $\varvec{A}$ is only available in distributed form as matrices $\varvec{A}_j$. Exploiting local support of basis functions, the coarse matrix $\varvec{A}_H$ breaks down into

$$\begin{aligned} ( \varvec{A}_H)_{i, j} = ( \varvec{R}_H \varvec{A}\varvec{R}_H^T)_{i, j} = \varphi _i \varvec{A}_i \varphi _j. \end{aligned}$$

We note that $\varphi _i \varvec{A}_i \varphi _j$ is zero for $\varOmega _i \cap \varOmega _j = \varnothing$, leading to a sparse structure in $A_H$. Therefore, all rows i of $\varvec{A}_H$ associated to basis functions $\varphi _i$ can be computed on the associated process locally while only requiring basis functions $\varphi _j$ from adjacent subdomains. In the implementation multiple basis functions are communicated in a single step.

The resulting blocks are combined into a matrix $\varvec{A}_H$ available on all processes, using direct MPI calls, while exploiting sparsity. Communication effort increases linearly with the dimension of $V_H$. This is a direct consequence of how two-level preconditioners are designed, and a good balance between coarse space size and preconditioner performance must be found.

The restriction and prolongation operators $\varvec{R}_H$ and $\varvec{R}_H^T$ are also only available locally. In case of the restriction $\varvec{R}_H v_h$ of a distributed vector $v_h \in V_{h, 0} ( \varOmega )$, it holds

$$\begin{aligned} ( \varvec{R}_H v_h)_i = \varphi _i \cdot v_h . \end{aligned}$$

Each row i can be computed by the process associated to $\varphi _i$, and the rows can be exchanged among all processes via MPI_Allgatherv. Again, the communication effort increases with the dimension of $V_H$.

Finally, the prolongation $\varvec{R}_H^T v_H$ of a global vector $v_H \in V_H$ fulfills

$$\begin{aligned} \varvec{R}_H^T v_H = \sum _i \varphi _i ( v_{H_{}})_i . \end{aligned}$$

Here, each part of the sum associated with a processor can be computed locally and combined by nearest-neighbor communication, scaling ideally. This completes the components needed for the two-level preconditioner according to Definition 1.

5 Numerical Experiments

In this section we demonstrate the solver’s salient features, including its high parallel scalability up to 15, 360 cores, its robustness to heterogeneous material parameters and its applicability to different elliptic PDEs. With exception of the final large-scale experiment all numerical examples in this section have been computed using the Balena HPC cluster of the University of Bath. Balena consists of 192 nodes each with two 8-core Intel Xeon E5-2650v2 Ivybridge processors, each running at 2.6 GHz, giving a total of 3072 available cores.

Fig. 2.

Coarse approximation error. From left to right: The parameter distribution and domain decomposition followed by the error $u - u_H$ with 1, 2 and 4 eigenvectors respectively.

5.1 GenEO Basis on Highly Structured Problems

With clearly structured problems, it can be visually seen that the GenEO coarse space systematically picks up inclusions or channels in the parameter distribution. In Fig. 2 the coarse approximation error is shown for a Darcy problem on a square domain. Dirichlet conditions are set to one at the top and zero at the bottom, Neumann conditions are set at the remaining boundary and a high-contrast parameter distribution with jumps and channels as shown on the left. We see that each inclusion has an effect on the approximation error. Adding additional eigenvectors from each subdomain to the coarse basis removes some of those error sources, the next eigenvectors pick up the skyscrapers and with only 4 eigenvectors per subdomain most channels are resolved. A total of 16 coarse basis functions is enough to almost entirely solve the given problem.

5.2 Demonstration of Robustness

Fig. 3.

Robustness of GenEO preconditioner

Robustness with respect to parameter contrast can be demonstrated solving the same Darcy problem as in Sect. 5.1. We choose a subdomain decomposition into 8 by 8 squares, a two-cell overlap region diameter and a total of 800 $Q_1$ elements in each direction. Figure 3 (left) shows the resulting condition number for increasing contrast when setting up a GenEO basis with various numbers of eigenvectors per subdomain. Clearly, the asymptotic robustness guaranteed by the analysis is achieved in practice.

When running the same setup with a parameter distribution of 40 horizontal equally thick layers, it becomes clear from Fig. 3 (right) that robustness is achieved exactly at four eigenvectors per subdomain. That stems from the fact that four coarse basis functions (together with the contribution of the one-level Schwarz method) are sufficient to represent the five layers contained in that subdomain. Similar relations can be observed with other strongly structured parameter distributions.

5.3 Comparison to Other Solvers

In this section we compare the performance of various preconditioned CG solvers. We compared with two different implementations of AMG, the implementation included in dune-istl and boomerAMG [18]. For this test we consider a flat composite plate made up of 12 composite layers stacked in a sequence of different angles, referred to as a stacking sequence. The composite layers are seperated by very thin layers of resin. There is a large jump in material strength between the composite and resin layer and due to the rotated layers the anisotropy cannot be grid aligned. We discretise with quadratic, 20-node serendipity elements to avoid shear locking and use full Gaussian integration.

Table 1. Demonstration of performance of different preconditioners for a problem of fixed size.

In Table 1 we compare the convergence of three iterative solvers. We record the condition number, the dimension of the coarse space $\text{ dim }(V_H)$ and the number of CG iterations required to achieve a residual reduction of $10^{-5}$. As expected the iteration counts increase steadily with the number of subdomains when no coarse space is used. In contrast, the iterations and the condition number estimates remain constant for the GenEO preconditioner as predicted by Theorem 1. The boomerAMG solver also retains a near constant number of iterations, although they are considerably higher. Due to a lower setup cost the boomerAMG solver is faster in actual CPU time than the GenEO solver in this small test case. However, for more complex geometries, boomerAMG does not perform very well and in our tests it does not scale beyond about 100 cores in composite applications [7]. In its current form the dune-istl implementation does not seem to be robust for composite problems, especially in parallel [12]. In the test setup used here the dune-istl AMG converges very slowly or not at all, thus we do not include it in Table 1.

5.4 Industrially-Motivated Example: Wingbox

In this section we describe an industrially motivated example in which we asses the strength of an airplane wingbox with a small localised wrinkle defect in one corner. Wrinkle defects often form during the manufacturing process and lead to strong local stress concentrations, which may cause premature failure [12, 13]. We perform a weak scaling and a strong scaling experiment. The experiments in this section were performed using the UK national HPC cluster Archer, which consists of 4, 920 Cray XC30 nodes with two 2.7 GHz, 12-core E5-2697 v2 CPUs each.

We model a single bay of a wingbox as shown in Fig. 4 (left). As in a typical aerospace application, the stacking sequence differs across the wingbox as shown in Fig. 4 (right). In total the wingbox is made up of 77 layers. One of the corner radii contains a localised wrinkle with a parametrisation matching an observed defect in a CT-Scan of a real corner section. An internal pressure of 0.109 MPa, arising from the fuel, is applied to the internal surface. The influence of ribs that constrain the wingbox are approximated by clamping all degrees of freedom at one end and tying the degrees of freedom at the other end using a multipoint constraint. A thermal pre-stress induced by the manufacturing process is also imposed. More details on this test setup can be found in [7].

Fig. 4.

Left: Geometry of the wingbox with dimensions; the colouring shows the number of eigenmodes used in GenEO in each of the subdomains. Right: the stacking sequence change around the corner containing a wrinkle. (Color figure online)

For the weak scaling experiment we refine the mesh, doubling the number of elements as we double the number of cores. Table 2 (left) contains the number of degrees of freedom, iteration numbers for the preconditioned CG, the dimension of the coarse space $\dim (V_H)$, as well as the total run time in seconds, time spent in setup of the preconditioner and in CG iterations for each test. As expected the weak scaling of the iterative CG solver with GenEO preconditioner is indeed almost optimal up to at least 15, 360 cores.

It should be noted that while the runtime consists mainly of CG iterations and the setup time for the GenEO preconditioner, which of these dominates depends on the eigenvalue threshold chosen and can be tuned to ensure a low total runtime. In this test case the same eigenvalue threshold is used for all problem sizes, in each the setup time dominates. The setup can be performed almost entirely in parallel and has very low MPI overhead as it is dominated by the solution of local eigenproblems. Conversely the CG iterations do show a slight increase in runtime for very large problems due to communication overhead.

Table 2. Parallel performance of the composites application on Archer. Left: Details of the weak scaling test. Right: details of the strong scaling test.

Table 2 (right) shows a strong-scaling experiment. The iterative CG solver with GenEO preconditioner scales almost optimally to at least 11, 320 cores. Memory constraints prevented tests with fewer than 2880 cores. Correspondingly we take 2880 as a baseline for these tests, leading in some cases to a parallel efficiency larger than 1. Table 2 shows that the number of iterations indeed remains almost constant. The last column gives the parallel efficiency, it remains high up to 11, 320 cores. Fluctuations are due mainly to the effects of the domain decomposition and eigenvalue threshold.