Analysis of Multiscale Theories for Viscoelastic Rubber Friction

Abstract

Rubber friction plays a fundamental role in the study of the tire-road interaction and still represents a topic of discussion for both academics and manufacturing companies, especially with the introduction of the concept of multiscale roughness [1, 2].

Taking into account that the road surface is a hard substrate, the two contributions to rubber friction can be considered to be (i) hysteretic phenomena deriving from time dependent viscoelastic deformations of the rubber due to the substrate asperities and (ii) adhesive effects.

From the modelling point of view, the estimation of each contribution represents a great challenge, and both formulations are inevitably affected by the presence of empirical constants. For example, hysteretic friction could be in principle computed by a full multiscale Persson’s theory [1, 3], but the latter one ultimately embraces an arbitrary choice of the cutoff frequency value, and, furthermore, the full multiscale theory can be in most cases simplified [4]. The adhesive contribution, instead, remains fundamentally empirically described by fitting functions and parameters, and, despite considerable progress and huge effort in this research field, it continues to represent the greatest challenge as well as to recognize the relative importance of the two contributions [5]. In this work, an analysis of the results obtained with the different formulations available in literature is proposed with particular reference to the empirical constants variability.

1 Introduction

Since the studies of the friction of rubber against hard surfaces by Grosch [6], it appears that friction arises from two contributions: the adhesion and the deformation losses. The latter contribution, also called viscoelastic friction, is due to the pulsating deformations the material is exposed to during sliding on the substrate asperities, meanwhile the first one depends on less obvious phenomena within the area of real contact. Therefore, from theoretical point of view, it is possible to write:

$$ \upmu =\upmu_{visc} +\upmu_{adh} $$

(1)

The friction master curve of rubber on a rough track shows, in general, two peaks. One of these occurs at high sliding velocity and it has been mainly attributed to viscoelastic contribution (although at very high speeds the effect of temperature further complicates the study generally lowering the friction coefficient) and the other one, occurring in general at much lower velocities, is considered attributable to the adhesion. In the Grosch studies, the latter peak appears much smaller than the viscoelastic one, giving a negligible contribution on the total friction especially on rough surfaces, but this may not be a general conclusion, as we shall see.

An elaborated theory to estimate the friction viscoelastic contribution was proposed by Persson [1]. This theory is based on exact solution for sliding of a rough rigid random surface in full contact with a viscoelastic medium. The exact formulation is described by the following equation:

$$ \mu \left( {q_{1} } \right) = \frac{1}{2}\int_{{q_{0} }}^{{q_{1} }} {dqq^{3} U\left( q \right) \times \int_{0}^{2\pi } {d\phi \,\cos \left( \phi \right)Im\frac{{E \left( {qv \,\cos \left( \phi \right)} \right)}}{{\left( {1 - \nu^{2} } \right)p_{0} }}} } $$

(2)

where p₀ is the nominal contact pressure, U(q) the surface displacements power spectrum (defined as a function of wavevector q), q₀ is the smallest (relevant) roughness wavevector and q₁ the (much more important) truncating one, E() is the complex viscoelastic modulus of the viscoelastic material.

Persson’s theory is obtained introducing various wise approximations in the real condition of partial contact, being the full contact a very remote condition in practical applications. The results of these corrections is (in the latest versions) a final calculation that involves four nested integrals:

$$ \mu \left( {q_{1} } \right) \cong \frac{1}{2}\int_{{q_{0} }}^{{q_{1} }} {dqq^{3} C\left( q \right)S\left( q \right)P\left( q \right) \times \int_{0}^{2\pi } {d\phi \,\cos \left( \phi \right)Im\frac{{E \left( {qv \,\cos \left( \phi \right)} \right)}}{{\left( {1 - \nu^{2} } \right)p_{0} }}} } $$

(3)

where:

$$ P\left( q \right) = \frac{1}{\sqrt \pi }\int_{0}^{\sqrt G } {dxe^{{ - x^{2} /4}} = erf\left( {\frac{1}{2\sqrt G }} \right)} $$

(4)

$$ G\left( q \right) = \frac{1}{8}\int_{{q_{0} }}^{q} {dqq^{3} C\left( q \right)\int_{0}^{2\pi } {d\phi \left| {\frac{{E \left( {qv \,\cos \left( \phi \right)} \right)}}{{\left( {1 - \nu^{2} } \right)p_{0} }}} \right|^{2} } } $$

(5)

and:

$$ S\left( q \right) = \gamma + \left( {1 - \gamma } \right) P^{2} \left( q \right) $$

(6)

where γ = 1/2 is an empirical fitting constant obtained to match numerical results. Notice that P(q) = A(q)/A₀ is the contact area, normalized respect to the nominal one, observed at the magnification q/q₀.

Ciavarella [4] proposes a much simpler formulations of Persson’s multiscale theory for the friction due to viscoelastic losses suggesting only the finest “single scale” at the so called large wavevector cutoff contributes to the integration process:

$$ \mu = h_{rms}^{'} \left( {q_{1} } \right)\frac{{Im E \left( {q_{1} v} \right)}}{{\surd 2\left| {E \left( {q_{1} v} \right)} \right|}} $$

(7)

where $h^{\prime}_{rms}$ is the rms slope of the surface that depend on the cutoff wavevector q₁ and E(q₁ v) is the complex viscoelastic modulus of the rubber (for a given temperature), at the circular frequency 2 $\pi$ f = q₁ v.

Notice that both formulation [1, 4] define the friction as a function of the truncating wavevector q₁ or, equivalently, as a function of the rms slope of the surface profile. Indeed, the rms slope of surfaces varies wildly at small scales and in principle would grow up to infinity, and at atomic scale, it is certainly badly defined. Lorenz et al. in [3], suggest to fix the cutoff wavevector so that including all the roughness scales with wavenumber q < q₁ gave $h^{\prime}_{rms} \left( {q_{1} } \right) \, = \, 1.3$. The reason for this choice is not so clear, and, more importantly, this aspect is not suggested by any other author, so it remains a best fit for a limited number of experimental results.

The modelling of the adhesive contribution, unfortunately, remains even more radically empirical. Although some simple models exist for dry clean surfaces in sliding contact, based on the consideration that the rubber molecules will interact stretching, detaching, relaxing, and reattaching to the surface of the substrate, ultimately (Schallamach [7] and Cherniak et al. [8], Persson and Volokitin [9]) the theory returns that the adhesive contribution is proportional to the frictional shear stress, which is a Gaussian-like curve as a function of the logarithm sliding velocity:

$$ \upmu_{adh} = \frac{{\tau_{f} }}{{p_{0} }}\frac{A}{{A_{0} }} $$

(8)

where this function is used by [9]:

$$ \tau_{f} = \tau_{f0} exp\left[ { - c\left( {\log_{10} \frac{v}{{v^{*} }}} \right)^{2} } \right] $$

(9)

which has the critical aspect that in large parts it resembles a bell-shaped curve like the viscoelastic contribution, as we shall see, not permitting to identify the relative contribution unambiguously. If one wants to add this contribution, hence, the parameters c, v* and τ_f0 must be estimated by subtracting the viscoelastic contribution from the total one. It worth noting that in Eq. (8) the dependency of µ_adh from the normalized contact area A(q)/A₀ appears and so, again, from the choice of the cutoff wavevector q_1.

A further complication of the problem stems from non-linear effects related to the viscoelastic modulus of the rubber. Indeed, generally the viscoelastic modulus E depends on the frequency of the excitation, on his temperature and on the level of strain, E = E (ω,T,ε). A recent approach proposed by Tolpekina et al. [10] is to assume a correction for a typical strain ε involved in the problem of interest. The authors suppose for sliding friction on the rough surfaces ε ≅ 1, needing knowledge of non-linear characterization of the rubber to evaluate the adhesive friction. Notice that the choice of ε ≅ 1 for sliding contact is also dependent on the choice of the cutoff wavevector q₁ and that this assumption implies a reduction of the small strain modulus E(ω) of a factor ≅ 0.1—i.e. a full order of magnitude, which is highly sensitive to the choice of the truncating wavevector of roughness. This strain softening causes an increase of µ_adh by means of the normalized contact area A(q)/A₀ (at the same conditions of τ_f).

It appear quite clear that the friction estimation is still a problem of great complexity where the present formulations only permit a vague possibility of interpreting experimental data, but hardly a “predictive” capability.

In this paper we show some examples of the challenge represented by the recognition of the importance of the two contribution by the friction curves. In particular, starting from the viscoelastic properties of the rubber and the PSD of a rough surface, an analysis of the results obtained with the different formulations is proposed, and compared with experimental results, with particular reference to the empirical constants variability.

2 Experimental Data

In order to analyse typical compound of interest in asphalt vs tyre contact and to give a quantitative example of the analysis made, all of the following is referred to the experimental data obtained Tolpekina and Persson [5, TP in the following] remarking that all the considerations made can be extended to any couple of rubber/substrate.

2.1 Viscoelastic Modulus

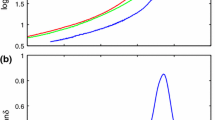
A full characterization of the viscoelastic properties of the rubber is fundamental for rubber friction calculations. The knowledge of the complex elastic modulus of the rubber over a rather large frequency range is necessary, as well as its behaviour at different strain values when the non-linear effects related to the viscoelastic modulus of the rubber would be taken into account. The standard way of measuring the viscoelastic modulus is to deform the rubber sample in an oscillatory manner with a constant strain or stress amplitude. This is done at different frequencies and then repeated at different temperatures. The results measured at different temperatures can be shifted according to the time-temperature superposition principle to form a master curve covering a wide range of frequencies at the chosen reference temperature. Tolpekina and Persson have performed measurements of the viscoelastic modulus in both shear and in tensile (elongation) modes, providing both the shear modulus G(ω) and the Young’s modulus E(ω). These moduli are related via E = 2G(1 + ν) where ν = 0.5 is the Poisson ratio.

In Fig. 1 are reported the real part of the Young’s modulus and the tanδ = ImE/ReE as a function of the logarithm of frequency for compound B of TP.

Fig. 1.

The real part of the Young’s modulus at the reference temperature T = 20 °C, as a function of frequency.

Fig. 2.

The tanδ = ImE/ReE as a function of the logarithm of frequency at the reference temperature T = 20 °C.

TP affirm that when a rubber tread block is sliding on a road surface, the strain in asperity contact regions is typically of order one, ε ≅ 1. To take this into account the effect of these large strain account, they perform strain sweep measurements up to a strain of order one, resulting in a reduction of the small strain modulus E(ω) of a factor S_f ≅ 0.1, where S_f is the strain softening factor [10].

2.2 Surface Roughness Power Spectrum

As rough surface for the rubber friction analysis a concrete block was considered. This type of substrate is very stable (negligible wear) and is easily available in a large number of nominally-identical blocks. The most important information about the substrate is the surface roughness power spectrum. Notice that it is possible to find different normalization of the PSD and therefore it is important to pay attention to the formulations used for the calculation of the quantities such as the root-mean-square (RMS) height ℎ_rms, the RMS slope $h^{\prime}_{{\text{rms}}}$, and the RMS curvature $h^{\prime\prime}_{{\text{rms}}}$ [11]. Referring to Persson formulation, Fig. 3 shows the 2D surface roughness power spectrum of the concrete surface and the significant range of interest of this self-affine fractal power spectra can be assumed to be a power law:

Fig. 3.

The surface roughness power spectrum of the concrete substrate.

$$ C\left( q \right) = C_{0} \cdot q^{{ - 2\left( {1 + H} \right)}} $$

(10)

where the Hurst exponent H = 0.86 and C₀ = 0.001152 m^(2-2H). The q₀ wavevector considered in this study is q₀ = 10^2.7, but fortunately the choice of this truncation is not very relevant for friction estimation, while the choice of the large wavenumber cut-off is extremely more sensible and arbitrary, as debated in the next section.

2.3 Friction

The available measured data for low velocities (LV) and higher velocity (HV) was obtained by TP using two different experimental setups. Friction for LV were obtained by means the Leonardo da Vinci experiment, which allows only to measure the friction coefficient on the branch of the µ(v)-curve where the friction coefficient increases with increasing sliding speed [12]. The friction coefficients for the sliding speeds of 0.1, 0.3, 1, and 1.8 m/s were obtained by means a Linear Friction Tester (LFT).

Figure 4 shows the measured data and calculated results, by using Persson formulation, for rubber sliding on concrete. Notice that the total friction curve is calculated as a sum of the viscoelastic and adhesive contribution plus a constant term µ_const = 0.2 (yet another empirical choice), which the authors refer to the “scratching of the concrete surface by the hard filler particles”.

Fig. 4.

The measured (symbols) and calculated (lines) friction coefficient using the Persson formulation.

The parameters adopted for the friction calculation are summarized in Table 1, where $h^{\prime}_{rms}$ is calculated as:

Table 1. Summary of the reference parameters adopted for the friction calculation.

$$ h'_{rms} = \smallint C\left( q \right) \cdot q^{3} dq $$

(11)

3 Analysis of Multiscale Theories

In this section, we want point out that the recognition of the importance of the adhesive and viscoelastic contribution is not at all simple and obvious. Indeed, starting from the viscoelastic properties of the rubber and the PSD of a rough surface, we propose different set of arbitrarily determined parameters, which return a different combination of Gaussian-like curves of the two contributions, allowing an equally good fitting of the experimental data.

Firstly, we investigate the theoretical results obtained calculating the viscoelastic contribution using the simplified formulation (Eq. 7). Again, the total friction curve is calculated as a sum of the viscoelastic and adhesive contribution plus the constant term µ_const = 0.2. The parameters are the same as those used for the calculation with the Persson theory and reported in Table 1.

Figure 5 shows the measured and calculated friction coefficient on the concrete surface as a function of the logarithm of sliding speed, using the simplified formulation. The lower red curve is the (calculated) viscoelastic contribution to the friction coefficient, the green is the adhesive contribution and the upper blue curve is the total calculated friction.

Fig. 5.

The measured (symbols) and calculated (lines) friction coefficient on concrete as a function of the logarithm of the sliding speed, using the simplified formulation for the viscoelastic contribution.

The results obtained with Persson theory and the simplified formulation do not show significant difference for low velocity friction data being these results considered as principally influenced by the adhesion. For high sliding velocity some difference can be appreciate but this data are often not predicted appropriately.

Here it should be empathized that these results are strongly influenced by the value of some parameters that are fixed in a non-rigorous way. In particular:

• the choice of the cutoff wavevector q₁ influences strongly both viscoelastic and adhesive contribution;

• the term µ_const = 0.2 which is attributed to scratching of the concrete surface by the hard filler particles is quite arbitrary;

• The reference velocity v* and the τ_f0 influence significantly the adhesive curve;

• The assumption that for sliding friction on the rough surfaces the deformation is ε ≅ 1 imply a reduction of the strain modulus E(ω) of a strain factor S_f ≅ 0.1. Due to the non-linear effects related to the viscoelastic modulus of the rubber, lower strain values would cause sensible variation of the S_f and therefore of the adhesive friction.

Adopting the simplified formulation for the viscoelastic friction and the Eqs. (8) and (9) for the adhesion, we propose different combinations in the choice of these parameters able to give an equally good fitting of the available experimental data. In Table 2, five different parameters’ set used for simulation are summarized, while Fig. 6 reports the corresponding friction results.

Table 2. Summary of the different parameters sets adopted for the friction calculation.

Fig. 6.

The measured (symbols) and calculated (lines) friction coefficient on concrete as a function of the logarithm of the sliding speed for different set of arbitrary parameters.

The experimental data at low velocity (red symbols in Fig. 6) seem well fitted by all parameters sets proposed. Notice that set A returns friction attributable almost exclusively to the viscous contribution, having considered null the constant term and resulting negligible the adhesive one because of the choice of a large cutoff wavevector q₁ and because of not considering the non-linear effect attributed to the viscoelastic modulus of the rubber. Despite this combination of parameters, with the formulations considered, the results do not seem acceptable for higher sliding velocity, that highlights the great influence the choice of the cutoff wavevector has on the recognition of the importance of the adhesive and viscoelastic contribution.

The other sets give results that appear satisfactory in relation to the available experimental data underlining that is not possible to determine these parameters unambiguously.

4 Conclusions

We have considered present multiscale theories for rubber-tyre friction and we have remarked, by means of actual examples that:

• unfortunately even the most elaborate theories to date (in particular those of Persson and co-authors), contain a number of empirical parameters, which are not uniquely defined, at least against the present experimental evidence

• the multiscale aspect of friction, which clearly complicates the theories significantly, in most cases doesn’t appear so fundamentally needed, since simplified formulations which permit immediate calculation without the need to implement any recursive integration, interpolation (with all the risks associated with incorrect coding of such models), seem to have comparable fitting capabilities

• the adhesive contribution seems in recent studies more important than in the earlier studies of Grosch. Unfortunately, this part is even more “fundamentally empirical” than the latter

• given the models of viscoelastic and adhesive contributions return friction curves which are very similar in large parts of the velocity spectrum, it remains difficult to attribute with precision the relative contribution

• non linear effects strongly affect the adhesive models, while they affect the viscoelastic friction less. These are also not simple to measure and to include unambiguously, as their role depends also on the true strain level at the truncating wavelength of roughness, which remains arbitrary.