Modeling of Carbon and Polyester Elastomeric Isolators in Unbounded Configuration by Using an Efficient Uniaxial Hysteretic Model

Abstract

This paper presents the application of a recently developed uniaxial phenomenological model to low-cost Fiber Reinforced Elastomeric Isolators (FREIs) in unbounded configuration. Prototypes under study represent the subject of a previous experimental investigation performed at the University of Naples Federico II [1], through which polyester FREIs demonstrated a very effective performance in comparison with carbone ones. A stable roll-over behavior was detected up to very large displacements (γ = 300%) both under monotonic and cyclic loading protocol. An accurate analytical model was also provided for preliminary design of the devices. In the present study, an uniaxial rate-independent hysteretic model [2] is proposed and calibrated in order to be employed in earthquake analysis problems of seismically base isolated structures. In particular, such a model, requiring only five parameters to be calibrated from experimental tests, is able to accurately reproduce the complex hysteretic behavior displayed by the tested FREIs as the result of combined rubber behavior and roll-over process. A satisfactory approximation is obtained up to 100% shear deformation, whereas a larger scatter comes out in the case of larger deformations. The paper also demonstrates that a very effective and easy to use calibration process is needed in order to accurately reproduce the experimental behavior of the tested seismic isolators. Furthermore, by implementation of the proposed hysteretic model, significant advantages arise in terms of reduced computational effort and processing time with respect to other accurate models available in the literature.

1 Introduction

In the last few years, the author has been studying fiber reinforced elastomeric isolators (FREIs) in unbounded configuration [1, 3,4,5] for development of novel and low cost seismic protection systems for developing regions of the world. Preliminary studies [2] have demonstrated the potential of FREIs as seismic isolators despite classical steel reinforced elastomeric isolators (SREIs) [6, 7]. Experimental shear and compression tests highlighted satisfactory performance of FREIs [1, 4]. An analytical model was also proposed [1] in order to properly take into account both geometric and mechanical non-linear behavior due to roll-over phenomenon. Softening phase in lateral force-displacement behavior of FREIs resulted more pronounced than SREIs [4].

Commercial software and numerical methods are often based on a Bouc-Wen model [8]. As an alternative approach, multi-linear spring models can be adopted with a pivot hysteresis model [9]. In both cases, computational efficiency of proposed algorithms is questionable and time history integration of large scale base isolated buildings may result challenging.

On the basis of experimental results shown by Losanno et al. [1], this paper provides a numerical modeling of carbon and polyester FREIs by an efficient uniaxial hysteretic model available from literature. Vaiana et al. [2, 10, 11] demonstrated that only five parameters have to be calibrated from experimental test in order to accurately reproduce the non-linear behavior of FREIs. This model seems very promising for application to passive control systems like classical SREIs and hysteretic like dampers [12]. In addition to this, the current paper demonstrates the effectiveness of the method proposed in [2] to model experimental behavior of FREIs, including roll-over deformation up to 300% deformation. A satisfactory response was obtained for a deformation level up to 100%, traducing in very accurate equivalent damping and stiffness estimate.

2 Experimental Program

The specimens under study were designed for a shaking-table test program on a prototype building to be isolated at a target period of 2,0 s.

Design process was conducted according to FEMA 450 provisions [13] and prototypes were assumed in a length scale factor of 1/3. The structure consisted of a steel frame having a total height of 2900 mm and plan dimensions of 2650 × 2150 mm. The total mass of the structure was 77 kN, with a base level of 36 kN and a top level of 41 kN. The vertical load at the base of each column was 19 kN.

The prototypes were designed for a target shear strain of 100%, providing a total rubber height of 30 mm. Under the assumption of a 10% damping ratio, target displacement of the scaled model was 30 mm, i.e. 90 mm for the real prototype. The fundamental period of the scaled model was 1,15 s, corresponding to a vibration frequency of 0,87 Hz.

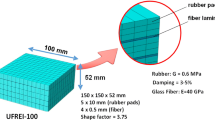
Two types of isolators were designed in order to test the influence of different fiber reinforcement, i.e. polyester (T1) and carbon (T2). A schematic drawing with a picture of the samples are given in Fig. 1:

Fig. 1.

Cross-section of the prototypes: (a) T1, and (b) T2.

2.1 Test Protocols

A total of four protocols (Fig. 2) were applied for assessing the shear behavior of the prototypes. A main protocol was defined according to FEMA 450 [13], including deformations up to 100% shear strain (protocol P1) applied at the design period (0,87 Hz). With the intention to test the devices under extreme conditions, a protocol P2 was introduced up to 300% deformation with a frequency of 0,87 Hz. Protocol P3 was similar to P1 but with a frequency of 0,5 Hz. Finally, protocol P4 included a monotonic test up to 300%.

Fig. 2.

Displacement protocols for the shear tests: (a) P1, (b) P2, (c) P3, and (d) P4.

A compression machine with a sliding table was used (Fig. 3). A constant vertical axial load was applied to the specimen in order to provide the same target stress of approximately 4 Mpa.

Fig. 3.

Shear test: (a) set up, and (b) specimen during the test.

2.2 Experimental Results

Even if two samples (a, b) for each type of isolators (T1, T2) were tested, results are only displayed for prototypes T1b and T2a. A stable hysteretic behavior was obtained from the shear tests (Fig. 4). A stiffness reduction due to Mullins effect [14] was observed for each deformation level with respect to the first cycle. The monotonic test is also displayed as representative of the skeleton curve. Even if the roll-over phenomenon significantly affected the softening phase of the response between 50 and 250% deformation, a non-negative tangent stiffness is recorder throughout the protocols.

Fig. 4.

Shear test results for prototype T1b (a, b, c) and T2a (d, e, f).

With the aim to numerical modeling hysteretic behavior, monotonic response is not explicitly considered. In addition to this, for 100% deformation level the protocol P3 will be assumed in lieu of P1. Due to Mullins effect, P3 provides a “scragged” behavior that is deemed more representative for predicting seismic response in numerical modeling.

3 Numerical Model

The Proposed Hysteretic Model (PHM) represents a specific instance of the more general class of uniaxial phenomenological models formulated by Vaiana et al. [8,9,10].

Figure 5 shows a typical restoring force-displacement hysteresis loop, bounded by two parallel curves, obtained by imposing a sinusoidal displacement and simulated by means of the PHM.

Fig. 5.

Branches $c_{1}$, $c_{2}$, $c_{3}$, and $c_{4}$ for a hysteresis loop bounded by two parallel curves.

Such a hysteresis loop can be divided into four different branches, each one corresponding to a different interval of displacement $u$ and sign of velocity $\dot{u}$ of the device along one of its transverse directions. The different branches are described as follows:

where $x_{2}$ ($x_{4}$), representing the model history variable, is the displacement where the generic loading (unloading) curve $c_{1}$ ($c_{3}$) intersects the upper (lower) limiting curve $c_{2}$ ($c_{4}$), whereas $x_{1} = x_{2} - 2\bar{x}$ ($x_{3} = x_{4} + 2\bar{x}$). Specifically, the expressions of such branches are:

$$ \begin{aligned} c_{1} & =\upbeta_{1} u^{3} +\upbeta_{2} u^{5} + k_{b} u + \left( {k_{a} - k_{b} } \right)\left[ {\frac{{\left( {1 + u - x_{2} + 2\bar{x}} \right)^{{\left( {1 -\upgamma} \right)}} }}{{1 -\upgamma}} - \frac{{\left( {1 + 2\bar{x}} \right)^{{\left( {1 -\upgamma} \right)}} }}{{1 -\upgamma}}} \right] + \bar{z}, \\ c_{2} & =\upbeta_{1} u^{3} +\upbeta_{2} u^{5} + k_{b} u + \bar{z}, \\ c_{3} & =\upbeta_{1} u^{3} +\upbeta_{2} u^{5} + k_{b} u + \left( {k_{a} - k_{b} } \right)\left[ {\frac{{\left( {1 - u + x_{4} + 2\bar{x}} \right)^{{\left( {1 -\upgamma} \right)}} }}{{\upgamma - 1}} - \frac{{\left( {1 + 2\bar{x}} \right)^{{\left( {1 -\upgamma} \right)}} }}{{\upgamma - 1}}} \right] - \bar{z}, \\ c_{4} & =\upbeta_{1} u^{3} +\upbeta_{2} u^{5} + k_{b} u - \bar{z}, \\ \end{aligned} $$

(1)

where $k_{a}$, $k_{b}$, $\upgamma$, $\beta_{1}$, and $\beta_{2}$ are model parameters to be identified from experimental tests, whereas $\bar{x}$ and $\bar{z}$ are the internal model parameters evaluated as a function of $k_{a}$, $k_{b}$, and $\upgamma$. In particular, $k_{a} > k_{b}$, $k_{a} > 0$, $\upgamma > 0$, $\upgamma \ne 1$, $\bar{x} > 0$, $\bar{z} > 0$, whereas $\beta_{1}$ and $\beta_{2}$ are reals; furthermore, the internal model parameters are computed as:

$$ \bar{x} = \frac{1}{2}\left[ {\left( {\frac{{k_{a} - k_{b} }}{{10^{ - 20} }}} \right)^{{\tfrac{1}{\upgamma}}} - 1} \right] , $$

(2)

$$ \bar{z} = \frac{{k_{a} - k_{b} }}{2}\left[ {\frac{{\left( {1 + 2\bar{x}} \right)^{{\left( {1 -\upgamma} \right)}} - 1}}{{1 -\upgamma}}} \right] , $$

(3)

whereas the model history variables are evaluated as:

$$ x_{2} = 1 + u_{P} + 2\bar{x} - \left\{ {\frac{{1 -\upgamma}}{{k_{a} - k_{b} }}\left[ {f_{P} -\upbeta_{1} u_{P}^{3} -\upbeta_{2} u_{P}^{5} - k_{b} u_{P} - \bar{z} + \left( {k_{a} - k_{b} } \right)\frac{{\left( {1 + 2\bar{x}} \right)^{{\left( {1 -\upgamma} \right)}} }}{{1 -\upgamma}}} \right]} \right\}^{{\left( {\frac{1}{{1 -\upgamma}}} \right)}} , $$

(4)

$$ x_{4} = - 1 + u_{P} - 2\bar{x} + \left\{ {\frac{{\upgamma - 1}}{{k_{a} - k_{b} }}\left[ {f_{P} -\upbeta_{1} u_{P}^{3} -\upbeta_{2} u_{P}^{5} - k_{b} u_{P} + \bar{z} + \left( {k_{a} - k_{b} } \right)\frac{{\left( {1 + 2\bar{x}} \right)^{{\left( {1 -\upgamma} \right)}} }}{{\upgamma - 1}}} \right]} \right\}^{{\left( {\frac{1}{{1 -\upgamma}}} \right)}} , $$

(5)

where $\left( {u_{P} , \, f_{P} } \right)$ are the coordinates of the initial point $P$ of the generic loading or unloading curve.

3.1 Parameter Calibration

According to experimental outcomes, model parameters were specifically calibrated. For each device (T1b, T2a), significant non-linear behavior required a specific calibration set for 300% (set a) and 100% (set b) protocols, respectively. In case (a), the calibration was aimed at reproducing the maximum force achieved during the test. In case (b), a very satisfactory approximation of the non-linear behavior was obtained throughout the test.

Parameters for T1b are resumed in Table 1 and corresponding hysteretic plots are displayed in Fig. 6. Unless 300% deformation cycle is considered, a satisfactory approximation of experimental results is obtained for both protocols.

Table 1. Model parameters used to simulate the hysteresis loops of T1b in Fig. 6.

Fig. 6.

Comparisons between analytical and experimental results for T1b: (a) protocol P2 and (b) P3.

For T2a, parameters are reported in Table 2 and corresponding hysteretic plots are displayed in Fig. 7. Despite to previous case, in the range of significant rollover during P2, a lightly different shape of the hysteretic cycles was obtained.

Table 2. Model parameters used to simulate the hysteresis loops in Fig. 7.

Fig. 7.

Comparisons between analytical and experimental results T2a: (a) protocol P2 and (b) P3.

3.2 Comparison

In order to evaluate effective parameters affecting non-linear behavior, equivalent stiffness and damping were estimated according to FEMA 450 [13].

For both prototypes, equivalent stiffness is satisfactorily matched for all deformation levels demonstrating a very similar response between experimental and numerical modeling.

As far as damping is concerned, it is worth to make a difference between P2 and P3. In particular, the parameters set (b) provided a satisfactory approximation with a 15% damping ratio at the target deformation of 100%. Differently, under protocol P2, a significant overestimate of damping was obtained between 50 and 200% shear strain. This is due to larger enclosed area of numerical cycles during unloading phase.

It can be argued that proposed model is sufficiently accurate in reproducing maximum force for any deformation level, whereas damping may results overestimated when set (a) is used and significant rollover is expected (Figs. 8 and 9).

Fig. 8.

Horizontal stiffness versus shear deformation: (a) T1b and (b) T2a.

Fig. 9.

Equivalent damping versus shear deformation: (a) T1b and (b) T2a.

4 Conclusions

This paper presented an interesting application of an algebraic hysteretic model to experimental behavior of unbounded FREIs.

FREIs represent a novel and promising technology for modern and low-cost seismic protection of structures. In order to apply the novel isolators to real buildings, hysteretic behavior has to properly be investigated and computationally efficient numerical models have to be developed for structural analysis programs.

On the basis of available experimental results, a 5-parameters polynomial model was suggested for modeling hysteretic behavior of unbounded isolators significantly affected by roll-over deformation. Due to significant influence of softening phenomenon on hysteretic behavior, a specific set of parameters was needed for target deformation level of 100% and 300%, respectively. Even if an excellent matching resulted for 100% deformation protocol, a satisfactory approximation was also obtained up to 300% deformation level.

A comparison between equivalent stiffness and damping for investigated deformation levels confirmed the effectiveness of the proposed model with a better approximation in case of shear deformation up to 100%. A looser approximation only affected damping estimate for deformation levels between 50 and 200% due to overestimation of dissipated area. Further research will be devoted to improve the model also taking into account degradation to reduce numerical damping. In future papers, the proposed hysteretic model will be also employed for the analysis of base-isolated structures by means of the seismic envelopes concept [15].