Keywords

1 Introduction

The use of robotic arms in industrial applications has significantly been increased. The robot motion tracking control which required high accuracy, stability, and safety is one of the challenging problems due to highly coupled and nonlinear dynamic. In the presence of model uncertainties such as dynamic parameters (e.g., inertia and payload conditions), dynamic effects (e.g., complex nonlinear frictions), and unmodeled dynamics, conventional controllers have many difficulties in treating these uncertainties. Sliding mode control (SMC) is one of the most robust approaches to overcome this problem. The most distinguished property of the sliding mode control lies in its insensitivity to dynamic uncertainties and external disturbances.

However, this approach exhibits high-frequency oscillations called chattering when the system state reaches the sliding surface, which has negative effects on the actuator control and excite the undesirable unmodeled dynamics.

Recently, sliding mode, integral sliding mode controllers (ISMC), and proportional integral sliding mode controllers (PI-SMC) were examined by many researchers as a powerful nonlinear controller in [1,2,3,4,5,6,7]. An adaptive sliding mode control is designed in several papers [8,9,10,11,12]. The proportional integral derivative sliding mode controller (PID-SMC) was designed to control the robot manipulator in several works. The investigation of fuzzy logic and neuro-fuzzy logic control to design an adaptive sliding mode control are found in [13,14,15,16].

Currently, evolutionary algorithms have appeared as an alternative design method for robotic manipulator. M. Vijay and Debaschisha design a PSO-based backstepping sliding mode controller and observer for robot manipulators [17]. This authors used PSO to tune the sliding surface parameters of SMC coupled with artificial neuro-fuzzy inference system (ANFIS) [18].

The optimization of the PID-SMC parameters using ALO is outperformed in comparison with GA and PSO algorithms by Mokeddem and Draidi to control a nonlinear system [19].

This paper presents the use of novel optimization algorithms to tune SMC with PID surface for the trajectory tracking control of robot manipulator. These algorithms are described in Sect. 3. Section 2 designates the mathematical model of robot manipulator. The principle of SMC and its application on the robot manipulator are titled in Sect. 4. The simulation results are presented in Sect. 5.

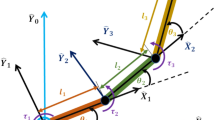
2 Dynamic Model of Robot Manipulator

By applying Lagrange’s principle, the dynamic model of two-degree-of-freedom (2DOF) robot manipulator is given by

$$ \tau =M(q)\ddot{q}+C\left(q,\dot{q}\right)\dot{q}+G(q)+F\left(\dot{q}\right) $$
(1)

where qi, \( {\dot{q}}_i \), and \( {\ddot{q}}_i \) present the link position, velocity, and acceleration vectors, respectively. M(q) is the matrix inertia given by

$$ M(q)=\left[\begin{array}{cc}{M}_{11}& {M}_{12}\\ {}{M}_{21}& {M}_{22}\end{array}\right] $$

where

$$ {M}_{11}={m}_1\bullet {l}_1^2+{m}_2\bullet \Big({l}_1^2+2{l}_1\bullet {l}_2\bullet \cos \left({q}_2\right)+{l}_2^2 $$
$$ {M}_{12}={M}_{12}={m}_2\bullet {l}_2\left({l}_2+{l}_1\bullet \cos \left({q}_2\right)\right) $$
$$ {M}_{22}={m}_2\bullet {l}_2^2 $$

\( C\left(q,\dot{q}\right) \) is the Coriolis centripetal force matrix given by

$$ C(q)=\left[\begin{array}{cc}{C}_{11}& {C}_{12}\\ {}{C}_{21}& {C}_{22}\end{array}\right] $$

where

$$ {C}_{11}=-{m}_2\bullet {l}_1\bullet {l}_2\bullet \sin \left({q}_2\right)\bullet 2{\dot{q}}_2 $$
$$ {C}_{12}=-{m}_2\bullet {l}_1\bullet {l}_2\bullet \sin \left({q}_2\right)\bullet {\dot{q}}_2 $$
$$ {C}_{21}={m}_2\bullet {l}_1\bullet {l}_2\bullet \sin \left({q}_2\right)\bullet {\dot{q}}_1 $$
$$ {C}_{22}=0 $$
$$ \mathrm{The}\ \mathrm{gravity}\ \mathrm{vector}\ G(q)={\left[{G}_{11}\kern0.5em {G}_{12}\right]}^T $$

is given by

$$ {G}_{11}=\left({m}_1+{m}_2\right)\bullet g\bullet {l}_1\bullet \cos \left({q}_1\right)+{m}_2\bullet g\bullet {l}_2\bullet \cos \left({q}_1+{q}_2\right) $$
$$ {G}_{12}={m}_2\bullet g\bullet {l}_2\bullet \cos \left({q}_1+{q}_2\right) $$

Finally, \( F\left(\dot{q}\right)={\left[{F}_{11}\kern0.5em {F}_{21}\right]}^T \) is the friction force vector given by

$$ {F}_{11}=2\bullet {\dot{q}}_1+0.8 \operatorname {sign}\ \left({\dot{q}}_1\right) $$
$$ {F}_{21}=4\bullet {\dot{q}}_2+0.1 \operatorname {sign}\ \left({\dot{q}}_2\right) $$

and τ is the vector of the torque control signal, where mi and li are the link mass and length, respectively.

3 Evolutionary Algorithms

3.1 Gray Wolf Optimizer (GWO)

GWO is a recent meta-heuristic optimizer inspired by gray wolves and proposed by [20]. It mimics the leadership hierarchy and the hunting mechanism of gray wolves in nature.

As described in literature, the GWO algorithm includes two mathematical models: encircling prey and hunting prey.

The encircling behavior: During the hunting, the gray wolves encircle prey. The mathematical model is presented in the following equations:

$$ \overset{\rightharpoonup }{D} = \left|\overset{\rightharpoonup }{C}\bullet \overset{\rightharpoonup }{X_p}(t)-\overset{\rightharpoonup }{X}(t)\right| $$
(2)
$$ \overset{\rightharpoonup }{X}\left(t+1\right)=\overset{\rightharpoonup }{X_p}(t)-\overset{\rightharpoonup }{A}\overset{\rightharpoonup }{D} $$
(3)

where D is the distance, \( \overset{\rightharpoonup }{\ {X}_p}(t) \) is the position vector of prey, \( \overset{\rightharpoonup }{\ X}(t) \) indicates the position of the gray wolf, t indicates the current iteration, and\( \overset{\rightharpoonup }{A} \) and \( \overset{\rightharpoonup }{C} \) are coefficient vectors calculated as follows:

$$ \overset{\rightharpoonup }{A}=2\overset{\rightharpoonup }{a}\overset{\rightharpoonup }{r_1}-\overset{\rightharpoonup }{a} $$
(4)
$$ \overset{\rightharpoonup }{C}=2\overset{\rightharpoonup }{r_2} $$
(5)

where components of a are linearly decreased from 2 to 0 over the course of iterations and r1 and r2 are random vectors in [0 1].

The hunting model: Four types of gray wolves participate in chasing prey; alpha, beta, delta, and omega denote the wolf group and are employed as solutions (fittest, best, and candidate) for simulating the leadership hierarchy.

The optimization algorithm is guided by α, β, and δ; with three best solutions obtained so far, the other search agents follow them and update their positions according to the best search agent as follows:

$$ \overset{\rightharpoonup }{D_{\upalpha}}=\left|\overset{\rightharpoonup }{C_1}\bullet \overset{\rightharpoonup }{X_{\upalpha}}(t)-\overset{\rightharpoonup }{X}(t)\right| $$
(6)
$$ \overset{\rightharpoonup }{D_{\upbeta}}=\left|\overset{\rightharpoonup }{C_2}\bullet \overset{\rightharpoonup }{X_{\upbeta}}(t)-\overset{\rightharpoonup }{X}(t)\right| $$
(7)
$$ \overset{\rightharpoonup }{D_{\updelta}}=\left|\overset{\rightharpoonup }{C_3}\bullet \overset{\rightharpoonup }{X_{\updelta}}(t)-\overset{\rightharpoonup }{X}(t)\right| $$
(8)
$$ \overset{\rightharpoonup }{X_1}=\overset{\rightharpoonup }{X_{\upalpha}}(t)-\overset{\rightharpoonup }{A_1}\bullet \overset{\rightharpoonup }{D_{\upalpha}} $$
(9)
$$ \overset{\rightharpoonup }{X_2}=\overset{\rightharpoonup }{X_{\upbeta}}(t)-\overset{\rightharpoonup }{A_2}\bullet \overset{\rightharpoonup }{D_{\upbeta}} $$
(10)
$$ \overset{\rightharpoonup }{X_3}=\overset{\rightharpoonup }{\ {X}_{\updelta}}(t)-\overset{\rightharpoonup }{A_3}\bullet \overset{\rightharpoonup }{D_{\updelta}} $$
(11)
$$ \mathrm{and}\ \overset{\rightharpoonup }{\ X}\left(t+1\right)=\frac{\overset{\rightharpoonup }{X_1}+\overset{\rightharpoonup }{X_2}+\overset{\rightharpoonup }{X_3}}{3} $$
(12)

3.2 The Ant Lion Optimizer

Another novel nature-inspired algorithm called ant lion optimizer (ALO) mimics the hunting mechanism of antlions in nature [21]. Five main steps of hunting prey such as the random walk of ants, building traps, entrapment of ants in traps, catching preys, and rebuilding traps are implemented in this algorithm.

Since ants move stochastically in nature when searching for food, a random walk is chosen for modeling ants’ movement as follows:

$$ X(t)=\left[0,\mathrm{cumsum}\left(2r\left({t}_1-1\right)\right),\mathrm{cumsum}\left(2r\left({t}_2-1\right)\right),\dots, \mathrm{cumsum}\left(2r\left({t}_n-1\right)\right)\right] $$
(13)

where cumsum calculates the cumulative sum, n is the maximum number of iteration, t shows the step of random walk (iteration in this study), and r(t) is a stochastic function defined as follows:

$$ r(t)=\left\{\begin{array}{c}1\ \mathrm{if} \operatorname {rand}>0.5\\ {}0\ \mathrm{if} \operatorname {rand}\le 0.5\end{array}\right\} $$
(14)

and rand is a random number generated with uniform distribution in the interval of [0,1]. The position of ants is saved and utilized during optimization in the following matrix:

$$ {M}_{\mathrm{Ant}}=\left[\begin{array}{c}{A}_{1.1}\ {A}_{1.2}\dots {A}_{1.d}\\ {}\begin{array}{c}{A}_{2.1}\ {A}_{2.2}\dots {A}_{2.d}\\ {}:\end{array}\\ {}{A}_{n.1}\ {A}_{n.2}\dots {A}_{n.d}\end{array}\right] $$
(15)

where Ai. j shows the value of the jth variable (dimension) of ith ant, n is the number of ants, and d is the number of variables. The position of an ant refers to the parameters for a particular solution. A fitness (objective) function is utilized during optimization, and the following matrix stores the fitness value of all ants:

$$ {M}_{\mathrm{OA}}=\left[\begin{array}{c}f\left(\left[{A}_{1.1},{A}_{1.2},\dots, {A}_{1.d}\right]\right)\\ {}\begin{array}{c}f\left(\left[{A}_{2.1},{A}_{2.2},\dots, {A}_{2.d}\right]\right)\\ {}:\end{array}\\ {}f\left(\left[{A}_{n.1},{A}_{n.2},\dots, {A}_{n.d}\right]\right)\end{array}\right] $$
(16)

where f is the objective function. In addition to ants, we assume the antlions are also hiding somewhere in the search space. In order to save their positions and fitness values, the following matrices are utilized:

$$ {M}_{\mathrm{Antlion}}=\left[\begin{array}{c}{AL}_{1.1}\ {AL}_{1.2}\dots {AL}_{1.d}\\ {}\begin{array}{c}{AL}_{2.1}\ {AL}_{2.2}\dots {AL}_{2.d}\\ {}:\end{array}\\ {}{AL}_{n.1}\ {AL}_{n.2}\dots {AL}_{n.d}\end{array}\right]\kern1.50em {M}_{\mathrm{OAL}}=\left[\begin{array}{c}f\left(\left[{AL}_{1.1},{AL}_{1.2},\dots, {AL}_{1.d}\right]\right)\\ {}\begin{array}{c}f\left(\left[{AL}_{2.1},{AL}_{2.2},\dots, {AL}_{2.d}\right]\right)\\ {}:\end{array}\\ {}f\left(\left[{AL}_{n.1},{AL}_{n.2},\dots, {AL}_{n.d}\right]\right)\end{array}\right] $$
(17)

ALi. j shows the jth dimension value of ith antlion, n is the number of antlions, and d is the number of variables (dimension), where MOAL is the matrix for saving the fitness of each antlion.

Random walks of ants: Random walks are all based on the Eq. (1). Ants update their positions with random walk at every step of optimization, which is normalized using the following equation (min–max normalization) in order to keep it inside the search space:

$$ {X}_i^t=\frac{\left({X}_i^t-{a}_i\right)\ast \left({d}_i-{c}_i^t\right)}{\left({d}_i^t-{a}_i\right)}+{c}_i $$
(18)

where ai is the minimum of random walk, di is the maximum of random walk, \( {c}_i^t \) is the minimum, and \( {d}_i^t \) indicates the maximum of ith variable at tth iteration.

Trapping in antlion’s pits: The ants walk in a hypersphere defined by the vectors c and d around a selected antlion are affected by antlions’ traps. In order to mathematically model this supposition, the following equations are proposed:

$$ {c}_i^t={\mathrm{Antlion}}_j^t+{c}^t $$
(19)
$$ {d}_i^t={\mathrm{Antlion}}_j^t+{d}^t $$
(20)

where ct is the minimum of all variables at tth iteration, dt indicates the vector including the maximum of all variables at tth iteration, \( {c}_i^t \) is the minimum of all variables for ith ant, \( {d}_i^t \) is the maximum of all variables for ith ant, and \( {\mathrm{Antlion}}_j^t \) shows the position of the selected jth antlion at tth iteration.

Building trap: In order to model the antlions’s hunting capability, a roulette wheel is employed for selecting antlions based of their fitness during optimization. Ants are assumed to be trapped in only one selected antlion. This mechanism gives high chances to the fitter antlions for catching ants.

Sliding ants towards antlion: Once antlions realize that an ant is in the trap they shoot sands outwards the center of the pit. This behavior slides down the trapped ant that is trying to escape. For mathematically modelling this behavior, the radius of ants’s random walks hyper-sphere is decreased adaptively. The following equations are proposed in this regard:

$$ {c}^t=\frac{c^t}{I} $$
(21)
$$ {d}^t=\frac{d^t}{I} $$
(22)

where I is a ratio, ct is the minimum of all variables at tth iteration, and dt indicates the vector including the maximum of all variables at tth iteration. In Eqs. (21) and (22), \( I={10}^W\frac{t}{T} \) where T is the maximum number of iterations and w is a constant defined based on the current iteration. Basically, the constant w can adjust the accuracy level of exploitation.

Catching prey and rebuilding the pit: For mimicking the final stage of hunt this process, it is assumed that catching prey occur when ants becomes fitter (goes insides and) than its corresponding antlion, which is required to update its position to the latest position of the hunted ant. The following equation is proposed in this regard:

$$ {\mathrm{Ant}\mathrm{lion}}_j^t={\mathrm{Ant}}_i^t\ \mathrm{if}\ f\left({\mathrm{Ant}}_j^t\right)>f\left({\mathrm{Ant}\mathrm{lion}}_j^t\right) $$
(23)

where \( {\mathrm{Antlion}}_j^t \)shows the position of selected jth antlion at tth iteration and \( {\mathrm{Ant}}_i^t \) indicates the position of ith ant at tth iteration.

Elitism: In this algorithm the best antlion obtained so far in each iteration is saved and considered as an elite.

Since the elite is the fittest antlion, it should be able to affect the movements of all the ants during iterations. Therefore, it is assumed that every ant randomly walks around a selected antlion by the roulette wheel and the elite simultaneously as follows:

$$ {\mathrm{Ant}}_i^t=\frac{R_A^t+{R}_E^t}{2} $$
(24)

where\( {R}_A^t \) is the random walk around the antlion selected by the roulette wheel at tth iteration, \( {R}_E^t \) is the random walk around the elite at tth iteration, and \( {\mathrm{Ant}}_i^t \) indicates the position of ith ant at tth iteration.

4 Sliding Mode Control

The principle of this type of control consists in bringing, whatever the initial conditions, the representative point of the evolution of the system on a hypersurface of the phase space representing a set of static relationships between the state variables.

The sliding mode control generally includes two terms:

$$ U={U}_{\mathrm{eq}}+{U}_n $$
(25)

Ueq: A continuous term, called equivalent command. Un: a discontinuous term, called switching command.

4.1 Equivalent Command

The method, proposed by Utkin, consists to admit that in sliding mode, everything happens as if the system was driven by a so-called equivalent command . The latter corresponds to the ideal sliding regime, for which not only the operating point remains on the surface but also for which the derivative of the surface function remains zero \( \dot{S}(t)=0 \)(that mean, invariant surface over time).

4.2 Switching Control

The switching command requires the operating point to remain at the neighborhood of the surface. The main purpose of this command is to check the attractiveness conditions:

$$ {U}_n=\lambda \operatorname{sign}(S) $$
(26)

The gain λ is chosen to guarantee the stability and the rapidity and to overcome the disturbances which can act on the system. The function sign (S(x, t)) is defined as

$$ \mathrm{Sign}\left(S\left(x,t\right)\right)=\left\{\begin{array}{c}1\ \mathrm{si}\ S>0\\ {}-1\ \mathrm{si}\ S<0\end{array}\right\} $$
(27)

The PID sliding surface for the sliding mode control can be indicated using the following equation:

$$ S(t)={k}_{\mathrm{d}}\dot{e}(t)+{k}_{\mathrm{p}}e(t)+{k}_{\mathrm{i}}\underset{0}{\overset{tf}{\int }}e(t)\mathrm{d}t $$
(28)

with kp, ki, and kd mentioned as PID parameters.\( e(t)={q}_{\mathrm{d}}-q,\dot{e(t)}={\dot{q}}_{\mathrm{d}}-\dot{q.} \)

qd and q are the desired and actual position of the robot articulations. \( {\dot{q}}_{\mathrm{d}} \) and \( \dot{q} \) are the desired and actual speed of the robot articulations.

According to Eq. (26)

$$ {U}_n=\lambda \operatorname{sign}\left({k}_{\mathrm{p}}e(t)+{k}_i\int e(t)\mathrm{d}t+{k}_{\mathrm{d}}\dot{e(t)}\right) $$

To calculate Ueq, it is necessary that\( \dot{S}(t)=0 \)

$$ {\displaystyle \begin{array}{l}{k}_{\mathrm{p}}\dot{e}(t)+{k}_{\mathrm{i}}e(t)+{k}_{\mathrm{d}}\ddot{e}(t)=0.\\ {}\ddot{e}(t)={k_{\mathrm{d}}}^{-1}\left({k}_{\mathrm{p}}\dot{e}(t)+{k}_{\mathrm{i}}e(t)\right)\end{array}} $$

with

$$ \ddot{e}(t)={\ddot{q}}_{\mathrm{d}}-\ddot{q} $$
$$ \ddot{q}=M{(q)}^{-1}\left({U}_{\mathrm{eq}}-H\left(q,\dot{q}\right)\dot{q}-G(q)-F\left(\dot{q}\right)\right)={\ddot{q}}_{\mathrm{d}}+{k_{\mathrm{d}}}^{-1}\left({k}_{\mathrm{p}}\dot{e}(t)+{k}_{\mathrm{i}}e(t)\right) $$
$$ {U}_{\mathrm{eq}}=M(q)\left({\ddot{q}}_{\mathrm{d}}+{k_{\mathrm{d}}}^{-1}\left({k}_{\mathrm{p}}\ \dot{e}(t)+{k}_{\mathrm{i}}e(t)\right)\right)+H\left(q,\dot{q}\right)\dot{q}+G(q)+F\left(\dot{q}\right) $$

Finally, the PID-SMC torque presented as in [18], with the demonstration of the Lyapunov stability condition, becomes

$$ U=M(q)\left({\ddot{q}}_{\mathrm{d}}+{k_{\mathrm{d}}}^{-1}\left({k}_{\mathrm{p}}\ \dot{e}(t)+{k}_{\mathrm{i}}e(t)\right)\right)+H\left(q,\dot{q}\right)\dot{q}+G(q)+F\left(\dot{q}\right)+M(q){k_{\mathrm{d}}}^{-1}\ \lambda \operatorname{sign}\left({k}_{\mathrm{p}}\ e(t)+{k}_{\mathrm{i}}\underset{0}{\overset{tf}{\int }}e(t)\mathrm{d}t+{k}_{\mathrm{d}}\dot{e}(t)\right) $$
(29)

5 Simulation and Results

The main goal of this work is to optimize the parameters of SMC with PID surface for the trajectory control of 2DOF robot manipulator by the minimization of ITAE and ISTE objective functions mentioned as

$$ {J}_1=\mathrm{ITAE}=\underset{t1}{\overset{tf}{\int }}\left|e(t)\ \right|\mathrm{d}t $$
(30)
$$ {J}_2=\mathrm{ISTE}=\underset{t1}{\overset{tf}{\int }}e{(t)}^2\mathrm{d}t $$
(31)

The parameters of the robot that have been taken in application are m1 = 10 kg, m2 = 5 kg, l1 = 1 m, l2 = 0.5 m, and the gravity g = 9.8 m/s2. First, we apply the algorithms described above to tune SMC controller. The objective function values for different optimization algorithms obtained with ITAE and ISTE criteria, defined in Eqs. (30) and (31), respectively, have been shown in Table 1.

Table 1 Cost function for the first and second articulation without disturbance
Full size table

It can be seen from the Table 1 that ALO algorithm gives minimum to the objective function compared with those of GWO, which means that ALO algorithm gives the best optimum that has minimum objective function better then GWO algorithm. The corresponding optimum parameters of PIDSMC were recapitulated in Table 2.

Table 2 SMCPID parameters for the first and second articulation
Full size table

Figure 1 shows the control input applied to the first and second articulations obtained so far by both optimization algorithms. In order to avoid the chattering effect of the “sign” function, used in Eq. (29), the latter is replaced by the “tanh” (hyperbolic tangent) function. It can be seen from Fig. 2 that the resulting torque was almost close for both chosen criteria and the two optimization algorithms.

Fig. 1
figure 1

Control torque of link 1 and link 2 with (sign) function ITAE criteria

Full size image
Fig. 2
figure 2

Control torque signal of SMCPID controller with (tanh) function: (a) ISTE criteria and (b) ITAE criteria

Full size image

Figures 3 and 4 show the error of the robot manipulator to track the desired trajectory by the minimization of ISTE and ITAE criteria, respectively. We can see from the figures that ALO algorithm, which has smaller cost function, outperforms GWO algorithm even if we change the objective function. The convergence curve of the used functions was represented in Fig. 5. The corresponding position of robot manipulator controlled by SMCPID controller optimized by the two algorithms was shown in Fig. 6.

Fig. 3
figure 3

Tracking error of both articulations with ISTE criteria and (tanh) function

Full size image
Fig. 4
figure 4

Tracking error of both articulations with ITAE criteria and (tanh) function

Full size image
Fig. 5
figure 5

Convergence curve of cost function: (a) ITAE criteria and (b) ISTE criteria

Full size image
Fig. 6
figure 6

Position of two articulations controlled by SMCPID controller with (tanh) function: (a) ITAE criteria and (b) ISTE criteria

Full size image

6 Conclusion

In this paper the optimization of the SMC with PID surface was realized with new techniques of optimization called ALO and GWO algorithms; the ALO presents more robustness in trajectory tracking control of 2DOF robot manipulator, regarding the convergence curve of the cost function, even if we change the objective function. From the observations of the simulations, we can realize the benefits of using evolutionary algorithms to tune the controller parameters than the traditional methods, especially when the system is highly nonlinear or in presence of disturbances where an online optimization is recommended.