Keywords

Latent Variable Models in Cognitive Science

Latent variable models have a long tradition in cognitive science (e.g., Hertzog and Schaie 1986; Sternberg 1978; see also Cochrane and Green, this volume) and offer characteristics which are particularly useful for studying cognitive performance. They allow not only to differentiate true score and error variance of a construct, but also to separate important sources of variance in cognitive tasks. For example, working memory updating tasks (Salthouse et al. 1991, see also Könen et al., this volume) require the continuous updating of the status of multiple stimuli (e.g., of spatial movements of multiple objects or of simple calculations with multiple numbers) before the final results must be recalled. Variance in this task performance can thus be attributed to task-specific (stimuli types), paradigm-specific (continuous updating), and ability-specific effects (simultaneous storage and processing). For almost all types of research questions, it is informative to know whether an effect of interest is valid on the ability level (e.g., working memory as system for simultaneous storage and processing, Baddeley and Hitch 1994), or is based on a specific mechanism which is captured by selected task paradigms (e.g., updating), or is task specific (e.g., updating of letters). Because a latent variable is equivalent to whatever is common among its indicators (and not a combination of its indicators; Rhemtulla et al. 2019), using different established task paradigms from more than one domain (spatial, numerical, verbal) and/or modality (e.g., visual, acoustic) as indicators for a latent variable allows for inferences on a cognitive ability level. For example, a latent variable with diverse working memory tasks (different paradigms and domains/modalities) as indicators captures simultaneous storage and processing as it is their central common requirement (Fig. 1). In this case, paradigm- and task-specific variances are considered an indicator-specific measurement error and are thus separated from the latent ability variance.

Fig. 1
A label working memory is categorized into Y 1 e 1, Y 2 e 2, and Y 3 e 3 via 1, L 2, and L 3, respectively.

Confirmatory factor model of a cognitive ability, for example, working memory. The circle represents a latent variable, squares represent observed variables, asterisks represent estimated parameters, and the triangle represents mean- and intercept-information (dashed lines are intercepts). For model identification, the first factor loading is fixed to one. Factor loadings (L2, L3), intercepts (i2, i3), and error terms (e1, e2, e3) are estimated. Observed indicator variables (Y1–Y3) could be, for example, a spatial updating, numerical n-back, and verbal complex span task (see Wilhelm et al. 2013, for task descriptions)

Full size image

Using tasks of the same paradigm but from different domains and/or modalities as indicators of a latent variable supports inferences about the central mechanism assessed by this paradigm. For example, updating is the central common requirement of spatial, numerical, and verbal updating tasks. This demonstrates how latent variable modeling supports testing effects on the level of interest in cognitive psychology. More general introductions highlight that many psychological constructs are inherently latent (i.e., not directly observable; Borsboom 2008, for details) and should be represented accordingly in statistical analyses.

The cognitive training literature could profit from an increased application of latent variable models. As Noack et al. (2014) argue, if training programs aim at improving a cognitive ability, then this ability should be theoretically defined and represented as latent. Its indicators should be multiple heterogeneous transfer tasks (i.e., non-trained tasks), which are sampled from the theoretically determined task space (Little et al. 1999). This strengthens claims of ability improvements as it rules out task-specific effects as alternative explanation for performance improvements, such as the development and automatization of task-specific strategies. Controversies in the cognitive training literature about the presence (Au et al. 2015, 2016; Karbach and Verhaeghen 2014) or absence (Melby-Lervåg and Hulme 2016; for details see Guye et al., this volume; Könen et al., this volume) of far transfer effects (i.e., improvements in cognitive functions other than the trained one/s) could also be addressed and possibly solved on the latent ability level.

In this chapter, we focus on a selected class of statistical models for analyzing latent change: latent change models. Latent change models are a particularly useful framework for cognitive training studies because they are especially eligible for typical applications with two or three groups (e.g., training, active control, passive control) and two or three time points (pretest, posttest, if applicable follow-up). Hence, they have been increasingly applied in the training literature over the last decade (e.g., McArdle and Prindle 2008; Schmiedek et al. 2010, 2014; Zelinski et al. 2014). Below, we present an introduction to latent change modeling and important concepts (e.g., measurement invariance) and further discuss possible practical challenges and limitations.

Introduction to Latent Change Modeling

Latent change models (McArdle and Hamagami 2001; for an overview see McArdle 2009) are also called latent change score models, latent difference (score) models, and latent true change models. They can be estimated as multiple-group latent change models and allow analyzing latent variables and latent changes in these variables across both time points and groups. Latent change models utilize a set of fixed coefficients (fixed to 1) to define a later measurement occasion (Fig. 2: f[2]) as the sum of an earlier occasion (f[1]) and the difference (Δf[2–1]) between both: f[2] = f[1] + Δf[2–1](McArdle 2009). The change between two time points (Δf[2–1]= f[2] – f[1]) is represented as a latent variable with a mean (i.e., average change), a variance (i.e., individual differences in change), a covariance with the initial factor f[1] and, if applicable, covariances with other variables in the model. Such a model allows estimating latent means, latent intraindividual mean changes, and interindividual differences in both. If a latent variable is considered free of measurement error at two time points (e.g., pretest and posttest) then the latent change between both is also considered free of measurement error (cf. McArdle and Prindle 2008). Thus, analyzing latent change scores is preferable to analyzing observed difference scores (Trafimow 2015, for a review of the latter).

Fig. 2
A label change is categorized into pretest and posttest with pretest and posttest categorized into Y 1 e 1, Y 2 e 2, and Y 3 e 3 via 1, L 2, and L 3, respectively.

Latent change model with strict measurement invariance across pretest and posttest. Circles represent latent variables, squares represent observed variables, asterisks represent estimated parameters, and the triangle represents mean- and intercept-information (dashed lines are intercepts). Parameters with the same name are constrained to be equal (are estimated on the same unstandardized value). For model identification, the first factor loading of each latent variable is fixed to one. Correlated error terms of the same indicator across time are allowed (exemplary shown for e3). Factor loadings (L2, L3), intercepts (i2, i3), and error terms (e1, e2, e3) are constrained to be equal across time. Observed indicator variables are named Y1–Y3

Full size image

As needed, models can include multiple latent change variables, for example, to capture the changes between pretest and posttest (e.g., Δf[2–1]) and between posttest and follow-up (e.g., Δf[3–2]). The latent mean score could increase over one period and be stable or even decrease over the next because the direction of change between the measurement occasions is independent. This is especially suitable for cognitive training studies, in which stability, decrease, or increase of transfer effects at follow-up is possible (the latter, for example, due to daily life training benefits). For example, transfer effects of a broad cognitive training were significantly reduced at a 2-year follow-up (in comparison to transfer at posttest) for episodic memory but not for reasoning (Schmiedek et al. 2014), which was analyzed with latent change models. Further, both latent change variables can have differential predictors, which is crucial, because the factors contributing to training-related gains may not be same as the factors contributing to maintenance after training.

As in all structural equation models with latent variables, one must evaluate how well the hypothesized model fits the observed data, usually with a χ2-test (chi square test) and multiple descriptive fit indices such as the Comparative Fit Index (CFI), the Root Mean Square Error of Approximation (RMSEA), and the Standardized Root Mean Square Residual (SRMR); see West et al. (2012) for details. An introduction to the statistical assumptions of structural equation modeling and common estimation methods (e.g., maximum likelihood estimation) can be found in Kline (2012). Particularly relevant in the context of latent change modeling are the assumptions that indicators are mutually uncorrelated after controlling for their common latent factor (i.e., local independence) and that relations between the indicators and other variables are attributed to relations between the common latent factor and those variables (e.g., Rhemtulla et al. 2019). However, an indicator usually correlates with itself over time over and above common latent factor correlations (e.g., in cognitive tasks due to task-specific effects). Thus, failing to represent these covariances in the model, for example, with correlated error terms (in Fig. 2 exemplary shown for parameter e3) or with method factors for the same indicator across time, can lead to biased estimations of structural relations and decreased model fit (e.g., Pitts et al. 1996). Generally, structural equation models are more flexible in testing and accounting for statistical assumptions than other statistical techniques (e.g., analysis of variance). For example, non-normality in the data distribution can be addressed by using robust estimation methods (Lei and Wu 2012, for details). Measurement invariance (across experimental groups and time points) and statistical power are discussed in later sections of this chapter. More detailed descriptions of latent change models with code examples are available in the literature (e.g., Ghisletta and McArdle 2012; Kievit et al. 2018; Klopack and Wickrama 2019).

Testing the Effectiveness of Training Programs

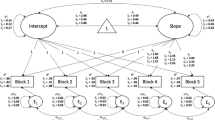
In randomized controlled trials, group mean differences between experimental and adequate control groups can serve as estimates of average causal treatment effects (Holland 1986; Schmiedek, this volume for details). When cognitive training studies are analyzed with multiple-group latent change models (Fig. 3), one can test for any training-related differences by comparing the fit of the model (with a Δχ2-test, i.e., chi square difference test) when a parameter is either constrained to be equal or free to vary across the training group and an adequate control group (McArdle and Prindle 2008).

Fig. 3
Two schematics are titled the training and control groups. The components change E G and C G are categorized into pretest E G, post-test E G, and follow-up E G in the training group and pretest C G, post-test C G, and follow-up C G in the control group.

Multiple-group latent change model with strict measurement invariance across group (training, control) and time (pretest, posttest, follow-up). Circles represent latent variables, squares represent observed variables, asterisks represent estimated parameters, and the triangle represents mean- and intercept-information (dashed lines are intercepts). Parameters with the same name are constrained to be equal (are estimated on the same unstandardized value). For model identification, the first factor loading of each latent variable is fixed to one. Correlated error terms of the same indicator across time are allowed (exemplary shown for e3). Factor loadings (L2, L3), intercepts (i2, i3), and error terms (e1, e2, e3) are constrained to be equal across groups and time. Observed indicator variables are named Y1–Y3

Full size image

One can test for average group effects by constraining the means of the latent change between the pre- and posttest (Δf[2–1]) of a training or transfer variable to be equal in the training group and control group (for an example see Stine-Morrow et al. 2014). If such a constraint significantly decreases model fit, the groups significantly differ in the latent change between the pretest and posttest. Latent effect sizes can be calculated equally as Cohen’s d by dividing the latent mean differences by the latent pooled standard deviations at pretest (when analyzing pretest and posttest, for an example see Schmiedek et al. 2014) or posttest (when analyzing posttest and follow-up). Please note that latent standard deviations might not be included in the output of software packages but can be easily calculated based on the provided variances. Alternatively, standardized indicators simplify the interpretation of latent means and latent mean changes (e.g., standardized to a T score distribution based on the pretest means and standard deviations as in Stine-Morrow et al. 2014).

It is possible that a training program has significant mean group effects on some indicators of a latent variable, but this effect is not valid on the latent level, which means that the common factor does not capture the effect (e.g., Estrada et al. 2015). Possible explanations can be substantive (e.g., task- or paradigm-specific training effects, such as the development and automatization of specific strategies) or more methodological (e.g., cognitive tasks differ in their reliability and sensitivity to change). At the same time, an effect can be significant on a latent level but not present in all indicators (e.g., Schmiedek et al. 2010). A solution to this issue is to report the average group findings on both a latent and an observed level (e.g., Schmiedek et al. 2010).

After this introduction to testing the effectiveness of training programs with latent change modeling, we also discuss two approaches which are no causal tests of cognitive training effects. First, the so-called responder analyses allow no causal inferences about cognitive training effects (Tidwell et al. 2014, for details). Applications of responder analyses aim at testing the effectiveness of training regimes for subgroups with specific characteristics. Individuals are classified on posttest (e.g., in high vs. low values) or change scores (e.g., more vs. less improvement, i.e., high and low responders) of an outcome variable and this classification is used as predictor of change in another outcome variable. Although latent change models are generally well-suited for predicting change, caution is necessary with responder analyses. Due to the post-hoc classification, they allow no clear distinction and attribution of cause and effect (see Tidwell et al. 2014 for more information).

Second, it can be informative to test for correlated gains on training and transfer scores because it is often reasonable to assume that individuals who benefit the most on the trained tasks are more likely to be the ones who demonstrate transfer to non-trained tasks (e.g., Zelinski et al. 2014). Correlated gains can descriptively support interpretations of training effects established on the mean group level, but they are no test of training effects. Correlated gains can be significant regardless of the group means (i.e., regardless of training-related improvements) because the magnitude of a correlation is invariant to linear transformations of the variables. In line with this, simulation studies demonstrated that transfer can be valid without any correlation in gain scores and correlated gain scores do not necessarily guarantee transfer (Jacoby and Ahissar 2015; Moreau et al. 2016).

Measurement Invariance

To be able to compare scores on a variable such as performance in a cognitive task across experimental groups and time (measurement occasions), the measurement needs to be equivalent (i.e., invariant) across groups and time (e.g., Widaman and Reise 1997). This applies for all types of variables, observed as well as latent variables. In most cases, it can only be assumed when using classical statistical procedures (e.g., analysis of variance) but can be explicitly tested and represented in models with latent variables. In training studies, one would typically test measurement invariance across groups first, separately for each measurement occasion, and then invariance across time (the latter in a multiple-group model were the invariance across groups is held constant). The advantage of this consecutive approach is that findings of non-invariance are directly attributable to either group or time. In a randomized controlled trial, measurement invariance across experimental groups at pretest/baseline is inherently expected due to the random assignment to the groups (Pitts et al. 1996) and any descriptive differences are the result of chance rather than bias (Moher et al. 2010).

The classical procedure of establishing measurement invariance consists of four steps (suggested by Meredith 1993; Widaman and Reise 1997), which are hierarchically ordered and are tested by comparing increasingly constrained models. The procedure is the same regardless of whether invariance across groups or time is investigated (which is why “groups or time” is used in the following). At first, configural invariance (the equivalence of model form) is established if the factors across groups or time have the same pattern of fixed and free loadings. Second, metric invariance or weak factorial invariance (the equivalence of factor loadings) is established if constraining the unstandardized factor loadings (see Fig. 3: parameters L2 and L3) to be equal across groups or time does not result in a substantial drop of model fit compared to a model with only configural invariance. Third, scalar invariance or strong factorial invariance (the equivalence of intercepts or thresholds) is established if additionally constraining the unstandardized intercepts (Fig. 3: parameters i2 and i3) or thresholds to be equal across groups or time does not result in a substantial drop of model fit compared to a model with only metric invariance (continuous indicators have intercepts, categorical indicators have thresholds). Scalar invariance implies that all substantial mean differences (across groups or time) in the indicators are captured by and attributable to the common latent construct, a necessary condition to compare latent means across groups or time (Widaman and Reise 1997). Fourth, strict invariance (the equivalence of residuals) is established if additionally constraining the unstandardized residuals (Fig. 3: parameters e1, e2, and e3) to be equal across groups or time does not result in a substantial drop of model fit compared to a model with only scalar invariance. This implies that all substantial (co)variance differences (across groups or time) in the indicators are captured by and attributable to the common latent construct (Widaman and Reise 1997). Across these four steps, the drop of model fit can be evaluated with a Δχ2-test (chi square difference test) and with descriptive fit indices (e.g., Cheung and Rensvold 2002; Meade et al. 2008).

Taken together, scalar measurement invariance is the necessary condition to compare latent means across groups or time and thus for testing the effectiveness of training programs on a latent level. Strict measurement invariance is even preferable as it implies that all substantial mean and (co)variance differences in the indicators across groups and time are captured by and attributable to the common latent construct, which supports their substantive interpretation. For example, comparing predictors of latent variables across groups or time is strengthened by strict measurement invariance. Finally, the model used for hypotheses testing should include invariance constraints across group and time (e.g., Fig. 3; for an empirical example see Schmiedek et al. 2010).

In case of violations of invariance (i.e., non-invariance), one should consider possible reasons for the violations in the given study, which can be practical (e.g., differential recruitment strategies for the training and control group) or theoretical (e.g., the relation of a task with the construct changed because the processes involved in task performance changed during skill acquisition, Ackerman 1988). There is no generally advisable strategy for all training studies, neither dropping the problematic indicator/s or refraining from analyzing the construct nor releasing the invariance constrains on the problematic indicator/s or continuing to impose all invariance constrains. The first two options are a threat to content validity (e.g., Pitts et al. 1996), and the latter two options can result in biased parameter estimates in the model, which are not necessarily indicated by the overall model fit (e.g., Clark et al. 2018). The strategy should depend on the specific research question and the specific measurement instruments used. Most importantly, one should compare and report whether the main findings and conclusions depend on this choice (i.e., are sensitive or not). Finally, the four steps described here are the current standard approach in psychology (Putnick and Bornstein 2016), but several alternatives for testing measurement invariance exist (e.g., Tay et al. 2015 used item-response theory; Van de Schoot et al. 2013 used a Bayesian approach).

Statistical Power Considerations

Simulations with the Monte Carlo method are the state of the art for estimating power in latent change modeling (Muthén and Muthén 2002, for a general introduction; Zhang and Liu 2019, for details on latent change modeling). Easy rule-of-thumbs such as “at least 10 or 20 cases per variable” can be misleading and should not be applied (e.g., Wolf et al. 2013). However, user-friendly online tools have been recently developed for estimating power in latent change modeling (e.g., Brandmaier et al. 2015 [www.brandmaier.de/lifespan]; Zhang and Liu 2019 [https://webpower.psychstat.org]). Still, collecting the basic information needed for power analyses (e.g., information on expected means and co/variances) could be difficult and might require a prestudy. Further, more research on the interplay of factors determining statistical power in latent change models is needed. Most studies investigated latent growth curve models (e.g., Hertzog et al. 2006, 2008; Rast and Hofer 2014), but one cannot generalize findings on statistical power to different classes of developmental models (cf. Hertzog et al. 2006) mostly because of differences in the underlying functions of change. Generally, low power represents not only a reduced chance to find a true effect, but also reduces the likelihood that a statistically significant finding reflects a true effect (cf. Button et al. 2013). Thus, estimating the statistical power of finding the main effects of a study is always worth the effort although this effort is admittedly likely higher for latent change modeling than for traditional approaches such as analysis of variance. Notably, regardless of power, when using frequentist statistics, a nonsignificant finding does not allow to infer the absence of an effect (e.g., Aczel et al. 2018; see De Simoni and Von Bastian 2018, for Bayesian evidence on the absence of effects).

Predictors and Correlates of Change Variables

The effectiveness of training programs is usually the first research question addressed in cognitive training studies. However, as Willis and Schaie (2009) pointed out, “programmatic intervention research should be aimed at the broader goal of answering a series of theoretically important empirical questions” such as “What specific mechanisms, processes, or components of the intervention are responsible for the desired change? What individual difference variables are associated with responsivity to change? How can the change be maintained?” (cf. Willis and Schaie 2009, p. 377). Latent change modeling offers some unique opportunities to address these and related questions because changes between two time points (e.g., pretest and posttest, posttest and follow-up) are represented as latent variables with means (i.e., average changes) and variances (i.e., individual differences in changes). If the variance of a latent change variable is significantly different from zero, it is reasonable to assume that this variance is not only random noise but includes reliable individual differences in change. Analyzing predictors or correlates of latent change variables allows to identify if, for example, some features of an individual or the situation make training or transfer gains more or less likely. Whether predictors or correlates are analyzed should depend on the given research question, but it is important to keep in mind that the mean of a latent change variable, which is predicted by other variables, should be interpreted conditional on the regression paths (i.e., does not represent “raw” mean changes; cf. Kievit et al. 2018).

A typical predictor of change is individual baseline cognitive performance, for example, when testing compensation or magnification effects (see Karbach and Kray, this volume; Katz et al., this volume). A compensation effect predicts that individuals with lower baseline performance tend to profit more from a training (i.e., higher gains over time) whereas a magnification effect predicts that individuals with higher baseline performance tend to profit more (Lövdén et al. 2012, for details). For example, Karbach et al. (2017) found that individuals with lower cognitive performance at baseline showed larger training and transfer benefits of an executive control training. They used multiple-group latent change models and compared models with a Δχ2-test (chi square difference test) in which the relation of baseline performance and change was either constrained to be equal or free to vary across the training and active control group. The relation of baseline and change was significantly higher in the training group compared to the active control group, which strengthens a substantive interpretation (e.g., because regression to the mean should occur in both groups, see Marsh and Hau 2002, for details on regression to the mean artifacts).

Other possible predictors are, for example, age, years of education, family income, need for cognition, or personality (e.g., Stine-Morrow et al. 2014; Zelinski et al. 2014). One might consider different predictors for different change variables (Fig. 3: Δf[2–1] and Δf[3–2]) because the factors contributing to training-related gains may not be the same as the factors contributing to maintenance after training. Of course, confirmatory and exploratory tests need to be explicitly distinguished, and a suitable correction of the statistical alpha level should be considered if multiple predictors or correlates are tested (e.g., Bonferroni-Holm method).

Further, it can be informative to test for correlated gains on training and transfer scores (e.g., McArdle and Prindle 2008; Zelinski et al. 2014) because it is often reasonable to assume that individuals who benefit the most on the trained tasks could also be the ones who demonstrate transfer to non-trained tasks. For example, Zelinski et al. (2014) analyzed correlations between gains in training and in transfer tasks in older adults with latent change models. Overall, correlations of training and transfer gains were mostly found for tasks with overlapping task demands, which is in line with an overlapping task demand model of transfer (cf. Zelinski et al. 2014). Notably, the effects were valid with and without controlling for covariates (age and education) related to both training and transfer gains. Taken together, predictors and correlates of latent change variables can provide valuable correlative information about possible mechanisms moderating (e.g., compensation or magnification effects) or fostering training outcomes (e.g., overlapping task demands). A more general introduction to analyzing predictors and correlates of intervention-related change is currently under review (Könen & Karbach, 2020).

Conclusion

On the one hand, latent change modeling of cognitive training data is arguably more time consuming than traditional analyses (e.g., analysis of variance), for example, because measurement invariance must be tested and the fit of the hypothesized model to the data must be evaluated. On the other hand, however, latent change modeling offers unique opportunities, which can enhance the practical and theoretical understanding of training and transfer effects. For example, it allows separating task-, paradigm-, and ability-specific effects and testing predictors and correlates of latent change variables. With this, one can not only evaluate whether a training program works on average but also understand which individual and situational characteristics make individual outcomes more likely.