Keywords

1 Introduction

A classical definition of the geological faults is that they are discontinuities of sedimentary, metamorphic or magmatic rock bodies. Thus, no physical properties are assigned to a fault; however, real geological faults have a complex structure which includes main fault body (“fault core”) and fractured or damage zones around [7, 25]. In particular, damage zone may be highly fractured, thus, permeable especially for carbonates [16], or it can be an impermeable due to the presence of deformation bonds which is typical for the sandstones [10]. Such differences of the local permeability near faults may strongly affect the reservoir performance [3]. Thus a detailed representation of the fault and damage zone is required for efficient oil and gas exploration.

Very often, to do field observations or laboratory studies of the real fault is difficult or impossible due to some natural reasons. Thus, numerical simulation is a reliable and efficient way to investigate the peculiarities of the structure’s forming and tectonic movement process. There are numerous techniques to simulate finite deformations in geological formations either grid-based methods such as finite differences [11], finite elements [13], boundary elements [26] or by meshless approaches also known as discrete elements method (DEM) [12, 22]. The letter is preferred because no predefined crack or fault geometry is needed for simulation. However, particle-based methods are more computationally intense and require calibration of the particle properties to match the mechanics of the whole body [22]. Despite this, the particle-based methods are incredibly flexible and can be used to generate multiple statistical realizations of the fault zones and study statistical features of the strongly deformed and highly-distorted zones. In our opinion, meshless methods of geological faults formation simulations can be used to generate faults geometries in realistic environments. After that simulated faults can be introduced in geological models which are used for seismic modeling and imaging [17, 28], moreover use advanced simulation techniques such as local mesh refinement [18, 21] allow studying seismic responses of the fine structure of near-fault damage zones.

In this paper, we present an algorithm based on the Discrete Elements Method (DEM). This approach is based on the media representation by a set of discrete particles. These particles interact as stiff elastic bodies according to the mechanical rules; i.e., elastic and frictional forces affect each particle, that leads to the particle movement according to the Newton mechanics [14]. Computation of the forces affecting a particle includes a high number of floating point and logical operations; thus it is computationally intense and hard to implement on CPU, using vectorization, etc. As a result, the efficiency of the CPU based realizations of DEM is low, and computation time to solve even a 2D problem may be as long as several thousand node-hours. On the contrary, GPU architecture is more appropriate for DEM implementation, because it can efficiently handle a big number of flops with a small amount of memory involved in computations.

2 Discrete Elements Method

To simulate the tectonic movements causing finite deformations and geological fault formation in the Earth’s crust we use the discrete element method, following [14, 23]. In this approach, the media is represented as an assembly of individual particles with a particular geometry and physical properties. Each particle is characterized by the coordinate of its center \(\varvec{x}^j\), radius \(R_j\), repulsion and attraction bulk moduli \(K_r^{+}\) and \(K_r^{-}\) respectively, tangential sliding stiffness \(K_s\), and two friction coefficients \(\mu _s\) is the static one and \(\mu _d\) is the dynamic friction coefficient. Having set these parameters, one may define the interaction forces between two adjoint particles.

2.1 Forces Computation

Consider two particles with the numbers i and j, with the coordinates \(\varvec{x}^i\) and \(\varvec{x}^j\) and radii \(R^i\) and \(R^j\) respectively. Particle j acts on particle i with the normal elastic forces:

$$\begin{aligned} \varvec{F}^{ji}_{n}= \left\{ \begin{array}{ccc} K_r^{-}(R^i+R^j-\Vert \varvec{X}^{ji}\Vert )\varvec{n}^{ji}, &{} R^i+R^j-\Vert \varvec{X}^{ji}\Vert>0, &{} repulsion, \\ K_r^{+}(R^i+R^j-\Vert \varvec{X}^{ji}\Vert )\varvec{n}^{ji}, &{} 0\le R^i+R^j-\Vert \varvec{X}^{ji}\Vert \le r_0, &{} active\ \ bond, \\ 0, &{} R^i+R^j-\Vert \varvec{X}^{ji}\Vert > r_0, &{} no\ \ bond, \end{array} \right. \end{aligned}$$
(1)

where \(r_0\) is the bond length, typically chosen equal to \(0.05(R_i+R_j)\), vector \(\varvec{X}^{ji}=\varvec{x}^i-\varvec{x}^j\) connects the centers of the particles and directed from particle j to particle i, vector \(\varvec{n}^{ji}=\varvec{X}^{ji}/\Vert \varvec{X}^{ji}\Vert \) is the unit vector directed from the centers of particle j to the center of particle i or normal vector, because it is normal to the contact plane. Note, that we use the model of linear elastic particles interaction and assume that the repulsion and attraction bulk moduli coincide, which is mainly valid for geomaterials across a wide range of scales.

Additionally frictional forces are taken into account if two particles are in a contact [23]:

$$\begin{aligned} \varvec{F}^{ji}_{t}= \left\{ \begin{array}{ccc} -K_s\delta _t \varvec{t}^{ji}, &{} K_s\delta _t\le \mu ^s\Vert \varvec{F}_n^{ji}\Vert , &{} static\ \ friction, \\ -\mu ^d \Vert \varvec{F}_n^{ji}\Vert \varvec{t}^{ji}, &{} K_s\delta _t > \mu ^s\Vert \varvec{F}_n^{ji}\Vert , &{} dynamic\ \ friction, \\ \end{array} \right. \end{aligned}$$
(2)

where \(K_s\) is the tangential sliding stiffness, usually considered to be equal to bulk modulus; i.e., \(K_s=K_r\), vector \(\varvec{t}^{ji}\) is the unitary tangential vector directed along the projection of the relative velocity onto the contact plane of two particles; i.e.,

$$\begin{aligned} \begin{array}{cc} \varvec{t}^{ji}=\frac{\varvec{v}^{ji}-(\varvec{v}^{ji},\varvec{n}^{ji})\varvec{n}^{ji}}{\Vert \varvec{v}^{ji}-(\varvec{v}^{ji},\varvec{n}^{ji})\varvec{n}^{ji}\Vert },&\varvec{v}^{ji}=\varvec{v}^i-\varvec{v}^j. \end{array} \end{aligned}$$
(3)

In this notations \(\varvec{v}^{ji}\) is the relative velocity of the particle i with respect to particle j. Parameter \(\delta ^{ji}\) denotes the tangential displacement of the contact point from its initial position. Tangential forces provided by formula (2) satisfy the Coulombs law; i.e., the static friction governs the particles interaction if the forces as below a critical value. If the tangential forces exceed the critical dynamical friction proportional to normal force is applied. Typically the static friction is much higher than the dynamical one.

Additionally, an artificial dissipation is introduced in the system to prevent elastic waves from propagating through the model and ensuring the media to remain stable at infinite instants:

$$\begin{aligned} \varvec{F}_d^i=-\nu \varvec{v}^i, \end{aligned}$$
(4)

where \(\nu \) is an artificial viscosity.

The Earth’s crust also remains under gravitational forces which are accounted as

$$\begin{aligned} \varvec{F}_g^i=M_i g \varvec{e}_3, \end{aligned}$$
(5)

where \(g=9.8\) m/s is the gravitational constant, \(\varvec{e}_3=(0,0,1)^T\), and \(M_i\) is the mass of the considered particle.

To compute the total forces acting at a particle one needs to account the forces due to interactions with all the neighbors, plus artificial dissipation, plus gravitational forces, as a result, one gets:

$$\begin{aligned} \varvec{F}^{i}=\sum _{j\in J(i)}\left[ \varvec{F}^{ji}_n+\varvec{F}^{ji}_t\right] +\varvec{F}_d^i+\varvec{F}_g^i, \end{aligned}$$
(6)

where J(i) is the set of indexes of the neighbors of i-th particle.

2.2 Time Integration

Having computed all external forces acting at j-th particle one may recompute its position using classical mechanics principles:

$$\begin{aligned} M^i\frac{d^2 \varvec{x}^i}{dt^2}=\varvec{F}^{i}\left( t,\varvec{x}^i,\varvec{x}^j,\frac{d\varvec{x}^i}{dt},\frac{d\varvec{x}^j}{dt}\right) , \end{aligned}$$
(7)

where dissipative \(\varvec{F}_d^i\) and frictional forces \(\varvec{F}_t^{ji}\) explicitly depend on the particles velocities \(\varvec{v}^i=\frac{d\varvec{x}^i}{dt}\).

To numerically resolve system of Eq. (7) we use the Verlet-like scheme with the velocity half-step [15]. Assume coordinates, velocities, and thus forces of all particles are known at instant \(t=t^n=\tau \cdot n\), then they can be updated to the instant \(t^{n+1}\) by the rule:

$$\begin{aligned} \begin{array}{l} \frac{(\varvec{v}^i)^{n+1/2}-(\varvec{v}^i)^{n}}{\tau /2}=\frac{1}{M^i}\varvec{F}^i\left( t^{n},(\varvec{x}^i)^n,(\varvec{x}^j)^n, (\varvec{v}^i)^n, (\varvec{v}^j)^n\right) , \\ \frac{(\varvec{x}^i)^{n+1}-(\varvec{x}^i)^{n}}{\tau }=(\varvec{v}^i)^{n+1/2}, \\ \frac{(\varvec{v}^i)^{n+1}-(\varvec{v}^i)^{n+1/2}}{\tau /2}=\frac{1}{M^i}\varvec{F}^i\left( t^{n+1},(\varvec{x}^i)^{n+1}, (\varvec{x}^j)^{n+1},(\varvec{v}^i)^{n+1/2}, (\varvec{v}^j)^{n+1/2}\right) , \\ j\in J(i). \end{array} \end{aligned}$$
(8)

In case of no explicit dependence of forces on the velocities the scheme is the second order accurate, however if applied to the equation of motion for DEM, this scheme possesses only the first order of approximation.

To ensure the stability of the finite-difference scheme we use the time step as suggested in [15]

$$\begin{aligned} \tau \le 0.2 \frac{D_{min}}{V_{max}}, \end{aligned}$$
(9)

where \(R_{min}\) is the minimum diameter of the particles, and \(V_{max}\) is the maximal velocity of perturbation propagation in the system.

2.3 Boundary Conditions

Proper implementation of the boundary conditions is a challenging task for the particles-based methods. In our research, we deal with two types of boundary conditions. First, we impose the rigid boundary condition; i.e., the surface \(\varGamma _s\) is fixed, or its movement is prescribed. Moreover, it is stiff; thus the particles cannot penetrate through it. Formally, this type of boundary condition can be stated as follows. Assume a boundary \(\varGamma _s=\{\varvec{x}|x_2=x_2^B\}\). If a particle is close enough to the boundary; i.e., if for the j-th particle \(|x_2^j-x_2^b|\le R^j\), then \(F^{jB}_2=K_r^{-}(R^j-|x_2^j-x_2^b|)\).

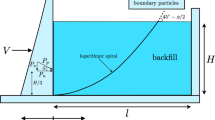
However, numerical implementation of this condition requires extra conditional operators. Thus it is worth implementing stiff-boundary as a series of particles, to make the simulation uniform either in the interior of the domain or near the boundary. To do so, we introduced the “boundary” particles with the same physical properties as those of the interior particles. However, we do not compute the forces acting on the “boundary” particles but allow the “boundary” particles to move according to a prescribed law. We specify the particular movement laws in the Sect. 4.

The second type of the boundary conditions is \(P_{over}=const\). This condition ensures the constant overburden pressure. Note that, condition \(P_{over}\) assumes that external forces act at the upper boundary of the domain \(\varGamma _p(t)\) along the normal direction to the boundary. This boundary is flexible, and it evolves in time; thus, to impose the boundary condition we need to follow the elements which form the upper boundary. This can be done, for example, by computing Voronoi diagrams for upper elements. However, such procedures are computationally intense. To overcome this difficulty, we suggest using the flexible membrane at the upper boundary [4, 29]. The idea of the approach is to introduce a layer of discrete elements so that the membrane elements are affected only by the normal forces.

If two adjoint membrane elements are interacting

$$\begin{aligned} \varvec{F}^{m,m\pm 1}_{n}= K_r(R^{m\pm 1}+R^m-\Vert \varvec{X}^{m,m\pm 1}\Vert )\varvec{n}^{m,m\pm 1}, \end{aligned}$$
(10)

if membrane element interacts with other elements

$$\begin{aligned} \varvec{F}^{mi}_{n}= \begin{array}{cc} K_r(R^i+R^m-\Vert \varvec{X}^{mi}\Vert )\varvec{n}^{mi}, &{} R^i+R^m-\Vert \varvec{X}^{mi}\Vert >0. \\ \end{array} \end{aligned}$$
(11)

It means that the adjoint membrane elements are bonded, and these bonds never bake, however no bonds of friction are considered when membrane elements interact with elements of other types. The membrane elements are ordered; thus it is easy to approximate constant pressure condition. If a membrane element with number m is considered then additional force, due to the pressure is

$$\begin{aligned} \varvec{F}_p^{m}=2PR^{m}\varvec{n}, \end{aligned}$$
(12)

where \(\varvec{n}\) is the vector normal to the boundary, which can be computed as:

$$ \varvec{n}=(x_2^{m-1}-x_2^{m+1},x_1^{m-1}-x_1^{m+1})^T, $$

the direction of the normal vector is defined uniquely due to the ordering of the membrane elements.

2.4 Output Parameters

Numerous parameters can be obtained as a result of discrete elements simulations. If rock properties are studied using uniaxial and triaxial stress tests, then the primary attention is paid to the distribution of the braked bonds [8, 19], stresses, and normal forces distribution [9] However, at the scale of the geological bodies a reliable parameter to determine fault zones is the strains distribution [1, 5, 14, 15, 24]. These strains can be further translated to the changes of physical parameters of rocks using the experimental laboratory measurements.

3 Implementation of the Algorithm

According to the general formulation of the particle-based methods, one has to compute the forces affecting each particle due to the interaction with all other particles. However, in geomechanical modeling by the discrete element method, for each particle only a small number of neighboring particles directly contact the considered one. The adjacency matrix is sparse, but it can evolve. Thus, two related problems should be solved. First, organizing the process of adjacency matrix construction (approximation). Second, computing forces and applying time stepping.

To construct the adjacency matrix, we suggest using the lattice method [20]. As it follows from the Eqs. (1) and (2), only directly contacting particles affect each other; thus, for each particle, the domain of dependence does not exceed \(2R_{max}+r_0\), where \(R_{max}\) is the maximal radius of the particles. Also, due to the stability criterion of the Verlet scheme, a single particle cannot move more than \(0.1R_{min}\) per a single time step, where \(R_{min}\) is the minimal radius over all particles. Thus, we can introduce a grid with the lattice size equal to \(2R_{max}+r_0\), so that each particle and all its neighbors belong to the same lattice of directly adjoint lattice. Now we can state the rule of adjacency matrix approximation - for each particle, all the particles belonging to the same or directly adjoint lattices are neighbors. In this case, we overestimate the number of connected particles but strictly simplify the process of the matrix construction.

The initial assignment of the particles to the lattices is performed by a sequential code by CPU. It is implemented particle-by-particle so that we determine the lattice number for considered particle and add the particle number to the list of particles for this lattice. This procedure is inapplicable under OMP of CUDA parallelization. Thus, the GPU implementation of the reassignment of the particles to the lattices is done lattice-by-lattice. The lattices are large enough, so that after one time step a particle may either stay in the same lattice or move to a directly adjoint lattice. Thus, to update the list of particles for each lattice, we need to check the particles which previously belonged to this lattice or the directly adjusted one. Similar ideas are used in the molecular dynamics and lattice Boltzmann methods but with different principles of lattices construction [2].

Computation of the forces and the numerical solution of the equation of motion is implemented on GPU. The parallelization is applied particle-by-particle so that a GPU core compute forces for one particle at a time.

4 Numerical Experiments

In this paper, we focus our attention on the effect of the direction and amplitude of tectonic movement on the geometry of the fault and damage zone. DEM-based simulations include uncertainties due to the particle’s positions and radii distributions. It means that for each scenario of the tectonic movements we need to perform a series of numerical simulations for different statistical realizations of the particles geometry distribution.

In all the experiments presented below, we use the following set of parameters. The size of the computational domain is 4000 m in horizontal and 500 m in the vertical direction. The repulsion/attraction modulus is 16 GPa, and same value is used for the tangential sliding stiffness. The coefficient of static friction is 0.8, which is typical for the majority of geomaterials, whereas the dynamic friction coefficient is 0.3, which is close to that of sandstone and limestone. We consider the bonds length proportional to the radii of the adjoint particles; i.e., \(r_0=0.05(R_j+R_i)\). We assume that the formation is buried at 3000 m; thus the overburden pressure of \(10^7\) Pa is applied at the top boundary of the model. The particles radii are homogeneously distributed from 1.25 to 2.5 m. So, the total number of elements is 390000.

We consider several scenarios of dipping normal tectonic movements with the dip angles equal to \(90^{\circ }\), \(75^{\circ }\), \(60^{\circ }\), \(45^{\circ }\), \(30^{\circ }\). Maximal vertical displacement is 100 m.

For each tectonic movement we simulate ten statistical realizations of the particles distributions; thus, 10 simulations are performed for each scenario. Also, we computed extra 20 realizations for the most common movement scenario with the dip angle equal to \(60^{\circ }\). Each simulation consists of two stages. First, the elements should be compacted under the overburden pressure and gravitational forces. This step takes about 60 % of the computational time. Second, the tectonic movements are applied. The total simulation time for one experiment (one realization) is about 8.7 h by a single GPU (NVIDIA Tesla M 2090).

We provide the strains distribution for each movement scenario in Figs. 1, 2 and 3. The main trend observed from the presented figures is that for big dip angles; i.e., for nearly vertical displacements no narrow fault cores are formed. When the dip angle gets smaller fault cores are formed (Fig. 1) and they are located within a narrow zone. Moreover, for low dip angles the form of the fault and its inclination is similar, thus might depend mainly on the medium properties rather than on the direction of tectonic movements. To verify this assumption, we perform clustering of the results and their statistical analysis in the following section.

Fig. 1.
figure 1

A single realizaton of hydrostatic (top) and shear (bottom) strains distribution in the fault zone for the displacement dip equal to \(30^\circ \).

Full size image
Fig. 2.
figure 2

A single realizaton of hydrostatic (top) and shear (bottom) strains distribution in the fault zone for the displacement dip equal to \(60^\circ \).

Full size image
Fig. 3.
figure 3

A single realizaton of hydrostatic (top) and shear (bottom) strains distribution in the fault zone for the displacement dip equal to \(90^\circ \).

Full size image

4.1 Clustering of the Results

Results of the numerical simulation tend to form narrow inclined faults if the dipping angle is small, whereas high dipping angles cause a wide V-shape damage zone. To quantify this observation, we applied k-means clustering of the computed strains distribution. Before processing to the formal analysis, we need to point out, that we performed two additional series of simulations (9 realizations in each series) corresponding to the tectonic movement dip angle equal to 60\(^\circ \). In total we have 27 statistical realizations corresponding to this scenario; however, we will still consider them as three independent series in our statistical analysis.

According to the Calinski-Harabasz Index [6] and the silhouette criterion [27] the optimal number of clusters of the considered data is two. We applied the k-means clustering technique to our data. We constructed clusters for each component of the strain tensor separately, as well as for all of them together. The panels in Fig. 4 represent the clustering results in two clusters applied to all components of the strain tensor. One may note that the displacement scenarios with dip angles equal to \(75^\circ \) and \(90^\circ \) form one cluster. This confirms the assumption that direction of the tectonic movement strictly affects the structure of the fault and near fault damage zone.

Fig. 4.
figure 4

Panels representing data clustering (two clusters) for all components of strain tensor. Left panel (A) corresponds to the optimal clustering with minimal distance, right panel (B) represents a case of local minimum of k-means functional. Different colors correspond to different clusters.

Full size image

5 Conclusions

We presented an algorithm for simulation of the Earth’s crust tectonic movements and formation of the geological faults and near-fault damage zones. The algorithms are based on the Discrete Elements Method, and it is implemented using CUDA technology. We used to simulate faults formation due to different scenarios of tectonic movements. We considered the displacements with dipping angles varied from 30 to 90 degrees; i.e., up to vertical throw. For each scenario, we performed simulations for some statistical realizations. According to clustering analysis shows that displacements with high (\(75^\circ \) and \(90^\circ \)) and low (\(30^\circ \) and \(45^\circ \)) dip angles form completely different geological structures. Nearly vertical displacements, high dip angles, form wide V-shaped deformation zones, whereas the flat displacements cause narrow fault-cores with rapidly decreasing strains apart from the fault core. Results of the presented simulations can be used to estimate mechanical and seismic properties of rocks in the vicinity of the faults and applied further to construct models for seismic modeling and interpretation, hydrodynamical simulations, history of matching simulation, etc.