Keywords

1 Introduction

The importance of the use of Bayesian methods as a natural methodology for implementation in Time Series Forecasting (TSF) has increased rapidly over the last decade. In particular, this technique provides a formal way to incorporate the prior information from the underlying process related with data generation before of its knowing. Then, this is seen as a resource in sequential learning and decision making, where it is possible to establish a direct relation between the exact results and the small samples. Moreover, the Bayesian paradigm takes into account all parameters and the uncertainty of the model [1], making relevant the relation between the predictive distribution and the sampling information, where the forecasting is allowed when all parameters are integrated based on a posterior distribution.

Commonly, the selection of a particular model is not specified by some theory or experience, and many adopted models can be trained with the purpose of obtaining that information [2]. Models comparison can be implemented based on a Bayesian framework through the so-called posterior odds, computed as the product of the prior odds and the Bayes factor. This Bayes factor measurement is obtained from any two models, estimated by the likelihood ratio of the marginal likelihood of two competing hypotheses represented by the models, quantifying the support of one model over another based on the available data.

Long short-term memory (LSTM) models are widely utilized for TSF because its architecture based on a special sort of recurrent neural network (RNN) [3, 4]. This kind of this artificial neural network (ANN) architecture is known due to the connections between units, which form a directed cycle. In this way, an internal state of the network is built up, which allows it to exhibit dynamic temporal behavior. In spite of the feedforward architecture of this network, their internal memory can process arbitrary sequences of inputs [5]. However, RNN are difficult to train using the stochastic gradient descent, according to the so-called “vanishing” gradient and/or “exploding” gradient phenomena. This limits the ability of simple RNN to learn sequences with relatively long dependencies [6], making that its employment was reconsidered. For this, proposals like vanilla RNN deal with the vanishing or exploding gradient problem, but remaining the long-term dependence problem, making very difficult the training [7]. Improving the mentioned problems, the LSTM introduces the gate mechanism to prevent back-propagated errors from vanishing or exploding problem, which has been shown to be more effective than conventional RNNs, preventing the overfitting and limitations with long-term sequences [8].

Applications of this kind of ANN can be seen in the work from Zhao et al. [9], which proposed a LSTM network for considering temporal–spatial correlation in traffic system. That ANN was composed of many memory units, comparing this architecture to other representative forecasting models, achieving a better performance. In addition, Kang et al. [10] employed the mentioned RNN to analyze the effect of various inputs settings on its performance. In [11] the authors used a model of ANN combined with a LSTM in a similar way that a Deep Neural Network (DNN), including the autocorrelation coefficients to improve the model accuracy and providing a better precision than traditional ones. Some recent works as in [12], where an adaptation of a LSTM to forecast sea surface temperature (SST) values was employed, including one day and three days information as past inputs. Then the RNN was compared to other models that employed information from weekly mean and monthly mean.

In this paper, a LSTM based on Bayesian Approach (LSTM-BA) method is proposed to predict time series data from well-known chaotic systems. The motivation to use this model is related to the property of this network with one full-connected layer to obtain a regression model for prediction. Also, the LSTM layer has been utilized to model the temporal relationship among time series data, using the Bayes information of the weights updated and a heuristic approach to adjust the number of training iterations. This requires the ability to integrate a sum of terms in the log joint likelihood using the factorized distribution. In some cases, the integral operations are not in closed form, which is typically handled by using a lower bound showed by Wang et al. [13], where a new method called improved Bayesian combined model.

This work is organized as follows: Section two describes LSTM with the proposed approach (RNN-BA) using Bayesian inference-based heuristic. Section three shows details about the architectures employed for forecasting and an experimental design. The fourth section offers results conducted throughout chaotic time series. Section five provides a discussion based on the used implementation. Finally, section six concludes about this work.

2 Recurrent Neural Networks: Long-Short Term Memory

Classical feedforward neural networks, whose connections are directed and without cycles, only maps the current input vector to output vector [14]. This represents a disadvantage because they cannot memorize previous input data, and in addition, a determination of an optimal time lags size cannot be obtained. The mentioned problems are increased due to the input data must be truncated into specific length for developing of the model, producing prediction results not desirable.

Opposite to the classical networks, the RNN allow cyclical or recurrent connections, mapping the complete historical input data to each output. At the same time, these recurrent connections provide a special aspect to memorize information from previous inputs that persists in the network’s internal state, influencing the network output. This attribute is useful when noisy signals or sequences with abrupt changes are treated, for example, chaotic series. Different applications have been developed with this architecture, which can change of complexity according to the number of units and connections. Likewise, for standard RNN architecture, the internal influence is given by the number of neurons in the hidden layer, which can decline or blowing up exponentially the value of the synaptic weights. This, according to the cycling behavior established by the recurrent connections. For this, some RNN models are trained with backpropagation through the time and real time recurrent learning for avoiding the vanishing and exploding error problem.

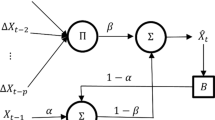
The main advantages of the LSTM are to model long-term dependencies and to determine the optimal time lags for TSF problems. These aspects are desirable for long-term future predictions specially, due to the lack of priori knowledge between samples. In addition, the problem of the sum of error signals increment, a proposal based on the constant error carrousel (CEC) was proposed in a first version. The LSTM architecture is modified, including a pair of gates, which can allow the flow from inputs to outputs. In the enhanced version, it adds a reset gate called forget gate [8], including the notion of memory cells as shown in Fig. 1 by the yellow blocks.

Fig. 1.
figure 1

Flow chart inside the LSTM RNN. (Color figure online)

Full size image

In the present proposal, a LSTM model is trained with focus on the exploration of solutions by employing a Bayesian heuristic method. In this way, an improvement given by the overfitting problem was searched [17]. Therefore, in order to make the topology of LSTM as simple as possible, it is important to delete unnecessary units, layers and connections, thus, to optimize the training and topology of RNN, we proposed a heuristic adjustment, as follows:

$$ 1 \le i_{t} \le 2\left( {H_{0} - KL} \right) $$
(1)
$$ H_{0} \le N_{p} \le KL + I_{x} $$
(2)

where lx is the dimension of the input vector, Np is the number patterns, and H0 is the initial value of hidden neurons. Then, a heuristic adjustment for the pair (it, Np), the number of iterations and patterns as function of the hidden units Ho and KL (Kullback-Leibler Information Criterion), according to the membership functions shown in Fig. 2. Finally, an approximation for the network weights and biases was developed, where all the model parameters were modelled as Gaussian distributions with a diagonal covariance. An exception for latent states, which was modelled as a Gaussian distribution with an almost diagonal covariance.

Fig. 2.
figure 2

Heuristic adjustment of (it, Np) in terms of KL after each epoch.

Full size image

3 Experimental Design

Experiments with data generated from an artificial chaotic systems, which were performed to obtain five common benchmark series with length of 1500 points. This length was chosen intentionally, for determining whether this a limitation in order to compare the model against other much simpler models with probable less overfitting.

For chaotic series, the generation of such aspect belongs to reaching the attractor. To do this, the system was allowed to evolve after one hundred samples, achieving the corresponding attractor. According to this, we assumed that the number of iterations guarantees the state of the dynamic system, ending the initial transient on the attractor. In spite of this, there are no reliability that the system will revisit future events similar to those observed during training.

3.1 Employed Datasets

For assessment of built models, seven datasets with artificial chaotic time series were used. Each of these series is describe next:

Mackey-Glass Series:

The dataset MG17 and MG30 are by sampling the Mackay-Glass (MG) equations, given by the expression (3), as follows:

$$ \dot{x}\left( t \right) = \frac{{ax\left( {t - \tau } \right)}}{{1 - x\left( {t - \tau } \right)^{c} }} - bx\left( t \right) $$
(3)

with a, b, c, τ setting parameters shown as follows in Table 1.

Table 1. Parameters to generate MG time series
Full size table

Logistic Time Series:

The dataset LOG01 and LOG02 series were mapped from logistic system and represent in (4), which is defined by:

$$ x\left( {t + 1} \right) = ax\left( t \right)\left[ {1 - x\left( t \right)} \right] $$
(4)

where a = 4, the iterations in Eq. (4) perform a chaotic time series (see Table 2).

Table 2. Parameters to generate LOG time series
Full size table

Henon Chaotic Time Series:

This time series can be constructed by following Eq. (5), however, it presents many aspects of dynamical behavior of more complicated chaotic systems.

$$ x\left( {t + 1} \right) = b + 1 - ax^{2} $$
(5)

where a and b were fixed as shown in Table 3. These same parameters were used in both cases.

Table 3. Parameters to generate HEN time series
Full size table

Lorentz Time Series:

The Lorenz model is given by the Eq. (6), the data is derived from the Lorenz system, which is given by three time-delay differential systems. Table 4 specifies the values employed to generate the data samples.

Table 4. Parameters to generate LOR time series
Full size table
$$ \left\{ {\begin{array}{*{20}l} {\frac{dx}{dt} = a\left( {y - x} \right)} \hfill \\ {\frac{dx}{dt} = bx - y - xz} \hfill \\ {\frac{dx}{dt} = xy - bz} \hfill \\ \end{array} } \right. $$
(6)

Rössler Chaotic Time Series:

In this example, the data was derived from the Rössler system, which is given by three time-delay differential systems represented in expression (7).

$$ \left\{ {\begin{array}{*{20}l} {\frac{dx}{dt} = - y\left( t \right) - z\left( t \right)} \hfill \\ {\frac{dx}{dt} = x\left( t \right) + ay\left( t \right)} \hfill \\ {\frac{dx}{dt} = b + z\left( t \right)\left( {x\left( t \right) - c} \right)} \hfill \\ \end{array} } \right. $$
(7)

The dataset was built by using four-order Runge–Kutta method with the initial value as shown in Table 5, and the step size was chosen as 0.01.

Table 5. Parameters to generate ROS time series
Full size table

Ikeda Time Series:

The Ikeda map was given in expression (8) as follows:

$$ \begin{array}{*{20}c} {\dot{x} = 1 - \mu \left[ {xcos\left( t \right) - ysin\left( t \right)} \right]} \\ {\dot{y} = \mu \left[ {xcos\left( t \right) - ysin\left( t \right)} \right]} \\ \end{array} $$
(8)

where \( t \, = \, 1/\left( {1 + x^{2} { + }y^{2} } \right). \) This system displays chaotic behavior over a range of values for the parameter, including the values chosen in Table 6.

Table 6. Parameters to generate IK time series
Full size table

In the experiments, the datasets were splitted into two parts: the training set and the test set. In the training phase, each of the individual models was trained with optimized parameters given by each filter. This means that every model was constructed with a sequence of data different to the test set samples. Figure 3 shows examples from each generated dataset for the five cases.

Fig. 3.
figure 3

Examples of the generated datasets.

Full size image

3.2 Neural Networks Models

The architecture of the LSTM model was composed by an input with length (ix) of 25 samples. The nonlinear gate was given by the sigmoid function and the nonlinearity from input to output was established by a hyperbolic tangent function. The number of epochs for training was adjusted to 50 as maximum. Learning rate was 2e-3 with a training percent of 0.80 and 512 units in just one hidden layer, dropout rate of 1.0 and weight decay of 1e-8.

As a way to compare the results in terms of ANN models, a nonlinear autoregressive model (NAR) was employed. This is an architecture that is based on feedforward connections as classical proposals of neural networks but with considerable results for forecasting tasks [15,16,17]. The main difference is determined by the recurrence that is missing in this model as previously mentioned. For developing the forecasting the expression (7) describes this model, in the way:

$$ y_{i} = tanh\left( {\sum\nolimits_{k = 1}^{p} {a_{i} y_{i - k} + b} } \right) $$
(9)

where yi is the time series to be modeled, ai are the coefficients of the model, which are called synaptic weights (wij) in other applications models. Parameter b is a bias value used to fix the function to be found. It is possible to see nonlinearity in the hyperbolic tangent (tanh) in (3) known as transfer function of the units or neurons in the neural model.

For NAR model, some equivalent parameters were fixed as LSTM model. For example, an input vector with 25 samples was used and 50 epochs for training. One hidden layer was also employed, modifying the number of neurons from two to ten and computing the results in an experimental mode. The resilient backpropagation algorithm was employed for adjusting the synaptic weights due to its fast convergence and low computational cost.

3.3 Prediction Error Metrics

To assess the performance of the forecasting, the symmetric mean absolute error (sMAPE) was employed as suggested in [18], and as shown in expression (10):

$$ sMAPE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \frac{{\left| {X_{t} - F_{t} } \right|}}{{\left( {\left| {X_{t} } \right| + \left| {F_{t} } \right|} \right)/2}}*100 $$
(10)

where t is the observation time, n is the size of the test set, Xt is the original series and Ft is the forecasted series.

Finally, the Root Mean Square Error (RMSE) was employed to obtain the error as in [19], given by the computation in (11) as follows:

$$ RMSE = \sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {X_{t} - F_{t} } \right)^{2} } } $$
(11)

where t, n, Xt and Ft are the same as in (10).

4 Results

Table 7 shows the results computed for sMAPE and RMSE average across all datasets when the LSTM model and its modification with the Bayesian Approach (LSTM-BA) were trained. Two horizons for this forecasting were highlighted because the best results. As a complement, Table 8 shows the results for NAR implemented models, where information about the neurons in the hidden layer and average for sMAPE and RMSE from computation in all datasets are shown.

Table 7. Mean forecast-error metrics computed by LSTM approaches employing all datasets.
Full size table
Table 8. Forecast-error metrics computed by NAR approaches employing all datasets.
Full size table

The BA approach shows a level improvement, indicating the necessity of information from prior distribution for an adequate model with better results in terms of prediction error. The evaluation of the results across the 10 series analyzed through its mean value evinced, with the use of sMAPE and RMSE indices, that there was an increment when the horizon is deeper for each series. Note that there is a little improvement of the forecasting given by LSTM-BA approach compared with the traditional LSTM one, which resulted from the use of a stochastic characteristic to generate a deterministic result for long-short-term prediction.

For the NAR model, the results remained under the results of the LSTM, showing the advantages of RNN compared with feedforward networks. In spite of the comparison was not equitable due to the number of units and optimization parameters to train the models, the results exhibit advantages of the recurrent strategies.

5 Discussion

The assessment of the obtained results, comparing the performance of the proposed algorithm, shows a significance improvement measured either by sMAPE and RMSE index for the LSTM-BA and LSTM ones contrasted to NAR models. According to the literature, it is not properly justified or experimentally proven that LSTM networks are appropriate for modeling chaotic series. However, as consequence of using the present proposal, there was an increment of the network in terms of learning of long sequences. This approach came from the idea that only the most recent data are important, and the sliding time window methods are very useful for pattern recognition, for datasets with highly dependence on the past bulk of observations.

LSTM models are powerful enough to learn the most important past behaviors and understand whether those past samples are important features in the making prediction process. This could not exposed by the NAR models, which, in spite of its utility in TSF, did not have better results than the RNN proposals. As mentioned, recurrent connections present capacity to memorize nonlinear relations between the samples, which allow to performance the forecasting in a better way. Other aspect for the NAR model is related with the number of neurons in the hidden layer. For both error measures, it was exhibited that with five neurons the models presented the best performance. After this number, the networks showed an overfitting incrementing the error in the test set.

In the specific case of chaotic time series, alternative models have been worked based on other Bayesian proposals. Examples of this, can be seen in [20], where a Bayesian enhanced ensemble approach, or in [21] with a Bayesian enhanced modified proposal, and in [22, 23] with BA extended and BA basic proposals, respectively. In all these models, the results were comparable and lightly under the present ones.

The limited amount of available input and a flexible prior over a large space of possible nonlinear models produces significant posterior uncertainty on the dynamics and the global prediction, converging to the long-term mean with large variance. This is due to the poor estimation of the mean error values using so little amount of data. In order to improve the value of the results, more prior information such as the apparent periodicity and trend of the signal must be considered.

6 Conclusions

In this paper, a proposal that includes a Bayesian heuristic approach to optimize the training and architecture of LSTM, allowing modifying its parameters in a better way. For this, the addition of information as the number of feedback layers, past input layers and incorporation of self-adaptive heuristic, adjusts the training process. Furthermore, we have shown that our model yields neural networks with higher prediction capability for time-series data, comparing the performances of the proposed algorithm and the existing one through the numerical experiments, using well-known benchmark series. An alternative proposal based on NAR models was presented with low performance compared to the LSTM ones.