Abstract
This chapter consists of two sections that cover algorithms and hardware architectures for modular addition and multiplication: (x + y) mod m and xy mod m. Subtraction and division are also included—as the addition of an inverse and as multiplication by an inverse. The underlying algorithms and hardware structures are those of Chap. 1, modified for modular arithmetic. For both operations we shall consider generic algorithms and hardware structures for arbitrary moduli and also those for special moduli.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
A primary difference between ordinary modular arithmetic and the modular arithmetic of cryptography is in the high precisions used in the latter, with operands represented in hundreds or even thousands of bits. One implication of this difference is that some of the algorithms and hardware designs for the former are not always appropriate for the latter, and this is especially so for multiplication. We will not make specific remarks on high-precision operations. The discussions in Sects. 1.1.5 and 1.2.4 largely carry over to the present context, and there is little to add.
The difference between ordinary addition and modular addition is not large; that is not so with multiplication. If the operands for a modular addition are within the correct range, then ensuring that the result too is within range is a relatively simple task. On the other hand, with modular multiplication ensuring that a result is within range generally requires modular reduction, which is generally almost equivalent to division. Thus the first part of the chapter is a short and straightforward one, whereas the second is not.
1 Addition
The first subsection is on “generic” modular adders, i.e., those for an arbitrary modulus. The second subsection is on adders for special moduli, of the form 2n ± 1. And the third section consists of a few remarks on subtraction.
1.1 Generic Structures
The result of adding, modulo m, two numbers x and y, where 0 ≤ x, y < m, is given by
This equation can be implemented directly or indirectly, in a variety of ways.
Let us suppose that we have an ordinary two-operand adder (Sect. 1.1), i.e., an adder that computes modulo-2k sums for k-bit operands. (We shall refer to such an adder as a “basic adder.”) Then a simple, direct algorithm to effect Eq. 5.1 is as follows.
-
(i)
x and y are added to yield an intermediate sum, s′.
-
(ii)
s′ is compared with m.
-
(iii)
If s′ < m , then s′ is the correct result.
-
(iv)
If s′≥ m , then m is subtracted from s′ , to yield a new value, s″, which is then the correct result.
The procedure just described suggests three sequential additions: the primary one; one for the “corrective” subtraction, which would be effected as the addition of the negation of the subtrahend; and one for the comparison, which would consist of a subtraction followed by sign determination. In practice the latter two additions can, as we show below, be combined into a single one, in the following way.
For the subtraction, we shall assume that the negation of the subtrahend is in two’s-complement representation. If x, y, and m are each represented in n bits, then the arithmetic will be in n + 1 bits, the additional bit being for sign.Footnote 1 We shall therefore assume (n + 1)-bit representations for the actual arithmetic, even with all operands and results representable in n bits each.
When interpreted as an unsigned number, the two’s-complement representation of negative m, which we shall denote \(\widetilde {m}\), corresponds to the numerical value 2n+1 − m (Section 1.1.6). With that interpretation
If x + y ≥ m, then \(x +y+\widetilde {m}\geq 2^{n+!}\), and the 2n+1 in the equation represents a carry out of the most significant bit-position; discarding that carry is equivalent to subtracting 2n+1 and leaves the correct result of x + y − m. On the other hand, if x + y < m, then \(x +y+\widetilde {m} < 2^{n+1}\), and there is no carry-out. Therefore, the carry-out from the second addition is equivalent to the result of the nominal comparison. As usual, the addition of \(\widetilde {m}\) will be as the addition of the ones’ complement and a 1 (injected as a carry-in to the adder).
Examples are given in Table 5.1. In the first case the second addition does not produce a carry, so the result (i.e., 9) from the first addition is correct. In the other case there is a carry, which is discarded, so the correct result (i.e., 3) is that from second addition is the correct one.
A straightforward arrangement to implement the preceding algorithm is one that uses a single adder, in three steps. First, x and y are added, and the result s′ is stored. Next, \(\widetilde {m}\) is added to s′, to obtain s″. Finally, s′ or s″ is selected as the result, according to the sign of the latter. The corresponding hardware architecture is shown in Fig. 5.1. The unit operates in two cycles, one for the computation of s′ = x + y and one for the computation of \(s{''}=x +y+\widetilde {m}\). Note that a carry-out cannot occur in the first cycle because x + y < 2n+1. A nominal overflow can occur, but it does not matter because the result is taken as an unsigned number.
An alternative to the organization of Fig. 5.1 is one that uses two basic adders arranged in sequence, as shown in Fig. 5.2. This new arrangement is more costly, but it can be faster on three grounds. First, the register delay in Fig. 5.1 is eliminated. Second, the new arrangement is more amenable to pipelining. And third, depending on the basic-adder design, the two adders in Fig. 5.2 can largely operate concurrently. The explanation for the last point is as follows.
Suppose, for example, that the two base adders are ripple adders. The result, s′, from the first adder will be available one bit at a time, starting from the least significant end. Therefore, the second addition, to compute s″, can start as soon as the first result bit from the first adder is available, and the computation of the first result bit from the second adder can be overlapped with that of second bit from the first adder. Extending this reasoning, we see that overlap is possible in the computation of the other sum bits. Similar reasoning may be applied to other adder designs. For example, where each adder is partitioned into blocks, with all the sum bits from a block available at the same time, the overlap can be at the level of blocks.
Two base adders can also be used in a different arrangement that is, in principle, faster than that of Fig. 5.2, by concurrently computing both s′ and s″ and then selecting one of the two. The computation of s″ requires that three operands be reduced to one, which is easily done by using a combination of a carry-save adder (CSA) and a carry-propagate adder (CPA), as shown in Fig. 5.3. Although two CPAs are shown, in practice the underlying design of a CPA may permit some sharing of logic, so the total cost need not be twice that of a single adder.
The essential idea in the aforementioned sharing will be found in the design of a carry-select adder, for example. Such an adder basically computes preliminary two sums, x + y and x + y + 1, one of which is then selected as the final result; but the detailed design is such that there is little replication of logic in the computation of the two intermediate results. One can envisage an extension of this arrangement into a more general one for the computation of x + y and \(x +y+\widetilde {m}\).
1.2 Special-Moduli
Moduli of the form 2n ± 1 find much use in modular arithmetic, and those that are prime are especially useful in cryptography. As we show below, modulo-(2n − 1) addition is almost exactly ones’-complement addition and is therefore much easier to implement than general modular addition. Modulo-(2n + 1) addition is somewhat more complex than modulo-(2n − 1) addition. We start with the latter.
Suppose the operands in addition are x and y, with 0 ≤ x, y < 2n − 1 and therefore representable in n bits each. We may distinguish between three cases in the addition:
-
(i)
0 ≤ x + y < 2n − 1
-
(ii)
x + y = 2n − 1
-
(iii)
x + y > 2n − 1, i.e., x + y = 2n + w, w ≥ 0
In (i), the value x + y is the correct modulo-(2n − 1) result. On the other hand, in each of (ii) and (ii), a nominal subtraction of 2n − 1 is required to obtain the correct result, which is zero in (ii) and w + 1 in (iii). It is easy to determine when (iii) is the case: the 2n is reflected as the carry-out from the addition. But there is no carry-out in either (i) or (ii). To distinguish between the two cases, the value 2n − 1 must be detected explicitly. How that is done is explained below.
Correction in case (iii) is straightforward. Subtracting 2n − 1 is equivalent to subtracting 2n and adding 1, which can be done by discarding the carry out (i.e., subtracting 2n) and adding 1. The carry-out also indicates the need to add the 1, so the desired effect can be achieved by adding the carry-out to the intermediate sum. Such “end-around-carry” addition is exactly what happens in ones’-complement addition (Sect. 1.2.1).
Case (ii) highlights the difference between ones’-complement addition and addition modulo 2n − 1. In ones’-complement notation, there are two representations for zero: 00⋯0 and 11⋯1. On the other hand, in modular arithmetic there is only one binary representation for zero, i.e., 00⋯0, and 11⋯1 represents 2n − 1. Thus, although no correction is required for an intermediate result of 11⋯1 in ones’-complement arithmetic, one is necessary in modular arithmetic. That correction is easily done by adding a 1 and ignoring the carry-out.
Let s′ denote the intermediate sum x + y in (i)–(iii), and x i, y i, and s′ i denote bits i of x, y, and s′. Then case (ii) holds when \(\prod _{i=0}^{n-1}s_i{'} =1\), which is possible only if
Note that P is just the block-propagate signal \(P_0^{n-1}\) in carry-lookahead and parallel-prefix adders (Eqs. 1.14 and 1.17); so its production in such adders will not require any extra logic or time.
On the basis of the preceding remarks, the computation of s = (x + y) mod (2n − 1) has three main parts:
-
(i)
Add x and y , to obtain the intermediate sum s′ and a carry-out c n−1.
-
(ii)
Form the signal z = P + c n−1.
-
(iii)
If z = 0, then the result s is s′ ; otherwise s is s′ + 1.
Some examples are given in Table 5.2.
The hardware implementation of a modulo-(2n − 1) adder consists of a straightforward modification to a ones’-complement adder (Figs. 1.12 and 1.13 in Sect. 1.2.1): the end-around-carry signal in such an adder is replaced with the z of (ii) above. A second addition will be required in most types of adders, but not with a conditional-sum adder or a parallel-prefix adder. At the penultimate stage of a conditional sum-adder, two intermediate sums that differ by one are available, with a selection made in the last stage. That selection may be made according to z, but the P signal must still be generated before that. In a parallel-prefix adder, the addition of a 1, conditional on z, is done by simply having an extra level of prefix operator, and the P signal will be the last block-propagate signal from the prefix tree.
Addition modulo 2n + 1 is not as easy as addition modulo 2n − 1. In both cases, when the intermediate result s′ = x + y is equal to or exceeds the modulus, it is necessary to subtract 2n and to also subtract 1 in the former case and subtract − 1 (i.e., add 1) in the latter case. In implementation, subtracting 1 is more difficult than adding 1 (as we explain below).
With the modulus 2n + 1, 0 ≤ x, y ≤ 2n; so the operands and modulus will be represented in n + 1 bits, and the arithmetic will be of n + 2 bits (with one bit for sign). Let the binary representation of s′ be s′ n+1s′ ns′ n−1⋯s 0, with a carry-out c n+1 from the addition that produces s′. Then a correction is required if either s′ n+1 = 1 and at least one of the other bits is a 1 (i.e., if the logical OR of the other bits is 1) or if c n+1 = 1; in both cases s′≥ 2n + 1, with x = y = 2n in the second case. To obtain the correct result, it is necessary to subtract 2n + 1. That can be done by subtracting 1 and then setting bit n of the subtraction-result to 0, the latter being equivalent to subtracting 2n. The order of the two corrective actions is important, because in the second case s n = 0. Note that a carry produced in the subtractive addition is discarded, according to the rules given in Sect. 1.1.6 (for operands of unlike sign).
Adding 1 (as in the modulo 2n − 1 case) is easy, since it can be done by injecting a carry into the least significant position of an adder. On the other hand, subtracting 1 (as in the modulo 2n + 1 case) requires the addition of 11⋯1 (assuming two’s-complement representation) and is more difficult.
Examples are given in Table 5.3. Subtraction is as the addition of a two’s complement of the subtrahend.
A special representation has been proposed to help solve the aforementioned subtraction problem. In diminished-one representation, the binary representation of a number z is taken to be what would ordinarily be the representation of the number z − 1 [1,2,3,4]. The requirement for a subtraction of 1 is thus converted to that of an addition of 1. Zero requires special handling in such a system: it is represented by the binary pattern that would normally be used to represent 2n—i.e., the pattern 100⋯00—and in the implementation of the arithmetic it is treated as an exceptional case.
Consider non-modular diminished-ones addition. If the operands are x ′ = x − 1 and y ′ = y − 1, adding them yields s′ = x + y − 2. To get the correct diminished value for x − y a 1 should be added to s′.
Now consider addition modulo 2n + 1 with diminished-one representation, excluding the special case of a zero operand, which would be handled in an obvious way. Let the binary representation of s′ above be s′ ns′ n−1⋯s′ 0. If x + y < 2n + 1, then s′ < 2n − 1; so \(s_n^{\prime }=0\), and a 1 should be added to get the correct result. On the other hand, if x + y ≥ 2n + 1, then \(s_n^{\prime }=1\); to get the correct modular result we should add 1, as before, and also subtract 2n + 1. Subtracting 2n is accomplished by setting \(s_n^{\prime }=0\). No additional action is required, as adding 1 and then subtracting 1 is equivalent to not doing anything.
Hardware for a diminished-ones modulo-(2n + 1) addition will be faster and less costly than for a generic modular adder (Figs. 5.1, 5.2, and 5.3). But, on the whole, diminished-one representations and arithmetic are of dubious practical worth. That is because conversion to and from the representation require full carry-propagate additions and subtractions, which are worthwhile only if there are numerous computations to be carried out and the intermediate operands are retained in the same form so that the “one-off” cost of conversions is therefore amortized. Such a situation does not often arise; so, despite a fair amount of study, diminished-ones representation finds little real use. We will therefore not consider the representation any further in the context of addition and refer the interested reader to the published literature [2, 3].
Given the preceding remarks, we may conclude that there is probably little value in devising addition units specifically for the modulus 2n + 1. Modulo-(2n + 1) multiplication might, in certain circumstances, be considered an exceptional case, which is considered below.
1.3 Subtraction
Given x and y such that 0 ≤ x, y < m, the definition of residue subtraction suggests that the computation of (x − y) mod m be carried out by first computing the additive inverse of y (i.e., m − y) and then adding x (modulo m). This would involve three additions: one to compute m − y, one to add x, and one (a subtraction) to correct the initial result that exceeds the modulus. A much better method is as to compute it as
This equation is similar to Eq. 5.1, but with the arithmetic operations changed to the converse. The condition that separates the two cases too is changed: the test for x − y ≥ 0 is easier than that for x + y > m, as the latter requires a nominal subtraction, and this difference can have practical implications in the implementation.
If x, y, and m are each represented in n bits, then the arithmetic will be in n + 1 bits, with one bit for sign. The subtraction is carried out by adding to x the negation (i.e., two’s complement) of the subtrahend. If \(\widetilde {y}\) is that negation, then the subtraction is equivalent to the addition of the unsigned number 2n+1 − y. That is, the intermediate result s′ of operating on the operands is
If x ≥ y, then s′≥ 2n+1; the 2n+1 in the expression for s′ indicates a carry out from the addition, and discarding that carry leaves the correct result of x − y. On the other hand, the absence of a carry out indicates that x < y, and so m should be added to s′. This addition will produce a carry, since x − y + m ≥ 0, and discarding that carry leaves the correct result of x − y + m. The algorithm for s = (x − y) mod m:
-
(i)
x and− y are added to yield an intermediate sum s′ with carry-out c n.
-
(ii)
If c n = 1, then s = s′ (after discarding the carry-out).
-
(iii)
Otherwise, add m to s′ to obtain s , with the carry-out discarded.
Examples are shown in Table 5.4.
Modulo-m subtractors will be similar to modulo-m adders, such as those of Figs. 5.1, 5.2, and 5.3. Thus, for example, simple changes to the inputs and outputs in Fig. 5.1 give the design of Fig. 5.4. The subtraction takes place in two cycles. The first cycle consists of the subtraction s′ = x − y, as the addition of the two’s complement of the subtrahend, which in turn is the addition of the ones’ complement and a 1 that is included as a carry into the adder. The second cycle consists of the addition of s″ = s′ + m. One of s′ and s″ is then chosen as the result.
The modifications required of Figs. 5.2 and 5.3 are similarly straightforward, as is the design of a combined modulo-m adder-subtractor.
1.3.1 Special Moduli
Subtraction with the moduli 2n ± 1 follows the general form above for an arbitrary modulus but with some simplifications. For the modulus 2n − 1, the negation of the subtrahend is the ones’-complement representation, and for 2n + 1 it is the two’s complement. The required precisions are n + 1 bits in the former case and n + 2 in the latter. The following is a discussion of modulo-(2n − 1) subtraction (Table 5.5).
When interpreted as the (n + 1)-bit representation of an unsigned number, the ones’-complement representation of − y is that of \(\widetilde {y}=2^{n+1}-y-1\) (Sect. 1.1.6). So
Three cases may be distinguished of the value of \(s{'} =x+\widetilde {y}\):
First, if x ≥ y + 1, then the 2n+1 represents a carry out, c n, from the addition. Discarding that carry leaves x − y − 1, and adding a 1 to that yields the correct result; the latter is just the addition of an end-around carry.
Second, if x = y, then s′ = 2n+1 − 1, and it is necessary to subtract 2n+1 − 1; i.e., subtract 2n+1 and add 1. Adding 1 to s′ produces a carry, and discarding that carry effects the subtraction of 2n+1. This case occurs if s′ ns′ n−1⋯s′ 0 = 11⋯, which corresponds to the carry-propagation signal (Sect. 1.1.1)
Third, if x < y, then there is no carry out. In this case 2n − 1 should be added to s′; i.e., 2n should be added and 1 subtracted. Since s′ is negative, s′ n = 1. So, adding 2n would change s′ to 0 and generate a carry that should be added as an end-around carry. Adding that carry and subtracting 1 is equivalent to doing nothing. Therefore, in this case the correct result may be obtained by simply setting s′ n = 0.
An algorithm for subtraction modulo 2n + 1 can be devised in a manner similar to that done above for addition modulo 2n + 1. Nevertheless, given the comments above on addition modulo 2n + 1, we will not bother with subtraction and leave it to the interested reader to look into the details.
2 Multiplication
The most straightforward method for the computation of xy mod m is to compute the ordinary product xy and then carry out a modular reduction. That is not always the best for cryptography applications, as the intermediate values can be very large, but it may nevertheless be considered for an implementation with “pre-built” units for the two basic functions. As both ordinary multiplication and reduction have been discussed in Chaps. 1 and 4, there is little to add to the matter. We shall therefore focus on those methods that include reduction as an intrinsic part of the computation of the modular product.
Ordinary multiplication consists of the addition of multiples of the multiplicand, with the multiples determined by the digits of the multiplier. In sequential multiplication, the multiples are added one at a time to running partial product that starts at zero and ends up as the sought product. In modular multiplication, reductions may be carried out on the partial products, on the basis that
Partial products are reduced as they are formed; so a corresponds to a partial product and b corresponds to a multiplicand multiple.
Let x and y be the two operands, each less than the modulus m and representable in n radix-r digits and with a product z: \(x =\sum _{i=0}^{n-1} x _ir^i\) and \(y=\sum _{i=0}^{n-1} y_ir^i\), and \(z=\sum _{i=0}^{n-1} z_ir^i\), where x i, y i and z i are digits i of x, y, and z. And let Z i denote the partial product in iteration i. Two algorithms for the sequential computation of z = xy are (Section 1.2.1)
for a right-to-left scan of the multiplier digits and
for left-to-right scan.
Ordinary sequential multiplication uses the first algorithm because the r i factor in the multiplicand multiple—a factor that in implementation implies a left shift of i digits positions—is removed by shifting the partial product one place to the right in each iteration instead of shifting the multiple i places to left in each iteration. Each digit that is shifted out is a digit of the final product, so the additions are of n digits each. On the other hand, the additions with the second algorithm must be of 2n digits, 2n being the precision of the largest multiplicand multiple.
If the two multiplication algorithms above are modified directly for modular arithmetic, then the situation of the preceding paragraph is reversed: the second algorithm is the better one. The implementation “optimization” mentioned above of the first algorithm is not directly possible in modular arithmetic, as all digits of a partial product must be included in a reduction; so, in general, the partial products will be of 2n digits, in contrast with n + 1 digits in the second algorithm. The former is therefore no better than an algorithm that consists of first computing xy and then reducing that. (The two examples in Tables 5.6 and 5.7 show this.) Nevertheless, we shall see that the first algorithm can still be applied in an efficient way in modular multiplication.
2.1 Multiplication with Direct Reduction
A straightforward algorithm for the computation of z = xy mod m based on Eqs. 5.4–5.6 is
of which an example is given in Table 5.6.
And an algorithm based on Eqs. 5.7–5.9 is
with an example given in Table 5.7.
A comparison of the magnitudes of the U i values in Table 5.6 and the U i values in Table 5.7 confirms the statements made above, to the effect that in the straightforward versions the second algorithm is the better of the two. The following discussion is therefore limited to that algorithm.
The computation of U i in Eq. 5.15 is largely straightforward. It consists of the computation of a small multiple of x, a left shift to effect the multiplication of Z i by r, and an addition. The complexity of the computation of y n−i−1x depends on the value of r, but in practice it is unlikely to be high. If r = 2, then the multiple is just 0 or x; and, for hardware implementation, other practical values of r will typically be restricted to 4 or 8, for easy multiplier recoding. On the other hand, the computation of U i mod m is fundamentally difficult, as it essentially implies (from the definition of a residue) a nominal division.
Now,
So, a subtraction of a multiple of m, up to (2r − 2)m, may be required to reduce U i to Z i+1 such that 0 ≤ Z i+1 ≤ m − 1. The difficulty is in determining the correct multiple to be subtracted—the classic problem in integer division. If r is sufficiently small, then the number of possible multiples will be small enough that all multiples may be checked efficiently against Z i+1—one at a time or concurrently—and the correct one chosen. With r = 2, Eq. 5.16 is now
which can be implemented with one adder used twice, as in Fig. 4.1. Nevertheless, for hardware implementation, the fundamental problem remains: exact results are required of the comparisons, which implies the use of carry-propagate adders. Therefore, the basic algorithm and obvious architecture are best suited to an implementation with “pre-built” units (especially adders), and such an implementation will be much slower than would be the case if carry-save adders could be used.
As in ordinary multiplication and division, the use of a carry-propagate adder (CPA) in the main loop will give an implementation that is quite slow. A faster implementation requires the use of a carry-save adder (CSA), but that raises the basic difficulty in division: in order to know when a subtraction is exactly necessary, a partial-carry and partial-sum must be assimilated, which requires the use of a CPA. As in division, the solution here is to use approximation. We next describe such a method [16].
Let C i denote the partial carry in iteration i and S i denote the partial sum in iteration i. And assume the radix is two. Then the starting algorithm, obtained directly from that of Eqs. 5.14–5.17, is
where the computations in the right-hand sides of the middle two equations are carry-save additions, SIGN is the exact sign of the result of assimilating the partial carry and partial sum, and the last addition is an assimilating carry-propagate addition. The algorithm requires exact determination of the sign. A better algorithm is obtained as follows.
Define the function T on as k-bit integer u as
T replaces the least significant t bits of u with 0s, so
Suppose the reduction of (C i, S i) is then by carrying out q times the two steps:
In the second step, the assimilation addition (or equivalent), which gives a sign approximation, involves only the most significant n − t bits of the operands.
Let (C J, S J) denote the values at the start of the q instances of Eqs. 4.18–4.19 and (C K, S K) denote the ending values. Then:
where the additions of C and S are assimilation ones. If the estimated value in Eq. 4.19 is positive in all q instances, then qm is subtracted from the starting values, so
And if the value is negative in any step, then it stays negative to the end, and the condition
in the last instance of Eq. 4.19 implies
since T(⋯ ) is always a multiple of 2t. Therefore:
and
In Eq. 4.18 C + S is reduced by m, and in the last instance there is no reduction, because the estimated value is negative. So
which implies
In the initial algorithm m is subtracted in each iteration, which would correspond to nq subtractions with the replacement of Eqs. 4.18–4.19. This can be improved upon by instead subtracting 2k−jm in iteration j, where q + 1 ≤ 2k and k = 1, 2, …, k. For example, if q = 3 and k = 2, then what would have been three subtractions of m are replaced with two subtractions—one of 2m and one of m.
Putting together all of the above, the final algorithm is
The final assimilation step is omitted, as it may require an additional correction, which is discussed below.
The value of t determines the precision and accuracy of the estimation and, therefore, of the complexity of the control logic and the required correction in the assimilation of C n and S n. After the second-last step of the algorithm:
So, after the next shift-add
With q = 3:
which implies 2t ≤ m or t ≤ n − 1.
Therefore:
And after the step in which 2m is subtracted:
If t = n − 1, then the sign estimation is computed from the five most significant bits of the partial carry and partial sum, and the result will be in the range [0, 2m). So, the final assimilation step is
This is just a case of Eq. 1.1 and may be implemented as described.
An example application of the algorithm is given in Table 5.8.
Figure 5.5 shows a straightforward architecture for the algorithm. The assimilation-and-correction part is omitted; an arrangement similar to that Fig. 4.5 (bottom half) will do for that. The y register is a left-shift register; and the PC-PS registers are initialized to zeros. Multiplication by two is as a wired left shift, and − m and − 2m are each added as the ones’ complement and a 1. A cheaper but slower implementation would avoid the duplication of logic and have just one carry-save adder, one logic estimation unit, and one carry-propagate adder—with all used twice.
Modifying direct-reduction algorithms, such as those above, for efficient high-radix computation is difficult; the modular reduction will require something close to actual division. We next give a brief description of such an algorithm.
If q i is the quotient from the division of U i by m, then we may express the algorithm of Eq. 5.14–5.17 as
Implementing this algorithm requires division—a costly operation—in each iteration, as well as the two multiplications (by x and m) that are not simple operations if r > 2 and the range of q i is unrestricted. In [17] these difficulties are dealt with as follows.
Instead of the exact q i, an approximation \(\widetilde {q}_i\) is used. This approximation is obtained by approximately dividing U i by 2km, where r = 2k; the subtraction U i − q im is then changed to \(U_i - \widetilde {q}_i 2^{2k}m\). Restrictions on the possible values of k and \(\widetilde {q}_i\) ensure that each Z i is less than 2m, and, therefore, that a single subtraction of m is sufficient to correct Z n.
The method used to compute \(\widetilde {q}_i\) is similar to that in SRT division (Sect. 1.3)—it involves, essentially, the comparison of a few leading bits of the partial dividend with a few leading bits of the divisor—but is more complex, as it requires the parallel computation of all the possible values of U i − q i2km. The arrangement and various restrictions also ensure that it is relatively easy to compute \(\widetilde {q}_i m\).
To facilitate the efficient computation of y n−i−1x, y n−i−1 is recoded into the radix-4 digit set \(\{ \overline {1}, 0, 1, 2 \}\). The multiplication is then carried out as the addition of easily computed, weighted powers of four.
The corresponding architecture employs carry-save adders in the primary arithmetic and so an implementation ought to be fast. Nevertheless, both the algorithm and the architecture are sufficiently complex that their real merits over, say, a fast radix-2 implementation are not easily ascertained.
2.2 Multiplication with Barrett Reduction
Barrett reduction (Sect. 4.1) consists of the computation of an approximation to the quotient from an integer division, the computation of an approximate remainder from that approximate quotient, and then, if necessary, a correction of that remainder. The radix-r computations for a = u mod m, with u < m 2, are
To compute xy mod m with this algorithm it suffices to add the computation u = xy. The algorithm can then be combined easily with the multiplication algorithm of Eqs. 5.14–5.17 to produce an algorithm that sequentially computes the xy mod m. As with the algorithm of Sect. 5.2.1, the essence of such an algorithm is to reduce the partial products as they are generated.
If 0 ≤ x, y < m, \(y=\sum _{i=0}^{n-1}y_ir^i\), and 2n−1 ≤ m < 2n, then the combined multiplication-reduction algorithm for the computation of z = xy mod m is
An example computation is given in Table 5.9, which corresponds to Tables 5.6 and 5.7. It is straightforward to devise a corresponding architecture, with two full multipliers, two carry-propagate adders, a multiplexer, etc.
A variant of the preceding algorithm, based on the “extension” described at the end of Sect. 4.1, and corresponding architectures for implementation will be found in [6]. Both the basic algorithm and the variant have an obvious shortcoming: the repeated multiplications, to compute \(\widetilde {q}_i\) and Z i+1, are not conducive to high-performance implementation, even with r = 2. The use of carry-save adders and recoding will help, but only partially. Nevertheless, they do have some merit—if cost, not performance, is the primary consideration. That is because the alternatives would require larger adders and multipliers. To see this, consider the first example in Table 5.9, and suppose the alternative consists of a straightforward multiplication followed by a reduction (e.g., Barrett reduction). The product of 456 and 123 is 56,088, which is far larger than any value in the table.
Residue number systems (Sect. 1.1.4) appear attractive for the high precisions in cryptography, since what would otherwise be high-precision operations are replaced with numerous low-precision ones, and there has been some work on adapting the Barrett algorithm to such representations. A fundamental problem in such an approach is the efficient computation of the approximate quotient of Eq. 5.27; a partially satisfactory solution for that is given in [15]. But the problem of conversions remains.
2.3 Multiplication with Montgomery Reduction
With u < mR and \(\gcd (m, R)=1\), Montgomery reduction (Sect. 4.2) computes z = uR −1 mod m, where R −1 is the multiplicative inverse of R with respect to m, through these steps:
z is the result, uR −1 mod m.
With R = r n, a serial-sequential version of the algorithm is
The Montgomery reduction algorithm can be used as the basis of one that computes xy mod m in two multiply-reduce steps, as follows.
Suppose we have a single algorithm that takes the operands, a, b, m, and R and computes abR −1 mod m; that is, multiplication is intrinsically part of the reduction process. Then xy mod m can be computed with two applications of the algorithm:
-
(i)
Apply the algorithm with a = x and b = y and obtain z = xyR −1 mod m.
-
(ii)
Apply the algorithm with a = z and \(b= \widetilde {R}\), where \(\widetilde {R}\) is the “pre-computed;; value R 2 mod m.
The result from (ii) is (xy) mod m:
The single algorithm is obtained by combining the steps of the basic multiplication algorithm (Eqs. 5.4–5.6), with operands a and \(b=\sum _{i=0}^{n-1} b_i r^{i}\), and the basic Montgomery-reduction multiplication algorithm for the computation of z = abR −1 mod m, with R = r n is
A single subtraction at the end of the iterative process suffices because 0 ≤ Z i < 2m − 1 for all i. This is evident for Z 0, and, by induction, if it is so for Z k, then
Note that with r as the representation radix, if the implementation radix is r or a power or r, then reduction modulo r is a trivial operation: it consists of simply taking the least significant digit of the operand. Therefore, Eq. 5.43 may be replaced with
where u 0 is the least significant digit of U i.
An example computation is shown in Table 5.10, which corresponds to Tables 5.6, 5.7, and 5.9.
In the multiplication shown in Table 5.10, the role of the second multiplication-reduction is essentially to remove the R −1 factor and thus obtain xy mod m from xyR −1 mod m. This is clearly seen if the factor of R 2 mod m is “split” into one R mod m for each operand; that is, each operand is multiplied by that factor before proceeding with any multiplication-reduction: Suppose that instead of x and y, the operands in the algorithm are xR mod m and yR mod m. Then one multiplication-reduction yields

from which another, similar, multiplication-reduction with 1 as the other operand, yields
If only a single modular multiplication is required, then the second multiplication-reduction can be done away with, by modifying only one of the operands in Eq. 5.47, say x to xR mod m:

But, as we explain below, it is the version with two modified operands that is of special interest.
The forms  and
and  are the Montgomery residues of x and y with respect to m and R. The set {kR mod m : 0 ≤ k ≤ m − 1} is a complete set of residues with respect to m, so it is permissible to work with this set instead of the “original” residues. Computing a Montgomery residue is, however, not an easy operation. One method that is routinely suggested in the standard literature is a Montgomery reduction in which
are the Montgomery residues of x and y with respect to m and R. The set {kR mod m : 0 ≤ k ≤ m − 1} is a complete set of residues with respect to m, so it is permissible to work with this set instead of the “original” residues. Computing a Montgomery residue is, however, not an easy operation. One method that is routinely suggested in the standard literature is a Montgomery reduction in which  is obtained from the reduction of the product of x and R
2 mod m:
is obtained from the reduction of the product of x and R
2 mod m:

This computation may be carried out by first computing  and then applying the Montgomery-reduction algorithm of Sect. 4.2 or by combining the multiplication and reduction, as in the algorithm of Sect. 5.2.3. Regardless of which of the two methods is used, R
2 mod m or xR
2 mod m must be computed by means other than Montgomery multiplication, and neither will be a simple computation. A careful consideration of what is involved also shows that for hardware implementation the aforementioned methods are probably no better than simply computing the product
and then applying the Montgomery-reduction algorithm of Sect. 4.2 or by combining the multiplication and reduction, as in the algorithm of Sect. 5.2.3. Regardless of which of the two methods is used, R
2 mod m or xR
2 mod m must be computed by means other than Montgomery multiplication, and neither will be a simple computation. A careful consideration of what is involved also shows that for hardware implementation the aforementioned methods are probably no better than simply computing the product  and then directly reducing that modulo m. Nevertheless, as we next explain, the one-time cost of computing Montgomery residues can be well worthwhile, depending on the circumstances.
and then directly reducing that modulo m. Nevertheless, as we next explain, the one-time cost of computing Montgomery residues can be well worthwhile, depending on the circumstances.
Equation 5.47 shows that the Montgomery multiplication of two Montgomery residues yields a Montgomery residue, and this is what is special about the algorithm. If there is a sequence of modular multiplications to be carried out—as in modular exponentiation—then all the intermediate values may held as Montgomery residues, with only one special, extra multiplication (Eqs. 5.48–5.51) for the conversion of the final result. The one-time costs of converting to and from Montgomery residues are then amortized. The key point, therefore, is that Montgomery multiplication is quite efficient if the cost of computing Montgomery residues is excluded. (We shall return to this in Chap. 6.)
In summary, if we wish to compute xy mod m, then we may convert x and y to the corresponding Montgomery residues and then use the algorithm of Eqs. 5.41–5.45 in two steps, the second of which converts from a Montgomery residue:
-
In the first step
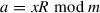 and
and  ; the result is
; the result is  .
. -
In the second step a = z and b = 1.
An example is shown in Table 5.11. (In practice, there will most likely be many computations between initial and final conversions.)
Assuming the availability of only carry-propagate adders, an architecture for Montgomery multiplication is shown in Fig. 5.6, for the computation of xyR −1 mod m, with r = 2. With this radix, Eq. 5.46 becomes \(\widetilde {q}_i=u_0\). (The explanation for this is given in Sect. 4.2.) The Z register is initialized to zero. The y register is a right-shift register that shifts once in each cycle, so that its least significant bit (y 0) is bit y i of the operand. The division by r is a wired shift that drops the least significant bit. The Correction part is as in Fig. 4.4.
A faster multiplier than that of Fig. 5.6 can be obtained by replacing the carry-propagate adders with carry-save adders, as shown in Fig. 5.7. Assimilation and Correction are as in Fig. 4.5.
The standard algorithmic technique for the design of high-performance multipliers is the use of a large radix, through multi-bit, fixed-length scanning of the multiplier operand—k bits at a time for radix 2k—combined with multiplier recoding (Sect. 1.2.2). The use of a large radix here is problematic: the computations of xy i and \(\widetilde {q}_i m\) (Fig. 5.7) are not simple operations if k > 1.
Let us briefly consider a straightforward modification of the architecture of Fig. 5.7, for radix-4 computation; that is, with the multiplier scanned two bits at a time, a digit \(y_i^{\prime }\). The y shift register, carry-save-adders (CSAs), Z registers, are appropriately modified. The AND gates that compute xy i are replaced with a Multiple-Formation unit that produces one of 0, x, 2x, and 3x, according to the value of \(y_i^{\prime }\). A simple way to do this is the use of two multiplexers: one with inputs 0, x, and 2x (obtained through a wired shift), and the other with inputs 0 and x; so the outputs of the multiplexers are 0 and 0 (0 + 0 = 0), or x and 0 (x + 0 = x), or 2x and 0 (2x + 0 = 2x), or 2x and x (2x + x = 3x). The two multiplexer outputs together with what were the two CSA inputs now go into a 4:2 compressor.Footnote 2 The logic for \(\widetilde {q}_i m\) is similarly replaced. Lastly, the logic to compute \(\widetilde {q}_i\) will now be a small, two-gate-level circuit that carries out a very small multiplication. Recoding may also be used. The modified multiplier will have a cycle that is slightly longer than that of the original, but there is a trade-off in the reduced number of cycles. The details would have to be worked out to determine any worthwhile benefit.
The alternative to fixed-length scanning is variable length scanning, which permits skipping past a string of any number of contiguous 0s or contiguous 1s in the multiplier operand without performing an arithmetic operation (for a string of 0s) or performing just two (for a string of 1s). The effect is to, essentially, recode the multiplier into a variable-length string. The two operations for a string of 1s are an addition and a subtraction (Eq. 1.33, Sect. 1.1.2):
So, implementing the technique requires a barrel shifter for y, another barrel shifter to compute 2j+1x (by shifting x), and a third to compute 2ix (by shifting x). The operational time of the multiplier will be variable, according to the operands at hand, which is why (in addition to cost) the technique is not normally used. Nevertheless, an implementation on such a basis has been devised for Montgomery multiplication [12], and we next give a very simplified description of that.
In [12], for the computation of xy i, the multiplier y is first recoded into the digit-set \(\{ \overline {1}, 0, 1\}\); this can be done with a simple circuit. Thus, in principle, the multiple to be produced is some power of two or zero, according to the sign and position of a digit. In order to determine the latter, another circuit is used to produce an “expanded” form of the recoded multiplier operand. The expansion consists of partitioning the operand into groups of bits, \((y_i^{\prime },\, z_i\)), where \(y_i^{\prime }\) is a digit of the recoded operand and z i is the number of 0s in the group. This expanded form is subsequently used in a circuit that includes a barrel shifter to produce the corresponding power of two. Relative to the architecture of Fig. 5.7, a single CSA is still used at the top level, but the third input now comes from a more complex circuit. The circuit used for the computation of \(\widetilde {q}_i m\) is more complex. In essence, it should consist of a barrel shifter for 2j+1m and a barrel shifter for 2im, with j + 1 and i supplied by the barrel shifter for y. The two values produced are then added together, in a 4:2 compressor, with what are the other inputs to the second-level CSA in Fig. 5.7. In practice, the implementation includes a lookup table that produces the equivalent of j + 1 and i and whose inputs are some low-order bits of U i (produced by a small carry-propagate adder that assimilates the corresponding bits of U i- PC and U i-PS), the output of the y barrel shifter, and some low-order bits of m.
The Montgomery-multiplication industry has been a substantial one, and the published literature is extensive. The work includes high-radix recoding, carry-save-adder design, and low-level techniques to improve performance or power consumption; examples will be found in [7, 8, 10,11,12,13]. As with the Barrett reduction algorithm, the use of residue number systems has been investigated [14]; but here too the fundamental problems are yet to be fully solved.
2.4 Multiplication with Special Moduli
Because reduction modulo 2n ± 1 is relatively simple (Sect. 4.4), the computation of xy mod (2n ± 1) may reasonably be carried out first computing xy and then reducing that. Such an approach is especially well suited to cases in which one has to work with “pre-built” units.
With the modulus 2n − 1, the operands will be of n bits each and the product xy will be of 2n bits. Suppose the product is split into two n-bit parts, x h and x l:
Since 2n mod (2n − 1) = [(2n − 1) + 1] mod (2n − 1) = 1,
This can readily be implemented with a single modulo-(2n − 1) adder. And for very large operands, xy may be split into more than two pieces that are then added in a tree of adders (consisting of carry-save adders and carry-propagate adders).
Similarly, with the modulus 2n + 1, the product will be of 2n + 1 bits, and splitting this into a one-bit and two n-bit parts:
Since 2n mod 2n + 1 = [(2n + 1) − 1] mod (2n + 1) = −1,
If diminished-one representation is used with the modulus 2n + 1, then the value 2n cannot be a direct operand, as its usual representation is used to represent zero, which is handled as an exceptional case. Therefore, xy will be of 2n bits that may be split into two n-bit parts, x h and x l:
This equation also holds if normal representation is used but the cases of one or both operands being 2n are excluded and treated as special cases. That is what we will assume in what follows.
The alternative to computing an entire product and then reducing it is to reduce each partial product as it is generated and added. The additions of partial products may be done in carry-save adders, with the final partial-carry and partial-sum from these adders assimilated in a modulo-(2n ± 1) carry-propagate adder. We shall assume that each operand in both cases is less than the modulus.
The algorithms given are based on the basic radix-2 multiplication algorithm of Eqs. 5.10–5.13, modified for modular arithmeticFootnote 3
The unreduced multiplicand multiple in Eq. 5.55 is
Modulus 2 n−1
Observe that the expression in the brackets corresponds to the binary pattern x n−i−1x n−i−2⋯x 0 x n−1x n−2⋯x n−i, which is just an i-place cyclic right shift of x n−1x n−1⋯x 0. And because x < 2n − 1, there must be some x k, 0 ≤ k ≤ n − 1, such that x k = 0. Therefore, the value represented by x n−i−1x n−i−2⋯x 0x n−1x n−2⋯x n−i must also be less than 2n − 1. And since y i is 0 or 1:
An example computation is shown in Table 5.12; |⋯| mod m denotes ⋯ mod m. Note that M i is not actually computed but is included solely for clarity the bits of x h are the bits shifted in at the low end (shown in bold font) to form M i mod m. The latter is, of course, a simple computation that involves addition of a 1 for and end-around-carry or to take into account the value 2n − 1 (Sect. 5.1.2). The relevant details in multiplication are given below.
The multiplication algorithm may be implemented with a single modulo-(2n − 1) adder used repeatedly, in a design that corresponds to that of Fig. 1.15. A much faster implementation for sequential multiplication would use a carry-save adder (CSA) in the loop and a modulo-(2n − 1) carry-propagate adder (CPA) to assimilate the final outputs of the CSA, in a design that corresponds to that of Fig. 1.16. An architecture for the latter is shown in Fig. 5.8. The y register is a right-shit register that shifts by one bit-position in each cycle. The multiplicand multiples, M i, are formed by cyclically the contents of the x register shifted by one bit-position in each cycle and then producing zero or the contents of that register, according to the value of y 0.
The reduction of a partial product as it is formed requires an addition modulo-(2n − 1), and such an addition involves the addition of an “end-around-carry.” With the arrangement of Fig. 5.8 this takes place at two places. First, during the “looping” the reduction is effected by turning the partial-carry output from the most significant bit of the CSA output in one cycle into the least significant bit of the CSA for the addition in the next cycle; in effect, we have a modulo-(2n − 1) CSA. Second, in the last cycle the partial-carry output bit is fed, as a carry-in, into the modulo-(2n − 1) CPA. We next explain one aspect of the design that might not be immediately apparent.
In modulo-(2n − 1) addition as described in Sect. 5.1.2, it is necessary to detect the value 2n − 1, which is represented by 11⋯1, and then make an adjustment in order to get the correct result. That is not necessary here, because each successive CSA makes any required correction and the final CPA makes any final correction required. To see this, ignore for the moment the fact that the intermediate results are in partial-carry/partial-sum form, or imagine that each CSA has been replaced by an ordinary adder (i.e., one with no end-around carry). Suppose, then, that the partial product is 2n − 1 and the multiplicand multiple is a. Now, (2n − 1) + a = 2n + (a − 1). If a > 0, then the 2n is a carry from the addition, and the addition of a 1 (the carry) at the next addition makes the necessary correction; otherwise, i.e., if a = 0, then the 2n − 1 is carried forward. At the last stage the modulo-(2n − 1) CPA contains logic that makes any necessary final correction.
With a parallel CSA array, similar to that of Fig. 1.19, the multiplicand multiples will be formed by appropriate wiring, and end-around-carries will be passed from one CSA to the next and finally to the CPA.
High-radix multiplier recoding, the primary technique used to speed up ordinary multiplication, can be used here too. The essential idea in recoding is exactly as described in Sect. 1.2.2, but with two points to note here. First, as indicated above, here it is the “full” shifted multiplicand multiple, 2ixy i, that is considered—but not actually computed—instead of assuming relative shifts to account for the 2i. Second, modulo-(2n − 1) arithmetic is essentially ones’-complement arithmetic, so subtractions are effected by adding the ones’ complement of the subtrahend. Putting all that together with Eq. 5.54, the table for radix-4 recoding is shown in Table 5.13, which corresponds to Table 1.8a. (The index i is incremented by two for each multiplicand multiple.) The values possible values added are ± 0, ±[2ix mod (2n − 1)], and ± [2(2ix) mod (2n − 1)], which correspond to ± 0, ±x, and ± 2x in Table 1.8a.
Modulus 2 n+1
Multiplication modulo 2n + 1 is more difficult than that modulo 2n − 1, and a multiplier for the former will not be as efficient as that for the latter. The basic difficulty is evident from a comparison of Eqs. 5.53 and 5.54. The addition of Eq. 5.53 translates into a simple cyclic shift because one operand has i trailing 0s and the other has n − i leading 0s. On the other hand, the operation in Eq. 5.54 is a subtraction, and in complement representation leading 0s in the subtrahend turn into 1s.
Much work has been done on the design of modulo-(2n + 1) multipliers, although mostly for diminished-one representation, e.g., [3,4,5, 9]. The following discussion, based on [1], is for a system with a normal representation but with the value zero not used for an operand and 2n represented by 00⋯0. The design can be modified easily to allow zero and instead use a special flag for 2n as well as for diminished-one representation.
Given two operands, x and y, with neither equal to 2n—special cases that are dealt with separately—the modulo-(2n + 1) product is
Each partial product, \(M_i^{\prime } \stackrel {\triangle }{=} 2^i xy_i\), is nominally represented in 2n bits, and we may split the representation of 2ix, which is
into two n-bit pieces, U and L:
Then 2ix = 2nU + L, and, with Eq. 5.54:
Now, from Sect. 1.1.6, the numeric value, \(\overline {z}\), of the 1s complement of a number U is
so
Therefore
That is
For simplification and correctness, two extra terms are added to the right-hand side of this equation. The first is a term that corresponds to \(\overline {y}_i(-0\cdots 00\cdots 0) = \overline {y}_i(1\cdots 11\cdots 1)+1\) and which allows some factoring. The second is an extra 1, because a normal adder performs modulo-2n operation, and
where c is the carry-out from the addition of a and b.
After some simplification, Eq. 5.58 yields

So, for fast multiplication, the process consists of addition of the terms of Eq. 5.59 in a structure of modulo-(2n + 1) CSAs and an assimilating modulo-(2n + 1) CPA, with each CSA having the extra precision to include the 2. A modulo-(2n + 1) CSA is similar to a modulo-(2n − 1), except that the end-around carry is inverted.
We now consider the special cases and the required corrections. Suppose x is 2n but y is not. Then
Similarly, if y is 2n but x is not, then \(xy \bmod (2^n+1) = (\overline {x}+2) \bmod (2^n+1) \). And if both are equal to 2n, then xy mod (2n + 1) = 1.
The general form of a modulo-(2n + 1) multiplier is shown in Fig. 5.9. The 2n Correction Unit: Since the assimilating carry-propagate adder adds in a 1 (C in above), in this case the inputs to the adder that are required to get the correct results (i.e., \(\overline {y}+2\), or \(\overline {x}+2\), or 1) are \(\overline {y}+1\), or \(\overline {x}+1\), or 0. That is,
Recoding here too is somewhat more complicated than with modulus 2n − 1. Table 5.14 gives one part of the actions for radix-4 recoding and corresponds to Table 5.12. (The index i is incremented by two for each multiplicand multiple.) Also, each multiplicand multiple now has added a two-bit correction term T = t i+1t i:
And the 2 in Eq. 5.59 is replaced with 1.
Notes
- 1.
Strictly, the first addition may be in n bits.
- 2.
Recall that such a compressor can be built to have a delay that is slightly larger than that through a 3:2 compressor.
- 3.
In ordinary multiplication the 2i factor is taken care of by shifting the partial product instead of the multiplicand multiple. That is possible because the lower order i bits of the ith partial product are not included in the corresponding addition. On the other hand, with modular multiplication—specifically the required reductions—all bits of a partial product must be included in the arithmetic; therefore, 2ixy i is taken in its entirety.
References
R. Zimmerman. 1999. Efficient VLSI implementation of modulo (2n ± 1) addition and multiplication. Proceedings, International Symposium on Computer Arithmetic, pp. 158–167.
H. T. Vergos and C. Efstathiou. 2008. A unifying approach for weighted and diminished-one modulo 2n + 1 addition. IEEE Transactions on Circuits and Systems II, 55:1041–1045.
L. Sousa and R. Chaves. 2005. A universal architecture for designing efficient modulo 2n + a multipliers. IEEE Transactions on Circuits and Systems I, 52(6):1166–1178.
R. Muralidharan and C.-H. Chang. 2012. Area-power efficient modulo 2n − 1 and modulo 2n + 1 multipliers for {2n − 1, 2n, 2n + 1} based RNS. IEEE Transactions on Circuits and Systems I, 59(10):2263–2274.
J. W. Chen, R. H. Yao, and W. J. Wu. 2011. Efficient modulo 2n + 1 multipliers. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 19(12):2149–2157.
M. Knezevic, F. Vercauteren, and I. Verbauwhede. 2010. Faster interleaved modular multiplication based on Barrett and Montgomery reduction methods. IEEE Transactions on Computers, 59(12):1715–17121.
H. Orup. 1995. Simplifying quotient determination in high-radix modular multiplication. In: Proceedings, 12th Symposium on Computer Arithmetic, pp. 193–199.
P. Kornerup. 1993. High-radix modular multiplication for cryptosystems. In: Proceedings, 12th Symposium on Computer Arithmetic, pp. 277–283.
A. V. Curiger, H. Bonennenberg, and H. Kaeslin. 1991. Regular VLSI architectures for multiplication modulo 2n + 1. IEEE Journal of Solid-State Circuits, 26(7):990–994.
M.-D. Shieh, J.-H. Chen, W.-C. Lin, and H.-H. Wu. 2009. A new algorithm for high-speed modular multiplication design. IEEE Transactions on Circuits and Systems I, 56(9): 2009–2019.
S.-R. Kuang, J. -P. Wang, K.-C. Chang, and H.-W. Hsu. 2013. Energy-efficient high-throughput Montgomery modular multipliers for RSA cryptosystems. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 21(11):1999–2009.
A. Reza and P. Keshavarzi. 2015. High-throughput modular multiplication and exponentiation algorithms using multibit-scan—multibit-shift technique. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 23(9): 1710–1719.
S.-R. Kung, K.-Y. Wu, and R.-Y. Lu. 2016. Low-cost high-performance VLSI architecture for Montgomery modular multiplication. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 24(2):434–443.
J.-C. Bajard, L.-S. Didier, and P. Kornerup. 1998. An RNS Montgomery modular multiplication algorithm. IEEE Transactions on Computers , 47(7):766–776.
H. K. Garg and H. Xiao. 2016. New residue based Barrett algorithms: modular integer computations. IEEE Access, 4:4882–4890.
C. K. Koc. 1995. RSA Hardware Implementation. Report, RSA Laboratories. Redwood City, California, USA.
H. Orup and P. Kornerup. 1991. A high-radix hardware algorithm for calculating the exponential M E modulo N. Proceedings, 10th IEEE Symposium on Computer Arithmetic, pp. 51–56.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
R. Omondi, A. (2020). Modular Addition and Multiplication. In: Cryptography Arithmetic. Advances in Information Security, vol 77. Springer, Cham. https://doi.org/10.1007/978-3-030-34142-8_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-34142-8_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34141-1
Online ISBN: 978-3-030-34142-8
eBook Packages: Computer ScienceComputer Science (R0)









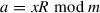
 ;
;  .
.


