A Fully Nonlinear Beam Model of Bernoulli–Euler Type

Abstract

This work presents a geometrically exact Bernoulli–Euler rod model. In contrast to Pimenta (1993b), Pimenta and Yojo (1993), Pimenta (1996), Pimenta and Campello (2001), where the hypothesis considered was Timoshenko’s, this approach is based on the Bernoulli–Euler theory for rods, so that transversal shear deformation is not accounted for. Energetically conjugated cross-sectional stresses and strains are defined. The fact that both the first Piola–Kirchhoff stress tensor and the deformation gradient appear again as primary variables is also appealing. A straight reference configuration is assumed for the rod, but, in the same way, as in Pimenta (1996), Pimenta and Campello (2009), initially curved rods can be accomplished, if one regards the initial configuration as a stress-free deformed state from the straight position. Consequently, the use of convective non-Cartesian coordinate systems is not necessary, and only components on orthogonal frames are employed. A cross section is considered to undergo a rigid body motion and parameterization of the rotation field is done by the rotation tensor with the Rodrigues formula that makes the updating of the rotational variables very simple. This parametrization can be seen in Pimenta et al. (2008), Campello et al. (2011). A simple formula for the incremental Rodrigues parameters in function of the displacements derivative and the torsion angle is also settled down. A 2-node finite element with Cubic Hermitian interpolation for the displacements, together with a linear approximation for the torsion angle, is displayed within the usual Finite Element Method, leading to adequate $C_{1}$ continuity.

1 Introduction

The first objective of this work is to present a geometrically exact Bernoulli–Euler rod formulation and its finite element implementation. The class of admissible motions, that follows from this assumption, is obtained by imposing that the cross sections of the rod, that are initially orthogonal to the chosen axis, remain rigid and orthogonal to it after deformation. Thus, the transversal shear deformation is not accounted for. This theory is called geometrically exact because no approximation is employed after the basic kinematical assumption made. Displacements and rotations can be unlimited large. The Bernoulli–Euler formulation for rods is analogous to the Kirchhoff–Love’s for shells presented in Viebahn et al. (2016), Pimenta et al. (2010).

As framework one uses the theory presented in Pimenta (1993b), Pimenta and Yojo (1993), which is now constrained to obey the Bernoulli–Euler assumption. This approach defines energetically conjugated generalized cross-sectional stress and strains. Besides their practical importance, cross-sectional quantities make the derivation of equilibrium equations easier, as well as the achievement of the corresponding tangent bilinear form, which is always symmetric for hyper-elastic materials and conservative loadings, even far from an equilibrium state.

The models are implemented using the finite element method with cubic Hermitian polynomial interpolation on the displacements and linear Lagrangian interpolation for the considered torsion degree of freedom. Usually in shear deformable rod theories, one needs to worry about shear-locking. With Bernoulli–Euler assumption, the shear deformation is not accounted for in the initial kinematics, therefore, there is no shear-locking. So, there is no need for reduced numerical integration or any other techniques to bypass this problem. Since only initially straight elements are considered here, membrane locking is not an issue too. Linear elastic constitutive equations for small strains are considered in the numerical examples of this paper. A forthcoming paper will address the issue of finite strain elastic and elastic–plastic constitutive equations.

As mentioned before, a straight reference configuration is assumed for the rod. Initially, curved rods can then be regarded as a stress-free deformation from this configuration. This approach was already employed for rods and shells in Pimenta (1996), Pimenta and Campello (2009). It precludes the use of convective non-Cartesian coordinate systems and other complicate entities like Christoffel symbols and fundamental forms. It simplifies, as well, the comprehension of tensor quantities, since only components on orthogonal systems are employed.

Throughout the text, italic Greek or Latin lowercase letters $\left( {a,b, \ldots ,\alpha ,\beta , \ldots } \right)$ denote scalars, bold italic Greek or Latin lowercase letters $\left( {\varvec{a},\varvec{b}, \ldots ,\varvec{\alpha},\varvec{\beta}, \ldots } \right)$ denote vectors and bold italic Greek or Latin capital letters $\left( {\varvec{A},\;\varvec{B},\; \ldots } \right)$ denote second-order tensors in a three-dimensional Euclidean space. Summation convention over repeated indices is adopted in the entire text, whereby Greek indices range from 1 to 2, while Latin indices range from 1 to 3. $\left\| \varvec{v} \right\| = \sqrt {\varvec{v} \cdot \varvec{v}}$ is the is the norm of vector $\varvec{v}$, where $\cdot$ denotes de scalar product of two vectors. The operator $\otimes$ denotes the dyadic or tensor product of two vectors. For instance, $\varvec{a} \otimes \varvec{b}$ is a second-order tensor such that $\left( {\varvec{a} \otimes \varvec{b}} \right)\varvec{c} = \left( {\varvec{b} \cdot \varvec{c}} \right)\varvec{a}$. Note that $\left( {\varvec{a} \otimes \varvec{b}} \right)^{T} = \left( {\varvec{b} \otimes \varvec{a}} \right)$, where $\left( \bullet \right)^{T}$ denotes the transpose. The operator axial $\left( \bullet \right)$ is such that, if $\varvec{v} =$ axial $\left( \varvec{V} \right)$, with $\varvec{V}$ skew-symmetric, then $\varvec{Vx} = \varvec{v} \times \varvec{x}$,$\forall \varvec{x}$, where $\times$ denotes the cross product of two vectors. If $\varvec{v} =$ axial $\left( \varvec{V} \right)$, then $\varvec{V} =$ Skew $\left( \varvec{v} \right)$, with $\varvec{V}$ skew-symmetric.

Rod models are of great interest in structural mechanics and flexible multibody systems. The first works on bending problems date back to Bernoulli investigating deflections of beams and Euler published the first systematic treatment of elastic curves. A full history can be seen in Timoshenko (1953). After these first discoveries, many authors wrote about rods. Until the 60s, most of these works were restricted to linear kinematics.

With the advent of computers, nonlinear problems started to be addressed. First as plane problems Reissner (1972, 1973) and then as three-dimensional ones Antman (1974), Whirman and De Silva (1974), Argyris (1982). The first geometrically exact problems in three-dimensional space were addressed by Simo (1985), resulting in a nonsymmetric tangent matrix far from the equilibrium state. Many authors solved geometrically exact rod problems based on this work, as to name just a few Simo and Vu-Quoc (1986, 1991), Simo (1992), Simo et al. (1992).

As Campello (2000) pointed out, it is evident that these early theories did not have rigor and precision in their conceptualizations, mainly because they are derived from simplifications imposed in the theories of three-dimensional solids.

Pimenta (1993b), Pimenta and Yojo (1993) presented a geometrically exact rod theory in three-dimensional space with the Fréchet derivative of the weak form of the equilibrium being exact and the rotations in three-dimensional space treated in a consistent and convenient way through the Euler–Rodrigues formula. Many authors extended these geometrically exact rod models to incorporate general cross-sectional in-plane changes and out-of-plane warping Pimenta and Campello (2003), distortion of the cross section Sokolov et al. (2015).

All those geometrically exact rod models are not constrained to obey the Bernoulli–Euler assumption as it is done herein. This class of rod models has drawn some attention in the last few years. Boyer and Primault (2004) present a geometrically exact nonlinear Euler–Bernoulli model for the special case of beams with circular cross sections and a straight initial configuration, in Boyer et al. (2011) the same theory is applied to cable dynamics. In the present approach, one can have arbitrary cross sections, the initial configuration is also straight, initially curved rods could be accomplished in the same it way as in Pimenta (1996, Pimenta and Campello 2009), if one regards the initial configuration as a stress-free deformed state from the plane position, this will be subject of future work. Bauer et al. (2016) extend Boyer and Primault (2004) into a nonlinear isogeometric spatial Bernoulli–Euler rod theory that is treated spatially curved and a rotation around the centerline of the rod is adopted as a degree of freedom, that also differs from this work, as it can be seen later. Greco and Cuomo (2013, 2016) have made some advances in nonlinear Bernoulli–Euler rod theory. They use an isogeometric approach. Meier et al. (2014, 2017) has a similar approach for the geometrically exact Bernoulli–Euler rod theory, in terms of initial kinematics configuration, but presents different parameterizations for the rotation. He also indicates two portions of motion on the beam axes, and 4 degrees of freedom, but they connect the elements through as usual in the finite element method, which imposes a continuous rotational degree of freedom. This cannot be true in many examples and is not consistent with the theory. Meier et al. (2016) extend Meier et al. (2014), a geometrically exact beam theory was developed considering discrete Bernoulli hypothesis of rigid cross sections that remain orthogonal to the chosen axis during deformation. Meier et al. (2016) focus on the development of finite element formulations that are capable of accurately modeling the dynamics of slender components and their contact interaction with circular cross sections. All the papers referred to above describes the rotation in a different way we do in this work.

Bernoulli–Euler theory can be widely applied to engineering problems. It can be used in the aerospace industry, oil drilling rods, robot arms and for rib-reinforced shells that are common in aerospace, naval and automobile industry. The hypothesis can be used whenever the rods are slender.

It is proposed a novel interpolation scheme for the rotation field representing the cross-sectional orientation, which is based on Rodrigues parameters and obeys the Bernoulli–Euler constraint. This formulation has continuous displacement degrees of freedom and can have discontinuous degrees of freedom for the derivatives of the displacements and the rotation. The connection between elements is enforced by the de Rodrigues parameter for the rotation being equal on both connecting ends. This is an advantage because one can address sudden changes of cross section or material along the rod, an example that is shown later in Sect. 6. And, there is the opportunity, in general, for the rod element to be used together with a Kirchhoff–Love shell element.

2 Geometrically Exact Bernoulli–Euler Rod Theory

2.1 Kinematics

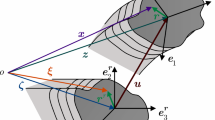
It is assumed at the outset that the rod is straight at the initial configuration, which is used as a reference. This formulation can be directly used for straight finite elements. The case of initially curved rods, which can be used for initially curved finite elements, can be treated as in Pimenta (1996) and is subject to future work. Let $\left\{ {\varvec{e}_{1}^{r} ,\varvec{e}_{2}^{r} ,\varvec{e}_{3}^{r} } \right\}$ be an orthogonal system placed at the reference (or initial) configuration of the rod. The vectors $\varvec{e}_{\alpha }^{r} ,\;\alpha = 1,2$, are placed on the cross sections of the rod, which are orthogonal to the axis at that configuration. Thus, $\varvec{e}_{3}^{r}$ is orthogonal to this plane and tangent to the rod axis.

The position of the rod material points in the reference configuration can be described by

$$\varvec{\xi}=\varvec{\zeta}+ \varvec{r}^{r} ,$$

(1)

where the vector

$$\varvec{\zeta}= \zeta \varvec{e}_{3}^{\varvec{r}} ,$$

(2)

describes the rod axis at reference configuration and $\varvec{r}^{r}$ is the director given by

$$\varvec{r}^{r} = \xi_{\alpha } \varvec{e}_{\alpha }^{\varvec{r}} .$$

(3)

One introduces the axial coordinate $\zeta = \left( {\varvec{\zeta}-\varvec{\zeta}_{0} } \right) \cdot \varvec{e}_{3}^{\varvec{r}}$, $\zeta \in \varOmega = \left( {0,\ell } \right)$, where $\ell$ is the rod length at reference configuration and $\varvec{\zeta}_{0}$ is the position of the axis for $\zeta = 0$. The boundary of the domain $\varOmega$ is denoted by $\varGamma$. Herein, $\varGamma$ contains the two ends of the rod, i.e., $\varGamma = \left\{ {0,\ell } \right\}$. $A \subset {\mathbb{R}}^{2}$ is the cross-sectional domain at the reference configuration. The contour of $A$ is denoted by $C$. Coordinates $\xi_{\alpha } = \varvec{r}^{r} \cdot \varvec{e}_{\alpha }^{r}$ are such that $\left\{ {\xi_{1} ,\;\xi_{2} } \right\}\; \in A$. Thus, $\xi_{1} ,\;\xi_{2} \;{\text{and}}\;\zeta$ build a Cartesian coordinate system.

At the current configuration, according to Fig. 1, the position of the material points is given by

Fig. 1

Rod description and basic kinematical quantities

$$\varvec{x} = \varvec{z} + \varvec{r},$$

(4)

where $\varvec{z} = \hat{\varvec{z}}\left( \zeta \right)$ describes the position of the rod axis at the current configuration and $\varvec{r}$ is the current director given by

$$\varvec{r} = \varvec{Qr}^{r} ,$$

(5)

where $\varvec{Q} = \hat{\varvec{Q}}\left( \zeta \right)$ is the cross-sectional rotation tensor.

The Bernoulli–Euler assumption states that the plane cross sections are subjected to a rigid body motion and remain orthogonal to the axis. After deformation the triad $\left\{ {\varvec{e}_{1}^{r} ,\varvec{e}_{2}^{r} ,\varvec{e}_{3}^{r} } \right\}$ is transformed to $\left\{ {\varvec{e}_{1},\varvec{e}_{2} ,\varvec{e}_{3}} \right\}$ at current configuration. $\varvec{e}_{3}$ is orthogonal to the cross sections and tangent to rod axis, while $\varvec{e}_{\alpha } , \alpha = 1,2$ remain attached to the cross sections. The axis of the rod at current configuration is defined by the axis placement. The vector $\varvec{e}_{3}$ is defined by the axis as well, but the unitary vectors $\varvec{e}_{\alpha } ,\;\alpha = 1,2$ the cross sections are not. They can be rotated around the rod axis and need an additional parameter, which is called herein torsion parameter. It can also be regarded as a rotation around a moving axis. We denote this scalar by $\varphi$. It follows that the rotation tensor can be expressed by

$$\varvec{Q} = \hat{\varvec{Q}}\left( {\varvec{e}_{3} ,\varphi } \right).$$

(6)

Note that no cross-sectional change is assumed. A general Bernoulli–Euler theory that incorporates cross section in-plane and out-of-plane changes will be presented in a coming work under preparation.

Remark 1: Back-Rotated Or Material Vectors

The following notation for vectors in ${\mathbb{R}}^{3}$ is used, $\left( \bullet \right) = \varvec{Q}\left( \bullet \right)^{r} \Leftrightarrow \left( \bullet \right)^{r} = \varvec{Q}^{T} \left( \bullet \right)$. The vector $\left( \bullet \right)^{r}$ is said to be the back-rotated or material counterpart of $\left( \bullet \right)$ and is not affected by superimposed rigid body motions. On the other hand, $\left( \cdot \right)$ is said to be the spatial counterpart of $\left( \cdot \right)^{r}$. Notice that the vector $\left( \bullet \right)$ has the same components on the local system $\left\{ {\varvec{e}_{i} = \varvec{Qe}_{i}^{r} ,\;i = 1,2,3} \right\}$ as the vector $\left( \bullet \right)^{r}$ has on the system $\left\{ {\varvec{e}_{i}^{r} ,\;i = 1,2,3} \right\}$.

2.2 Rodrigues Parameterization

Let $\theta$ denote a rotation around an axis defined by the unitary vector $\varvec{e}$. Let $\varvec{\theta}$ represent the vector of Euler parameters. Then, one defines the following vector of Rodrigues parameters $\varvec{\alpha}= \alpha \,\varvec{e}$, where $\alpha = 2\tan {\theta \mathord{\left/ {\vphantom {\theta 2}} \right. \kern-0pt} 2}$. The rotation tensor is then given by Pimenta and Campello (2001), Campello et al. (2003), Argyris (1982)

$$\hat{\varvec{Q}}\left(\varvec{\alpha}\right) = \left( {\varvec{I} - \frac{1}{2}\varvec{A}} \right)^{ - 1} \left( {\varvec{I} + \frac{1}{2}\varvec{A}} \right),$$

(7)

where $\varvec{A} = {\text{Skew}}\left(\varvec{\alpha}\right)$. An alternative to (7) is

$$\hat{\varvec{Q}}\left(\varvec{\alpha}\right) = \varvec{I} + \frac{4}{{4 + \alpha^{2} }}\left( {\varvec{A} + \frac{1}{2}\varvec{A}^{2} } \right),$$

(8)

where $\alpha^{2} =\varvec{\alpha}\cdot\varvec{\alpha}$.

For the spin vector

$$\varvec{\omega}= {\text{axial}}\left(\varvec{\varOmega}\right),\quad {\text{where}}\quad\varvec{\varOmega}= \dot{\varvec{Q}}\varvec{Q}^{T} ,$$

(9)

the following relation holds

$$\varvec{\omega}=\varvec{\varXi}\dot{\varvec{\alpha }},\quad {\text{where}}\quad\varvec{\varXi}= \frac{4}{{4 + \alpha_{{}}^{2} }}\left( {\varvec{I} + \frac{1}{2}\varvec{A}} \right),$$

(10)

which has been derived for the first time in Pimenta and Campello (2001).

2.3 Incremental Description of the Rotation

The use of Rodrigues parameters is restricted to $- \pi < \theta < \pi$. To overcome this drawback, we describe the rotation by the incremental approach, as in Pimenta et al. (2008). This limitation is then restricted to a load increment in Statics or to a time increment in Dynamics.

Let $\left( \cdot \right)_{i}$ and $\left( \cdot \right)_{i + 1}$ denote a quantity $\left( \cdot \right)$ at instants $t_{i}$ and $t_{i + 1}$, respectively. And let $\left( \cdot \right)_{\Delta }$ be an incremental quantity. Thus, one gets for the rotation tensor the following relations

$$\begin{aligned} \varvec{Q}_{i + 1} & = \varvec{Q}_{\Delta } \varvec{Q}_{i}, {\text{where}} \\ \varvec{Q}_{i + 1} & = \hat{\varvec{Q}}\left( {\varvec{\alpha}_{i + 1} } \right),\varvec{Q}_{\Delta } = \hat{\varvec{Q}}\left( {\varvec{\alpha}_{\Delta } } \right)\quad {\text{and}}\quad \varvec{Q}_{i} = \hat{\varvec{Q}}\left( {\varvec{\alpha}_{i} } \right). \\ \end{aligned}$$

(11)

We recall the following result by Rodrigues, which is probably the most relevant result by him,

$$\varvec{\alpha}_{i + 1} = \frac{4}{{4 -\varvec{\alpha}_{i} \cdot\varvec{\alpha}_{\Delta } }}\left( {\varvec{\alpha}_{i} +\varvec{\alpha}_{\Delta } - \frac{1}{2}\varvec{\alpha}_{i} \times\varvec{\alpha}_{\Delta } } \right).$$

(12)

In the incremental description one has for the spin vector

$$\varvec{\omega}= {\text{axial}}\left(\varvec{\varOmega}\right),\quad {\text{where}}\quad\varvec{\varOmega}= \dot{\varvec{Q}}_{\Delta } \varvec{Q}_{\Delta }^{T} ,$$

(13)

the following relation

$$\varvec{\omega}=\varvec{\varXi}_{\Delta } \dot{\varvec{\alpha }}_{\Delta } ,\quad {\text{where}}\quad\varvec{\varXi}_{\Delta } = \frac{4}{{4 + \alpha_{\Delta }^{2} }}\left( {\varvec{I} + \frac{1}{2}\varvec{A}_{\Delta } } \right),$$

(14)

where $\varvec{A}_{\Delta } = {\text{Skew}}\left( {\varvec{\alpha}_{\Delta } } \right)$ and $\alpha_{\Delta }^{2} =\varvec{\alpha}_{\Delta }^{{}} \cdot\varvec{\alpha}_{\Delta }^{{}}$.

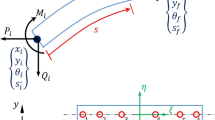
At instants $t_{i}$ and $t_{i + 1}$ triad $\left\{ {\varvec{e}_{1}^{{}} ,\varvec{e}_{2}^{{}} ,\varvec{e}_{3}^{{}} } \right\}$ is denoted by $\left\{ {\varvec{e}_{1}^{i} ,\varvec{e}_{2}^{i} ,\varvec{e}_{3}^{i} } \right\}$ and $\left\{ {\varvec{e}_{1}^{i + 1} ,\varvec{e}_{2}^{i + 1} ,\varvec{e}_{3}^{i + 1} } \right\}$, respectively. We denote the incremental torsion parameter by $\varphi_{\Delta }$. This is schematically shown in Fig. 2. From (7) and $\varvec{e}_{3}^{i + 1} = \varvec{Q}_{\Delta } \varvec{e}_{3}^{i}$, one arrives at the important result below

Fig. 2

Description of the incremental motion of the vector that describes de axis of the rod

$$\varvec{e}_{3}^{i + 1} - \varvec{e}_{3}^{i} =\varvec{\alpha}_{\Delta } \times \varvec{e}_{3}^{m} ,\quad {\text{where}}\quad \varvec{e}_{3}^{m} = \frac{1}{2}\left( {\varvec{e}_{3}^{i + 1} + \varvec{e}_{3}^{i} } \right).$$

(15)

We remark that $\varvec{e}_{3}^{m}$ is not a unitary vector, but $\left\| {\varvec{e}_{3}^{m} } \right\|^{ - 1} \varvec{e}_{3}^{m}$ is. Now we state

$$\varvec{\alpha}_{\Delta } = \left\| {\varvec{e}_{3}^{m} } \right\|^{ - 2} \left( {\varvec{e}_{3}^{i} \times \varvec{e}_{3}^{i + 1} } \right) + \varphi_{\Delta } \left\| {\varvec{e}_{3}^{m} } \right\|^{ - 1} \varvec{e}_{3}^{m} .$$

(16)

We can show that (16), after some algebraic manipulation, preserves (15)₁. Note that

$$\varphi_{\Delta } = \left\| {\varvec{e}_{3}^{m} } \right\|^{ - 1}\varvec{\alpha}_{\Delta } \cdot \varvec{e}_{3}^{m} .$$

(17)

Thus, assuming that the configuration at $t_{i}$ is known, the incremental rotation tensor in (11) can be expressed as

$$\varvec{Q}_{\Delta } = \hat{\varvec{Q}}_{\Delta } \left( {\varvec{e}_{3}^{i + 1} ,\varphi_{\Delta } } \right),$$

(18)

which is the incremental counterpart of (6).

Meier et al. (2014) uses a similar rotation parameter, but their conclusion on this matter is that an Hermite interpolation of the relative angle $\varphi_{\Delta }$‘(s) would lead to a non-objective element formulation. $\varphi_{\Delta }$ in Meier et al. (2014) is used within the context of the “smallest rotation” triad, but not within the Rodrigues parameterization.

Remark 2: Alternative Definition of Incremental Torsion Parameter

In place of (16), we could define

$$\varvec{\alpha}_{\Delta } = \left\| {\varvec{e}_{3}^{m} } \right\|^{ - 2} \left( {\varvec{e}_{3}^{i} \times \varvec{e}_{3}^{i + 1} } \right) + 2\tan \frac{{\varphi_{\Delta } }}{2}\left\| {\varvec{e}_{3}^{m} } \right\|^{ - 1} \varvec{e}_{3}^{m} ,$$

which seems to be more adequate when the rotation is a torsion around a fixed axis. (16) simplifies the resulting equations. We recall that both are equal to second order with respect to the torsion parameter $\varphi_{\Delta }$.

Remark 3: Objectivity

Objectivity is a major issue for any formulation dealing with large deformations. We remark that the rod theory presented herein entirely fulfills objectivity requirements in the sense of continuum mechanics. Objectivity of the strain and stress measures is assured since one uses only material (back-rotated) quantities in the constitutive equations and thus are invariant under superposed rigid body motions. An analytical proof of this property is straightforward and will be omitted here. It is easy to verify that (16) is also objective. The torsion parameter $\varphi_{\Delta }$ is a scalar, therefore it is objective as well, as (17) show.

Remark 4: Path-Dependency

It is also important to mention that by adopting an incremental description for the rotations, this description for the rotation turns out to be path-dependent. But one should keep in mind that path-dependency is a natural consequence when the time variable is discretized in the framework of a time-stepping scheme, which is mandatory for the numerical simulation of dynamical processes. Moreover, upon time increment refinement the dependence on the history of incrementation decreases and in an asymptotic manner path-independence is reached, as also discussed in Pimenta et al. (2008), Campello et al. (2011), Crisfield and Jelenic (1999). This is an obvious consequence, since (16) is numerically consistent.

2.4 Strains

According to the Bernoulli–Euler assumption the unitary vector $\varvec{e}_{3}$ is given by

$$\varvec{e}_{3} = \left\| {\varvec{z^{\prime}}} \right\|^{ - 1} \varvec{z^{\prime}},$$

(19)

whereby the following notation for derivative along the axis has been defined

$$\left( \bullet \right)^{\prime } = \frac{d\left( \bullet \right)}{d\zeta }.$$

(20)

$\varvec{e}_{3}$ is tangent to the rod axis in the current configuration and orthogonal to the cross sections (19) makes this formulation different from Pimenta (1993b), Pimenta and Yojo (1993) and the geometrically exact theory is constrained ab initio to obey the Bernoulli–Euler assumption.

Displacements of the points on the rod axis are defined by

$$\varvec{u} = \varvec{z} -\varvec{\zeta}.$$

(21)

Note also that

$$\varvec{z^{\prime}} = \varvec{e}_{3}^{r} + \varvec{u^{\prime}}\quad {\text{and}}\quad \varvec{z^{\prime\prime}} = \varvec{u^{\prime\prime}}.$$

(22)

Analogously to (9), the curvature vector of the axis at the current configuration is given by

$$\varvec{\kappa}= {\text{axial}}\left( {\varvec{Q^{\prime}Q}^{T} } \right).$$

(23)

Since $\left( {\dot{\varvec{Q}}} \right)^{\prime } = \left( {\varvec{Q^{\prime}}} \right)^{ \cdot }$, one has

$$\varvec{\omega^{\prime}} = \dot{\varvec{\kappa }} -\varvec{\omega}\times\varvec{\kappa}.$$

(24)

Time differentiation of $\varvec{\kappa}^{r} = \varvec{Q}^{T}\varvec{\kappa}$ leads to $\dot{\varvec{\kappa }}^{r} = \varvec{Q}^{T} \left( {\dot{\varvec{\kappa }} -\varvec{\omega}\times\varvec{\kappa}} \right)$. Hence, from (24), one arrives at the important relation displayed below

$$\dot{\varvec{\kappa }}_{{}}^{r} = \varvec{Q}^{T} \varvec{\omega^{\prime}}\varvec{.}$$

(25)

The deformation gradient can then be expressed by

$$\varvec{F} = \varvec{QF}^{r} ,$$

(26)

where

$$\varvec{F}^{r} = \varvec{I} +\varvec{\gamma}_{{}}^{r} \otimes \varvec{e}_{3}^{r}$$

(27)

is the back-rotated deformation gradient, $\varvec{I}$ is the identity tensor and

$$\varvec{\gamma}_{{}}^{r} =\varvec{\eta}_{{}}^{r} +\varvec{\kappa}_{{}}^{r} \times \varvec{r}^{r}$$

(28)

are back-rotated cross section strains. In (28) the following generalized back-rotated strain has been introduced

$$\varvec{\eta}^{r} = \varvec{Q}^{T} \varvec{z^{\prime}} - \varvec{e}_{3}^{r} .$$

(29)

We remark that

$$\varvec{\eta}^{r} \cdot \varvec{e}_{\alpha }^{r} =\varvec{\eta}^{r} \times \varvec{e}_{3}^{r} = 0.$$

(30)

due to the Bernoulli–Euler assumption. Note that

$$\varvec{\eta}^{r} = \varepsilon \varvec{e}_{3}^{r} ,\quad {\text{where}}\quad \varepsilon = \left\| {\varvec{z^{\prime}}} \right\| - 1$$

(31)

(28) and (29) are the back-rotated counterparts of the following cross-sectional generalized strains

$$\varvec{\gamma}=\varvec{\eta}+\varvec{\kappa}\times \varvec{r}\quad {\text{and}}\quad\varvec{\eta}= \varvec{z^{\prime}} - \varvec{e}_{3} .$$

(32)

From (19) and (22)₁, it follows that $\varvec{e}_{3}^{{}} = \hat{\varvec{e}}_{3}^{{}} \left( {\varvec{u^{\prime}}} \right)$, which together with (18) leads to

$$\varvec{\alpha}_{\Delta } = \hat{\varvec{\alpha }}_{\Delta } \left( {\varvec{u^{\prime}}_{i + 1} ,\varphi_{\Delta } } \right).$$

(33)

Hence, one may write

$$\dot{\varvec{\alpha }}_{\Delta } = \varvec{W\dot{u}^{\prime}} + \varvec{w}\dot{\varphi }_{\Delta } ,$$

(34)

where

$$\varvec{W} = \frac{{\partial\varvec{\alpha}_{\Delta } }}{{\partial \varvec{u^{\prime}}}}\quad {\text{and}}\quad \varvec{w} = \frac{{\partial\varvec{\alpha}_{\Delta } }}{{\partial \varphi_{\Delta } }}.$$

(35)

With the aid of (14), (35) and (34), the spin vector can be written as

$$\varvec{\omega}=\varvec{\varXi}_{\Delta } \varvec{W\dot{u}^{\prime}} +\varvec{\varXi}_{\Delta } \varvec{w}\dot{\varphi }_{\Delta } .$$

(36)

On the other hand, the curvature vector needs to be updated at instant $t_{i + 1}$ from the curvature vector at instant $\varvec{\kappa}_{i}$. From (23) one gets

$$\varvec{\kappa}_{i + 1} = {\text{axial}}\left( {\varvec{Q^{\prime}}_{i + 1} \varvec{Q}_{i + 1}^{T} } \right) = {\text{axial}}\left( {\left( {\varvec{Q}_{\Delta } \varvec{Q}_{i} } \right)^{\prime } \varvec{Q}_{i}^{T} \varvec{Q}_{\Delta }^{T} } \right)$$

(37)

This delivers

$$\varvec{\kappa}_{i + 1} = \varvec{Q}_{\Delta }\varvec{\kappa}_{i} +\varvec{\varXi}_{\Delta } \varvec{\alpha^{\prime}}_{\Delta } .$$

(38)

Introducing (33) in (38), and using definitions (35), one gets

$$\varvec{\alpha^{\prime}}_{\Delta } = \varvec{Wu^{\prime\prime}} + \varvec{w}\varphi^{\prime}_{\Delta } ,$$

(39)

Similarly, the back-rotated curvature vector at instant $t_{i + 1}$ is given by

$$\varvec{\kappa}_{i + 1}^{r} =\varvec{\kappa}_{i}^{r} + \varvec{Q}_{i + 1}^{T}\varvec{\varXi}_{\Delta } \varvec{\alpha^{\prime}}_{\Delta } .$$

(40)

The derivatives in (35) are now displayed below,

$$\begin{aligned} \varvec{W} & = \left[ {\left\| {\varvec{e}_{3}^{m} } \right\|^{ - 2} \varvec{E}_{3}^{i} - \left\| {\varvec{e}_{3}^{m} } \right\|^{ - 4} \left( {\varvec{e}_{3}^{i} \times \varvec{e}_{3}^{i + 1} } \right) \otimes \varvec{e}_{3}^{m} } \right]\left\| {\varvec{z^{\prime}}} \right\|^{ - 1} \varvec{M}^{b} \\ & \quad + \frac{1}{2}\varphi_{\Delta } \left\| {\varvec{e}_{3}^{m} } \right\|^{ - 1} \left( {\varvec{I} - \left\| {\varvec{e}_{3}^{m} } \right\|^{ - 2} \varvec{e}_{3}^{m} \otimes \varvec{e}_{3}^{m} } \right)\left\| {\varvec{z^{\prime}}} \right\|^{ - 1} \varvec{M}^{b} \\ \end{aligned}$$

(41)

and

$$\varvec{w} = \left\| {\varvec{e}_{3}^{m} } \right\|^{ - 1} \varvec{e}_{3}^{m} .$$

(42)

In (41), one has introduced $\varvec{E}_{3}^{i} = {\text{Skew}}\left( {\varvec{e}_{3}^{i} } \right)$, and $\varvec{M}^{b} = \varvec{I} - \varvec{e}_{3}^{i + 1} \otimes \varvec{e}_{3}^{i + 1}$. Note that $\left( {\varvec{M}^{b} } \right)^{k} = \varvec{M}^{b}$, so that $\varvec{W}$ in (35) has following property

$$\varvec{WM}^{b} = \varvec{W}\varvec{.}$$

(43)

Note that, with assistance from (15), one gets

$$\varvec{\varXi}_{\Delta } \varvec{w} = \frac{4}{{4 + \alpha_{\Delta }^{2} }}\left\| {\varvec{e}_{3}^{m} } \right\|^{ - 1} \varvec{e}_{3}^{i + 1} .$$

(44)

Hence, in place of (36) and (40), one has

$$\varvec{\omega}=\varvec{\omega}^{m} +\varvec{\omega}^{b} \quad {\text{and}}\quad\varvec{\kappa}_{i + 1}^{r} =\varvec{\kappa}_{i}^{r} + \varvec{Q}_{i + 1}^{T} \left( {\varvec{\kappa}_{\Delta }^{m} +\varvec{\kappa}_{\Delta }^{b} } \right),$$

(45)

respectively, where, with aid of (43), one has

$$\begin{aligned}\varvec{\omega}^{m} & = \left( {\frac{4}{{4 + \alpha_{\Delta }^{2} }}\left\| {\varvec{e}_{3}^{m} } \right\|^{ - 1} \dot{\varphi }_{\Delta } } \right)\varvec{e}_{3}^{i + 1} ,\quad\varvec{\omega}^{b} =\varvec{\varXi}_{\Delta } \varvec{WM}^{b} \varvec{\dot{u}^{\prime}}, \\\varvec{\kappa}_{\Delta }^{m} & = \left( {\frac{4}{{4 + \alpha_{\Delta }^{2} }}\left\| {\varvec{e}_{3}^{m} } \right\|^{ - 1} \varphi^{\prime}_{\Delta } } \right)\varvec{e}_{3}^{i + 1} \quad {\text{and}}\quad\varvec{\kappa}_{\Delta }^{b} =\varvec{\varXi}_{\Delta } \varvec{WM}^{b} \varvec{u^{\prime\prime}}. \\ \end{aligned}$$

(46)

Remark 5: Variance of the Axis Position

It is remarked that $\varvec{\gamma}^{r} \cdot \varvec{e}_{\alpha }^{r} = 0$ only at the chosen rod axis $\left( {\xi_{\alpha } = 0} \right)$. Therefore, the Bernoulli–Euler theory is not invariant with respect to the axis position. One can show that the axis should be placed on the cross-section shear centers.

Remark 6: Axial and Transversal Parts of a Vector

According to (45), one defines the axial (membrane) and transversal (bending) parts of a vector $\varvec{v}$ by $\varvec{v}^{m} = \left( {\varvec{e}_{3} \otimes \varvec{e}_{3} } \right)\varvec{v}$ and $\varvec{v}^{b} = \varvec{M}^{b} \varvec{v}$, respectively. (46) shows that only the bending parts of $\varvec{u^{\prime}}$ and $\varvec{u^{\prime\prime}}$ affect the spin and incremental curvature vectors, respectively.

Remark 7: Number of Turns Around a Moving Axis

The number of turns around the moving axis $\varvec{e}_{3}$ can be computed through

$$N = \sum\limits_{i} {\frac{{\varphi_{\Delta } }}{2\pi }} .$$

(47)

(47) allows us to count the number of turns that a cross section did from the initial to the current configuration.

2.5 Strain Rates

The velocity gradient is given by time differentiation of (26)

$$\dot{\varvec{F}} =\varvec{\varOmega}\varvec{F} + \varvec{Q}\left( {\dot{\varvec{\gamma }}_{{}}^{r} \otimes \varvec{e}_{3}^{r} } \right),$$

(48)

where

$$\dot{\varvec{\gamma }}^{r} = \dot{\varvec{\eta }}^{r} + \dot{\varvec{\kappa }}^{r} \times \varvec{r}^{r} .$$

(49)

Finally, from (25) and (40), one gets

$$\dot{\varvec{\kappa }}_{i + 1}^{r} = \varvec{Q}_{i + 1}^{T} \varvec{\omega^{\prime}}_{i + 1} = \varvec{Q}_{i}^{T} \varvec{Q}_{\Delta }^{T} \left( {\varvec{\varXi}_{\Delta } \dot{\varvec{\alpha }}_{\Delta } } \right)^{\prime } .$$

(50)

Hence, one may write

$$\dot{\varvec{\kappa }}_{i + 1}^{r} = \varvec{Q}_{i}^{T} \varvec{Q}_{\Delta }^{T} \varvec{\varXi^{\prime}}_{\Delta } \dot{\varvec{\alpha }}_{\Delta } + \varvec{Q}_{i}^{T} \varvec{Q}_{\Delta }^{T}\varvec{\varXi}_{\Delta } \varvec{\dot{\alpha }^{\prime}}_{\Delta } .$$

(51)

On the other hand, time differentiation of (29) yields

$$\dot{\varvec{\eta }}^{r} = \varvec{Q}^{T} \varvec{\dot{u}^{\prime}} + \dot{\varvec{Q}}^{T} \varvec{z^{\prime}} = \varvec{Q}^{T} \left( {\varvec{\dot{u}^{\prime}} + \varvec{z^{\prime}} \times\varvec{\omega}} \right).$$

(52)

Thus, with $\varvec{Z^{\prime}} = {\text{Skew}}\left( {\varvec{z^{\prime}}} \right)$, one may write

$$\dot{\varvec{\eta }}_{i + 1}^{r} = \varvec{Q}_{i + 1}^{T} \left( {\varvec{\dot{u}^{\prime}}_{i + 1} + \varvec{Z^{\prime}}_{i + 1}\varvec{\varXi}_{\Delta } \dot{\varvec{\alpha }}_{\Delta } } \right).$$

(53)

2.6 Stresses

Let the 1^st Piola–Kirchhoff stress tensor be expressed by its columns as follows

$$\varvec{P} =\varvec{\tau}_{i} \otimes \varvec{e}_{i}^{r} = \varvec{Q}\left( {\varvec{\tau}_{i}^{r} \otimes \varvec{e}_{i}^{r} } \right).$$

(54)

One can now introduce the back-rotated 1^st Piola-Kirchhoff stress tensor by

$$\varvec{P}^{r} = \varvec{Q}^{T} \varvec{P} =\varvec{\tau}_{i}^{r} \otimes \varvec{e}_{i}^{r} ,$$

(55)

where

$$\varvec{\tau}_{i}^{r} = \varvec{Q}^{T}\varvec{\tau}_{i} ,\quad i = 1,2,3,$$

(56)

are the back-rotated nominal stress vectors.

The following cross-sectional resultants are obtained by integration of the stresses $\varvec{\tau}=\varvec{\tau}_{3}$ on the cross section

$$\varvec{n} = \int_{A} {\varvec{\tau}dA} \quad {\text{and}}\quad \varvec{m} = \int_{A} {\left( {\varvec{r} \times\varvec{\tau}} \right)dA} .$$

(57)

$\varvec{n}$ are the true forces and $\varvec{m}$ are the true moments that are acting on a cross section. The axial (membrane) and transversal (bending) parts of the force $\varvec{n}$ are expressed by

$$\varvec{n}^{m} = \left( {\varvec{e}_{3} \otimes \varvec{e}_{3} } \right)\varvec{n} = N\varvec{e}_{3} \quad {\text{and}}\quad \varvec{n}^{b} = \varvec{M}^{b} \varvec{n} = V_{\alpha } \varvec{e}_{\alpha } ,$$

(58)

respectively, where $N = \varvec{n} \cdot \varvec{e}_{3}$ and $V_{\alpha } = \varvec{n} \cdot \varvec{e}_{\alpha }$ are the normal and shear forces that are acting on the cross section, respectively.

Their back-rotated counterparts are

$$\varvec{n}^{r} = \varvec{Q}^{T} \varvec{n}\quad {\text{and}}\quad \varvec{m}^{r} = \varvec{Q}^{T} \varvec{m}.$$

(59)

Hence, one may also write

$$\varvec{n}^{r} = \int_{A} {\varvec{\tau}^{r} dA} \quad {\text{and}}\quad \varvec{m}^{r} = \int_{A} {\left( {\varvec{r}^{r} \times\varvec{\tau}^{r} } \right)dA} .$$

(60)

$\varvec{n}_{{}}^{r}$ and $\varvec{m}_{{}}^{r}$ are the back-rotated cross section forces and moments, respectively. The back-rotated counterparts of (58) are

$$\varvec{n}^{mr} = N\varvec{e}_{3}^{r} \quad {\text{and}}\quad \varvec{n}^{br} = V_{\alpha } \varvec{e}_{\alpha }^{r} ,$$

(61)

For the bending moments and the torsion moment, $M_{\alpha } = \varvec{m} \cdot \varvec{e}_{\alpha } = \varvec{m}^{{_{{}}^{{}} }} \cdot \varvec{e}_{\alpha }^{r}$ and $T = \varvec{m} \cdot \varvec{e}_{3} = \varvec{m}^{r} \cdot \varvec{e}_{3}^{r}$ are written, respectively. Hence, one has

$$\begin{aligned} \varvec{n} & = V_{\alpha } \varvec{e}_{\alpha } + N\varvec{e}_{3} \quad {\text{and}}\quad \varvec{m} = M_{\alpha } \varvec{e}_{\alpha } + T\varvec{e}_{3} ,\quad {\text{or}} \\ \varvec{n}^{r} & = V_{\alpha } \varvec{e}_{\alpha }^{r} + N\varvec{e}_{3}^{r} \quad {\text{and}}\quad \varvec{m}^{r} = M_{\alpha } \varvec{e}_{\alpha }^{r} + T\varvec{e}_{3}^{r} . \\ \end{aligned}$$

(62)

2.7 Kinetics

From (54) and (48) and the angular momentum balance $\varvec{PF}^{T} :\varvec{\varOmega}= 0$, one gets the following result:

$$\varvec{P}:\dot{\varvec{F}} =\varvec{\tau}^{r} \cdot \dot{\varvec{\gamma }}^{r} .$$

(63)

(63) is the stress power per unit of reference volume. Introducing (49) in (63) and after some manipulation with the cross product, one gets

$$\varvec{P}:\dot{\varvec{F}} =\varvec{\tau}^{r} \cdot \dot{\varvec{\eta }}^{r} + \left( {\varvec{r}^{r} \times\varvec{\tau}^{r} } \right) \cdot \dot{\varvec{\kappa }}^{r} .$$

(64)

Note that $\varvec{\tau}_{\alpha }^{r}$ are powerless in this model. With the aid of the definitions (60), the integration of (64) over the cross section furnishes

$$\int_{A} {\left( {\varvec{P}:\dot{\varvec{F}}} \right)dA} = \varvec{n}^{r} \cdot \dot{\varvec{\eta }}^{r} + \varvec{m}^{r} \cdot \dot{\varvec{\kappa }}^{r} .$$

(65)

(65) is the stress power per unit length of the reference axis. It is important to remark that $\varvec{n}^{r} ,\varvec{m}^{r} ,\varvec{\eta}^{r} {\text{and}}\;\varvec{\kappa}^{r}$ are not affected by superimposed rigid body motions. Regarding (61)₁, one has

$$\varvec{n}^{r} \cdot \dot{\varvec{\eta }}^{r} + \varvec{m}^{r} \cdot \dot{\varvec{\kappa }}^{r} = \varvec{n}^{mr} \cdot \dot{\varvec{\eta }}^{r} + \varvec{m}^{r} \cdot \dot{\varvec{\kappa }}^{r} . .$$

(66)

The internal power on the domain $\varOmega$ is then given by

$$P_{\text{int}}^{\varOmega } = \int_{\varOmega } {\left( {\varvec{n}^{r} \cdot \dot{\varvec{\eta }}^{r} + \varvec{m}^{r} \cdot \dot{\varvec{\kappa }}^{r} } \right)d\varOmega } .$$

(67)

On the other hand, the external power on the same domain can be expressed by

$$P_{\text{ext}}^{\varOmega } = \int_{\varOmega } {\left[ {\int_{C} {\left( {\bar{\varvec{t}} \cdot \dot{\varvec{x}}} \right)dC} + \int_{A} {\left( {\bar{\varvec{b}} \cdot \dot{\varvec{x}}} \right)dA} } \right]d\varOmega } ,$$

(68)

where $\bar{\varvec{t}}$ is the surface traction per unit reference area that is prescribed on the lateral surface of the rod and $\bar{\varvec{b}}$ is the body force per unit reference volume. The time differentiation of (4) yields

$$\dot{\varvec{x}} = \dot{\varvec{u}} +\varvec{\omega}\times \varvec{r}.$$

(69)

With following definitions

$$\bar{\varvec{n}}^{\varOmega } = \int_{C} {\bar{\varvec{t}}dC} + \int_{A} {\bar{\varvec{b}}dA} \;{\text{and}}\;\bar{\varvec{m}}^{\varOmega } = \int_{C} {\left( {\varvec{r} \times \bar{\varvec{t}}} \right)dC} + \int_{A} {\left( {\varvec{r} \times \bar{\varvec{b}}} \right)dA} ,$$

(70)

Together with (69), one may write

$$P_{\text{ext}}^{\varOmega } = \int_{\varOmega } {\left( {\bar{\varvec{n}}^{\varOmega } \cdot \dot{\varvec{u}} + \bar{\varvec{m}}^{\varOmega } \cdot\varvec{\omega}} \right)d\varOmega } = \int_{\varOmega } {\left( {\bar{\varvec{n}}^{\varOmega } \cdot \dot{\varvec{u}} +\varvec{\varXi}_{\Delta }^{T} \bar{\varvec{m}}^{\varOmega } \cdot \dot{\varvec{\alpha }}_{\Delta } } \right)d\varOmega } .$$

(71)

$\bar{\varvec{n}}^{\varOmega }$ is the applied external force per unit length at reference configuration and $\bar{\varvec{m}}^{\varOmega }$ is the applied external moment per unit length at reference configuration. Introducing (34) in (71), it furnishes

$$P_{\text{ext}}^{\varOmega } = \int_{\varOmega } {\left( {\bar{\varvec{n}}^{\varOmega } \cdot \dot{\varvec{u}} + \bar{\varvec{\mu }}^{\varOmega } \cdot \varvec{\dot{u^{\prime}}} + \bar{\mu }^{\varOmega } \dot{\varphi }_{\Delta } } \right)d\varOmega } ,$$

(72)

where

$$\bar{\varvec{\mu }}^{\varOmega } = \varvec{W}^{T}\varvec{\varXi}_{\Delta }^{T} \bar{\varvec{m}}^{\varGamma } \quad {\text{and}}\quad \bar{\mu }^{\varOmega } = \varvec{w} \cdot\varvec{\varXi}_{\Delta }^{T} \bar{\varvec{m}}^{\varGamma }$$

(73)

are the pseudo-bending-moments and the pseudo-torsion-moments per unit reference length applied along the rod, respectively. Note that $\bar{\varvec{\mu }}^{\varOmega b} = \bar{\varvec{\mu }}^{\varOmega }$ and $\bar{\varvec{\mu }}^{\varOmega } \cdot \varvec{\dot{u^{\prime}}} = \bar{\varvec{\mu }}^{\varOmega } \cdot \left( {\varvec{\dot{u^{\prime}}}} \right)^{b}$.

Similarly to (70), one defines

$$\bar{\varvec{n}}^{\varGamma } = \int_{C} {\bar{\varvec{t}}dC} + \int_{A} {\bar{\varvec{b}}dA} \;{\text{and}}\;\bar{\varvec{m}}^{\varGamma } = \int_{C} {\left( {\varvec{r} \times \bar{\varvec{t}}} \right)dC} + \int_{A} {\left( {\varvec{r} \times \bar{\varvec{b}}} \right)dA} .$$

(74)

Thus, with the aid of (69), one may write for the rod ends

$$P_{\text{ext}}^{\varGamma } = \left( {\bar{\varvec{n}}^{\varGamma } \cdot \dot{\varvec{u}} + \bar{\varvec{m}}^{\varGamma } \cdot\varvec{\omega}} \right)_{\varGamma } = \left( {\bar{\varvec{n}}^{\varGamma } \cdot \dot{\varvec{u}} +\varvec{\varXi}_{\Delta }^{T} \bar{\varvec{m}}^{\varGamma } \cdot \dot{\varvec{\alpha }}_{\Delta } } \right)_{\varGamma } .$$

(75)

$\bar{\varvec{n}}^{\varGamma }$ and $\bar{\varvec{m}}^{\varGamma }$ are the applied external forces and moments at rod ends, respectively. In (75), the notation $\left( \cdot \right)_{\varGamma } = \left( \cdot \right)_{\zeta = \ell } - \left( \cdot \right)_{\zeta = 0}$ has been introduced. With (34), (71) furnishes

$$P_{\text{ext}}^{\varGamma } = \left( {\bar{\varvec{n}}^{\varGamma } \cdot \dot{\varvec{u}} + \bar{\varvec{\mu }}^{\varGamma } \cdot \varvec{\dot{u^{\prime}}} + \bar{\mu }^{\varGamma } \dot{\varphi }_{\Delta } } \right)_{\varGamma } ,$$

(76)

where

$$\bar{\varvec{\mu }}^{\varGamma } = \varvec{W}^{T}\varvec{\varXi}_{\Delta }^{T} \bar{\varvec{m}}^{\varGamma } \quad {\text{and}}\quad \bar{\mu }^{\varGamma } = \varvec{w} \cdot\varvec{\varXi}_{\Delta }^{T} \bar{\varvec{m}}^{\varGamma }$$

(77)

are the pseudo-bending-moments and the pseudo-torsion-moments applied on the rod ends, respectively. Note that $\bar{\varvec{\mu }}^{\varGamma b} = \bar{\varvec{\mu }}^{\varGamma }$ .

2.8 Weak Form of the Local Equilibrium Equation

The internal virtual work on a domain $\varOmega \subset {\mathbb{R}}$ is given by

$$\delta W_{\text{int}}^{\varOmega } = \int_{\varOmega } {\left( {\varvec{n}^{mr} \cdot \delta\varvec{\eta}_{i + 1}^{r} + \varvec{m}^{r} \cdot \delta\varvec{\kappa}_{i + 1}^{r} } \right)d\varOmega } ,$$

(78)

while the external virtual work on the domain $\varOmega \subset {\mathbb{R}}$ is, in a similar manner, given by

$$\delta W_{\text{ext}}^{\varOmega } = \int_{\varOmega } {\left( {\bar{\varvec{n}}^{\varOmega } \cdot \delta \varvec{u}_{i + 1} +\varvec{\varXi}_{\Delta }^{T} \bar{\varvec{m}}^{\varOmega } \cdot \delta\varvec{\alpha}_{\Delta } } \right)d\varOmega ,}$$

(79)

where

$$\begin{aligned} & \delta\varvec{\eta}_{i + 1}^{r} = \varvec{Q}_{i + 1}^{T} \left( {\delta \varvec{u^{\prime}}_{i + 1} + \varvec{Z^{\prime}}_{i + 1}\varvec{\varXi}_{\Delta } \delta\varvec{\alpha}_{\Delta } } \right) ,\\ & \delta\varvec{\kappa}_{i + 1}^{r} = \varvec{Q}_{i + 1}^{T} \left( {\varvec{\varXi}_{\Delta } \delta\varvec{\alpha}_{\Delta } } \right)^{\prime } \quad {\text{and}} \\ & \delta\varvec{\alpha}_{\Delta } = \varvec{W}\delta \varvec{u^{\prime}}_{i + 1} + \varvec{w}\delta \varphi_{\Delta } . \\ \end{aligned}$$

(80)

Introducing (80) in (78), one gets

$$\begin{aligned} \delta W_{\text{int}}^{\varOmega } & = \int_{\varOmega } {\varvec{n}_{{}}^{m} \cdot \left( {\delta \varvec{u^{\prime}}_{i + 1} + \varvec{Z^{\prime}}_{i + 1}\varvec{\varXi}_{\Delta } \delta\varvec{\alpha}_{\Delta } } \right)d\varOmega } \\ & \quad + \int_{\varOmega } {\varvec{m} \cdot \left( {\varvec{\varXi}_{\Delta } \left( {\varvec{W}\delta \varvec{u^{\prime}}_{i + 1} + \varvec{w}\delta \varphi_{\Delta } } \right)} \right)^{\prime } d\varOmega } . \\ \end{aligned}$$

(81)

Similarly, from (79) one arrives at

$$\delta W_{\text{ext}}^{\varOmega } = \int_{\varOmega } {\left( {\bar{\varvec{n}}^{\varOmega } \cdot \delta \varvec{u} + \bar{\varvec{\mu }}^{\varOmega } \cdot \delta \varvec{u^{\prime}} + \bar{\mu }^{\varOmega } \delta \varphi_{\Delta } } \right)d\varOmega } .$$

(82)

The rod local equilibrium equations are obtained by applying the Virtual Work Theorem as follows:

$$\delta W_{\text{int}}^{\varOmega } - \delta W_{\text{ext}}^{\varOmega } = \delta W_{\text{ext}}^{\varGamma } ,\quad \forall \delta \varvec{u},\delta \varphi_{\Delta } \;{\text{in}}\;\varOmega .$$

(83)

where $\delta W_{\text{ext}}^{\varGamma }$ is the external virtual work on the boundary $\varGamma$, which is given by

$$\delta W_{\text{ext}}^{\varGamma } = \left( {\bar{\varvec{n}}^{\varGamma } \cdot \delta \varvec{u} + \bar{\varvec{\mu }}^{\varGamma } \cdot \delta \varvec{u^{\prime}} + \bar{\mu }^{\varGamma } \delta \varphi_{\Delta } } \right)_{\varGamma } .$$

(84)

Introducing (81) and (82) in (83), and taking into account that $\varvec{z^{\prime}}_{i + 1} \times \varvec{n}_{{}}^{m} = \varvec{o}$, one gets

$$\begin{aligned} & \int_{\varOmega } {\left( {\varvec{n}_{{}}^{m} \cdot \delta \varvec{u^{\prime}}_{i + 1} + \varvec{m} \cdot \left( {\varvec{\varXi}_{\Delta } \left( {\varvec{W}\delta \varvec{u^{\prime}}_{i + 1} + \varvec{w}\delta \varphi_{\Delta } } \right)} \right)^{\prime } } \right)d\varOmega } + \\ & \quad - \int_{\varOmega } {\left( {\bar{\varvec{n}}^{\varOmega } \cdot \delta \varvec{u}_{i + 1} + \bar{\varvec{\mu }}^{\varOmega } \cdot \delta \varvec{u^{\prime}} + \bar{\mu }^{\varOmega } \delta \varphi_{\Delta } } \right)d\varOmega } = \delta W_{\text{ext}}^{\varGamma } . \\ \end{aligned}$$

(85)

By integration by parts of (85), one obtains

$$\begin{aligned} & - \int_{\varOmega } {\left( {\left( {\left( {\varvec{n}^{m} } \right)^{\prime } + \bar{\varvec{n}}^{\varOmega } } \right) \cdot \delta \varvec{u}_{i + 1} } \right)d\varOmega } + \\ & \quad - \int_{\varOmega } {\left( {\left( {\varvec{W}^{T}\varvec{\varXi}_{\Delta }^{T} \varvec{m^{\prime}} + \bar{\varvec{\mu }}^{\varOmega } } \right) \cdot \delta \varvec{u^{\prime}}_{i + 1} + \left( {\varvec{w} \cdot\varvec{\varXi}_{\Delta }^{T} \varvec{m^{\prime}} + \bar{\mu }^{\varOmega } } \right)\delta \varphi_{\Delta } } \right)d\varOmega } \\ & \quad + \left. {\left( {\varvec{n}^{m} \cdot \delta \varvec{u}_{i + 1} + \varvec{m} \cdot\varvec{\varXi}_{\Delta } \left( {\varvec{W}\delta \varvec{u^{\prime}}_{i + 1} + \varvec{w}\delta \varphi_{\Delta } } \right)} \right)} \right|_{\varGamma } = \delta W_{\text{ext}}^{\varGamma } \\ \end{aligned}$$

(86)

and again on (86), one arrives at

$$\begin{aligned} & - \int_{\varOmega } {\left[ {\left( {\tilde{\varvec{n}}^{\prime } + \bar{\varvec{n}}^{\varOmega } } \right) \cdot \delta \varvec{u}_{i + 1} } \right]d\varOmega } - \int_{\varOmega } {\left( {\left( {\varvec{w} \cdot\varvec{\varXi}_{\Delta }^{T} \varvec{m^{\prime}} + \bar{\varvec{\mu }}^{\varOmega } } \right)\delta \varphi_{\Delta } } \right)d\varOmega } \\ & \quad + \left. {\left( {\tilde{\varvec{n}} \cdot \delta \varvec{u}_{i + 1} + \varvec{m} \cdot\varvec{\varXi}_{\Delta } \left( {\varvec{W}\delta \varvec{u^{\prime}}_{i + 1} + \varvec{w}\delta \varphi_{\Delta } } \right)} \right)} \right|_{\varGamma } = \delta W_{\text{ext}}^{\varGamma } , \\ \end{aligned}$$

(87)

where

$$\tilde{\varvec{n}} = \varvec{n}^{m} - \varvec{W}^{T}\varvec{\varXi}_{\Delta }^{T} \varvec{m^{\prime}} - \bar{\varvec{\mu }}^{\varOmega } .$$

(88)

By standard arguments of Calculus of Variation, (87) delivers the following local equilibrium equations in $\varOmega$

$$\tilde{\varvec{n}}^{\prime } + \bar{\varvec{n}}^{\varOmega } = \varvec{o}\quad {\text{and}}\quad \varvec{w} \cdot\varvec{\varXi}_{\Delta }^{T} \varvec{m^{\prime}} + \bar{\varvec{\mu }}^{\varOmega } = 0.$$

(89)

It remains the following boundary term on $\varGamma$

$$\begin{aligned} & \left( {\tilde{\varvec{n}} \cdot \delta \varvec{u}_{i + 1} + \varvec{m} \cdot\varvec{\varXi}_{\Delta } \left( {\varvec{W}\delta \varvec{u^{\prime}}_{i + 1} + \varvec{w}\delta \varphi_{\Delta } } \right)} \right)_{\varGamma } \\ & = \left( {\bar{\varvec{n}}^{\varGamma } \cdot \delta \varvec{u} + \bar{\varvec{\mu }}^{\varGamma } \cdot \delta \varvec{u^{\prime}} + \bar{\mu }^{\varGamma } \delta \varphi_{\Delta } } \right)_{\varGamma } . \\ \end{aligned}$$

(90)

Thus, one can conclude that the natural (Neumann) boundary conditions are

$$\bar{\varvec{n}}^{\varGamma } = \tilde{\varvec{n}},\quad \bar{\varvec{\mu }}^{\varGamma } = \varvec{W}^{T}\varvec{\varXi}_{\Delta }^{T} \varvec{m}\quad {\text{and}}\quad \bar{\mu }^{\varGamma } = \varvec{w} \cdot\varvec{\varXi}_{\Delta }^{T} \varvec{m,}$$

(91)

while the essential (Dirichlet) boundary conditions are

$$\varvec{u} = \bar{\varvec{u}},\quad \left( {\varvec{u^{\prime}}} \right)^{b} = \left( {\varvec{\bar{u}^{\prime}}} \right)^{b} \quad {\text{and}}\quad \varphi_{\Delta } = \bar{\varphi }_{\Delta } .$$

(92)

2.9 Statics

The rod local equilibrium equations can be directly derived by Statics (see, for example, Pimenta (1993a), Pimenta and Yojo (1993)). They are displayed below

$$\varvec{n^{\prime}} + \bar{\varvec{n}}^{\varOmega } = \varvec{o}\quad {\text{and}}\quad \varvec{m^{\prime}} + \varvec{z^{\prime}} \times \varvec{n} + \bar{\varvec{m}}^{\varOmega } = \varvec{o}.$$

(93)

From (93)₂, one gets $\varvec{z^{\prime}} \times \varvec{n} = - \left( {\varvec{m^{\prime}} + \bar{\varvec{m}}^{\varOmega } } \right)$, which, with the aid of (58), i.e., $\varvec{n} = \varvec{n}^{m} + \varvec{n}^{b}$, and $\varvec{z^{\prime}} \times \varvec{n}^{m} = \varvec{o}$, leads to the result below

$$\varvec{z^{\prime}} \times \varvec{n}^{b} = - \left( {\varvec{m^{\prime}} + \bar{\varvec{m}}^{\varOmega } } \right).$$

(94)

From (94), with $\varvec{n}^{b} = V_{\alpha } \varvec{e}_{\alpha }$, one can derive

$$\begin{aligned} \varvec{e}_{\beta }^{{}} \cdot \left( {\varvec{z^{\prime}} \times \varvec{n}^{b} } \right) & = \left\| {\varvec{z^{\prime}}} \right\|V_{\alpha } \left( {\varvec{e}_{\beta }^{{}} \cdot \varvec{e}_{3} \times \varvec{e}_{\alpha } } \right) \\ & = \varepsilon_{\alpha \beta } \left\| {\varvec{z^{\prime}}} \right\|V_{\alpha } = - \varvec{e}_{\beta } \cdot \left( {\varvec{m^{\prime}} + \bar{\varvec{m}}^{\varOmega } } \right), \\ \end{aligned} ,$$

(95)

where $\varepsilon_{\alpha \beta } = \varvec{e}_{\alpha } \cdot \varvec{e}_{\beta } \times \varvec{e}_{3}$ is a permutation symbol. From (95), one arrives at

$$V_{\alpha } = - \left\| {\varvec{z^{\prime}}} \right\|^{ - 1} \varepsilon_{\alpha \beta } \varvec{e}_{\beta }^{{}} \cdot \left( {\varvec{m^{\prime}} + \bar{\varvec{m}}^{\varOmega } } \right).$$

(96)

An alternative to (96) is

$$\begin{aligned} \varvec{n}^{b} & = V_{\alpha } \varvec{e}_{\alpha } = - \left\| {\varvec{z^{\prime}}} \right\|^{ - 1} \left[ {\varepsilon_{\alpha \beta } \varvec{e}_{\beta }^{{}} \cdot \left( {\varvec{m^{\prime}} + \bar{\varvec{m}}^{\varOmega } } \right)} \right]\varvec{e}_{\alpha } = \\ & = - \left\| {\varvec{z^{\prime}}} \right\|^{ - 1} \left( {\varvec{e}_{1} \otimes \varvec{e}_{2} - \varvec{e}_{2} \otimes \varvec{e}_{1} } \right)\left( {\varvec{m^{\prime}} + \bar{\varvec{m}}^{\varOmega } } \right). \\ \end{aligned}$$

(97)

From (97), with the assistance of $\varvec{e}_{2} \otimes \varvec{e}_{1} - \varvec{e}_{1} \otimes \varvec{e}_{2} = {\text{Skew}}\left( {\varvec{e}_{3} } \right)$, one arrives at

$$\varvec{n}^{b} = \left\| {\varvec{z^{\prime}}} \right\|^{ - 1} \varvec{e}_{3} \times \left( {\varvec{m^{\prime}} + \bar{\varvec{m}}^{\varOmega } } \right) = \left\| {\varvec{z^{\prime}}} \right\|^{ - 2} \varvec{z^{\prime}} \times \left( {\varvec{m^{\prime}} + \bar{\varvec{m}}^{\varOmega } } \right)\;.$$

(98)

3 Elastic Constitutive Equations

Only elastic small strains have been considered in this work. In a later work under preparation, other constitutive equations will be considered. If the rod axis is placed along with the cross-sectional shear centers, the following linear elastic constitutive equation for small strain isotropic elasticity can be adopted:

$$\varvec{\sigma}^{r} = \varvec{D}\varvec{\varepsilon}^{r} ,$$

(99)

where

$$\varvec{\sigma}^{r} = \left[ {\begin{array}{*{20}c} {\varvec{n}^{mr} } \\ {\varvec{m}^{r} } \\ \end{array} } \right],\quad\varvec{\varepsilon}^{r} = \left[ {\begin{array}{*{20}c} {\varvec{\eta}^{r} } \\ {\varvec{\kappa}^{r} } \\ \end{array} } \right]\quad {\text{and}}\quad \varvec{D} = \left[ {\begin{array}{*{20}c} {\varvec{D}_{\eta \eta } } & {\varvec{D}_{\eta \kappa } } \\ {\varvec{D}_{\kappa \eta } } & {\varvec{D}_{\kappa \kappa } } \\ \end{array} } \right].$$

(100)

The strain energy per unit reference length, in this case, is given by

$$\psi = \frac{1}{2}\varvec{\varepsilon}^{r} \cdot \varvec{D}\varvec{\varepsilon}^{r} .$$

(101)

In (100)₃, one has

$$\begin{aligned} \varvec{D}_{\eta \eta } & = EA\varvec{e}_{3}^{r} \otimes \varvec{e}_{3}^{r} \\ \varvec{D}_{\eta \kappa } & = ES_{\alpha } \varvec{e}_{3}^{r} \otimes \varvec{e}_{\alpha }^{r} = \varvec{D}_{\kappa \eta }^{T} {\text{ and}} \\ \varvec{D}_{\kappa \kappa } & = EJ_{\alpha \beta } \varvec{e}_{\alpha }^{r} \otimes \varvec{e}_{\beta }^{r} + GJ_{T} \varvec{e}_{3}^{r} \otimes \varvec{e}_{3}^{r} , \\ \end{aligned}$$

(102)

where $E$ is the elasticity modulus, $G$ is the shear modulus, $A$ is the cross-sectional area, $J_{T}$ is the cross-sectional torsion constant, $S_{\alpha } = \varepsilon_{\alpha \beta } \int_{A}^{{}} {\xi_{\beta } } dA$ are the cross-sectional static moments and $J_{\alpha \beta } = \varepsilon_{\alpha \gamma } \varepsilon_{\beta \delta } \int_{A} {\xi_{\gamma } \xi_{\delta } dA}$ are the cross-sectional inertia moments. It is recalled that $J_{T}$ is given by

$$J_{T} = J_{0} - \int_{A} {\varepsilon_{\alpha \beta } \xi_{\beta } \phi_{,\alpha } dA} ,$$

(103)

where $\phi = \hat{\phi }\left( {\xi_{\alpha } } \right)$ is the St.Venant warping function, $\phi_{,\alpha } = \partial \phi /\partial \xi_{\alpha }$ and

$$J_{0} = \int_{A} {\xi_{\alpha } \xi_{\alpha } dA} = J_{11} + J_{22}$$

(104)

is the cross-sectional polar inertia moment. For circular or annular sections, with the origin at the barycenter $S_{\alpha } = 0, \, J_{12} = J_{21} = 0,$ $\phi = 0$ and $J_{T} = J_{0}$. For bisymmetrical cross sections with the origin at the barycenter and $\varvec{e}_{\alpha }^{r}$ along the principal axes of the cross section, one has $S_{\alpha } = 0, \, J_{12} = J_{21} = 0,{\text{ and }}J_{T}$ given by (103).

Remark 8: Strain Energy Density

According to (40) and (100), we may write

$$\psi = \hat{\psi }\left( {\varvec{u},\varphi_{\Delta } } \right).$$

(105)

4 Finite Element Implementation

The simulations can be performed within the AceFEM finite element software. Both AceGen and AceFEM programs are developed and maintained by Joze Korelc (University of Ljubljana). The interested reader is referred to Korelc and Wriggers (2016).

Within the class of conservative problems, only the formulation of the total potential energy is required, which can be given by

$$\varPi = \sum\limits_{e} {\left( {\varPi_{\text{int}}^{e} + \varPi_{\text{ext}}^{e} } \right)} ,$$

(106)

where $\left( \cdot \right)^{e}$ is the contribution of each element $e = 1,2, \ldots N_{elements}$ . The strain energy of an element is

$$\varPi_{\text{int}}^{e} = \int_{{\varOmega^{e} }} {\psi d\varOmega } ,$$

(107)

with $\psi$ given by (101). Regarding (105), we may write

$$\varPi_{\text{int}}^{e} = \hat{\varPi }_{\text{int}}^{e} \left( {\varvec{u},\varphi_{\Delta } } \right)$$

(108)

The potential energy of an element, for the case of constant forces and constant pseudo-moments along the rods, is given by

$$\varPi_{\text{ext}}^{e} = - \int_{{\varOmega^{e} }} {\left( {\bar{\varvec{n}}^{\varOmega } \cdot \varvec{u} + \bar{\varvec{\mu }}^{\varOmega } \cdot \varvec{u^{\prime}} + \bar{\mu }^{\varOmega } \varphi_{\Delta } } \right)d\varOmega } .$$

(109)

In view of (109), we may write

$$\varPi_{\text{ext}}^{e} = \hat{\varPi }_{\text{ext}}^{e} \left( {\varvec{u},\varphi_{\Delta } } \right)$$

(110)

According to (92), for a smooth axis at reference configuration, the finite element approximation must be continuous for $\varvec{u}$, $\left( {\varvec{u^{\prime}}} \right)^{b}$ and $\varphi_{\Delta }$. If there is no sudden cross-sectional change, sudden material change nor concentrated loads at a connection node, a $C_{1}$ interpolation for the displacements $\varvec{u}$ and a $C_{0}$ interpolation for the incremental rotation $\varphi_{\Delta }$ and a standard connection between elements is adequate. This has been done in [46]. In these cases, the element can be directly employed with the usual finite element tying procedure. However, a continuity of $\left( {\varvec{u^{\prime}}} \right)^{m}$, i.e. the axial part of $\varvec{u^{\prime}}$, is also achieved, what is not required by the theory. Moreover, the imposition of general Dirichlet boundary conditions can be complicated.

For the general case, i.e., for nonsmooth axis, multiple connections or for the case of cross section or material change from an element to the other, the connection of elements must be carefully performed. The appropriate connection can be generally formulated by imposing the equality of $\varvec{u}$ and $\varvec{\alpha}_{\Delta }$ at connecting ends.

Herein, the connection is achieved in a more standard way, as follows. The proposed element has only 2 nodes. Displacements $\varvec{u}$ are approximated by cubic Hermitian polynomials, as usual

$$\varvec{u}\left( \zeta \right) = N_{1}^{u} \varvec{u}_{1} + N_{1}^{{u^{\prime}}} \varvec{u^{\prime}}_{1} + N_{2}^{u} \varvec{u}_{2} + N_{2}^{{u^{\prime}}} \varvec{u^{\prime}}_{2} ,$$

(111)

where

$$\begin{aligned} N_{1}^{u} & = 1 - \frac{{3\zeta^{2} }}{{\ell^{2} }} + \frac{{2\zeta^{3} }}{{\ell^{3} }}, \, N_{1}^{{u^{\prime}}} = \zeta - \frac{{2\zeta^{2} }}{\ell } + \frac{{\zeta^{3} }}{{\ell^{2} }}, \\ N_{2}^{u} & \varvec{ = }\frac{{3\zeta^{2} }}{{\ell^{2} }} - \frac{{2\zeta^{3} }}{{\ell^{3} }}\;{\text{and}}\;N_{2}^{{u^{\prime}}} = \frac{{\zeta^{3} }}{{\ell^{2} }} - \frac{{\zeta^{2} }}{\ell }. \\ \end{aligned}$$

(112)

At nodes $I = 1,2$, from the nodal values $\varvec{\alpha}_{\Delta I}$ and $\varepsilon_{I}^{i + 1}$, we get

$$\varvec{e}_{iI}^{i + 1} = \varvec{Q}_{\Delta I} \varvec{e}_{iI}^{i} = \hat{\varvec{Q}}\left( {\varvec{\alpha}_{\Delta I} } \right)\varvec{e}_{iI}^{i} ,$$

(113)

$$\varphi_{\Delta I} = \left\| {\varvec{e}_{3I}^{m} } \right\|^{ - 1} \left( {\varvec{\alpha}_{\Delta I} \cdot \varvec{e}_{3I}^{m} } \right)$$

(114)

and

$$\varvec{u^{\prime}}_{I}^{i + 1} = \left( {1 + \varepsilon_{I}^{i + 1} } \right)\varvec{e}_{3I}^{i + 1} - \varvec{e}_{3}^{r} .$$

(115)

Along the rod, we compute $\varvec{u}\left( \zeta \right)$ and $\varvec{u^{\prime}}\left( \zeta \right)$ with the aid of (111). When necessary, we obtain $\varvec{e}_{3}^{i + 1} \left( \zeta \right)$ with the help from (19) and $\varvec{\alpha}_{\Delta } \left( \zeta \right)$ with the assistance from (16) together with the following linear approximation:

$$\begin{array}{*{20}c} {\varphi_{\Delta } \left( \zeta \right) = \varphi_{\Delta 1} N_{1}^{\varphi } \left( \zeta \right) + \varphi_{\Delta 2} N_{2}^{\varphi } \left( \zeta \right),\quad {\text{where}}} \\ {N_{1}^{\varphi } \left( \zeta \right) = 1 - \frac{\zeta }{\ell }\quad {\text{and}}\quad N_{2}^{\varphi } \left( \zeta \right) = \frac{\zeta }{\ell }.} \\ \end{array}$$

(116)

This 2-node finite element has 7 DOFs, namely, $\varvec{u},\;\varvec{\alpha}_{\Delta }$ and $\varepsilon$, at each extremity, but only $\varvec{u}$ and $\varvec{\alpha}_{\Delta }$ can be shared with neighboring elements.

Remark 9: Quadratic Approximation for $\varphi_{\Delta }$

A quadratic approximation for the incremental torsion angle $\varphi_{\Delta }$ could also be used, but an extra mid-length node with a DOF for $\varphi_{\Delta }$ will be needed. This can be interesting for coupling with Kirchhoff–Love shell elements and to achieve a better convergence.

5 Conclusions

The geometrically exact rod formulation presented in Pimenta (1993b), Pimenta and Yojo (1993) was extended to a Bernoulli–Euler-type rod. Thereby, the present work is based on rotational parametrization via the Rodrigues rotation vector, which is used to propose an incremental update that a priory fulfills the shear rigidity constraint. It also introduces the ability to formulate inter-element connections in a more flexible manner. As in Pimenta (1993b), Pimenta and Yojo (1993), the approach has defined energetically conjugated generalized cross-sectional stress and strains based on the concept of a cross section. Besides their practical importance, cross-sectional quantities make the derivation of equilibrium equations easy, as well as the achievement of the corresponding tangent bilinear form, which is always symmetric for hyper-elastic materials and conservative loadings, even far from an equilibrium state.

A straight reference configuration was assumed for the rod on this work. Initially, curved rods are then regarded as a stress-free deformation from the straight configuration. This approach was already employed for rods in Pimenta (1996) and for shells in Pimenta and Campello (2009). It precludes the use of convective non-Cartesian coordinate systems and simplifies the comprehension of tensor quantities, since only components on orthogonal systems are employed.

Some examples were computed to show the capabilities of the formulation presented. As exposed throughout the paper, some examples with this Bernoulli–Euler rod theory were compared to benchmark problems and presented satisfying results. This formulation shows great promises and can be used to accurately describe the stresses, strains, displacements of flexible structures with great efficiency.

The derived beam formulation will be implemented in a finite element framework and investigated in various aspects. The authors aim to consider non-straight reference configurations on the element level in future studies. Further work is planned on extending the formulation to a pointwise approach, to incorporate general three-dimensional material laws. Consideration of out of plane warping is on the schedule as well.