Data Acquisition System for Solar Panel Analysis

Abstract

This project introduces a data acquisition system for solar panel technologies, mainly for analysis and report purposes. The measured variables are the current and voltage generated by the panel so that the power and voltage curve can be plotted to analyze. The system is made up of two parts, the hardware that will be designed using an Arduino circuit board with a voltage sensor, a current sensor and a temperature sensor that feedback the modeled circuit based on Matlab and Simscape platforms. As an addition to the hardware system, an embedded system is designed using operational amplifiers to simulate a solar panel, this emulation is based on the mathematical model that gives our values for variables generated by solar technologies. For simulation of the modeling and plotting of the generated data, we propose the use of Wahba’s method, for smoothing noisy data using spline function. This model will serve as a research/experimentation tool for technologies that improve the efficiency range of a solar cell.

1 Introduction

In the last 15 years, there has been an unprecedented change in the consumption of energy resources. The high growth in the renewable energy market, in terms of investment, new capacities and high growth rates in developing countries, has changed the landscape for the energy sector. We have seen the growth of unconventional resources and improvements in the evolution of technology for all forms of energy resources [1]. In particular, solar energy has proven to meet up this energy scenario [2].

Solar cells, also called photovoltaic (PV) cells, convert solar radiation directly into electricity. They capture photons by exciting electrons through the band gap of a semiconductor, which creates electron pairs and holes that are then separated by charge, usually by PN junctions introduced by doping. The bonding interface conducts the electrons in one direction and the holes in the other, which creates a potential difference in the external electrodes equal to the band gap.

The concept and configuration are similar to those of a semiconductor diode, except that the electrons and holes are introduced into the junction by the excitation of the photon and are removed at the electrodes [3]. Currently solar cells reach a wide variety of applications and contribute to the massive or isolated generation of electrical energy. Crystalline silicon is a well-studied material and its technology is mature, it is the most common material used in Photo Voltaic (PV) technologies, the global production of solar cells increases rapidly and the amount of silicon used exceeds the set of semiconductor devices such as diodes, transistors and circuits.

The huge gap between the potential of solar energy and its use is due to the cost and conversion capacity. Fossil fuels satisfy our energy demands at lower cost than solar alternatives, in part because fossil fuel deposits are concentrated sources of energy, while the sun distributes photons quite evenly on Earth at a more modest energy density. The use of biomass as a fuel is limited by the production capacity of the available land and water. The limitations of cost and capacity in the use of solar energy are addressed more effectively with a single research objective: to increase conversion efficiency in a cost-effective manner.

Several mathematical models have been developed that describe the behavior of a solar cell. All the models are based on the current-voltage ratio resulting from a diode, whose manufacture represents the n-type and p-type doped semiconductors, used in the manufacture of a solar cell [4]. These models can be used in the design and development of data acquisition (DAQ) systems which measure physical phenomenon such as voltage, current, temperature, pressure, or sound converting them into digital signals. These signals in turn, are processed and conditioned by a computer with programmable software to allow their easy analysis and visualization.

In this work a circuit is designed in Simscape to simulate the behavior of a real PV panel. A sensor board was constructed to collect the current, voltage and power values generated by the photovoltaic panel. The DAQ system was completed by a computer code programed to process and smooth the signals into a format that could be used for analysis purposes.

2 Process and Development

2.1 Mathematical Modeling of a Solar Panel

A solar cell is the building block of a solar panel. A photovoltaic module is formed by connecting many solar cells in series and parallel. Generally, the equivalent electrical circuit of a solar cell consists of a photo-current source generated by the action of solar radiation, a diode, a resistance in parallel and a shunt resistance (representing the internal resistance of the material to the flow of the current), as shown in Fig. 1.

Fig. 1.

Electrical representation of a solar cell

Applying Kirchhoff’s law to the representation of a solar cell as seen in Fig. 1. The next equation can be obtained.

$$ I = I_{PH} - I_{D} - I_{SH} $$

(1)

Where I_PH is the photo-generated current, I_D is the current of the diode, I_SH is the shunt resistance loss in parallel and I is the output current of the cell. The first term can be determined from next equation and depends on the irradiance, area and temperature in which the cell is being exposed.

$$ I_{PH} = \frac{G}{{G_{STC} }}\left[ {A \cdot J_{SC} + \alpha J_{SC} \left( {T - T_{STC} } \right)} \right] $$

(2)

where G is the irradiance value under given conditions, G_STC is the irradiance value under standard conditions, A is the area of the cell, J_SC is the short-circuit current density of the cell, $\upalpha{\text{J}}_{\text{SC}}$ is the temperature coefficient of the short-circuit current density, T is the temperature under given conditions, T_STC is the temperature under standard conditions.

The second term from Eq. (1) is the current of the diode which can be determined from the Shockley equation.

$$ I_{D} = I_{O} \left( {e^{{\frac{{V_{D} }}{{nV_{T} }}}} - 1} \right) $$

(3)

Where I_O is the saturation current, V_D is the voltage of the diode, n is equal to the ideality factor of the diode and V_T is the thermal voltage. From Eq. (3) the diode saturation current is obtained, which is that part of the reverse current in a semiconductor diode caused by diffusion of minority carriers from the neutral regions to the depletion region

$$ I_{O} = \frac{{J_{SC} \cdot A - \frac{{V_{OC} }}{{R_{SH} }}}}{{\left( {e^{{\frac{{V_{OC} }}{{nV_{T} }}}} - 1} \right)}} $$

(4)

Where J_SC is the short-circuit current density of the cell, A is the area of the cell, V_OC is the open circuit voltage of the cell, R_SH is the resistance in parallel, V_T is the thermal voltage and n is equal to the ideality factor of the diode.

The third term from Eq. (1) is shunt resistance loss current which corresponds to the current leakage is usually suppressed in some models because the parallel resistance (RSH) usually has a very high value with respect to the series resistance.

$$ I_{RSH} = \frac{{V + R_{S} I}}{{R_{SH} }} $$

(5)

Where V is the output voltage of the solar cell, RS is the series resistance, RSH is the parallel resistance and I is the resistance current in parallel.

Equations 2, 3 and 4 are substituted in Eq. 1, so the general modeling equation for a solar cell is obtained.

$$ I = I_{PH} - I_{O} \left( {e^{{\frac{{V + R_{S} I}}{{nV_{T} }}}} - 1} \right) - \frac{{V + R_{S} I}}{{R_{SH} }} $$

(6)

A solar panel is formed by grouping cells in series, in order to obtain the output current (I) of a solar panel the output voltage (V) in the Eq. 6 is divided by the number of cells (Ns) [5, 6].

$$ I = I_{PH} - I_{O} \left( {e^{{\frac{{\frac{V}{{N_{S} }} + R_{S} I}}{{nV_{T} }}}} - 1} \right) - \frac{{\frac{V}{{N_{S} }} + R_{S} I}}{{R_{SH} }} $$

(7)

3 Data Validation

To represent the mathematical equation and to model a solar panel, the Matlab and Simulink platform tools are used, this model is visualized as a set of subsystems connected and configured to calculate the variables needed to be analyzed.

3.1 Cell Modeling

Using the tools from Matlab and the mathematical equations, a model is built for the PV cell; this model represents the circuit equations of a PV cell taking into account the effects of physical and environmental parameters such as the solar radiation and cell temperature, as shown in Fig. 2.

Fig. 2.

Simulink model designed to represent a PV module.

Inside the block that represents the PV module, the values and elements from Eq. 7 are modeled in subsystems Fig. 3.

Fig. 3.

The subsystems within the designed Simulink model.

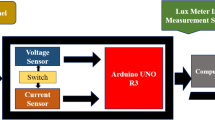
The fundamental parameters related to solar cell are short circuit current (I_sc), open circuit voltage (V_oc), efficiency of solar cell and fill factor. These values are measured using the hardware circuit built in an arduino board using voltage, current and temperature sensors. Short Circuit Current is the condition when the impedance is low and it is calculated when the voltage equals to zero.

I_sc occurs at the beginning of the forward-bias sweep and is the maximum current value in the power quadrant. For an ideal cell, this maximum current value is the total current produced in the solar cell by photon excitation. I_sc is the short-circuit current of cell at 25 °C and an Irradiance 1000 W/m², I_ph is the light generated current directly proportional to the solar irradiation, Io is the diode saturation current of the cell varies with the cell temperature, Irs is the reverse saturation current of a cell at a reference temperature and a solar irradiation, Eg is the band gap energy of the semiconductor used in the cell and I_sh stands for Parallel resistance loss current, this term of the equation that corresponds to the current leakage is usually suppressed in some models because the parallel resistance usually has a very high value with respect to the series resistance [6].

Modeling the Solar Panel in Simscape.

To Model the PV cell in Simscape involves the estimation of the I-V and P-V characteristics curves to emulate the real cell under various environmental conditions. The most popular approach is to utilize the electrical equivalent circuit, which is primarily based on diode. The Solar Cell block in SimElectronics Fig. 4. represents a single solar cell as a parallel current source, I_ph, an exponential diode, D and a shunt resistance, R_sh that are connected in series with a resistance R_s.

Fig. 4.

Solar cell element in Simscape.

The Solar panel circuit is modeled using elements from Simscape and Simulink. Solar cell was connected with blocks such as current sensor and voltage sensor to measure the current and voltage across solar cell. Blocks for varying Irradiance level and Temperature, were also connected in the above model. Rest of the blocks were the interface between major blocks and used for plotting I-V characteristics (Fig. 5).

Fig. 5.

Simscape array for a solar panel

This model circuit works with the data we acquired from the readings of our experimental solar cell at a lab.

Parameter Estimation Methodology.

Smoothing splines are well known to provide nice curves which smooth discrete, noisy data, in this case it is proposed a system based on parameter estimation theory which will allow the system to filter measurements which can be considered error. In signal processing, an autoregressive (AR) model is a representation of a type of random process; as such, it is used to describe certain time-varying processes, the model specifies that the output variable depends linearly on its own previous values and on a stochastic term.

The AR model is a widely used model to understand time series data. Traditionally, the innovation noise of the AR is modeled as Gaussian. However, many time series applications, for example, situations arising in applications of signal processing where the time series are non-Gaussian and heavy-tailed, either due to intrinsic data generation mechanism or existence of outliers, the AR model with more general heavy tailed innovations is preferred.

Another issue that frequently occurs in time series is missing values, due to system data record failure or unexpected data loss. In the recent era of data deluge, many applications collect and process time series data for inference, learning, parameter estimation, and decision making. The AR model is a commonly used model to analyze time series data, where observations taken closely in time are statistically dependent on others. In an AR time series, each sample is a linear combination of some previous observations with a stochastic innovation.

An AR model of order p, AR(p), is defined as.

$$ y_{t} = \varphi_{0} + \sum\nolimits_{i = 1}^{p} {\varphi_{i} y_{t - i} + \varepsilon_{t} } $$

(8)

Where $y_{t}$ is the t-th observation, $\varphi_{0}$ is a constant, $\varphi_{i}$ are autoregressive coefficients, and $\varepsilon_{t}$ is the innovation associated with the t-th observation, which is assumed to be Gaussian distributed, as a result of the linearity of the AR model, means that the observations are also Gaussian distributed.

The method of generalized cross validation has been shown both theoretically and by example, to be an effective method for estimating that value of the spline smoothing parameter which minimizes the mean square error. Excellent estimates of the derivative are also obtained in examples involving roughly 1% and 1/10 of 1% noise, Wahba posed the problem of finding the proper orthogonal matrix A that minimizes the cost function [6, 7].

$$ f\left( x \right) = \frac{1}{2}\left[ {\mu \left( {\sum\nolimits_{{{\text{j}} = 1}}^{\text{n}} { \left( {MesEstimated - v_{mes} \left( j \right)} \right)^{2} } } \right)} \right] $$

(9)

This paper defines the evolution of the value of the current density in the proposed function $f\left( x \right)$, so that the minimum error is chosen, but it takes in account the prediction of the state x and the coefficients of value for the state $\mu$ and the measures estimated (MesEstimated = MS) at the instant k.

The motivation for this cost function is that if the vectors are error-free and the true matrix $f\left( x \right)true$, is assumed to be the same for all the measurements, then $MesEstimated$ is equal to $v_{mes} true\left( j \right)$ for all $j$ and the cost function is equal to zero, which is clearly the minimum value, for $f\left( x \right)$ equal to $f\left( x \right)true$.

So for this method we define $f\left( x \right)$ as our current density $I_{x}$ and adapted it to get the next formula.

$$ I_{x} = \frac{1}{2}\left[ {\mu \left( {\sum\nolimits_{j = 1}^{n} {\left( {I_{est} - I_{mes} \left( j \right)} \right)^{2} } } \right)} \right] $$

(10)

Where I_X stands for the parameter estimation in which the optimal values considered for each test are, I_est for the estimated current values, I_mes is for the current date measured and n will stand for the number of readings we get each in a minute [8].

4 Results

In this section, part of the simulation and results are represented in order to show the performance of the proposed system, from our readings captured by our circuit, this data is inserted in the Simscape modeling.

The readings obtained from the test are fluctuating and represent a certain percent of noise and error; we must determine the optimal value to get the plot needed to analyze Fig. 6.

Fig. 6.

I-V and power curve plotted from variable sample reading in the laboratory

Applying the Eq. 10 in each of the sampling readings from our test the optimal value can be determined with the minimum range of error.

As presented in the Table 1 the values obtained for I_SC are calculated as the optimal and with less percentage of error.

Table 1. Data obtained from readings

This percentage error calculated using the value for short circuit current stabilizes rapidly in the range of 1% which can be interpreted as an acceptable range; the test results we registered have an acceptable percentage error Fig. 7. This data reading represents the values of a single solar cell which has been modeled and plotted Fig. 8.

Fig. 7.

Percentage error obtained by our optimal value compared to the highest and lowest values of variation in the test.

Fig. 8.

Plotting for the I-V and power curve obtained from experimentation data for a single solar cell.

To get the power curve we have programed a code that calculates the value using Watt’s law, so when the plotting process in Matlab starts both curves are sent to us to analyze.

The simscape model we designed can be modified to represent a complete solar panel, the element we configured with our readings can be connected in series or parallel to represent the model of Solar panel we desire Fig. 9.

Fig. 9.

Solar cell series connection

Depending of the number and connection type of the solar panel, a subsystem configuration can be created to represent the PV module needed to analyze Fig. 10.

Fig. 10.

Solar panel created in a subsystem

This way, the PV panel designed can be analyzed in solitary, or add more panels to represent a PV array, the curves obtained from the readings in this solar panel can be saved for report or analysis Fig. 11.

Fig. 11.

I-V curve and power curve for a photovoltaic panel.

5 Conclusion

This paper has analyzed the development of a method for the mathematical modeling of PV arrays, using a simulation platform and an embedded system which simulates these systems.

The method obtains the parameters of the I–V equation by measuring the values generated by our solar panel, which are the open circuit voltage, short-circuit current, and maximum output power. To accomplish our main objective which is to reduce error and represent a clean and smooth curve for analysis and report purposes, we used the cross validation method proposed with Wahba’s problem.