Abstract
This paper proposes a notion of branching bisimilarity for non-deterministic probabilistic processes. In order to characterize the corresponding notion of rooted branching probabilistic bisimilarity, an equational theory is proposed for a basic, recursion-free process language with non-deterministic as well as probabilistic choice. The proof of completeness of the axiomatization builds on the completeness of strong probabilistic bisimilarity on the one hand and on the notion of a concrete process, i.e. a process that does not display (partially) inert \(\tau \)-moves, on the other hand. The approach is first presented for the non-deterministic fragment of the calculus and next generalized to incorporate probabilistic choice, too.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
In [11], in a setting of a process language featuring both non-deterministic and probabilistic choice, Yuxin Deng and Catuscia Palamidessi propose an equational theory for a notion of weak bisimilarity and prove its soundness and completeness. Not surprisingly, the axioms dealing with a silent step are reminiscent to the well-known \(\tau \)-laws of Milner [26, 27]. The process language treated in [11] includes recursion, thereby extending the calculus and axiomatization of [6]. While the weak transitions of [11] can be characterized as finitary, infinitary semantics is treated in [15], providing a sound and complete axiomatization also building on the seminal work of Milner [27].
In this paper we focus on branching bisimilarity in the sense of [17], rather than on weak bisimilarity as in [6, 11, 15]. In the non-probabilistic setting branching bisimilarity has the advantage over weak bisimilarity that it has far more efficient algorithms [18, 19]. Furthermore, it has a strong logical underpinning [9]. It would be very attractive to have these advantages available also in the probabilistic case, where model checking is more demanding. See also the initial work reported in [21].
For a similarly basic process language as in [11], without recursion though, we propose a notion of branching probabilistic bisimilarity as well as a sound and complete equational axiomatization. Hence, instead of lifting all \(\tau \)-laws to the probabilistic setting, we only need to do this for the B-axiom of [17], the single axiom capturing inert silent steps. For what is referred to as the alternating model [22], branching probabilistic bisimilarity has been studied in [2, 3]. Also [28] discusses branching probabilistic bisimilarity. However, the proposed notions of branching bisimilarity are either no congruence for the parallel operator, or they invalidate the identities below which we desire. The paper [1] proposes a complete theory for a variant of branching bisimilarity that is not consistent with the first \(\tau \)-law unfortunately.
Our investigation is led by the wish to identify the three processes below, involving as a subprocess a probabilistic choice between P and Q. Essentially, ignoring the occurrence of the action a involved, the three processes represent (i) a probabilistic choice of weight \(\frac{3}{4}\) between to instances of the subprocess mentioned, (ii) the subprocess on its own, and (iii) a probabilistic choice of weight \(\frac{1}{3}\) for the subprocess and a rescaling of the subprocess, in part overlapping.

In our view, all three processes starting from \(s_0\), \(t_0\), and \(u_0\) are equivalent. The behavior that can be observed from them when ignoring \(\tau \)-steps and coin tosses to resolve probabilistic choices is the same. This leads to a definition of probabilistic branching bisimilarity that hitherto was not proposed in the literature and appears to be the pendant of weak distribution bisimilarity defined by [13].
As for [11] we seek to stay close to the treatment of the non-deterministic fragment of the process calculus at hand. However, as an alternate route in proving completeness, we rely on the definition of a concrete process. We first apply the approach for strictly non-deterministic processes and mutatis mutandis for the whole language allowing processes that involve both non-deterministic and probabilistic choice. For now, let’s call a process concrete if it doesn’t exhibit inert transitions, i.e. \(\tau \)-transitions that don’t change the potential behavior of the process essentially. The approach we follow first establishes soundness for branching (probabilistic) bisimilarity and soundness and completeness for strong (probabilistic) bisimilarity. Because of the non-inertness of the silent steps involved, strong and branching bisimilarity coincide for concrete processes. The trick then is to relate a pair of branching (probabilistically) bisimilar processes to a corresponding pair of concrete processes. Since these are also branching (probabilistically) bisimilar as argued, they are consequently strongly (probabilistically) bisimilar, and, voilà, provably equal by the completeness result for strong (probabilistic) bisimilarity.
The remainder of the paper is organized as follows. In Sect. 2 we gather some notation regarding probability distributions. For illustration purposes Sect. 3 treats the simpler setting of non-deterministic processes reiterating the completeness proof for the equational theory of [17] for rooted branching bisimilarity. Next, after introducing branching probabilistic bisimilarity and some of its fundamental properties in Sects. 4 and 5, respectively, in Sect. 6 we prove the main result, viz. the completeness of an equational theory for rooted branching probabilistic bisimilarity, following the same lines set out in Sect. 3. In Sect. 7 we wrap up and make concluding remarks.
2 Preliminaries
Let \(\textit{Distr}(X)\) be the set of distributions over the set X of finite support. The support of a distribution \(\mu \) is denoted as \( spt (\mu )\). Each distribution \(\mu \in \textit{Distr}(X)\) can be represented as \(\mu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * x_i\) when \(\mu (x_i) = p_i\) for \(i \in I\) and \(\textstyle \sum _{i {\in } I}\, p_i = 1\). We assume I to be a finite index set. In concrete cases, when no confusion arises, the separator \(*\) is omitted from the notation. For convenience later, we do not require \(x_i \ne x_{i'}\) for \(i \ne i'\) nor \(p_i > 0\) for \(i, i' \in I\).
We use \(\delta (x)\) to denote the Dirac distribution for \(x \in X\). For \(\mu , \nu \in \textit{Distr}(X)\) and \(r \in [0,1]\) we define \(\mu \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\nu \in \textit{Distr}(X)\) by \((\mu \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\nu )(x) = r \mathop {\cdot }\mu (x) + (1{-}r) \mathop {\cdot }\nu (x)\). By definition \(\mu \mathbin {{}_{\scriptscriptstyle 0 } \oplus \,} \nu = \nu \) and \(\mu \mathbin {{}_{\scriptscriptstyle 1 } \oplus \,} \nu = \mu \). For an index set I, \(p_i \in [0,1]\) and \(\mu _i \in \textit{Distr}(X)\), we define \(\textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \mu _i \in \textit{Distr}(X)\) by \((\textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \mu _i)(x) = \textstyle \sum _{i {\in } I}\, p_i \mathop {\cdot }\mu _i(x)\) for \(x \in X\). For \(\mu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \mu _i\), \(\nu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \nu _i\), and \(r \in [0,1]\) it holds that \(\mu \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\nu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, ( \mu _i \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\nu _i )\).
For a binary relation \(\mathcal {R}\subseteq \textit{Distr}(X)\times \textit{Distr}(X)\) we use \(\mathcal {R}^\dagger \) to denote its symmetric closure.
3 Completeness: The Non-deterministic Case
In this section we present an approach to prove completeness of an axiomatic theory for branching bisimilarity exploiting the notion of a concrete process in the setting of a basic process language. In the remainder of the paper we extend the approach to a process language involving probabilistic choice.
We assume to be given a set of actions \(\mathcal {A}\) including the so-called silent action \(\tau \). The process language we consider is called a Minimal Process Language in [4]. It provides inaction \( \mathbf{0 }\), a prefix construct for each action \(a \in \mathcal {A}\), and non-deterministic choice.
Definition 3.1
(Syntax). The class \(\mathcal {E}\) of non-deterministic processes over \(\mathcal {A}\), with typical element E, is given by

with actions \(\alpha \) from \(\mathcal {A}\).
The process \( \mathbf{0 }\) cannot perform any action, \(\alpha \mathop {.}E\) can perform action \(\alpha \) and subsequently behave as E, and \(E_1+E_2\) represents the choice in behavior between \(E_1\) and \(E_2\).
For \(E \in \mathcal {E}\) we define its complexity c(E) by \(c( \mathbf{0 }) = 0\), \(c(\alpha \mathop {.}E) = c(E) + 1\), and \(c(E + F) = c(E) + c(F)\).
The behavior of processes in \(\mathcal {E}\) is given by a structured operational semantics going back to [24].
Definition 3.2
(Operational semantics). The transition relation \({\rightarrow } \subseteq \mathcal {E}\times \mathcal {A}\times \mathcal {E}\) is given by

We have auxiliary definitions and relations derived from the transition relation of Definition 3.2. A process \(E' \in \mathcal {E}\) is called a derivative of a process \(E \in \mathcal {E}\) iff \(E_0, \ldots , E_n \in \mathcal {E}\) and \(\alpha _1, \ldots , \alpha _n\) exist such that  , and \(E_n \equiv E'\). We define \(\textit{der} (E) = \lbrace \,E' \in \mathcal {E}\mid E'{} { derivativeof}~E \, \rbrace \). Furthermore, for \(E, E' \in \mathcal {E}\) and \(\alpha \in \mathcal {A}\) we write
, and \(E_n \equiv E'\). We define \(\textit{der} (E) = \lbrace \,E' \in \mathcal {E}\mid E'{} { derivativeof}~E \, \rbrace \). Furthermore, for \(E, E' \in \mathcal {E}\) and \(\alpha \in \mathcal {A}\) we write  iff
iff  , or \(\alpha = \tau \) and \(E = E'\). We use
, or \(\alpha = \tau \) and \(E = E'\). We use  to denote the reflexive transitive closure of
to denote the reflexive transitive closure of  .
.
The definitions of strong and branching bisimilarity for \(\mathcal {E}\) are standard and adapted from [17, 26].
Definition 3.3
(Strong and branching bisimilarity).
-
(a)
A symmetric relation \(\mathcal {R}\subseteq \mathcal {E}\times \mathcal {E}\) is called a strong bisimulation relation iff for all \(E, E', F \in \mathcal {E}\) if \(E \,{\mathcal {R}}\,F\) and
 then there is an \(F' \in \mathcal {E}\) such that
then there is an \(F' \in \mathcal {E}\) such that 
-
(b)
A symmetric relation \(\mathcal {R}\subseteq \mathcal {E}\times \mathcal {E}\) is called a branching bisimulation relation iff for all \(E, E', F \in \mathcal {E}\) if \(E \,{\mathcal {R}}\,F\) and
 , then there are \(\bar{F}, F' \in \mathcal {E}\) such that
, then there are \(\bar{F}, F' \in \mathcal {E}\) such that 
-
(c)
Strong bisimilarity, denoted by
 , and branching bisimilarity, written as
, and branching bisimilarity, written as  , are defined as the largest strong bisimulation relation on \(\mathcal {E}\) and the largest branching bisimulation relation on \(\mathcal {E}\), respectively.
, are defined as the largest strong bisimulation relation on \(\mathcal {E}\) and the largest branching bisimulation relation on \(\mathcal {E}\), respectively.
Clearly, in view of the definitions, strong bisimilarity between two processes implies branching bisimilarity between the two processes.
If for a transition  we have that
we have that  , the transition is called inert. A process \(\bar{E}\) is called concrete iff it has no inert transitions, i.e., if \(E'\in \textit{der} (\bar{E})\) and
, the transition is called inert. A process \(\bar{E}\) is called concrete iff it has no inert transitions, i.e., if \(E'\in \textit{der} (\bar{E})\) and  , then
, then  . We write \(\mathcal {E}_{ cc }= \lbrace \,\bar{E}\in \mathcal {E}\mid \bar{E} \text{ concrete } \, \rbrace \).
. We write \(\mathcal {E}_{ cc }= \lbrace \,\bar{E}\in \mathcal {E}\mid \bar{E} \text{ concrete } \, \rbrace \).
Next we introduce a restricted form of branching bisimilarity, called rooted branching bisimilarity, instigated by the fact that branching bisimilarity itself is not a congruence for the choice operator. This makes branching bisimilarity unsuitable for equational reasoning where it is natural to replace subterms by equivalent terms. Note that weak bisimilarity has the same problem [26].
For example, we have for any process E that E and \(\tau \mathop {.}E\) are branching bisimilar, but in the context of a non-deterministic alternative they may not, i.e., it is not necessarily the case  . More concretely, although
. More concretely, although  , it does not hold that
, it does not hold that  . The \(\tau \)-move of \(\tau \mathop {.} \mathbf{0 }+ b \mathop {.} \mathbf{0 }\) to \( \mathbf{0 }\) has no counterpart in \( \mathbf{0 }+ b \mathop {.} \mathbf{0 }\) because
. The \(\tau \)-move of \(\tau \mathop {.} \mathbf{0 }+ b \mathop {.} \mathbf{0 }\) to \( \mathbf{0 }\) has no counterpart in \( \mathbf{0 }+ b \mathop {.} \mathbf{0 }\) because  .
.
Definition 3.4
A symmetric \(\mathcal {R}\mathbin \subseteq \mathcal {E}\times \mathcal {E}\) is called a rooted branching bisimulation relation iff for all \(E, F \in \mathcal {E}\) such that \(E \,{\mathcal {R}}\,F\) it holds that if  for \(\alpha \in \mathcal {A}\), \(E' \in \mathcal {E}\) then
for \(\alpha \in \mathcal {A}\), \(E' \in \mathcal {E}\) then  and
and  for some \(F' \in \mathcal {E}\). Rooted branching bisimilarity, denoted by
for some \(F' \in \mathcal {E}\). Rooted branching bisimilarity, denoted by  , is defined as the largest rooted branching bisimulation relation.
, is defined as the largest rooted branching bisimulation relation.
The definition of rooted branching bisimilarity boils down to calling processes \(E, F \in \mathcal {E}\) rooted branching bisimilar, notation  , iff (i)
, iff (i)  implies
implies  and
and  for some \(F' \in \mathcal {E}\) and, vice versa, (ii)
for some \(F' \in \mathcal {E}\) and, vice versa, (ii)  implies
implies  and
and  for some \(E' \in \mathcal {E}\). The formulation of Definition 3.4 for the nondeterministic processes of this section corresponds directly to the definition of rooted branching probabilistic bisimulation that we will introduce in Sect. 4, see Definition 4.5.
for some \(E' \in \mathcal {E}\). The formulation of Definition 3.4 for the nondeterministic processes of this section corresponds directly to the definition of rooted branching probabilistic bisimulation that we will introduce in Sect. 4, see Definition 4.5.
Direct from the definitions we see  . As implicitly announced we have a congruence result for rooted branching bisimilarity.
. As implicitly announced we have a congruence result for rooted branching bisimilarity.
Lemma 3.5
([17]).  is a congruence on \(\mathcal {E}\) for the operators \(\mathop {.}\) and \(+\).
is a congruence on \(\mathcal {E}\) for the operators \(\mathop {.}\) and \(+\).
It is well-known that strong and branching bisimilarity for \(\mathcal {E}\) can be equationally characterized [4, 17, 26].
Definition 3.6
(Axiomatization of  and
and  ). The theory \( A X \) is given by the axioms A1 to A4 listed in Table 1. The theory \( A X ^b\) contains in addition the axiom B.
). The theory \( A X \) is given by the axioms A1 to A4 listed in Table 1. The theory \( A X ^b\) contains in addition the axiom B.
If two processes are provably equal, they are rooted branching bisimilar.
Lemma 3.7
(Soundness). For all \(E,F \in \mathcal {E}\), if \( A X ^b\vdash E = F\) then  .
.
Proof
(Sketch). First one shows that the left-hand side and the right-hand side of the axioms of \( A X ^b\) are rooted branching bisimilar. Next, one observes that rooted branching bisimilarity is a congruence. \(\square \)
Strong bisimilarity is equationally characterized by the axioms A1 to A4 of Table 1. See for example [26, Sect. 7.4] for a proof.
Theorem 3.8
(AX sound and complete for  ). For all processes \(E, F \in \mathcal {E}\) it holds that \( A X \vdash E = F\) iff
). For all processes \(E, F \in \mathcal {E}\) it holds that \( A X \vdash E = F\) iff  .
.
For concrete processes that have no inert transitions, branching bisimilarity and strong bisimilarity coincide. Hence, in view of Theorem 3.8, branching bisimilarity implies equality for \( A X \).
Lemma 3.9
For all concrete \(\bar{E},\bar{F}\in \mathcal {E}_{ cc }\), if  then both
then both  and \( A X \vdash \bar{E}= \bar{F}\).
and \( A X \vdash \bar{E}= \bar{F}\).
Proof
(Sketch). Consider \(\bar{E}, \bar{F}\in \mathcal {E}_{ cc }\) such that  . Let \(\mathcal {R}\) be a branching bisimulation relation relating \(\bar{E}\) and \(\bar{F}\). Define \(\mathcal {R}'\) as the restriction of \(\mathcal {R}\) to the derivatives of \(\bar{E}\) and \(\bar{F}\), i.e., \(\mathcal {R}' = \mathcal {R}\cap ( (\textit{der} (\bar{E}) \times \textit{der} (\bar{F})) \cup (\textit{der} (\bar{F}) \times \textit{der} (\bar{E})) )\). Then \(\mathcal {R}'\) is a strong bisimulation relation, since none of the processes involved admits an inert \(\tau \)-transition. By the completeness of \( A X \), see Theorem 3.8, it follows that \( A X \vdash \bar{E}= \bar{F}\). \(\square \)
. Let \(\mathcal {R}\) be a branching bisimulation relation relating \(\bar{E}\) and \(\bar{F}\). Define \(\mathcal {R}'\) as the restriction of \(\mathcal {R}\) to the derivatives of \(\bar{E}\) and \(\bar{F}\), i.e., \(\mathcal {R}' = \mathcal {R}\cap ( (\textit{der} (\bar{E}) \times \textit{der} (\bar{F})) \cup (\textit{der} (\bar{F}) \times \textit{der} (\bar{E})) )\). Then \(\mathcal {R}'\) is a strong bisimulation relation, since none of the processes involved admits an inert \(\tau \)-transition. By the completeness of \( A X \), see Theorem 3.8, it follows that \( A X \vdash \bar{E}= \bar{F}\). \(\square \)
We are now in a position to prove the main technical result of this section, viz. that branching bisimilarity implies equality under a prefix. In the proof the notion of a concrete process plays a central role.
Lemma 3.10
-
(a)
For all processes \(E \in \mathcal {E}\), a concrete process \(\bar{E}\in \mathcal {E}_{ cc }\) exists such that
 and \( A X ^b\vdash { \alpha \mathop {.}E = \alpha \mathop {.}\bar{E}}\) for all \(\alpha \in \mathcal {A}\).
and \( A X ^b\vdash { \alpha \mathop {.}E = \alpha \mathop {.}\bar{E}}\) for all \(\alpha \in \mathcal {A}\). -
(b)
For all processes \(F,G \in \mathcal {E}\), if
 then \( A X ^b\vdash { \alpha \mathop {.}F = \alpha \mathop {.}G }\) for all \(\alpha \in \mathcal {A}\).
then \( A X ^b\vdash { \alpha \mathop {.}F = \alpha \mathop {.}G }\) for all \(\alpha \in \mathcal {A}\).
Proof
We prove statements (a) and (b) by simultaneously induction on c(E) and \(\max \lbrace c(F), c(G) \rbrace \), respectively.
Basis, \(c(E) = 0\). We have that \(E= \mathbf{0 }+\cdots + \mathbf{0 }\). Hence, take \(\bar{E}= \mathbf{0 }\). Clearly, part (a) of the lemma holds as \( \mathbf{0 }\) is concrete,  and \( A X ^b\vdash \alpha \mathop {.}E = \alpha \mathop {.} \mathbf{0 }\) for all \(\alpha \in \mathcal {A}\).
and \( A X ^b\vdash \alpha \mathop {.}E = \alpha \mathop {.} \mathbf{0 }\) for all \(\alpha \in \mathcal {A}\).
Induction step for (a): \(c(E) > 0\). The process E can be written as \({ \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}E_i }\) for some finite I and suitable \(\alpha _i\in \mathcal {A}\) and \(E_i\in \mathcal {E}\).
First suppose that for some \(i_0\in I\) we have \(\alpha _{i_0} = \tau \) and  . Then \( A X \vdash E = H + \tau .E_{i_0}\), where
. Then \( A X \vdash E = H + \tau .E_{i_0}\), where  . By the induction hypothesis (a), there is a term \(\bar{E}_{i_0} \in \mathcal {E}_{ cc }\) such that
. By the induction hypothesis (a), there is a term \(\bar{E}_{i_0} \in \mathcal {E}_{ cc }\) such that  . We claim that
. We claim that  .
.
For suppose  . Then
. Then  where
where  and
and  . In case \(E_{i_0} = E'_{i_0}\) it follows that
. In case \(E_{i_0} = E'_{i_0}\) it follows that  . Since \(\bar{E}_{i_o}\) is concrete, either \(\alpha \ne \tau \) or
. Since \(\bar{E}_{i_o}\) is concrete, either \(\alpha \ne \tau \) or  . Hence, \(\alpha \ne \tau \) or
. Hence, \(\alpha \ne \tau \) or  . So
. So  . Consequently,
. Consequently,  . In case \(E_{i_0} \ne E'_{i_0}\) we have
. In case \(E_{i_0} \ne E'_{i_0}\) we have  .
.
Now suppose  . Then either
. Then either  or
or  . In the first case we have
. In the first case we have  where
where  and
and  , while in the latter case
, while in the latter case  , and since
, and since  we have
we have  where
where  and
and  . Because \(\bar{E}_{i_0}\) is concrete, \(\bar{E}'_{i_o} = \bar{E}_{i_0}\). Thus
. Because \(\bar{E}_{i_0}\) is concrete, \(\bar{E}'_{i_o} = \bar{E}_{i_0}\). Thus  with
with  , which was to be shown.
, which was to be shown.
Hence  . Clearly \(c(E_{i_0}), c(E_{i_0}+H) < c(E)\). Therefore, by the induction hypothesis (b), \( A X ^b\vdash \tau \mathop {.}E_{i_0} = \tau \mathop {.}( E_{i_0} + H )\). By the induction hypothesis (a), there is a term \(\bar{E}\in \mathcal {E}_{ cc }\) such that
. Clearly \(c(E_{i_0}), c(E_{i_0}+H) < c(E)\). Therefore, by the induction hypothesis (b), \( A X ^b\vdash \tau \mathop {.}E_{i_0} = \tau \mathop {.}( E_{i_0} + H )\). By the induction hypothesis (a), there is a term \(\bar{E}\in \mathcal {E}_{ cc }\) such that  and \( A X ^b\vdash \alpha \mathop {.}\bar{E}= \alpha \mathop {.}( E_{i_0} + H )\). Now we have
and \( A X ^b\vdash \alpha \mathop {.}\bar{E}= \alpha \mathop {.}( E_{i_0} + H )\). Now we have  . Therefore,
. Therefore,

Hence, we have shown the existence of a desired process \(\bar{E}\) with the required properties.
Now suppose, for all \(i \in I\) we have \(\alpha _i \ne \tau \) or  . Clearly \(c(E_i) < c(E)\) for all \(i \in I\). By the induction hypothesis we can find, for all \(i \in I\), concrete \(\bar{E}_i\) such that
. Clearly \(c(E_i) < c(E)\) for all \(i \in I\). By the induction hypothesis we can find, for all \(i \in I\), concrete \(\bar{E}_i\) such that  and \( A X ^b\vdash \alpha \mathop {.}\bar{E}_i = \alpha \mathop {.}E_i\) for all \(\alpha \in \mathcal {A}\). Define \(\bar{E}= { \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}\bar{E}_i }\). Then
and \( A X ^b\vdash \alpha \mathop {.}\bar{E}_i = \alpha \mathop {.}E_i\) for all \(\alpha \in \mathcal {A}\). Define \(\bar{E}= { \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}\bar{E}_i }\). Then  and \(\bar{E}\) is concrete too, since
and \(\bar{E}\) is concrete too, since  for \(i \in I\) in case \(\alpha _i = \tau \). Moreover, \( A X ^b\vdash E = \bar{E}\), since \(E = \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}E_i = \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}\bar{E}_i = \bar{E}\). Hence, for \(\alpha \in \mathcal {A}\), \( A X ^b\vdash \alpha \mathop {.}E = \alpha \mathop {.}\bar{E}\).
for \(i \in I\) in case \(\alpha _i = \tau \). Moreover, \( A X ^b\vdash E = \bar{E}\), since \(E = \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}E_i = \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}\bar{E}_i = \bar{E}\). Hence, for \(\alpha \in \mathcal {A}\), \( A X ^b\vdash \alpha \mathop {.}E = \alpha \mathop {.}\bar{E}\).
Both the base and the induction step for (b): \(\max \lbrace c(F), c(G) \rbrace \geqslant 0\). Suppose  . Pick \(\bar{F}, \bar{G}\in \mathcal {E}_{ cc }\) such that
. Pick \(\bar{F}, \bar{G}\in \mathcal {E}_{ cc }\) such that  and \( A X ^b\vdash \alpha \mathop {.}F = \alpha \mathop {.}\bar{F}\) for all \(\alpha \in \mathcal {A}\), and similarly for G and \(\bar{G}\). Then we have
and \( A X ^b\vdash \alpha \mathop {.}F = \alpha \mathop {.}\bar{F}\) for all \(\alpha \in \mathcal {A}\), and similarly for G and \(\bar{G}\). Then we have  . Since \(\bar{F}\) and \(\bar{G}\) are concrete it follows that \( A X \vdash \bar{F}= \bar{G}\), see Lemma 3.9. Now pick any \(\alpha \in \mathcal {A}\). Then we have \( A X ^b\vdash \alpha \mathop {.}F = \alpha \mathop {.}\bar{F}= \alpha \mathop {.}\bar{G}= \alpha \mathop {.}G\). \(\square \)
. Since \(\bar{F}\) and \(\bar{G}\) are concrete it follows that \( A X \vdash \bar{F}= \bar{G}\), see Lemma 3.9. Now pick any \(\alpha \in \mathcal {A}\). Then we have \( A X ^b\vdash \alpha \mathop {.}F = \alpha \mathop {.}\bar{F}= \alpha \mathop {.}\bar{G}= \alpha \mathop {.}G\). \(\square \)
By now we have gathered sufficient building blocks to prove the main result of this section.
Theorem 3.11
(\({ A X ^b}\) sound and complete for  ). For all processes \(E, F \in \mathcal {E}\) it holds that
). For all processes \(E, F \in \mathcal {E}\) it holds that  iff \( A X ^b\vdash E = F\).
iff \( A X ^b\vdash E = F\).
Proof
In view of Lemma 3.7 we only need to prove completeness of \( A X ^b\) for rooted branching bisimilarity. Suppose \(E, F \in \mathcal {E}\) and  . Let \(E = \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}E_i\) and \(F= \textstyle \sum _{j {\in } J}\, \beta _j \mathop {.}F_j\) for suitable index sets I and J, \(\alpha _i, \beta _j \in \mathcal {A}\), \(E_i, F_j \in \mathcal {E}\). Since
. Let \(E = \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}E_i\) and \(F= \textstyle \sum _{j {\in } J}\, \beta _j \mathop {.}F_j\) for suitable index sets I and J, \(\alpha _i, \beta _j \in \mathcal {A}\), \(E_i, F_j \in \mathcal {E}\). Since  we have (i) for all \(i \in I\) there is a \(j \in J\) such that \(\alpha _i = \beta _j \) and
we have (i) for all \(i \in I\) there is a \(j \in J\) such that \(\alpha _i = \beta _j \) and  , and, symmetrically, (ii) for all \(j \in J\) there is an \(i \in I\) such that \(\alpha _i = \beta _j\) and
, and, symmetrically, (ii) for all \(j \in J\) there is an \(i \in I\) such that \(\alpha _i = \beta _j\) and  . Put
. Put  . Define the processes \(G, H \in \mathcal {E}\) by
. Define the processes \(G, H \in \mathcal {E}\) by
where, for \(i \in I\), \(\gamma _k = \alpha _i\) and \(G_k \equiv E_i\) if \(k = (i,j)\) for some \(j \in J\), and, similarly for \(j \in J\), \(\zeta _k = \beta _j\) and \(H_k \equiv F_j\) if \(k = (i,j)\) for some \(i \in I\). Then G and H are well-defined. Moreover, \( A X \vdash E = G\) and \( A X \vdash F = H\).
For \(k \in K\), say \(k = (i,j)\), it holds that \(\gamma _k = \alpha _i = \beta _j = \zeta _k\) and  , by definition of K. By Lemma 3.10b we obtain, for all \(k \in K\), \( A X ^b\vdash { \gamma _k \mathop {.}G_k = \zeta _k \mathop {.}H_k }\). From this we get \( A X ^b\vdash E = \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}E_i = \textstyle \sum _{k {\in } K}\, \gamma _k \mathop {.}G_k = \textstyle \sum _{k {\in } K}\, \zeta _k \mathop {.}H_k = \textstyle \sum _{j {\in } J}\, \beta _j \mathop {.}F_j = F \) which concludes the proof of the theorem. \(\square \)
, by definition of K. By Lemma 3.10b we obtain, for all \(k \in K\), \( A X ^b\vdash { \gamma _k \mathop {.}G_k = \zeta _k \mathop {.}H_k }\). From this we get \( A X ^b\vdash E = \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}E_i = \textstyle \sum _{k {\in } K}\, \gamma _k \mathop {.}G_k = \textstyle \sum _{k {\in } K}\, \zeta _k \mathop {.}H_k = \textstyle \sum _{j {\in } J}\, \beta _j \mathop {.}F_j = F \) which concludes the proof of the theorem. \(\square \)
4 Branching Bisimilarity for Probabilistic Processes
In this section we define branching bisimilarity for probabilistic processes. Following [6], we start with adapting the syntax of processes, now distinguishing non-deterministic processes \(E \in \mathcal {E}\) and probabilistic processes \(P \in \mathcal {P}\).
Definition 4.1
(Syntax). The classes \(\mathcal {E}\) and \(\mathcal {P}\) of non-deterministic and probabilistic processes over \(\mathcal {A}\), respectively, ranged over by E and P, are given by

with actions \(\alpha \) from \(\mathcal {A}\) where \(r \in (0,1)\).
The probabilistic process \(P_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,}P_2\) executes the behavior of \(P_1\) with probability r and the behavior \(P_2\) with probability \(1-r\). By convention, \(P \mathbin {{}_{\scriptscriptstyle 1 } \oplus \,} Q\) denotes P and \(P \mathbin {{}_{\scriptscriptstyle 0 } \oplus \,} Q\) denotes Q.
We again introduce the complexity measure c, now for non-deterministic and probabilistic processes, based on the depth of a process. The complexity measure  is given by \(c( \mathbf{0 }) = 0\), \(c(\alpha \mathop {.}P) = c(P) + 1\), \(c(E+F) = c(E)+c(F)\), and \(c(\partial (E)) = c(E) + 1\), \(c(P \mathbin {{}_{\scriptscriptstyle r } \oplus \,}Q) = c(P) + c(Q)\).
is given by \(c( \mathbf{0 }) = 0\), \(c(\alpha \mathop {.}P) = c(P) + 1\), \(c(E+F) = c(E)+c(F)\), and \(c(\partial (E)) = c(E) + 1\), \(c(P \mathbin {{}_{\scriptscriptstyle r } \oplus \,}Q) = c(P) + c(Q)\).
As usual SOS semantics for \(\mathcal {E}\) and \(\mathcal {P}\) makes use of two types of transition relations [6, 22].
Definition 4.2
(Operational semantics).
-
(a)
The transition relations \({\rightarrow } \subseteq \mathcal {E}\times \mathcal {A}\times \textit{Distr}(\mathcal {E})\) and \({\mapsto } \subseteq \mathcal {P}\times \textit{Distr}(\mathcal {E})\) are given by

-
(b)
The transition relation \({\rightarrow } \subseteq \textit{Distr}(\mathcal {E})\times \mathcal {A}\times \textit{Distr}(\mathcal {E})\) is such that
 whenever \(\mu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * E_i\), \(\mu ' = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \mu '_i \), and
whenever \(\mu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * E_i\), \(\mu ' = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \mu '_i \), and  for all \(i \in I\).
for all \(i \in I\).
With \([[P]]\), for \(P\in \mathcal {P}\), we denote the unique distribution \(\mu \) such that \(P\mapsto \mu \).
The transition relation \(\rightarrow \) on distributions allows for a probabilistic combination of non-deterministic alternatives resulting in a so-called combined transition, cf. [28, 29]. For example, for \(E \equiv a \mathop {.}(P \mathbin {{}_{\scriptscriptstyle 1/2 } \oplus \,} Q) + a \mathop {.}(P \mathbin {{}_{\scriptscriptstyle 1/3 } \oplus \,} Q)\), the Dirac process \(\delta (E) \equiv \delta ( a \mathop {.}(P \mathbin {{}_{\scriptscriptstyle 1/2 } \oplus \,} Q) + a \mathop {.}(P \mathbin {{}_{\scriptscriptstyle 1/3 } \oplus \,} Q) )\) provides an a-transition to \([[P \mathbin {{}_{\scriptscriptstyle 1/2 } \oplus \,} Q]]\) as well as an a-transition to \([[P \mathbin {{}_{\scriptscriptstyle 1/3 } \oplus \,} Q]]\). However, since for distribution \(\delta (E)\) it holds that \(\delta (E) = \frac{1}{2} \delta (E) \oplus \frac{1}{2} \delta (E)\) there is also a transition

As noted in [30], the ability to combine transitions is crucial for obtaining transitivity of probabilistic process equivalences that take internal actions into account.
Referring to the example in the introduction, the processes of \(t_0\) and \(u_0\) will be identified. However, without the splitting of the source distribution \(\mu \) as provided by Definition 4.2, we are not able to relate \(t_0\) and \(u_0\) directly, or rather their direct derivatives, while meeting the natural transfer conditions (see Definition 4.4). The difficulty arises when both P and Q can do a \(\tau \)-transition to non-bisimilar processes.
In preparation to the definition of the notion of branching probabilistic bisimilarity below we introduce some notation.
Definition 4.3
For \(\mu , \mu ' \mathbin \in \textit{Distr}(\mathcal {E})\) and \(\alpha \mathbin \in \mathcal {A}\) we write  iff (i)
iff (i)  , or (ii) \(\alpha = \tau \) and \(\mu = \mu _1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\mu _2\), \(\mu ' = \mu '_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\mu '_2\) such that
, or (ii) \(\alpha = \tau \) and \(\mu = \mu _1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\mu _2\), \(\mu ' = \mu '_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\mu '_2\) such that  and \(\mu _2 = \mu '_2\) for some \(r \in [0,1]\). We use
and \(\mu _2 = \mu '_2\) for some \(r \in [0,1]\). We use  to denote the reflexive transitive closure of
to denote the reflexive transitive closure of  .
.
Thus, for example,

We are now in a position to define strong probabilistic bisimilarity and branching probabilistic bisimilarity. Note that the notion of strong probabilistic bisimilarity is the variant with combined transitions as defined in [6, 29].
Definition 4.4
(Strong and branching probabilistic bisimilarity).
-
(a)
A symmetric relation \(\mathcal {R}\subseteq \textit{Distr}(\mathcal {E})\times \textit{Distr}(\mathcal {E})\) is called decomposable iff for all \(\mu , \nu \in \textit{Distr}(\mathcal {E})\) such that \(\mu \,{\mathcal {R}}\,\nu \) and \(\mu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \mu _i\) there are \(\nu _i \in \textit{Distr}(\mathcal {E})\), for \(i \in I\), such that

-
(b)
A decomposable relation \(\mathcal {R}\subseteq \textit{Distr}(\mathcal {E})\times \textit{Distr}(\mathcal {E})\) is called a strong probabilistic bisimulation relation iff for all \(\mu , \nu \in \textit{Distr}(\mathcal {E})\) such that \(\mu \,{\mathcal {R}}\,\nu \) and
 there is a \(\nu ' \in \textit{Distr}(\mathcal {E})\) such that
there is a \(\nu ' \in \textit{Distr}(\mathcal {E})\) such that 
-
(c)
A symmetric relation \(\mathcal {R}\subseteq \textit{Distr}(\mathcal {E})\times \textit{Distr}(\mathcal {E})\) is called weakly decomposable iff for all \(\mu , \nu \in \textit{Distr}(\mathcal {E})\) such that \(\mu \,{\mathcal {R}}\,\nu \) and \(\mu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \mu _i\) there are \(\bar{\nu }, \nu _i \in \textit{Distr}(\mathcal {E})\), for \(i \in I\), such that

-
(d)
A weakly decomposable relation \(\mathcal {R}\subseteq \textit{Distr}(\mathcal {E})\times \textit{Distr}(\mathcal {E})\) is called a branching probabilistic bisimulation relation iff for all \(\mu , \nu \in \textit{Distr}(\mathcal {E})\) such that \(\mu \,{\mathcal {R}}\,\nu \) and
 , there are \(\bar{\nu }, \nu ' \in \textit{Distr}(\mathcal {E})\) such that
, there are \(\bar{\nu }, \nu ' \in \textit{Distr}(\mathcal {E})\) such that 
-
(e)
Strong probabilistic bisimilarity, denoted by
 , and branching probabilistic bisimilarity, written as
, and branching probabilistic bisimilarity, written as  , are respectively defined as the largest strong probabilistic bisimulation relation on \(\textit{Distr}(\mathcal {E})\) and as the largest branching probabilistic bisimulation relation on \(\textit{Distr}(\mathcal {E})\).
, are respectively defined as the largest strong probabilistic bisimulation relation on \(\textit{Distr}(\mathcal {E})\) and as the largest branching probabilistic bisimulation relation on \(\textit{Distr}(\mathcal {E})\).
By comparison, on finite processes, as used in this paper, the branching probabilistic bisimilarity of Segala and Lynch [29] can be defined in our framework exactly as in (d) and (e) above, but taking a decomposable instead of a weakly decomposable relation. This yields a strictly finer equivalence, distinguishing the processes \(s_0\), \(t_0\) and \(u_0\) from the introduction.
The notion of decomposability has been adopted from [23] and weak decomposability from [25]. The underlying idea stems from [10]. These notions provide a convenient dexterity to deal with behavior of sub-distributions, e.g., to distinguish \(\textstyle {\frac{1}{2}} \partial ( a \mathop {.}\partial ( \mathbf{0 })) \oplus \textstyle {\frac{1}{2}} \partial ( b \mathop {.}\partial ( \mathbf{0 }))\) from \(\partial ( \mathbf{0 })\), as well as combined behavior.
Our definition of branching probabilistic bisimilarity is based on distributions rather than on states and has similarity with the notion of weak distribution bisimilarity proposed by Eisentraut et al. in [13]. Consider the running example of [13], reproduced in Fig. 1 and reformulated in terms of the process language at hand. The states
 and
and
 are identified with respect to weak distribution bisimilarity as detailed in [13]. Correspondingly, putting
are identified with respect to weak distribution bisimilarity as detailed in [13]. Correspondingly, putting

the non-deterministic processes \(E_1\) and \(E_6\) are identified with respect to branching probabilistic bisimilarity.
Probabilistic automaton of [13]
Note that strong and branching probabilistic bisimilarity are well-defined since any union of strong or branching probabilistic bisimulation relations is again a strong or branching probabilistic bisimulation relation. In particular, (weak) decomposability is preserved under arbitrary unions.
As we did for the non-deterministic setting, we introduce a notion of rooted branching probabilistic bisimilarity for distributions over processes.
Definition 4.5
A symmetric and decomposable relation \(\mathcal {R}\mathbin \subseteq \textit{Distr}(\mathcal {E})\times \textit{Distr}(\mathcal {E})\) is called a rooted branching probabilistic bisimulation relation iff for all \(\mu , \nu \in \textit{Distr}(\mathcal {E})\) such that \(\mu \,{\mathcal {R}}\,\nu \) it holds that if  for \(\alpha \in \mathcal {A}\), \(\mu ' \in \textit{Distr}(\mathcal {E})\) then
for \(\alpha \in \mathcal {A}\), \(\mu ' \in \textit{Distr}(\mathcal {E})\) then  and
and  for some \(\nu ' \in \textit{Distr}(\mathcal {E})\). Rooted branching probabilistic bisimilarity, denoted by
for some \(\nu ' \in \textit{Distr}(\mathcal {E})\). Rooted branching probabilistic bisimilarity, denoted by  , is defined as the largest rooted branching probabilistic bisimulation relation.
, is defined as the largest rooted branching probabilistic bisimulation relation.
Since any union of rooted branching probabilistic bisimulation relations is again a rooted branching probabilistic bisimulation relation, rooted branching probabilistic bisimilarity  is well-defined.
is well-defined.
Note, the two probabilistic processes \(P = \partial ( \tau \mathop {.}\partial (a \mathop {.}\partial ( \mathbf{0 }))) \mathbin {{}_{\scriptscriptstyle 1/2 } \oplus \,} \partial (b \mathop {.}\partial ( \mathbf{0 }))\) and \(Q = \partial (a \mathop {.}\partial ( \mathbf{0 })) \mathbin {{}_{\scriptscriptstyle 1/2 } \oplus \,} \partial (b \mathop {.}\partial ( \mathbf{0 }))\) are not rooted branching probabilistically bisimilar. Any rooted branching probabilistic bisimulation relation is by decomposability required to relate the respective probabilistic components \(\partial ( \tau \mathop {.}\partial (a \mathop {.}\partial ( \mathbf{0 })))\) and \(\partial (a \mathop {.}\partial ( \mathbf{0 }))\), which clearly do not meet the transfer condition. Thus, since  also
also  .
.
Two non-deterministic processes are considered to be strongly, rooted branching, or branching probabilistically bisimilar iff their Dirac distributions are, i.e.,  iff
iff  ,
,  iff
iff  , and
, and  iff
iff  . Two probabilistic processes are considered to be strongly, rooted branching, or branching probabilistically bisimilar iff their associated distributions over \(\mathcal {E}\) are.
. Two probabilistic processes are considered to be strongly, rooted branching, or branching probabilistically bisimilar iff their associated distributions over \(\mathcal {E}\) are.
We show that branching probabilistic bisimilarity, although not a congruence for non-deterministic choice, is a congruence for probabilistic choice. We first need a technical result, the proof of which is omitted here, see [16].
Lemma 4.6
Let I and J be finite index sets, \(p_i,q_j\in [0,1]\) and \(\xi , \mu _i,\nu _j \in \textit{Distr}(\mathcal {E})\), for \(i \in I\) and \(j \in J\), with \(\xi = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i*\mu _i\) and \(\xi =\textstyle {\bigoplus _{j \mathord {\in } J}}\, q_j * \nu _j\). Then there are \(r_{ij} \in [0,1]\) and \(\varrho _{ij} \in \textit{Distr}(\mathcal {E})\) such that \(\sum _{i\in I} \, r_{ij}=q_j\), \(\sum _{j\in J} \, r_{ij}=p_i\), \( p_i * \mu _i = \textstyle {\bigoplus _{j \mathord {\in } J}}\, r_{ij} * \varrho _{ij} \text { for all}~i \in I, \text { and } q_j * \nu _j = \textstyle {\bigoplus _{i \mathord {\in } I}}\, r_{ij} * \varrho _{ij} \text { for all}~j \in J. \)
The next result states that the operator \(\mathbin {{}_{\scriptscriptstyle r } \oplus \,}\) respects branching probabilistic bisimilarity.
Lemma 4.7
Let \(\mu _1,\mu _2,\nu _1,\nu _2\in \textit{Distr}(\mathcal {E})\) and \(r\in (0,1)\). If  and
and  then
then  .
.
Also for a proof of Lemma 4.7 we refer to [16]. A direct consequence of the lemma is that if  and
and  then
then  .
.
Lemma 4.8
(Congruence). The relations  ,
,  , and
, and  on \(\mathcal {E}\) and \(\mathcal {P}\) are equivalence relations, and the relations
on \(\mathcal {E}\) and \(\mathcal {P}\) are equivalence relations, and the relations  and
and  are congruences on \(\mathcal {E}\) and \(\mathcal {P}\).
are congruences on \(\mathcal {E}\) and \(\mathcal {P}\).
Proof
The proof of  ,
,  , and
, and  being equivalence relations involves a number of straightforward auxiliary results, in particular for the case of transitivity, and are omitted here.
being equivalence relations involves a number of straightforward auxiliary results, in particular for the case of transitivity, and are omitted here.
Regarding congruence the interesting cases are for non-deterministic and probabilistic choice with respect to rooted branching probabilistic bisimilarity. Suppose  and
and  . Then \(\mathcal {R}= \lbrace { \langle \delta (E_1+E_2) , \delta (F_1+F_2) \rangle } \rbrace ^\dagger \) is a rooted branching probabilistic bisimulation relation. Clearly, \(\mathcal {R}\) is symmetric and decomposable. Moreover, if
. Then \(\mathcal {R}= \lbrace { \langle \delta (E_1+E_2) , \delta (F_1+F_2) \rangle } \rbrace ^\dagger \) is a rooted branching probabilistic bisimulation relation. Clearly, \(\mathcal {R}\) is symmetric and decomposable. Moreover, if  , then either
, then either  ,
,  , or
, or  ,
,  and \(\mu ' = \mu '_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \mu '_2\) for suitable \(\mu '_1, \mu '_2 \in \textit{Distr}(\mathcal {E})\) and \(r \in (0,1)\). We only consider the last case, as the first two are simpler. Hence, we can find \(\nu '_1, \nu '_2 \in \textit{Distr}(\mathcal {E})\) such that
and \(\mu ' = \mu '_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \mu '_2\) for suitable \(\mu '_1, \mu '_2 \in \textit{Distr}(\mathcal {E})\) and \(r \in (0,1)\). We only consider the last case, as the first two are simpler. Hence, we can find \(\nu '_1, \nu '_2 \in \textit{Distr}(\mathcal {E})\) such that  ,
,  ,
,  , and
, and  . From this it follows that
. From this it follows that  and
and  for \(\nu ' = \nu '_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \nu '_2\) using Lemma 4.7.
for \(\nu ' = \nu '_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \nu '_2\) using Lemma 4.7.
Suppose  and
and  with \(\mathcal {R}_1\) and \(\mathcal {R}_2\) rooted branching probabilistic bisimulation relations relating \([[P_1]]\) with \([[Q_1]]\), and \([[P_2]]\) with \([[Q_2]]\), respectively, and fix some \(r\in (0,1)\). Then \(\mathcal {R}= \lbrace \,\langle {\mu }_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} {\mu }_2 , \nu _1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \nu _2 \rangle \mid {\mu }_1 \mathcal {R}_1 \nu _1 ,\, {\mu }_2 \mathcal {R}_2 \nu _2 \, \rbrace \) is a rooted branching probabilistic bisimulation relation relating \([[P_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} P_2]]\) with \([[Q_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} Q_2]]\). Symmetry is straightforward and decomposability can be shown by application of Lemma 4.6.
with \(\mathcal {R}_1\) and \(\mathcal {R}_2\) rooted branching probabilistic bisimulation relations relating \([[P_1]]\) with \([[Q_1]]\), and \([[P_2]]\) with \([[Q_2]]\), respectively, and fix some \(r\in (0,1)\). Then \(\mathcal {R}= \lbrace \,\langle {\mu }_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} {\mu }_2 , \nu _1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \nu _2 \rangle \mid {\mu }_1 \mathcal {R}_1 \nu _1 ,\, {\mu }_2 \mathcal {R}_2 \nu _2 \, \rbrace \) is a rooted branching probabilistic bisimulation relation relating \([[P_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} P_2]]\) with \([[Q_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} Q_2]]\). Symmetry is straightforward and decomposability can be shown by application of Lemma 4.6.
So we are left to prove the transfer property. Suppose \(({\mu }_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} {\mu }_2) \mathcal {R}(\nu _1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \nu _2)\), thus \(\mu _1 \mathcal {R}_1 \mu _2\) and \(\nu _1 \mathcal {R}_2 \nu _2\). If  then
then  and \(\mu ' = \mu '_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \mu '_2\) for suitable \(\mu '_1, \mu '_2 \in \textit{Distr}(\mathcal {E})\). By assumption, \(\nu '_1\) and \(\nu '_2\) exist such that
and \(\mu ' = \mu '_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \mu '_2\) for suitable \(\mu '_1, \mu '_2 \in \textit{Distr}(\mathcal {E})\). By assumption, \(\nu '_1\) and \(\nu '_2\) exist such that  ,
,  , and
, and  . From this we obtain
. From this we obtain  and by Lemma 4.7
and by Lemma 4.7  for \(\nu ' = \nu '_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \nu '_2\). \(\square \)
for \(\nu ' = \nu '_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \nu '_2\). \(\square \)
5 A Few Fundamental Properties of Branching Bisimilarity
In this section we show two fundamental properties of branching probabilistic bisimilarity that we need further on: the stuttering property, known from [17] for non-deterministic processes, and cancellativity of probabilistic choice with respect to  .
.
Lemma 5.1
(Stuttering Property). If  and
and  then
then  .
.
Proof
We show that the relation  is a branching probabilistic bisimulation.
is a branching probabilistic bisimulation.
First suppose  . Then there are \(\bar{\nu }, \nu ' \in \textit{Distr}(\mathcal {E})\) such that
. Then there are \(\bar{\nu }, \nu ' \in \textit{Distr}(\mathcal {E})\) such that

Since  , we have
, we have  , which had to be shown. Now suppose
, which had to be shown. Now suppose  . Then certainly
. Then certainly  .
.
To show weak decomposability, suppose \(\mu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \mu _i\). Then there are \(\bar{\nu }, \nu _i \in \textit{Distr}(\mathcal {E})\), for \(i \in I\), such that

Again it suffices to point out that  . Conversely, suppose \(\bar{\mu }= \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \bar{\mu }_i\). Then
. Conversely, suppose \(\bar{\mu }= \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \bar{\mu }_i\). Then  . \(\square \)
. \(\square \)
Lemma 5.2
(Cancellativity). Let \(\mu , \mu ', \nu , \nu ' \in \textit{Distr}(\mathcal {E})\). If  with \(r \in (0,1]\) and
with \(r \in (0,1]\) and  , then
, then  .
.
A proof can be found in [16].
6 Completeness: The Probabilistic Case
In this section we provide a sound and complete equational characterization of rooted branching probabilistic bisimilarity. The completeness result is obtained along the same lines as the corresponding result for branching bisimilarity for the non-deterministic processes in Sect. 3. We extend and adapt the non-deterministic theories \( A X \) and \( A X ^b\) of Sect. 3.
Definition 6.1
(Axiomatization of  and
and  ). The theory \( A X _{p}\) is given by the axioms A1 to A4, the axioms P1 to P3 and C listed in Table 2. The theory \( A X ^b_{p}\) contains in addition the axioms BP and G.
). The theory \( A X _{p}\) is given by the axioms A1 to A4, the axioms P1 to P3 and C listed in Table 2. The theory \( A X ^b_{p}\) contains in addition the axioms BP and G.
The axioms A1–A4 for non-deterministic processes are as before. Regarding probabilistic processes, for the axioms P1 and P2 dealing with commutativity and associativity, we need to take care of the probabilities involved. For P2, it follows from the given restrictions that also \((1{-}r)s = (1{-}r')s'\), i.e., the probability for Q to execute is equal for the left-hand and right-hand side of the equation. Axiom P3 expresses that a probabilistic choice between equal processes can be eliminated. Axiom C expresses that any two nondeterministic transitions can be executed in a combined fashion: one with probability r and one with the complementary probability \(1{-}r\).
The axioms P1 and P2 allow us to write each probabilistic process P as
for non-deterministic processes \(E_i\). In the sequel we denote such a process by \(\textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * E_i\) with \(p_i=r_i\prod _{j=1}^{i-1}(1-r_j)\). More specifically, if a probabilistic process P corresponds to a distribution \(\textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * E_i\), then we have \( A X _{p}\vdash P = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * E_i\), as can be shown by induction on the structure of P.
For axioms BP and G of Table 2 we introduce the notation \(E \sqsubseteq P\) for \(E \in \mathcal {E}\), \(P \in \mathcal {P}\). We define

Thus, we require that every transition of the non-deterministic process E can be directly matched by the probabilistic process P. Note, if \(E \sqsubseteq P\) and  , then
, then  for some \(\nu \in \textit{Distr}(\mathcal {E})\) such that
for some \(\nu \in \textit{Distr}(\mathcal {E})\) such that  : If
: If  , then \(\mu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \mu _i\) and
, then \(\mu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \mu _i\) and  for suitable \(p_i \geqslant 0\), \(\mu _i \in \textit{Distr}(\mathcal {E})\). Since \(E \sqsubseteq P\), we have for each \(i \in I\) that
for suitable \(p_i \geqslant 0\), \(\mu _i \in \textit{Distr}(\mathcal {E})\). Since \(E \sqsubseteq P\), we have for each \(i \in I\) that  for some \(\nu _i \in \textit{Distr}(\mathcal {E})\) satisfying
for some \(\nu _i \in \textit{Distr}(\mathcal {E})\) satisfying  . Hence
. Hence  and
and  by Lemma 4.7.
by Lemma 4.7.
Axiom BP is an adaptation of axiom B of the theory \( A X ^b\) to the probabilistic setting of \( A X ^b_{p}\). In the setting of non-deterministic processes the implication  \(\Longrightarrow \)
\(\Longrightarrow \)  \(\wedge \)
\(\wedge \)  for some \(E'\) is captured by
for some \(E'\) is captured by  . If we reformulate axiom B as \(E + F = E\) \(\Longrightarrow \) \(\alpha \mathop {.}( F + \tau \mathop {.}E ) = \alpha \mathop {.}E\), then it becomes more similar to axiom BP in Table 2.
. If we reformulate axiom B as \(E + F = E\) \(\Longrightarrow \) \(\alpha \mathop {.}( F + \tau \mathop {.}E ) = \alpha \mathop {.}E\), then it becomes more similar to axiom BP in Table 2.
As to BP, in the context of a preceding action \(\alpha \) and a probabilistic process Q, a non-deterministic alternative E that is also offered by a probabilistic process after a \(\tau \)-prefix can be dispensed with, together with the prefix \(\tau \). In a formulation without the prefix \(\alpha \) and the probabilistic alternative Q, but with the specific condition \(E \sqsubseteq P\), and retaining the \(\tau \)-prefix on the right-hand side, the axiom BP shows similarity with axioms T2 and T3 in [15] which, in turn, are reminiscent of axioms T1 and T2 of [11]; these axioms stem from Milner’s second \(\tau \)-law [26].
Let us illustrate the working of axiom BP. Consider the non-deterministic process \(E = b \mathop {.}\partial ( \mathbf{0 })\) and the probabilistic process \(P = \partial ( a \mathop {.}\partial ( \mathbf{0 })+ b \mathop {.}\partial ( \mathbf{0 })) \mathbin {{}_{\scriptscriptstyle 1/2 } \oplus \,} \partial ( b \mathop {.}\partial ( \mathbf{0 }))\). Then we have \(E \sqsubseteq P\), i.e.

Therefore, we have by application of axiom BP the provable equality

Another example is  , so
, so

An example illustrating the use of \((\alpha )\), rather than \(\alpha \), as label of the matching transition of \([[P]]\) in the definition of \(\sqsubseteq \) is

from which we obtain

The axiom G roughly is a variant of BP without the \(\tau \) prefixing the process P. A typical example, matching the one above, is

The occurrences of the prefix \(\alpha \mathop {.}{\_}\) in BP and G are related to the root condition for non-deterministic processes, cf. axiom B in Sect. 3.
Lemma 6.2
The following simplifications of the axiom BP are derivable:

See [16] for a proof of the above lemma. Similar simplifications of axiom G can be found. Using the properties given by Lemma 6.2 the process identities mentioned in the introduction can easily be proven. Returning to the processes \(E_1\) and \(E_6\) related to Fig. 1, we have

Soundness of the theory \( A X _{p}\) for strong probabilistic bisimilarity and of the theory \( A X ^b_{p}\) for rooted branching probabilistic bisimilarity is straightforward.
Lemma 6.3
(Soundness). For all \(P,Q \in \mathcal {P}\), if \( A X _{p}\vdash P = Q\) then  , and if \( A X ^b_{p}\vdash P = Q\) then
, and if \( A X ^b_{p}\vdash P = Q\) then  .
.
Proof
As usual, in view of  and
and  being congruences, one only needs to prove the left-hand and right-hand sides of the axioms to be strongly or rooted branching probabilistically bisimilar. We only treat the cases of the axioms BP and G with respect to rooted branching probabilistic bisimilarity.
being congruences, one only needs to prove the left-hand and right-hand sides of the axioms to be strongly or rooted branching probabilistically bisimilar. We only treat the cases of the axioms BP and G with respect to rooted branching probabilistic bisimilarity.
For BP, by Definition 4.5 and Lemma 4.7, it suffices to show that  if \(E \sqsubseteq P\). Suppose
if \(E \sqsubseteq P\). Suppose  . We distinguish two cases: (i)
. We distinguish two cases: (i)  ; (ii) \(\alpha = \tau \),
; (ii) \(\alpha = \tau \),  and \(\mu = [[P]] \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \mu '\) for some \(r \in (0,1]\). For (i), by definition of \(E \sqsubseteq P\), we have
and \(\mu = [[P]] \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \mu '\) for some \(r \in (0,1]\). For (i), by definition of \(E \sqsubseteq P\), we have  and
and  for suitable \(\nu \in \textit{Distr}(\mathcal {E})\). For (ii), again by \(E \mathbin \sqsubseteq P\), we have
for suitable \(\nu \in \textit{Distr}(\mathcal {E})\). For (ii), again by \(E \mathbin \sqsubseteq P\), we have  and
and  . Thus
. Thus  and
and  for \(\nu = [[P]] \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \nu '\), as was to be shown. Conversely,
for \(\nu = [[P]] \mathbin {{}_{\scriptscriptstyle r } \oplus \,} \nu '\), as was to be shown. Conversely,  trivially implies that
trivially implies that  . The requirement on weak decomposability also holds trivially.
. The requirement on weak decomposability also holds trivially.
For G, by Definition 4.5 and Lemma 4.7, it suffices to show that  if \(E \sqsubseteq \partial (F)\). Put
if \(E \sqsubseteq \partial (F)\). Put  . We verify that \(\mathcal {R}\) is a branching probabilistic bisimulation. Naturally,
. We verify that \(\mathcal {R}\) is a branching probabilistic bisimulation. Naturally,  implies
implies  , and also weak decomposability is easy. Finally, suppose
, and also weak decomposability is easy. Finally, suppose  . Since \(E \sqsubseteq \partial (F)\) now we have
. Since \(E \sqsubseteq \partial (F)\) now we have  for some \(\nu \) with
for some \(\nu \) with  . \(\square \)
. \(\square \)
As for the process language with non-deterministic processes only, we aim at a completeness proof that is built on completeness of strong bisimilarity and the notion of a concrete process. Equational characterization of strong probabilistic bisimilarity has been addressed by various authors. The theory \( A X _{p}\) provides a sound and complete theory. For a proof, see e.g. [23].
Lemma 6.4
The theory \( A X _{p}\) is sound and complete for strong bisimilarity.
The next lemma provides a more state-based characterization of strong probabilistic bisimilarity.
Lemma 6.5
Let \(\mathcal {R}\subseteq \textit{Distr}(\mathcal {E})\times \textit{Distr}(\mathcal {E})\) be a decomposable relation such that
and for each pair \(E,F \in \mathcal {E}\)

for a suitable \(\nu ' \in \textit{Distr}(\mathcal {E})\). Then \(\mu \,{\mathcal {R}}\,\nu \) implies  .
.
Proof
We show that \(\mathcal {R}\) is a strong probabilistic bisimulation relation. So, let \(\mu , \nu \in \textit{Distr}(\mathcal {E})\) such that \(\mu \,{\mathcal {R}}\,\nu \) and  . By Definition 4.2(b) we have \(\mu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * E_i\), \(\mu ' = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \mu '_i \), and
. By Definition 4.2(b) we have \(\mu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * E_i\), \(\mu ' = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \mu '_i \), and  for all \(i \in I\). Since \(\mathcal {R}\) is decomposable, there are \(\nu _i \in \textit{Distr}(\mathcal {E})\), for \(i \in I\), such that
for all \(i \in I\). Since \(\mathcal {R}\) is decomposable, there are \(\nu _i \in \textit{Distr}(\mathcal {E})\), for \(i \in I\), such that

Let, for each \(i\in I\), \(\nu _i = \bigoplus _{j\in J_i} \, p_{ij} * F_{ij}\). Since \(\mathcal {R}\) is decomposable, there are \(\mu _{ij} \in \textit{Distr}(\mathcal {E})\), for \(j \in J_i\), such that

Here \(\mu _{ij} = \delta (E_i)\). Writing \(E_{ij} \, {:=} \, E_i\), \(q_{ij} \, {:=} \, p_i\cdot p_{ij}\) and \(K = \lbrace \,(i,j) \mid i \in I \wedge j \in J_i \, \rbrace \) we obtain

Let \(\mu '_{ij} {:=} \mu '_i\) for all \(i \in I\) and \(j \in J_i\). Then \(\mu ' = \textstyle {\bigoplus _{k \mathord {\in } K}}\, q_{k} * \mu '_k\). Using that  for all \(k \in K\), there must be distributions \(\nu '_k\) for \(k \in K\) such that
for all \(k \in K\), there must be distributions \(\nu '_k\) for \(k \in K\) such that

By Definition 4.2(b) this implies  , for
, for  . Moreover, (1) yields \(\mu ' \,{\mathcal {R}}\,\nu '\). \(\square \)
. Moreover, (1) yields \(\mu ' \,{\mathcal {R}}\,\nu '\). \(\square \)
The following technical lemma expresses that two rooted branching probabilistically bisimilar processes can be represented in a similar way.
Lemma 6.6
For all \(Q, R \in \mathcal {P}\), if  then there are an index set I as well as for all \(i\in I\) suitable \(p_i > 0\) and \(F_i, G_i \in \mathcal {E}\) such that
then there are an index set I as well as for all \(i\in I\) suitable \(p_i > 0\) and \(F_i, G_i \in \mathcal {E}\) such that  , \( A X _{p}\vdash Q = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * F_i\) and \( A X _{p}\vdash R = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * G_i\).
, \( A X _{p}\vdash Q = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * F_i\) and \( A X _{p}\vdash R = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * G_i\).
Proof
Suppose  . Since
. Since  and
and  is decomposable, the process R can be written as
is decomposable, the process R can be written as  with \(R_j \in \mathcal {P}\) for \(j \in J\), such that
with \(R_j \in \mathcal {P}\) for \(j \in J\), such that  . Therefore, each distribution \(R_j\) can be written as
. Therefore, each distribution \(R_j\) can be written as  where
where  for all \(j \in J\) and \(k \in K_j\). We now define \(F_{jk} = F'_j\) for \(j \in J\) and \(k \in K_j\). Then, using the axioms P1, P2 and P3 we can derive
for all \(j \in J\) and \(k \in K_j\). We now define \(F_{jk} = F'_j\) for \(j \in J\) and \(k \in K_j\). Then, using the axioms P1, P2 and P3 we can derive

with  for \(j \in J\) and \(k \in K_j\). This proves the lemma. \(\square \)
for \(j \in J\) and \(k \in K_j\). This proves the lemma. \(\square \)
Similar to the non-deterministic case, a transition  is called inert iff
is called inert iff  . Typical cases of inert transitions include
. Typical cases of inert transitions include

Furthermore, a transition  with \(r \in (0,1]\) and
with \(r \in (0,1]\) and  is called partially inert. A typical case is
is called partially inert. A typical case is

Here  because
because  .
.
In Sect. 3 a process is called concrete if it does not exhibit an inert transition. In the setting with probabilistic choice we need to be more careful. For example, we also want to exclude processes of the form
from being concrete, although they cannot perform a transition by themselves at all. Therefore, we define the derivatives \(\textit{der} (P)\subseteq \mathcal {E}\) of a probabilistic process \(P\in \mathcal {P}\) by
and define a process \(\bar{P}\in \mathcal {P}\) to be concrete iff none of its derivatives can perform a partially inert transition, i.e., if there is no transition  with \(E \in \textit{der} (\bar{P})\), \(r \in (0,1]\) and
with \(E \in \textit{der} (\bar{P})\), \(r \in (0,1]\) and  . A non-deterministic process \(\bar{E}\) is called concrete if the probabilistic process \(\partial (\bar{E})\) is. Moreover, we define two sets of concrete processes:
. A non-deterministic process \(\bar{E}\) is called concrete if the probabilistic process \(\partial (\bar{E})\) is. Moreover, we define two sets of concrete processes:

Furthermore, we call a process \(E \in \textit{Distr}(\mathcal {E})\) rigid iff there is no inert transition  , and write
, and write  . Naturally, \(\mathcal {E}_{ cc }\subseteq \mathcal {E}_r\).
. Naturally, \(\mathcal {E}_{ cc }\subseteq \mathcal {E}_r\).
We use concrete and rigid processes to build the proof of the completeness result for rooted branching probabilistic bisimilarity on top of the completeness proof of strong probabilistic bisimilarity. The following lemma lists all properties of concrete and rigid processes we need in our completeness proof.
Lemma 6.7
-
(a)
If \(E = \textstyle \sum _{i {\in } I}\, \alpha _i \cdot P_i\) with \(P_i \in \mathcal {P}_{\! cc }\) and, for all \(i \in I\), \(\alpha _i \ne \tau \) or \([[P_i]]\) cannot be written as \(\mu _1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\mu _2\) with \(r \mathbin \in (0,1]\) and
 , then \(E \in \mathcal {E}_{ cc }\).
, then \(E \in \mathcal {E}_{ cc }\). -
(b)
If \(P_1,P_2\in \mathcal {P}_{\! cc }\) then \(P_1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,}P_2\in \mathcal {P}_{\! cc }\).
-
(c)
If \(\mu = \textstyle {\bigoplus _{i \mathord {\in } I}}\, p_i * \mu _i \in \textit{Distr}(\mathcal {E}_{ cc })\) with each \(p_i>0\), then each \(\mu _i\in \textit{Distr}(\mathcal {E}_{ cc })\).
-
(d)
If \(\mu \in \textit{Distr}(\mathcal {E}_{ cc })\) and
 then
then  .
. -
(e)
If \(\mu \in \textit{Distr}(\mathcal {E}_r)\) and
 with
with  then \(\mu = \mu '\).
then \(\mu = \mu '\). -
(f)
If \(E \mathbin \in \mathcal {E}_{ cc }\), \(F \mathbin \in \mathcal {E}\), and \(\mu ,\nu \mathbin \in \textit{Distr}(\mathcal {E})\) are such that
 ,
,  ,
,  and
and  , then
, then  .
.
Proof
Properties (a), (b), (c) and (d) follow immediately from the definitions, in the case of (d) also using Definition 4.2(b).
For (e), let \(\mu \mathbin \in \textit{Distr}(\mathcal {E}_r)\) and  with
with  . Towards a contradiction, suppose \(\mu \ne \mu '\). Then there must be a distribution \(\bar{\mu }\ne \mu \) such that
. Towards a contradiction, suppose \(\mu \ne \mu '\). Then there must be a distribution \(\bar{\mu }\ne \mu \) such that  and
and  . We may even choose \(\bar{\mu }\) such that the transition
. We may even choose \(\bar{\mu }\) such that the transition  acts on only one (rigid) state in the support of \(\mu \), i.e. there are \(E \in \mathcal {E}\), \(r \in (0,1]\) and \(\rho ,\nu \in \textit{Distr}(\mathcal {E})\) such that \(\mu = \delta (E) \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\rho \),
acts on only one (rigid) state in the support of \(\mu \), i.e. there are \(E \in \mathcal {E}\), \(r \in (0,1]\) and \(\rho ,\nu \in \textit{Distr}(\mathcal {E})\) such that \(\mu = \delta (E) \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\rho \),  and \(\bar{\mu }= \nu \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\rho \). By Lemma 5.1
and \(\bar{\mu }= \nu \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\rho \). By Lemma 5.1 . Hence by Lemma 5.2
. Hence by Lemma 5.2  . So the transition
. So the transition  is inert, contradicting \(E \in \mathcal {E}_r\).
is inert, contradicting \(E \in \mathcal {E}_r\).
To establish (f), suppose \(E \in \mathcal {E}_{ cc }\), \(F \in \mathcal {E}\), and \(\mu ,\nu \in \textit{Distr}(\mathcal {E})\) are such that  ,
,  and
and  . Assume \(\alpha = \tau \), for otherwise the statement is trivial. Then
. Assume \(\alpha = \tau \), for otherwise the statement is trivial. Then  and
and  for some \(\nu _1 \in \textit{Distr}(\mathcal {E})\) and \(r \in [0,1]\). Since
for some \(\nu _1 \in \textit{Distr}(\mathcal {E})\) and \(r \in [0,1]\). Since  is weakly decomposable, there are \(\bar{\mu }, \mu _1, \mu _2 \in \textit{Distr}(\mathcal {E})\) such that
is weakly decomposable, there are \(\bar{\mu }, \mu _1, \mu _2 \in \textit{Distr}(\mathcal {E})\) such that  ,
,  , \(\bar{\mu }= \mu _1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\mu _2\),
, \(\bar{\mu }= \mu _1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\mu _2\),  and
and  . Since \(\mu \) is concrete, using case (d) of the lemma, \(\bar{\mu }= \mu \) by case (e). Thus
. Since \(\mu \) is concrete, using case (d) of the lemma, \(\bar{\mu }= \mu \) by case (e). Thus  with
with  . Since E is concrete, this transition cannot be partially inert. Thus, we must have \(r = 1\). It follows that
. Since E is concrete, this transition cannot be partially inert. Thus, we must have \(r = 1\). It follows that  . \(\square \)
. \(\square \)
Lemma 6.8
For all \(\bar{P},\bar{Q}\in \mathcal {P}_{\! cc }\), if  then
then  and \( A X _{p}\vdash \bar{P}= \bar{Q}\).
and \( A X _{p}\vdash \bar{P}= \bar{Q}\).
Proof
Let  . Then, by Lemma 6.7(c)–(d), \(\mathcal {R}\) is a branching probabilistic bisimulation relation relating \(\bar{P}\) and \(\bar{Q}\). We show that \(\mathcal {R}\) moreover satisfies the conditions of Lemma 6.5. Condition (1) is a direct consequence of Lemmas 4.7 and 6.7(b). That \(\mathcal {R}\) is decomposable follows since it is weakly decomposable, in combination with Lemma 6.7(e). Now, in order to verify condition (2), suppose \(\delta (E) \,{\mathcal {R}}\,\delta (F)\) and
. Then, by Lemma 6.7(c)–(d), \(\mathcal {R}\) is a branching probabilistic bisimulation relation relating \(\bar{P}\) and \(\bar{Q}\). We show that \(\mathcal {R}\) moreover satisfies the conditions of Lemma 6.5. Condition (1) is a direct consequence of Lemmas 4.7 and 6.7(b). That \(\mathcal {R}\) is decomposable follows since it is weakly decomposable, in combination with Lemma 6.7(e). Now, in order to verify condition (2), suppose \(\delta (E) \,{\mathcal {R}}\,\delta (F)\) and  . Then
. Then  for some \(\bar{\nu },\nu \in \mathcal {P}\) with \(\delta (E) \,{\mathcal {R}}\,\bar{\nu }\) and \(\mu \,{\mathcal {R}}\,\nu \). By Lemma 6.7(e) we have \(\bar{\nu }= \delta (F)\). Thus
for some \(\bar{\nu },\nu \in \mathcal {P}\) with \(\delta (E) \,{\mathcal {R}}\,\bar{\nu }\) and \(\mu \,{\mathcal {R}}\,\nu \). By Lemma 6.7(e) we have \(\bar{\nu }= \delta (F)\). Thus  . Hence, using Lemma 6.7(f) it follows that
. Hence, using Lemma 6.7(f) it follows that  . With \(\mathcal {R}\) satisfying conditions (1) and (2), Lemma 6.5 yields
. With \(\mathcal {R}\) satisfying conditions (1) and (2), Lemma 6.5 yields  . By Lemma 6.4 we obtain \( A X _{p}\vdash \bar{P}= \bar{Q}\). \(\square \)
. By Lemma 6.4 we obtain \( A X _{p}\vdash \bar{P}= \bar{Q}\). \(\square \)
Before we are in a position to prove our main result we need one more technical lemma. Here we write \( A X ^b_{p}\vdash P_1 \approx P_2\) as a shorthand for
For example, using axiom BP, if \(E\sqsubseteq P\) then \( A X ^b_{p}\vdash \partial (E + \tau \mathop {.}P ) \approx P\). Likewise, using G, if \(E \sqsubseteq \partial (F)\) then \(\partial (E+F)\approx \partial (F)\). As in the proof of Lemma 6.2(i), from \( A X ^b_{p}\vdash P_1 \approx P_2\) it also follows that \( A X ^b_{p}\vdash \alpha \mathop {.}P_1 \approx \alpha \mathop {.}P_2\) for all \(\alpha \in \mathcal {A}\).
For a complete proof of the lemma we refer the reader to [16]. Note, in the proof we rely on the axioms BP and G.
Lemma 6.9
-
(a)
For each non-deterministic process \(E \in \mathcal {E}\) there is a concrete probabilistic process \(\bar{P}\in \mathcal {P}_{\! cc }\) such that \( A X ^b_{p}\vdash \partial (E) \approx \bar{P}\).
-
(b)
For each probabilistic process \(P \in \mathcal {P}\) there is a concrete probabilistic process \(\bar{P}\in \mathcal {P}_{\! cc }\) such that \( A X ^b_{p}\vdash { \alpha \mathop {.}P = \alpha \mathop {.}\bar{P}}\) for all \(\alpha \in \mathcal {A}\).
-
(c)
For all probabilistic processes \(Q,R \in \mathcal {P}\), if
 then \( A X ^b_{p}\vdash { \alpha \mathop {.}Q = \alpha \mathop {.}R }\) for all \(\alpha \in \mathcal {A}\).
then \( A X ^b_{p}\vdash { \alpha \mathop {.}Q = \alpha \mathop {.}R }\) for all \(\alpha \in \mathcal {A}\).
Proof
(Sketch). We proceed by simultaneous induction on c(E), c(P), and \(\max \lbrace c(Q), c(R) \rbrace \). For part (a) we write a process E with \(c(E) > 0\) as \(\textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}P_i \) for some index set I and suitable \(\alpha _i \in \mathcal {A}\) and \(P_i \in \mathcal {P}\). By the induction hypothesis (b), we can pick for each \(i \in I\) a concrete probabilistic process \(\bar{P}_i \mathbin \in \mathcal {P}_{\! cc }\) with \( A X ^b_{p}\vdash { \alpha _i \mathop {.}\bar{P}_i = \alpha _i \mathop {.}P_i }\). Now \( A X _{p}\vdash E = \bar{E}\) for \(\bar{E} := \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}\bar{P}_i\). We then distinguish two subcases: (i) for some \(i_0\in I\), \(\alpha _{i_0} = \tau \) and  ; (ii) for all \(i \in I\), \(\alpha _i \ne \tau \) or
; (ii) for all \(i \in I\), \(\alpha _i \ne \tau \) or  , i.e., \(\bar{E}\) is rigid.
, i.e., \(\bar{E}\) is rigid.
Subcase (i) is relatively easy. We make use of the axiom BP. For the axiom to apply we need to verify that \(H \sqsubseteq \bar{P}_{i_0}\) where  .
.
For subcase (ii) we show that a concrete process \(\bar{C}\in \mathcal {E}_{ cc }\) exists such that \( A X ^b_{p}\vdash \partial (\bar{E}) \approx \partial (\bar{C})\) for which we proceed by induction on the number of indices \(k \in I\) such that \(\alpha _{k} \mathbin = \tau \) and \([[P_{k}]]\) can be written as \(\mu _1 \mathbin {{}_{\scriptscriptstyle r } \oplus \,}\mu _2\) with \(r \mathbin \in (0,1)\) and  . For the induction step we prove that \(\tau \mathop {.}P_{i_0} \sqsubseteq H\) and we make use of axiom G. As an intermediate result we show
. For the induction step we prove that \(\tau \mathop {.}P_{i_0} \sqsubseteq H\) and we make use of axiom G. As an intermediate result we show  .
.
Parts (b) and (c) follow directly from parts (a) and (b), respectively, with the help of Lemmas 6.7 and 6.8. \(\square \)
By now we have gathered all ingredients for showing that the theory \( A X ^b_{p}\) is an equational characterization of rooted branching probabilistic bisimilarity. In the proof of the theorem we make use of axiom C.
Theorem 6.10
(\( A X ^b_{p}\) sound and complete for  ). For all non-deterministic processes \(E, F \in \mathcal {E}\) and all probabilistic processes \(P,Q \in \mathcal {P}\) it holds that
). For all non-deterministic processes \(E, F \in \mathcal {E}\) and all probabilistic processes \(P,Q \in \mathcal {P}\) it holds that  iff \( A X ^b_{p}\vdash {E = F}\) and
iff \( A X ^b_{p}\vdash {E = F}\) and  iff \( A X ^b_{p}\vdash {P = Q}\).
iff \( A X ^b_{p}\vdash {P = Q}\).
Proof
As we have settled the soundness of \( A X ^b_{p}\) in Lemma 6.3, it remains to show that  is complete. So, let \(E, F \in \mathcal {E}\) such that
is complete. So, let \(E, F \in \mathcal {E}\) such that  . Suppose \(E = \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}P_i\) and \(F = \textstyle \sum _{j {\in } J}\, \beta _j \mathop {.}Q_j\) for suitable index sets I, J, actions \(\alpha _i, \beta _j\), and probabilistic processes \(P_i, Q_j\).
. Suppose \(E = \textstyle \sum _{i {\in } I}\, \alpha _i \mathop {.}P_i\) and \(F = \textstyle \sum _{j {\in } J}\, \beta _j \mathop {.}Q_j\) for suitable index sets I, J, actions \(\alpha _i, \beta _j\), and probabilistic processes \(P_i, Q_j\).
Since, for each \(i \in I\),  we have
we have  and
and  for some subset \(J_i \subseteq J\) and suitable \(q_{ij} \geqslant 0\). Similarly, there exist for \(j \in J\) a subset \(I_j \subseteq I\) and \(p_{ij} \geqslant 0\) such that
for some subset \(J_i \subseteq J\) and suitable \(q_{ij} \geqslant 0\). Similarly, there exist for \(j \in J\) a subset \(I_j \subseteq I\) and \(p_{ij} \geqslant 0\) such that  and
and  series of applications of axiom C we obtain
series of applications of axiom C we obtain
Since  and
and  we obtain by Lemma 6.9
we obtain by Lemma 6.9
for \(i \in I\), \(j \in J\). Combining this with Eqs. (3) and (4) yields \( A X ^b_{p}\vdash E = F\).
Now, let \(P, Q \in \mathcal {P}\) such that  . By Lemma 6.6 we have
. By Lemma 6.6 we have

for a suitable index set I, \(p_i > 0\), \(E_i, F_i \in \mathcal {E}\), for \(i \in I\). By the conclusion of the first paragraph of this proof we have \( A X ^b_{p}\vdash { E_i = F_i }\) for \(i \in I\). Hence \( A X ^b_{p}\vdash { P = Q }\). \(\square \)
7 Concluding Remarks
We presented an axiomatization of rooted branching probabilistic bisimilarity and proved its soundness and completeness. In doing so, we aimed to stay close to a straightforward completeness proof for the axiomatization of rooted branching bisimilarity for non-deterministic processes that employed concrete processes, which is also presented in this paper. In particular, the route via concrete processes guided us to find the right formulation of the axioms BP and G for branching bisimilarity in the probabilistic case.
Future work will include the study of the extension of the setting of the present paper with a parallel operator [12]. In particular a congruence result for the parallel operator should be obtained, which for the mixed non-deterministic and probabilistic setting can be challenging. Also the inclusion of recursion [11, 15] is a clear direction for further research.
The present conditional form of axioms BP and G is only semantically motivated. However, the axiom G has a purely syntactic counterpart of the form

whereas BP can be written as

with \(I \cap J = \emptyset \), where \(\alpha _i = \tau \) for all \(i \in I\), \(P_i = \textstyle {\bigoplus _{k \mathord {\in } K}}\, r_k*P_{ik}\) for all \(i \in {I \cup J}\), and

Admittedly, this form is a bit complicated to work with. An alternative approach could be to axiomatize the relation \(\sqsubseteq \), or perhaps to introduce and axiomatize an auxiliary process operator \(+'\) such that \(E \sqsubseteq P\) can be translated into the condition \(E +' P = P\) or similar.
Also, we want to develop a minimization algorithm for probabilistic processes modulo branching probabilistic bisimilarity. Eisentraut et al. propose in [13] an algorithm for deciding equivalence with respect to weak distribution bisimilarity relying on a state-based characterization, a result presently not available in our setting. Other work and proposals for weak bisimilarity include [8, 14, 31], but these do not fit well with the installed base of our toolset [7]. For the case of strong probabilistic bisimilarity without combined transitions we recently developed in [20] an algorithm improving upon the early results of [5]. In [31] a polynomial algorithm for Segala’s probabilistic branching bisimilarity, which differs from our notion of probabilistic branching bisimilarity, is defined. We hope to arrive at an efficient algorithm by combining ideas from [31,32,33] and of [18, 19].
References
Andova, S., Georgievska, S.: On compositionality, efficiency, and applicability of abstraction in probabilistic systems. In: Nielsen, M., Kučera, A., Miltersen, P.B., Palamidessi, C., Tůma, P., Valencia, F. (eds.) SOFSEM 2009. LNCS, vol. 5404, pp. 67–78. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-540-95891-8_10
Andova, S., Georgievska, S., Trcka, N.: Branching bisimulation congruence for probabilistic systems. Theoret. Comput. Sci. 413, 58–72 (2012)
Andova, S., Willemse, T.A.C.: Branching bisimulation for probabilistic systems: characteristics and decidability. Theoret. Comput. Sci. 356, 325–355 (2006)
Baeten, J.C.M., Basten, T., Reniers, M.A.: Process Algebra: Equational Theories of Communicating Processes. Cambridge Tracts in Theoretical Computer Science, vol. 50. CUP, Cambridge (2010)
Baier, C., Engelen, B., Majster-Cederbaum, M.E.: Deciding bisimilarity and similarity for probabilistic processes. J. Comput. Syst. Sci. 60, 187–231 (2000)
Bandini, E., Segala, R.: Axiomatizations for probabilistic bisimulation. In: Orejas, F., Spirakis, P.G., van Leeuwen, J. (eds.) ICALP 2001. LNCS, vol. 2076, pp. 370–381. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-48224-5_31
Bunte, O., et al.: The mCRL2 toolset for analysing concurrent systems. In: Vojnar, T., Zhang, L. (eds.) TACAS 2019. LNCS, vol. 11428, pp. 21–39. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17465-1_2
Cattani, S., Segala, R.: Decision algorithms for probabilistic bisimulation*. In: Brim, L., Křetínský, M., Kučera, A., Jančar, P. (eds.) CONCUR 2002. LNCS, vol. 2421, pp. 371–386. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45694-5_25
De Nicola, R., Vaandrager, F.W.: Three logics for branching bisimulation. J. ACM 42(2), 458–487 (1995)
Deng, Y., van Glabbeek, R.J., Hennessy, M., Morgan, C.C.: Testing finitary probabilistic processes. In: Bravetti, M., Zavattaro, G. (eds.) CONCUR 2009. LNCS, vol. 5710, pp. 274–288. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04081-8_19
Deng, Y., Palamidessi, C.: Axiomatizations for probabilistic finite-state behaviors. Theoret. Comput. Sci. 373, 92–114 (2007)
Deng, Y., Palamidessi, C., Pang, J.: Compositional reasoning for probabilistic finite-state behaviors. In: Middeldorp, A., van Oostrom, V., van Raamsdonk, F., de Vrijer, R. (eds.) Processes, Terms and Cycles: Steps on the Road to Infinity. LNCS, vol. 3838, pp. 309–337. Springer, Heidelberg (2005). https://doi.org/10.1007/11601548_17
Eisentraut, C., Hermanns, H., Krämer, J., Turrini, A., Zhang, L.: Deciding bisimilarities on distributions. In: Joshi, K., Siegle, M., Stoelinga, M., D’Argenio, P.R. (eds.) QEST 2013. LNCS, vol. 8054, pp. 72–88. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40196-1_6
Ferrer Fioriti, L.M., Hashemi, V., Hermanns, H., Turrini, A.: Deciding probabilistic automata weak bisimulation: theory and practice. Formal Aspects Comput. 28, 09–143 (2016)
Fisher, N., van Glabbeek, R.J.: Axiomatising infinitary probabilistic weak bisimilarity of finite-state behaviours. J. Logical Algebraic Methods Program. 102, 64–102 (2019)
van Glabbeek, R.J., Groote, J.F., de Vink, E.P.: A complete axiomatization of branching bisimilarity for a simple process language with probabilistic choice. Technical report, Eindhoven University of Technology (2019). http://rvg.web.cse.unsw.edu.au/pub/AxiomProbBranchingBis.pdf
van Glabbeek, R.J., Weijland, W.P.: Branching time and abstraction in bisimulation semantics. J. ACM 43, 555–600 (1996)
Groote, J.F., Jansen, D.N., Keiren, J.J.A., Wijs, A.: An O(m log n) algorithm for computing stuttering equivalence and branching bisimulation. ACM Trans. Comput. Logic 18(2), 13:1–13:34 (2017)
Groote, J.F., Vaandrager, F.: An efficient algorithm for branching bisimulation and stuttering equivalence. In: Paterson, M.S. (ed.) ICALP 1990. LNCS, vol. 443, pp. 626–638. Springer, Heidelberg (1990). https://doi.org/10.1007/BFb0032063
Groote, J.F., Rivera Verduzco, H.J., de Vink, E.P.: An efficient algorithm to determine probabilistic bisimulation. Algorithms 11(9), 131, 1–22 (2018)
Groote, J.F., de Vink, E.P.: Problem solving using process algebra considered insightful. In: Katoen, J.-P., Langerak, R., Rensink, A. (eds.) ModelEd, TestEd, TrustEd. LNCS, vol. 10500, pp. 48–63. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68270-9_3
Hansson, H., Jonsson, B.: A calculus for communicating systems with time and probabilities. In: Proceedings of the RTSS 1990, pp. 278–287. IEEE (1990)
Hennessy, M.: Exploring probabilistic bisimulations, part I. Formal Aspects Comput. 24, 749–768 (2012)
Hennessy, M., Milner, R.: On observing nondeterminism and concurrency. In: de Bakker, J., van Leeuwen, J. (eds.) ICALP 1980. LNCS, vol. 85, pp. 299–309. Springer, Heidelberg (1980). https://doi.org/10.1007/3-540-10003-2_79
Lee, M.D., de Vink, E.P.: Logical characterization of bisimulation for transition relations over probability distributions with internal actions. In: Faliszewski, P., Muscholl, A., Niedermeier, R. (eds.) Proceedings of the MFCS 2016. LIPIcs, vol. 58, pp. 29:1–29:14. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2016)
Milner, R.: Communication and Concurrency. Prentice Hall, Upper Saddle River (1989)
Milner, R.: A complete axiomatization for observational congruence of finite-state behaviours. Inf. Comput. 81(2), 227–247 (1989)
Segala, R.: Modeling and verification of randomized distributed real-time systems. PhD thesis, MIT (1995). Technical report MIT/LCS/TR-676
Segala, R., Lynch, N.: Probabilistic simulations for probabilistic processes. In: Jonsson, B., Parrow, J. (eds.) CONCUR 1994. LNCS, vol. 836, pp. 481–496. Springer, Heidelberg (1994). https://doi.org/10.1007/978-3-540-48654-1_35
Stoelinga, M.: Alea Jacta est: verification of probabilistic, real-time and parametric systems. Ph.D. thesis, Radboud Universiteit (2002)
Turrini, A., Hermanns, H.: Polynomial time decision algorithms for probabilistic automata. Inf. Comput. 244, 134–171 (2015)
Valmari, A.: Simple bisimilarity minimization in O(m log n) time. Fundam. Inf. 105(3), 319–339 (2010)
Valmari, A., Franceschinis, G.: Simple O(m log n) time Markov chain lumping. In: Esparza, J., Majumdar, R. (eds.) TACAS 2010. LNCS, vol. 6015, pp. 38–52. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-12002-2_4
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
van Glabbeek, R.J., Groote, J.F., de Vink, E.P. (2019). A Complete Axiomatization of Branching Bisimilarity for a Simple Process Language with Probabilistic Choice. In: Alvim, M., Chatzikokolakis, K., Olarte, C., Valencia, F. (eds) The Art of Modelling Computational Systems: A Journey from Logic and Concurrency to Security and Privacy. Lecture Notes in Computer Science(), vol 11760. Springer, Cham. https://doi.org/10.1007/978-3-030-31175-9_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-31175-9_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-31174-2
Online ISBN: 978-3-030-31175-9
eBook Packages: Computer ScienceComputer Science (R0)


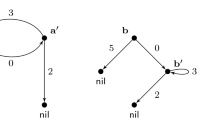


 then there is an
then there is an 
 , then there are
, then there are 
 , and branching bisimilarity, written as
, and branching bisimilarity, written as  , are defined as the largest strong bisimulation relation on
, are defined as the largest strong bisimulation relation on  and
and  then
then 
 whenever
whenever  for all
for all 
 there is a
there is a 

 , there are
, there are 
 , and branching probabilistic bisimilarity, written as
, and branching probabilistic bisimilarity, written as  , are respectively defined as the largest strong probabilistic bisimulation relation on
, are respectively defined as the largest strong probabilistic bisimulation relation on 
 , then
, then  then
then  .
. with
with  then
then  ,
,  ,
,  and
and  , then
, then  .
. then
then