Abstract
Succinct non-interactive arguments (SNARGs) enable verifying NP computations with substantially lower complexity than that required for classical NP verification. In this work, we construct a zero-knowledge SNARG candidate that relies only on lattice-based assumptions which are claimed to hold even in the presence of quantum computers.
Central to our construction is the notion of linear-targeted malleability introduced by Bitansky et al. (TCC 2013) and the conjecture that variants of Regev encryption satisfy this property. Then, using the efficient characterization of NP languages as Square Arithmetic Programs we build the first quantum-resilient zk-SNARG for arithmetic circuits with a constant-size proof consisting of only 2 lattice-based ciphertexts.
Our protocol is designated-verifier, achieves zero-knowledge and has shorter proofs and shorter CRS than the previous such schemes, e.g. Boneh et al. (Eurocrypt 2017).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
1.1 Zero-Knowledge Arguments
Zero-knowledge arguments are cryptographic protocols between two parties, a prover \({\mathsf {P}}\) and a verifier \(\mathsf {V}\), in which the prover can convince the verifier about the validity of a statement without leaking any extra information beyond the fact that the statement is true.
Since their introduction in [25] zero-knowledge (ZK) proofs have been shown to be a very powerful instrument in the design of secure cryptographic protocols.
Related to efficiency and to optimization of communication complexity, it has been shown that statistically-sound proof systems are unlikely to allow for significant improvements in communication [13, 23, 24, 42]. When considering proof systems for \(\mathsf {NP}\) this means that, unless some complexity-theoretic collapses occur, in a statistically sound proof system any prover has to communicate, roughly, as much information as the size of the \(\mathsf {NP}\) witness. The search for ways to beat this bound motivated the study of computationally-sound proof systems, also called argument systems [15], where soundness is required to hold only against computationally bounded provers.
1.2 SNARG: Succinct Non-interactive Arguments
Assuming the existence of collision-resistant hash functions, Kilian [30] showed a four-message interactive argument for \(\mathsf {NP}\). In this protocol, membership of an instance x in an \(\mathsf {NP}\) language can be proven with communication and verifier’s running time significantly smaller than required in the classical \(\mathsf {NP}\) verification. Argument systems of this kind are called succinct. A challenge, which is of both theoretical and practical interest, is the construction of non-interactive succinct arguments. Starting from Kilian’s protocol that requires four messages, Micali [35] used the Fiat-Shamir heuristic [17] to construct a one-message succinct argument for \(\mathsf {NP}\) whose soundness is set in the random oracle model.
In the plain model, a non-interactive argument requires the verifier \(\mathsf {V}\) (or a trusted party) to generate a common reference string \(\mathsf {crs}\) ahead of time and independently of the statement to be proved by the prover \({\mathsf {P}}\). Such systems are called succinct non-interactive arguments (SNARGs) [22]. Several SNARGs constructions have been proposed [8, 16, 19, 26, 27, 33, 39], and the area of SNARGs has become popular in the last years with the proposal of constructions which introduced significant improvements in efficiency. Many of these SNARGs are also arguments of knowledge – so called SNARKs [7, 8].
In parallel with improvements in efficiency, there has been interesting work on understanding SNARGs. An important remark is that all such constructions are based on non-falsifiable assumptions [38], a class of assumptions that is likely to be inherent in proving the security of SNARGs for general NP languages (without random oracles), as shown by Gentry and Wichs [22]. Bitansky et al. [8] proved that designated verifier SNARKs exist if and only if extractable collision-resistant hash functions exist. Bitansky et al. [9] give an abstract model of SNARKs that rely on linear encodings of field elements. Their information theoretic framework called linear interactive proofs (LIPs) capture proof systems where the prover is restricted to using linear operations in computing the expected proof. They give a generic conversion of a 2-move LIP to a publicly verifiable SNARK using pairing-based techniques or to a designated verifier SNARK using additively homomorphic encryption techniques.
1.3 SNARGs for Arithmetic Circuits
The methodology for building SNARGs common to a family of constructions, some of which represent the state of the art [16, 20, 27, 34, 39], has as a central starting point the framework based on quadratic programs introduced by Gennaro et al. in [19]. This common framework allows to build SNARGs and SNARKs for programs instantiated as boolean or arithmetic circuits.
This approach has led to fast progress towards practical verifiable computations. For instance, using span programs for arithmetic circuits (QAPs), Pinocchio [39] provides evidence that verified remote computation can be faster than local computation. At the same time, their construction is zero-knowledge, enabling the server to keep intermediate and additional values used in the computation private.
1.4 Post-quantum SNARGs
Most of the SNARGs constructed so far are based on discrete-logarithm type assumptions, that do not hold against quantum polynomial-time adversaries [41], hence the advent of general-purpose quantum computers would render insecure the constructions based on these assumptions. Efforts were made to design such systems based on quantum resilient assumptions. We note that the original protocol of Micali [35] is a zk-SNARG which can be instantiated with a post-quantum assumption since it requires only a collision-resistant hash function – however (even in the best optimized version recently proposed in [6]) the protocol does not seem to scale well for even moderately complex computations.
Some more desirable assumptions that withstand quantum attacks are the lattice assumptions [1, 37]. Nevertheless, few non-interactive proof systems are built based on lattices. Some recent works that we can mention are the NIZK constructions for specific languages, like [5, 31, 32] and the two designated verifier SNARG constructions [10, 11], designed by Boneh et al. using encryption schemes instantiated with lattices. A similar approach is used by [20] to design a designated-verifier zk-SNARK (that is a SNARG of knowledge) for boolean circuits.
We attempt to make a step forward in this direction by building a designated-verifier zk-SNARG from quantum-resilient assumptions with better efficiency and succinctness than previous such schemes.
1.5 Our Contribution
We introduce in this work a new lattice-based designated-verifier zk-SNARG.
Our scheme uses as a main building block encodings that rely on the Learning With Errors (LWE) assumption, more precisely, we employ a variant of the encryption scheme proposed by Regev in 2005 [40]. We further assume linear-only properties of this lattice encryption scheme conjectured before by [10, 11].
The underlying relation of our zk-SNARG is a square arithmetic program, which is a very efficient characterization of arithmetic circuits. Square arithmetic programs are closely related to quadratic arithmetic programs [19], but use only squarings instead of arbitrary multiplications. As suggested by Groth [27] the use of squarings give nice symmetry properties and a more compact proof. This efficient language allow us to build a zk-SNARG that achieves better succinctness, CRS size and verification time than the previous similar schemes.
We provide a generalization to our scheme, in the spirit of [19, 20], by using encoding schemes with certain properties. We achieve the most compact proofs known to date, consisting in just 2 lattice-based encodings and verification time in the size of the arithmetic circuit representing the statement. This contribution is of independent interest and consists in a generic framework for SNARGs from Square Arithmetic Programs (SAPs). The stronger notion of knowledge soundness (which leads to zk-SNARKs) can be achieved by replacing the linear-targeted malleability property of our encoding schemes with a stronger (extractable) assumption [9].
1.6 Related Work
Recently, in two companion papers [10, 11], Boneh et al. provided the first designated-verifier SNARGs construction based on lattice assumptions.
The first paper [10] has two main results: an improvement on the LPCP construction in [9] and a construction of linear-only encryption based on LWE. The second paper [11] presents a different approach where the information-theoretic LPCP is replaced by a LPCP with multiple provers, which is then compiled into a SNARG again via linear-only encryption. The main advantage of this approach is that it reduces the overhead on the prover, achieving what they call quasi-optimalityFootnote 1.
Then, [20] exploits the square span program language for boolean circuits in order to introduce a general-purpose framework for SNARGs that can accomodate lattice-based encodings. The main improvements over the previous lattice-based SNARGs showed by [20] are zero-knowledge property and knowledge soundness, this being the first construction of a lattice-based zk-SNARK.
1.7 Techniques and Comparison to Other SNARGs
Our new framework for building SNARGs exploits the advantages of previous proposals taking the best of these approaches. It uses the simple and efficient representation of a arithmetic circuit satisfiability problem, SAP and minimizes the proof size. Also, our scheme does need only plausible hardness assumptions for the underlying encoding scheme for proving computational soundness.
Although conceptually similar to the recent scheme by Gennaro et al. [20], our construction is designed for arithmetic circuits and achieves better properties and efficiency:
SNARG for Arithmetic Circuit Satisfiability. In contract to previous lattice-based constructions, designed for boolean circuit satisfiability, our SNARG is built for proving satisfiability of arithmetic circuits which makes it a better candidate for practical applications.
Standard results show that polynomially sized arithmetic circuits are equivalent (up to a logarithmic factor) to Turing machines that run in polynomial time, though of course the actual efficiency of computing via circuits versus on native hardware depends heavily on the application; for example, an arithmetic circuit for matrix multiplication adds essentially no overhead, whereas a boolean circuit for integer multiplication is far less efficient.
While we describe a SNARG for arithmetic circuit satisfiability (over a field \(\mathbb {F}=\mathbf {Z}_p\)), the problem of boolean circuit satisfiability easily reduces to arithmetic circuit satisfiability with only constant overhead (see [9] Claim A.2).
We remark also that we compare well in terms of efficiency with the quasi-optimal SNARG of [10, 11] in the case of arithmetic circuit satisfiability over large fields (\(\mathbf {Z}_p\), where \(p=2^\lambda \)).Footnote 2 In this case, their proof system is no longer a SNARG (not quasi-optimally succinct).
SAP Language for Arithmetic Circuits. Our scheme exploits the simplicity of Square Arithmetic Program to optimize the size of the proofs. Due to their conceptual simplicity, SAPs offer several advantages over previous constructions for arithmetic circuits. Their reduced number of constraints lead to smaller programs, and to lower sizes and degrees for the polynomials required to represent them, which in turn reduce the computation complexity required in SNARG schemes. Notably, their simpler “square” form requires only a single polynomial to be evaluated for verification (instead of two for earlier QSPs, and three for QAP) leading to a simpler and more compact setup, smaller \(\mathsf {crs}\), and fewer operations required for proof and verification.
Long-Standing Assumptions. Another simplification is the use of the more general long-standing assumption of linear-targeted malleability of the encoding (see Sect. 5.1 for details) instead of the recent introduced knowledge of exponent assumptions for lattice encodings of [20]. The soundness of our SNARG is based on a plausible intractability assumption, which is in the spirit of assumptions on which previous SNARGs were based. Moreover, with minimal modifications, based on a stronger variant of the assumption, we can get a SNARK (i.e., a SNARG of knowledge) with similar complexity.
Designated-Verifier. One limitation is that our new constructions are designated-verifier, while existing constructions are publicly verifiable.
2 Definitions
2.1 Notation
Let \(\lambda \in \mathbb {N}\) be the computational security parameter, and \(\kappa \in \mathbb {N}\) the statistical security parameter. We say that a function is negligible in \(\lambda \), and we denote it by \(\mathsf {negl}\), if it is a \(f(\lambda ) = \mathcal {O}(\lambda ^{-c})\) for any fixed constant c. We also say that a probability is overwhelming in \(\lambda \) if it is \(1 - \mathsf {negl}\)(\(\lambda \)).
When sampling uniformly at random the value a from the set S, we employ the notation  . When sampling the value a from the probabilistic algorithm \(\mathsf {M}\), we employ the notation \(a \leftarrow \mathsf {M}\). We use \(:=\) to denote assignment. For an n-dimensional column vector \(\mathbf{a}\), we denote its i-th entry by \(a_i\). In the same way, given a polynomial f, we denote its i-th coefficient by \(f_i\). Unless otherwise stated, the norm
. When sampling the value a from the probabilistic algorithm \(\mathsf {M}\), we employ the notation \(a \leftarrow \mathsf {M}\). We use \(:=\) to denote assignment. For an n-dimensional column vector \(\mathbf{a}\), we denote its i-th entry by \(a_i\). In the same way, given a polynomial f, we denote its i-th coefficient by \(f_i\). Unless otherwise stated, the norm  considered in this work is the \(\ell _2\) norm. We denote by \(\mathbf{a}\cdot \mathbf{b}\) the dot product between vectors \(\mathbf{a}\) and \(\mathbf{b}\).
considered in this work is the \(\ell _2\) norm. We denote by \(\mathbf{a}\cdot \mathbf{b}\) the dot product between vectors \(\mathbf{a}\) and \(\mathbf{b}\).
Unless otherwise specified, all the algorithms defined throughout this work are assumed to be probabilistic Turing machines that run in time \(\mathsf {poly}\) - i.e., \(\mathsf {PPT}\). An adversary is denoted by \(\mathcal {A}\).
2.2 Succinct Non-interactive Arguments
In this section we provide formal definitions for the notion of succinct non-interactive arguments (SNARGs).
A SNARG can be defined for a specific efficiently decidable binary relation \(\mathcal {R}\). Let \(\mathfrak {R}\) be a relation generator that given a security parameter \(\lambda \) in unary returns a polynomial time decidable binary relation \(\mathcal {R}\). The relation generator may also output some side information, an auxiliary input z, which will be given to the adversary.
For pairs \((u,w) \in \mathcal {R}\) we call u the statement and w the witness. Let \(L_{\mathcal {R}}\) be the language consisting of statements for which there exist matching witnesses in \(\mathcal {R}\).
Definition 1
(zk-SNARG for \(\mathsf {NP}\mathbf{).}\) An efficient prover designated-verifiable non-interactive argument for \(\mathcal {R}\) is a quadruple of probabilistic polynomial algorithms \(\mathsf {\Pi }=(\mathsf {Gen}, {\mathsf {P}}, \mathsf {V}, \mathsf {Sim})\) such that:
-
 the CRS generation algorithm takes as input some security parameter \(\lambda \) and outputs a common reference string \(\mathsf {crs}\), a verification state \(\mathsf {vrs}\), and a trapdoor \(\mathsf {td}\).
the CRS generation algorithm takes as input some security parameter \(\lambda \) and outputs a common reference string \(\mathsf {crs}\), a verification state \(\mathsf {vrs}\), and a trapdoor \(\mathsf {td}\). -
\(\pi \leftarrow {\mathsf {P}}(\mathsf {crs}, u, w)\) the prover algorithm takes as input the \(\mathsf {crs}\), a statement u, and a witness w. It outputs some argument \(\pi \).
-
\(b \leftarrow \mathsf {V}(\mathsf {vrs}, u, \pi )\) the verifier algorithm takes as input a statement \(u\) together with an argument \(\pi \), and \(\mathsf {vrs}\). It outputs \(b=1\) (accept) if the proof was accepted, \(b=0\) (reject) otherwise.
-
\(\pi \leftarrow \mathsf {Sim}(\mathsf {crs}, \mathsf {td}, u)\) the simulator takes as input a simulation trapdoor \(\mathsf {td}\) and a statement \(u\) together with a proof \(\pi \) and returns an argument \(\pi \).
In the same line of past works [16, 18, 20], we will assume for simplicity that \(\mathsf {crs}\) can be extracted from the verification key \(\mathsf {vrs}\), and that the unary security parameter \({1^{\lambda }}\) as well as the relation \(\mathcal {R}\) can be inferred from the \(\mathsf {crs}\).
Non-interactive proof systems are generally asked to satisfy some security properties that simultaneously protect the prover from the disclosure of the witness, and the verifier from a forged proof. We now state the security notions necessary to define a zk-SNARG:
-
Completeness. For every relation \(\mathcal {R}\), given a true statement, a honest prover \({\mathsf {P}}\) with a valid witness should convince the verifier \(\mathsf {V}\) with overwhelming probability. More formally, for all
 , for all
, for all  and for all \((u, w) \in \mathcal {R}\):
and for all \((u, w) \in \mathcal {R}\): 
-
Computational Soundness. An argument system requires that no computationally bounded adversary can make an honest verifier accept a proof of a false statement \(u \not \in L_{\mathcal {R}}\). More formally, for every \(\mathsf {PPT}\) adversarial prover \(\mathcal {A}\), for any relation
 there is a negligible function \(\mathsf {negl}\) such that:
there is a negligible function \(\mathsf {negl}\) such that: 
-
Succinctness. A non-interactive argument where the verifier runs in polynomial time in \(\lambda + |u|\) and the proof size is polynomial in \(\lambda \) is called a preprocessing succinct non-interactive argument (SNARG). If we also restrict the common reference string to be polynomial in \(\lambda \) we say the non-interactive argument is a fully succinct SNARG. Bitansky et al. [8] show that preprocessing SNARKs can be composed to yield fully succinct SNARKs. The focus of this paper is on preprocessing SNARKs, where the common reference string may be long.
-
Statistical Zero-Knowledge. An argument is zero-knowledge if it does not leak any information besides the truth of the statement. Formally, if for all \(\lambda \in \mathbb {N}\), for all
 , for all \((u, w) \in \mathcal {R}\) and for all \(\mathsf {PPT}\) adversaries \(\mathcal {A}\) the following two distributions are statistically close:
, for all \((u, w) \in \mathcal {R}\) and for all \(\mathsf {PPT}\) adversaries \(\mathcal {A}\) the following two distributions are statistically close: 
Adaptive Soundness. A SNARG is called adaptive if the prover can choose the statement u to be proved after seeing the reference string \(\mathsf {crs}\) and the argument remains sound.
SNARG vs. SNARK. If we replace the computational soundness with computational Knowledge Soundness we obtain what we call a SNARK, a succinct non-interactive argument of knowledge.
-
Knowledge Soundness. The notion of knowledge soundness implies that there is an extractor that can compute a witness whenever the adversary produces a valid argument. The extractor gets full access to the adversary’s state, including any random coins. Formally, we require that for all \(\mathsf {PPT}\) adversaries \(\mathcal {A}\) there exists a \(\mathsf {PPT}\) extractor \(\varepsilon _\mathcal {A}\) such that
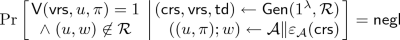
Publicly Verifiable vs. Designated Verifier. We define a SNARG such that the setup algorithm for the argument system also outputs a secret verification state \(\mathsf {vrs}\) which is needed for proof verification. If adaptive soundness holds against adversaries that also have access to the verification state \(\mathsf {vrs}\), then the SNARG is called publicly verifiable; otherwise it is designated verifier. A key question that arises in the design and analysis of designated verifier arguments is whether the same common reference string can be reused for multiple proofs. Formally, this “multi-theorem” setting is captured by requiring soundness to hold even against a prover that makes adaptive queries to a proof verification oracle. If the prover can choose its queries in a way that induces noticeable correlations between the outputs of the verification oracle and the secret verification state, then the adversary can potentially compromise the soundness of the scheme. Thus, special care is needed to construct designated-verifier argument systems in the multi-theorem setting.
3 Building Blocks
3.1 Arithmetic Circuits
Informally, an arithmetic circuit consists of wires that carry values from a field \(\mathbb {F}\) and connect to addition and multiplication gates.
We designate some of the input/output wires as specifying a statement and use the rest of the wires in the circuit to define a witness. This gives us a binary relation \(\mathcal {R}\) consisting of statement wires and witness wires that satisfy the arithmetic circuit, i.e., make it consistent with the designated input/output wires.
3.2 Square Arithmetic Programs
We characterize \(\mathsf {NP}\) as Square Arithmetic Programs (SAPs) over some field \(\mathbb {F}\) of order \(p\ge 2^{\lambda -1}\). SAPs were introduced first by Groth et al. in [28].
The main idea is to represent each gate input and each gate output as a variable. Then we may rewrite each gate as an equation in some variables representing the gate’s input and output wires. These equations are satisfied only by the values of the wires that meet the gate’s logical specification. By composing such constraints for all the gates in the circuit, a satisfying assignment for any arithmetic circuit can be specified first as a set of quadratic equations, then modified to a square equivalent, and finally, seen as a constraint on the span of a set of polynomials, defining the SAP for this circuit. As a consequence, the prover needs to convince the verifier that all the quadratic equations are satisfiable by finding a solution of the equivalent polynomial problem.
Definition 2 (SAP)
A Square Arithmetic Program \(\mathsf {SAP}\) over the field \(\mathbb {F}\) contains two sets of polynomials \(\{v_0(x), \ldots , v_m(x)\} , \{w_0(x), \ldots , w_m(x)\} \in \mathbb {F}[x]\) and a target polynomial t(x) such that \(\deg (v_i(x)), \deg (w_i(x))\le d:=\deg (t(x))\) for all \( i= 0, \dots , m\).
We say that SAP accepts an input \( a_1, \ldots , a_\ell \in \mathbb {F}\) if and only if there exist \(\{a_i \}_{i=\ell +1}^m \in \mathbb {F}\) satisfying:
A \(\mathsf {SAP}\) with such a description defines the following binary relation \(\mathcal {R}\), where we define \(a_0=1\),

3.3 Encoding Schemes
The main ingredient for an efficient preprocessing SNARG is an encoding scheme E over a field \(\mathbb {F}\) with some important properties that allow proving and verifying on top of encoded values. Well-known schemes use deterministic pairing-based encodings, where the values are hidden in the exponent and the security is guaranteed by discrete logarithm type assumptions, e.g. [16, 27, 34, 39]. A formalisation of these encoding schemes was initially introduced in [19]. Here, we recall a variant of this definition that was used for a recent SNARK construction based on lattices in [20]. This definition has the advantage that it accommodates for encodings with noise.
An encoding scheme \(E=(\mathsf {K}, \mathsf {E})\) over a field \(\mathbb {F}\) is composed of the following algorithms
-
 : a key generation algorithm that outputs some secret state \(\mathsf {sk}\) together with some public information \(\mathsf {pk}\).
: a key generation algorithm that outputs some secret state \(\mathsf {sk}\) together with some public information \(\mathsf {pk}\). -
\(\mathsf {E}(a) \rightarrow C\): a (non-deterministic) encoding algorithm mapping \(a \in \mathbb {F}\) to some encoding space C, such that \(\{\{{\mathsf {E}(a)}: a \in \mathbb {F}\}\) partitions C, where \(\{\mathsf {E}(a)\}\) denotes the set of the possible evaluations of the algorithm \(\mathsf {E}\) on a.
Depending on the encoding algorithm, \(\mathsf {E}\) will be either deterministic or not and will require either only the public information \(\mathsf {pk}\), or the secret state \(\mathsf {sk}\). For our application, it will be the case of \(\mathsf {sk}\). To ease notation, we will omit this additional argument.
The above algorithms must satisfy the following properties:
-
d -linearly homomorphic: there exists a \(\mathsf {poly}\) algorithm \(\mathsf {Eval}\) that, given as input the public parameters \(\mathsf {pk}\), a vector of encodings \((\mathsf {E}(a_1), \dots , \mathsf {E}(a_d))\), and coefficients \(\mathbf{c}= (c_1, \dots , c_d) \in \mathbb {F}^d\), outputs a valid encoding of \(\mathbf{a} \cdot \mathbf{c}\) where \(\mathbf{a} = (a_1, \dots a_d)\) with probability overwhelming in \(\lambda \).
-
quadratic root detection: there exists an efficient algorithm that, given some parameter \(\delta \) (either \(\mathsf {pk}\) or \(\mathsf {sk}\)), \(\mathsf {E}(a_0), \dots , \mathsf {E}(a_t)\), and the quadratic polynomial \(\mathsf {p}\in \mathbb {F}[x_0, \dots , x_t]\), can distinguish if \(\mathsf {p}(a_1, \dots , a_t) = 0\). With a slight abuse of notation, we will adopt the writing \(\mathsf {p}(\mathsf {ct}_0, \dots , \mathsf {ct}_t) = 0\) to denote the quadratic root detection algorithm with inputs \(\delta \), \(\mathsf {ct}_0, \dots , \mathsf {ct}_t\), and \(\mathsf {p}\).
-
image verification: there exists an efficiently computable algorithm \(\in \) that, given as input some parameter \(\delta \) (again, either \(\mathsf {pk}\) or \(\mathsf {sk}\)), can distinguish if an element c is a correct encoding of a field element.
Decoding Algorithm. When using a homomorphic encryption scheme in order to instantiate an encoding scheme, we simply define the decoding algorithm \(\mathsf {Dec}\) as the decryption procedure of the scheme. More specifically, since we study encoding schemes derived from encryption functions, quadratic root detection and image verification for designated-verifiers are trivially obtained by using the decryption procedure \(\mathsf {Dec}\) together with the secret key \(\mathsf {sk}\).
One-Way Encodings. If such a secret state is not needed to perform the quadratic root detection, we will consider \(\mathsf {sk}=\perp \) and call it “one-way” or publicly-verifiable encoding. At present, the only candidates for such a “one-way” encoding scheme that we know of are based on bilinear groups, where the bilinear maps support efficient testing of quadratic degrees without any additional secret information.
4 zk-SNARG for Arithmetic Circuits
The idea of our SNARG is simple and follows the common paradigm of many well-known pairing-based constructions. The prover has to convince the verifier that it knows some polynomials, such that a division property between them holds (a solution to SAP problem). Instead of sending the entire polynomials as a proof, it evaluates them in a secret point s (hidden by the encoding) to obtain some scalar values. The verifier, instead of checking a polynomial division, has only to check a division between scalars, which makes the task extremely fast.
4.1 Framework for zk-SNARGs from SAP
In a nutshell, in order to construct succinct proofs of knowledge using our framework, one must use the following building blocks:
-
an SAP, a way of “translating” the circuit satisfiability problem into a polynomial division problem, meaning that we reduce the proof of computing a circuit to the proof of a solution to this SAP problem,
-
an \(\mathsf {E}\) encoding scheme that hides scalar values, but allows linear operations on the encodings for the prover to evaluate polynomials, and some quadratic check property for the verifier to validate the proofs,
-
a CRS generator that uses this encoding scheme to hide a secret random point s and all the necessary powers of s needed later by the prover to compute polynomial evaluations on s.
Our new framework for building SNARGs exploits the advantages of previous such proposals taking the best of each one. It uses the simple and efficient representation of a arithmetic circuit satisfiability problem, SAP and minimizes the proof size of our SNARG scheme. Also, our scheme does need only plausible hardness assumptions for the underlying encoding scheme for proving computational soundness.
Efficiency. The proof size is 2 encodings. The common reference string contains a description of \(\mathcal {R}\) and implicitly the polynomials in \(\mathsf {SAP}\), a public key for an encoding scheme and \(m+ 2d+1-\ell _u\) encodings of field elements. The verification consists of checking one quadratic equation on the encoded values.
The prover has to compute the polynomial h(x). It depends on the relation how long time this computation takes; if it arises from an arithmetic circuit where each multiplication gate connects to a constant number of wires, the relation will be sparse and the computation will be linear in d. The prover also computes the coefficients of the representation \( v(x) :=\textstyle \sum _{i=0}^m a_i v_i(x)\). Having all these coefficients, the prover applies \(m+ 2d+1-\ell _u\) linear homomorphic operations on the encodings from the given \(\mathsf {crs}\).
Besides the improvements mentioned above, one of the most remarkable features of this framework is the fact that it can accommodate for lattice-based encodings, meaning that we can use it to obtain a quantum-resilient SNARGs.
4.2 Lattice-Based Instantiation
In this section, we describe a possible encoding scheme based on learning with errors (LWE) that will be used as a building block for our post-quantum SNARG scheme.
Lattice-Based Encoding Scheme. In order to instantiate our SNARG encoding, we just use \(Enc=(\mathsf {K}, \mathsf {E},\mathsf {Dec})\) encryption scheme depicted in Fig. 2. This is the same encoding used to construct lattice-based SNARKs in [20], a slight variation of the classical LWE cryptosystem initially presented by Regev [40] and later extended in [14].
The encryption scheme Enc is described by parameters \(\varGamma :=(p,q, n, \alpha )\), with \(q,n,p \in \mathbb {N}\) such that \((p, q) =1 \), and \(0<\alpha <1\). In the corresponding description of our building block E, the public information is constituted by the LWE parameters \(\mathsf {pk}= \varGamma \) and an encoding of m is simply an LWE encryption of m. The LWE secret key constitutes the secret state \(\mathsf {sk}=\mathbf{s}\) of the encoding scheme.
Basic Properties. We briefly recall the main properties Enc should satisfy as a building block in a SNARG scheme.
-
correctness. Let \(\mathsf {ct}= (-\mathbf{a}, \mathbf{a}\cdot \mathbf{s}+ pe + m)\) be an encoding. Then \(\mathsf {ct}\) is a valid encoding of a message \(m \in \mathbf {Z}_p\) if \(e < \frac{q}{2p}\).
-
d -linearly homomorphicity. Given a vector of d encodings \(\mathbf {\mathsf {ct}}\in \mathbb {Z}_q^{d \times (n+1)}\) and a vector of coefficients \(\mathbf{c}\in \mathbb {Z}_p^d\), the homomorphic evaluation algorithm is defined as follows: \(\mathsf {Eval}(\mathbf {\mathsf {ct}}, \mathbf{c}):=\mathbf{c}\cdot \mathbf {\mathsf {ct}}\).
-
quadratic root detection. The algorithm for quadratic root detection can be implemented using \(\mathsf {Dec}\) and the secret key (i.e., \(\mathsf {sk}:=\mathbf{s}\)): decrypt the message and evaluate the polynomial, testing if it is equal to 0.
-
image verification. Using the decryption algorithm \(\mathsf {Dec}\) and \(\mathsf {sk}\), we can implement image verification (algorithm \(\in \)).
4.3 Technical Challenges
Noise growth. During the homomorphic evaluation, the noise grows as a result of the operations which are performed on the encodings. Consequently, in order to ensure that the output of \(\mathsf {Eval}\) is a valid encoding of the expected result, we need to start with a sufficiently small noise in each of the initial encodings.
In order to bound the size of the noise, we first need a basic theorem on the tail bound of discrete Gaussian distributions due to Banaszczyk [3]:
Lemma 1
([3]). For any \(\sigma , T \in \mathbb {R}^+\) and \(\mathbf{a}\in \mathbb {R}^n\):

At this point, this corollary follows:
Corollary 1
Let  be a secret key and \(\mathbf{m} = (m_0, \dots , m_{d-1}) \in \mathbf {Z}_p^d\) be a vector of messages. Let \(\mathbf {\mathsf {ct}}\) be a vector of d fresh encodings so that \(\mathsf {ct}_i \leftarrow \mathsf {E}(\mathbf{s}, m_i)\), and \(\mathbf{c}\in \mathbf {Z}_p^d\) be a vector of coefficients. If \(q > 2 p^2 \sigma \sqrt{\frac{\in d}{\pi }}\), then \(\mathsf {Eval}(\mathbf{c}, \mathbf {\mathsf {ct}})\) outputs a valid encoding of \(\mathbf{m} \cdot \mathbf{c}\) under the secret key \(\mathbf{s}\).
be a secret key and \(\mathbf{m} = (m_0, \dots , m_{d-1}) \in \mathbf {Z}_p^d\) be a vector of messages. Let \(\mathbf {\mathsf {ct}}\) be a vector of d fresh encodings so that \(\mathsf {ct}_i \leftarrow \mathsf {E}(\mathbf{s}, m_i)\), and \(\mathbf{c}\in \mathbf {Z}_p^d\) be a vector of coefficients. If \(q > 2 p^2 \sigma \sqrt{\frac{\in d}{\pi }}\), then \(\mathsf {Eval}(\mathbf{c}, \mathbf {\mathsf {ct}})\) outputs a valid encoding of \(\mathbf{m} \cdot \mathbf{c}\) under the secret key \(\mathbf{s}\).
Smudging. When computing a linear combination of encodings, the distribution of the error term in the final encoding does not result in a correctly distributed fresh encoding. The resulting error distribution depends on the coefficients used for the linear combination, and despite correctness of the decryption still holds, the error could reveal more than just the plaintext. We combine homomorphic evaluation with a technique called noise smudging [2, 4, 21], which “smudges out” any difference in the distribution that is due to the coefficients of the linear combination, thus hiding any potential information leak.
Zero-Knowledge. We now present a version of the the famous “leftover hash lemma” introduced in [29] that will be useful later when proving the zero-knowledge property of our construction. In a nutshell, it says that a random linear combination of the columns of a matrix is statistically close to a uniformly random vector, for some particular choice of coefficients.
Lemma 2 (Specialized leftover hash lemma)
Let n, p, q, d be non-negative integers. Let  , and
, and  . Then we have
. Then we have
where \( A \mathbf {r}\) is computed modulo q, and  .
.
Practical Considerations. A single encoded value has size \((n+1) \log q = \widetilde{O}(\lambda )\). Therefore, as long as the prover sends only 2 encodings, the proof is guaranteed to be (quasi) succinct.
Although the scheme requires the noise terms to be sampled from a discrete Gaussian distribution, for practical purposes we can sample them from a bounded uniform distribution (see, e.g., [36] for a formal assessment of the hardness of LWE in this case).
5 Security of Our zk-SNARG
Following our framework for SAP and implementing it with the encryption scheme Enc as described above and making some modification for the zero-knowledge, we obtain a new lattice-based zk-SNARG scheme with short proofs consisting in 2 ciphertexts instead of 5 in [20]. The soundness of the resulting SNARG scheme relies on the long-standing hardness assumption of linear targeted malleability of the encoding scheme.
Moreover, the same construction yields a zk-SNARK (a zero-knowledge succinct non-interactive argument of knowledge) if the soundness property is replaced with a corresponding knowledge property, and the scheme \(\mathsf {E}\) satisfies linear-only encryption, where the simulator is required to be efficient (i.e., \(\mathsf {PPT}\)). For more details, we refer to [9]. Roughly, the knowledge property states that there exists an extractor such that for every linear strategy that convinces the verifier of some statement u with high probability, the extractor outputs a witness w such that \((u,w)\in \mathcal {R}\).
5.1 Hardness Assumptions
Linear-Only Encoding Schemes. A linear-only encoding scheme is an encoding scheme where any adversary can output a valid new encoding only if this is a linear combination of some previous encodings that the adversary had as input. At high-level, a linear-only encoding scheme does not allow any other form of homomorphism than linear operations. If we require from the adversary to actually know the coefficients of the linear combination, we assume extractable linear-only, and model this knowledge by the existence of a non-black-box polynomial time extractor.
In this work, we use the weaker notion of linear-targeted malleability, employed also in [9]. This is closer to the definition template of Boneh et al. [12]. In such a notion, the extractor is replaced by an efficient simulator. Relying on this weaker variant, if the simulator is allowed to be inefficient, we are only able to prove soundness of the SNARG, though not knowledge soundness as needed for SNARKs. Concretely, the linear-only property rules out any encryption scheme where ciphertexts can be sampled obliviously; instead, the weaker notion does not, and thus allows for shorter ciphertexts.
Definition 3
(Linear-Targeted Malleability, [9]). An encoding scheme satisfies linear-targeted malleability property if for all \(\mathsf {PPT}\) adversaries \(\mathcal {A}\) and plaintext generation algorithm \(\mathsf {M}\) there exists a simulator \(\mathsf {S}\) such that, for any sufficiently large \(\lambda \in \mathbb {N}\), any “benign” auxiliarly input z the following two distributions \(\mathcal {D}_0(\lambda ), \mathcal {D}_1(\lambda )\) in Fig. 3 are computationally inistinguishable.
5.2 Security Proof
Before formally proving this is a SNARG, let us give a little intuition behind the different components in the scheme (see Fig. 1). The role of \(\beta \) is to ensure A and B are consistent with each other in the choice of coefficients \(a_0, \ldots , a_m\). In the verification equation the product \(A(A+\beta )\) involves a linear dependence on \(\beta \), and we will later prove that this linear dependence can only be balanced out by the term B with a consistent choice of \(a_0, \ldots , a_m\) in A and B. The role of \(\delta \) to make the product \(\delta B\) of the verification equation independent from the first product and preventing mixing and matching of elements intended for different products in the verification equation. Finally, the prover algorithm uses r to randomize the proof to get zero-knowledge.
Theorem 1
Assuming that the scheme Enc is a linear-targeted malleable encoding scheme, the protocol given in Fig. 1 is a non-interactive zero-knowledge argument.
Completeness. Completeness holds by direct verification.
Zero-Knowledge. To obtain a zero-knowledge protocol, we do two things: we add a smudging term to the noise of the encoding, in order to make the distribution of the final noise independent of the coefficients \(a_i\), and we randomize the target polynomial t(x) to hide the witness from the verifier. The random vectors constituting the first element of the ciphertext are guaranteed to be statistically indistinguishable from uniformly random vectors by leftover hash lemma (cf. Lemma 2).
To see that the simulated proofs are indistinguishable from the real proofs, first observe that the simulation procedure always produces verifying proofs. Next, observe that for a given instance and proof \(\pi = (A,B)\) the element A uniquely determines B through the verification equation. In a real proof the random choice of r makes the value encoded in A uniformly random, and in a simulated proof the random choice of \(\mu \) makes the value inside A uniformly random. So in both cases, we get the same probability distribution over the values hidden by the encodings A, B with uniformly random A and the unique matching B.
We are left with showing that after applying our encoding scheme on these values, the two proofs, the real one and the simulated one, are statistically indistinguishable.
In both worlds, the proof is a couple of encodings (A, B). Once the \(\mathsf {vrs}\) is fixed, each encoding can be written as \((-\mathbf{a}, \mathbf{a}\cdot \mathbf{s}+ pe + m)\), for some \(\mathbf{a}\in \mathbb {Z}_q^n\) and some \(m \in \mathbb {Z}_p\) satisfying the verification equations. Due to Lemma 2, the random vectors \(\mathbf{a}\) are indistinguishable from uniformly random in both worlds. The error terms are statistically indistinguishable due to smudging techniques applied to the ciphertexts. The zero-knowledge follows from these claims, since the simulator can use re-randomization to ensure that its actual encodings (not just what is encoded) are appropriately uniform.
Computational Soundness. The linear-targeted malleability property of the encryption scheme constrains the prover to only use affine strategies. This ensures soundness for our SNARG. To check a proof, the verifier decrypts the prover’s responses and checks the corresponding quadratic equation on these values.
What remains is to demonstrate that for any affine prover strategy that is able to produce a couple statement-proof \((\mathbf{u}, \pi )\) that passes the verification test, there exists the simulator \(\mathsf {S}\) as defined in Fig. 3 that outputs a valid witness \(\mathbf{w}\) for the statement \(\mathbf{u}\).
For any prover algorithm \(\mathcal {A}(\mathsf {crs}) \rightarrow (\mathbf{u}, \pi )\), by our linear-targeted malleability assumption the values A, B encoded in the proof \(\pi =(A,B)\) are identically distributed as two simulated linear combination of some initial values \(\sigma = ( \delta t(s)^2,~ \beta t(s),~ \{ \delta s^i)\}_{i=0}^{d-1},~ \{\delta s^i t(s)\}_{i=0}^{d-2}, ~ \{ \delta w_i(s)+ \beta v_i(s)\}_{i=\ell +1}^{m})\) encoded in the \(\mathsf {crs}\). More formally, we consider the simulator \(\mathsf {S}\) that on input \(\sigma \) and some auxiliary input z (which corresponds to the rest of the SNARG’s \(\mathsf {crs}\)) outputs a pair of coefficients such that the resulting values c, d are indistinguishable from the values encoded by the proof \(\pi \):

If \(\mathcal {A}\) convinces the verifier to accept with probability at least \(\varepsilon (\lambda )\), then, with at least \(\varepsilon (\lambda )-\mathsf {negl}\) probability, the distribution on the left satisfies that \(\mathsf {V}(\mathsf {vrs}, \mathbf{u}, (\mathsf {E}(c), \mathsf {E}(b))) = 1 \). However, in this distribution, the generation of \((\{m_i\})\) is independent of the generation of the simulated affine function coefficients \((c', \mathbf{c}, b', \mathbf{b}) \). Therefore, by averaging, there exists some \((c', \mathbf{c}, b', \mathbf{b}) \) such that, with probability at least \(\varepsilon (\lambda )/2\) over the choice of \(\{m_i\}_i\) it holds that \(\pi '=(\mathsf {E}(c), \mathsf {E}(b))\) is a valid proof for \(\mathbf{u}\). We can use some basic linear algebra techniques to recombine the coefficients \((c', \mathbf{c}, b', \mathbf{b}) \) and extract an actual witness \(\mathbf{w}=(a_{\ell _u+1}, \dots a_m)\) for the statements \(\mathbf{u} = (a_1, \dots a_{\ell _u})\).
Given that the number of variables and the lenght of the equation is significant we will not detail all the computations, but the intuition of how we recover these coefficients from the values c, b is the following:
We can rewrite c as
for known field elements \(c_1, c_2, \{c_{5i}\}_{i>\ell _u}\) and polynomials \( c_3(x),c_{4}(x)\) of degrees \(d-1\) and \(d-2\), respectively. We can write out \(b :=b(\beta , \delta , s)\) in a similar fashion from the values in \(\sigma \). By the Schwartz-Zippel lemma the proof \(\pi '=(c,b)\) has negligible probability to pass the check unless the verification equation \( c^2 + \beta c = \delta (b +\phi (\mathbf{u})) \) holds not only for the values c, b, but for some actual polynomials \(c(x_\beta , x_\delta , x_s), b(x_\beta , x_\delta , x_s)\) in indeterminates \(x_\beta , x_\delta , x_s\). We now view the verification equation as an equality of multivariate polynomials in \(x_\beta , x_\delta , x_s\) and by cancelling the respective terms in this polynomial equality (for example the terms with indeterminate \(x_\beta ^2\), then the ones with \(x_\delta x_\beta \), etc.), we eventually remain only with the terms involving powers of \(x_s\) that should satisfy:
This shows that \((a_{\ell _u+1}, \dots a_{m} )=(c_{\ell _u+1}, \dots c_{m}) \) is a witness for the statement \((a_{1}, \dots a_{\ell _u} )\).
Lower Bounds for SNARGs. It is an intriguing question how efficient non-interactive arguments can be and what is the minimal size of the proof. Groth showed in [27] that a pairing-based non-interactive argument with generic group algorithms must have at least two group elements in the proof. We do not have an equivalent result for lower bounds in the post-quantum setting, but recent construction aim to minimize the number of lattice-encodings in the proof and the verification overhead. Our lattice-based SNARG seems to be the most optimal to date in the size of the proof and the number of verification equations, we achieve proofs of size 2 encodings and only one verification equation.
Notes
- 1.
This is the first scheme where the prover does not have to compute a cryptographic group operation for each wire of the circuit, which is instead true e.g., in QSP-based protocols.
- 2.
Quasi-optimal succinctness refers to schemes where the argument size is quasilinear in the security parameter.
References
Ajtai, M.: Generating hard instances of lattice problems (extended abstract). In: Miller, G.L. (ed.) STOC, pp. 99–108. ACM (1996). http://dblp.uni-trier.de/db/conf/stoc/stoc1996.html#Ajtai96
Asharov, G., Jain, A., López-Alt, A., Tromer, E., Vaikuntanathan, V., Wichs, D.: Multiparty computation with low communication, computation and interaction via threshold FHE. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 483–501. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_29
Banaszczyk, W.: Inequalities for convex bodies and polar reciprocal lattices inRn. Discret. Comput. Geom. 13(2), 217–231 (1995)
Banerjee, A., Peikert, C., Rosen, A.: Pseudorandom functions and lattices. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 719–737. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_42
Baum, C., Bootle, J., Cerulli, A., del Pino, R., Groth, J., Lyubashevsky, V.: Sub-linear lattice-based zero-knowledge arguments for arithmetic circuits. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 669–699. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_23
Ben-Sasson, E., Bentov, I., Horesh, Y., Riabzev, M.: Scalable, transparent, and post-quantum secure computational integrity. Cryptology ePrint Archive, Report 2018/046 (2018). https://eprint.iacr.org/2018/046
Bitansky, N., et al.: The hunting of the SNARK. Cryptology ePrint Archive, Report 2014/580 (2014). http://eprint.iacr.org/2014/580
Bitansky, N., Canetti, R., Chiesa, A., Tromer, E.: From extractable collision resistance to succinct non-interactive arguments of knowledge, and back again, pp. 326–349 (2012). https://doi.org/10.1145/2090236.2090263
Bitansky, N., Chiesa, A., Ishai, Y., Paneth, O., Ostrovsky, R.: Succinct non-interactive arguments via linear interactive proofs. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 315–333. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_18
Boneh, D., Ishai, Y., Sahai, A., Wu, D.J.: Lattice-based SNARGs and their application to more efficient obfuscation, pp. 247–277 (2017). https://doi.org/10.1007/978-3-319-56617-79
Boneh, D., Ishai, Y., Sahai, A., Wu, D.J.: Quasi-optimal SNARGs via linear multi-prover interactive proofs. Cryptology ePrint Archive, Report 2018/133 (2018). https://eprint.iacr.org/2018/133
Boneh, D., Segev, G., Waters, B.: Targeted malleability: homomorphic encryption for restricted computations, pp. 350–366 (2012). https://doi.org/10.1145/2090236.2090264
Boppana, R.B., Hastad, J., Zachos, S.: Does co-np have short interactive proofs? Inf. Process. Lett. 25(2), 127–132 (1987). https://doi.org/10.1016/0020-0190(87)90232-8
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE, pp. 97–106 (2011). https://doi.org/10.1109/FOCS.2011.12
Brassard, G., Chaum, D., Crépeau, C.: Minimum disclosure proofs of knowledge. J. Comput. Syst. Sci. 37(2), 156–189 (1988). https://doi.org/10.1016/0022-0000(88)90005-0
Danezis, G., Fournet, C., Groth, J., Kohlweiss, M.: Square span programs with applications to succinct NIZK arguments, pp. 532–550 (2014). https://doi.org/10.1007/978-3-662-45611-828
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Fuchsbauer, G.: Subversion-zero-knowledge SNARKs. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10769, pp. 315–347. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_11
Gennaro, R., Gentry, C., Parno, B., Raykova, M.: Quadratic span programs and succinct NIZKs without PCPs. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 626–645. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_37
Gennaro, R., Minelli, M., Nitulescu, A., Orrù, M.: Lattice-based zk-SNARKs from square span programs. In: Lie, D., Mannan, M., Backes, M., Wang, X. (eds.) ACM Conference on Computer and Communications Security, pp. 556–573. ACM (2018). http://dblp.uni-trier.de/db/conf/ccs/ccs2018.html#GennaroMNO18
Gentry, C.: Fully homomorphic encryption using ideal lattices, pp. 169–178 (2009). https://doi.org/10.1145/1536414.1536440
Gentry, C., Wichs, D.: Separating succinct non-interactive arguments from all falsifiable assumptions, pp. 99–108 (2011). https://doi.org/10.1145/1993636.1993651
Goldreich, O., Håstad, J.: On the complexity of interactive proofs with bounded communication. Inf. Process. Lett. 67(4), 205–214 (1998). https://doi.org/10.1016/S0020-0190(98)00116-1
Goldreich, O., Vadhan, S., Wigderson, A.: On interactive proofs with a laconic prover. Comput. Complex. 11(1–2), 1–53 (2002). https://doi.org/10.1007/s00037-002-0169-0
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Groth, J.: Short pairing-based non-interactive zero-knowledge arguments. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 321–340. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_19
Groth, J.: On the size of pairing-based non-interactive arguments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 305–326. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_11
Groth, J., Maller, M.: Snarky signatures: minimal signatures of knowledge from simulation-extractable SNARKs. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 581–612. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_20
Håstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999)
Kilian, J.: A note on efficient zero-knowledge proofs and arguments (extended abstract), pp. 723–732 (1992). https://doi.org/10.1145/129712.129782
Kim, S., Wu, D.J.: Multi-theorem preprocessing NIZKs from lattices. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 733–765. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_25
Libert, B., Ling, S., Nguyen, K., Wang, H.: Lattice-based zero-knowledge arguments for integer relations. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 700–732. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_24
Lipmaa, H.: Progression-free sets and sublinear pairing-based non-interactive zero-knowledge arguments. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 169–189. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_10
Lipmaa, H.: Succinct non-interactive zero knowledge arguments from span programs and linear error-correcting codes. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 41–60. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_3
Micali, S.: CS proofs (extended abstracts), pp. 436–453 (1994). https://doi.org/10.1109/SFCS.1994.365746
Micciancio, D., Peikert, C.: Hardness of SIS and LWE with small parameters. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 21–39. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_2
Micciancio, D., Regev, O.: Worst-case to average-case reductions based on Gaussian measures, pp. 372–381 (2004). https://doi.org/10.1109/FOCS.2004.72
Naor, M.: On cryptographic assumptions and challenges (invited talk), pp. 96–109 (2003). https://doi.org/10.1007/978-3-540-45146-46
Parno, B., Howell, J., Gentry, C., Raykova, M.: Pinocchio: nearly practical verifiable computation, pp. 238–252 (2013). https://doi.org/10.1109/SP.2013.47
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography, pp. 84–93 (2005). https://doi.org/10.1145/1060590.1060603
Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 41(2), 303–332 (1999). http://dblp.uni-trier.de/db/journals/siamrev/siamrev41.html#Shor99
Wee, H.: On round-efficient argument systems. In: Caires, L., Italiano, G.F., Monteiro, L., Palamidessi, C., Yung, M. (eds.) ICALP 2005. LNCS, vol. 3580, pp. 140–152. Springer, Heidelberg (2005). https://doi.org/10.1007/11523468_12
Acknowledgements
Research founded by: the European Research Council (ERC) under the European Unions’s Horizon 2020 research and innovation programme under grant agreement No 803096 (SPEC); the Danish Independent Research Council under Grant-ID DDF-6108-00169 (FoCC).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Nitulescu, A. (2019). Lattice-Based Zero-Knowledge SNARGs for Arithmetic Circuits. In: Schwabe, P., Thériault, N. (eds) Progress in Cryptology – LATINCRYPT 2019. LATINCRYPT 2019. Lecture Notes in Computer Science(), vol 11774. Springer, Cham. https://doi.org/10.1007/978-3-030-30530-7_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-30530-7_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-30529-1
Online ISBN: 978-3-030-30530-7
eBook Packages: Computer ScienceComputer Science (R0)



 the CRS generation algorithm takes as input some security parameter
the CRS generation algorithm takes as input some security parameter  , for all
, for all  and for all
and for all 
 there is a negligible function
there is a negligible function 
 , for all
, for all 
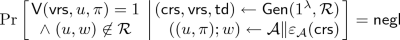
 : a key generation algorithm that outputs some secret state
: a key generation algorithm that outputs some secret state 

