Soft Subspace Growing Neural Gas for Data Stream Clustering

Abstract

Subspace clustering aims at discovering the clusters embedded in multiple, overlapping subspaces of high dimensional data. It has been successfully applied in many domains such as financial transactions, telephone records, sensor network monitoring, website analysis, weather monitoring, etc. Data stream are ordered and potentially unbounded sequences of data points created by a typically non-stationary data generating process. Clustering this type of data requires both time and memory restrictions. In this paper, we propose S2G-Stream based on growing neural gas and soft subspace clustering. We introduce two types of entropy weighting for both features and subspaces. Experiments on public datasets showed the ability of S2G-Stream to: (1) detect relevant features and subspaces; (2) detect clusters of arbitrary shape; (3) enhance the clustering results.

1 Introduction

As opposed to traditional data forms which are unchanging and static, a data stream has its own characteristics: (1) it consists of a flow of infinite data. (2) it is rapidly evolving data that occurs in real time with quick response requirements. (3) only one (or few) pass is possible through the data. (4) storage of the data stream is restricted, thus only a synopsis of the data can be saved. Data stream clustering is a technique that performs cluster analysis on data stream and is able to produce results in real time. The ability to process data through a single pass and summarize it, while using limited memory, is crucial to stream clustering. Subspace clustering is an extension of feature selection which tries to identify clusters in different subspaces of the same dataset. As feature selection, subspace clustering needs both a search method and an evaluation criterion. In addition, subspace clustering must somehow restrict the scope of the evaluation criterion so as to consider different subspaces for each different cluster.

Table 1. Comparison between stream data clustering algorithms

In the previous work [1], authors consider all features equally important to the clustering task. Our main contribution in this paper is to introduce a double weight system for features and subspaces in order to make relevant features and subspaces contribute more to the clustering. The rest of the paper is organized as follows: In Sect. 2, we present related literature. In Sect. 3, we explain our algorithm called Soft Subspace Neural Gas for Data Stream Clustering (S2G-Stream) and evaluate its performance in Sect. 4. Finally, we conclude this paper in Sect. 5.

2 Related Works

2.1 Data Stream

Several algorithms and methods have been proposed to deal with clustering data stream constraints. A large number of algorithms relies on two phases. An online phase processes data stream points and produces summary statistics. Then an offline component phase uses the summary data to generate the clusters [2,3,4]. Alternative solutions also propose to generate final clusters without using an offline phase [5, 6]. Table 1 lists the differences between some methods of clustering data stream.

Table 2. Comparison between subspace clustering algorithms

2.2 Subspace Clustering

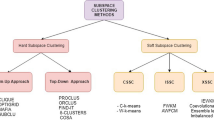
Based on the way cluster subspaces are determined, subspace clustering can be classified into two main categories: Hard Subspace Clustering (HSC) and Soft Subspace Clustering (SSC). SSC algorithms perform clustering in high dimensional spaces by assigning a weight to each dimension to measure the contribution of individual dimensions to the formation of a particular cluster [7]. SSC methods can be classified into three categories. CSSC (Conventional Subspace Clustering) uses a feature weighting process in a two steps clustering process. First, it uses some weighting strategies to find subspaces. Then, clustering is performed on the subspace that was obtained. This is referred to as separated feature weighting. Clustering can also be obtained by performing the two processes simultaneously, this is known as coupled feature weighting. ISSC(Independent Subspace Clustering) associates with each cluster its own weight vector so that every cluster forms its own subspace. XSSC(Extended Subspace Clustering) has been proposed to enhance the performance of both CSSC and ISSC.

In HSC a feature in a subspace equally contributes to the clustering process. HSC algorithms can be divided into bottom-up and top-down subspace search methods [8]. Top-down algorithms find an initial clustering in the full set of dimensions and evaluate the subspaces of each cluster. Bottom-Up approaches define an histogram to each dimension, a range with a density higher than a fixed threshold represent a cluster. Table 2 presents a comparison between some subspace clustering methods.

3 Model Proposition

In this section we introduce soft subspace clustering (S2G-Stream) based on the Growing Neural Gas (GNG) model. Which is an incremental self-organizing approach that belongs to the family of topological maps such as Self-Organizing Maps (SOM) [9]. We assume that the data stream consists in a sequence $\mathcal X = \{\mathbf x_1,\mathbf x_2,...,\mathbf x_n\}$ of n (potentially infinite) elements arriving at times $t_1, t_2, ..., t_n$, where $\mathbf x_i = (x_{i}^1, x_{i}^2, ...,x_{i}^d )$. At each time, S2G-Stream is represented by a graph $\mathcal C$, where each node represents a cluster. Each node $c \in \mathcal C$ is associated with: (1) a prototype $\mathbf {w}_c=(w_c^1, w_c^2, \dots , w_c^d)$ representing its position (2) a weight $\pi _c$ (3) an error variable error(c) representing the distance between this node and the assigned data points. For each pair of nodes (r, c), we denote the shortest path between r and c on the graph by $\delta (c,r)$. Finally we denote by $\mathcal{K}^T(\delta ) = \mathcal{K}(\delta /T)$ the neighborhood function, T controls the width of $\mathcal K$.

In our previous work [1], we consider all features equally important to the clustering task. However, in most applications some variables may be irrelevant and, among the relevant ones, some may be more or less relevant than others. Therefore, and based on [10, 11], we introduce a double weight system for both features, denoted by $\beta$, and subspaces, denoted by $\alpha$, in order to make relevant features and subspaces contribute more to the clustering. Figure 1 illustrates the representation of the weights and prototypes. The features $\mathcal F$ are divided into P subspaces $\mathcal F =\cup _{b=1}^P \mathcal F_b$ where $\mathcal F_b = \{x^j, j = 1,...,d_b\}$ is the feature set where $d_1+...+d_b+...+d_P = d$. Thus, $\alpha$ can be represented as a $K \times P$ matrix where $\alpha _{c}^b$ is the weight of the subspace b in the node c. $\beta$ is a $K \times d$ matrix where $\beta _b$ is a $K \times d_b$ matrix, where $\beta _{cb}^j(j=1,...,d_b)$ is the weight of the $j^{th}$ feature in the subspace b for the node c with $\sum _{j=1}^{d_b} \beta _{cb}^{j}=1$ and $\sum _{b=1}^{P} \alpha _{c}^{b}=1$, $\forall c \in \mathcal C$. Cluster subspaces can be retrieved from both weight matrices.

Fig. 1.

Representation of $\alpha$ and $\beta$. $\alpha _{c}^b$ is the weight of the subspace b in the node c and $\beta _{cb}^j(j=1,...,d_b)$ is the weight of the $j^{th}$ feature in the subspace b for the node c. ${w}_c$ is the prototype of node c.

Based on [1], we propose to minimize the new cost function defined below for data batch $\mathcal X^{(t+1)}=\{ \mathbf X_1, \mathbf X_2, ..., \mathbf X_{t+1}\}$:

$$\begin{aligned} \jmath ^{(t+1)}(\phi ,\mathcal W,\alpha ,\beta ) = \sum _{c \in C} \sum _{b = 1}^{P} \quad \sum _{\mathbf x_i \in \mathcal X^{(t+1)}} {\mathcal K}^ T \left( \delta (c,\phi (\mathbf x_i))\right) \alpha _{c}^b {\mathcal D}_{\beta _{cb} } + J _{cb}+I_{c} \end{aligned}$$

(1)

where ${\mathcal D}_{\beta _{cb}} = \sum _{j=1}^{d_b} \beta _{cb}^j(x_{i}^j - \omega _{c}^j)^2$. $I_{c}=\lambda \sum _{b=1}^{P} \alpha _{c}^b \log (\alpha _{c}^b)$ and $J_{cb}= \eta \sum _{j=1}^{d_b} \beta _{cb}^j \log (\beta _{cb}^j)$ represent respectively the weighted negative entropies associated with the subspaces weight vectors and the features weight vectors. The parameters $\lambda$ and $\eta$ are used to adjust the relative contributions made by the features and subspaces to the clustering.

3.1 Optimization Algorithm

The optimization of the cost function is performed alternately for each batch $\mathcal X^{(t+1)}$ through four steps corresponding to the four parameters $\mathcal {W},\phi ,\alpha$ and $\beta$:

• 1. Assignment function: For a fixed $\mathcal {W},\alpha$ and $\beta$, the assignment function $\phi (\mathbf {x}_{i})$ is described in Eq. (2). In order to reduce the computational time, neighborhood nodes are not considered in the assignment.

  $$\begin{aligned} \phi (\mathbf {x}_{i}) = \arg \min _{c \in \mathcal {C}}\left( \sum _{b=1}^{P}\alpha _{c}^{b}\sum _{j=1}^{d_b} \beta _{cb}^j \left( x_{i}^j - \omega _{c}^j \right) ^2 \right) \end{aligned}$$

  (2)

• 2. Update prototypes $\mathcal {W}$: For a fixed $\phi ,\alpha$ and $\beta$, $\mathbf w_c$ prototypes are updated for every batch of data following the equation defined below.

  $$\begin{aligned} \mathbf w_{c}^{(t+1)}=\frac{\mathbf {w}_{c}^{(t)}n_{c}^{(t)}\gamma +\sum _{r \in C} {\mathcal K}^T(\delta (r,c))\mathbf w_{r}^{(t)}m_{r}^{(t)}}{n_{c}^{(t)}\gamma +\sum _{r \in C} {\mathcal K}^T(\delta (r,c))m_{r}^{(t)}} \end{aligned}$$

  (3)

  where $\mathbf w_{c}^{(t)}$ is the previous prototype, $n_{c}^{(t)}$ is the number of points assigned to the cluster, $\mathbf w_{r}^{(t)}$ is the previous prototype for the cluster r (which is a neighbor of c) and $m_{r}^{(t)}$ is the number of points added to the cluster r in the current batch: $n_{c}^{(t+1)} = n_{c}^{(t)}+m_{c}^{(t)}$.

• 3. Update weights $\alpha$: for a fixed $\phi$, $\mathcal W$ and $\beta$, we minimize the objective function 1 with respect to $\alpha _{c}^{b}$ the weight of the subspace b in c-th cluster. Since there exist a constraint $\sum _{b=1}^{P} \alpha _{c}^{b}=1$, we form the Lagrangian by isolating the terms which contain $\alpha$ then adding Lagrangian multipliers $\mu$ as follows:

  $$\begin{aligned} \mathcal {L}(\alpha ,\lambda ) = \jmath ^{(t+1)}(\phi ,\mathcal W,\alpha ,\beta ) - \sum _{b \in P} \mu _c \left( \sum _{b=1}^P \alpha _{cb} - 1\right) \end{aligned}$$

  (4)

  Taking the derivative with respect to $\alpha _{c}^{b}$ and setting it to zero yields a minimum of $\alpha _{c}^{b}$ at:

  $$\begin{aligned} \alpha _{c}^{b} = \frac{e^{\frac{-D_{cb}}{\lambda } }}{\sum \nolimits _{s=1}^{P} e^{\frac{-D_{cs}}{\lambda } }} \end{aligned}$$

  (5)

  with $D_{cb} = \sum _{\mathbf x_{i} \in \mathcal X^{(t)}}{\mathcal K}^ T(\delta (\phi (\mathbf x_i),c))\sum _{j=1}^{d_b}\beta _{cb}^j \left( \mathbf x_{i}^j - w_{c}^{j}\right) ^2$

• 4. Update weights $\beta$: for a fixed $\phi$, $\mathcal W$ and $\beta$, we minimize the objective function 1 with respect to $\beta ^{j}_{cb}$ the weight of the feature j of subspace b in c-th cluster. Since there exist a constraint $\sum _{j=1}^{d_b} \beta _{cb}^{j}=1$, we form the Lagrangian by isolating the terms which contain $\beta$ then adding Lagrangian multipliers $\mu$ as follows:

  $$\begin{aligned} \mathcal {L}(\alpha ,\lambda ) = \jmath ^{(t+1)}(\phi ,\mathcal W,\alpha ,\beta ) - \sum _{c \in C} \mu _{cb} \left( \sum _{j=1}^{d_b} \beta ^{j}_{cb} - 1\right) \end{aligned}$$

  (6)

  Taking the derivative with respect to $\beta ^{j}_{cb}$ and setting it to zero yields a minimum of $\beta ^{j}_{cb}$ at:

  $$\begin{aligned} \beta ^{j}_{cb} = \frac{e^{\frac{-E_{cb}^j}{\eta }}}{\sum \nolimits _{h \in \mathcal F_{P_j}} e^{\frac{-E_{ch}}{\eta } }} \end{aligned}$$

  (7)

  with $E_{cb}^j = \sum _{\mathbf x_i \in \mathcal X^{(t)}}\alpha _{c}^{P_j}{\mathcal K}^ T(\delta (\phi (\mathbf x_i),c)) \left( \mathbf x_{i}^j - w_{c}^{j}\right) ^2$, where $P_j$ is the subspace the $j^{th}$ feature belongs to.

3.2 S2G-Stream Algorithm

S2G-Stream aims at extending the G-Stream algorithm [12] to subspace clustering by introducing subspace and feature entropy weighting. Starting with two nodes, and whenever a new data point is available, we link the nearest and the second-nearest nodes by an edge. The nearest node and its topological neighbors are moved towards the data point. We present the main functions for the S2G-Stream algorithm below.

Fading Function. Most data stream algorithms consider most recent data as more important and reflect better the changes in the data distribution. For that, the notion of time windows is used. There are three window models commonly studied: landmark, sliding and damped [13]. We consider in this paper the damped window model, in which the weight of each node decreases exponentially with time via a fading function by introducing a decay factor parameter $0<\gamma <1$.

$$\begin{aligned} \pi _{c}^{(t+1)}=\pi _{c}^{(t)}\gamma \end{aligned}$$

(8)

If the weight of a node is below a threshold value, this node is considered outdated and removed (along with its links).

Edge Management. An edge linking two nodes can be either strengthened or removed. Its age grows with the exponential function $2^{\tau _{age}^{(t-t_0)}}$, where $\tau _{age} > 0$ defines age growth rate over time, t denotes the current time and $t_0$ is the edge creation time. A new edge can be added to connect two nodes and can be removed if it exceeds a maximum age.

Node Insertion. Nodes can be inserted into the graph between the two nodes having the highest error value. If the weight of a node is lower than a threshold value then this node is considered as outdated and removed (along with its links).

The complete description of the S2G-Stream algorithm can be found in Algorithm 3.

4 Experimental Results

4.1 Clustering Evaluation

The S2G-Stream method described in this article was implemented in Spark/Scala and will be available on Clustering4Ever github repository¹. We evaluated clustering quality of S2G-Stream on real datasets from the UCI repository [14] described in Table 4. For the quality measures, we used Normalized Mutual Information (NMI) and Adjusted Rand index (ARAND).

Assuming large high-dimensional data arrives as a continually, S2G-Stream divides the streaming data into batches and processes each batch continuously. The batch size depends on the available memory and the size of the original dataset. We set the time interval between two batches to 1 s. We repeated our experiments with different initialization and have chosen those giving the best results. We set $\mu =3$, $\gamma =0.99$ and $age_{max}=250$. $\lambda$ and $\eta$ and the batch size for each dataset are described in Table 3. The weights $\alpha$ and $\beta$ are initialized randomly under the two constraints $\sum _{j=1}^{d_b} \beta _{cb}^{j}=1$ and $\sum _{b=1}^{P} \alpha _{c}^{b}=1$, $\forall c \in \mathcal C$.

Table 3. Initialization of $\lambda$, $\eta$ and batch size parameters for each dataset

To show the effectiveness of our method, we compare it to four algorithms: Growing Neural Gas (GNG) from the Scala Smile repository², CluStream and DStream from R package streamMOA³. The results are reported in Table 4. It is noticeable that S2G-Stream gives better results than the other methods except for DStream on CTG and waveform with NMI metric, and on CTG with ARAND metric. These results are due to the fact that S2G-Stream detects relevant features and subspaces, and allow those subspaces to contribute more to clustering. This is also due to the notion of fading which reduces the impact of non-significant data.

Table 4. Comparing S2G-stream with different algorithms. The value after ± correspond to standard deviation.

Figure 2 shows an example of evolution of the graph S2G-Stream on waveform dataset (using Sammon’s nonlinear mapping), as the data flows (colored points represent labelled data points and black points represent nodes of the graph with edges in black lines). We can clearly see that S2G-Stream, beginning with two randomly chosen nodes (Fig. 2(a)), is able to recognize gradually the structure of the data stream (Fig. 2(b, c)). At the end of the training we can observe that the topology recover all the data structure (Fig. 2(d)). It is noticeable that our method manages to recognize the structures of the data stream and can separate these structures with the best visualization. It can also detect clusters of arbitrary shapes.

Fig. 2.

Evolution of graph creation of S2G-Stream on waveform dataset (colored points represent labelled data points and black points represents nodes of the graph with edges in black lines) (Color figure online)

4.2 Subspace and Feature Weighting Analysis

For this section, we focus on CTG dataset due to space limitation. CTG dataset describes fetal cardiotocograms and is composed of 3 subspaces, subspace 1 contains 7 variables related to the heart rate of a fetus. Subspace 2 contains four variables describing heart rate variability. Subspace 3 is composed of 10 variables defining histograms of fetal cardiography.

Figure 3 represents prototypes $\mathcal W$, $\beta$ weights and $\alpha$ weights for the final batch of CTG dataset. We observe in Fig. 3(b) that weights of features (8, 9, 10, 11) which are respectively ASTV(percentage of time with abnormal short term variability), MSTV(mean value of short term variability), ALTV(percentage of time with abnormal long term variability) and MLTV(mean value of long term variability) are higher than the weights of the other features for most clusters. We observe that this 4 features influence better the clustering process and are more important than the other features for most clusters. In Fig. 3(c) we observe that the $\alpha$ weight of the second subspace that contains this four features is also higher than the weights of the other two subspaces. We conclude from this experiment that heart rate variability influences better the fetal cardiotocograms clustering.

Fig. 3.

Results of weights $\alpha$ and $\beta$, and prototypes $\mathcal W$ for the final batch for CTG dataset. Each color represent a node. (Color figure online)

Based on the previous experiments, we performed S2G-Stream on only the reduced dataset i.e. only the relevant subspaces from the dataset based on the average of subspace weights $\alpha$. We present the NMI and ARAND results compared with the results on the whole dataset in Fig. 4. For CTG dataset, both NMI and ARAND results on the reduced dataset are better than the results using all features and subspaces. The subspace 1 with subspace 2 provide a lower ARAND value. We conclude that subspace 1 gives better results compared to other subspaces, which confirms previous results. Waveform dataset contains two subspaces of 20 features each, the second subspace being composed of only noisy features. NMI and ARAND measured on the reduced dataset (subspace 1) are higher than the whole dataset since the noisy features on the whole dataset affect the results. The same results are observed on the IS dataset. For pendigits dataset the results of NMI and ARAND on the reduced dataset are lower, since both subspaces contain features that are required for the pen-based recognition.

Fig. 4.

NMI and ARAND for all real datasets comparing to results on reduced datasets.

5 Conclusion

In this paper, we have proposed S2G-Stream, an efficient method for subspace clustering of an evolving data stream in an online manner. Unlike the previous works that consider all subspaces equally important to the clustering task, our method introduces a double weighting system for both features and subspaces. Thus, the proposed algorithm is able to select the most important features for the clustering task. We also introduced the notion of fading to delete outdated nodes. Experimental evaluation and comparison with well-known clustering methods demonstrates the effectiveness and efficiency of S2G-Stream in clustering results, discovering clusters of arbitrary shape and also detecting relevant features and subspaces. Future works include several experiments by varying the data ordering and also generalize our method to deal with different types of data. We plan also to visualise our results based on the topology of GNG.