1 Introduction

Crew scheduling is an important step of the operational planning in railways. It deals with generating duties to cover all trips at minimal cost while considering numerous real-world requirements. This work deals with the problem of scheduling conductors for multiple regional railway networks with the network-specific constraints of attendance rates, a problem arising at a large railway company.

Railway passenger transportation on regional level connects smaller cities and towns with each other and, if existing, with larger cities in the same area. It serves the regional and local travel demand, e.g., for commuting, leisure activities, or connection to larger cities and other transportation modes. The train lines are typically designed for stopping at almost every station within the range of a certain distance. In Germany, local state transport authorities plan these railway networks for each geographical area. These separately defined networks are interlinked to ensure travel connections as can be seen from Fig. 1.

Fig. 1.
figure 1

Geographical extend of three regional passenger transportation networks with 15 important intersections

Full size image

After defining a network by its train lines and corresponding timetable, the authorities select an railway company by means of a public tender. The transportation contract also formalizes service requirements such as the type and quality of the rolling stock, the ticket pricing structure or attendance rates for conductors. The latter is a special characteristic in the German regional railway passenger transportation and has to be considered when scheduling conductors to operate the network. Conductors’ work mainly consists of passenger services (e.g., controlling tickets) and sometimes of operational tasks (e.g., securing departures). Hence, in contrast to drivers, they are not required on a train during the total driving time. Mainly due to cost reasons, the state transport authorities assign each train kilometer an attendance rate g which may vary depending on product type, time of day and other factors. Attendance rate g is satisfied when the g-share of all kilometers assigned to g is covered by at least one conductor. It can be defined as

$$\begin{aligned} g \le \dfrac{\text {train kilometers}_{g, \text {attended}}}{\text {train kilometers}_{g, \text {total}}} . \end{aligned}$$
(1)

Based on the terms of the transportation contract and further operational and legal restrictions, the nominated railway company schedules its resources, i.e. rolling stock and crews, to operate the network. The cost for rolling stock and personnel are two main cost factors of railway operations. Since companies strive for resource-efficient schedules, they commonly support these scheduling tasks with software based on Operations Research techniques. Due to the public tender process, companies plan each single network separately, even though schedules that operate across multiple interlinked networks could achieve economies of scale. Only in few cases, planners use their knowledge and experience to create duties across single networks manually. In our project, we investigate the cost saving potential of planning crews across multiple networks with attendance rates, a problem arising at the largest German railway operator.

Solving single networks with attendance rates has been extensively discussed by [8, 9]. Our solution approach for solving multiple networks with attendance rates builds on the hybrid column generation genetic algorithm developed by [8]. In a previous study, we have shown that partitioning the original multi-network problem into smaller sub-problems enables parallel computation and thus acceleration of the solution procedure. By sub-sequentially solving the original problem building on the solutions of the previous phase, the algorithm regains solution quality. With this approach, cost savings up to 2% for 12 networks with a planning horizon of one day could be realized [6]. In this study, each single network represented a sub-problem which led to two drawbacks: Firstly, the needed CPU capacity for parallel computation increases proportionally with the number of sub-problems to be solved. Secondly, the different sizes and complexities of the sub-problems led to a high variance in computational times in the partitioning phase. We aim for a limited use of CPU capacity and balanced computational times by creating few sub-problems of similar size and complexity. To achieve this, different decomposition strategies suitable for the multi-network crew scheduling problem with attendance rates are investigated.

In this work, we describe the multiple network crew scheduling problem with attendance rates and its size and complexity (Sect. 2). We discuss related work (Sect. 3) and present an improved 2-phase optimization method based on a hybrid column generation genetic algorithm (Sect. 4). In Sect. 5, we outline problem-specific considerations to decompose the original problem which translate into three different decomposition approaches. We assess their performance with two real-world instances and benchmark the results against the solution method without decomposition (Sect. 6). We conclude with a summary of our findings and potential for further research (Sect. 7).

2 Problem Description

Crew scheduling is part of the planning process for tenders as well as the operational planning at a railway company. Its objective is to select a set of feasible duties, a schedule, which covers all trips at minimum cost. A trip represents an atomic unit of a train run and is characterized by a departure/arrival time and a departure/arrival station (relief points). Relief points are stations where crew members can change trains. Some of them are equipped for taking breaks. Trips i and j can be combined into feasible duties, if

  1. 1.

    the starting relief point of trip j is the end relief point of trip i (geographical condition) and

  2. 2.

    trip j starts after trip i with a maximum waiting time (chronological condition).

If the trips i and j are not on the same train run, the walking distance from one train to the other must be considered. We set the maximum waiting time and the walking time to 120 and 5 min, respectively. Also, duties can only start and end at a few defined stations (crew depots) which have to be identical (duty symmetry). Further restrictions include additional operational conditions (e.g., break opportunities at relief points) and legal work regulations (e.g., maximum working time, break time rules). A comprehensive discussion of all restrictions that apply to our real-world problem for the single network case can be found in [8, 9].

2.1 Attendance Rates in the Multi-network Railway Crew Scheduling Problem

For being able to schedule crews across multiple networks, it is necessary to combine separately defined networks and their specific restrictions into a crew scheduling problem (multi-network railway crew scheduling problem).

We define a single railway network as the entity of train lines and the corresponding parameters determined by a transportation contract. Obviously, it is only reasonable to combine two single networks if they are interlinked, i.e. the two networks share at least one relief point (an intersection of two or more networks). Otherwise, crews cannot change between the trains of different networks. Combining two or more single networks results in a very large synthetic network of trips and relief points with their corresponding characteristics and restrictions.

Not all restrictions apply to every network. Attendance rates for conductors, in particular, are defined for each network individually. However, other restrictions and characteristics such as the aforementioned operational conditions or legal work regulations usually apply to a station (e.g., walking distances), to a duty (e.g., maximum working time, break time rules, symmetry of starting/end crew depot) or to the schedule in total (e.g., average working time). Hence, we define the problem in such a way that attendance rates are the only network-specific restrictions, i.e. must be satisfied for the set of trips of each network individually.

2.2 Mathematical Formulation

We formulate the multi-network railway crew scheduling problem with attendance rates (MNRCSPAR) as set covering model. Let M and N denote the set of trips i and the set of duties k, respectively. Furthermore, we define R as the set of networks r and \(G_r\) as the set of required attendance rates g per network r. The binary decision variable \(x_k\) indicates whether duty k is selected in the solution schedule, i.e. \(x_k = 1\), 0 otherwise. Let \(y_i\) be a binary decision variable such that \(y_i = 1\) if trip i is covered by the schedule, 0 otherwise. We define the travel distance of trip i which is assigned to attendance rate g as \(d_{ig}\) and the cost of duty k as \(c_k\). The binary assignment matrix A indicates whether trip i is covered by duty k (\(a_{ik} = 1\)) or not (\(a_{ik} = 0\)). The model formulation is:

$$\begin{aligned}&\min \displaystyle \sum _{k \in N} c_k x_k \end{aligned}$$
(2)
$$\begin{aligned}&s{.}t.\, \displaystyle \sum _{i \in M_r} d_{ig} y_i \ge g \displaystyle \sum _{i \in M_r} d_{ig} \quad \forall g \in G_r, \forall r \in R \end{aligned}$$
(3)
$$\begin{aligned}&\displaystyle \sum _{k \in N} a_{ik} x_k \ge y_i \qquad \qquad \, \forall i \in M \end{aligned}$$
(4)
$$\begin{aligned}&y_i \qquad \quad \,\, \ge a_{ik} x_k \qquad \,\,\,\, \forall i \in M , \forall k \in N \end{aligned}$$
(5)
$$\begin{aligned}&x_k , y_i \quad \,\,\,\,\, \in \{0,1\} \qquad \,\,\,\, \forall i \in M, \forall k \in N. \end{aligned}$$
(6)

The objective (2) is to minimize the total cost of all duties. Constraints (3) ensure that the total distance of attended trips of network r with attendance rate g satisfies the by attendance rate g defined minimum (see Eq. (1) in Sect. 1). Constraints (4) and (5) link the trip coverage by the duties of the solution schedule to the attendance rate constraints (cf. constraints (3)): if the minimal attended distance for attendance rate g requires that trip i is covered, then at least one duty k has to cover trip i. Vice-versa, constraints (5) ensure that if trip i is covered by at least one duty of the solution schedule, its distance \(d_i\) adds to the corresponding attendance rate fulfillment.

2.3 Size and Complexity of the MNRCSPAR

A MNRCSPAR is more complex than single network problems for two reasons. First, the total number of trips to be covered is much larger since it consists of the sum of all trips of each network plus additional trips. These are created when a network serves a station which is not defined as relief point, but is a relief point in another network. As a consequence, some trips are broken up into two or more trips as compared to the single network case. This adds both restrictions and variables, i.e. duties to cover all trips, to the problem.

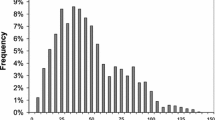
Secondly, the total number of possible trip combinations, i.e. duties, increases with the higher number of possible successors per trip. Figure 2 illustrates the typical distribution of possible successors per trip for different network types.

Fig. 2.
figure 2

Typical distribution of the number of possible successors per trip for a small to medium-size network, a large and complex network and multiple networks

Full size image

Typical small to medium-size networks are composed of a low to medium number of lines with a moderate frequency (e.g., every 60 min). Most trips can be combined with 1 to 10 successors, the maximum ranges from 10 to 15. In contrast, large and complex networks are characterized by a high number of train lines and/or a high frequency of train services with a short average trip duration. In our example, the distribution of the number of possible trip successors shows the highest peak at 38. Those are trips which end at one of the most important junction of the network where several train lines interconnect. The service frequency of these lines is relatively high, every 20 or 30 min, and remains constant throughout the day. Additionally, the frequencies of the train lines are synchronized in such a way that passengers have enough time to change trains. Hence, each trip which ends at this junction shows the same pattern of possible successors throughout the day.

If both of such network types are combined to multiple networks, the maximum number of possible trip successors increases, in this example up to 48. The median is slightly reduced as compared to the large and complex single network, but is higher than for the typical small to medium-size network. The average trip duration in our real-case data set is about 18 min. As a consequence, duties consist of 15 to 20 trips on average, in extreme cases up to 40. With the higher number of potential successors, the possibilities for combining trips to feasible duties increases to an even larger extend resulting an immense number of variables in the MNRCSPAR.

Crew scheduling problems are known to be NP-hard and therefore require high computational times for optimal solutions. This is not suitable for the planning tasks of our railway company. Its planners generate crew schedules for tender offers and for the daily operations. Planning for tenders commonly occurs every 10 years per network, depending on the duration of the transportation contract, and is a complex task including many dependencies with the previous planning steps. Typically, it takes several months until a tender offer is ready for submission. Operational planning occurs more frequently but is a little less extensive as it can build on the knowledge and experience of the previous schedules. It is common to review and adjust the crew schedule for each network on a yearly or half-yearly basis, following the changes of the time tables. However, due to potential short-term changes (e.g., construction sites), intrayear adjustments to the schedule might become necessary. For both planning tasks, the planners test different schedule parameters and modify the data set in order to improve the overall cost in a number of iterations. Hence, to support the planning tasks, our software tool should generate feasible and high quality solutions which achieve lower cost than the sum of the solutions of the single network problems within less than a few days. These requirements necessitate a tailored method to compute high quality results for the multi network railway crew scheduling problem in reasonable time.

3 Related Work

Researchers have dealt with crew scheduling problems in the transportation industry since the 1950s. Originally, their focus was on problems in the public transit and airlines industries which still are areas of high interest (see, e.g., the recent surveys of [10, 15]). In the 1990s, due to the advances of computational power, research extended to the more complex problems of crew scheduling in railway systems (e.g., see [2, 7]). Since then, a large number of real-world applications have been studied varying in, among others, transportation modes, countries and their specific requirements, as well as the integration level of planning stages.

Heuristic procedures and meta-heuristics are frequently employed to achieve faster computational times. By far the most popular solution method is column generation (see [18] for a methodological overview) with various forms and modifications to fit the specific real-world case. In the context of crew scheduling, the problem of selecting duties for the best schedule starts with a small subset of feasible duties (restricted master problem). It is stepwise enlarged by newly generated duties, i.e. columns, which potentially improve the current solution. Generating these duties is an optimization problem by itself (pricing problem). Since the master problem is relaxed by linear or Lagrangean relaxation, integer solutions are either generated by a branch-and-bound scheme (branch-and-price) or in a subsequent step.

Due to its slow convergence, researchers investigate problem-specific techniques to achieve better solutions in less time. In general, we distinguish between acceleration techniques for the solution method itself, problem size management by merging and restrictions and problem size management by decomposition. For common acceleration techniques such as column deletion and column fixation, [3] provide an comprehensive overview.

Problem size management by merging and restrictions includes approaches to reduce the graph size of the original problem by dissolving defined parts of it or to reduce the solution space by adding limits. [17] discuss three main ways of controlling the search space to extend their column generation approach by iteratively deriving new sub-problems of manageable size for the commercial solver (to continuously improve the current solution). These search space controllers include, among others, dissolving relief opportunities using experienced-based rules and limiting the number of trips per duty. Additional restrictions such as a minimal threshold for the share of working time or minimal duty duration reduce the solution space further. Likewise, [5] add limits to the number of possible connections per trip.

Problem size management by decomposition uses strategies to partition the graph of the original problem into a number of smaller sub-graphs which are solved either independently or remain linked to each other. Logical dimensions to decompose a problem are time, geography, train lines and historical schedule information (see [13]). [11] leverage the periodic element of a weekly RCSP to transform it into smaller one-period problems using the concept of time frames. Geographical and train line aspects are used by [16] who limit the trips for a problem instance to certain railway lines or train types or by a maximum distance from a depot. Likewise, [19] formulate individual problems per geographical crew district in order to cope with the large problem size. [4] develop two overlapping sub-problems based on the geographical position of the origin and destination of the trips. [1] experiment with all of the above mentioned partitioning dimensions: weekday partitioning, geographical partitioning, line based partitioning and partitioning based on information on good trip combinations from previous optimization runs. They show that combining the partitioning methods with the original solution procedure achieves a solution improvement by up to \(2\%\). Some researchers investigate the use of algorithms to decompose the problem. [20] use a genetic algorithm to assign trips to depots and solve the smaller instances independently. Extensive research to partition graphs for problems at a freight railway operator was done by [12, 13]. They explore and compare different edge weights for a graph partitioning problem and solve the resulting sub-problems dynamically using a divide-and-price algorithm.

With such problem size management approaches, computational times can be reduced significantly, but with a trade-off between reduction of solution space and loss of quality (see [17]).

4 Solution Approach

We build on the existing approach for the single network multi-day crew scheduling problem with attendance rates: a hybrid column generation genetic algorithm referred to as CGGA in the following (see [8] for a detailed discussion). In order to accelerate computational time for the MNRCSPAR, we experiment with the decomposition of the original problem into a number of sub-problems. Besides reducing the problem size, this enables parallel computation. However, as we aim for a better solution quality as the sum of the single network problems, it seems not sufficient to only decompose the original problem into smaller sub-problems and add up their solutions in the end. Instead, we expect to generate more cost savings by solving the complete original problem in a later phase. As a consequence, we suggest a 2-phase optimization method (see Fig. 3).

Fig. 3.
figure 3

Framework of the 2-phase optimization method with variable selection between phase 1 and 2

Full size image

Phase 1 starts with the decomposition of the original problem into smaller sub-problems which are solved in parallel thereafter. We discuss different decomposition strategies and algorithms in Sect. 5. The sub-problems as well as the original problem in the later phase are solved using CGGA modified for network-specific constraints. Within CGGA, the linear relaxation at the root node of the master problem is solved with column generation. It utilizes a genetic algorithm for generating new duties, i.e. columns. The initial set of duties consists of efficient trip combinations which are built by three different graph search strategies. The column generation procedure applies column deletion to manage the size of the master problem and ends as soon as no new column with negative reduced cost could be generated by the genetic algorithm. Other stopping criteria such as time limits or limiting the number of iterations can also be applied. Instead of computing an integer solution for each sub-problem, we select every column \(x_k\) with a primal value greater than a defined threshold \(\alpha \) and pass it on to the second phase. Subsequently, in phase 2, we solve the original problem using CGGA building on an initial set of duties which combines the selected duties of each sub-problem and additional efficient trip combinations. In the last step, the integer solution is generated using a commercial solver.

Note that the initial set of duties of the second phase does not necessarily represent a feasible solution. The quality of the duty set per sub-problem highly depends on the decomposition which affects the sub-problems structure and its solvability, in particular with regard to the attendance rates requirements. Hence, suitable decomposition strategies are required.

5 Decomposition Strategies

An essential characteristic of the MNRCSPAR is that some restrictions, i.e. attendance rates, only apply to a subset of trips. Maintaining this structure of restrictions might support the solvability of the sub-problems. Additionally, to build a powerful initial set of duties to be further improved by the genetic algorithm of CGGA in phase 2, it seems beneficial to combine two sets of duties: duties which represent good solutions of the sub-problems considering attendance rate restrictions and duties which are efficient trip combination across all networks without considering attendance rate restrictions. The latter are built from the in the first step of CGGA, while the first must be derived from the sub-problem solutions using a suitable decomposition strategy. To test this assumption, we compare the performance of different strategies with the 2-phase optimization method.

5.1 Guidelines for Decomposing the Graph of a MNRCSPAR

Our objective is to decompose the MNRCSPAR into a defined number of sub-problems by cutting as few “good” trip combinations as possible.

The underlying structure of the MNRCSPAR can be interpreted as directed, weighted graph \(G = (V,E)\) with vertices \(v~\in ~V\) representing trips. An edge \((i,j)~\in ~E~\subset ~V~\times ~V\) with edge weight \(w_{ij}\) exists, if two trips i and j can be connected in accordance with the geographical and chronological conditions and the maximum waiting time (see Sect. 2). Finding a good decomposition is a graph partitioning problem [1, 13]. It is formally described for a graph G to find a partition of V into k equal-sized subsets \(V_{1}, ..., V_{k}\) with minimum edge cut \(w_{p}\), where

$$\begin{aligned} w_{p} = \sum _{n = 1}^{k} (\sum _{(i,j) \in E: i \in {V_{n}}, j \in {V \setminus V_{n}}} w_{ij} + \sum _{(i,j) \in E: i \in {V \setminus V_{n}}, j \in {V_{n}}} w_{ij}) \end{aligned}$$
(7)

In our case, the importance of an edge, represented by its weight, is determined by three factors (see [13] for a detailed discussion of the first two items):

  • Cost efficiency - Unproductive times, e.g., crews waiting for the next trip, increase the cost of an schedule and, therefore, should be minimized.

  • Exclusiveness of a connection - With an increasing number of outgoing edges of a vertex, the importance of one of these edges decreases as other alternatives exist. However, if a connection between two trips is unique for one of them, it should not been cut. Otherwise, the trip can only become the first or last trip of a duty which might lead to an insolvable problem instance.

  • Network or train run affiliation - Trips of the same network or train run should be kept together in one sub-problem to reflect the problem structure with attendance rates.

Furthermore, the decomposition method applied should generate an adjustable number of sub-problem, e.g., ranging from 2 to 8 or more. The reasonable number of sub-problems depends on the problem size, its network structure and the available computational power for solving the MNRCSPAR.

5.2 Decomposition by a Graph Partitioning Algorithm

The NP-hard graph partitioning problem has been studied extensively. Various heuristics have been proposed to generate good solutions in very short time. In the context of railway crew scheduling problems, [13] show that adjusted edge weights and subset size modifications improve the performance of their solution method.

For our purpose, we define problem-specific edge weights (cf. Eq. 8) to represent cost efficiency, exclusiveness of a connection and train run affiliation. Cost efficiency is driven by the unproductive time, i.e. the waiting time \(t_{ij}\) in minutes, of a connection. We use the inverse of the waiting time as indicator (cf. first addend of 8). The exclusiveness of an edge can be measured by the inverse of the number of alternative edges. An edge \(e_{ij}\) is always both one of the outgoing edges (\(e_{iv}\)) of vertex i as well as one of the incoming edges (\(e_{vj}\)) of vertex j. It will therefore be assigned two values of which the maximum is chosen (cf. second addend of 8). Lastly, if the two vertices i and j belong to the same train run, indicated by the train number tNo, the weight of their linking edge is increased by a constant \(z_{ij} = 1\) (cf. third addend of 8). With this, the addends are defined in such way that all three factors are considered equally with a value range of (0, 1] and [0, 1], respectively.

$$\begin{aligned} w_{ij} = \frac{1}{t_{ij}} + \max \left\{ \frac{1}{\sum _{v \in V} e_{vj}}, \frac{1}{\sum _{v \in V} e_{iv}}\right\} + z_{ij} \text { with } z_{ij} = {\left\{ \begin{array}{ll} 1 &{} \text {if } tNo_{i} = tNo_{j} \\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$
(8)

We use the algorithm developed by [14], a multilevel recursive-bisection which has proven to achieve good and fast results. The algorithm and further improvements are implemented in the open-source software tool METISFootnote 1, version 5.1. It enables k-partitioning of an undirected, weighted graph into k subsets which fits our purpose.

5.3 Decomposition by Network-Based Greedy Heuristics

As we assume that maintaining the single network structure supports our solution procedure, we also define a network-based greedy heuristic for decomposing the MNRCSPAR. Next to maintaining the single network structure, we aim for a balanced number of trips across the sub-problems in order to achieve comparable computational time and effort. The basic idea is that, given the trips of the original problem and a target number of sub-problems, a set of trips of a network is selected according to a defined rule and added to a sub-problem. The number of trips per sub-problem is hereby limited to \(110\%\) of the average number of trips per sub-problem.

Variant 1. First, we order the single networks by their count of trips. Then, starting with the network with the highest count of trips, the sets of trips per network are iteratively added to the sub-problem with the currently lowest number of trips. If the limit for trips is exceeded after adding a set of trips to a sub-problem, the sub-problem is “closed” and cannot be considered any further. The procedure continues until all sets of trips, i.e. single networks, are assigned.

This variant considers only the number of trips in order to achieve balanced sub-problem sizes. However, the degree of connectivity between single networks can vary significantly. For instance, if the MCRCSPAR includes more than two networks, it is possible that some of them are only indirectly connected via other networks. i.e. they do not share any edge. Since phase 1 of the solution procedure should already generate feasible duties which potentially are part of the final solution, considering connectivity between networks seems to be useful.

Variant 2. In the first step, we calculate the connectivity between all single networks defined as the number of edges connecting the sets of trips of two networks. The connectivity values between each network and each sub-problem are set to 0. We start with the highest connectivity value and add the trips of both networks \(r_1\) and \(r_2\) to the same sub-problem \(sp_{1}\). It follows the update of the connectivity values in such a way that the connectivity between a network \(r_3\) and sub-problem \(sp_1\) is updated to the sum of the connectivity values between network \(r_3\) and the networks \(r_1\) and \(r_2\), respectively. The latter are set to 0 afterwards. We iterate this procedure of selecting the highest connectivity value, assigning the trips to a sub-problem and updating the connectivity values until all sets of trips are assigned. As soon as the limit number of trips is exceeded after adding a set of trips to a sub-problem, all connectivity values of the corresponding sub-problem are set to 0 (“closing” of sub-problem). If a network remains with connectivity values of 0 to all of the open sub-problems, its trips are added to the sub-problem with the lowest number of trips.

6 Computational Results

We apply the decomposition strategies (see Sect. 5) to the partitioning step in phase 1 of the 2-phase optimization method (2PH, see Sect. 4). As a result, three alternative solution methods are derived: 2PH in combination with the graph partitioning algorithm (2PH\(\_\)GP) and with the two variants of the network-based greedy decomposition heuristic (2PH\(\_\)H1 and 2PH\(\_\)H2). We evaluate the performance of the three alternatives with two real-world test instances (see Table 1).

Table 1. Structure and size of two real-world test instances
Full size table

All tests are executed on a Intel(R) Xenon(R) CPU E5-2630 with 3.3 GHz clock speed (768 GB RAM) and 32 kernels. The linear and integer programming problems within CGGA are solved using the commercial solver Gurobi, version 8.1, restricted to maximal 6 kernels. We limit the computational time of each step in 2PH. Phase 1 is limited to 2 and 3 h for test instances 1 and 2, respectively. Phase 2 is limited to 9 h, thereof 3 h for the column generation procedure and 6 h for computing the integer solution.

We benchmark the test runs against a run without decomposition (CGGA) with the same time limits. For instance, the time limits of the column generation procedure and the computation of the integer solution for instance 1 are set to 5 h (equals the time limits of phase 1 plus the column generation procedure in phase 2) and 6 h, respectively.

Table 2 shows the minimum (Min.) and maximum (Max.) as well as the median (Median) of the best objective value found (Obj.) and its gap to the current lower bound (Gap) of 5 test runs per solution approach. We also include the share of mixed duties covering trips of more than one network (MixD) and the relative improvement of the objective value (\(\varDelta _{Obj}\)) in comparison to the non-decomposition benchmark. If the solution of the best objective value found includes infeasible duties, the value is marked with (*) and additional penalty cost (500,000 per infeasible duty) are added to the objective value. Test instance 1 consists of 2 networks. Hence, the number of sub-problems for all decomposition approaches is set to 2. As H1 and H2 produce the same decomposition, we only show the results for H1 in this case. Test instance 2 is decomposed into 4 sub-problems. Other experiments have shown that this number of sub-problems provides a good trade-off between solution time versus computational power consumption and solution quality in phase 1. The non-decomposition benchmarks could not produce feasible solutions in the given time limits. The best objective values found (with gaps) are \(27,315,360^{(*)}\) (\(10.0\%\)) and \(10,171,075^{(*)}\) (\(4.1\%\)) for test instance 1 and 2, respectively.

Table 2. Computational results of three decomposition strategies with test instances 1 and 2
Full size table

It can be seen that all decomposition strategies lead to an improvement of the non-decomposition benchmark. However, similar to CGGA, the 2PH\(\_\)GP approach does not achieve a feasible solution within the given time limits for both instances. In contrast, only one run of the network-based decomposition heuristics, the maximum of 2PH\(\_\)H1 for test instance 2, produces an infeasible duty. All other runs lead to feasible solutions which indicates that maintaining the network structure during the decomposition supports the solution of the MNRCSPAR. Moreover, the minimum, maximum and median of 2PH\(\_\)H2 are slightly better than the comparable results of 2PH\(\_\)H1 for instance 2 in terms of best objective found the related gaps. It also results in a higher share of mixed duties (43 up to 53%). Hence, considering the degree of connectivity between the networks further improves the already good results of the network-based decomposition without connectivity. Finally, the gaps of instance 1 of more than \(8\%\) indicate that great improvement of the best integer solution found is possible with longer computational times.

7 Conclusion

This paper presents a multi-network railway crew scheduling problem with application to the German regional passenger transportation and its specific requirement of attendance rates for conductors. We especially focus on the development of a problem-specific solution approach with the aim to achieve high quality solutions in reasonable time. Therefore, we develop a 2-phase optimization method which builds on a hybrid column generation and genetic algorithm, an existing solution approach for solving the single network case (see [8])). In the first phase, sub-problems are built and solved in parallel. By a variable selection mechanism, the duties of the solutions of the relaxed master problems are passed to the second phase in which the original problem is solved and an integer solution is generated.

We experiment with three different decomposition strategies: a graph partitioning algorithm developed by [14] with problem-specific adjusted edge weights and two variants of a network-based greedy decomposition heuristics. The decision rules build on the number of trips per network (variant 1) plus the degree of connectivity between networks (variant 2). We test the decomposition strategies with the 2-phase optimization method. The test results of two real-world instances show that maintaining the network structure by using the network-based greedy decomposition heuristics performs best within the given time limits. Hereby, considering the connectivity degree between the networks, next to keeping the number of trips across sub-problems balanced, achieves slightly better results than the decomposition without connectivity. Moreover, we show that feasible solutions for test instances with more than 18,000 trips can be generated within less than 12 h, but with potential for further improvement.

A disadvantage of 2PH\(\_\)H1 and 2PH\(\_\)H2 is that they are very problem-specific to the multi-network case and cannot be applied to a very large and complex single network. Still, they work well for our purpose. Further research involves testing the performance of 2PH\(\_\)H2 with even larger instances, in particular planning test instance 2 with 11 networks for one week which is the standard planning period of the railway company. In this context, further solution method extensions with focus on accelerating the integer solution generation (e.g., variable fixing heuristics) should be investigated.