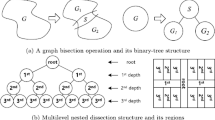The Introduction of Multi-level Parallelism Solvers in Multibody Dynamics

Abstract

The paper deals with the problem of the scaling speed-up of time-consuming computations on the example of the dynamic stress-strain state (DSS) modelling for the multibody systems. Speed-up is achieved through the introduction of multilevel parallelism at the levels of decomposition of the model and the distribution of calculations on the computational nodes of the cluster, at the level of multithreaded computations within the part of the model at one node and at the level of vectorization of calculations and their transfer to GPU/ FPGA accelerators within a single computational flow. Vectorization is considered for both conventional multicore CPUs and the MIC architecture. Accelerators are used using OpenCL technology for heterogeneous systems. The possibility of computations speed-up up to 50 times for the considered problem due to the introduction of multilevel parallelism is shown.

1 Introduction

At present, many areas of science and industry use special software systems that perform mathematical modeling of various physical processes and phenomena. Such programs include solvers, similar to the one considered in this work as part of the system of formation of solutions of nonlinear dynamics equations (FRUND), which performs the calculation of the stress-strain state of a multibody model. The multibody approach presents the studied objects as a system of discrete bodies, connected with elastic links, as shown in Fig. 1. Discrete body dynamics is described with a system of differential equations (DE) ${\text{M}}\mathop {\text{y}}\limits^{..} + {\text{Ky}} = {\text{q}}$, where M – is a mass matrix, K – inertia forces vector, q – vector of forces, influencing bodies.

Fig. 1.

Multibody system representation.

Due to a large amount of data processed and the high computational complexity of processing algorithms (matrix computations, coordinate transformations from local to global coordinate systems, calculation of forces for right-side of the differential equations on each iteration of integration of DE), such calculations can take a long time and require speed-up. For example, the calculation of stresses in the suspension arms of the car in the dynamics on a conventional computer in single-threaded mode can take more than 24 h.

To perform such calculations and computationally complex modeling, multicomputer systems (clusters) are used [1, 2]. Such systems are often heterogeneous (or hybrid), for example, a computer system includes processors of different architectures: multi-core CPUs, GPU accelerators, accelerators or autonomous processors with a large number of cores (MIC), reconfigurable accelerators based on FPGAs and others. When performing computations on a multiprocessor system or computing cluster, it makes sense to reduce time costs, using all available computing resources of the system at the same time. Though, very often we face the situation when software cannot use heterogeneous or even homogeneous computers of a cluster, obtaining their maximum or even close to maximum performance.

In general, it is necessary to implement all needed algorithms suitable to use all available computing nodes regarding their types, to obtain a system that can work on a heterogeneous computing cluster. This will allow using of clusters with different computing nodes for calculations, achieving their maximum utilization.

The approach to parallelization considered in this paper, namely, multilevel implementation of parallelism, is quite universal [2], though it is applied to the area of DSS analysis. Approbation of various methods of computing acceleration, their combination, and evaluation of their efficiency for the DSS solver is interesting both in itself and as an example, which in the future can allow extending the developed approach to other problems having a similar computational structure.

The paper has the following structure. In Sect. 2 brief problem state for the dynamic stress-strain solver is presented. In Sect. 3 general algorithm of solving the DE, the system is described and possibilities of parallel implementation of its stages are estimated. The main approaches to parallelize the DSS are observed in Sect. 4. In Sect. 5 the multi-level approach to solver implementation is described at each level. Experimental results for multi-level parallel solver testing on the homogeneous cluster are presented in Sect. 6. Some test results, as well as approaches to the use of the heterogeneous cluster, are presented in Sect. 7.

2 Brief Problem State for DSS Solver

Dynamic stress-strain solver, based on discrete elements method [3], or multi-body approach, uses a basic system of differential equations in the form [4]:

$$ M\ddot{y} = q\left( {\dot{y},y,t} \right) - Ma\left( t \right) + s(\dot{y},y) $$

(1)

where a – acceleration vector, M – matrix of masses, ${\text{s}}\left( {{\dot{\text{y}}}, {\text{y}}} \right)$ – stabilization forces, ${\text{q}}\left( {{\dot{\text{y}}}, {\text{y}}, {\text{t}}} \right)$ – the function describing the forces between discrete elements.

The model presented is described mathematically in two ways: with the help of absolute coordinates in one common (global) coordinate system, as well as with the help of relative coordinates describing the position of the body relative to the reference, focusing on the center of mass and the central axis of inertia.

Since all the data for the calculation is stored in the global coordinate system, we must introduce the transformation of the body position from local coordinates to global. For this purpose, rotation matrices are used – square matrices, which make it possible to determine the position of the body described in one coordinate system, in another coordinate system. Rotations are based on the form of Euler angles (ψ, θ, and φ), aircraft (ship) angles, or angles of Tait-Bryan, which allow taking into account small displacements.

At each step of the calculations, the Euler angles for each discrete element are recalculated relative to the previous ones to obtain the actual rotation matrices for the transfer of bodies from one coordinate system to another. These matrices have the following form

$$ \begin{array}{*{20}c} {{\text{A}} = {\text{X}}_{\upvarphi } {\text{Y}}_{\uptheta} {\text{Z}}_{\uppsi} } \\ { = \left[ {\begin{array}{*{20}c} {\cos\uptheta\cos\uppsi} & { - \cos\uptheta \sin\uppsi} & {\sin\uptheta} \\ {\cos {\upvarphi } \sin\uppsi + \sin {\upvarphi } \sin\uptheta \cos\uppsi} & {\cos {\upvarphi }\cos\uppsi - \sin {\upvarphi } \sin\uptheta \sin\uppsi} & { - \sin {\upvarphi } \cos\uptheta} \\ {\sin {\upvarphi } \sin\uppsi - \sin {\upvarphi } \cos\uptheta\sin\uppsi} & {\sin {\upvarphi } \cos\uppsi + \cos {\upvarphi } \sin\uptheta \sin\uppsi} & {\cos {\upvarphi } \cos\uptheta} \\ \end{array} } \right]} \\ \end{array} $$

(2)

The use of the described scheme makes it possible to apply explicit methods of numerical integration, in which, unlike implicit ones, it is not required to calculate the roots of the system of linear algebraic equations (SLAE) at each iteration, which also simplifies the problem of calculations. In the considered DSS solver the Eq. (1) is solved by the Runge-Kutta method of the 4th order of accuracy. According to the method, the approximate value at the points of the model is calculated by the iterative formula:

$$ {\text{y}}_{{{\text{n}} + 1}} = {\text{y}}_{\text{n}} + \frac{\text{h}}{6}\left( {{\text{k}}_{1} + 2{\text{k}}_{2} + 2{\text{k}}_{3} + {\text{k}}_{4} } \right), $$

(3)

$$ {\text{k}}_{1} = {\text{f}}\left( {{\text{x}}_{\text{n}} , {\text{y}}_{\text{n}} } \right) , $$

(4)

$$ {\text{k}}_{2} = {\text{f}}\left( {{\text{x}}_{\text{n }} + \frac{\text{h}}{2}, {\text{y}}_{\text{n}} + \frac{\text{h}}{2}{\text{k}}_{1} } \right), $$

(5)

$$ {\text{k}}_{3} = {\text{f}}\left( {{\text{x}}_{\text{n }} + \frac{\text{h}}{2}, {\text{y}}_{\text{n}} + \frac{\text{h}}{2}{\text{k}}_{2} } \right), $$

(6)

$$ {\text{k}}_{4} = {\text{f}}\left( {{\text{x}}_{\text{n }} + {\text{h}}, {\text{y}}_{\text{n}} + {\text{hk}}_{3} } \right), $$

(7)

where x_n and y_n are parameters of the function f in general differential equation system ${\text{y}}^{{\prime }} = {\text{f}}\left( {{\text{x}}_{\text{n}} , {\text{y}}_{\text{n}} } \right)$, h is the size of the grid step for x.

3 The General Algorithm for Calculating the Dynamic Stress-Strain State

To make a general algorithm for calculating the dynamic stress-strain state, it is necessary to proceed from the mathematical model of calculations and identify the main stages. The algorithm shown in Fig. 2 is typical for all multibody dynamics systems, at least for FRUND system [4, 5].

Fig. 2.

The general algorithm for calculating the dynamic stress-strain state.

Let us consider each stage from the point of view of the possibilities of its parallelization.

The zero stage (preparation, or model initialization) includes the preparation of computational models and includes the definition of constants, setting calculation parameters, generation of computational domains and other operations. It can be concluded that this stage is rather consistent.

The main calculation is performed at the first stage in a cycle with a given number of iterations, and each iteration corresponds to a certain point in time. Since at this stage, a strict sequence of calculations is specified, and each subsequent iteration uses the result calculated on the previous one, then due to the presence of information dependencies, complete parallelization of the main cycle is impossible.

However, it is possible to parallelize stages 1.1, 1.2 and 1.3 separately, which are performed for each step of numerical integration.

The calculation of the coefficients of the Runge-Kutta method is performed for each discrete element in the model. Since according to the problem statement all elements are identical and initialized with constant values, the calculation of the i-th coefficients can be carried out independently. But the computational complexity of this stage is small and its contribution to the total time of the calculation is insignificant.

Stage 1.2 includes a set of trigonometric operations that implement the formula for calculating the rotation matrix to translate a discrete element in the coordinate system of the reference body and auxiliary calculations. Many actions can be performed separately for each item: the initialization, the updating of matrices of rotation, the steps for the numerical integration of the kinematic Euler and others. If we take into account the short calculation time, we can assume that the efficiency of parallelized computations can be significantly reduced due to frequent memory access and multiple data transfers, as they cause large overhead.

Stage 1.2 is used to update the data on the rotation matrices and is also preparatory for the calculation of the right-hand side of the Eq. (1).

In stage 1.3, new force values are calculated, which are used by numerical integration at each step of the Runge-Kutta method. The calculation of the right parts is the most important and resource-intensive stage of DSS calculation.

Since calculating the right-hand side is performed for each discrete element, it can be performed in parallel. It includes many vector and matrix transformations and operations, which provides additional parallelization capability.

The main reason for improving performance difficulties is the need to constantly access different areas of memory, which does not allow efficient use of the data cache and creates overhead.

Thus, we can distinguish the main features of the algorithm in terms of parallelization of calculations:

• 1. Iterative calculation scheme: the numerical method can be parallelized only within one iteration since each iteration uses the results obtained on the previous one.

• 2. On small models, the parallelization effect is negligible due to the small computational complexity of one iteration. A more significant effect can be achieved on larger models.

• 3. The presence of cycles without information dependencies, as well as the presence of vector and matrix operations, makes it possible to speed up the calculation due to parallelization at a lower level.

4 Approaches to Parallelize the Calculation of DSS

Existing actual methods of parallelization can be conventionally combined into several groups. The first group includes approaches using “fine-grained” parallelism.

Since the solution of the problem under consideration involves numerical integration with dependent iterations, it is difficult to effectively parallelize methods for high-dimensional problems while maintaining the accuracy of calculations due to the fact that most of the computations are described by sequential code and there are few potentially parallelized computations among them. However, the model has significant internal parallelism, which makes it possible to perform many operations on discrete elements in parallel. Multithreaded computing is best suited for this task. Thus, in [1] different parallel algorithms of sparse matrix processing allow achieving acceleration up to 60% in the MST dynamics solver on 6 cores. Similarly, the calculation is accelerated by 20–30% using OpenMP when using “fine-grained” parallelism.

The use of various accelerators and coprocessors is an alternative to the use of multi-core CPU, the number of threads of which is limited. For example, it is possible to use coprocessors with MIC architecture with a large number of cores, on which it is also possible to organize parallel calculations using OpenMP in native mode.

As another alternative, we can consider the use of massively parallel computing devices – graphics coprocessors or even FPGA, which allow achieving a higher degree of parallelism due to the fact that computing units process one discrete element at a time. To work with such devices, you can use OpenCL technology. This approach to the parallelization of engineering calculations is quite popular among foreign and domestic authors and, for example, is considered in [6]. The use of accelerators in the process of calculating the DSS has such a drawback as the complicity of full transfer of the solver implementation to the device, due to the lack of computing and/or memory resources, which makes it necessary to implement a joint calculation of the CPU with the GPU/FPGA, which in turn makes it difficult to actively exchange data between the host and devices.

In addition to multithreaded computing, there are technologies that provide support for “fine-grained” parallelism within a single compute core. Among them is vectorization, which is well suited for parallelizing the code of linear algebra operations. This area of research is relatively new, but there are works showing the possibilities of using vectorization in engineering calculations, including the MIC architecture [7].

There is also a group of approaches that implement the concept of “coarse-grained” parallelism. As a rule, these approaches use some kind of distributed computing using MPI or other ones [8]. Within the framework of the approach, calculations of individual models are paralleled, for example, when using a multivariate calculation, when the same calculations are performed on different input data.

To effectively implement this approach within the framework of one DSS calculation task, it is necessary to decompose the computational domain into several subdomains, which will be processed in parallel by different computing devices.

5 Development of the General Multi-level Scheme of Parallelization of the Dynamic DSS Solver

In order to implement the task of significantly accelerating the dynamic DSS solver via parallelism, in our opinion, it is necessary to use a multi-level scalable approach to parallel calculations, that is necessary to parallelize calculations at several interrelated levels at the same time:

• At the level of decomposition of computational domains for systems with distributed memory;

• At the level of decomposition of computational domains for systems with multithreaded calculations on shared memory;

• At the level of data parallelism for SIMD processing on multi-core processors with support for vector instructions, for SIMT computing using multi-core MIC and GPU accelerators, as well as FPGA.

Figures 3 and 4 show a diagram of the proposed approach at the upper first and two lower levels.

Fig. 3.

Higher-level for DSS parallelization.

Fig. 4.

Lower levels for DSS parallelization.

At the top level is a spatial decomposition, which involves the separation of the original geometry of the model into several related parts and their parallel processing separately for each part, followed by the combining of results in the root process [9].

The computational domain is divided into N fragments, each of which can be processed by one of the M involved computing devices. It is also possible to perform parallel calculations with both shared and distributed memory within the same node.

It is not advisable to divide the computational domain into too many subdomains since in this case there will be a need for data exchange between the executive nodes, and as the number of subdomains increases, the amount of data transferred will also increase. In addition, in order to achieve the greatest efficiency, it is necessary to split the model into submodels of such a size that internal parallelism at lower levels gives an increase in productivity, that is, the calculation of one submodel should not occur too quickly.

Decomposition and synchronization is a complicated process, involving many stages and details, starting from implementing special DEC-files (DECompisition files), containing decomposition information about submodels, as shown in Fig. 5(a–d), to supporting SYNC-data files (SYNCronization data files) for synchronization procedures, shown in Fig. 6, and choosing appropriate MPI – functions for data transfers (in our case –MPI_Sendrecv with user’s data types, shown in Fig. 7).

Fig. 5.

Blocks of data on the decomposition of the model: (a) initial model, (b) submodels, (c) boundary areas, (d) addressing elements of the submodels in the original model.

Fig. 6.

Data synchronization (a) buffer table, (b) graphical interpretation of data transfer.

Fig. 7.

Map of user’s MPI data type: (a) to send data, (b) to receive data.

The next level is multithreading – it calculates the individual stages of numerical integration, there is an additional decomposition of the computational domain – in each flow, a part of the discrete elements of the submodel is processed. This step can be performed on a single compute node (GPU or CPU) or jointly on the CPU and GPU or FPGA.

At the lowest level, the vectorization of individual calculation operations is used [10]. This step is performed on a single compute node with support for vector registers of a certain type and does not require additional processing power. Also, depending on the hardware platform, it is possible to use different types of vector registers.

Figure 8 shows some classes, implementing vectorization for various processor architectures in DSS solver.

Fig. 8.

Some classes implementing vectorization for different SIMD instructions in DSS solver.

However, if the number of vector processors or coprocessors is limited, it is recommended to reduce the number of executive threads to avoid performance degradation by attempting to access the same register at the same time.

Thus, we can highlight the following advantages that are achieved in the proposed multiscale approach:

• The flexibility to change the scheme depending on the configuration of the hardware platform.

• Overcoming the limitations of technologies implementing the concept of coarse-grained parallelism by internal parallelization of the calculation within a single subtask.

• The opportunity to further speed-up the computation by the use of vector instructions for the calculation parallelized on other levels.

This approach is quite universal and makes it possible to use the maximum available computing power to solve large-size problems of modeling the dynamics of body systems, as well as other types of engineering calculations.

6 Experimental Results for Multi-level Parallelization on Homogeneous Cluster

The table below shows the results achieved by decomposition on a homogeneous cluster of Xeon E5 nodes with the maximum available number of OpenMP threads and vectorization using a set of AVX2 with FMA instructions (model with 300 elements per side and 100 × 100 iterations is considered).

The calculations were also performed on a homogeneous cluster of KNL (MIC) nodes. The calculation results are shown in the table below (same model as in Table 1, but for 1 × 100 iterations).

Table 1. The results of the calculation using a multi-level parallelization approach on a homogeneous cluster with Intel Xeon E5 nodes (using AVX2 FMA vectorization).

Table 2. The results of the calculation using a multi-level parallelization approach on a homogeneous cluster with KNL nodes.

The results obtained for the speed-up of the calculation on both types of hardware platforms indicate good scalability of the proposed parallelization algorithm. It can be concluded that the increase in performance is proportional to the number of computing nodes of a cluster involved in the calculations.

In general, proposed a multi-level approach and its implementation via vectorized algorithms of base operations with matrices and right-side of differential equations, multi-treading and model decomposition for multiple process calculations via MPI let us obtain scalable speed-up from 27–30 times for Xeon E5 CPUs nodes up to 50 times for KNL many-core (MIC) processor nodes. Though, the performance achieved is far from peak, especially for MIC computers, which is probably due to low memory optimizations. The low performance of MIC nodes and cluster complicates the joint use of MIC and general CPU nodes in a heterogeneous cluster of Xeon and MIC (Xeon Phi) nodes. Still, such a combination could be improved by appropriate load balancing.

7 The Alternatives for the Parallelization of the DSS Calculation Using Heterogeneous Cluster

The considered approach to the acceleration of the dynamic stress-strain state solver is quite effective, but its efficiency can be improved for a heterogeneous environment (with GPUs and CPUs) by using OpenCL technology. Thus, it was used to develop a parallel code for GPU [5]. Originally only the calculation of the right-hand sides of the equations was made in OpenCL kernel since this part of the calculations takes the largest part of the calculation time.

This approach had been leading to a significant additional time spent on data transfer from the CPU to the GPU, though the calculation on the GPU was faster than on the CPU.

There are several factors that limit the performance of this approach:

• Intensive data exchange between CPU and GPU;

• Non-optimized calculation algorithm;

• The need to speed-up the numerical integration and recalculation of rotation matrices.

The alternative approach is to perform all the needed calculations for the part of the initial multi-body system inside OpenCL kernel on GPU withing an MPI process. In this case, we can perform some processes on GPUs and other processes on CPUs or other accelerators.

To get a rough idea of the solver performance when running on different hardware configurations for models of different dimensions, the calculations were performed on two processes: one for the host – CPU, one for GPU. Also, the program was run separately for the CPU on two processes and one GPU solely.

Let us combine the results into a table, where the intersection of the rows will indicate the time for which the calculation is performed, in seconds (Table 3).

Table 3. The results of running the solver with OpenCL on CPU and GPU, s.

Let us also build a graph to visualize the results (Fig. 9).

Fig. 9.

The results of running the solver with OpenCL on CPU and GPU, s.

Plate models with the side size of 50, 100, and 200 discrete elements in the model and 10,000 iterations are calculated faster on two processes on CPU and GPU bundles than on two processes on the CPU, but calculations on GPU only are much faster than on bundle of GPU and CPU. From the above results it can be seen that server accelerator NVIDIA TESLA itself makes it possible to speed up the calculations of DSS more than 30 times compared to using server CPU E5 (which is surprisingly much more compared to results in [5], though they were obtained on less powerful GPU, this should still be verified). Bundle of GPU and CPU processes is faster than CPU (up to 2–3 times), though it makes no sense yet compared to calculations held on GPU only. The problem is probably in the interaction overhead of GPU and CPU processes via MPI. We still can expect that optimizing this interaction and competent load balancing will allow us to achieve extra speed-up when using decomposition into heterogeneous nodes compared to the results given in Tables 1 and 2 for a homogeneous cluster. But this needs to be studied more thoroughly, confirmed experimentally and has gone beyond the scope of this work.

8 Conclusions and Future Research

The paper shows an approach to solving the problem of extracting the maximum parallelism from both homogeneous and heterogeneous computing clusters equipped with multi-core processors and accelerators when modeling the dynamic stress-strain state via a multibody discrete-element representation of models as an illustrative example. Maximum concurrency and, as a consequence, a high real performance is achieved through the introduction of multilevel parallelism at the levels of submodel-node (process), part of the submodel – flow, and vectorization of calculations within the flow. The speed-up of calculations up to 50 times on 6 homogeneous multicore nodes of the computing cluster is achieved, the possibility to accelerate calculations up to 3 times on each heterogeneous node equipped with a powerful GPU is shown (though performing calculations on sole GPU turned to be more efficient, as MPI interaction of nodes with GPU needs to be improved). It is stated that it is possible to increase the whole speed-up when using heterogeneous nodes with and without GPU due to appropriate model decomposition and load balancing (though the real benefit of such heterogeneous computations should be studied more thoroughly and confirmed experimentally).

As mentioned above, some approaches should be studied in more detail, first of all – the load balancing issues for the heterogeneous cluster, especially with CPU and GPU nodes. As for MIC nodes, their performance for the considered task could be improved if we take into consideration memory optimizations. A reduction of overheads for MPI communication is very important to increase the performance of the cluster, equipped with GPU accelerators. The considered approach for DSS could be also applied to basic multibody dynamics solver.