Keywords

1 Introduction

SPASS-SATT (v1.1) is a sound and complete CDCL(LA) solver for quantifier-free linear rational and linear mixed/integer arithmetic. It is a from-scratch implementation except for some basic data structures taken from the SPASS [32] superposition theorem prover. It is available through the SPASS-Workbench [3]. We participated with SPASS-SATT in the main track of the 13th International Satisfiability Modulo Theories Competition (SMT-COMP 2018) and ranked first in the category QF_LIA (quantifier-free linear integer arithmetic) [1] and second in the category QF_LRA (quantifier-free linear rational arithmetic) [2]. This system description explains the main features that led to the success of SPASS-SATT. We do not only describe the relevant techniques, but also show their specific impact on dedicated groups of examples from the SMT-LIB by experiments.

By far not all techniques presented in this system description are unique features of SPASS-SATT. The techniques that appeared first in SPASS-SATT are the unit cube test and bounding transformations explained in Sect. 2. Concerning preprocessing, SPASS-SATT is the first SMT solver implementing the small-clause-normal-form algorithm, see Sect. 4. Further important techniques implemented in SPASS-SATT have already been available in other SMT solvers such as CVC4 [4], MathSAT [12], Yices [16], and Z3 [14], but not all in one tool: (i) the implementation of branch and bound as a separate theory solver and a number of improvements to the simplex implementation such as a priority queue for pivot selection, integer coefficients instead of rational coefficients, dynamically switching between native and arbitrary precision integers, and backing-up versus recalculating simplex states, all in Sect. 2, (ii) decision recommendations, unate propagations, and bound refinements for the interaction between the SAT and theory solver, in Sect. 3, and (iii) preprocessing techniques for if-then-else operators and pseudo-boolean inequalities, in Sect. 4. Although these techniques are contained in existing SMT solvers, not all have been described in the respective literature. The paper ends with a discussion of future extensions to SPASS-SATT in Sect. 5.

The benchmark experiments with SPASS-SATT consider the 6947 SMT-LIB benchmarks for quantifier-free linear integer arithmetic (QF_LIA) [5]. For the experiments, we used a Debian Linux cluster and gave SPASS-SATT for each problem one core of an Intel Xeon E5620 (2.4 GHz) processor, 8 GB RAM, and 40 min. The results are depicted as scatter plots and in each of them we compare the default configuration (i.e., without any command line options) of SPASS-SATT (horizontal axis) with an alternative configuration of SPASS-SATT (vertical axis). (The SMT-COMP results were obtained with the default configuration; by default all presented techniques are turned on.)

Fig. 1.
figure 1

Impact of our BnB extensions on the QF LIA benchmarks (a) QF_LIA with(out) unit cube tests (b) QF_LIA with(out) bounding transf.

Full size image

2 SPASS-IQ: An LA Theory Solver

SPASS-SATT’s theory solver, called SPASS-IQ, decides conjunctions of linear arithmetic inequations. It is divided into two main components: a simplex implementation for handling linear rational arithmetic and a branch-and-bound implementation for handling linear mixed/integer arithmetic.

However, the division between the two components is in all truth not that strict. The branch-and-bound implementation is more of a supervisor for the simplex implementation. To be more precise, the branch-and-bound implementation coordinates the search for a mixed or integer solution, but the majority of the actual search/calculation is still done by the simplex implementation. For most QF_LIA benchmark instances (4894 out of 6947 instances), this supervision is not even necessary; i.e., SPASS-SATT solves these instances with just the simplex implementation as its theory solver. This means that SPASS-SATT’s efficiency on the QF_LIA benchmarks also highly depends on the efficiency of our simplex implementation and not just on the extensions and optimizations to our branch-and-bound implementation.

The simplex implementation inside SPASS-IQ is based on a specific version [17] of the dual simplex algorithm [29]. The overall efficiency of our simplex implementation is heavily influenced by the efficiency of the data structures that we use. Our most important data structure features are:

  1. (1)

    Priority Queue for Pivot Selection: Instead of iterating over all basic variables when searching for violated basic variables, we collect the basic variables in a priority queue as soon as they become violated.

  2. (2)

    Integer Coefficients Instead of Rational Coefficients: We avoid rational coefficients in our simplex tableau by multiplying each equation in the tableau with the common denominator of the equations coefficients. As a result, each basic variable also has a coefficient, but all coefficients are integers. This transformation roughly halves the cost of most tableau operations because we do not need to consider rationals which are typically represented by two integers (the numerator and the denominator).

  3. (3)

    Dynamically Switching between Native and Arbitrary-Precision Integers: We use the arbitrary-precision arithmetic library FLINT to represent our integers [21]. It dynamically switches between native C integer and arbitrary-precision types.

  4. (4)

    Backup vs. Recalculation: In contrast to Dutertre and de Moura’s version of the simplex algorithm, our simplex backtrack function recalculates a satisfiable assignment instead of loading a backup of the last satisfiable assignment.

SPASS-IQ’s second set of decision procedures revolves around an implementation of the branch-and-bound (BnB) algorithm [29]. Most SMT solvers implement branch and bound through a technique called splitting-on-demand [6], which delegates some of the branch-and-bound reasoning to the SAT solver. In order to keep more control over the branch-and-bound reasoning, we decided against splitting-on-demand and implemented branch and bound as a theory solver separate from the SAT solver. This also made it easier to complement branch and bound with other decision procedures:

The first two extensions that we discuss here are simple rounding and bound propagation  [29], which are both classical additions to most branch-and-bound implementations. For simple rounding, we round any rational solution computed during the branch-and-bound search to the closest integer assignment and check whether this is already an integer solution. For bound propagation, we propagate new bounds from existing bounds at every node in our branching tree. Although both techniques are very popular, we could only measure a minor impact on SPASS-SATT’s performance on the QF_LIA benchmarks. With simple rounding we solve only one instance faster and with bound propagations we solve only 10 additional instances. In part, this is due to our next two extensions that make simple rounding and bound propagation in many cases unnecessary.

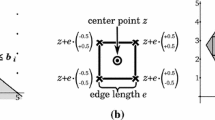
The next extension we discuss is the unit cube test . It determines in polynomial time whether a polyhedron, i.e., the geometric representation of a system of inequalities, contains a hypercube parallel to the coordinate axes with edge length one [9, 10]. The existence of such a hypercube guarantees a mixed/integer solution for the system of inequalities.

The unit cube test is only a sufficient and not a necessary test for the existence of a solution. There is at least one class of inequality systems, viz., absolutely unbounded inequality systems [9, 10], where the unit cube test is also a necessary test and which are much harder for many complete decision procedures.

The plot in Fig. 1(a) shows that SPASS-SATT employing the unit cube test solves 56 additional benchmark instances from the QF_LIA benchmarks and solves 705 instances more than twice as fast.Footnote 1 Moreover, the unit cube test causes only a minor overhead on problems where it is not successfully applicable.

The final extension that we discuss are bounding transformations . Branch and bound alone is an incomplete decision procedure and only guarantees termination on bounded problems, i.e., problems where all variables have an upper and a lower bound. For this reason, we developed two transformations that reduce any unbounded problem into an equisatisfiable problem that is bounded [7]. The transformed problem can then be solved with our branch-and-bound implementation because it is complete for bounded problems.

The plot in Fig. 1(b) shows that SPASS-SATT employing the bounding transformation solves 169 additional benchmark instances from the QF_LIA benchmarks and solves 167 instances more than twice as fast.Footnote 2 Moreover, the bounding transformation causes only a minor, almost immeasurable overhead on problem instances where it is not successfully applicable.

Fig. 2.
figure 2

CDCL(LA) as implemented in SPASS-SATT

Full size image
Fig. 3.
figure 3

Impact of decision recommendations on the QF_LIA benchmarks (a) QF_LIA with(out) decision recom. (b) convert with(out) decision recom.

Full size image

3 CDCL(LA): SAT and Theory Solver Interaction

SPASS-SATT uses at its core a CDCL(LA) implementation that combines our CDCL (conflict-driven-clause-learning)-based SAT solver SPASS-SAT with our LA theory solver SPASS-IQ. The result is a decision procedure for ground linear-arithmetic formulae in clause normal form. In this section, we quickly explain how our theory solver and SAT solver interact. To this end, we list in Fig. 2 the main interface functions of our SAT solver and theory solver and show through a flow graph how they interact. The main focus of this section, however, is to explain in which way our implementation of CDCL(LA) differs from more general frameworks for CDCL(T), also called DPLL(T) [6, 18, 26, 27].

There are three key points that we have changed compared to the more general frameworks for CDCL(T). First of all, we rely on “weakened early pruning” [30], i.e., we only use a weaker but faster check to determine theory satisfiability for partial (propositionally abstracted) models. We do so because IntCheck(), i.e., checking for an integer solution, is too expensive and not incrementally efficient enough to be checked more than once per complete (propositionally abstracted) model. As a compromise, we at least check the partial model with RatCheck(), i.e., we check for a rational solution, before we add a(nother) decision literal to the model with Decide(L,P).

As our second key change, we let the theory solver select via GetPhase(L) the phase of the next decision literal L, i.e., whether Decide(L,P) will add the positive or the negated version of L to the model. We call this technique a decision recommendation .Footnote 3 Finally, we use theory reasoning via the function LearnClauses() to find and learn new clauses implied by the input formula. The reasoning techniques we use for this purpose are unate propagations and bound refinements as proposed in [17].

In Fig. 3(a), we examine the impact that decision recommendations have on SPASS-SATT’s performance on the QF_LIA benchmarks. With decision recommendations it can solve 129 additional problems. Moreover, it becomes more than twice as fast on 389 problems, but only twice as slow on 58 problems. The benchmark family that is impacted the most by decision recommendations is convert with 116 additionally solved problems (see Fig. 3(b)). Although SPASS-SATT frequently and regularly performs unate propagations on the QF_LIA benchmarks, we are unable to observe any consistent benefit or drawback from this interaction technique. The impact of bound refinements is also relatively minor and SPASS-SATT solves only 24 additional problem instances if they are activated.

Fig. 4.
figure 4

Impact of our preprocessing techniques on (a) the QF_LIA benchmarks and more specifically (b) nec_smt, (c) rings, and (d) pb2010

Full size image

4 Preprocessing

Many real world applications can be encoded as linear integer arithmetic formulas, and some of those applications are too specialized to be efficiently handled by our rather general CDCL(LA) implementation. To resolve this, we have complemented SPASS-SATT with several specialized preprocessing techniques.Footnote 4

Complex input formulas are typically transformed into CNF by a Tseitin-style renaming [31] using a static criterion which subformula to replace by a fresh propositional variable. SPASS-SATT includes the small clause normal form algorithm [28]. Instead of a static criterion, the number of clauses with or without a renaming is compared and a fresh propositional variable is introduced only if a renaming eventually yields fewer clauses. This results in a more compact CNF with strictly fewer additional propositional variables. To this end we extended the small clause normal form algorithm to ITE formulas. For an ITE formula \((\text {ite} \; t_1 \; t_2 \; t_3)\), simplified by the below techniques and potentially contained in some formula f, we compare the number of clauses generated out of replacing the formula with a fresh variable P in f and adding \(P \leftrightarrow [(t_1 \rightarrow t_2) \wedge (\lnot t_1 \rightarrow t_3)]\) with a direct replacement of the ITE formula by the before mentioned conjunction of two implications. This test can be carried out in constant time after having once filled respective data structures. The set up of the data structures needs one run on the overall formula, i.e., can be computed in linear time [28].

SPASS-SATT also has five specialized preprocessing techniques for if-then-else expressions (ITE). Our first technique, if-then-else reconstruction , rebuilds if-then-else operations that were already preprocessed-away by the creators of the input problem. The reconstruction then allows us to apply simplifications missed during the creation of the input problem. To this end, we check whether the first conjunctive layer of our formula \(f := (\text {and} \; \ldots \; t_i \; \ldots \; t'_i \; \ldots )\) contains any pair of clauses \(t_i\), \(t'_i\) that match the clauses added by the standard if-then-else elimination, i.e., \(t_i \in T_i\) and \(t'_i \in T_i {\setminus } \{t_i\}\), where \(T_i = \{(\text {or} \; t_{i1} \; (= \; y_i \; t_{i3})), (\text {or} \; (\text {not} \; t_{i1}) \; (= \; y_i \; t_{i2})), (\text {or} \; (= \; y_i \; t_{i2}) \; (= \; y_i \; t_{i3}))\}\) and \(y_i\) is an arithmetic variable. If we find such pairs \(t_i\), \(t'_i\), then we remove them from f and replace all remaining occurrences of \(y_i\) in f with \((\text {ite} \; t_{i1} \; t_{i2} \; t_{i3})\).

The next three techniques are all dedicated to so-called constant if-then-else expressions (CITEs). A CITE is either a leaf, i.e., an arithmetic expression that can be simplified to a number \(a_{ij} \in \mathbb {Q}\), or a branch, i.e., an if-then-else expression \((\text {ite} \; t_1 \; t_2 \; t_3)\) where \(t_2\) and \(t_3\) are again CITEs.

The first CITE technique is called shared monomial lifting and we use it to increase the number of CITEs in our formula. It traverses the subterms in our formula in bottom-up order and transforms all subterms \(t := (\text {ite} \; t_1 \; (+ \; q \; q') \; (+ \; q \; \hat{q}))\) into \((+ \; q \; (\text {*} \; 1 \; (\text {ite} \; t_1 \; (+ \; q') \; (+ \; \hat{q}))))\). (We assume here for simplicity that the shared part q appears after the unshared parts \(q'\) and \(\hat{q}\). In reality SPASS-SATT has to find and extract the shared parts.)

The second technique is called CITE simplification and it simplifies atoms \((o \; t_1 \; t_2)\), where \(t_1\) and \(t_2\) are CITEs and o is one of the operators \(<=\), \(=\), \(>=\). To be more precise, the technique essentially pushes the comparison operator o recursively down the CITE branches and greedily simplifies any branch to true or false if possible. For more details, see Sect. 4 in the paper by Kim et al. on efficient term-ITE conversion [24].

The third technique is called CITE bounding and eliminates the remaining CITEs. Thanks to it, we only introduce one new variable for each topmost CITE instead of one variable for each CITE branch. Moreover, this new variable describes only a small set of values (often equivalent to just the CITE leaves) because it is bounded as tightly as possible. As its first step, CITE bounding creates one new integer variable \(x_j\) for each topmost CITE expression \(t_j\) and replaces the occurrences of \(t_j\) in our formula f with \(x_j\). As its second step, CITE bounding extends f to the formula \(f' := (\text {and} \; f \; f_1 \; f'_1 \; \ldots \; f_m \; f'_m)\), where (i) \(f_j\) is equivalent to \(t_j\) except that all leaves \(a_{ij}\) of \(t_j\) are replaced by the equations \((= \; x_j \; a_{ij})\), (ii) \(f'_j := (\text {and} \; (>= \; x_j \; a_\mathrm{minj}) \; (<= \; x_j \; a_{\mathrm{maxj}}))\), and (iii) \(a_{\mathrm{minj}}\) is the smallest leaf in \(t_j\) and \(a_{\mathrm{maxj}}\) is the largest leaf in \(t_j\). As its last step, CITE bounding replaces all occurrences of \(x_j\) in \(f'\) with \((* \; a_{gj} \; x_j)\), where \(a_{gj}\) is the greatest common divisor of the leaves \(a_{ij}\) in \(t_j\).

The final ITE technique handles nested conjunctive if-then-else expressions (AND-ITEs). An AND-ITE is a series of nested if-then-else expressions that can be simplified to a conjunction. For instance, if \(t_i := (\text {ite} \; t'_i \; t_{i+1} \; \textit{false})\) for \(i = 1, \ldots , n\), then \(t_1\) is an AND-ITE equivalent to \((\text {and} \; t'_1 \; \ldots \; t'_n \; t_{n+1})\). Naturally, we transform these AND-ITEs into actual conjunctions and we call this process compression. However, we compress an AND-ITE \(t_1\) only if all of its actual AND-ITE subterms \(t_i\) appear only inside \(t_1\) and only once. If this is the case, then we first replace all occurrences of \(t_1\) in f by a new propositional variable \(p_j\) and extend our formula f to the formula \((\text {and} \; f \; (= \; p_j \; t'_1))\), where \(t'_1\) is the compressed form of \(t_1\). (If this is not the case, then we simply replace and compress the AND-ITE subterms in \(t_i\) first.) We do the compression in this way to strengthen the connection of the AND-ITEs that have multiple occurrences in f. The above described technique is called if-then-else compression and it was first presented by Burch in [11]. However, Burch used it to simplify control circuits and not SMT input problems.

Last but not least, SPASS-SATT also provides a preprocessing technique for pseudo-boolean problems [20], i.e., linear arithmetic problems where all integer variables \(x_j\) have bounds \(0 \le x_j \le 1\), which we call pseudo-boolean variables. To be more precise, SPASS-SATT recognizes clauses that are encoded as linear pseudo-boolean inequalities (i.e., inequalities containing just pseudo-boolean variables) and turns them into actual clauses . (This technique goes back to the NP-hardness proof of 0-1 programming [23].) However, SPASS-SATT only transforms inequalities containing at most three variables because it would otherwise fail to solve some of the problems from the pidgeons benchmark family.

The convert benchmark family contains problems that are relatively hard unless SPASS-SATT uses the right combination of techniques. To be more precise, SPASS-SATT solves only two-thirds of the 319 instances if one of the following three techniques is missing: (i) recalculating simplex states during backtracking (Sect. 2), (ii) decision recommendations (Sect. 3), or (iii) the small CNF transformation. SPASS-SATT with all three techniques solves all instances in less than 2 s (see Fig. 3(b)).

The nec_smt benchmark family contains problems with many nested if-then-else and let expressions. SPASS-SATT can handle most of them if we first apply our constant if-then-else simplifications and our conjunctive if-then-else compression. In Fig. 4(b), we see that SPASS-SATT without our preprocessing techniques solves only 1422 out of the 2800 benchmark instances and is by far slower on the instances it can solve. SPASS-SATT with our preprocessing techniques solves 2782 out of the 2800 benchmark instances.

The rings benchmark family encodes associative properties on modular arithmetic with the help of if-then-else expressions. With a combination of shared monomial lifting and constant if-then-else bounding, these problems become almost trivial to solve. In fact, SPASS-SATT needs less than one second for each problem instance and needs only techniques for linear rational arithmetic to solve each of them (Fig. 4(c)).

The rings_preprocessed benchmark family is equivalent to the rings benchmark family except that all if-then-else-operations were eliminated by standard if-then-else elimination [19]. We can use the same trick as for the rings benchmark family if we first use our if-then-else reconstruction technique that reverses the standard if-then-else elimination.

The pb2010 benchmark family is a set of industrial problems taken from the pseudo-boolean competition 2010. With its pseudo-boolean preprocessing, SPASS-SATT solves 22 additional benchmark instances from the 81 instances in the pb2010 benchmark family (see Fig. 4(e)). Moreover, SPASS-SATT solves all of these instances without its branch-and-bound implementation.

5 Conclusion and Future Work

We have presented SPASS-SATT our complete solver for ground linear arithmetic and have explained which techniques make it so efficient in practice. To summarize, SPASS-SATT is so efficient because (i) we have optimized the data structures in our simplex implementation, (ii) we have combined branch and bound with the unit cube test and the bounding transformation, (iii) we have added decision recommendations to our CDCL(LA) framework, (iv) we have added a small CNF transformation, and (v) we have added specialized preprocessing techniques for if-then-else expressions and pseudo-boolean inequalities.

Almost all of the presented techniques can be applied incrementally, however this is not always useful. For the partial models computed by the SAT solver, we only apply the simplex method, unate propagation, and bound refinements incrementally. If we ever extend SPASS-SATT to handle theory combinations or incremental SMT-LIB problems, then we would also apply branch-and-bound, unit cubes, and bounding transformations incrementally; but only on the models generated during Nelson-Oppen combination or between two (check-sat) calls.

For future research, we plan to extend SPASS-SATT to quantified linear arithmetic. Moreover, we plan to complement SPASS-SATT with several specialized decision procedures. For instance, SPASS-SATT could handle (almost) pseudo-boolean problems (e.g., benchmark families pb2010, miplib2003) much more efficiently if we extended branch and bound with a SAT based arithmetic decision procedure [8, 22, 25].