Abstract
We present an abstract development of Gödel’s incompleteness theorems, performed with the help of the Isabelle/HOL theorem prover. We analyze sufficient conditions for the theorems’ applicability to a partially specified logic. In addition to the usual benefits of generality, our abstract perspective enables a comparison between alternative approaches from the literature. These include Rosser’s variation of the first theorem, Jeroslow’s variation of the second theorem, and the Świerczkowski–Paulson semantics-based approach. As part of our framework’s validation, we upgrade Paulson’s Isabelle proof to produce a mechanization of the second theorem that does not assume soundness in the standard model, and in fact does not rely on any notion of model or semantic interpretation.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Gödel’s incompleteness theorems [10, 13] are landmark results in mathematical logic. Both theorems refer to consistent logical theories that satisfy some assumptions, notably that of “containing enough arithmetic.” The first incompleteness theorem (\(\mathcal {IT}_{1}\)) says that there are sentences that the theory cannot decide (i.e., neither prove nor disprove); the second theorem (\(\mathcal {IT}_{2}\)) says that the theory cannot prove (an internal formulation of) its own consistency. It is generally accepted that \(\mathcal {IT}_{1}\) and \(\mathcal {IT}_{2}\) have a wide scope, covering many logics and logical theories. However, when it comes to rigorous presentation, typically these results are only proved for particular, albeit paradigmatic cases, such as theories of arithmetic or hereditarily finite (HF) sets, within classical first-order logic (FOL); and even in these cases the constructions and proofs tend to be “incomplete and (apparently) irremediably messy” [4, p. 16]. Hence, the theorems’ scope remains largely unexplored on a rigorous/formal basis.
The emergence of powerful theorem provers has changed the rules of the game and, we argue, the expectation. Using interactive theorems provers, we can reliably keep track of all the constructions and their properties. Proof automation (often powered by fully automatic provers [18, 28]), makes complete, fully rigorous proofs feasible. And indeed, researchers have successfully met the challenge of mechanizing \(\mathcal {IT}_{1}\) [15, 25, 27, 35] and recently \(\mathcal {IT}_{2}\) [27]. Besides reassurance, these verification tours de force have brought superior technical insight into the theorems. But they have taken place within the same solitary confinement of scope as the informal proofs.
This paper takes steps towards a more comprehensive prover-backed exploration of the incompleteness theorems, by a detailed analysis of their assumptions. We use Isabelle/HOL [24] to establish general conditions under which the theorems apply to a partially specified logic. Our formalization is publicly available [31]. An extended technical report gives more details [30].
We start with a notion of logic (Sect. 2) whose terms, formulas and provability relation are kept abstract (Sect. 2.1). In particular, substitution and free variables are not defined, but axiomatized by some general properties. On top of this logic substratum, we consider an arithmetic substratum, consisting of a set of closed terms called numerals and an order-like relation (Sect. 2.2). Also factored in our abstract framework are encodings of formulas and proofs into numerals, the representability of various functions and relations as terms or formulas (Sect. 2.3), variations of the Hilbert-Bernays-Löb derivability conditions [16, 23] (Sect. 2.4), and standard models (Sect. 2.5).
Overall, our assumptions capture the notion of “containing enough arithmetics” in a general and flexible way. It is general because only few assumptions are made about the exact nature of formulas and numerals. It is flexible because different versions of the incompleteness theorems consider their own “amount of arithmetics” that makes it “enough,” as proper subsets of these assumptions. Indeed, our formalization of the theorems (Sect. 3) proceeds in an austere-buffet style: Every result picks just enough infrastructure needed for it to hold—ranging from diagonalization which requires very little (Sect. 3.1) to Rosser’s version of \(\mathcal {IT}_{1}\) which is quite demanding. This approach caters for a sharp comparison between different formulations of the theorems, highlighting their trade-offs: Gödel’s original formulation of \(\mathcal {IT}_{1}\) versus Rosser’s improvement (Sect. 3.2), proof-theoretic versus semantic versions of \(\mathcal {IT}_{1}\) (Sect. 3.2), and Gödel’s original formulation of the \(\mathcal {IT}_{2}\) versus Jeroslow’s improvement (Sect. 3.3).
Abstractness is our development’s main strength, but also a potential weakness: Are our hypotheses reasonable? Are they consistent? These questions particularly concern our axiomatization of free variables and substitution—a notoriously error-prone area. As a remedy, we instantiate our framework to Paulson’s semantics-based \(\mathcal {IT}_{1}\) and \(\mathcal {IT}_{2}\) for HF set theory [27], also performing an upgrade of Paulson’s \(\mathcal {IT}_{2}\) to a more general and standard formulation: for consistent (not necessarily sound) theories (Sect. 4). In the rest of this section, we discuss some formalization principles and related work.
Formal Design Principles. Our long-term goal is a framework that makes it easy to instantiate the incompleteness theorems and related results to different logics. This is a daunting task, especially for \(\mathcal {IT}_{2}\), where a lot of seemingly logic-specific technicalities are required to even formulate the theorem. The challenge is to push as much as possible of the technical constructions and lemmas to a largely logic-independent layer.
To this end, we strive to make minimal assumptions in terms of structure and properties when inferring the results—we will call this the Economy principle. For example, we do not define, but axiomatize syntax in terms of a minimalistic infrastructure. We assume a generic single-point substitution, then define simultaneous substitution and infer its properties. This is laborious, but worthwhile: Any logic that provides a single-point substitution satisfying our assumptions gets the simultaneous substitution for free.
As another instance of Economy, when faced with two different ways of formulating a theorem’s conclusion we prefer the one that is stronger under fewer assumptions. (And dually, we prefer weakness for a theorem’s assumptions.) For example, we discuss two variants of consistency: (1) “does not prove false” or (2) “there exists no formula such that itself and its negation are provable” (Sect. 3.3). While the statements are equivalent at the meta-level, their representations as object-logic formulas are not necessarily equivalent; in fact, (1) implies (2) under mild assumptions but not vice versa. So in our abstract theorems we prefer (1). Indeed, even if (2) implies (1) in all reasonable instances, why postpone for the instantiation time any fact that we can show abstractly?
Applying the Economy principle not only stocks up generality for instantiations, but also accurately outlines trade-offs: How much does it cost (in terms of other added assumptions) to improve the conclusion, or to weaken an assumption of a theorem? For example, an Economy-based proof of Rosser’s variant of \(\mathcal {IT}_{1}\) reveals how much arithmetic we must factor in for weakening the \(\omega \)-consistency assumption into consistency.
Related Work. Gödel initially gave a proof of \(\mathcal {IT}_{1}\) and the rough proof idea of \(\mathcal {IT}_{2}\) [13]. Hilbert and Bernays gave a first detailed proof of \(\mathcal {IT}_{2}\) [16]. A vast literature was dedicated to the (re)formulation, proof, and analysis of these results [4, 33, 38, 39]. The now canonical line of reasoning goes through the derivability conditions devised by Bernays and Hilbert [16] and simplified by Löb [23]. These conditions have inspired a new branch of modal logic called provability logic [4]. Jeroslow has argued that, unlike previously believed, one condition is redundant when proving \(\mathcal {IT}_{2}\) [17].
Kreisel [20] and Jeroslow [17] were the first to study abstract conditions on logics under which the incompleteness theorems apply. Buldt [5] surveys the state of the art focusing on \(\mathcal {IT}_{1}\). Our abstract approach, based on generic syntax and provability and truth predicates, resembles the style of institution-independent model theory [9, 14] and our previous work on abstract completeness [3] and completeness of ordered resolution [34]. Dimensions of generality that our formalized work does not (yet) explore include quantifier-free logics [17] and arithmetical hierarchy refinements [19]. Our syntax axiomatization is inspired by algebraic theories of the \(\lambda \)-calculi syntax [11, 12, 29].
In the realm of mechanical proofs, the earliest substantial development was due to Sieg [36], who used a prover based on TEM (Theory of Elementary Meta-Mathematics) to formalize parts of the proofs of both \(\mathcal {IT}_{1}\) and \(\mathcal {IT}_{2}\). But the first full proof of \(\mathcal {IT}_{1}\) was achieved by Shankar [35] in the Boyer-Moore prover, followed by Harrison in HOL Light [15] and O’Connor in Coq [25]. \(\mathcal {IT}_{2}\) has only been fully proved recently—by Paulson in Isabelle/HOL [26, 27] (who also proved \(\mathcal {IT}_{1}\)). All these mechanizations target theories over a fixed language in classical FOL: that of arithmetic (Harrison and O’Connor) and that of HF sets or a variation of it (Sieg, Shankar and Paulson). These mechanizations are mostly focused on “getting all the work done” in a particular setting (although Harrison targets a more abstract class of theories in the given language). On their way to \(\mathcal {IT}_{1}\), Shankar and O’Connor also prove representability of all partial, respectively primitive recursive functions—important standalone results. Also, there has been work on fully automating parts of the proofs of these theorems [1, 6, 32, 37].
By contrast, we explore conditions that enable different formulations for an abstract logic, where aspects such as recursiveness are below our abstraction level. The two approaches are complementary, and they both contribute to formally taming the complex ramifications of the incompleteness theorems. When instantiating our abstract assumptions to recover and upgrade Paulson’s results, we took advantage of Paulson’s substantial work on proving the many low-level lemmas towards the derivability conditions. More should be done at an abstract level to avoid duplicating some of these laborious lemmas when instantiating the theorems to different logics. This will be future work.
2 Abstract Assumptions
Roughly, the incompleteness theorems are considered to hold for logical theories that (1) contain enough arithmetic and (2) are “effective” in that they themselves can be arithmetized. Our goal is to give a general expression of these favorable conditions. To this end, we identify some logic and arithmetic substrata consisting of structure and axioms that express the containment of (various degrees of) arithmetic more abstractly and flexibly than relative interpretations [41]. We also identify abstract notions of encodings and representability that have just what it takes for a working arithmetization.
2.1 The Logical Substratum
We start with some unspecified sets of variables (\(\mathsf {{Var}}\), ranged over by x, y, z), terms (\({{\mathsf {Term}}}\), ranged over by s, t) and formulas (\({{\mathsf {Fmla}}}\), ranged over by \(\varphi ,\psi ,\chi \)). We assume that variables are particular terms, \(\mathsf {{Var}}\subseteq {{\mathsf {Term}}}\), and that \(\mathsf {{Var}}\) is infinite. Free-variables and substitution operators, \({{\mathsf {FVars}}}\) and \(\_\,[\_/\_]\), are assumed for both terms and formulas. We think of \({{\mathsf {FVars}}}(t)\) as the (finite) set of free variables of the term t, and similarly for formulas. We call sentence any formula with no free variable, and let \({{\mathsf {Sen}}}\) denote the set of sentences. We think of \(s\,[t/x]\) as the term obtained from s by the (capture-avoiding) substitution of t for the free occurrences of variable x; we think of \(\varphi \,[t/x]\) as the formula obtained from \(\varphi \) by the substitution of t for the free occurrences of variable x.
In FOL, terms introduce no bindings, so any occurring variable is free. FOL terms fall under our framework, and so do terms with bindings as in \(\lambda \)-calculi and higher-order logic (HOL). To achieve this degree of inclusiveness while also being able to prove interesting results, we work under some well-behavedness assumptions about the free-variables and substitution operators. For example, free-variables distribute over substitution, \({{\mathsf {FVars}}}\,(\varphi \,[s/x]) = {{\mathsf {FVars}}}(\varphi ) - \{x\} \,\cup \, {{\mathsf {FVars}}}(s)\) if \(x \in {{\mathsf {FVars}}}(\varphi )\), and substitution is compositional, \(\varphi \,[s_1/x_1]\,[s_2/x_2] = \varphi \,[s_2/x_2]\,[(s_1\,[s_2/x_2]) \,/\, x_1]\) if \(x_1 \not = x_2\) and \(x_1 \notin {{\mathsf {FVars}}}(s_2)\). Our extended report [30] contains the full list of our generic syntax axioms.
The incompleteness theorems rely heavily on simultaneous substitution, written \(\varphi \,[t_1/x_{1},\ldots , t_{n}/x_{n}]\), whose properties are tricky to formalize—for example, Paulson’s formalization paper dedicates them ample space [27, 6.2]. To address this problem once and for all generically, we define simultaneous substitution from the single-point substitution, \(\varphi \,[t/x]\), and infer its properties from the single-point substitution axioms. For example, we prove that  . The technicalities are delicate: To avoid undesired variable replacements, \(\varphi \,[s_1/x_1,\ldots ,s_n/x_n]\) must be defined as \(\varphi \,[y_1/x_1]\ldots [y_n/x_n]\,[s_1/y_1]\ldots [s_n/y_n]\) for some fresh \(y_1,\ldots ,y_n\), the choice of which we must show to be immaterial. This definition’s complexity is reflected in the properties’ proofs. But again, this one-time effort benefits any “customer” logic: In exchange for a well-behaved single-point substitution, it gets back a well-behaved simultaneous substitution.
. The technicalities are delicate: To avoid undesired variable replacements, \(\varphi \,[s_1/x_1,\ldots ,s_n/x_n]\) must be defined as \(\varphi \,[y_1/x_1]\ldots [y_n/x_n]\,[s_1/y_1]\ldots [s_n/y_n]\) for some fresh \(y_1,\ldots ,y_n\), the choice of which we must show to be immaterial. This definition’s complexity is reflected in the properties’ proofs. But again, this one-time effort benefits any “customer” logic: In exchange for a well-behaved single-point substitution, it gets back a well-behaved simultaneous substitution.
We let \(v_1,v_2,\ldots \) be fixed mutually distinct variables. We write \({{\mathsf {Fmla}}}_k\) for the set of formulas whose free variables are precisely \(\{v_1,\ldots ,v_k\}\), and \({{\mathsf {Fmla}}}^\subseteq _k\) for the set of formulas whose variables are among \(\{v_1,\ldots ,v_{k}\}\). Note that \({{\mathsf {Fmla}}}_k \subseteq {{\mathsf {Fmla}}}^\subseteq _k\) and \({{\mathsf {Fmla}}}_0 = {{\mathsf {Fmla}}}^\subseteq _0 = {{\mathsf {Sen}}}\). Given \(\varphi \in {{\mathsf {Fmla}}}^\subseteq _k\), we write \(\varphi \,(t_1,\ldots ,t_n)\) instead of \(\varphi \,[t_1/v_1,\ldots ,t_n/v_n]\).
In addition to free variables and substitution, our theorems will require formulas to be equipped with term equality (\(\equiv \)), Boolean connectives (\(\bot \), \(\top \), \(\rightarrow \), \(\lnot \), \(\wedge \), \(\vee \)), universal and existential quantifiers (\(\forall \), \(\exists \)). In our formalization, we assume a minimal list of the above with respect to intuitionistic logic, and define the rest from this minimal list. They are not assumed to be constructors (syntax builders), but operators on terms and formulas, e.g., \(\equiv \;\,: {{\mathsf {Term}}}\rightarrow {{\mathsf {Term}}}\rightarrow {{\mathsf {Fmla}}}\), \(\bot \in {{\mathsf {Fmla}}}\), \(\forall \,:\, \mathsf {{Var}}\times {{\mathsf {Fmla}}}\rightarrow {{\mathsf {Fmla}}}\). This caters for logics that do not have them as primitives. For example, HOL defines all connectives and quantifiers from \(\lambda \)-abstraction and either equality or implication.
We fix a unary relation \(\vdash \; \subseteq {{\mathsf {Fmla}}}\) on formulas, called provability. We write \(\vdash \varphi \) instead of \(\varphi \in \; \vdash \), and say the formula \(\varphi \) is provable. Whenever certain formula connectives or quantifiers are assumed present, we will assume that \(\vdash \) behaves intuitionistically w.r.t. them—namely, we assume the usual (Hilbert-style) intuitionistic FOL axioms with respect to the abstract connectives and quantifiers. Stronger systems, such as those of classical logic, also satisfy these assumptions.
Consistency, denoted Con, is defined as the impossibility to prove false, namely \(\not \vdash \bot \). Another central concept is \(\omega \)-consistency—we carefully choose a formulation that works intuitionistically, with conclusion reminiscent of Gödel’s negative translation [8]:
-
OCon: For all \(\varphi \in {{\mathsf {Fmla}}}_1^{\subseteq }\), if \(\vdash \lnot \;\varphi (n)\) for all \(n\in {{\mathsf {Num}}}\) then
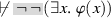 .
.
Assuming classic deduction in \(\vdash \), this is equivalent to the standard formulation: For all \(\varphi \in {{\mathsf {Fmla}}}_1^{\subseteq }\), it is not the case that \(\vdash \varphi (n)\) for all \(n\in {{\mathsf {Num}}}\) and \(\vdash \lnot \;(\forall x.\;\varphi (x))\).
Occasionally, we will consider not only provability but also explicit proofs. We fix a set \({{\mathsf {Proof}}}\) of (entities we call) proofs, ranged over by p, q, and a binary relation between proofs p and sentences \(\varphi \), written \(p {\,\mathrel {\Vdash }\,}\varphi \) and read “p is a proof of \(\varphi \).” We assume \(\vdash \) and \({\,\mathrel {\Vdash }\,}\) to be related as expected, in that provability is the same as the existence of a proof:
-
 For all \(\varphi \in {{\mathsf {Sen}}}\), \(\vdash \varphi \) iff there exists \(p\in {{\mathsf {Proof}}}\) such that \(p {\,\mathrel {\Vdash }\,}\varphi \).
For all \(\varphi \in {{\mathsf {Sen}}}\), \(\vdash \varphi \) iff there exists \(p\in {{\mathsf {Proof}}}\) such that \(p {\,\mathrel {\Vdash }\,}\varphi \).
2.2 The Arithmetic Substratum
We extend the generic syntax assumptions with a subset \({{\mathsf {Num}}}\subseteq {{\mathsf {Term}}}\), of numerals, ranged over by m, n, which are assumed to be closed, i.e., have no free variables.
Convention 1
In all the shown results we implicitly assume: (1) the generic syntax (free variable and substitution) axioms, (2) at least \(\rightarrow \) and \(\bot \) plus whatever connectives and quantifiers appear in the statement, (3) closedness of \(\vdash \) under intuitionistic deduction rules, and (4) the existence of numerals. Other assumptions (e.g., order-like relation axioms, consistency, standard models, etc.) will be indicated explicitly.
On one occasion, we will assume an order-like binary relation modeled by a formula \(\prec \; \in {{\mathsf {Fmla}}}_2\). We write \(t_1 \prec t_2\) instead of \(\prec (t_1,t_2)\) and \(\forall x \prec n.\,\varphi \) instead of \(\forall x.\, x \prec n \rightarrow \varphi \). It turns out that at our level of abstraction it does not matter whether \(\prec \) is a strict or a non-strict order. Indeed, we only require the following two properties, where \(x \in M\) denotes \(\bigvee _{m \in M} x \equiv m\) and \(\bigvee \) expresses the disjunction of a finite set of formulas:
-
\(\textsf {Ord}_{1}\): For all \(\varphi \in {{\mathsf {Fmla}}}_1\) and \(n\in {{\mathsf {Num}}}\), if \(\vdash \varphi (m)\) for all \(m \in {{\mathsf {Num}}}\), then \(\vdash \forall x \prec n.\, \varphi (x)\).
-
\(\textsf {Ord}_{2}\): For all \(n\in {{\mathsf {Num}}}\), there exists a finite set \(M \subseteq {{\mathsf {Num}}}\) such that \(\vdash \forall x.\,x \in M \vee n \prec x\).
\(\textsf {Ord}_{1}\) states that if a property \(\varphi \) is provable for all numerals, then its universal quantification bounded by any given numeral n is also provable. Having in mind the arithmetic interpretation of numerals, it would also make sense to assume a stronger version of \(\textsf {Ord}_{1}\), replacing “if \(\vdash \varphi (m)\) for all \(m \in {{\mathsf {Num}}}\)” by the weaker hypothesis “if \(\vdash \varphi (m)\) for all \(m \in {{\mathsf {Num}}}\) such that \(\vdash m \prec n\)”. But this stronger version will not be needed.
\(\textsf {Ord}_{2}\) states that, for any numeral n, any element x in the domain of discourse is either greater than n or equal to one of a finite set M of numerals. If we instantiate our syntax to that of first-order arithmetic, then the natural number model satisfies \(\textsf {Ord}_{1}\) and \(\textsf {Ord}_{2}\) when interpreting \(\prec \) as either < or \(\le \). Moreover, these properties are provable in intuitionistic Robinson arithmetic, again for both < and \(\le \).
2.3 Encodings and Representability
Central in the incompleteness theorems are functions that encode formulas and proofs as numerals, \(\langle \_\rangle : {{\mathsf {Fmla}}}\rightarrow {{\mathsf {Num}}}\) and \(\langle \_\rangle : {{\mathsf {Proof}}}\rightarrow {{\mathsf {Num}}}\). For our abstract results, the encodings are not required to be injective or surjective.
Let \(A_1,\ldots ,A_m\) be sets, and let, for each of them, \(\langle \_\rangle : A_i \rightarrow {{\mathsf {Num}}}\) be an “encoding” function to numerals. Then, an m-ary relation \(R \subseteq A_1 \times \ldots \times A_m\) is said to be represented by a formula  if the following hold for all \((a_1,\ldots ,a_m) \in A_1 \times \ldots \times A_m\):
if the following hold for all \((a_1,\ldots ,a_m) \in A_1 \times \ldots \times A_m\):
-
\((a_1,\ldots ,a_m) \in R\) implies

-
\((a_1,\ldots ,a_m) \notin R\) implies

Let A be another set with \(\langle \_\rangle : A \rightarrow {{\mathsf {Num}}}\). An m-ary function \(f : A_1 \times \ldots A_{m} \rightarrow A\) is said to be represented by a formula  if for all \((a_1,\ldots ,a_{m}) \in A_1 \times \ldots \times A_{m}\):
if for all \((a_1,\ldots ,a_{m}) \in A_1 \times \ldots \times A_{m}\):
The notion of a function being represented is stronger than that of its graph being represented (as a relation)—but with enough deductive power they are equivalent [38, §16]. We will need an even stronger notion: A function f as above is term-represented by an operator  if
if  for all \((a_1,\ldots ,a_{m}) \in A_1 \times \ldots \times A_{m}\). When the formula by which a relation/function P is represented or term-represented is irrelevant, we call P representable or term-representable.
for all \((a_1,\ldots ,a_{m}) \in A_1 \times \ldots \times A_{m}\). When the formula by which a relation/function P is represented or term-represented is irrelevant, we call P representable or term-representable.
We will also need an enhancement of relation representability: Given \(i < m\), we call the representation of an m-ary relation R by  i -clean if
i -clean if  for all numbers \(n_1,\ldots ,n_m\) such that \(n_i\) (the i’th number among them) is outside the image of \(\langle \_\rangle \) (i.e., there is no \(a\in A_i\) with \(n_i = \langle a\rangle \)). Cleanness would be trivially satisfied if the encodings were surjective. However, surjectivity is not a reasonable assumption. For example, most of the numeric encodings used in the literature are injective but not surjective.
for all numbers \(n_1,\ldots ,n_m\) such that \(n_i\) (the i’th number among them) is outside the image of \(\langle \_\rangle \) (i.e., there is no \(a\in A_i\) with \(n_i = \langle a\rangle \)). Cleanness would be trivially satisfied if the encodings were surjective. However, surjectivity is not a reasonable assumption. For example, most of the numeric encodings used in the literature are injective but not surjective.
We let \({{\mathsf {S}}}: {{\mathsf {Fmla}}}_1 \rightarrow {{\mathsf {Sen}}}\) be the self-substitution function, which sends any \(\varphi \in {{\mathsf {Fmla}}}_1\) to \(\varphi (\langle \varphi \rangle )\), i.e., to the sentence obtained from \(\varphi \) by substituting the encoding of \(\varphi \) for the unique variable of \(\varphi \). An alternative is the following “soft” version of \({{\mathsf {S}}}\), which sends any \(\varphi \in {{\mathsf {Fmla}}}_1\) to \(\exists v_1.\;v_1 \equiv \langle \varphi \rangle \wedge \varphi \), where \(v_1\) is the single free variable of \(\varphi \). The soft version yields provably equivalent formulas and has the advantage that it is easier to represent inside the logic, since it does not require formalizing the complexities of capture-avoiding substitution. All our results involving \({{\mathsf {S}}}\) have been proved for both versions.
We will consider the properties \(\textsf {Repr}_\lnot \), \(\textsf {Repr}_{{\mathsf {S}}}\), and \(\textsf {Repr}_{\Vdash }\), stating the representability of the functions \(\lnot \) and \({{\mathsf {S}}}\), and of the relation \({\,\mathrel {\Vdash }\,}\!\). In addition, \(\textsf {Clean}_{\Vdash }\) will state that the considered representation of \({\,\mathrel {\Vdash }\,}\!\) is 1-clean, i.e., it is clean on the proof component. For the representing formulas for the above relations and functions we will use their circled names,  ,
,  , etc.; for example, \(\textsf {Repr}_{\Vdash }\) means that (1) \(p {\,\mathrel {\Vdash }\,}\varphi \) implies
, etc.; for example, \(\textsf {Repr}_{\Vdash }\) means that (1) \(p {\,\mathrel {\Vdash }\,}\varphi \) implies  and (2) \(p \,{\not \Vdash }\,\varphi \) implies
and (2) \(p \,{\not \Vdash }\,\varphi \) implies  for all \(p\in {{\mathsf {Proof}}}\) and \(\varphi \in {{\mathsf {Sen}}}\).
for all \(p\in {{\mathsf {Proof}}}\) and \(\varphi \in {{\mathsf {Sen}}}\).
2.4 Derivability Conditions
Most of our assumptions refer to representability. An important exception is the provability relation \(\vdash \), for which only a weakening of representability is reasonable. Let  be the formula for this task. We consider the following assumptions about
be the formula for this task. We consider the following assumptions about  , known as the Hilbert-Bernays-Löb derivability conditions:
, known as the Hilbert-Bernays-Löb derivability conditions:
-
\(\textsf {HBL}_{1}\): \(\vdash \varphi \) implies
 for all \(\varphi \in {{\mathsf {Sen}}}\).
for all \(\varphi \in {{\mathsf {Sen}}}\). -
\(\textsf {HBL}_{2}\):
 for all \(\varphi ,\psi \in {{\mathsf {Sen}}}\).
for all \(\varphi ,\psi \in {{\mathsf {Sen}}}\). -
\(\textsf {HBL}_{3}\):
 for all \(\varphi \in {{\mathsf {Sen}}}\).
for all \(\varphi \in {{\mathsf {Sen}}}\).
Above and elsewhere, to lighten notation we omit parentheses when instantiating one-variable formulas with encodings of formulas—e.g., writing  instead of
instead of  .
.
\(\textsf {HBL}_{1}\) states that, if a sentence is provable, then its encoding is also provable inside the representation. \(\textsf {HBL}_{3}\) is roughly a formulation of \(\textsf {HBL}_{1}\) “one level up,” inside the proof system \(\vdash \). Finally, note that the provability relation is closed under modus ponens, in that \(\vdash \varphi \) and \(\vdash \varphi \rightarrow \psi \) implies \(\vdash \psi \) for all \(\varphi ,\psi \in {{\mathsf {Sen}}}\). Thus, \(\textsf {HBL}_{2}\) roughly states the same property inside the proof system. In short, the derivability conditions state that the representation of provability acts partly similarly to the provability relation. Note that the representability of “proof of” implies \(\textsf {HBL}_{1}\), taking  to be
to be  .
.
Convention 2
We focus on the standard provability representation in this paper: Whenever we assume explicit proofs and representability of “proof of,” the formula  will be defined from
will be defined from  as shown above.
as shown above.
We will also be interested in the following variations of the derivability conditions:
-
\(\textsf {HBL}_{4}\):
 for all \(\varphi ,\psi \in {{\mathsf {Sen}}}\).
for all \(\varphi ,\psi \in {{\mathsf {Sen}}}\). -
\(\textsf {HBL}^{\Leftarrow }_{1}\):
 implies \(\vdash \varphi \) for all \(\varphi \in {{\mathsf {Sen}}}\).
implies \(\vdash \varphi \) for all \(\varphi \in {{\mathsf {Sen}}}\). -
\(\textsf {SHBL}_{3}\):
 for all closed terms t.
for all closed terms t. -
\(\textsf {WHBL}_2\): \(\vdash \varphi \rightarrow \psi \) implies
 for all \(\varphi ,\psi \in {{\mathsf {Sen}}}\).
for all \(\varphi ,\psi \in {{\mathsf {Sen}}}\).
\(\textsf {HBL}_{4}\) has a similar flavor as \(\textsf {HBL}_{2}\), but refers to conjunction: It states that the conjunction introduction rule holds inside the proof system. \(\textsf {HBL}^{\Leftarrow }_{1}\) is the converse of \(\textsf {HBL}_{1}\). Finally, \(\textsf {SHBL}_{3}\) is a strengthening of \(\textsf {HBL}_{3}\) holding for all closed terms and not only those that encode sentences, and (if we assume \(\textsf {HBL}_{1}\)) \(\textsf {WHBL}_2\) is a weakening of \(\textsf {HBL}_{2}\).
2.5 Standard Models
We fix a unary relation \(\models \; \subseteq {{\mathsf {Sen}}}\), representing truth of a sentence in the standard model. We write \(\models \varphi \) instead of \(\varphi \in \;\models \), and read it as “\(\varphi \) is true.” We consider the assumptions:
-
\(\textsf {Syn}_{\models }\): Syntactic entities (logical connectives and quantifiers) handle truth as expected:
-
(1)
\(\not \models \bot \); (2) for all \(\varphi ,\psi \in {{\mathsf {Sen}}}\), \(\models \varphi \) and \(\models \varphi \rightarrow \psi \) imply \(\models \psi \);
-
(3)
for all \(\varphi \in {{\mathsf {Fmla}}}_1\), if \(\models \varphi (n)\) for all \(n\in {{\mathsf {Num}}}\) then \(\models \forall x.\,\varphi (x)\);
-
(4)
for all \(\varphi \in {{\mathsf {Fmla}}}_1\), if \(\models \exists x.\,\varphi (x)\) then \(\models \varphi (n)\) for some \(n\in {{\mathsf {Num}}}\);
-
(5)
for all \(\varphi \in {{\mathsf {Sen}}}\), \(\models \varphi \) or \(\models \lnot \,\varphi \).
-
(1)
-
Soundness (of provability with respect to truth): \(\vdash \varphi \) implies \(\models \varphi \) for all \(\varphi \in {{\mathsf {Sen}}}\).
\(\textsf {Syn}_{\models }\)(1–4) only contains a partial description of the syntactic entities’ behavior—corresponding to elimination rules for \(\bot \), \(\rightarrow \) and \(\exists \) and introduction rule for \(\forall \). For our results this suffices. \(\textsf {Syn}_{\models }\)(5) states that standard models decide every sentence.
On his way to formalizing \(\mathcal {IT}_{2}\) for extensions of the HF set theory, after proving \(\textsf {HBL}_{1}\) Paulson notes [27, p. 21]: “The reverse implication [namely \(\textsf {HBL}^{\Leftarrow }_{1}\)], despite its usefulness, is not always proved.” In his abstract account, Buldt also assumes \(\textsf {HBL}^{\Leftarrow }_{1}\) in his most general formulation of \(\mathcal {IT}_{1}\) [5, Theorem 3.1]; that formulation has in mind not necessarily the standard provability representation (our Convention 2), but any formula that weakly represents \(\vdash \), which is acceptable for \(\mathcal {IT}_{1}\) but not for \(\mathcal {IT}_{2}\) [2].
We avoid such an \(\mathcal {IT}_{1}\) versus \(\mathcal {IT}_{2}\) divergence by remaining focused on the standard provability representation. In this case, for arithmetics and related theories, \(\textsf {HBL}^{\Leftarrow }_{1}\) cannot be inferred without assuming soundness in the standard model (which Paulson does), or at least \(\omega \)-consistency. We can depict the situation abstractly, without knowing what standard models look like:
Lemma 3
(1) Assume  , \(\textsf {Repr}_{\Vdash }\), \(\textsf {Clean}_{\Vdash }\) and OCon. Then \(\textsf {HBL}^{\Leftarrow }_{1}\) holds.
, \(\textsf {Repr}_{\Vdash }\), \(\textsf {Clean}_{\Vdash }\) and OCon. Then \(\textsf {HBL}^{\Leftarrow }_{1}\) holds.
(2) Assume Soundness and \(\textsf {Syn}_{\models }\)(1, 2, 3). Then OCon holds.
(3) Assume  , \(\textsf {Repr}_{\Vdash }\), \(\textsf {Clean}_{\Vdash }\), Soundness and \(\textsf {Syn}_{\models }\)(1, 2, 4). Then
, \(\textsf {Repr}_{\Vdash }\), \(\textsf {Clean}_{\Vdash }\), Soundness and \(\textsf {Syn}_{\models }\)(1, 2, 4). Then  implies \(\vdash \varphi \) for all \(\varphi \in {{\mathsf {Sen}}}\). In particular, \(\textsf {HBL}^{\Leftarrow }_{1}\) holds.
implies \(\vdash \varphi \) for all \(\varphi \in {{\mathsf {Sen}}}\). In particular, \(\textsf {HBL}^{\Leftarrow }_{1}\) holds.
Thus, staying in a proof-theoretic world, \(\omega \)-consistency ensures \(\textsf {HBL}^{\Leftarrow }_{1}\) if the “proof of” relation is cleanly represented (1). In turn, \(\omega \)-consistency is ensured by minimal semantic requirements, including the soundness of provability (2). Finally, putting together representability and semantics, we can infer something stronger than \(\textsf {HBL}^{\Leftarrow }_{1}\): That the mere truth (and not just the provability) of a sentence’s provability representation implies the provability of the sentence itself (3).
It follows from either points (1, 2) or point (3) of the lemma that, in the presence of standard models and soundness, clean representability of the “proof of” relation implies \(\textsf {HBL}^{\Leftarrow }_{1}\); and recall that it also implies \(\textsf {HBL}_{1}\). So it implies an “iff” version of \(\textsf {HBL}_{1}\): \(\vdash \varphi \) if an only if  . Interestingly, a converse of this implication also holds. To state it, we initially assume there is no “outer” notion of proof (i.e., no set \({{\mathsf {Proof}}}\) and no relation \({\,\mathrel {\Vdash }\,}\!\)), but only an “inner” one, given by a formula \({{\mathsf {P}}}\in {{\mathsf {Fmla}}}_2\) such that:
. Interestingly, a converse of this implication also holds. To state it, we initially assume there is no “outer” notion of proof (i.e., no set \({{\mathsf {Proof}}}\) and no relation \({\,\mathrel {\Vdash }\,}\!\)), but only an “inner” one, given by a formula \({{\mathsf {P}}}\in {{\mathsf {Fmla}}}_2\) such that:
-
 .
. -
\(\textsf {Compl}_{{{\mathsf {P}}}}\): \(\models {{\mathsf {P}}}(n,\langle \varphi \rangle )\) implies \(\vdash {{\mathsf {P}}}(n,\langle \varphi \rangle )\) for all \(n \in {{\mathsf {Num}}}\) and \(\varphi \in {{\mathsf {Sen}}}\).
-
\(\textsf {Compl}_{\lnot {{\mathsf {P}}}}\): \(\models \lnot \,{{\mathsf {P}}}(n,\langle \varphi \rangle )\) implies \(\vdash \lnot \,{{\mathsf {P}}}(n,\langle \varphi \rangle )\) for all \(n \in {{\mathsf {Num}}}\) and \(\varphi \in {{\mathsf {Sen}}}\).
 is the inner version of
is the inner version of  It expresses that, inside the representation, proofs and provability are connected as expected. \(\textsf {Compl}_{{{\mathsf {P}}}}\) and \(\textsf {Compl}_{\lnot {{\mathsf {P}}}}\) state that provability is complete on \({{\mathsf {P}}}\) statements about formula encodings, as well as their negations; in traditional settings, this is true thanks to \({{\mathsf {P}}}\) being a bounded arithmetical formula (\(\varDelta _0\)). Now the converse result states that, thanks to (standard models and) the “iff” version of \(\textsf {HBL}_{1}\), we can define an outer notion of proof that is represented by the inner notion \({{\mathsf {P}}}\):
It expresses that, inside the representation, proofs and provability are connected as expected. \(\textsf {Compl}_{{{\mathsf {P}}}}\) and \(\textsf {Compl}_{\lnot {{\mathsf {P}}}}\) state that provability is complete on \({{\mathsf {P}}}\) statements about formula encodings, as well as their negations; in traditional settings, this is true thanks to \({{\mathsf {P}}}\) being a bounded arithmetical formula (\(\varDelta _0\)). Now the converse result states that, thanks to (standard models and) the “iff” version of \(\textsf {HBL}_{1}\), we can define an outer notion of proof that is represented by the inner notion \({{\mathsf {P}}}\):
Lemma 4
Assume
 , \(\textsf {Compl}_{{{\mathsf {P}}}}\), \(\textsf {Compl}_{\lnot {{\mathsf {P}}}}\), Soundness, \(\textsf {Syn}_{\models }\)(4,5), \(\textsf {HBL}_{1}\) and \(\textsf {HBL}^{\Leftarrow }_{1}\). Take \({{\mathsf {Proof}}}= {{\mathsf {Num}}}\) and define \({\,\mathrel {\Vdash }\,}\!\) by \(n {\,\mathrel {\Vdash }\,}\varphi \) iff \(\vdash {{\mathsf {P}}}\,(n,\langle \varphi \rangle )\). Then
, \(\textsf {Compl}_{{{\mathsf {P}}}}\), \(\textsf {Compl}_{\lnot {{\mathsf {P}}}}\), Soundness, \(\textsf {Syn}_{\models }\)(4,5), \(\textsf {HBL}_{1}\) and \(\textsf {HBL}^{\Leftarrow }_{1}\). Take \({{\mathsf {Proof}}}= {{\mathsf {Num}}}\) and define \({\,\mathrel {\Vdash }\,}\!\) by \(n {\,\mathrel {\Vdash }\,}\varphi \) iff \(\vdash {{\mathsf {P}}}\,(n,\langle \varphi \rangle )\). Then  , \(\textsf {Repr}_{\Vdash }\) and \(\textsf {Clean}_{\Vdash }\) hold, with \({\,\mathrel {\Vdash }\,}\!\) being represented by \({{\mathsf {P}}}\).
, \(\textsf {Repr}_{\Vdash }\) and \(\textsf {Clean}_{\Vdash }\) hold, with \({\,\mathrel {\Vdash }\,}\!\) being represented by \({{\mathsf {P}}}\).
3 Abstract Incompleteness Theorems
After last section’s preparations, we are now ready to discuss different versions of the incompleteness theorems and their major lemmas, based on alternative assumptions.
3.1 Diagonalization
The formula diagonalization technique (due to Gödel and Carnap [7]) yields “self-referential” sentences. All we need for it to work is the representability of substitution.
Proposition 5
Assuming \(\textsf {Repr}_{{\mathsf {S}}}\), for all \(\psi \in {{\mathsf {Fmla}}}_1\) there exists \(\varphi \in {{\mathsf {Fmla}}}_1\) with \(\vdash \varphi \mathrel {\;\leftarrow \rightarrow \;}\psi \langle \varphi \rangle \).
A sentence \(\varphi \in {{\mathsf {Sen}}}\) is called a Gödel sentence if  ; it is called a Rosser sentence if
; it is called a Rosser sentence if  , where we define
, where we define  . The existence of Gödel and Rosser sentences follows immediately from diagonalization.
. The existence of Gödel and Rosser sentences follows immediately from diagonalization.
Proposition 6
Assuming \(\textsf {Repr}_{{\mathsf {S}}}\), there exist Gödel and Rosser sentences.
Thus, any Gödel sentence is provably equivalent to the negation of its own provability; in Gödel’s words [13], it “says about itself that it is not provable.” A Rosser sentence \(\varphi \) asserts its own unprovabilty in a weaker fashion: Rather than saying “Myself, \(\varphi \), am not provable” (i.e., “it is not the case that there exists a proof p of \(\varphi \)”), it says “it is not the case that there exists a proof p of \(\varphi \) such that, for all smaller proofs q, q is not a proof of \(\lnot \,\varphi \).” Here, “smaller” refers to the order the encoding of proofs as numerals imposes.
3.2 The Incompleteness Theorems
\(\mathcal {IT}_{1}\) identifies sentences that are neither provable nor disprovable—which often holds for Gödel and Rosser sentences with the help of a provability relation satisfying \(\textsf {HBL}_{1}\).
Proposition 7
Assume Con and \(\textsf {HBL}_{1}\). Then \(\not \vdash \textsf {G}\) for all Gödel sentences \(\textsf {G}\).
For showing that the Gödel sentences are not disprovable, a standard route is to assume explicit proofs, strengthen the consistency assumption to \(\omega \)-consistency, and strengthen \(\textsf {HBL}_{1}\) to representability of the “proof of” relation.
Proposition 8
Assume OCon,  , \(\textsf {Repr}_{\Vdash }\), \(\textsf {Clean}_{\Vdash }\). Then \(\not \vdash \lnot \,\textsf {G}\) for all Gödel sentences \(\textsf {G}\).
, \(\textsf {Repr}_{\Vdash }\), \(\textsf {Clean}_{\Vdash }\). Then \(\not \vdash \lnot \,\textsf {G}\) for all Gödel sentences \(\textsf {G}\).
Proof
Let \(\textsf {G}\) be a Gödel sentence. We prove \(\not \vdash \lnot \,\textsf {G}\) by contradiction. Assume (1) \(\vdash \lnot \,\textsf {G}\).
-
By consistency (which is implied by OCon), we obtain \(\not \vdash \textsf {G}\).
-
From this and
 , we obtain \(p \,{\not \Vdash }\,\textsf {G}\) for all \(p\in {{\mathsf {Proof}}}\).
, we obtain \(p \,{\not \Vdash }\,\textsf {G}\) for all \(p\in {{\mathsf {Proof}}}\). -
From this, \(\textsf {Repr}_{\Vdash }\) and \(\textsf {Clean}_{\Vdash }\), we obtain
 for all \(n \in {{\mathsf {Num}}}\).
for all \(n \in {{\mathsf {Num}}}\). -
From this and OCon, we obtain
 , i.e.,
, i.e.,  .
. -
Hence, since \(\textsf {G}\) is a Gödel sentence, we obtain \(\not \vdash \lnot \, \textsf {G}\), which contradicts (1).
\(\square \)
While the line of reasoning in the above proof is mostly well-known, it contains two subtle points about which the literature is not explicit (due to the usual focus on classical first-order arithmetic and particular choices of encodings).
First, we must assume the representation of the “proof of” relation to be 1-clean, i.e., clean with respect to the proof component. Indeed, the argument crucially relies on converting the statement “\(p \,{\not \Vdash }\,\textsf {G}\) for all \(p\in {{\mathsf {Proof}}}\)” into “ for all \(n \in {{\mathsf {Num}}}\),” which is only possible for 1-clean encodings. This assumption will be repeatedly needed in later results. By contrast, cleanness is never required with respect to the sentence component of “proof of” or for the provability relation (which only involves sentence encodings). In short, cleanness is only needed for proofs, not for sentences.
for all \(n \in {{\mathsf {Num}}}\),” which is only possible for 1-clean encodings. This assumption will be repeatedly needed in later results. By contrast, cleanness is never required with respect to the sentence component of “proof of” or for the provability relation (which only involves sentence encodings). In short, cleanness is only needed for proofs, not for sentences.
Second, to reach the desired contradiction for our intuitionistic proof system \(\vdash \), from “ for all \(n \in {{\mathsf {Num}}}\)” it is not sufficient to employ standard \(\omega \)-consistency, which would only give us
for all \(n \in {{\mathsf {Num}}}\)” it is not sufficient to employ standard \(\omega \)-consistency, which would only give us  , i.e.,
, i.e.,  ; the last together with
; the last together with  would be insufficient for obtaining \(\not \vdash \lnot \,\textsf {G}\). However, our stronger version of \(\omega \)-consistency, OCon, does the trick. \(\mathcal {IT}_{1}\) now follows by putting together Propositions 6–8:
would be insufficient for obtaining \(\not \vdash \lnot \,\textsf {G}\). However, our stronger version of \(\omega \)-consistency, OCon, does the trick. \(\mathcal {IT}_{1}\) now follows by putting together Propositions 6–8:
Theorem 9
(\(\mathcal {IT}_{1}\)) Assume  ,
,  , \(\textsf {Repr}_{\Vdash }\), \(\textsf {Clean}_{\Vdash }\), and \(\textsf {Repr}_{{\mathsf {S}}}\). Then:
, \(\textsf {Repr}_{\Vdash }\), \(\textsf {Clean}_{\Vdash }\), and \(\textsf {Repr}_{{\mathsf {S}}}\). Then:

Rosser’s contribution to \(\mathcal {IT}_{1}\) was an ingenious trick for weakening the \(\omega \)-consistency assumption into plain consistency—as such, it is usually seen as a strict improvement over Gödel’s version. While this is true for the concrete case of FOL theories extending arithmetic, from an abstract perspective the situation is more nuanced: The improvement is achieved at the cost of asking more from the logic. Our framework makes this trade-off clearly visible. The idea is to use Rosser sentences instead of Gödel sentences to “repair” the \(\omega \)-consistency assumption of Theorem 9 (inherited from Proposition 8):
Theorem 10
(\(\mathcal {IT}_{1}\) à la Rosser) Assume  ,
,  ,
,  ,
,  ,
,  , \(\textsf {Repr}_{\Vdash }\), \(\textsf {Clean}_{\Vdash }\), and \(\textsf {Repr}_{{\mathsf {S}}}\). Then:
, \(\textsf {Repr}_{\Vdash }\), \(\textsf {Clean}_{\Vdash }\), and \(\textsf {Repr}_{{\mathsf {S}}}\). Then:

Highlighted is the assumption trade-off between the two versions: Rosser’s weakening of \(\omega \)-consistency into consistency is paid by additionally assuming representability of negation and an order-like relation satisfying \(\textsf {Ord}_{1}\) and \(\textsf {Ord}_{2}\). Certainly, negation representability is not a big price, since for concrete logics this tends to be a lemma that is anyway needed when proving \(\textsf {HBL}_{1}\). On the other hand, the ordering assumptions seem to be a significant generality gap in favor of Gödel’s version. A clear manifestation of this gap is in our inference of a semantic version of \(\mathcal {IT}_{1}\)—which we obtain from Theorem 9 with the help of Lemmas 3(2) and 4:
Theorem 11
(Semantic \(\mathcal {IT}_{1}\)) Assume  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and \(\textsf {Repr}_{{\mathsf {S}}}\). Then:
, and \(\textsf {Repr}_{{\mathsf {S}}}\). Then:

We have highlighted the assumptions specific to the semantic treatment. They replace OCon,  , \(\textsf {Repr}_{\Vdash }\) and \(\textsf {Clean}_{\Vdash }\) from the proof-theoretic Theorem 9. Also highlighted is the additional fact concluded: that the Gödel sentences are true.
, \(\textsf {Repr}_{\Vdash }\) and \(\textsf {Clean}_{\Vdash }\) from the proof-theoretic Theorem 9. Also highlighted is the additional fact concluded: that the Gödel sentences are true.
We have inferred the semantic version from Gödel’s proof-theoretic version (Theorem 9), and not from Rosser’s variation (Theorem 10). This is because in the semantic version \(\omega \)-consistency comes for free (from Lemma 3(2)). By contrast, for deploying Rosser’s version we would need to explicitly consider the order-like relation with its own hypotheses. This would have led to a strictly less general abstract result (if we ignore the difference in the way Gödel and Rosser sentences are actually defined).
The semantic \(\mathcal {IT}_{1}\) relies on \(\textsf {HBL}^{\Leftarrow }_{1}\). If we commit to classical logic (i.e., assume \(\vdash \lnot \,\lnot \,\varphi \rightarrow \varphi \)), we can more directly show, taking advantage of \(\textsf {HBL}^{\Leftarrow }_{1}\), that the Gödel sentences are not disprovable, which immediately proves \(\mathcal {IT}_{1}\):
Theorem 12
(Classical \(\mathcal {IT}_{1}\)) Assume classical logic, Con, \(\textsf {HBL}_{1}\), \(\textsf {HBL}^{\Leftarrow }_{1}\), \(\textsf {Repr}_{{\mathsf {S}}}\). Then:

Classical logic also offers two alternatives to our semantic Theorem 11 (where the second is strictly more general than the first):
Theorem 13
(Classical Semantic \(\mathcal {IT}_{1}\)) The conclusions of Theorem 11 still hold if we assume classical logic and perform either of the following changes in its assumptions: (1) remove \(\textsf {Compl}_{\lnot {{\mathsf {P}}}}\), or (2) replace
 , \(\textsf {Compl}_{{{\mathsf {P}}}}\) and \(\textsf {Compl}_{\lnot {{\mathsf {P}}}}\) with “
, \(\textsf {Compl}_{{{\mathsf {P}}}}\) and \(\textsf {Compl}_{\lnot {{\mathsf {P}}}}\) with “ implies \(\vdash \varphi \) for all \(\varphi \in {{\mathsf {Sen}}}\).”
implies \(\vdash \varphi \) for all \(\varphi \in {{\mathsf {Sen}}}\).”
Even though \(\mathcal {IT}_{1}\) needs a predicate  that satisfies \(\textsf {HBL}_{1}\) (and sometimes also \(\textsf {HBL}^{\Leftarrow }_{1}\), meaning that it weakly represents provability), its conclusion, the existence of undecided sentences, is meaningful regardless of whether
that satisfies \(\textsf {HBL}_{1}\) (and sometimes also \(\textsf {HBL}^{\Leftarrow }_{1}\), meaning that it weakly represents provability), its conclusion, the existence of undecided sentences, is meaningful regardless of whether  adequately expresses provability. By contrast, the meaning of \(\mathcal {IT}_{2}\)’s conclusion, the theory cannot prove its own consistency, relies on this (non-mathematical) “intensional” assumption [2]. In this case, consistency is adequately expressed by the sentence \(\lnot \,\langle \bot \rangle \). The standard formulation (and proof) of \(\mathcal {IT}_{2}\) uses all three derivability conditions:
adequately expresses provability. By contrast, the meaning of \(\mathcal {IT}_{2}\)’s conclusion, the theory cannot prove its own consistency, relies on this (non-mathematical) “intensional” assumption [2]. In this case, consistency is adequately expressed by the sentence \(\lnot \,\langle \bot \rangle \). The standard formulation (and proof) of \(\mathcal {IT}_{2}\) uses all three derivability conditions:
Theorem 14
(\(\mathcal {IT}_{2}\)) Assume Con, \(\textsf {HBL}_{1}\), \(\textsf {HBL}_{2}\), \(\textsf {HBL}_{3}\) and \(\textsf {Repr}_{{\mathsf {S}}}\). Then  .
.
3.3 Jeroslow’s Approach
Next we study an alternative line of reasoning due to Jeroslow [17], often cited as a simplification of the canonical route to prove \(\mathcal {IT}_{2}\) [33, 38, 39]. To study its features and pitfalls, we need some standard notation used by Jeroslow. A pseudo-term is a formula \(\varphi \in {{\mathsf {Fmla}}}_{m+1}\) expressing a provably functional relation via “exists unique”: \(\vdash \forall x_1,\ldots ,x_m.\, \;\exists ! y.\,\varphi (x_1,\ldots ,x_m,y)\). We only discuss the case \(m=2\); the general case is similar.
Notation 15
Given a pseudo-term \(\varphi \in {{\mathsf {Fmla}}}_2\), we treat it as if it is a one-variable term:
-
for any terms s and t, we write \(t \equiv \varphi (s)\) instead of \(\varphi (s,t)\);
-
for any term s and formula \(\psi \in {{\mathsf {Fmla}}}_1\), we write \(\psi (\varphi (s))\) instead of \(\exists y.\,\varphi (s,y) \wedge \psi (y)\).
This notation smoothly integrates pseudo-terms with terms: If \(\vdash t \equiv \varphi (s)\) and \(\vdash \psi (\varphi (s))\) then \(\vdash \psi (t)\), where \(\psi (t)\) denotes actual substitution of terms in formulas.
Jeroslow relies on an abstract class of m-ary functions, \(\mathcal {F}_m \subseteq {{\mathsf {Num}}}^m \rightarrow {{\mathsf {Num}}}\), for all arities \(m \in \mathbb {N}\), on which he considers the following assumptions:
-
\(\textsf {Repr}_{\mathcal {F}}\): Every \(f\in \mathcal {F}_m\) is represented by some pseudo-term
 under the identity encoding \({{\mathsf {Num}}}\rightarrow {{\mathsf {Num}}}\).
under the identity encoding \({{\mathsf {Num}}}\rightarrow {{\mathsf {Num}}}\). -
CapN: Some \({{\mathsf {N}}}\in \mathcal {F}_1\) correctly captures negation: \({{\mathsf {N}}}\langle \varphi \rangle = \langle \lnot \,\varphi \rangle \) for all \(\varphi \in {{\mathsf {Sen}}}\).
-
CapSS: Some \({{\mathsf {ssap}}}: {{\mathsf {Fmla}}}_1 \rightarrow \mathcal {F}_1\) correctly captures substituted self-application:
 for all \(\psi \in {{\mathsf {Fmla}}}_1\) and \(f \in \mathcal {F}_1\).
for all \(\psi \in {{\mathsf {Fmla}}}_1\) and \(f \in \mathcal {F}_1\).
In CapSS, following Jeroslow we employed Notation 15 taking advantage of the fact that  are pseudo-terms: The highlighted text denotes
are pseudo-terms: The highlighted text denotes  . Moreover, using the same notation, the statement of \(\textsf {Repr}_{\mathcal {F}}\) for some \(f\in \mathcal {F}_1\) and \(n\in {{\mathsf {Num}}}\) would be written as
. Moreover, using the same notation, the statement of \(\textsf {Repr}_{\mathcal {F}}\) for some \(f\in \mathcal {F}_1\) and \(n\in {{\mathsf {Num}}}\) would be written as  . Similarly, combining CapN with the instance of \(\textsf {Repr}_{\mathcal {F}}\), we obtain a fact that can be written as
. Similarly, combining CapN with the instance of \(\textsf {Repr}_{\mathcal {F}}\), we obtain a fact that can be written as  .
.
When our logical theory is a recursive extension of Robinson arithmetic and \({{\mathsf {Num}}}= \mathbb {N}\), \(\mathcal {F}_m\) could be the set of m-ary computable functions. Then every \(f \in \mathcal {F}_m\) would indeed be represented by a formula  . Moreover, assuming a computable and injective encoding of formulas, \(\langle \_\rangle : {{\mathsf {Fmla}}}_1 \rightarrow \mathbb {N}\), we can take \({{\mathsf {N}}}: \mathbb {N}\rightarrow \mathbb {N}\) to be the following computable function: Given input n, it checks if n has the form \(\langle \varphi \rangle \); if so, it returns \(\langle \lnot \;\varphi \rangle \); if not, it returns any value (e.g., 0). And \({{\mathsf {ssap}}}\;\psi \) can be defined similarly, obtaining the desired property for every \(\varphi \in {{\mathsf {Fmla}}}_2\), not necessarily of the form
. Moreover, assuming a computable and injective encoding of formulas, \(\langle \_\rangle : {{\mathsf {Fmla}}}_1 \rightarrow \mathbb {N}\), we can take \({{\mathsf {N}}}: \mathbb {N}\rightarrow \mathbb {N}\) to be the following computable function: Given input n, it checks if n has the form \(\langle \varphi \rangle \); if so, it returns \(\langle \lnot \;\varphi \rangle \); if not, it returns any value (e.g., 0). And \({{\mathsf {ssap}}}\;\psi \) can be defined similarly, obtaining the desired property for every \(\varphi \in {{\mathsf {Fmla}}}_2\), not necessarily of the form  . In short, Jeroslow’s assumptions cover arithmetic (but also potentially many other systems).
. In short, Jeroslow’s assumptions cover arithmetic (but also potentially many other systems).
At the heart of Jeroslow’s approach lies an alternative diagonalization technique, producing term fixpoints, not just formula fixpoints:
Lemma 16
Assume CapSS and \(\textsf {Repr}_{\mathcal {F}}\) and let \(\psi \in {{\mathsf {Fmla}}}_1\). Then there exists a closed pseudo-term t such that \(\vdash t \equiv \langle \psi (t)\rangle \). Moreover, taking \(\varphi = \psi (t)\), we have \(\vdash \varphi \mathrel {\;\leftarrow \rightarrow \;}\psi \langle \varphi \rangle \).
Proof
Let \(f = {{\mathsf {ssap}}}\;\psi \) and  . From CapSS, we obtain \(f \langle \textcircled {{f}}\rangle = \langle \psi (\textcircled {{f}}\langle \textcircled {{f}}\rangle )\rangle \). From this and \(\textsf {Repr}_{\mathcal {F}}\), we obtain
. From CapSS, we obtain \(f \langle \textcircled {{f}}\rangle = \langle \psi (\textcircled {{f}}\langle \textcircled {{f}}\rangle )\rangle \). From this and \(\textsf {Repr}_{\mathcal {F}}\), we obtain  , i.e., \(\vdash t \equiv \langle \psi (t)\rangle \). With the equality rules, we obtain \(\vdash \psi (t) \!\mathrel {\;\leftarrow \rightarrow \;}\! \psi (\langle \psi (t)\rangle ) \), i.e., \(\vdash \varphi \!\mathrel {\;\leftarrow \rightarrow \;}\! \psi \langle \varphi \rangle \). \(\square \)
, i.e., \(\vdash t \equiv \langle \psi (t)\rangle \). With the equality rules, we obtain \(\vdash \psi (t) \!\mathrel {\;\leftarrow \rightarrow \;}\! \psi (\langle \psi (t)\rangle ) \), i.e., \(\vdash \varphi \!\mathrel {\;\leftarrow \rightarrow \;}\! \psi \langle \varphi \rangle \). \(\square \)
This lemma offers us Gödel and Rosser sentences, which can be used like in Sects. 3.1 and 3.2, leading to corresponding variants of \(\mathcal {IT}_{1}\). But Jeroslow’s main innovation affects \(\mathcal {IT}_{2}\): While traditionally \(\mathcal {IT}_{2}\) requires all three derivability conditions, Jeroslow’s version does not make use of the second, \(\textsf {HBL}_{2}\):
Theorem 17
(\(\mathcal {IT}_{2}\) à la Jeroslow) Assume Con, \(\textsf {HBL}_{1}\),  , \(\textsf {Repr}_{\mathcal {F}}\), CapN, CapSS. Then
, \(\textsf {Repr}_{\mathcal {F}}\), CapN, CapSS. Then  , where \(\textsf {jcon}\) denotes
, where \(\textsf {jcon}\) denotes  .
.
Like with Rosser’s trick, we analyze this innovation’s trade-offs from an abstract perspective. A first trade-off is in the employment of a stronger version of the third condition, \(\textsf {SHBL}_{3}\) (extended to affect all closed pseudo-terms via Notation 15). Another is in the way consistency is expressed in the logic. Jeroslow does not conclude  , but something more elaborate, namely \(\not \vdash \textsf {jcon}\). While the formula
, but something more elaborate, namely \(\not \vdash \textsf {jcon}\). While the formula  internalizes the statement \(\not \vdash \bot \), \(\textsf {jcon}\) internalizes the equivalent statement “for all \(\varphi \), it is not the case that \(\vdash \varphi \) and \(\vdash \lnot \,\varphi \).” But are the internalizations themselves equivalent, i.e., is it the case that
internalizes the statement \(\not \vdash \bot \), \(\textsf {jcon}\) internalizes the equivalent statement “for all \(\varphi \), it is not the case that \(\vdash \varphi \) and \(\vdash \lnot \,\varphi \).” But are the internalizations themselves equivalent, i.e., is it the case that  iff \(\vdash \textsf {jcon}\)? This surely holds for many concrete logics, but it is one direction that we can infer logic-independently: Assuming \(\textsf {HBL}_{1}\), \(\textsf {Repr}_{\mathcal {F}}\) and CapN, \(\vdash \textsf {jcon}\) implies
iff \(\vdash \textsf {jcon}\)? This surely holds for many concrete logics, but it is one direction that we can infer logic-independently: Assuming \(\textsf {HBL}_{1}\), \(\textsf {Repr}_{\mathcal {F}}\) and CapN, \(\vdash \textsf {jcon}\) implies  . And it seems we cannot infer the other direction without knowing what
. And it seems we cannot infer the other direction without knowing what  looks like more concretely. Therefore,
looks like more concretely. Therefore,  , the conclusion of the original \(\mathcal {IT}_{2}\), is abstractly stronger than, hence preferable to \(\not \vdash \textsf {jcon}\). In short, Jeroslow somewhat weakens the theorem’s conclusion.
, the conclusion of the original \(\mathcal {IT}_{2}\), is abstractly stronger than, hence preferable to \(\not \vdash \textsf {jcon}\). In short, Jeroslow somewhat weakens the theorem’s conclusion.
Let us now look at (a slight rephrasing of) Jeroslow’s proof:
Proof of Theorem 17. We assume (1) \(\vdash \textsf {jcon}\) and aim to reach a contradiction.
-
Applying Lemma 16 to
 , obtain a closed term t where (2)
, obtain a closed term t where (2)  .
. -
By \(\textsf {SHBL}_{3}\) applied to
 , we obtain
, we obtain  .
. -
From (2) and the equality rules, we obtain
 .
. -
The last two facts give us
 , where \(\varphi \) denotes
, where \(\varphi \) denotes  .
. -
On the other hand, (1) instantiated with \(\langle \varphi \rangle \) gives us
 .
. -
From the last two facts, we obtain (3) \(\vdash \lnot \,\varphi \).
-
With \(\textsf {HBL}_{1}\), we obtain
 and with CapN and \(\textsf {Repr}_{\mathcal {F}}\), we obtain
and with CapN and \(\textsf {Repr}_{\mathcal {F}}\), we obtain  .
. -
From (2) and the equality rules, we obtain
 , i.e.,
, i.e., 
-
From the last two facts, we obtain \(\vdash \varphi \). With (3) this contradicts (1). \(\square \)
A first major observation is that, under the stated assumptions, the above proof is incorrect. It uses an implicit assumption, hidden under Notation 15: When we disambiguate the notation, we see that Lemma 16 gives us a pseudo-term t that does not exactly satisfy (1) \(\vdash t \equiv \langle \psi (t)\rangle \) (which is what the theorem’s proof needs), but something weaker, namely (2) \(\vdash t \equiv \langle \chi \rangle \), where \(\chi \) is  . And although \(\vdash \chi \!\mathrel {\;\leftarrow \rightarrow \;}\! \psi (t)\), we still cannot infer (1) from (2), unless the encodings of provably equivalent formulas are assumed provably equal. But this assumption is unreasonable: Usually formula equivalence is undecidable, so no computable encoding can achieve that. (Incidentally, this problem is also the reason why we need \(\textsf {SHBL}_{3}\) instead of \(\textsf {HBL}_{3}\): In the proof’s application of \(\textsf {SHBL}_{3}\) to obtain
. And although \(\vdash \chi \!\mathrel {\;\leftarrow \rightarrow \;}\! \psi (t)\), we still cannot infer (1) from (2), unless the encodings of provably equivalent formulas are assumed provably equal. But this assumption is unreasonable: Usually formula equivalence is undecidable, so no computable encoding can achieve that. (Incidentally, this problem is also the reason why we need \(\textsf {SHBL}_{3}\) instead of \(\textsf {HBL}_{3}\): In the proof’s application of \(\textsf {SHBL}_{3}\) to obtain  , we cannot work with \(\langle \lnot \,\varphi \rangle \) instead of
, we cannot work with \(\langle \lnot \,\varphi \rangle \) instead of  , even though
, even though  .)
.)
To repair that, we can replace representation by pseudo-terms with actual term-representation. More precisely (also factoring in the observation that Jeroslow’s proof does not need \(\mathcal {F}_n\) for all n, but \(\mathcal {F}_1\) suffices), we change \(\textsf {Repr}_{\mathcal {F}}\) into:
-
\(\textsf {Repr}_{\mathcal {F}}\): Every \(f\in \mathcal {F}_1\) is term-represented, under the identity encoding \({{\mathsf {Num}}}\rightarrow {{\mathsf {Num}}}\), by some
 taken from a set \({{\mathsf {Ops}}}\subseteq ({{\mathsf {Term}}}\rightarrow {{\mathsf {Term}}})\) for which an encoding as numerals \(\langle \_\rangle : {{\mathsf {Ops}}}\rightarrow {{\mathsf {Num}}}\) is given, and such that \({{\mathsf {FVars}}}(g(t)) = {{\mathsf {FVars}}}(t)\) and \((g(t))[s/x]= g(t[s/x])\) for all \(g\in {{\mathsf {Ops}}}\), \(s,t\in {{\mathsf {Term}}}\) and \(x\in \mathsf {{Var}}\).
taken from a set \({{\mathsf {Ops}}}\subseteq ({{\mathsf {Term}}}\rightarrow {{\mathsf {Term}}})\) for which an encoding as numerals \(\langle \_\rangle : {{\mathsf {Ops}}}\rightarrow {{\mathsf {Num}}}\) is given, and such that \({{\mathsf {FVars}}}(g(t)) = {{\mathsf {FVars}}}(t)\) and \((g(t))[s/x]= g(t[s/x])\) for all \(g\in {{\mathsf {Ops}}}\), \(s,t\in {{\mathsf {Term}}}\) and \(x\in \mathsf {{Var}}\).
(In concrete logics, the elements of \({{\mathsf {Ops}}}\) can be constructors or derived operators on terms.) Then CapSS, Lemma 16, and all proofs work with terms rather than pseudo-terms and everything becomes formally correct. In summary, Jeroslow’s approach to \(\mathcal {IT}_{2}\) seems to fail for pseudo-terms representing computable functions, but to require actual terms. This usually means that the logic has built-in Skolem symbols and axioms.
Finally, let us see what it takes to alleviate the second trade-off: from \(\not \vdash \textsf {jcon}\) to the more desirable  . We see that Theorem 17’s proof uses \(\vdash \textsf {jcon}\) not at \(\textsf {jcon}\)’s full generality but only instantiated with formula encodings, which thanks to \(\textsf {Repr}_{\mathcal {F}}\) and CapN would follow from (*)
. We see that Theorem 17’s proof uses \(\vdash \textsf {jcon}\) not at \(\textsf {jcon}\)’s full generality but only instantiated with formula encodings, which thanks to \(\textsf {Repr}_{\mathcal {F}}\) and CapN would follow from (*)  . And it only takes \(\textsf {WHBL}_2\) (a weaker version of \(\textsf {HBL}_{2}\)) and \(\textsf {HBL}_{4}\) to prove
. And it only takes \(\textsf {WHBL}_2\) (a weaker version of \(\textsf {HBL}_{2}\)) and \(\textsf {HBL}_{4}\) to prove  , allowing us to infer (*) from
, allowing us to infer (*) from  ; meaning that the latter could have been used. We obtain:
; meaning that the latter could have been used. We obtain:
Theorem 18
If in the (corrected) Theorem 17 we additionally assume \(\textsf {WHBL}_2\) and \(\textsf {HBL}_{4}\), its conclusion can be upgraded to  .
.
Whether \(\textsf {WHBL}_2\) and \(\textsf {HBL}_{4}\) are a good trade-off for \(\textsf {HBL}_{2}\) will of course depend on the logic’s specificity, in particular, on its primitive rules of inference.
Jeroslow presented his approach for an abstract logical theory over a FOL language, which is not necessarily a FOL theory—so it found a natural fit in our generic framework. To our knowledge, very few subsequent authors present Jeroslow’s approach rigorously, and none at its original level of generality. Smith’s monograph gives a rigorous account for arithmetic [38, §33], silently performing the correction we have shown here, but failing to detect the need for \(\textsf {SHBL}_{3}\) instead of \(\textsf {HBL}_{3}\) (which Jeroslow had noticed). A mechanical prover is of invaluable help with detecting such nuances and pitfalls.
Summary. Using our generic infrastructure (Sect. 2), we have formally proved several abstract incompleteness results. They include four versions of \(\mathcal {IT}_{1}\):
-
Gödel’s original \(\mathcal {IT}_{1}\) (Theorem 9) and an \(\mathcal {IT}_{1}\) based on classical logic (Theorem 12) required the formalization of some well-known arguments without change.
-
Rosser’s \(\mathcal {IT}_{1}\) (Theorem 10) involved the generalization of a well-known argument: distilling two abstract conditions, \(\textsf {Ord}_{1}\) and \(\textsf {Ord}_{2}\).
-
Novel semantic variants of \(\mathcal {IT}_{1}\) (Theorems 11 and 13) were born from abstractly connecting standard models, the “iff” version of \(\textsf {HBL}_{1}\) and proof representability.
They also include two versions of \(\mathcal {IT}_{2}\):
4 Instances of the Abstract Results
We first validate the assumptions about our abstract logic and arithmetic:
Proposition 19
(1) Any FOL theory that extends Robinson arithmetic or the HF set theory satisfies all the axioms in our logical and arithmetical substrata (in Sects. 2.1 and 2.2).
(2) If, in addition, the theory is sound, then, together with its corresponding standard model, it also satisfies all our model-theoretic axioms (in Sect. 2.5).
In particular, point (2) shows that our discussion of standard models applies equally well to \(\mathbb {N}\) and the datatype of HF sets. (In the latter case, \({{\mathsf {Num}}}\) becomes the entire set of closed terms, so that numerals can denote arbitrary HF sets. This shows the versatility of our abstract concept of numeral.) Then we instantiate three of our main theorems:
Theorem 20
(1) Any FOL theory that extends the HF set theory with a finite set of axioms and  satisfies the hypotheses of Theorems 13 and 14. Hence \(\mathcal {IT}_{1}\) (semantic version) and \(\mathcal {IT}_{2}\) hold for it.
satisfies the hypotheses of Theorems 13 and 14. Hence \(\mathcal {IT}_{1}\) (semantic version) and \(\mathcal {IT}_{2}\) hold for it.
(2) Any FOL theory that extends the HF set theory with a finite set of axioms and  satisfies Theorem 14’s hypotheses. Hence \(\mathcal {IT}_{2}\) holds for it.
satisfies Theorem 14’s hypotheses. Hence \(\mathcal {IT}_{2}\) holds for it.
These instances are heavily based on the lemmas proved by Paulson in his formalization of \(\mathcal {IT}_{1}\) and \(\mathcal {IT}_{2}\) [26, 27], who follows and corrects Świerczkowski’s detailed informal account [40]. Point (1) is a restatement of Paulson’s formalized results: theorems Goedel\(\_\)I and Goedel\(\_\)II in [27]. (His theorems also assume consistency, but that is redundant: Consistency follows from his underlying soundness assumption.)
By contrast, point (2) is an upgrade of Paulson’s Goedel\(\_\)II, applicable to any consistent, though possibly unsound theory. This stronger version is in fact \(\mathcal {IT}_{2}\)’s standard form, free from any model-theoretic considerations. Paulson had proved both \(\textsf {HBL}_{1}\) and \(\textsf {HBL}^{\Leftarrow }_{1}\) taking advantage of soundness, so we needed to discard \(\textsf {HBL}^{\Leftarrow }_{1}\) and re-prove \(\textsf {HBL}_{1}\) by replacing any semantic arguments with proofs within the HF calculus. We also removed all invocations of a convenient “truth implies provability for \(\varSigma \)-sentences” lemma, which depended on soundness due to Paulson’s choice of \(\varSigma \)-sentence definition.
This instantiation process has offered important feedback into the abstract results. A formal development such as ours is (largely) immune to reasoning errors, but not to missing out on useful pieces of generality. We experienced this firsthand with our assumptions about substitution. An a priori natural choice was to assume representability of the numeral substitution \({{\mathsf {Sb}}}: {{\mathsf {Fmla}}}_1 \times {{\mathsf {Num}}}\rightarrow {{\mathsf {Sen}}}\) (defined as \({{\mathsf {Sb}}}(\varphi ,n) = \varphi (n)\)), part of which means (1)  . But Paulson had instead proved (2)
. But Paulson had instead proved (2)  . The key difference from (1) is that (2) applies the term encoding function \(\langle \_\rangle : {{\mathsf {Term}}}\rightarrow {{\mathsf {Num}}}\) to numerals as well (as particular terms); and since his \(\langle \_\rangle \) function is injective, it is far from the case that \(\langle n\rangle = n\) for all numerals n. Paulson’s version makes more sense than ours when building the results bottom-up: Representability should not discriminate numerals, but filter them through the encodings like other terms. However, top-down our version also made sense: It yielded the incompleteness theorems under reasonable assumptions, which do hold, by the way, for the HF set theory—even though in a bottom-up development one is unlikely to prove them. We resolved this discrepancy through a common denominator: the representability of self-substitution \({{\mathsf {S}}}: {{\mathsf {Fmla}}}_1 \rightarrow {{\mathsf {Sen}}}\) (Sect. 2.3), which made our results more general.
. The key difference from (1) is that (2) applies the term encoding function \(\langle \_\rangle : {{\mathsf {Term}}}\rightarrow {{\mathsf {Num}}}\) to numerals as well (as particular terms); and since his \(\langle \_\rangle \) function is injective, it is far from the case that \(\langle n\rangle = n\) for all numerals n. Paulson’s version makes more sense than ours when building the results bottom-up: Representability should not discriminate numerals, but filter them through the encodings like other terms. However, top-down our version also made sense: It yielded the incompleteness theorems under reasonable assumptions, which do hold, by the way, for the HF set theory—even though in a bottom-up development one is unlikely to prove them. We resolved this discrepancy through a common denominator: the representability of self-substitution \({{\mathsf {S}}}: {{\mathsf {Fmla}}}_1 \rightarrow {{\mathsf {Sen}}}\) (Sect. 2.3), which made our results more general.
Paulson’s formalization has also inspired our abstract treatment of standard models (Sect. 2.5). Since Paulson proves \(\textsf {HBL}^{\Leftarrow }_{1}\) and uses classical logic, an obvious “port of entry” of his \(\mathcal {IT}_{2}\) into our framework is Theorem 12. But this theorem tells us nothing about the Gödel sentences’ truth. Delving deeper into Paulson’s proof, we noted that he (unconventionally) completely avoids \(\textsf {Repr}_{\Vdash }\), and does not even define \({\,\mathrel {\Vdash }\,}\!\). This raised the question of whether \(\textsf {HBL}^{\Leftarrow }_{1}\) and \(\textsf {Repr}_{\Vdash }\) are somehow interchangeable in the presence of standard models—and we found that they indeed are, under mild assumptions about truth. Incidentally, these assumptions were also sufficient for establishing the Gödel sentences’ truth, leading to our semantic \(\mathcal {IT}_{1}\) (Theorem 11). However, Theorem 11 was not easy to instantiate to Paulson’s \(\mathcal {IT}_{1}\). All its assumptions were easy to prove, except for \(\textsf {Compl}_{\lnot {{\mathsf {P}}}}\). Whereas Paulson proved that his proof-of predicate is a \(\varSigma \)-formula (which implies \(\textsf {Compl}_{{{\mathsf {P}}}}\) by \(\varSigma \)-completeness), he did not prove the same for its negation (which would imply \(\textsf {Compl}_{\lnot {{\mathsf {P}}}}\)). We are confident that this is true (any reasonable proof-of predicate is a \(\varDelta \)-formula), but we leave the laborious formal proof of this fact as future work. Instead, we recovered Paulson’s result as an instance of our Theorem 13.
As future work, we will consider even more general variants of our semantic Theorems 11 and 13, as in Smorynski’s account [39]: by distinguishing between a sound “base” provability relation \(\vdash _0\) and an extension \(\vdash \) only required to be consistent or \(\omega \)-consistent. For example, \(\vdash _0\) could be deduction in HF set theory or a weaker theory and \(\vdash \) deduction in a consistent (not necessarily sound) extension of the HF set theory. This two-layered approach would have also benefited Paulson’s original formalization.
Many other logics and logical theories satisfy our theorems’ assumptions. We do not require the logic to be reducible to a single syntactic category of formulas, \({{\mathsf {Fmla}}}\), a single syntactic judgment, \(\vdash \), etc.; but only that such (well-behaved) formulas, provability relation, etc. are identifiable as part of that logic, e.g., localized to a given type and/or relativised by a given predicate. This allows our framework to capture most variants of higher-order logic and type theory (including the variant underlying Isabelle/HOL itself [21, 22]), and also, we believe, many of the logics surveyed by Buldt [5], including non-classical and fuzzy. But enabling “mass instantiation” that is both formal and painless requires more progress on the agenda we started here: recognizing reusable construction and proof patterns and formalizing them as abstract results.
References
Ammon, K.: An automatic proof of Gödel’s incompleteness theorem. Artif. Intell. 61(2), 291–306 (1993)
Auerbach, D.: Intensionality and the Gödel theorems. Philos. Stud. Int. J. Philos. Anal. Tradit. 48(3), 337–351 (1985)
Blanchette, J.C., Popescu, A., Traytel, D.: Unified classical logic completeness. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) IJCAR 2014. LNCS (LNAI), vol. 8562, pp. 46–60. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08587-6_4
Boolos, G.: The Logic of Provability. Cambridge University Press, Cambridge (1993)
Buldt, B.: The scope of Gödel’s first incompleteness theorem. Log. Univers. 8(3), 499–552 (2014)
Bundy, A., Giunchiglia, F., Villafiorita, A., Walsh, T.: An incompleteness theorem via abstraction. Technical report, Istituto per la Ricerca Scientifica e Tecnologica, Trento (1996)
Carnap, R.: Logische syntax der sprache. Philos. Rev. 44(4), 394–397 (1935)
Davis, M.: The Undecidable: Basic Papers on Undecidable Propositions, Unsolvable Problems, and Computable Functions. Dover Publication, Mineola (1965)
Diaconescu, R.: Institution-Independent Model Theory, 1st edn. Birkhäuser, Basel (2008)
Feferman, S., Dawson Jr., J.W., Kleene, S.C., Moore, G.H., Solovay, R.M., van Heijenoort, J. (eds.): Kurt Gödel: Collected Works. Vol. 1: Publications 1929–1936. Oxford University Press, Oxford (1986)
Fiore, M.P., Plotkin, G.D., Turi, D.: Abstract syntax and variable binding. In: Logic in Computer Science (LICS) 1999, pp. 193–202. IEEE Computer Society (1999)
Gabbay, M.J., Mathijssen, A.: Nominal (universal) algebra: equational logic with names and binding. J. Log. Comput. 19(6), 1455–1508 (2009)
Gödel, K.: Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte für Mathematik und Physik 38(1), 173–198 (1931)
Goguen, J.A., Burstall, R.M.: Institutions: abstract model theory for specification and programming. J. ACM 39(1), 95–146 (1992)
Harrison, J.: HOL light proof of Gödel’s first incompleteness theorem. http://code.google.com/p/hol-light/, directory Arithmetic
Hilbert, D., Bernays, P.: Grundlagen der Mathematik, vol. II. Springer, Heidelberg (1939)
Jeroslow, R.G.: Redundancies in the Hilbert-Bernays derivability conditions for Gödel’s second incompleteness theorem. J. Symb. Log. 38(3), 359–367 (1973)
Kaliszyk, C., Urban, J.: HOL(y)Hammer: online ATP service for HOL light. Math. Comput. Sci. 9(1), 5–22 (2015)
Kikuchi, M., Kurahashi, T.: Generalizations of Gödel’s incompleteness theorems for \(\sum \) n-definable theories of arithmetic. Rew. Symb. Logic 10(4), 603–616 (2017)
Kossak, R.: Mathematical Logic. SGTP, vol. 3. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-97298-5
Kunčar, O., Popescu, A.: A consistent foundation for Isabelle/HOL. In: Urban, C., Zhang, X. (eds.) ITP 2015. LNCS, vol. 9236, pp. 234–252. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22102-1_16
Kunčar, O., Popescu, A.: Comprehending Isabelle/HOL’s consistency. In: Yang, H. (ed.) ESOP 2017. LNCS, vol. 10201, pp. 724–749. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54434-1_27
Löb, M.: Solution of a problem of Leon Henkin. J. Symb. Log. 20(2), 115–118 (1955)
Nipkow, T., Wenzel, M., Paulson, L.C. (eds.): Isabelle/HOL. LNCS, vol. 2283. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9
O’Connor, R.: Essential incompleteness of arithmetic verified by Coq. In: Hurd, J., Melham, T. (eds.) TPHOLs 2005. LNCS, vol. 3603, pp. 245–260. Springer, Heidelberg (2005). https://doi.org/10.1007/11541868_16
Paulson, L.C.: A machine-assisted proof of Gödel’s incompleteness theorems for the theory of hereditarily finite sets. Rew. Symb. Logic 7(3), 484–498 (2014)
Paulson, L.C.: A mechanised proof of Gödel’s incompleteness theorems using Nominal Isabelle. J. Autom. Reason. 55(1), 1–37 (2015)
Paulson, L.C., Blanchette, J.C.: Three years of experience with Sledgehammer, a practical link between automatic and interactive theorem provers. In: The 8th International Workshop on the Implementation of Logics, IWIL 2010, Yogyakarta, Indonesia, 9 October 2011, pp. 1–11 (2010)
Popescu, A., Roşu, G.: Term-generic logic. Theor. Comput. Sci. 577, 1–24 (2015)
Popescu, A., Trayel, D.: A formally verified abstract account of Gödel’s incompleteness theorems (extended report) (2019). https://bitbucket.org/traytel/abstract_incompleteness/downloads/report.pdf
Popescu, A., Traytel, D.: Formalization associated with this paper (2019). https://bitbucket.org/traytel/abstract_incompleteness/
Quaife, A.: Automated proofs of Löb’s theorem and Gödel’s two incompleteness theorems. J. Autom. Reason. 4(2), 219–231 (1988)
Raatikainen, P.: Gödel’s incompleteness theorems. In: The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University (2018)
Schlichtkrull, A., Blanchette, J.C., Traytel, D., Waldmann, U.: Formalizing Bachmair and Ganzinger’s ordered resolution prover. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 89–107. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_7
Shankar, N.: Metamathematics, Machines, and Gödel Proof. Cambridge University Press, Cambridge (1994)
Sieg, W.: Elementary proof theory. Technical report, Institute for Mathematical Studies in the Social Sciences, Stanford (1978)
Sieg, W., Field, C.: Automated search for Gödel’s proofs. Ann. Pure Appl. Logic 133(1–3), 319–338 (2005)
Smith, P.: An Introduction to Gödel’s Incompleteness Theorems. Cambridge University Press, Cambridge (2007)
Smorynski, C.: The incompleteness theorems. In: Barwise, J. (ed.) Handbook of Mathematical Logic, pp. 821–865. North-Holland, Amsterdam (1977)
Świerczkowski, S.: Finite sets and Gödel incompleteness theorems. Diss. Math. 422, 1–58 (2003)
Tarski, A., Mostowski, A., Robinson, R.: Undecidable Theories. Studies in Logic and the Foundations of Mathematics. North-Holland, Amsterdam (1953). 3rd edn. 1971
Acknowledgments
We thank Bernd Buldt for his patient explanations on material in his monograph, and the reviewers for insightful comments and suggestions.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Popescu, A., Traytel, D. (2019). A Formally Verified Abstract Account of Gödel’s Incompleteness Theorems. In: Fontaine, P. (eds) Automated Deduction – CADE 27. CADE 2019. Lecture Notes in Computer Science(), vol 11716. Springer, Cham. https://doi.org/10.1007/978-3-030-29436-6_26
Download citation
DOI: https://doi.org/10.1007/978-3-030-29436-6_26
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29435-9
Online ISBN: 978-3-030-29436-6
eBook Packages: Computer ScienceComputer Science (R0)




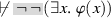 .
. For all
For all 



 for all
for all  for all
for all  for all
for all  for all
for all  implies
implies  for all closed terms t.
for all closed terms t. for all
for all  .
. , we obtain
, we obtain  for all
for all  , i.e.,
, i.e.,  .
. under the identity encoding
under the identity encoding  for all
for all  , obtain a closed term t where (2)
, obtain a closed term t where (2)  .
. , we obtain
, we obtain  .
. .
. , where
, where  .
. .
. and with
and with  .
. , i.e.,
, i.e., 
 taken from a set
taken from a set