Abstract
Several decision procedures for the Bernays-Schoenfinkel (BS) fragment of first-order logic rely on explicit model assumptions. In particular, the procedures differ in their respective model representation formalisms. We introduce a new decision procedure SCL deciding the BS fragment. SCL stands for clause learning from simple models. Simple models are solely built on ground literals. Nevertheless, we show that SCL can learn exactly the clauses other procedures learn with respect to more complex model representation formalisms. Therefore, the overhead of complex model representation formalisms is not always needed. SCL is sound and complete for full first-order logic without equality.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
There has been intensive research into the development of decision procedures for the Bernays-Schoenfinkel (BS) first-order clause fragment without equality [1, 3, 4, 7, 9, 14, 17]. Even classical tableau can be turned into a decision procedure for BS [2]. The procedures follow three different paradigms. They either employ an explicit CDCL-style [12] partial model assumption [1, 3, 4, 14], or they implement an abstraction-refinement approach [9, 17], or merely rely on syntactic restrictions on inferences [7] yielding finite saturations.
The BS fragment is a natural generalization of propositional logic but still enjoys the finite-model property. Furthermore, any finite BS clause set can be transformed into a satisfiability equivalent SAT problem by finite instantiation at the price of a, worst case, exponentially larger clause set. For example, this relationship is used as a reasoning principle in Answer Set Programming (ASP) [8]. The exponential “overhead” is, in the worst case, unavoidable for any decision procedure, because BS satisfiability is NEXPTIME-complete [11, 15]. This means, worst case, that an explicit model representation gets exponentially large, or satisfiability testing with respect to the model representation cannot be done in polynomial time. This justifies and motivates the research for procedures with different model representation formalisms as well as alternative approaches through abstraction or saturation. Actually, the leading systems at recent CASCs [16] have implemented a portfolio containing procedures from all of the aforementioned paradigms.
One contribution of this paper is a CDCL-style calculus deciding the BS fragment and being sound and complete for full first-order logic without equality. The model representation is simple: it consists of a sequence of ground literals. It is therefore properly contained in known model representation formalisms [1, 3, 4, 14]. However, we show that this model representation formalism together with the respective inference rules is sufficient to learn the very same clauses as in NRCL [1]. NRCL has one of the most expressive model representation formalisms. We call the procedure SCL for clause learning from simple models. The most important computations with respect to a model representation are the consistent extension of the current trail and the detection of a propagating literal or a false clause. The currently available procedures can be further divided into procedures where these computations can be done in polynomial time [3, 6] and procedures where such computations are worst case NP-complete [1, 14].Footnote 1 The advantages of the latter two formalisms are exponentially more compact model representations where the model representation language of the NRCL calculus [1] is more general than [3, 6, 14]. One contribution of this paper is that for model-driven clause learning, sophisticated model representations are not needed (Theorem 24). More precisely, we prove that any clause learned by the NRCL calculus can also be learned by our new SCL calculus, where the model representation consists of ground literals only. One of the simplest but also most efficient model representations known with respect to computations. This result holds for full first-order logic without equality. Model representations for BS clause sets with respect to ground literals can become exponentially larger compared to the above-mentioned more sophisticated model representations. The model size is exponential in the maximal arity of a predicate, which we will discuss in detail in Sect. 5. The implication of our result is that SCL can be efficiently used on problems where the ground literal model representation does not become “too large”, further discussed in Sect. 6.
Another contribution in addition to SCL being sound, complete, and a decision procedure for the BS fragment is the fact that it only learns non-redundant clauses with respect to so-called reasonable strategies, see Sect. 3. A clause is redundant with respect to a clause set, if it is implied by smaller clauses, see Sect. 2. Non-redundancy is a powerful property: in the BS context, we prove it NEXPTIME-complete, Theorem 14. Practically, this implies that a clause generated by SCL with a reasonable strategy does not need to be tested for forward redundancy, e.g., forward Subsumption. Saturation-based theorem provers spent a substantial share of their run time on testing forward redundancy.
A third contribution concerning SCL is its ability to simulate resolution, Sect. 4, Theorem 20. Arbitrary resolution steps may generate redundant clauses, hence giving up a reasonable strategy is a prerequisite for the simulation. In this context we also discuss the performance of SCL with respect to proof length, Sect. 4, following [13].
Finally, we investigate a so called weakly-reasonable strategy, where propagations need not to be exhaustive, specifically unit clauses need not to be propagated. Although propagating unit clauses is typically a good strategy for SAT, for the BS fragment this depends already on the actual problem, because one unit clause may cause exponentially many subsequent propagation steps. In summary, the weakly-reasonable strategy generates non-redundant clauses with the exception of unit instances, Theorem 12, and allows for exponentially shorter proofs compared to a reasonable strategy, which exhausts propagation, Example 9. We end the paper with a short summary and discussion of the obtained results, Sect. 6.
2 Preliminaries
We assume a first-order language without equality where N denotes a clause set; C, D denote clauses; L, K, H denote literals; A, B denote atoms; P, Q, R denote predicates; t, s terms; f, g, h function symbols; a, b, c constants; and x, y, z variables. Atoms, literals, clauses and clause sets are considered as usual. The complement of a literal is denoted by the function
 . Semantic entailment \(\models \) is defined as usual where variables in clauses are assumed to be universally quantified. Substitutions \(\sigma , \tau \) are total mappings from variables to terms, where
. Semantic entailment \(\models \) is defined as usual where variables in clauses are assumed to be universally quantified. Substitutions \(\sigma , \tau \) are total mappings from variables to terms, where
 is finite and
is finite and
 . Their application is extended to literals, clauses, and sets of such objects in the usual way. A term, atom, clause, or a set of these objects is ground if it does not contain any variable. A substitution \(\sigma \) is ground if
. Their application is extended to literals, clauses, and sets of such objects in the usual way. A term, atom, clause, or a set of these objects is ground if it does not contain any variable. A substitution \(\sigma \) is ground if
 is ground. A substitution \(\sigma \) is grounding for a term t, literal L, clause C if \(t\sigma \), \(L\sigma \), \(C\sigma \) is ground, respectively. A closure is denoted as \(C\cdot \sigma \) and is a pair of a clause C and a ground substitution \(\sigma \). The function
is ground. A substitution \(\sigma \) is grounding for a term t, literal L, clause C if \(t\sigma \), \(L\sigma \), \(C\sigma \) is ground, respectively. A closure is denoted as \(C\cdot \sigma \) and is a pair of a clause C and a ground substitution \(\sigma \). The function
 computes the set of all ground instances of a literal, clause, or clause set. Note that for BS this set is always finite, whereas for first-order logic it is infinite, in general. The function
computes the set of all ground instances of a literal, clause, or clause set. Note that for BS this set is always finite, whereas for first-order logic it is infinite, in general. The function
 denotes the most general unifier of two terms, atoms, literals. We assume that any
denotes the most general unifier of two terms, atoms, literals. We assume that any
 of two terms or literals does not introduce any fresh variables and is idempotent.
of two terms or literals does not introduce any fresh variables and is idempotent.
In addition, we assume a well-founded, total, strict ordering \(\prec \) on ground literals. This ordering is then lifted to clauses and clause sets by its respective multiset extension. We overload \(\prec \) for literals, clauses, clause sets if the meaning is clear from the context. The ordering is lifted to the non-ground case via instantiation: we define \(C \prec D\) if for all grounding substitutions \(\sigma \) it holds \(C\sigma \prec D\sigma \). We define \(\preceq \) as the reflexive closure of \(\prec \) and \(N^{\preceq C} := \{D \mid D\in N \;\text {and}\; D\preceq C\}\).
Definition 1
(Clause Redundancy). A ground clause C is redundant with respect to a ground clause set N and an order \(\prec \) if \(N^{\preceq C}\,\models \,C\). A clause C is redundant with respect to a clause set N and an order \(\prec \) if for all
 \(C'\) is redundant with respect to
\(C'\) is redundant with respect to
 .
.
3 SCL Rules and Properties
The inference rules of SCL are represented by an abstract rewrite system. They operate on a problem state, a five-tuple \((\varGamma ; N; U; k; u)\) where \(\varGamma \) is a sequence of annotated ground literals, the trail; N and U are the sets of initial and learned clauses; k counts the number of decisions; and u is a status that is either true \(\top \), false \(\bot \), or a closure \(C\cdot \sigma \). Literals in \(\varGamma \) are either annotated with a number, a level; i.e., they have the form \(L^k\) meaning that L is the k-th guessed decision literal, or they are annotated with a closure that propagated the literal to become true. A ground literal L is of level i with respect to a problem state \((\varGamma ; N; U; k; u)\) if L or
 occurs in \(\varGamma \) and the first decision literal left from L (
occurs in \(\varGamma \) and the first decision literal left from L (
 ) in \(\varGamma \), including L, is annotated with i. If there is no such decision literal then its level is zero. A ground clause D is of level i with respect to a problem state \((\varGamma ; N; U; k; u)\) if i is the maximal level of a literal in D; the level of the empty clause \(\bot \) is 0. Recall u is a non-empty closure or \(\top \) or \(\bot \).
) in \(\varGamma \), including L, is annotated with i. If there is no such decision literal then its level is zero. A ground clause D is of level i with respect to a problem state \((\varGamma ; N; U; k; u)\) if i is the maximal level of a literal in D; the level of the empty clause \(\bot \) is 0. Recall u is a non-empty closure or \(\top \) or \(\bot \).
A literal L is undefined in \(\varGamma \) if neither L nor
 occur in \(\varGamma \). The initial state for a first-order clause set N is \((\epsilon , N, \emptyset , 0, \top )\). The rules for conflict search are
occur in \(\varGamma \). The initial state for a first-order clause set N is \((\epsilon , N, \emptyset , 0, \top )\). The rules for conflict search are

These rules construct a (partial) model via the trail \(\varGamma \) for \(N\cup U\) until a conflict, i.e., a false clause with respect to \(\varGamma \) is found. The above rules always terminate with respect to the BS fragment, but not for first-order logic, in general. In the special case of a unit clause L, the rule Propagate actually annotates the literal L with a closure of itself. So the propagated literals on the trail are annotated with the respective propagating clause and the decision literals with the respective level. If a conflict is found, it is resolved by the rules below. Before any Resolve step, we assume that the respective clauses are renamed such that they do not share any variables and that the grounding substitutions of closures are adjusted accordingly.

The clause \(D\vee L\) added by the rule Backtrack to U is called a learned clause. The empty clause \(\bot \) can only be generated by rule Resolve or be already present in N, hence, as usual for CDCL style calculi, the generation of \(\bot \) together with the clauses in \(N\cup U\) represent a resolution refutation. The rules for SCL are applied in a don’t-care style, hence, the calculus offers freedom with respect to factorization. Literals in the conflict clause can, but do not have to be factorized. In particular, the Factorize rule may remove duplicate literals. The rule Resolve does not remove the literal resolved upon from the trail. Actually, Resolve is applied as long as the rightmost propagated trail literal occurs in the conflict clause. This literal is eventually removed by rule Skip from the trail.
For example, consider the clause set \(N = \{ D = Q \vee R(a,y)\vee R(x,b), C = Q\vee S(x,y)\vee P(x)\vee P(y)\vee \lnot R(x,y)\}\) and a problem state:
derived by SCL. The rule Conflict is applicable and yields the conflict state
from which we can either learn the clause
or the clause
depending on whether we first resolve or factorize. Note that \(C_2\) does not subsume \(C_1\). Both clauses are non-redundant. In order to learn \(C_1\) we need to resolve twice with \(R(a,b)^{C\cdot \{x\mapsto a, y\mapsto b\}}\).
The first property we prove about SCL is soundness. We prove it via the notion of a sound state.
Definition 2
(Sound States). A state \((\varGamma ;N;U;k;u)\) is sound if the following conditions hold
-
1.
\(\varGamma \) is a consistent sequence of annotated ground literals,
-
2.
for each decomposition \(\varGamma = \varGamma _1,L\sigma ^{C\vee L\cdot \sigma },\varGamma _2\) we have that \(C\sigma \) is false under \(\varGamma _1\) and \(L\sigma \) is undefined under \(\varGamma _1\), \(C\vee L\in (N \cup U)\),
-
3.
for each decomposition \(\varGamma = \varGamma _1,L^k,\varGamma _2\) we have that L is undefined in \(\varGamma _1\),
-
4.
\(N\,\models \,U\),
-
5.
if \(u=C\cdot \sigma \) then \(C\sigma \) is false under \(\varGamma \) and \(N\,\models \,C\).
Note that an initial state \((\epsilon , N, \emptyset , 0, \top )\) is sound. A rule is sound if it maps sound states to sound states.
Theorem 3
(Soundness of SCL). The rules of SCL are sound, hence SCL starting with an initial state is sound.
Proof
(Idea) By induction on the length of an SCL derivation and a case analysis for the different rules preserving soundness of states. \(\square \)
Next we introduce regular and weakly-regular runs. Regular runs always generate non-redundant clauses, but require exhaustive propagation. Weakly-regular runs do not require exhaustive propagation and almost always generate non-redundant clauses except for instances of unit clauses. However, although exhaustive propagation is typically done in CDCL style SAT, already for the BS fragment it should not always be preferred, because unit clauses can have already exponentially many ground instances.
Definition 4
(Regular States). A state \((\varGamma ;N;U;k;u)\) is regular if and only if the following hold:
-
1.
for every decomposition \(\varGamma = \varGamma _1,L^k,\varGamma _2\) there is no clause in \(N\cup U\) that could propagate from \(\varGamma _1\),
-
2.
for each decomposition \(\varGamma = \varGamma _1,L,\varGamma _2\) where L may be either propagated or decided, there is no clause from
 false under \(\varGamma _1\).
false under \(\varGamma _1\).
Definition 5
(Weakly-Regular States). A state \((\varGamma ;N;U;k;u)\) is weakly-regular if and only if the following hold:
-
1.
for every decomposition \(\varGamma = \varGamma _1,L^k,\varGamma _2\) there is no non-unit clause in \(N\cup U\) that could propagate from \(\varGamma _1\),
-
2.
for each decomposition \(\varGamma = \varGamma _1,L,\varGamma _2\) where L may be either propagated or decided, there is no clause from
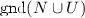 false under \(\varGamma _1\).
false under \(\varGamma _1\).
Some of the below results hold both for regular and weakly-regular states or runs. In this case we write “(weakly-) regular” meaning both cases.
Theorem 6
(Correct Termination). If no rules are applicable to a (weakly-) regular state \((\varGamma ;N;U;k;u)\) then either \(u=\bot \) and N is unsatisfiable or N is satisfiable and \(\varGamma \,\models \,N\).
Proof
For a state \((\varGamma ;N;U;k;u)\) where \(u\not \in \{\top , \bot \}\), one of the rules Resolve, Skip, Factorize or Backtrack is applicable. If the top level literal is a propagated literal then either Resolve or Skip are applicable. If the top level literal is a decision then one of the rules Backtrack or Factorize is applicable. If \(u=\top \) and Propagate, Decide, and Conflict are not applicable it means that there are no undefined ground literals in \(\varGamma \), so \(\varGamma \,\models \,N\). \(\square \)
Definition 7
(Regular Runs). A derivation of regular states is regular or a regular run if the rules Conflict and Propagate are always applied before all other rules in decreasing order of priority.
Definition 8
(Weakly-Regular Runs). A derivation of regular states is weakly-regular or a weakly-regular run if the following conditions hold:
-
1.
Conflict has higher priority than all other rules,
-
2.
if Conflict is not applicable and we can apply Propagate to a non-unit clause then Propagate has higher priority than any other rule,
-
3.
Decide never adds a literal L to the trail if
 is a unit clause in
is a unit clause in
 ,
, -
4.
Resolve has higher priority than Backtrack if the current conflict clause is subsumed in N by a unit clause.
Example 9
(Comparing Proof Length of Regular and Weakly-Regular Runs). Proofs generated by weakly-regular runs can be exponentially shorter than proofs generated by regular runs. Consider the simple BS clause set
A weakly-regular run can ignore generating the \(2^n\) different ground instances of \(R(x_1,\ldots ,x_n,a,b)\) and directly proceed in refuting the propositional part of N in the usual CDCL style by starting with a decision on P or Q. For the example it is obvious that the instances of \(R(x_1,\ldots ,x_n,a,b)\) can be ignored, but in general it is not. This phenomenon already occurs for NP-complete problems: when deciding linear integer arithmetic in a CDCL style, exhaustive propagation is not required by respective calculi for the very same reason [5].
Definition 10
(State Induced Ordering). Let \((L_1, L_2,\ldots ,L_n;N;U;k;u)\) be a sound state of SCL where the annotations of the \(L_i\) are ignored. The trail induces a total well-founded strict order on the defined literals by

We extend \(\prec _\varGamma \) to a strict total order on all literals where all undefined literals are larger than
 . We also extend \(\prec _\varGamma \) to a strict total order on ground clauses by multiset extension and also on multisets of ground clauses and overload \(\prec _\varGamma \) for all these cases. With \(\preceq _\varGamma \) we denote the reflexive closure of \(\prec _\varGamma \).
. We also extend \(\prec _\varGamma \) to a strict total order on ground clauses by multiset extension and also on multisets of ground clauses and overload \(\prec _\varGamma \) for all these cases. With \(\preceq _\varGamma \) we denote the reflexive closure of \(\prec _\varGamma \).
Theorem 11
(Learned Clauses in Regular Runs). Let \((\varGamma ;N;U;k;C_0\cdot \sigma _0)\) be the state resulting from the application of Conflict in a regular run and let C be the clause learned at the end of the conflict resolution, then C is not redundant with respect to \(N\cup U\) and \(\prec _\varGamma \).
Proof
Consider the following fragment of a derivation learning a clause:
By soundness \(N\cup \,\models \,C\) and \(C\sigma \) is false under both \(\varGamma \) and \(\varGamma '\). We prove that \(C\sigma \) is non-redundant.
Assume there is an
 s.t. \(S\,\models \,C\sigma \). There is a clause \(D\in S\) false under \(\varGamma \), \(S \preceq _\varGamma \{C\sigma \}\) and \(C\sigma \not \in S\). All clauses in S have a defined truth value (as all undefined literals are greater than all defined literals) and if \(\varGamma \,\models \,S\) then \(\varGamma \,\models \,C\sigma \), a contradiction.
s.t. \(S\,\models \,C\sigma \). There is a clause \(D\in S\) false under \(\varGamma \), \(S \preceq _\varGamma \{C\sigma \}\) and \(C\sigma \not \in S\). All clauses in S have a defined truth value (as all undefined literals are greater than all defined literals) and if \(\varGamma \,\models \,S\) then \(\varGamma \,\models \,C\sigma \), a contradiction.
We distinguish whether the two trails \(\varGamma \) and \(\varGamma '\) are equal or \(\varGamma '\) is a strict prefix of \(\varGamma \).
If \(\varGamma \ne \varGamma '\) then at least one Skip application was performed during conflict resolution, so \(C\sigma \) does not contain the rightmost literal of \(\varGamma \) and since \(D\prec _{\varGamma }C\sigma \) neither does D. So at a previous point in the derivation there must be a conflict search state such that D was false under the current trail but was not chosen as conflict instance, a contradiction to the exhaustive application of Conflict.
If \(\varGamma =\varGamma '\) we distinguish two sub-cases according to whether the rightmost literal in \(\varGamma \) is the result of a Decision or a Propagation.
If the rightmost literal of \(\varGamma =\varGamma '',L^k\) is a decision literal, then D is either true in \(\varGamma ''\) or has at least two literals undefined or of level k. Since D must be false under \(\varGamma \), D must have two or more occurrences of literals undefined under \(\varGamma \) or of
 . Since \(C\sigma \) has no undefined literal and exactly one occurrence of
. Since \(C\sigma \) has no undefined literal and exactly one occurrence of
 we have a contradiction with \(D\prec _{\varGamma }C\sigma \).
we have a contradiction with \(D\prec _{\varGamma }C\sigma \).
If \(\varGamma =\varGamma '',L^{C'\cdot \delta }\) then at most one literal in \(C\sigma \) is of level k and all other literals, if any, are of level at most \(k-1\). Moreover, D is also either true in \(\varGamma ''\) or has at least two literals undefined under \(\varGamma ''\) or of level k or \(k = 0\). Backtrack requires the presence of at least one decision literal on the trail and so \(k > 0\) so D must have at least two literals of level k. If both of those literal are different from
 then by regularity, we would have applied Conflict instead of Propagate on the trail \(\varGamma ''\). So at least one of the literals of level k in D must be
then by regularity, we would have applied Conflict instead of Propagate on the trail \(\varGamma ''\). So at least one of the literals of level k in D must be
 . Simple case analysis shows that under these conditions \(C\sigma \prec _\varGamma D\), a contradiction. \(\square \)
. Simple case analysis shows that under these conditions \(C\sigma \prec _\varGamma D\), a contradiction. \(\square \)
Theorem 12
(Learned Clauses in Weakly-Regular Runs). Let the state \((\varGamma ;N;U;k;C_0\cdot \sigma _0)\) the result of a Conflict application in a weakly-regular run and let C be the clause learned at the end of the conflict resolution, then C is not redundant w.r.t. \(N\cup U\) and \(\prec _\varGamma \) or C is an instantiation of a unit clause in \(N\cup U\).
Proof
Consider the following fragment of a derivation learning a clause:
By soundness \(N\cup U\,\models \,C\) and \(C\sigma \) is false under both \(\varGamma \) and \(\varGamma '\). We need to prove that there exists a ground instantiation of C that is non-redundant or that C is unit; we assume that C is not a unit and prove by contradiction that \(C\sigma \) is non-redundant.
Assume there is an
 s.t. \(S\,\models \,C\). There is a clause \(D\in S\) false under \(\varGamma \); indeed since \(S \prec _\varGamma \{C\sigma \}\) all clauses in S have a defined truth value and if all clauses in S were to be true under \(\varGamma \) we would also have that \(C\sigma \) would be true under \(\varGamma \) by transitivity of entailment.
s.t. \(S\,\models \,C\). There is a clause \(D\in S\) false under \(\varGamma \); indeed since \(S \prec _\varGamma \{C\sigma \}\) all clauses in S have a defined truth value and if all clauses in S were to be true under \(\varGamma \) we would also have that \(C\sigma \) would be true under \(\varGamma \) by transitivity of entailment.
We distinguish whether the two trails \(\varGamma \) and \(\varGamma '\) are equal or \(\varGamma '\) is a strict prefix of \(\varGamma \).
If \(\varGamma \ne \varGamma '\) then rule Skip was applied at least once during conflict resolution, so \(C\sigma \) does not contain the rightmost literal of \(\varGamma \) and since \(D\prec _{\varGamma }C\sigma \) neither does D. So at a previous point in the derivation there must be a conflict search state such that D was false under the current trail but was not chosen as conflict instance, a contradiction to the exhaustive application of Conflict.
If \(\varGamma =\varGamma '\) we distinguish two sub-cases according to whether the rightmost literal in \(\varGamma \) is the result of a Decision or a Propagation.
If the rightmost literal of \(\varGamma =\varGamma '',L^k\) is a decision literal then D is either true in \(\varGamma ''\), a unit clause, or has at least two literals undefined or of level k. If D is a unit clause then it must be true or undefined in \(\varGamma ''\), and since decisions are restricted to never falsify unit clauses D cannot be false in \(\varGamma ''\). Otherwise, D must have two or more occurrences of literals undefined under \(\varGamma ''\) or of
 . Since \(C\sigma \) has no undefined literal and exactly one occurrence of
. Since \(C\sigma \) has no undefined literal and exactly one occurrence of
 , we have a contradiction with \(D\prec _{\varGamma }C\sigma \).
, we have a contradiction with \(D\prec _{\varGamma }C\sigma \).
If \(\varGamma =\varGamma '',L^{C'\cdot \delta }\) then at most one literal in \(C\sigma \) is of level k and all other literals, if any, are of level at most \(k-1\), moreover D is either true in \(\varGamma ''\), a unit clause, or has at least two literals undefined or of level k. Under these conditions \(D\prec _\varGamma C\sigma \) and \(\varGamma \,\models \,\lnot D\) imply \(D = \lnot L\) and \(C\sigma = C''\vee \lnot L\), but then the next rule cannot be a Backtrack as by weak regularity Resolve would have higher priority. \(\square \)
Proposition 13
All regular runs are weakly-regular runs.
Proof
There are four conditions that a weakly-regular run needs to satisfy. A regular run clearly respects the first two conditions, so we prove that regular runs respect the last two. In a regular run Propagate has always higher priority than Decide, so whenever we could decide a literal L s.t.
 the literal
the literal
 must have already been propagated and so L is not undefined. By Theorem 11 whenever we can apply Backtrack the conflict clause is not redundant in N and so not subsumed in N. \(\square \)
must have already been propagated and so L is not undefined. By Theorem 11 whenever we can apply Backtrack the conflict clause is not redundant in N and so not subsumed in N. \(\square \)
Theorem 14
(BS Non-redundancy is NEXPTIME-Complete). Deciding non-redundancy of a BS clause C with respect to a finite BS clause set \(N^{\preceq C}\) is NEXPTIME-Complete.
Proof
We only show hardness, because containment of the problem in NEXPTIME is obvious. To this end, let \(N = \{C_1,\ldots ,C_n\}\) be an arbitrary, finite BS clause set. We consider an LPO ordering \(\prec _{\text {LPO}}\). Next we add two fresh predicates of arity zero, P, Q with \(P \prec _{\text {LPO}} Q\), where P, Q are larger in the LPO precedence than any other symbol from N. Then obviously N is satisfiable iff the finite BS clause set \(N' = \{P, Q, C_1\vee \lnot Q, C_2\vee \lnot P, C_3, \ldots , C_n\}\) is satisfiable. Furthermore, the clause \(\lnot P\vee \lnot Q\) is \(\prec _{\text {LPO}}\) larger than any clause in \(N'\setminus \{P, Q\}\). The clause \(\lnot P\vee \lnot Q\) is non-redundant with respect to \(N'\setminus \{P, Q\}\) iff \(N'\) is satisfiable. \(\square \)
Theorem 15
(Termination). If N is a clause set and
 is finite then any (weakly-) regular run of SCL terminates.
is finite then any (weakly-) regular run of SCL terminates.
Proof
Any infinite run learns infinitely many clauses. Firstly, for a regular run, by Theorem 11, all learned clauses are non-redundant. The number of different ground clauses and literals is finite. So there is no infinite regular run. Secondly, for weakly-regular runs, the learned clause is either non-redundant, or an instance of a unit clause from N or from the set of learned clauses. However, there are also only finitely many instances of unit clauses from N. So there is no infinite weakly-regular run. \(\square \)
Theorem 16
(SCL Refutational Completeness). If N is unsatisfiable, then there is a (weakly-) regular run of SCL deriving \(\bot \).
Proof
If N is unsatisfiable, then as a consequence of Herbrand’s Theorem there is a finite set of ground instances \(N'\) from N that is unsatisfiable. Now restrict the rules Decide and Propagate to ground literals from \(N'\). By Theorems 15 and 6 any (weakly-) regular run on this restriction derives \(\bot \). \(\square \)
Theorem 17
(SCL decides the BS fragment). SCL restricted to weakly-regular runs decides satisfiability of a BS clause set.
Proof
There are only finitely many ground instances of a BS clause set. Following the proof of Theorem 15, any SCL (weakly-) regular run will terminate on a BS clause set. \(\square \)
4 Simulating Resolution by SCL
It is well-known that resolution inferences may generate redundant clauses. Therefore, by Theorems 11 and 12 (weakly-) regular runs cannot simulate resolution. However, the SCL calculus is still flexible enough to simulate arbitrary resolution inferences that do not result in tautologies by a non-regular strategy.
Lemma 18
(SCL Simulates Resolution). Let N be a clause set, \(C = C'\vee H\) and \(D = D'\vee H'\) be clauses in N such that \(C'\) and \(D'\) are non-empty,
 exists, the literals H and \(H'\) are not duplicated in either C or D and the three clauses \(C\eta \), \(D\eta \) and \((C'\vee D')\eta \) are not tautologies. Then, there is an SCL run starting from the state \((\epsilon ;N;\emptyset ;0;\top )\) where the first learned clause is \((C'\vee D')\eta \).
exists, the literals H and \(H'\) are not duplicated in either C or D and the three clauses \(C\eta \), \(D\eta \) and \((C'\vee D')\eta \) are not tautologies. Then, there is an SCL run starting from the state \((\epsilon ;N;\emptyset ;0;\top )\) where the first learned clause is \((C'\vee D')\eta \).
Proof
Let \(\theta \) be a grounding substitution on the variables of \(C\eta \) and \(D\eta \) such that distinct literals are mapped to distinct ground literals, also let \(\{L_1,\ldots ,L_n\} = (C' \vee D')\eta \theta \).
We can start our derivation with n Decisions where at the i-th step we decide the literal
 to obtain the state \((K_1^1,\ldots ,K_n^n; N;U;n;\top )\),
to obtain the state \((K_1^1,\ldots ,K_n^n; N;U;n;\top )\),
 . This is possible as \((C' \vee D')\) is not a tautology.
. This is possible as \((C' \vee D')\) is not a tautology.
\(H\eta \theta \) is still undefined but every other literal in \(C'\eta \theta \) is falsified under the current trail; so in the next step we can propagate \(H\eta \theta \) on the trail.
Now the rule Conflict is applicable to \((D' \vee H')\eta \theta \) resulting in
We apply Resolve once and we reach the state
From this state we can backtrack to
\(\square \)
Lemma 19
(SCL Simulates Factoring). Let N be a clause set, \(C = C'\vee H\vee H'\) a non-tautological clause with unifiable literals H and \(H'\). There is a run starting from the state \((\epsilon ;N;\emptyset ;0;\top )\) where the first learned clause is \((C'\vee H)\eta \) where
 .
.
Proof
Let \(\{L_1,\dots ,L_k\} = C\eta \) and let \(\rho \) be a grounding of C injective on the literals of \(C\eta \). By applying Decide k times we can reach a state \((K_1^1\rho ,\ldots ,K_k^k\rho ;N;\emptyset ;k;\top )\),
 , from which we can apply rule Conflict to \(C\eta \rho \) resulting in \((K_1^1\rho ,\ldots , K_k^k\rho ;N;\emptyset ;k;C\cdot \eta \rho )\). Now we can factorize H and \(H'\), deriving \(\Rightarrow ^{\text {Factorize}}_{\text {SCL}}(K_1^1\rho ,\ldots ,K_k^k\rho ;N;\emptyset ;k;(C'\vee H)\eta \cdot \rho )\) and, finally, backtrack and learn \((C'\vee H)\eta \). \(\square \)
, from which we can apply rule Conflict to \(C\eta \rho \) resulting in \((K_1^1\rho ,\ldots , K_k^k\rho ;N;\emptyset ;k;C\cdot \eta \rho )\). Now we can factorize H and \(H'\), deriving \(\Rightarrow ^{\text {Factorize}}_{\text {SCL}}(K_1^1\rho ,\ldots ,K_k^k\rho ;N;\emptyset ;k;(C'\vee H)\eta \cdot \rho )\) and, finally, backtrack and learn \((C'\vee H)\eta \). \(\square \)
In order to simulate an overall refutation of the resolution calculus, an additional Restart rule is needed. Note that tautologies can be ignored in refutations by the resolution calculus.

Theorem 20
(SCL Simulates the Resolution Calculus). SCL together with the Restart rule can simulate a resolution refutation by a non-regular strategy.
Proof
By Lemmas 18 and 19. \(\square \)
Consider another example, taken from [13], where exhaustive propagation leads to exponentially longer proofs compared to the shortest resolution proof. Let i be a positive integer and consider the clause set \(N^i\) with one predicate P of arity i consisting of the following clauses, where we write \({\bar{x}}, {\bar{0}}\) and \({\bar{1}}\) to denote sequences of the appropriate length of variables and constants to meet the arity of P:
and i clauses of the form
where the length of \({\bar{1}}\) varies between 0 and \(i-1\). The example encodes an i-bit counter. A regular run of SCL (NRCL) on this clause set would find a conflict after \(O(2^i)\) propagations without any application of Decide. For example, for \(i=4\) we get the clauses of \(N^4\):

For this clause set a regular SCL (NRCL) generates all unit clauses from P(0, 0, 0, 0) to P(1, 1, 1, 1) via \(2^4\) applications of Propagate, then finds a conflict with clause 6 and then uses \(2^4\) times Resolve to end up in \(\bot \).
Instead a short resolution refutation can be obtained by

In general, O(2i) many resolution steps are sufficient to refute \(N^i\). The above resolution proof cannot be simulated by an SCL weakly-regular run. As soon as we decide a ground literal \([\lnot ] P(\ldots )\) propagation using the two literal clauses yields a conflict with either \(\lnot P(1,1,1,1)\) or P(0, 0, 0, 0). The above resolution proof can only be simulated by a non-regular SCL run, Theorem 20. It is an open problem to find a notion of regularity that both guarantees non-redundant clause learning and can simulate resolution proofs of the above type.
5 Simulating NRCL by SCL
In this section we show that even under the restriction of a ground trail, SCL can generate any clause learned by NRCL. In the worst case, the trail generated by SCL may be exponentially longer than the NRCL trail, see Example 25. We use \(\varGamma , \varGamma _1, \varGamma _2\) to denote SCL trails and \(\varGamma ', \varGamma '_1, \varGamma '_2\) to denote NRCL trails.
The ordering \(\prec _{\varGamma '}\) is defined as in [1] and concerning NRCL we exactly stick to the notions from [1]. Nevertheless, the most important notions from NRCL are recalled below.
Definition 21
(Constrained Clauses [1]). A constrained clause \((C\cdot \sigma ;\pi )\) is a pair of a closure \(C\cdot \sigma \) and a constraint \(\pi \) of the form \(\bigwedge _{i=0}^n \vec s_i \ne \vec t_i\) where \(\vec s_i\) and \(\vec t_i\) are tuples of terms of equal length. The set of ground instances of \((C\cdot \sigma ;\pi )\) denoted as
 is
is
 . A constraint \(\pi = \bigwedge _{i=0}^n \vec s_i \ne \vec t_i\) is true if for all \(0\le i\le n\) \(\vec s_i\) and \( \vec t_i\) are not unifiable. A ground clause \(C'\) is covered by a constrained clause \((C\cdot \sigma ;\pi )\) if
. A constraint \(\pi = \bigwedge _{i=0}^n \vec s_i \ne \vec t_i\) is true if for all \(0\le i\le n\) \(\vec s_i\) and \( \vec t_i\) are not unifiable. A ground clause \(C'\) is covered by a constrained clause \((C\cdot \sigma ;\pi )\) if
 . We similarly define constrained literals \((L\cdot \sigma ;\pi )\) and say that a ground literal \(L'\) is defined true by \((L\cdot \sigma ;\pi )\) if it is covered by \((L\cdot \sigma ;\pi )\) and defined false if it covered by
. We similarly define constrained literals \((L\cdot \sigma ;\pi )\) and say that a ground literal \(L'\) is defined true by \((L\cdot \sigma ;\pi )\) if it is covered by \((L\cdot \sigma ;\pi )\) and defined false if it covered by
 .
.
Definition 22
(State induced ordering in NRCL [1]). A ground literal L is defined under a trail \(\varGamma '\) if L or
 is covered by some constrained literals \(L'\) in \(\varGamma '\). Such a literal is necessarily unique and is denoted by
is covered by some constrained literals \(L'\) in \(\varGamma '\). Such a literal is necessarily unique and is denoted by
 . Given two defined ground literals \(L_1,L_2\) we say
. Given two defined ground literals \(L_1,L_2\) we say
 if
if
 .
.
The proof of the simulation is done in two steps. Firstly, we show that we can generate via SCL a suitable ground instance of any NRCL trail, Lemma 23. Then we show that on this basis, we can actually learn exactly the clause NRCL learns, Theorem 24.
Lemma 23
(Simulating the NRCL Trail). Let \((\varGamma ';N;U;k;\top )\) be a regular state in an NRCL run and let \(\prec _0\) be a total order on ground literals compatible with \(\prec _{\varGamma '}\). Then there is an SCL derivation starting from \((\epsilon ;N;U;0;\top )\) which produces a trail \(\varGamma \) such that for any ground literal L, L is true, false, undefined under \(\varGamma \) if and only if it is so under \(\varGamma '\), and for all ground literals
 : \(L_1 \prec _{\varGamma } L_2\) if and only if \(L_1 \prec _{0} L_2\). We call \(\varGamma \) a grounding of \(\varGamma '\).
: \(L_1 \prec _{\varGamma } L_2\) if and only if \(L_1 \prec _{0} L_2\). We call \(\varGamma \) a grounding of \(\varGamma '\).
Proof
By induction on the length of \(\varGamma '\). If \(\varGamma '=\epsilon \) then we choose \(\varGamma =\epsilon \) satisfying the conjecture. If \(\varGamma '=\varGamma '_1,(L;\sigma ;\pi )^k\) then all ground literals
 are undefined in \(\varGamma _1\) so we can simply decide every literal in
are undefined in \(\varGamma _1\) so we can simply decide every literal in
 in increasing order according to \(\prec _{\varGamma '}\) to obtain a trail \(\varGamma _2\) that clearly satisfies the conjecture. If the rightmost literal of \(\varGamma '\) is a propagation then we apply Propagate instead of Decide on the SCL trail. \(\square \)
in increasing order according to \(\prec _{\varGamma '}\) to obtain a trail \(\varGamma _2\) that clearly satisfies the conjecture. If the rightmost literal of \(\varGamma '\) is a propagation then we apply Propagate instead of Decide on the SCL trail. \(\square \)
A consequence of Lemma 23 is that SCL can simulate the derivation of \(\bot \) from a state without decisions. So this needs not to be considered anymore. The most sophisticated rule of NRCL to be considered for the simulation is Backjump, because its side conditions are substantially different from the side conditions of the SCL Backtrack rule.

Theorem 24
(SCL Simulates NRCL). If from an NRCL conflict state we can learn a clause \(C \ne \bot \), then we can learn the same clause C from a grounding of that state by SCL.
Proof
Let \(w'_1 = (\varGamma '_1;N;U;k;(C_1;\sigma _1;\pi _1))\) be an NRCL conflict state from which we learn the clause C. We prove by induction on the length of conflict resolution that there exists an SCL state \(w_1 = (\varGamma _1;N;U;k;C_1\cdot \delta _1)\) obtained by grounding \(w'_1\) from which we can learn C.
As a base case, we prove that if we can apply Backjump to an NRCL state \((\varGamma '_2;N;U;k';(C_2;\sigma _2;\pi _2))\) then we can also apply Backtrack to a grounding \((\varGamma _2;N;U;k;C_2\cdot \delta _2)\). In particular, we choose \(\delta _2 = \sigma _2\rho \) where \(\rho \) is an injective mapping from the variables of \(C_2\) to a set of fresh constants. If we can apply Backjump in NRCL then one of the three cases of the rule applies. We consider them separately. The first case cannot apply as we have assumed a clause different from \(\bot \). The second case implies that we can backtrack to the very same level via SCL. For the third case, we note that in SCL there is no equivalent of the concept of blocking decisions or blocking clauses as they can only arise when a decision defines multiple ground literals. In SCL all literals defined by decisions in a conflict clause have different levels and thus we can always apply Backtrack from any grounding of the conflict clause if the third case of Backjump applies.
For the inductive step, consider a rule application \((\varGamma '_1;N;U;k';(C_1;\sigma _1;\pi _1))\) \(\Rightarrow _{\text {NRCL}}(\varGamma '_2;N;U;k';(C_2;\sigma _2;\pi _2))\) in a conflict resolution. For any grounding \((\varGamma _2;N;U;k;C_2\cdot \delta _2)\) of \((\varGamma '_2;N;U;k';(C_2;\sigma _2;\pi _2))\) we build a grounding \((\varGamma _1;N;U;k;\) \(C_1\cdot \delta _1)\) of \((\varGamma '_1;N;U;k';(C_1;\sigma _1;\pi _1))\) from which we can still learn the clause C. In particular we will need to define \(\varGamma _1\) and \(\delta _1\) in terms of \((\varGamma _2;N;U;k;C_2\cdot \delta _2)\)
Case Resolve: we consider the NRCL rule application
by the conditions of Resolve in NRCL we have
-
1.
there exists \(\eta _0= {\text {mgu}}(\mathrm{comp}(L_0),L_1)\)
-
2.
there exists \(\eta = {\text {mgu}}(\mathrm{comp}(L_0)\sigma _0,L_1\sigma _1)\)
-
3.
\(\eta _0\sigma _2 = \sigma _1\sigma _0\eta \)
-
4.
\(C_2 = (C_1\vee C_0)\eta _0\)
and from the grounding we have \(\delta _i = \sigma _i\delta '_i\) for some \(\delta _i'\), \(i=0,1,2\). It is clear that any grounding substitution \(\delta _2\) on the variables of \((C_1\vee C_0)\eta _0\) can be induced by choosing opportune grounding substitutions \(\delta _0\) and \(\delta _1\). In particular, we can define \(\delta _i\) for \(i=0,1\) as the restriction of \(\eta _0\delta _2\rho \) to the variables of \(C_i\vee L_i\) where \(\rho \) is a grounding on
 . If there is a grounding \(\rho \) such that \(L_0\eta _0\delta _2\rho \) is undefined in \(\varGamma _2\) then we define \(\varGamma _1\) as \(\varGamma _2,L_0\eta _0\delta _2\rho ^{C_0\vee L_0\cdot \eta _0\delta _2\rho }\). If such a substitution \(\rho \) does not exist then the literal \(L_0\rho '^{C_0\vee L_0\cdot \rho '}\) is already defined in \(\varGamma _2\) obtained from grounding the same literal \((L_0;\sigma _0;\pi _0)^{C_0\vee L_0}\); we can then define \(\varGamma _1\) equal to \(\varGamma _2\) and resolve once more with the literal \(L_0\rho '^{C_0\vee L_0\cdot \rho '}\).
. If there is a grounding \(\rho \) such that \(L_0\eta _0\delta _2\rho \) is undefined in \(\varGamma _2\) then we define \(\varGamma _1\) as \(\varGamma _2,L_0\eta _0\delta _2\rho ^{C_0\vee L_0\cdot \eta _0\delta _2\rho }\). If such a substitution \(\rho \) does not exist then the literal \(L_0\rho '^{C_0\vee L_0\cdot \rho '}\) is already defined in \(\varGamma _2\) obtained from grounding the same literal \((L_0;\sigma _0;\pi _0)^{C_0\vee L_0}\); we can then define \(\varGamma _1\) equal to \(\varGamma _2\) and resolve once more with the literal \(L_0\rho '^{C_0\vee L_0\cdot \rho '}\).
Case Factorize: we consider the NRCL rule application
by the conditions on Factorize in NRCL we have
-
1.
there exists \(\eta _0= {\text {mgu}}(L_1,L'_1)\)
-
2.
\(C_2 = C_1\eta _0\) and \(L_2 = L_1\eta _0\)
-
3.
there exists \(\eta = {\text {mgu}}(\mathrm{comp}(L_0)\sigma _0,L_1\sigma _1,L'_1\sigma _1)\)
-
4.
\(\eta _0\sigma _2 = \sigma _1\eta \)
and from the grounding we have \(\delta _i = \sigma _i\delta '_i\). We can define \(\delta _1 = \eta _0\delta _2\) which produces an acceptable grounding of \((C_1\vee L_1\vee L'_1;\sigma _1;\pi _1)\) as \(\eta _0\delta _2=\eta _2\sigma _2\) and so \(\delta _1= \sigma _1\delta '_1\) for \(\delta '_1 = \eta \delta '_2\). We can, moreover, define \(\varGamma _1= \varGamma _2\) as in SCL Factorize is not restricted to the rightmost literal.
Case Skip: we consider the NRCL rule application
We can simply define \((\varGamma _1;N;U;k;C_1\cdot \delta _1)=(\varGamma _2;N;U;k;C_2\cdot \delta _2)\) where Factorize is independent from the trail in SCL and the induction step for Resolve can add any needed literal. \(\square \)
Example 25
(SCL Trails may be Exponentially Longer). Consider an unsatisfiable clause set
NRCL can refute the clause set \(N^n\) at level \(k=0\) in linear time by building through rule Propagate the trail \(\lnot Q_0,Q_n(x_1,\dots ,x_n), Q_{n-1}(x_1,\dots ,x_{n-1}),\ldots ,\) \(Q_1(x_1)\), where we do not show the clauses annotated to the literals, resulting in a conflict with \(\lnot Q_1(1) \vee \lnot Q_1(0) \vee Q_0\). For SCL all ground instances of the \(Q_i(x_1,\ldots ,x_i)\) have to be enumerated and there are \(2^i\) many such ground instances for each \(Q_i\).
Another relevant aspect is whether the SCL run constructed in Theorem 24 is (weakly-) regular. The example below shows it is not, in general, however at least for the example below, it is the case that SCL can actually learn a more general clause by a regular run.
Example 26
(Simulating SCL Runs are not (Weakly-) Regular). Consider the clauses

In NRCL we can decide the literal \(\lnot Q(x)\), propagate \(\lnot P(x)\) and result in a conflict with \(P(x)\vee P(a)\vee P(b)\vee P(c)\). After factorization and resolution with \(Q(x)\vee \lnot P(x)\), NRCL learns the clause \(Q(a)\vee Q(b)\vee Q(c)\). This clause cannot be learned with a (weakly-) regular run in SCL. After deciding any ground instance of \(\lnot Q(x)\), immediately all ground literals \(\lnot P(a)\), \(\lnot P(b)\), \(\lnot P(c)\) are propagated through the two literal clauses. Now the conflict does not only rely on the first two clauses but also involves the two literal clauses. After resolution and factoring steps, if SCL started with \(\lnot Q(a)\) it eventually learns the clause Q(a) which makes the NRCL learned clause \(Q(a)\vee Q(b)\vee Q(c)\) redundant.
6 Conclusion
The contributions of this paper are: (i) a sound, complete, SCL calculus for full first-order logic learning non-redundant clauses with respect to regular runs, (ii) weakly-regular runs do not exhaustively propagate unit clauses but still learn non-redundant clauses except for unit instances, (iii) the used notion of non-redundancy is NEXPTIME-complete for the BS fragment, (iv) SCL simulates resolution by non-regular runs, (v) SCL simulates NRCL by non-regular runs, (vi) exhaustive propagation is not always a good strategy for the BS fragment and beyond, and (vii) SCL is a decision procedure for the BS fragment.
The price for the simple SCL models is that trails can be exponentially longer compared to trails of calculi with more expressive model representation languages. For a BS clause set N the overall trail size is bound by \(mr^k\) where k is the maximal arity of a predicate in N, m the number of predicates, and r the number of constant symbols in N. Exploiting the actual recursive structure of N this bound can be further refined for a specific problem [10]. So in a simple preprocessing step, it can be checked whether an SCL trail potentially becomes “too large”. Then a procedure can either start with a more expressive trail language [1, 3, 4, 7, 9, 14, 17] or dynamically decide to switch the trail model representation formalism. In practice, there are many interesting problems where the maximal predicate arity is not larger than three and there are not “too many” constants. Recall that all our examples inducing an exponentially growing trail or an exponentially growing proof length include the encoding of some type of binary counter.
Although SCL with a regular strategy and also all other calculi with exhaustive propagation cannot simulate resolution, the resolution calculus has also drawbacks. Worst case, the resolution calculus may generate more clauses, even in a terminating setting [7], than there are potential ground model assumptions as they are explored by SCL. Still one open question is whether the advantages of resolution and SCL can be combined: learning only non redundant clauses via partial model assumptions and being able to simulate non-redundant resolution inferences, in general. Such a result would unify both paradigms.
Notes
- 1.
For [4] no complexity result has been published so far.
References
Alagi, G., Weidenbach, C.: NRCL - a model building approach to the Bernays-Schönfinkel fragment. In: Lutz, C., Ranise, S. (eds.) FroCoS 2015. LNCS (LNAI), vol. 9322, pp. 69–84. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24246-0_5
Baumgartner, P.: Hyper tableau—the next generation. In: de Swart, H. (ed.) TABLEAUX 1998. LNCS (LNAI), vol. 1397, pp. 60–76. Springer, Heidelberg (1998). https://doi.org/10.1007/3-540-69778-0_14
Baumgartner, P., Fuchs, A., Tinelli, C.: Lemma learning in the model evolution calculus. In: Hermann, M., Voronkov, A. (eds.) LPAR 2006. LNCS (LNAI), vol. 4246, pp. 572–586. Springer, Heidelberg (2006). https://doi.org/10.1007/11916277_39
Bonacina, M.P., Plaisted, D.A.: Semantically-guided goal-sensitive reasoning: model representation. J. Autom. Reason. 56(2), 113–141 (2016)
Bromberger, M., Sturm, T., Weidenbach, C.: Linear integer arithmetic revisited. In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 623–637. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6_42
Fermüller, C.G., Pichler, R.: Model representation over finite and infinite signatures. J. Log. Comput. 17(3), 453–477 (2007)
Hillenbrand, T., Weidenbach, C.: Superposition for bounded domains. In: Bonacina, M.P., Stickel, M.E. (eds.) Automated Reasoning and Mathematics. LNCS (LNAI), vol. 7788, pp. 68–100. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36675-8_4
Kaufmann, B., Leone, N., Perri, S., Schaub, T.: Grounding and solving in answer set programming. AI Mag. 37(3), 25–32 (2016)
Korovin, K.: Inst-Gen – a modular approach to instantiation-based automated reasoning. In: Voronkov, A., Weidenbach, C. (eds.) Programming Logics. LNCS, vol. 7797, pp. 239–270. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37651-1_10
Korovin, K.: Non-cyclic sorts for first-order satisfiability. In: Fontaine, P., Ringeissen, C., Schmidt, R.A. (eds.) FroCoS 2013. LNCS (LNAI), vol. 8152, pp. 214–228. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40885-4_15
Lewis, H.R.: Complexity results for classes of quantificational formulas. J. Comput. Syst. Sci. 21(3), 317–353 (1980)
Nieuwenhuis, R., Oliveras, A., Tinelli, C.: Solving sat and sat modulo theories: from an abstract Davis-Putnam-Logemann-Loveland procedure to DPLL (T). J. ACM 53, 937–977 (2006)
Navarro, J.A., Voronkov, A.: Proof systems for effectively propositional logic. In: Armando, A., Baumgartner, P., Dowek, G. (eds.) IJCAR 2008. LNCS (LNAI), vol. 5195, pp. 426–440. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-71070-7_36
Piskac, R., de Moura, L.M., Bjørner, N.: Deciding effectively propositional logic using DPLL and substitution sets. J. Autom. Reason. 44(4), 401–424 (2010)
Plaisted, D.A.: Complete problems in the first-order predicate calculus. J. Comput. Syst. Sci. 29, 8–35 (1984)
Sutcliffe, G.: The CADE ATP system competition - CASC. AI Mag. 37(2), 99–101 (2016)
Teucke, A., Weidenbach, C.: First-order logic theorem proving and model building via approximation and instantiation. In: Lutz, C., Ranise, S. (eds.) FroCoS 2015. LNCS (LNAI), vol. 9322, pp. 85–100. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24246-0_6
Acknowledgments
This work was funded by DFG grant 389792660 as part of TRR 248.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Fiori, A., Weidenbach, C. (2019). SCL Clause Learning from Simple Models. In: Fontaine, P. (eds) Automated Deduction – CADE 27. CADE 2019. Lecture Notes in Computer Science(), vol 11716. Springer, Cham. https://doi.org/10.1007/978-3-030-29436-6_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-29436-6_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29435-9
Online ISBN: 978-3-030-29436-6
eBook Packages: Computer ScienceComputer Science (R0)





 false under
false under 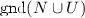 false under
false under  is a unit clause in
is a unit clause in
 ,
,