Keywords

1 Introduction

Modeling and analysis of human walking motion is essential in human health monitoring, medical diagnoses, design of prostheses and orthoses, humanoid robot, and energy supply to wearable devices [1,2,3]. Therefore, lots of efforts have been devoted to model and analysis in human walking. The walking motion requiring interaction among joints of the body, especially the hip and knee in the lower limb [4]. Therefore, the development of an appropriate human lower limb model is highly desired.

Many human lower limb models have been developed these years, such as inverted pendulum model, multiple-mass inverted pendulum model, and multi-segment-rigid body model [5, 6]. In inverted pendulum model, the body mass concentrates at one point (center of gravity), and the massless leg acts as the supporting rod. It’s simple but is unable to generate natural and realistic human motion. Multiple-mass inverted pendulum model is more stable as it considered the dynamic effect of the swing leg [7]. Multi-rigid-body model shares appropriate fidelity which can produce kinematic outputs similar to natural gait [8].

The human lower limb model needs to be described by some equations to represent its moving characteristics. Generally, the equations are obtained by kinematics and dynamics. The Kinematic representations of many open-loop robotic applications are commonly based on the Denavit-Hartenberg (D-H) notion [9]. Qiu used D-H notation to calculate the position of knee and hip when the limb at the stand phase [10]. Roberson-Wittenburg (R-S) algorithm utilize the system graph theory to replace the connection of multi-rigid-body system structure [11].

As for dynamic characters analysis, there are different dynamic modeling methods to calculate the forces and moments of each joint during gait. To solve the dynamic parameters at the joint, Newton-Euler equation is applied to establish the human lower limb dynamic equations [12]. Pejhan et al. applied classical Lagrange dynamic equations to build the model of human lower limb for optimizing an above-knee prosthesis based on the kinematics of gait [13]. As Kane equation is ideally suited for the analysis of multi-body system dynamics, Mu used Kane equation in the impact prediction of human motion [14]. Nasir applied Kane equation to model the motion of human lower limb [15].

Both the kinematic and dynamic modeling methods have been widely used in human lower limb motion. However, the previous studies lack distinct comparison among these methods. This paper aims to find an applicable dynamic modeling method toward human lower limb to describe the moving characteristics during human’s walking.

The rest of this paper is organized as follows. In Sect. 2, human lower limbs are simplified as a plant model which moves in the two-dimensional sagittal plane. In Sect. 3, the kinematic analysis methods are illustrated to establish relationships of human lower limb joints. Dynamic methods are displayed to exhibit the dynamic characteristics of joints. In addition, a comparison among the methods was also made. In Sect. 4, the experimental data of an adult man walking at 5 km/h are analyzed and the comparison between the torques calculated by the Lagrange equation and the simulation results is also discussed. The conclusion is drawn in the final section.

2 Plant Model of Human Lower Limb

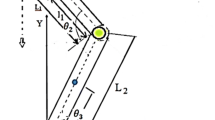
Lower limb motion produce the walking of human. As the three joints of hip, knee and ankle play an important role in human lower limb motion, hip and knee mainly stretch and flex the thigh and shank, which acute the whole body to move. Considering the ankle presents no obvious influence in forward motion as it rotates by a slight angle, rotation of the ankle can be ignored. The swing leg can then be simplified as two rigid links, and the stance leg is simplified as a rigid rod fixed to the ground. Therefore, the structure of human lower limbs are reduced to planar rigid body model as shown in Fig. 1.

Fig. 1.
figure 1

A plant model of human lower limb

Full size image

In the model, H, K and A respectively represent the hip, knee and ankle of swing leg, T and S are respectively the centers of mass of swing thigh and shank. L represents the centers of mass of stance leg. The stance foot is taken as the origin of coordinate. p1 is the distance from origin to mass center of the stance foot, p2 is the distance from hip to mass center of swing thigh, p3 is the distance between mass center of swing shank and knee. l1 is the length of stance leg, l2 and l3 are the length of thigh and shank of swing leg, θ1 is the angle from Y axis to stance leg, θ2 is the angle from Y axis to thigh, θ3 is the angle from Y axis to shank.

3 Analysis Methods of the Plant Model

3.1 Kinematic Analysis Method

Denavit-Hartenberg Notion.

D-H method fixes a coordinate in each link, and then the homogeneous transformation matrix is applied to describe the space relation between two adjacent links. Based on the plant model, D-H parameters of the plant model are established as Table 1.

Table 1. D-H parameters
Full size table

Based on Table 1, the homogeneous transformation matrix is calculated as follows,

$$ T_{i,i + 1} = \left[ {\begin{array}{*{20}c} {{ \cos }\theta_{i} } & { - { \sin }\theta_{i} { \cos }\alpha_{i} } & {{ \sin }\theta_{i} { \sin }\alpha_{i} } & {a_{i} { \cos }\theta_{i} } \\ {{ \sin }\theta_{i} } & {{ \cos }\theta_{i} { \cos }\alpha_{i} } & { - { \cos }\theta_{i} { \sin }\alpha_{i} } & {a_{i} { \sin }\theta_{i} } \\ 0 & {{ \sin }\alpha_{i} } & {{ \cos }\alpha_{i} } & {d_{i} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] $$
(1)

The kinematic equations can be derived based on the transformation matrix to obtain the position of knee and hip. The D-H method describes the position changes of each link in the plant model, which is comprehensible and convenient. In some closed-loop or tree structures, the transmission shaft may exceed one and results in the ambiguous relationship. Fortunately, modified D-H has developed and compensated this shortage [16]. For the human lower limb model, D-H is enough and concise.

Roberson-Wittenburg Algorithm.

The structure and path relationship of the system are described by the incidence matrix and path matrix in graph theory. A pair of adjacent rigid bodies of each hinge is taken as the independent unit, one rigid body act as the reference, and the generalized coordinates of the hinge express the other rigid body. The generalized coordinate is usually the hinge displacement between adjacent rigid bodies, so that the position of the open loop system can be determined through the generalized coordinate matrix of all the hinges. In the plant model of human lower limb, the incidence matrix and path matrix can be shown as follow,

$$ S = \left[ {\begin{array}{*{20}c} { - 1} & 1 & 1 \\ 0 & { - 1} & 1 \\ 0 & 0 & { - 1} \\ \end{array} } \right]\quad \quad T = \left[ {\begin{array}{*{20}c} { - 1} & { - 1} & { - 1} \\ 0 & { - 1} & { - 1} \\ 0 & 0 & { - 1} \\ \end{array} } \right] $$
(2)

Based on the theorem of motion of mass center and theorem of momentum, the dynamic equations can be established.

3.2 Dynamic Analysis Method

Newton Euler Equation.

As a classical mechanics method, Newton Euler method simplifies human body as rigid links. The plane motion of a body is decomposed as translation from a point and rotation around a point. Newton Euler equation of thigh and shank can be written as follow respectively,

$$ \left\{ {\begin{array}{*{20}c} {\vec{f}_{1} - \vec{f}_{2} + m_{1} g = m_{1} p_{1} \ddot{\theta }_{1} } \\ {} \\ {M_{1} = I_{1} \ddot{\theta }_{1} + \dot{\theta }_{1} \times I_{1} \dot{\theta }_{1} } \\ \end{array} } \right. \, \begin{array}{*{20}c} {} \\ \Rightarrow \\ {} \\ \end{array} \, I_{1} \ddot{\theta }_{1} + \dot{\theta }_{1} \times I_{1} \dot{\theta }_{1} = M_{h} - \vec{f}_{1} \times p_{1} + \vec{f}_{2} \times (l{}_{1} - p_{1} ) $$
(3)
$$ \left\{ {\begin{array}{*{20}c} {\vec{f}_{2} - \vec{f}_{3} + m_{2} g = m_{2} p_{2} \ddot{\theta }_{2} } \\ {} \\ {M_{2} = I_{2} \ddot{\theta }_{2} + \dot{\theta }_{2} \times I_{2} \dot{\theta }_{2} } \\ \end{array} } \right. \, \begin{array}{*{20}c} {} \\ \Rightarrow \\ {} \\ \end{array} \, \begin{array}{*{20}c} {} \\ {I_{2} \ddot{\theta }_{2} + \dot{\theta }_{2} \times I_{2} \dot{\theta }_{2} = M_{h} - M_{k} - \vec{f}_{2} \times p_{2} + \vec{f}_{3} \times (l_{2} - p_{2} )} \\ {} \\ \end{array} $$
(4)
$$ \left\{ {\begin{array}{*{20}c} {m_{3} g + \vec{f}_{3} = m_{3} p_{3} \ddot{\theta }_{3} } \\ {} \\ {M_{3} = I_{3} \ddot{\theta }_{3} + \dot{\theta }_{3} \times I_{3} \dot{\theta }_{3} } \\ \end{array} } \right. \, \begin{array}{*{20}c} {} \\ \Rightarrow \\ {} \\ \end{array} \, \begin{array}{*{20}c} {} \\ {I_{3} \ddot{\theta }_{3} + \dot{\theta }_{3} \times I_{3} \dot{\theta }_{3} = M_{k} - \vec{f}_{3} \times p_{3} } \\ {} \\ \end{array} $$
(5)

where I1 and M1 are the inertia tensor and moment of stance leg, I2 and I3 are the inertia tensor of swing thigh and shank. M2 and M3 are the moment of swing thigh and shank. Moreover, f1 is the ground support force applied to stance leg, f2 is the constraint force that thigh react to the stance leg and f3 denotes the force that thigh act to shank in swing leg.

The moment of hip and knee can be derived as Mh and Mk respectively as follows,

$$ \left\{ {\begin{array}{*{20}l} {M_{k} = f_{2} p_{2} \sin \theta_{2} + I_{2} \ddot{\theta }_{2} + \dot{\theta }_{2} \times I_{2} \dot{\theta }_{2} } \hfill \\ {M_{h} = I_{1} \ddot{\theta }_{1} + \dot{\theta }_{1} \times I_{1} \dot{\theta }_{1} + f_{2} p_{2} \sin \theta_{2} + I_{2} \ddot{\theta }_{2} + \dot{\theta }_{2} \times I_{2} \dot{\theta }_{2} + f_{1} p_{1} \cos \theta_{1} - f_{2} (l_{1} - p_{1} )\cos \theta_{1} } \hfill \\ \end{array} } \right. $$
(6)

In the Newton Euler equation, the existence of constraint reaction forces increase the dynamic analysis complexity. In addition, Newton Euler equation illustrates the dynamic characteristics of one rigid body. The human lower limb model consists of three rigid bodies, the dynamic equation of the plant model is a simultaneous equations composed of multiple equations.

Lagrange Equation.

Based on the viewpoint of energy, the kinetic energy function is represented by generalized coordinates and velocity. It avoids the complicated calculation of force, velocity, acceleration and other vectors. The Lagrange equation of the plant model can be formed as follows.

$$ \left\{ {\begin{array}{*{20}l} {E_{k} = \frac{1}{2}m_{1} p_{{_{1} }}^{2} \dot{\theta }_{1}^{2} + \frac{1}{2}m_{2} l_{1}^{2} \dot{\theta }_{1}^{2} + \frac{1}{2}m_{2} p_{2}^{2} \dot{\theta }_{2}^{2} + \frac{1}{2}m_{2} l_{2}^{2} \dot{\theta }_{2}^{2} + \frac{1}{2}m_{3} p_{3}^{2} \dot{\theta }_{3}^{2} } \hfill \\ {E_{p} = m_{1} gp_{1} (1 - \cos \theta_{1} ) + m_{2} gp_{2} (1 - \cos \theta_{2} ) + m_{3} gp_{3} (1 - \cos \theta_{3} ) + m_{3} gl_{2} (1 - \cos \theta_{2} )} \hfill \\ \end{array} } \right. $$
(7)
$$ \begin{aligned} L = & \,E_{k} - E_{p} = \frac{1}{2}m_{1} p_{{_{1} }}^{2} \dot{\theta }_{1}^{2} + \frac{1}{2}m_{2} l_{1}^{2} \dot{\theta }_{1}^{2} + \frac{1}{2}m_{2} p_{2}^{2} \dot{\theta }_{2}^{2} + \frac{1}{2}m_{2} l_{2}^{2} \dot{\theta }_{2}^{2} + \frac{1}{2}m_{3} p_{3}^{2} \dot{\theta }_{3}^{2} \\ \quad - & m_{1} gp_{1} (1 - \cos \theta_{1} ) - m_{2} gp_{2} (1 - \cos \theta_{2} ) - m_{3} gp_{3} (1 - \cos \theta_{3} ) - m_{3} gl_{2} (1 - \cos \theta_{2} ) \\ \end{aligned} $$
(8)
$$ \left\{ {\begin{array}{*{20}l} {M_{k} = \frac{d}{dt}\frac{\partial L}{{\partial \dot{\theta }_{3} }} - \frac{\partial L}{{\partial \theta_{3} }} = m_{3} p_{3}^{2} \ddot{\theta }_{3} - m_{3} gp_{3} \sin \theta_{3} } \hfill \\ {M_{h} = \frac{d}{dt}\frac{\partial L}{{\partial \dot{\theta }_{2} }} - \frac{\partial L}{{\partial \theta_{2} }} = (m_{2} p_{2}^{2} + m_{2} l_{2}^{2} )\ddot{\theta }_{2} - (m_{2} p_{2} + m_{3} l_{2} )g\sin \theta_{2} } \hfill \\ \end{array} } \right. $$
(9)

Compared with Newton Euler equation, Lagrange illustrates the multi-rigid-body system in one equation, and no constrain force is included. As for the plant model of human lower limb, Lagrange equation is more simple and distinct.

Kane Equation.

Kane equation is established using Alembert principle and virtual displacement principle. (The system is composed of n particles, with ideal constraints and n degrees of freedom)

$$ F_{r} + \, F_{r}^{*} = 0\,(r = 1, \ldots ,n) $$
(10)

\( F_{r} \) and \( F_{r}^{*} \) are generalized applied force and inertia force which depend on the generalized coordinates respectively. That is,

$$ F_{r} = \sum\limits_{i = 1}^{N} {f_{i} } = m_{1} g + m_{2} g $$
(11)
$$ F_{r}^{*} = \sum\limits_{i = 1}^{N} {( - m_{i} a_{i} )} = - m_{1} P_{1} \ddot{\theta }_{1} - m_{2} P_{2} \ddot{\theta }_{2} + 2m_{1} \dot{\theta }_{1} \times P_{1} \ddot{\theta }_{1} + 2m_{2} \dot{\theta }_{2} \times P_{2} \ddot{\theta }_{2} $$
(12)

3.3 Summary of Analysis Method

To summarize these analysis methods when they describe the plant model, Table 2 is shown as follow.

Table 2. Analysis methods comparisons
Full size table

We can see that Lagrange method is more straightforward than Newton Euler and Kane method to characterize the dynamic features of knee and hip, and it’s the reason why Lagrange method is widely used in human motion modeling and analysis.

4 Comparison Between Simulation and Experimental Results

The plant model is simulated in the Simulink to imitate the motion of human. The experiment on the treadmill is conducted to verify the plant model and the dynamic analysis method. The subject is a health man (24 years old, 65 kg, 1.78 m) without previous history musculoskeletal injury. The experiment setup is shown in Fig. 2 and the acceleration sensors (CXL04GP3) are used to collect the human walking information when the treadmill’s speed is controlled at 3, 4, 5, 6, 7 km/h.

Fig. 2.
figure 2

Experiment setup

Full size image

The torques of hip and knee are then calculated by Lagrange method based on the experiment data. This paper uses motion data at 5 km/h as it is close to the normal walking speed mostly. Both the numerical calculated torques and experiment calculated torques of hip and knee respectively are shown in Fig. 3.

Fig. 3.
figure 3

(a) The torque of hip (b) The torque of knee

Full size image

Some errors exist between the experimental analysis and simulation, it may result from the relative motion between clothes and human body. Compared with the simulation, the experiment result line presents many glitch impulses which come from the muscles jitter, damp characteristic and flexibility of human body. Moreover, the period of simulation and experiment at hip are totally coincide, but they are not as well at the knee. It implies that knee and hip may have relative hysteresis in the real motion, which hasn’t been considered in the plant model and simulation. Aiming at these phenomena, further research work will be carried out in the future to quantify these influences.

5 Conclusion

The human lower limb was simplified to a three-rigid-link system which moves in a two-dimensional sagittal plane, and it is named as plant model. To explore the properties of the pant model in walking motion, Denavit-Hartenberg notion and Roberson-Wittenburg algorithm were used to deploy the relation of each joints. Moreover, Newton Euler, Lagrange equation and Kane equation were compared when they build the dynamic equation of the plant model. The superiority of Lagrange equation was demonstrated. Therefore, the torques of experiment data were analyzed by Lagrange equation. The comparisons of simulation and experiment results show that the dynamic properties of plant model is similar to the real human, thus the fidelity of the plant model is validated.