Whale Optimization Algorithm with Local Search for Open Shop Scheduling Problem to Minimize Makespan

Abstract

In this paper, a hybrid whale optimization algorithm (HWOA) with local search strategy is proposed to minimize the makespan for the Open-shop Scheduling Problem (OSP), which is one of the most important scheduling types in practical applications. Firstly, the large-order-value (LOV) encoding rule is presented to transform HWOA’s individuals from continuous vectors into job permutations, which makes HWOA suitable for dealing with the OSP and performing global search in the solution space. Secondly, a local search mechanism guided by different neighborhoods is designed to enhance the search depth in the promising regions of excellent solutions. Computational experiments and comparisons show that HWOA performs well on random generation problems. This is the first time that HWOA has been used to address the OSP.

1 Introduction

With the introduction of “Industry 4.0” and “Made in China 2025”, the manufacturing industry will face severe challenges of transformation and upgrading and scheduling is the core and key technology of the manufacturing process. Reasonable scheduling can shorten the manufacturing period, reduce resource waste, and improve economic and management benefits. Open-shop Scheduling Problem (OSP) is a kind of special production scheduling problem that exists in practice. OSP can be applied not only to enterprise production management, industrial process modeling, but also to inspection and service industries, such as: inspection and diagnosis of machine network operations in hospitals [1], inspection and maintenance of large equipment such as automobiles and aircraft [2], logistics and road construction [3], medical examination [4], teacher or student examination arrangement [5] and so on, the common feature of the above examples is that there is no order constraint between the operations, so this type of problem can be simplified to OSP, it can be seen that it has a strong application background. Therefore, this paper studies the effective algorithm for OSP with the minimum makepsan as the optimization goal. In terms of computational complexity, OSP is an optimal combination of complexity and difficulty. Gonzalez and Sahni [6] have shown that when there are more than two machines, OSP is an NP-Hard problem, meaning that with a few exceptions, it is basically impossible to find the optimal solution in polynomial time. In summary, the study of the algorithm for solving the OSP that minimizes the makepsan is not only important for the development of operations research and combinatorial optimization theory, but also has important practical significance.

The OSP is more complex and it is more difficult to find the optimal solution in a limited time. In the past few decades, domestic and foreign scholars have conducted extensive research on OSP, and mainly focused on minimizing the makespan. Gonzalez and Sahni [6] first studied the OSP, gave the definition and a linear time solving algorithm for the case of two machines. Brucker and Hurink [7] used the branch and bound method based on Disjunctive Graph (DG) to minimize the optimal solution of some examples of Taillard [8]. Liaw [9] proposed a local search algorithm based on tabu search for non-preemptive OSP to minimizing makespan. At the same time, using the neighborhood structure by defining the block structure on the critical path to improve the current solution. The optimal solution of most examples and the calculation time is reasonable. Research on OSP focuses more on artificial heuristics based on artificial intelligence. Prins [10] aimed at minimizing the makespan of OSP, pointing out that the OSP’s no-process constraint is the reason that the performance of the meta-heuristic algorithm based on DG-based branch and bound method and tabu search is weak in solving OSP. Several genetics are proposed to solve OSP, not only obtained the optimal solution of the Taillard [8] example, but also improved the optimal solution of an example. Sha [11] proposed a new particle swarm optimization algorithm for minimizing makespan. It can solve the discrete OSP by using the priority and interpolation operators to modify the particle position and motion representation respectively, it obtains many new optimal solution of the Taillard [8] example. Gao [12] proposed the PSO-OSP algorithm for minimizing makespan. By analyzing the defects of particle swarm optimization (PSO) in information sharing mechanism, a new information sharing mechanism based on swarm intelligence was proposed. The neighborhood knowledge guides the local search and overcomes the blind search caused by the randomness of the meta heuristic algorithm.

The whale optimization algorithm (WOA) is a novel biomimetic group intelligence proposed by Mirjalili [13] in 2016. WOA has been proved to be superior to PSO, DE, gravitational search algorithm (GSA) and GWO algorithm in solving accuracy and convergence speed [13]. At present, the research on whale optimization algorithm is still in its preliminary stage. In the field of shop scheduling: Yan [14] aimed at minimizing the maximum completion time of the job shop, a quantum whale optimization algorithm is proposed. The algorithm makes use of the quantum computing and optimization ideas to some extent to make up for the shortcomings of WOA with low convergence precision and easy to fall into local optimum. Abdel-Basset et al. [15] proposed a simple hybrid whale optimization algorithm for the replacement flow shop problem. It can be seen that there is no literature report on solving the open shop scheduling problem, so it is very important to carry out relevant research.

This paper proposes a hybrid whale optimization algorithm to minimize makespan of OSP. Firstly, the Large-order-value (LOV) coding rule is presented to transform HWOA’s individuals from continuous vectors into job permutations, which can make OSP solve the problem solution space effectively. Then, a local search mechanism guided by perturbation and exploitation is designed to enhance the optimization accuracy of the algorithm. Finally, the experimental results show that HWOA has good performance on random generation problems.

In Sect. 2, the mixed integer linear programming (MILP) model of OSP is briefly introduced. In Sect. 3, WOA is described briefly. In Sect. 4, HWOA is proposed and described in detail. In Sect. 5, simulation results and comparisons are provided. Finally, we end the paper with some verdicts and future work in Sect. 6.

2 Problem Description of OSP

Firstly, define the symbols required in this article, including parameters, indicators and variables as shown in Table 1.

Table 1. Symbols and definitions

2.1 Problem Description

Given a set $\varvec{J = }\,\left\{ {J_{i} \left| {i = 1,2, \ldots ,n} \right.} \right\}$ of n jobs and a set $\varvec{M}\text{ = }\left\{ {M_{j} |j = 1,2, \ldots ,m} \right\}$ of m machines. Each job $J_{i}$ consists of m operations $(O_{ij} ,\forall i,\forall j)$, where $O_{ij}$ has to be processed on machine $M_{j}$ for $(p_{ij} \text{ > }0,\forall i,\forall j)$ time units. The operations of each job can be processed in any order; each machine can process at most one operation at a time. The goal of OSP scheduling is to determine the sequential combination of all jobs and machines while satisfying the above assumptions and constraints, so that the scheduling performance metrics are optimal.

2.2 Mathematical Models of OSP

Before describing the model, we need to define the decision variables

$$ Y_{ikj} = \left\{ {\begin{array}{*{20}l} {1,\,for\,machine \, j, if\,process\,O_{kj} \,when\,finish\,O_{ij} ,\,0 \le j \le m,\,0 \le i \ne k \le n} \hfill \\ { 0 ,\,or\,else} \hfill \\ \end{array} } \right. $$

$$ X_{ijf} = \left\{ {\begin{array}{*{20}l} { 1 ,\,for\,job\,i,\,if\,process\,O_{if} \,when\,\,finish\,O_{ij} ,\,0 \le i \le n,\,0 \le j \ne f \le m} \hfill \\ { 0 ,\,or\,else} \hfill \\ \end{array} } \right. $$

Under the symbols and decision variables defined above, let $C_{\hbox{max} }$ be the objective function, which represents makespan. The mixed integer linear programming model of OSP can be given as follows

$$ Min\,\,\,C_{\hbox{max} } $$

(1)

$$ s.t. \, \sum\nolimits_{i = 0,i \ne k}^{n} {Y_{ikj} = 1,\forall k,j} $$

(2)

$$ \sum\nolimits_{k = 1,k \ne i}^{n} {Y_{ikj} \le 1,\forall i,j} $$

(3)

$$ \sum\nolimits_{k}^{n} {Y_{0kj} = 1,\forall j} $$

(4)

$$ Y_{ikj} + Y_{kij} \le 1,\forall j,0 < i \ne k < n $$

(5)

$$ S_{kj} - S_{ij} \ge P_{ij} ,\forall j,0 < i \ne k < n $$

(6)

$$ S_{if} - S_{ij} \ge P_{ij} ,\forall i,0 < j \ne f < m $$

(7)

$$ C_{i} \ge F_{ij} > 0,\forall i,j $$

(8)

Among them, formula (2) means that each job can be processed once on any machine; formula (3) means that only one job can be processed after machining one job per machine; formula (4) means that the 0 process can be a pre-process of any one of the job; formula (5) means that one process cannot be the former or the latter of the other process at the same time; formula (6) indicates that the same machine cannot process two job at the same time; formula (7) indicates that for the same process, it cannot be processed on two machines at the same time; formula (8) means that the completion time of one job is not less than the processing time of any one of the processes.

3 Whale Optimization Algorithm

The WOA is a novel meta-heuristic that simulate the social behavior of humpback whales in chasing their prey. The modeling process can be described as follows

3.1 Bubble-Net Attacking Method (Exploitation Phase)

The humpback whale’s bubble-net attack method swims around the prey along a spiral path within a gradually constricted circle, the strategy of encircling the prey can be represented by the following equations

$$ \varvec{D} = \left| {\varvec{C} \times \varvec{X}^{ * } (t) - \varvec{X}(t)} \right| $$

(9)

$$ \varvec{X}(t + 1) = \varvec{X}^{ * } (t) - \varvec{A} \times \varvec{D} $$

(10)

$$ \varvec{A} = 2 \times \varvec{a} \times \varvec{r} - \varvec{a} $$

(11)

$$ \varvec{C} = 2 \times \varvec{r} $$

(12)

where $t$ indicates the current iteration, $\varvec{A}$ and $\varvec{C}$ are coefficient vectors, $\varvec{X}^{ * }$ is the position vector of the best solution obtained so far, $\varvec{X}$ is the position vector; $\varvec{X}^{ * }$ would be updated in each iteration if there is a better solution. $\varvec{a}$ is linearly decreased from 2 to 0 over the process of iterations and $\varvec{r}$ is a random vector in [0, 1].

The behavior of the spiral-shaped path can be formulated and assuming a 50% probability of selecting the position of the whale in the shrink-wrap or spiral model. Set $p$ to a random value in [0, 1], the bubble network attack process can be fully described as follows

$$ \varvec{X}(t + 1)\text{ = }\left\{ {\begin{array}{*{20}l} {\varvec{X}^{ *} (t) - \varvec{A} \times \varvec{D}} \hfill & {p < 0.5} \hfill \\ {\varvec{D}^{{\prime }} \times e^{bl} \times \cos (2 \times \pi \times l)\text{ + }\varvec{X}^{ *} (t)} \hfill & {p \ge 0.5} \hfill \\ \end{array} } \right. $$

(13)

Where $b$ is a constant for defining the shape of the logarithmic spiral, $l$ is a random number in [−1, 1].

3.2 Search for Prey (Exploration Phase)

In fact, humpback whales search randomly according to the position of each other, the mathematical model is as follows:

$$ \varvec{D} = \left| {\varvec{C} \times \varvec{X}_{rand} - \varvec{X}} \right| $$

(14)

$$ \varvec{X}(t + 1) = \varvec{X}_{rand} - \varvec{A} \times \varvec{D} $$

(15)

where $\varvec{X}_{rand}$ is a random position vector (a random whale) chosen from the current population.

4 HWOA for OSP with Makespan

Since traditional WOA is suitable for solving continuous problems, it is usually combined with several methods to solve discrete problems. This paper proposes a hybrid whale optimization algorithm, which combines WOA with local search strategy to improve the performance of WOA. HWOA consists of four main steps: encoding, decoding, population initialization, and local search design. All four steps will be discussed in the following sections.

4.1 Encoding and Solution Expression

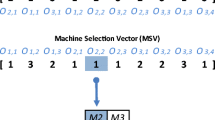
The important problem in applying WOA to OSP is to find a suitable mapping between job sequence and individuals (continuous vectors) in WOA. For the n job and m machine problem, each vector contains n number of dimensions corresponding to n operations. In this paper, we adopt a largest-order-value (LOV) rule [16] to convert the ith individual of WOA $\varvec{X}_{i} = \left[ {x_{i,1} ,x_{i,2} , \ldots ,x_{i,n} } \right]$ to the job solution $\varvec{\pi}_{i} = \left[ {\pi_{i,1} ,\pi_{i,2} , \ldots ,\pi_{i,n} } \right]$. According to LOV rule, $\varvec{X}_{i} = \left[ {x_{i,1} ,x_{i,2} , \ldots ,x_{i,n} } \right]$ are firstly ranked by descending order to get the sequence $\varvec{\varphi }_{i} = \left[ {\varphi_{i,1} ,\varphi_{i,2} , \ldots ,\varphi_{i,n} } \right]$. Then the job permutation $\pi_{i}$ is calculated by the following formula:

$$ \pi_{{i,{\varphi }_{i,k} }} = k $$

(16)

To better understand the LOV rule, a simple example is provided in Table 2. In this instance, when k = 1, $\varphi_{i,1} = 6$, $\pi_{{i,{\varphi }_{i,1} }} = \pi_{i,6} = 1$; when k = 2, $\varphi_{i,2} { = }3$, $\pi_{{i,{\varphi }_{i,2} }} = \pi_{i,3} = 2$, and so on. This representation is unique and simple in terms of finding new permutations (Table 2).

Table 2. Solution representation

Permutation list is one of the widely used encoding schemes. It is purely the relative order of all the $g$ operations in which they are processed ($g = n \times m$). For example, consider a problem of two machines and three jobs. It sums up to six operations: $O_{12}$, $O_{22}$, $O_{32}$, $O_{11}$, $O_{21}$, $O_{31}$. Every permutation of these six operations, like $\theta \,{ = }\,\left\{ {O_{12} ,O_{22} ,O_{32} ,O_{11} ,O_{31} ,O_{21} } \right\}$, corresponds to one solution.

4.2 Decoding

It is known that in terms of makespan, the search space is reduced in such a way that it does not eliminate the optimal solution by this decoding. In this paper, we mean to examine the performance of decoding by the set of non-delay schedule. We apply the procedure proposed by Giffler and Thompson [17]: all operations are put into a set including unscheduled ($\varvec{U}$) operations. $S_{ij}$ means the earliest possible at which the operation $O_{ij}$ could be started. We count $y$ which equals the minimum of $S_{ij}$ of operations in $\varvec{U}$. All the operations whose starting time is equal to $y$ are put into a set called $\varvec{R}$. Among all operations in $\varvec{R}$, the operation $O^{ * }$ with the earliest relative position in permutation is scheduled and extracted from $\varvec{U}$.

4.3 Population Initialization

For population initialization, because the solution space of OSP is large and there is no prior knowledge of the global optimal solution to the problem, we will generate the initial population randomly, that is, each individual is randomly generated $g$ ($g = n \times m$) non-repeating continuous real numbers.

4.4 Local Search

It is known that the neighborhood can lead the search to a more various region and then enhance the search ability of HWOA in a way, so, we employ insert and cut here as the neighborhood for local search. Two operators can be described as follows.

Insert: randomly select two different locations of the sequence and insert the back one before the front one.

Cut: randomly select two different locations of the sequence and insert the job between the two locations before the front of the sequence.

These operators are executed in the given order to generate another solution, and then the new solution replaces the old one if it precedes the old. The above procedure is designed as follows:

Step 1: Convert individual $\varvec{X}_{i} (t)$ to a job permutation $\varvec{\pi}_{i\_0}$ according to the LOV rule.

Step 2: Perturbation phase.

Randomly select u and v, where u $\ne$ v; $\varvec{\pi}_{i} = insert(\varvec{\pi}_{i\_0} ,u,v)$.

Step 3: Exploitation phase.

Set k = 1;

Do

Randomly select u and v, where u $\ne$ v;

$\varvec{\pi}_{i\_1} = cut(\varvec{\pi}_{i} ,u,v)$;

If $f_{i\_1} \text{ < }f_{i}$, then $\varvec{\pi}_{i} \varvec{ = \pi }_{i - 1}$;

$k = k{ + }1$;

While $k\text{ < }(n \times (n - 1))$;

Step 4: If $f_{i} \text{ < }f_{i\_0}$, then $\varvec{\pi}_{i\_0} \varvec{ = \pi }_{i}$.

Step 5: Convert $\varvec{\pi}_{i\_0}$ back to $\varvec{X}_{i} (t)$.

With the above design, the procedure of HWOA for solving the OSP with makespan is illustrated in Fig. 1.

Fig. 1.

Framework of HWOA

5 Simulation Result and Comparisons

5.1 Experimental Setup

To test the performances of WOA, we will test the effectiveness of algorithm on randomly generated test questions. For OSP, n jobs are randomly machined on $m$ machines, and the processing time of each process is the integers generated in [1, 30], we compare the effective algorithms proposed by Naderi et al. [18].

HWOA and HGA are coded in Delphi 2010 and run on a PC with Intel 7700HQ 2.80 GHz. The proposed HWOA’s parameters are set as follows: Since the number of instances of different scales measured by the algorithm is huge, and the running time of each generation is quite different, the running generation (gen) and the population of the corresponding problem (pop) will be respectively given. The comparison algorithm runs 20 times independently for each test problem at the same runtime as HWOA, where min, max, avg, and std are the minimum, maximum, average, and standard deviation, respectively. The optimal results corresponding to each problem are shown in bold, and the test results are shown in Table 3.

Table 3. Comparisons of HWOA and HGA

5.2 Results and Comparison

In the comparison of the algorithms, four indicators min, max, avg and std are used to evaluate the advantages and inferiority of the algorithm. It can be seen from Table 3 that the avg and min values of HWOA are almost better than HGA in each instance of various problems, and with the increase of the scale of the problem, the superiority of HWOA is more obvious, and a few individuals can ensure the performance of the algorithm, which verifies the rationality of the design of the local search mechanism. On the other hand, the std of HWOA is bigger than HGA, it means that HWOA is not stable enough. Through experimental comparison, we can conclude that HWOA can search for larger and more detailed solution space under the condition of running the same algebra. HWOA is an effective and excellent algorithm for solving the makespan of OSP, and there is room for further improvement and application.

6 Conclusion

In this paper, a hybrid whale optimization algorithm (HWOA) with local search strategy is proposed to minimize the makespan for the Open-shop Scheduling Problem (OSP), which is one of the most important scheduling types in practical applications. Firstly, the large-order-value (LOV) encoding rule is presented to transform HWOA’s individuals from continuous vectors into job permutations, which makes HWOA suitable for dealing with the OSP and performing global search in the solution space. Secondly, a local search mechanism guided by inter-based perturbation and cut-based exploitation is designed to enhance the search depth in the promising regions of excellent solutions and improve the ability of WOA. Computational experiments and comparisons show that HWOA performs well on random generation problems. This is the first time that HWOA has been used to address the OSP. The future research work is to solve the multi-objective OSP and design a more efficient WOA.