A New Manifold-Based Feature Extraction Method

Abstract

Many traditional feature extraction methods takes the global or the local characteristics of training samples into consideration during the process of feature extraction. How to fully utilize the global or the local characteristics to improve the feature extraction efficiencies is worthy of research. In view of this, a new Manifold-based Feature Extraction Method (MFEM) is proposed. MFEM takes both the advantage of Linear Discriminant Analysis (LDA) in keeping the global characteristics and the advantage of Locality Preserving Projections (LPP) in keeping the local characteristics into consideration. In MFEM, Within-Class Scatter based on Manifold (WCSM) and Between-Class Scatter based on Manifold (BCSM) are introduced and the optimal projection can be obtained based on the Fisher criterion. Compared with LDA and LPP, MFEM considers the global information and local structure and improves the feature extraction efficiency.

1 Introduction

Linear Discriminant Analysis (LDA) [1] is popular in practice, in which the non-singularity problem has greatly influent its improvement of efficiencies. In view of this, many effective improvements are made by scientists: Regularized Discriminant Analysis (RDA) proposed by Friedman [2] efficiently solves the above problem; 2D-LDA is proposed to directly extract the features based on Fisher criterion [3]; Orthogonal LDA (OLDA) tries to diagonalize the scatter matrix so as to obtain the discriminant vectors [4]; Direct LDA (DLDA) [5] carries no discriminative information by modifying the simultaneous diagonalization procedure. Besides, the commonly-used improvement approach include Pseudo-inverse LDA (PLDA) [6], Two-stage LDA [7], Penalized Discriminant Analysis (PDA) [8], Enhanced Fisher Linear Discriminant Model (EFM) [9]. In recent years, as to the under-sampled problems, we proposed Scalarized LDA (SLDA) [10], and Matrix Exponential LDA (MELDA) [11].

The general strategy of above approach is to solve the singularity problem firstly and then uses the Fisher criterion to obtain the optimal projections. LDA only takes the sample global information into consideration but always neglects the local structure. On the other hand, many popular manifold learning approach such as Locality Preserving Projection (LPP) [12], only focus on the local structure.

Therefore, all the sample information including the global characteristics and local structure is taken into consideration, and propose a new Manifold-based Feature Extraction Method (MFEM). MFEM inherits the advantage of Fisher criterion and manifold learning and effectively improve the feature extraction efficiency.

2 Background Knowledge

2.1 LDA

Given a dataset matrix X = [x₁, x₂, …, x_N] = [x₁, x₂, …, x_c] where x_i(i = 1, …, N), N and c are respectively the training size and the class size. N_i denoting the number of sample in the i th class.

In LDA, two scatters named between-class scatter S_B and within-class scatter S_W are defined as:

$$ \varvec{S}_{\varvec{B}} = \sum\limits_{i = 1}^{c} {\frac{{N_{i} }}{N}} (\bar{\varvec{x}}_{\varvec{i}} \text{ - }\bar{\varvec{x}})(\bar{\varvec{x}}_{\varvec{i}} \text{ - }\bar{\varvec{x}})^{\text{T}} $$

(1)

$$ \varvec{S}_{\varvec{W}} \text{ = }\sum\limits_{{i\text{ = 1}}}^{c} {\sum\limits_{{j\text{ = 1}}}^{{N_{i} }} {\frac{\text{1}}{N}} } \text{(}\varvec{x}_{{\varvec{ij}}} - \bar{\varvec{x}}_{\varvec{i}} \text{)(}\varvec{x}_{{\varvec{ij}}} - \bar{\varvec{x}}_{\varvec{i}} \text{)}^{\text{T}} $$

(2)

where $\bar{\varvec{x}}_{\varvec{i}} = \frac{1}{{N_{i} }}X_{i} e_{i}$ with $e_{i} = [1, {\ldots}, 1]^{T} \in R^{{N_{i} }}$ is the centroid of class i and $\bar{\varvec{x}} = \frac{1}{N}Xe$ with $e_{i} = [1, {\ldots}, 1]^{T} \in R^{N}$ is the global centroid.

The optimal function of LDA is:

$$ J(\varvec{W}_{{\varvec{opt}}} ) = \mathop {\hbox{max} }\limits_{W} \frac{{\varvec{W}^{\text{T}} \varvec{S}_{\varvec{B}} \varvec{W}}}{{\varvec{W}^{\text{T}} \varvec{S}_{\varvec{W}} \varvec{W}}} $$

(3)

The Eq. (3) is equivalent to:

$$ \mathop {\hbox{max} }\limits_{\varvec{W}} \;\varvec{W}^{\text{T}} \varvec{S}_{\varvec{B}} \varvec{W} $$

(4)

and

$$ \mathop {\hbox{min} }\limits_{\varvec{W}} \;\varvec{W}^{\text{T}} \varvec{S}_{\varvec{W}} \varvec{W} $$

(5)

where W is the optimal projection.

The projection W can be obtained by calculating the eigenvectors.

It can be seen from the above analysis, LDA tries to preserve the global characteristics invariant before and after feature extraction. Its efficiency can not be improved because it neglects the local structure of each class.

2.2 LPP

The optimal problem of LPP is:

$$ \mathop {min}\limits_{\varvec{W}} \;\sum\limits_{i,j} {\text{(}\varvec{W}^{\text{T}} \varvec{x}_{\varvec{i}} } - \varvec{W}^{\text{T}} \varvec{x}_{\varvec{j}} )^{2} S_{ij} $$

(6)

$$ s.t\;\sum\limits_{i} {\varvec{W}^{\text{T}} \varvec{x}_{\varvec{i}} } \varvec{D}_{{\varvec{ii}}} \varvec{x}_{\varvec{i}}^{\text{T}} \varvec{W} = 1 $$

(7)

where W is the optimal projection, S_ij is the weight function which reflects the similarity of samples, $\varvec{D}_{{\varvec{ii}}} = \sum\nolimits_{j} {S_{ij} }$.

The above optimization problem can be transformed as follows based on the linear algebra theory:

$$ \mathop {min}\limits_{\varvec{W}} \varvec{W}^{\text{T}} \varvec{XLX}^{\text{T}} \varvec{W} $$

(8)

$$ s.t.\;\varvec{W}^{\text{T}} \varvec{XDX}^{\text{T}} \varvec{W}{ = }\text{1} $$

(9)

where L = D − S.

The optional projection matrix is obtained by computing all the nonzero eigenvectors of $\varvec{XLX}^{\text{T}} \varvec{W}\text{ = }\varvec{\lambda XDX}^{\text{T}} \varvec{W}$.

In conclusion, LPP tries to preserve the local characteristic but does not take the global characteristics into consideration, especially, when encountering noise, the feature extraction efficiency of LPP is greatly influenced.

3 MFEM

Feature extraction is a classical preprocessed approach in dealing with the high-dimensional samples. Though they are widely-used in practice, the feature extraction efficiency is limited due to neglecting the global characteristics and local structure. In order to take all the characteristics of the training samples, a new Manifold-based Feature Extraction Method (MFEM) is proposed. In MFEM, Within-Class Scatter based on Manifold (WCSM) and Between-Class Scatter based on Manifold (BCSM) are introduced and the optimal projection can be obtained based on the Fisher criterion.

3.1 Between-Class Scatter Based on Manifold

Inspired by manifold learning, we firstly construct the adjacency graph $\varvec{G}_{\varvec{D}} = \{ \varvec{X},\varvec{D}\}$ where $\varvec{G}_{\varvec{D}}$ donates a graph with different classes, X and D donate the dataset and the weight of different classes respectively. The different-class weight function of two random samples x_i and x_j can be defined:

$$ D_{ij} = \left\{ {\begin{array}{*{20}c} {\exp ({{ - d} \mathord{\left/ {\vphantom {{ - d} {\left\| {\varvec{x}_{\varvec{i}} - \varvec{x}_{\varvec{j}} } \right\|^{2} }}} \right. \kern-0pt} {\left\| {\varvec{x}_{\varvec{i}} - \varvec{x}_{\varvec{j}} } \right\|^{2} }}) ,} & {l_{i} \ne l_{j} } \\ { 0,} & { l_{i} = l_{j} } \\ \end{array} } \right. $$

(10)

where l_i (i = 1, 2, …, N) donates the class label and d is a constant.

The different-class weight function verifies that if the samples x_i and x_j belong to different classes, the weight of them is large; or else, the weight is zero.

In order to preserve the local characteristics of different classes, the samples x_i and x_j belonged to different classes will be far away after feature extraction. The optimization problem can be described as follows.

$$ \mathop {\hbox{max} }\limits_{\varvec{W}} \;\sum\limits_{i,j} {(\varvec{y}_{\varvec{i}} - \varvec{y}_{\varvec{j}} )^{2} D_{ij} } $$

(11)

Where $\varvec{y}_{\varvec{i}} = \varvec{W}^{\text{T}} \varvec{x}_{\varvec{i}}$, W donates the projection matrix and $\varvec{x}_{\varvec{i}} \in \varvec{X}$.

$\sum\limits_{i,j} {(\varvec{y}_{\varvec{i}} - \varvec{y}_{\varvec{j}} )^{2} D_{ij} }$ is reformulated to the following equations based on the algebraic transformation.

$$ \begin{array}{*{20}l} {\frac{1}{2}\sum\limits_{i,j} {(\varvec{y}_{\varvec{i}} - \varvec{y}_{\varvec{j}} )^{2} D_{ij} } } \hfill \\ { = \frac{1}{2}\sum\limits_{i,j} {(\varvec{W}^{\text{T}} \varvec{x}_{\varvec{i}} - \varvec{W}^{\text{T}} \varvec{x}_{\varvec{j}} )^{2} D_{ij} } } \hfill \\ { = \sum\limits_{i,j} {(\varvec{W}^{\text{T}} \varvec{x}_{\varvec{i}} D_{ii} \varvec{x}_{\varvec{i}}^{\text{T}} \varvec{W} - \varvec{W}^{\text{T}} \varvec{x}_{\varvec{i}} D_{ij} \varvec{x}_{\varvec{j}}^{\text{T}} \varvec{W})} } \hfill \\ { = \varvec{W}^{\text{T}} \varvec{XD}^{{\prime }} \varvec{X}^{\text{T}} \varvec{W} - \varvec{W}^{\text{T}} \varvec{XDX}^{\text{T}} \varvec{W}} \hfill \\ { = \varvec{W}^{\text{T}} \varvec{X}(\varvec{D}^{{\prime }} - \varvec{D})\varvec{X}^{\text{T}} \varvec{W}} \hfill \\ { = \varvec{W}^{T} \varvec{S}_{\varvec{D}} \varvec{W}} \hfill \\ \end{array} $$

(12)

where $\varvec{S}_{\varvec{D}} = \varvec{X}(\varvec{D}^{{\prime }} - \varvec{D})\varvec{X}^{\text{T}}$, $\varvec{D}^{{\prime }}$ is a diagonal matrix and $\varvec{D}^{{\prime }} = \sum\nolimits_{j} {D_{ij} }$.

By taking (12) to (11), (11) is reformulated to

$$ \mathop {\hbox{max} }\limits_{\varvec{W}} \;\varvec{W}^{\text{T}} \varvec{S}_{\varvec{D}} \varvec{W} $$

(13)

Based on the above analysis, we can see Eqs. (4) and (13) reflect the global characteristics of different classes and local structure of each class respectively. In order to fully utilize all the above information, we can obtain the following optimization expression based on (4) and (13).

$$ \begin{array}{*{20}l} {\mathop {\hbox{max} }\limits_{\varvec{W}} \;\alpha \varvec{W}^{\text{T}} \varvec{S}_{\varvec{B}} \varvec{W} + (1 - \alpha )\varvec{W}^{\text{T}} \varvec{S}_{\varvec{D}} \varvec{W}} \hfill \\ { = \mathop {\hbox{max} }\limits_{\varvec{W}} \;\varvec{W}^{\text{T}} [\alpha \varvec{S}_{\varvec{B}} + (1 - \alpha )\varvec{S}_{\varvec{D}} ]\varvec{W}} \hfill \\ { = \mathop {\hbox{max} }\limits_{\varvec{W}} \;\varvec{W}^{\text{T}} \varvec{M}_{\varvec{B}} \varvec{W}} \hfill \\ \end{array} $$

(14)

where $\varvec{M}_{\varvec{B}} = \alpha \varvec{S}_{\varvec{B}} + (1 - \alpha )\varvec{S}_{\varvec{D}}$ and $\alpha$ is a parameter balancing $\varvec{S}_{\varvec{B}}$ and $\varvec{S}_{D}$. $\varvec{M}_{\varvec{B}}$ is called Between-Class Scatter based on Manifold (BCSM).

3.2 Within-Class Scatter Based on Manifold

Similarity with BCSM, the same-class weight function of two random samples x_i and x_j is defined:

$$ S_{ij} = \left\{ {\begin{array}{*{20}c} {\exp ({{ - \left\| {\varvec{x}_{\varvec{i}} - \varvec{x}_{\varvec{j}} } \right\|^{2} } \mathord{\left/ {\vphantom {{ - \left\| {\varvec{x}_{\varvec{i}} - \varvec{x}_{\varvec{j}} } \right\|^{2} } s}} \right. \kern-0pt} s}),} & {l_{i} = l_{j} } \\ {0,} & {l_{i} \ne l_{j} } \\ \end{array} } \right. $$

(15)

where l_i (i = 1, 2, .., N) donates the class label and s is a constant.

The same-class weight function verifies that if the samples x_i and x_j with the same class label, the weight of them is large; or else, the weight is zero.

In order to keep the neighborhood close, it can be described as:

$$ \mathop {\hbox{min} }\limits_{\varvec{W}} \;\sum\limits_{i,j} {(\varvec{y}_{\varvec{i}} - \varvec{y}_{\varvec{j}} )^{2} S_{ij} } $$

(16)

where $\varvec{y}_{\varvec{i}} = \varvec{W}^{\text{T}} \varvec{x}_{\varvec{i}}$, W donates the projection matrix and $\varvec{x}_{\varvec{i}} \in \varvec{X}$.

$\sum\limits_{i,j} {(\varvec{y}_{\varvec{i}} - \varvec{y}_{\varvec{j}} )^{2} S_{ij} }$ is reformulated to the following equations based on the algebraic transformation.

$$ \begin{array}{*{20}l} {\frac{1}{2}\sum\limits_{i,j} {(\varvec{y}_{\varvec{i}} - \varvec{y}_{\varvec{j}} )^{2} S_{ij} } } \hfill \\ { = \frac{1}{2}\sum\limits_{i,j} {(\varvec{W}^{\text{T}} \varvec{x}_{\varvec{i}} - \varvec{W}^{\text{T}} \varvec{x}_{\varvec{j}} )^{2} S_{ij} } } \hfill \\ { = \sum\limits_{i,j} {(\varvec{W}^{\text{T}} \varvec{x}_{\varvec{i}} S_{ii} \varvec{x}_{\varvec{i}}^{\text{T}} \varvec{W} - \varvec{W}^{\text{T}} \varvec{x}_{\varvec{i}} S_{ij} \varvec{x}_{\varvec{j}}^{\text{T}} \varvec{W})} } \hfill \\ { = \varvec{W}^{\text{T}} \varvec{XS}^{{\prime }} \varvec{X}^{\text{T}} \varvec{W} - \varvec{W}^{\text{T}} \varvec{XSX}^{\text{T}} \varvec{W}} \hfill \\ { = \varvec{W}^{\text{T}} \varvec{X}(\varvec{S}^{{\prime }} - \varvec{S})\varvec{X}^{\text{T}} \varvec{W}} \hfill \\ { = \varvec{W}^{\text{T}} \varvec{S}_{\varvec{S}} \varvec{W}} \hfill \\ \end{array} $$

(17)

where $\varvec{S}_{\varvec{S}} = \varvec{X}(\varvec{S}^{{\prime }} - \varvec{S})\varvec{X}^{T}$, $\varvec{S}^{{\prime }}$ is a diagonal matrix and $\varvec{S}^{\varvec{'}} = \sum\nolimits_{j} {S_{ij} }$.

By taking (17) to (16), (16) is reformulated to

$$ \mathop {\hbox{max} }\limits_{\varvec{W}} \;\varvec{W}^{\text{T}} \varvec{S}_{\varvec{S}} \varvec{W} $$

(18)

The following optimization expression based on (5) and (18).

$$ \begin{array}{*{20}l} {\mathop {\hbox{max} }\limits_{\varvec{W}} \;\beta \varvec{W}^{\text{T}} \varvec{S}_{\varvec{W}} \varvec{W} + (1 - \beta )\varvec{W}^{\text{T}} \varvec{S}_{\varvec{S}} \varvec{W}} \hfill \\ { = \mathop {\hbox{max} }\limits_{\varvec{W}} \;\varvec{W}^{\text{T}} [\beta \varvec{S}_{\varvec{W}} + (1 - \beta )\varvec{S}_{\varvec{S}} ]\varvec{W}} \hfill \\ { = \mathop {\hbox{max} }\limits_{\varvec{W}} \;\varvec{W}^{T} \varvec{M}_{\varvec{W}} \varvec{W}} \hfill \\ \end{array} $$

(19)

where $\varvec{M}_{\varvec{W}} = \beta \varvec{S}_{\varvec{W}} + (1 - \beta )\varvec{S}_{\varvec{S}}$ and $\beta$ is a parameter balancing $\varvec{S}_{W}$ and $\varvec{S}_{S}$. $\varvec{M}_{W}$ is called Within-Class Scatter based on Manifold (WCSM).

3.3 The Optimization Problem

Inspired by the Fisher criterion, the above optimization problem can be described as follows.

$$ J = \mathop {\hbox{max} }\limits_{\varvec{W}} \frac{{\varvec{M}_{\varvec{B}} }}{{\varvec{M}_{\varvec{W}} }} = \mathop {\hbox{max} }\limits_{\varvec{W}} \frac{{\varvec{W}^{\text{T}} (\alpha \varvec{S}_{\varvec{B}} + (1 - \alpha )\varvec{S}_{\varvec{D}} )\varvec{W}}}{{\varvec{W}^{\text{T}} (\beta \varvec{S}_{\varvec{W}} + (1 - \beta )\varvec{S}_{\varvec{S}} )\varvec{W}}} $$

(20)

The solution of the maximization of (20) is given by computing all the nonzero eigenvectors of $\varvec{M}_{\varvec{B}} \varvec{W} = \lambda \varvec{M}_{\varvec{W}} \varvec{W}$.

From the optimization expression of MFEM, it can be seen MFEM not only takes the global characteristics into consideration, but also preserves the local structure. MFEM inherits the advantages of LDA and LPP and improves the feature extraction efficiency to some extent. When $\alpha = \beta = 1$ or $d = s = \infty$, MFEM is equivalent to LDA; When $\alpha = \beta = 0$, $d = \infty$ and $s < \infty$, MFEM is equivalent to LPP.

In practice, $\varvec{M}_{\varvec{W}}$ maybe singular and the optimal projection can not be obtained by the above approach. For the sake of convenience, the singular value perturbation by adding a little positive number to the diagonal of $\varvec{M}_{\varvec{W}}$ is introduced to solve the singular problem.

3.4 Optimization Algorithm

Input: the original dataset X and the reduced dimension d

Output: the corresponding lower dimensional dataset Y = [y₁, y₂, …, y_d]

Step1: Construct the adjacency graph $\varvec{G}_{\varvec{D}} = \{ \varvec{X},\varvec{D}\}$ and $\varvec{G}_{\varvec{S}} = \{ \varvec{X},\varvec{S}\}$ where $\varvec{X} = {\{ }\varvec{x}_{{\mathbf{1}}} \text{,}\varvec{x}_{{\mathbf{2}}} ,\ldots, \varvec{x}_{\varvec{N}} \}$ donates the original dataset, D and S respectively donate the weights of different classes and the same class. We put an edge between x_i and x_j if they are in different classes in the G_D, or else, put an edge between them in the G_s.

Step2: Compute the different-class weights and the same-class weights. If different-class samples x_i and x_j are connected, utilize Eq. (10) to compute the different-class weights; else utilize Eq. (15) to compute the same-class weights.

Step3: Compute $\varvec{S}_{W}$, $\varvec{S}_{\varvec{B}}$, $\varvec{M}_{W}$ and $\varvec{M}_{\varvec{B}}$.

Step4: Solving the singular problem of $\varvec{M}_{W}$. The singular value perturbation is introduced to solve the singular problem. Let $\varvec{M}_{W}$ transform to $\varvec{M}_{W}^{{\prime }}$ after perturbation.

Step5: Compute the optimal projection W. The solution of the optimal projection W is given by computing all the nonzero eigenvectors of $\varvec{M}_{W}^{ - 1} \varvec{M}_{\varvec{B}} \varvec{W}\text{ = }\lambda \varvec{W}$ or $\varvec{M^{\prime}}_{W}^{ - 1} \varvec{M}_{\varvec{B}} \varvec{W}\text{ = }\lambda \varvec{W}$. The nonzero eigenvectors corresponding to the biggest d eigen-values are combine to form the optimal projection W = [w₁, …, w_d].

Step6: As to a certain sample $\varvec{x}_{i} \in X$, the corresponding lower dimensional sample can be obtained by $\varvec{y}_{\varvec{i}} = \varvec{W}^{\text{T}} \varvec{x}_{\varvec{i}}$.

4 Experimental Analysis

4.1 UCI Two-Dimensional Visualization

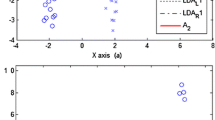
Wine dataset, including 178 samples with 3 classes, in UCI machine learning repository is used in the experiment. Set the reduced dimension is two, successively run PCA, LPP, LDA, MFEM on the wine dataset, and we can obtain the experimental results, shown in Table 1.

Table 1. Recognition rates of PCA, LPP, LDA, MFEM on the face datasets

It can be seen from Fig. 1, some different-class samples are overlapped after feature extraction by PCA. LPP, LDA and MFEM can mainly fulfill the feature extraction task but the efficiencies are different. After feature extraction by LPP, some samples lying near the three-class boundary are overlapped. Therefore, compared with LDA and MFEM, the efficiency of LPP is lowest. The efficiencies of LDA and MFEM are both high, but in the respect of distribution, MFEM shows much more perfect than LDA. This is because MFEM tries to preserve the original distribution by taking both the global and local characteristics, while LDA only focus on the global characteristics based on the Fisher criterion so as to make the different-class samples far and the same-class samples close. Although the within-class scatter reflects the closeness of the same-class samples, yet it does not take the relationship of adjacent samples before and after feature exaction.

Fig. 1.

The experiment results of 2-dimensional visualization

4.2 Experiments on Face Datasets

Experiment datasets include ORL face dataset and Yale face dataset. We will discuss the relationship between the sizes of training samples and recognition rates as well as the relationship between the reduced dimensions and recognition rates.

Relationship Between the Size of Training Samples and the Recognition Rate.

The training dataset consists of the first k images of each subject, and the remainders are used for test. The values of k in ORL and Yale dataset are selected from 3, 4, 5, 6, 7 and from 3, 5, 7, 9 respectively. The comparative experimental results are show in Table 1. In order to overcome the small size problem in LDA, we utilize PCA + LDA instead for LDA in the experiment.

It can be seen from Table 1, compared with PCA, LPP, LDA, MFEM performs best on the ORL dataset and except k = 8, the efficiency of MFEM is highest on the Yale dataset.

Relationship Between the Reduced Dimensions and Recognition Rates.

The training dataset consists of the first 5 images of each subject, and the remainders are used for test. We can obtain the experiment results shown in Fig. 2.

Fig. 2.

Relationship between reduced dimensions and recognition rates

It can be seen from Fig. 2, as the reduced dimension becomes higher, the corresponding recognition rate mainly has an upward tendency. Compared with PCA, LPP, LDA, MFEM performs best.

5 Conclusions

Researches on current feature extraction approaches can be reduced to two ways, one pays more attention on the global structure, and the other originates from local structure and tries to make the relationship between samples before and after feature extraction be invariant. In view of shortages of classical feature extraction approaches, MFEM is proposed. MFEM considers all the information and improves the feature extraction efficiency. Experiments on some standard datasets verify the effectiveness of MFEM. In practice, linear inseparability is a quite common problem and how to solve it is attracting more and more researchers’ interest. MFEM proposed in this paper is suitable to the linear separability situation, how to expand MFEM to linear inseparability is our next work.