Keywords

1 Introduction

Robot manipulators are high nonlinear systems – which have very complex dynamics with coupling terms. It is arduous to get its exact dynamics or even impossible in practice because of the frictions, disturbances, and payload changes – well-known as dynamic uncertainties. In rare case, unavoidable faults happen when the robot working. To deal with these uncertainties and faults, various control methods have been proposed in literature, such as PID control [1, 2], adaptive control [3], fuzzy control [4, 5], neural network control [6, 7], sliding mode control (SMC) [8,9,10]. Compared with other controllers, SMC standouts with salient features such as easy design procedure, robustness against the effect of dynamic uncertainties and faults. Basically, SMC uses a proportional-derivative (PD) sliding function to deal with the overshoot problem and get a fast response, respectively. To archive higher accuracy, an integral part has been added into the sliding function which is called proportional-integral-derivative SMC (PID-SMC) [11]. However, both conventional SMC and PID-SMC still include the disadvantages, such as: (1) chattering phenomenon; (2) do not provide the finite-time convergence; (3) require the prior knowledge of the dynamic uncertainties and faults, and (4) the design procedure need the velocity information.

In order to eliminate the chattering problem, this paper employs super-twisting algorithm (STA) to provide continuous control signal instead of the discontinuous one. On the other hand, the finite-time convergence of STA has been successfully proved in literature [12, 22]. Unfortunately, its design procedure still requires the velocity measurement information and the prior knowledge of the lumped uncertainties and faults which do not exist in realization. In order to obtain the dynamic uncertainties and faults information, a lot of estimation methods have been developed, such as time delay estimation [13, 14], neural network observer [15], third-order sliding mode observer (TOSMO) [16, 17]. Among them, TOSMO is the remarkable estimation method because of its ability to estimate not only the lumped dynamic uncertainties and faults but also the velocity information without the need of a lowpass filter.

Although the requirement of the prior knowledge of uncertainties and faults is eliminated in controller design procedure, however, it is still needed in the process of designing of TOSMO. Generally, the observer’s parameters are selected based on experience and the upper bound of the lumped dynamic uncertainties and faults. In literature, various methods have been developed to estimate system parameters, such as adaptive law [18], fuzzy logic [19], radial basis function neural network (RBFN) [20]. In this paper, RBFN is used to approximate the parameters of TOSMO because of its fast learning ability, high approximation accuracy, and simple structure [17].

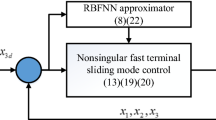
This paper proposes a neural TOSMO which can estimate both the velocities and the dynamic uncertainties and faults with high accuracy fast response without the need of lowpass filter. Additionally, the assumption of prior knowledge of the lumped uncertainties and faults are eliminated. Based on the obtained information of the observer, a PID-SMC control method based on super-twisting algorithm is designed to deal with the robot dynamic uncertainties and faults. The proposed control strategy provides high position tracking accuracy with less chattering, highly robust against the effects of the uncertainties and faults with only position measurement. The global stability and finite-time convergence are guaranteed by Lyapunov theory.

The structure of this paper is as follows. The dynamic equation of a n-link robotic manipulator is first described in Sect. 2. Then, the process of designing of TOSMO and neural TOSMO for robotic manipulators is presented in Sect. 3. Section 4 introduces the controller design procedure. In Sect. 5, the simulation results of the proposed control method are shown for a PUMA560 robotic manipulator. Finally, conclusions are presented in Sect. 6.

2 Problem Statement

The dynamic equation of a serial n-link robotic manipulator with faults is given as

$$ \ddot{\theta } = M^{ - 1} \left( \theta \right)\left[ {\tau - C\left( {\theta ,\dot{\theta }} \right)\dot{\theta } - G\left( \theta \right) - F\left( {\theta ,\dot{\theta }} \right) - \tau_{d} } \right] + \gamma \left( {t - T_{f} } \right)\Psi \left( t \right) $$
(1)

where \( \theta ,\dot{\theta },\ddot{\theta } \in {\mathbb{R}}^{n} \) denote position, velocity, and acceleration of robot joints, respectively. \( \tau \in {\mathbb{R}}^{n} \), \( M\left( \theta \right) \in {\mathbb{R}}^{n \times n} \), \( C\left( {\theta ,\dot{\theta }} \right) \in {\mathbb{R}}^{n} \), \( G\left( \theta \right) \in {\mathbb{R}}^{n} \) represent the control input torque, inertia matrix, Coriolis and centripetal forces, gravitational force term, respectively. \( F\left( {\theta ,\dot{\theta }} \right) \in {\mathbb{R}}^{n} \), \( \tau_{d} \in {\mathbb{R}}^{n} \) denote the friction vector and disturbance vector, respectively, these two elements constitute the dynamic uncertainties. \( \Psi \left( t \right) \in {\mathbb{R}}^{n} \) indicates unknown faults with the time of occurrence \( T_{f} \).

\( \gamma \left( {t - T_{f} } \right) = diag\left\{ {\gamma_{1} \left( {t - T_{f} } \right),\gamma_{2} \left( {t - T_{f} } \right), \ldots ,\gamma_{n} \left( {t - T_{f} } \right)} \right\} \) is the time profile of the faults

$$ \gamma_{1} \left( {t - T_{f} } \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {if\,t \le T_{f} } \hfill \\ {1 - e^{{ - \varsigma_{i} \left( {t - T_{f} } \right)}} } \hfill & {if\,t \ge T_{f} } \hfill \\ \end{array} } \right. $$
(2)

where \( \varsigma_{i} > 0 \) is the unknown faults evolution rate. The small and large values of \( \varsigma_{i} \) characterize incipient faults and abrupt faults, respectively.

For simpler in design procedure, the robot dynamics of (1) can be rewritten in state space as

$$ \begin{aligned} & \dot{x}_{1} = x_{2} \\ & \dot{x}_{2} = \Upsilon \left( x \right) + M^{ - 1} \left( {x_{1} } \right)u(t) +\Xi (x,t) \\ \end{aligned} $$
(3)

where \( x_{1} = \theta , \) \( x_{2} = \dot{\theta }, \)\( x = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } \\ \end{array} } \right]^{T} \), \( u(t) = \tau , \) \( \Upsilon \left( x \right) = M^{ - 1} \left( \theta \right)\left[ { - C\left( {\theta ,\dot{\theta }} \right)\dot{\theta } - G\left( \theta \right)} \right] \) and \( \Xi \left( {x,t} \right) = M^{ - 1} \left( \theta \right)\left[ { - F\left( {\theta ,\dot{\theta }} \right) - \tau_{d} } \right] + \gamma \left( {t - T_{f} } \right)\Psi \left( t \right) \) indicates the lumped dynamic uncertainties and faults.

The purpose of this paper is to design a continuous PID-SMC based on neural TOSMO which can handle the effect of lumped dynamic uncertainties and faults with only available position measurement. This controller is designed based on the following assumption.

Assumption 1:

The lumped dynamic uncertainty and fault \( \Xi \left( {x,t} \right) \) of the system and its time derivative are bounded as

$$ \left| {\Xi \left( {x,t} \right)} \right| \le \bar{\Xi } $$
(4)
$$ \left| {\dot{\Xi }\left( {x,t} \right)} \right| \le \bar{\Lambda } $$
(5)

where \( \bar{\Xi } \) and \( \bar{\Lambda } \) are positive constants.

3 Observer Design

3.1 Third-Order Sliding Mode Observer

Based on robot dynamics (3), the third-order sliding mode observer is designed as [17]

$$ \begin{aligned} & \dot{\hat{x}}_{1} = \mu_{1} \left| {x_{1} - \hat{x}_{1} } \right|^{2/3} sign\left( {x_{1} - \hat{x}_{1} } \right) + \hat{x}_{2} \\ & \dot{\hat{x}}_{2} = \Upsilon (\hat{x}) + M^{ - 1} \left( {\hat{x}_{1} } \right)u(t) + \mu_{2} \left| {x_{1} - \hat{x}_{1} } \right|^{1/3} sign\left( {x_{1} - \hat{x}_{1} } \right) + \hat{z} \\ & \dot{\hat{z}} = \mu_{3} sign\left( {x_{1} - \hat{x}_{1} } \right) \\ \end{aligned} $$
(6)

where \( \hat{x} \) is the estimation of \( x \) and \( \mu_{i} \) denotes the sliding mode gains.

The estimation error can be obtained by subtracting (6) from (3)

$$ \begin{aligned} & \dot{\tilde{x}}_{1} = - \mu_{1} \left| {\tilde{x}_{1} } \right|^{2/3} sign\left( {\tilde{x}_{1} } \right) + \tilde{x}_{2} \\ & \dot{\tilde{x}}_{2} = - \mu_{2} \left| {\tilde{x}_{1} } \right|^{1/3} sign\left( {\tilde{x}_{1} } \right) + \Xi (x,t) + d\left( {\tilde{x},t} \right) - \hat{z} \\ & \dot{\hat{z}} = \mu_{3} sign\left( {\tilde{x}_{1} } \right) \\ \end{aligned} $$
(7)

where \( \tilde{x} = x - \hat{x} \) and \( d\left( {\tilde{x},t} \right) = \Upsilon (x) + M^{ - 1} \left( {x_{1} } \right)u(t) - \left( {\Upsilon (\hat{x}) + M^{ - 1} \left( {\hat{x}_{1} } \right)u(t)} \right) \).

Defining \( \tilde{x}_{3} = - \hat{z} + \Xi_{o} (x,t) \), where \( \Xi_{o} (x,t) = \Xi (x,t) + d\left( {\tilde{x},t} \right) \). Equation (7) becomes

$$ \begin{aligned} & \dot{\tilde{x}}_{1} = - \mu_{1} \left| {\tilde{x}_{1} } \right|^{2/3} sign\left( {\tilde{x}_{1} } \right) + \tilde{x}_{2} \\ & \dot{\tilde{x}}_{2} = - \mu_{2} \left| {\tilde{x}_{1} } \right|^{1/3} sign\left( {\tilde{x}_{1} } \right) + \tilde{x}_{3} \\ & \dot{\tilde{x}}_{3} = - \mu_{3} sign\left( {\tilde{x}_{1} } \right) + \dot{\Xi }_{o} (x,t) \\ \end{aligned} $$
(8)

By choosing the candidate Lyapunov function \( L_{0} \) and using the same proving procedure as in [21], we can prove that the system (8) is stable and the estimation errors \( \tilde{x}_{1} ,\, \)\( \tilde{x}_{2} ,\, \) and \( \tilde{x}_{3} \) converge to zero in finite time with convergence time as

$$ T_{0} \left( {\tilde{x}_{0} } \right) \le \frac{{L_{0}^{{{1 \mathord{\left/ {\vphantom {1 5}} \right. \kern-0pt} 5}}} \left( {\tilde{x}_{0} } \right)}}{{\tfrac{1}{5}\chi }} $$
(9)

where \( \tilde{x}_{0} \) is the initial condition of (8) and \( 0 \le \chi \le 2.8 \times 10^{ - 4} . \)

After the convergence process, the estimated states will achieve the real states \( \left( {\hat{x}_{1} = x_{1} ,\,\hat{x}_{2} = x_{2} } \right) \) and \( d\left( {\tilde{x},t} \right) = 0 \), the third term of system (8) becomes

$$ \dot{\tilde{x}}_{3} = - \mu_{3} sign\left( {\tilde{x}_{1} } \right) + \dot{\Xi }(x,t) \equiv 0 $$
(10)

The lumped dynamic uncertainties and the faults can be reconstructed as

$$ \hat{\Xi }\left( {x,t} \right) = \int {\mu_{3} sign\left( {\tilde{x}_{1} } \right)} $$
(11)

We can see that the estimated dynamic uncertainties and faults in (11) can be reconstructed directly without the need of lowpass filter. Besides, an integral element is included, therefore, the chattering of the estimated function is partially eliminated.

Although the TOSMO provides high estimation accuracy and finite time convergence, its parameters in still selected based on experience and the upper bound of the lumped dynamic uncertainties and faults. In the next Section, the neural TOSMO will be designed to surpass this drawback of TOSMO.

3.2 Neural Third-Order Sliding Mode Observer

Based on robot dynamics (3), the neural TOSMO is designed as

$$ \begin{aligned} & \dot{\hat{x}}_{1} = {\kern 1pt} \;\hat{\mu }_{1} \left| {\tilde{x}_{1} } \right|^{2/3} sign\left( {\tilde{x}_{1} } \right) + \hat{x}_{2} \\ & \dot{\hat{x}}_{2} = \Upsilon (\hat{x}) + M^{ - 1} \left( {\hat{x}_{1} } \right)u(t) + \hat{\mu }_{2} \left| {\tilde{x}_{1} } \right|^{1/3} sign\left( {\tilde{x}_{1} } \right) + \hat{z} \\ & \dot{\hat{z}} = \hat{\mu }_{3} sign\left( {\tilde{x}_{1} } \right) \\ \end{aligned} $$
(12)

where \( \hat{\mu }_{i} \) is the estimation of \( \mu_{i} \)

$$ \hat{\mu }_{i} = \hat{V}_{i}^{T} \Phi_{i} \left( {X_{k} } \right),\,i = 1,2,3 $$
(13)

where \( X_{k} = \left[ {e_{1} \,e_{2} } \right]^{T} \) is the neural network input with \( e_{1} = x_{1} - \hat{x}_{1} \) and \( e_{2} = \dot{\hat{x}}_{1} - \hat{x}_{2} \).

The RBFN is used as an activation function

$$ \Phi_{i} \left( {X_{k} } \right) = \exp \left( {\frac{{\left\| {X_{k} - c_{ij} } \right\|^{2} }}{{\sigma_{ij}^{2} }}} \right) $$
(14)

where \( c_{ij} \) denotes the center vector, \( \sigma_{ij} \) denotes the spread factor, \( j = 1,2, \ldots ,N \) denotes the number of nodes in the hidden layer.

The weigh update law is as

$$ \dot{\hat{V}}_{i} = \eta_{i} \Phi_{i} \left( {X_{k} } \right)\left\| {X_{k} } \right\| $$
(15)

where \( \eta_{i} \) denote the learning rate.

By the same procedure with Sect. 3.1, we can reconstruct the lumped dynamic uncertainties and faults as

$$ \hat{\Xi }\left( {x,t} \right) = \int {\hat{\mu }_{3} sign\left( {\tilde{x}_{1} } \right)} $$
(16)

Consequently, the requirement of prior knowledge of the lumped dynamic uncertainties and faults has been removed. The obtained velocities and faults information are used to design controller in Sect. 4. The effectiveness of the proposed observer will be shown in simulation results.

4 Controller Design

We define the tracking error and velocity error as

$$ \hat{e} = \hat{x}_{1} - x_{d} $$
(17)
$$ \hat{\dot{e}} = \hat{x}_{2} - \dot{x}_{d} $$
(18)

where \( x_{d} \,{\text{and}}\,\dot{x}_{d} \) describe the desired trajectory and velocity, respectively.

The PID sliding function is selected as [11]

$$ \hat{s} = K_{p} \hat{e} + K_{i} \int {\hat{e} + K_{d} } \hat{\dot{e}} $$
(19)

where \( K_{i} ,K_{p} ,\,and\,K_{d} \) denote the proportional, integral, and derivative gains, respectively.

Taking the first-time derivative of sliding function, we obtain

$$ \begin{aligned} \dot{\hat{s}} = & \,K_{p} \dot{\hat{e}} + K_{i} \hat{e} + K_{d} \dot{\hat{\dot{e}}} \\ = & \,K_{p} \left( {\dot{\hat{x}}_{1} - \dot{x}_{d} } \right) + K_{i} \hat{e} + K_{d} \left( {\dot{\hat{x}}_{2} - \ddot{x}_{d} } \right) \\ = & \,K_{p} \left( {\dot{\hat{x}}_{1} - \dot{x}_{d} } \right) + K_{i} \hat{e} + K_{d} \left( {\begin{array}{*{20}l} {\Upsilon (\hat{x}) + M^{ - 1} \left( {\hat{x}_{1} } \right)u(t)} \hfill \\ { + \hat{\mu }_{2} \left| {\tilde{x}_{1} } \right|^{1/3} sign\left( {\tilde{x}_{1} } \right) + \hat{\mu }_{3} \int {sign\left( {\tilde{x}_{1} } \right) - \ddot{x}_{d} } } \hfill \\ \end{array} } \right) \\ \end{aligned} $$
(20)

The control law is designed as follows

$$ u = - \frac{1}{{K_{d} }}M\left( {x_{1} } \right)\left( {u_{eq} + u_{smc} } \right) $$
(21)

where the equivalent control law \( u_{eq} \) is designed as

$$ u_{eq} = K_{p} \left( {\dot{\hat{x}}_{1} - \dot{x}_{d} } \right) + K_{i} \hat{e} + K_{d} \left( {\Upsilon (\hat{x}) + \hat{\mu }_{2} \left| {\tilde{x}_{1} } \right|^{1/3} sign\left( {\tilde{x}_{1} } \right) + \hat{\mu }_{3} \int {sign\left( {\tilde{x}_{1} } \right) - \ddot{x}_{d} } } \right) $$
(22)

and the switching control law \( u_{smc} \) is designed based on super-twisting algorithm as

$$ \begin{aligned} & u_{smc} = \rho_{1} \left| {\hat{s}} \right|^{1 /2} \text{sgn} \left( {\hat{s}} \right) + \vartheta \\ & \dot{\vartheta } = \rho_{2} \text{sgn} \left( {\hat{s}} \right) \\ \end{aligned} $$
(23)

Substituting the control laws (21–23) into (20), we obtain

$$ \begin{aligned} & \dot{\hat{s}} = \rho_{1} \left| {\hat{s}} \right|^{1 /2} \text{sgn} \left( {\hat{s}} \right) + \vartheta \\ & \dot{\vartheta } = \rho_{2} \text{sgn} \left( {\hat{s}} \right) + \dot{\delta } \\ \end{aligned} $$
(24)

Since the estimation of the lumped dynamic uncertainties and faults \( \hat{\mu }_{3} \int {sign\left( {\tilde{x}_{1} } \right)} \) is included in the equivalent control signal, the stability and finite time convergence of the system (24) will be guaranteed in [22] if the sliding gains are chosen as

$$ \begin{aligned} & \rho_{1} > 0 \\ & \rho_{2} > \left( {3 + 2\frac{{\bar{\delta }}}{{\rho_{1}^{2} }}} \right)\bar{\delta } \\ \end{aligned} $$
(25)

where \( \delta = \hat{\Xi } - \Xi \) denotes the uncertainties and faults estimation error and \( \left| {\dot{\delta }} \right| \le \bar{\delta } \).

The stability and finite time convergence of system (24) have been successfully proved by using Lyapunov theory in [22].

5 Simulation Results

In this section, the effectiveness of control method is proved by computer simulation for a PUMA560 robot with the last three links are locked. The explicit dynamic model and parameter values of PUMA560 robot are given in [23].

The friction \( F\left( {\theta ,\dot{\theta }} \right) \in {\mathbb{R}}^{n} \) and disturbance \( \tau_{d} \in {\mathbb{R}}^{n} \) vectors are assumed as

$$ F\left( {\theta ,\dot{\theta }} \right) = \left[ {\begin{array}{*{20}c} {0.8\dot{\theta }_{1} + 1.2\cos \left( {3\theta_{1} } \right)} \\ {1.3\dot{\theta }_{2} + 0.5sin\left( {5\theta_{2} } \right)} \\ {0.7\dot{\theta }_{3} + 0.3\sin \left( {3.5\theta_{3} } \right)} \\ \end{array} } \right]\,\,\,\,\,{\text{and}}\,\,\,\,\,\tau_{d} = \left[ {\begin{array}{*{20}c} {1.2\sin \left( {0.95\dot{\theta }_{1} } \right)} \\ {0.9\cos \left( {1.7\dot{\theta }_{2} } \right)} \\ {0.5\sin \left( {3.2\dot{\theta }_{3} } \right)} \\ \end{array} } \right] $$
(26)

The fault occurs at \( T_{f} = 10s \) and is assumed as

$$ \Psi = \left[ {\begin{array}{*{20}c} {2\cos (0.8t)} & {3\sin (t)} & {1.2\sin (t)} \\ \end{array} } \right]^{T} $$
(27)

In this simulation, three RBFNs with 20 neurons in each hidden layer are used to approximate three parameters of the proposed observer, respectively. The learning rates are chosen as \( \eta_{i} = 2.5,\,i = 1,2,3 \). The sliding gains of TOSMO are selected as \( \mu_{1} = 3L^{1/3} ,\,\mu_{2} = 1.5L^{1/2} ,\,\mu_{3} = 1.1L \) with \( L = 6 \) [24]. The estimation of velocities and the lumped uncertainties and faults are shown in Figs. 1 and 2. We can see that the obtained information are almost the same with the results of TOMSO, however, the upper bound of the lumped uncertainties and faults is not needed.

Fig. 1.
figure 1

Comparison of velocity estimation error between TOSMO and neural TOSMO among three joints.

Full size image
Fig. 2.
figure 2

Comparison of lumped uncertainty and fault estimation error between TOSMO and neural TOSMO among three joints.

Full size image

In order to verify the effectiveness of the proposed controller, the parameters of proposed controller are selected as \( K_{i} = 7,\,K_{p} = 3,\,K_{d} = 0.5,\rho_{1} = 1.5,\rho_{2} = 1.1 \). Figure 3 shows the comparison of position tracking error between the proposed controller and the conventional PID-SMC which is designed as follows:

Fig. 3.
figure 3

Comparison of position tracking error between conventional PID-SMC and proposed controller among three joints.

Full size image

The PID sliding function is selected as

$$ s = K_{p} e + K_{i} \int {e + K_{d} } \dot{e} $$
(28)

where \( e = x_{1} - x_{d} \) and \( \dot{e} = x_{2} - \dot{x}_{d} \)

The control law is designed as follows

$$ u = - \frac{1}{{K_{d} }}M\left( {x_{1} } \right)\left( {u_{eq} + u_{smc} } \right) $$
(29)
$$ u_{eq} = K_{p} \dot{e} + K_{i} e + K_{d} \left( {\Upsilon (x) - \ddot{x}_{d} } \right) $$
(30)
$$ u_{smc} = \Pi \text{sgn} \left( s \right) $$
(31)

where \( \Pi \ge \bar{\Xi } \) is sliding gain.

From the results, the proposed controller provides higher tracking accuracy, however, its convergence time becomes longer. This phenomenon is a consequence of the velocity estimation delay. The output control signal is shown in and Fig. 4. The results show that the chattering phenomenon is eliminated thanks to the effectiveness of super-twisting algorithm.

Fig. 4.
figure 4

Comparison of control signal between conventional PID-SMC and proposed controller among three joints.

Full size image

6 Conclusions

This paper proposes a continuous PID-SMC strategy based neural TOSMO for uncertainty robotic manipulator without velocity measurement. The neural TOSMO provides high estimation accuracy without the requirement of the prior knowledge of lumped dynamic uncertainties and the faults. The tracking error accuracy is improved by using the proposed control algorithm. The global stability and finite-time convergence of system is guaranteed. The simulation results on a 3-DOF PUMA560 robot verify the effectiveness of the proposed strategy.