Self-Assembly from a Single-Molecule Perspective

Abstract

As manipulating the self-assembly of supramolecular and nanoscale constructs at the single-molecule level increasingly becomes the norm, new theoretical scaffolds must be erected to replace the thermodynamic and kinetics based models used to describe traditional bulk phase active syntheses. Like the statistical mechanics underpinning these latter theories, the framework we propose uses state probabilities as its fundamental objects; but, contrary to the Gibbsian paradigm, our theory directly models the transition probabilities between the initial and final states of a trajectory, foregoing the need to assume ergodicity. We leverage these probabilities in the context of molecular self-assembly to compute the overall likelihood that a specified experimental condition leads to a desired structural outcome. We demonstrate the application of this framework to a simple toy model in which three identical molecules can assemble in one of two ways and conclude with a discussion of how the high computational cost of such a fine-grained model can be overcome through approximation when extending it to larger, more complex systems.

1 Introduction

The concept of structure-driven communication is first grasped at a very young age, when one first puzzles out that the square peg must be inserted into the square hole. But at a much earlier stage of development, this “lock and key” motif is already ingrained into our bodies on the microscale, where evolution has engineered countless proteins whose native states form a pocket that is sized and shaped to bind only a single, specific molecular partner. In the macroworld, we make locks that admit only a single key shape so that we may exclude others from our privacy. Exclusivity is the objective of structural communication in the microworld as well, though it is not volitional interlopers who are the concern but rather stochastic ones. In the noisy environment of our cells, structural exclusion is the only way to ensure that a protein does not bind the first molecule to diffuse into it.

While structural specificity may combat the stochasticity inherent to molecular binding, the stochasticity inherent to the self-assembly of these structures themselves is a much higher hurdle to surpass. Even nature, with four billion years of evolutionary experience, has not perfected this art. The misfolding of proteins like the neuronal amyloid-beta ($A\beta$) protein or the pancreatic amylin, for example, can seed the formation of plaques that have been implicated as a potential cause for Alzheimer’s disease and type II diabetes, respectively [1]. Human efforts to synthesize nanoscale structures that can interact with or leverage biology have thus understandably struggled with precise structural control. Gold nanoparticle [2] and liposome [3] syntheses have difficulty achieving acceptable levels of monodispersity, biofilm [4] and other monolayer surface depositions [5] are prone to disorder and defects, and supramolecular assemblies [6] are often plagued by competing interactions that lead to disparate products.

Newer techniques such as optical and magnetic tweezers [7], molecular beams [8], and micro- and nanofluidics [9] have shown potential for greatly improving our control over molecular self-assembly processes by reducing the scale of the experiments from the macroscopic bulk phase to systems involving only a few relevant molecules. The current theories used to model self-assembling systems, however, still largely rely on bulk statistical thermodynamics and kinetics [10,11,12], which are insufficient for this new experimental scale. In this paper we attempt to address this gap by modeling the distribution of self-assembled states by considering the stochastic dynamics of a single self-assembly sequence and its branching structural end states. The result is a probabilistic model that requires neither an ergodic hypothesis nor a thermodynamic limit.

2 The Model

The framework of our model is to assign to each molecule two sets of stochastic variables. The first set, which we denote as the state $\psi$, characterizes the molecule’s entry into the system. This set of parameters might include the time at which it is injected or emitted, its initial position and velocity, and its starting orientation. These are parameters over which the experimenter exercises some degree of control. The second set, which we denote by the state $\phi$, describes the molecule’s interaction with the self-assembling core. Whether or not the molecule adds to the growing structure and in what manner it adds will depend upon the same sorts of parameters, but evaluated at the time of first interaction, which itself may be one of the random variables in $\phi$. We denote the set of all possible end states of the self-assembly process under consideration as S, and the probability that self-assembly terminates at some structure $s\in S$ will depend upon the states $\phi$ of each interacting molecule–even those that interacted without binding to the structure. We call this set of states $\{\phi \}$ and the probability linking this set to a specified outcome as $p_{R}(s\in S\vert \{\phi \})$, where the R index stands for “result.”

The set of states $\{\phi \}$ evolve dynamically from the set of initial states $\{\psi \}$ as a result of some stochastic transport process. This process might be simple diffusion through a volume or across a surface, or it might be some facilitated process. The probability of observing a specific set of interacting states given a set of initial states is defined as the conditional transport probability $p_{T}(\{\phi \}\vert \{\psi \})$. We further define the source probability $p_S(\{\psi \}\vert \sigma )$ as the likelihood that a set of initial states $\{\psi \}$ are observed given specified values of a set of externally tunable parameters $\sigma$. This set can consist of variables like temperature and emission frequency that are directly manipulated by the experimenter. The ultimate probability that we wish to compute is $p_F(s\vert \sigma )$, the overall final probability that a set of input parameters will result in molecules assembling into structure s. This probability can be related to the latter three by the following integral:

$$\begin{aligned} p_{F}(s\vert \sigma )=\int d\{\phi \} d\{\psi \}\, p_{R}(s\vert \{\phi \})p_{T}(\{\phi \}\vert \{\psi \})p_S(\{\psi \}\vert \{\sigma \}). \end{aligned}$$

(1)

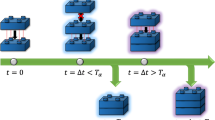
The complexity involved in actually evaluating Eq. (1) will naturally depend upon the details of the system under consideration. In this paper, we restrict our attention to a simple toy model that demonstrates how this theoretical framework might be applied and what sort of predictions it can be used to make. In this model, we assume that three identical molecules are released at randomly selected times into a one-dimensional drift-diffusion channel characterized by a drift speed v, a diffusion constant D, and a channel length $\ell$. The first molecule to traverse the channel binds to a receptor site that catalyzes a self-assembly process with the second molecule to arrive, resulting in a dimer state. We assume that this assembly process takes a finite amount of time, which we denote as the assembly time $T_{\alpha }$. If the third molecule arrives while dimer assembly is still occurring, it will be repelled and the final state of the system will be the dimer. If, on the other hand, it arrives once the dimer is complete, then a trimer state will result. Figure 1 depicts a cartoon representation of our toy model and summarizes its possible outcomes.

Fig. 1.

Toy model timeline. If $t=0$ is the time at which the first two monomers initiate their self-assembly into a dimer, then $t=\varDelta t$ is the time at which the third monomer arrives. Depending upon whether this time is smaller or larger than the self-assembly time scale $T_{\alpha }$, the final state of the model will either be the original dimer or a trimer.

If the three molecules are labeled 0, 1, and 2 based on the order in which they are released into the channel, we may define the initial state of the $i^{th}$ particle $\psi _i$ as its injection time $\tau _i$, and its interaction state $\phi _i$ can be defined analogously as its arrival time $t_i$ at the channel terminus. Because the first such arrival time may be thought of as the start of the experiment, the absolute release and arrival times are irrelevant, and we can replace these six time variables with four time intervals. We define the intervals $\varDelta \tau _1$ and $\varDelta \tau _2$ as the differences between the injection times of particle 1 and particle 0 and particle 2 and particle 0, respectively. Analogously, the intervals $\varDelta t_1$ and $\varDelta t_2$ are the equivalent differences in the arrival times of the particles at the self-assembly site. Because the order in which the particles arrive is not fixed, due to the stochasticity of the transport down the channel, these latter time intervals can potentially be negative. The space of self-assembled structures S in this case contains only the dimer and trimer configurations, which we shall denote as $s_2$ and $s_3$, respectively. The probability of observing a dimer at the end of the experiment depends upon whether or not the third molecule to interact does so within a time $T_{\alpha }$ of the second molecule’s arrival. We can thus write the dimer result probability $p_{R}(s_2\vert \varDelta t_1,\varDelta t_2)$ as the following conditional:

$$\begin{aligned} p_R(s_2\vert \varDelta t_1,\varDelta t_2)= {\left\{ \begin{array}{ll} 1-\varTheta (\vert \varDelta t_2-\varDelta t_1\vert -T_{\alpha }) &{} \text { for } \varDelta t_1\ge 0, \varDelta t_2\ge 0 \\ 1-\varTheta (\vert \varDelta t_2\vert -T_{\alpha }) &{} \text { for } \varDelta t_2\ge \varDelta t_1, \varDelta t_1< 0 \\ 1-\varTheta (\vert \varDelta t_1\vert -T_{\alpha }) &{} \text { for } \varDelta t_1\ge \varDelta t_2, \varDelta t_2< 0. \end{array}\right. } \end{aligned}$$

(2)

In the above, $\varTheta (t)$ is the Heaviside step function. We adopt the convention that it takes value unity when its argument exceeds zero and has value zero otherwise. Since the only other possibility is that a trimer is formed, $p_{R}(s_3\vert \varDelta t_1,\varDelta t_2)=1-p_{R}(s_2\vert \varDelta t_1,\varDelta t_2)$.

The first passage time across a drift-diffusion channel is distributed according to the standard inverse Gaussian distribution $IG(\mu ,\lambda ;t)$ [13], analytically continued to be zero for negative values of its time argument:

$$\begin{aligned} IG(\mu ,\lambda ;t)= {\left\{ \begin{array}{ll} \sqrt{\frac{\lambda }{2\pi t^3}} \, \exp {\left[ \frac{-\lambda (t-\mu )^2}{2\mu ^2 t}\right] } &{} t>0 \\ &{} \\ 0 &{} t\le 0 \end{array}\right. } \end{aligned}$$

(3)

The parameter $\mu \equiv \ell /v$ is the time it takes to cross the channel in the absence of diffusion, and $\lambda \equiv \ell ^2/2D$ is the average time it would take in the absence of drift. This suggests the following form for the transport distribution $p_{T}(\varDelta t_1,\varDelta t_2\vert \varDelta \tau _1,\varDelta \tau _2)$:

(4)

Finally, we will assume that each molecule has an equal chance of being released into the channel at any moment in time after the previous molecule’s emission, which results in the release time intervals being exponentially distributed (as in a radioactive decay process). Assuming an average injection rate $1/\tau$, we get

$$\begin{aligned} p_{S}(\varDelta \tau _1,\varDelta \tau _2\vert \tau )&=\frac{1}{\tau ^2}e^{-(\varDelta \tau _2-\varDelta \tau _1)/\tau }e^{-\varDelta \tau _1/\tau } \nonumber \\&=\frac{1}{\tau ^2}e^{-\varDelta \tau _2/\tau }. \end{aligned}$$

(5)

Note that the dependence of this distribution on $\varDelta \tau _1$ cancels out of the exponent and that $\tau$ is the presumptive tuning parameter of the experiment.

Equations (2), (4), and (5) can be substituted into Eq. (1) to calculate the total dimer probability $p_F(s_2\vert \tau )$. The simple conditional form of the result probability $p_R(s_2\vert \varDelta t_1,\varDelta t_2)$ will lead to a modification in the limits of integration over the arrival time intervals. This leads to a more complicated looking expression for $p_F(s_2\vert \tau )$ that is nonetheless more straightforward to evaluate numerically:

$$\begin{aligned}&p_F(s_2\vert \tau )=\frac{1}{\tau ^2}\int _{0}^{\infty }d\varDelta \tau _2\int _{0}^{\infty }d\varDelta \tau _1\, e^{-\varDelta \tau _2/\tau } \nonumber \\&\times \, \left[ 2\int _{0}^{\infty }d\varDelta t_2\int _{\max (\varDelta t_2-T_{\alpha },0)}^{\varDelta t_2}d\varDelta t_1\, p_T(\varDelta t_1,\varDelta t_2\vert \varDelta \tau _1,\varDelta \tau _2)\right. \nonumber \\&+\,\left. 2\int _{0}^{T_{\alpha }}d\varDelta t_2\int _{0}^{\infty }d\varDelta t_1\, p_T(-\varDelta t_1,\varDelta t_2\vert \varDelta \tau _1,\varDelta \tau _2)\right. \nonumber \\&+\, \left. 2\int _{0}^{T_{\alpha }}d\varDelta t_2\int _{\varDelta t_2}^{\infty }d\varDelta t_1\, p_T(-\varDelta t_1,-\varDelta t_2\vert \varDelta \tau _1,\varDelta \tau _2)\right] . \end{aligned}$$

(6)

The three integrals over the arrival time intervals in the above expression correspond, respectively, to the cases in which particle 0 arrives first, second, and third. The factors of 2 account for the symmetry, in each case, of swapping the index labels 1 and 2.

3 Results and Discussion

Even for such a simple toy system, the numerical integration required to calculate $p_F(s_2\vert \tau )$ is computationally intensive, with the principal time sink being the repeated evaluations of Eq. (4) for all the different values of the release and arrival time intervals needed to evaluate Eq. (6). We resolved this difficulty by parallelizing the computation, evaluating each instance of $p_T(\varDelta t_1,\varDelta t_2\vert \varDelta \tau _1,\varDelta \tau _2)$ on a separate thread of an Nvidia GeForce GTX TITAN GPU with 3,072 cores, 12 GB of RAM, and 1,000 MHz clock speed. This reduced the total computational time by a factor of roughly 1,000. For our integration mesh, we chose a lattice spacing (bin width) of 0.02 time units, and a mesh domain defined in terms of model time units by the inequalities $0\le \varDelta \tau _1\le \varDelta \tau _2$, $0\le \varDelta \tau _2\le r$, $-10\le \varDelta t_1\le r+10$, and $-10\le \varDelta t_2\le r+10$, where the integration range r was set equal to 20 time units. For each point on this mesh, the formally infinite upper limit of each of the parallelized time integrals was approximated as 50 time units. These restricted integration ranges were sufficient to approximately normalize all of the probability distributions of the model to within an acceptable tolerance.

After computing the transport probability at each point of the chosen integration mesh, it became tractable to evaluate the integrals over the release and arrival time intervals serially, using an Intel Core i7-2600 CPU with 3.40 GHz clock speed and 8 GB of memory. We demonstrate how this computational time varies with integration range r in Fig. 2 for three different bin widths. As the logarithmic scale makes clear, the serial computation time grows roughly exponentially with the integration range. It also grows approximately as an inverse power law of the bin width, with a negative exponent of about 4.

Fig. 2.

Computational time (in seconds) plotted versus the integration range (in model time units) for three different bin widths (also in model time units): from top to bottom, 0.02 (red), 0.05 (green), and 0.1 (blue). The ordinate axis is on a log scale to better illustrate the exponential growth of the computational time for sufficiently large integration ranges. (Color figure online)

We plot our numerically evaluated probability $p_F(s_2\vert \tau )$ in Fig. 3(A) as a function of the self-assembly time scale $T_{\alpha }$ for values of the mean release interval $\tau = 0.5$, 1.5, 2.5, and 3.5, in descending order. For all curves, the time scales $\mu$ and $\lambda$ were both fixed at unity. As expected, when self-assembly is instantaneous ($T_{\alpha }=0$), there is no interval of time during which the third molecule can be repelled, so trimer formation is inevitable ($p_F(s_2\vert \tau )=0$). At the other extreme, as $T_{\alpha }\rightarrow \infty$, the dimer becomes the only possible product ($p_F(s_2\vert \tau )\rightarrow 1$). As molecule emissions into the channel become more infrequent (larger $\tau )$, the window to avoid trimer trapping becomes smaller, depressing the dimer probability. These curves are all fit very well by a function of the form $1-\exp [-c_1(T_{\alpha }/\tau )^{c_2}]$, where $c_1$ and $c_2$ are fitting parameters that may depend in a complicated manner upon some dimensionless combination of the time scales $\tau$, $\mu$, and $\lambda$. These best fit functions are plotted as solid curves over the numerical data in Fig. 3(A).

Fig. 3.

Plots of the final dimer formation probability $p_F(s_2\vert \tau )$ versus the self-assembly time scale $T_{\alpha }$ for (A) fixed $\mu$ and $\lambda$ equal to unity, with $\tau$ varying, from top to bottom, as 0.5, 1.5, 2.5, and 3.5; and for (B) fixed $\tau =1.5$ with $(\mu ,\lambda )$ varying, from top to bottom, as (1, 1), (2, 2), (2, 1), and (4, 2). The data points are the computationally evaluated probabilities, while the solid curves are the analytic fits of the function $1-\exp [-c_1(T_{\alpha }/\tau )^{c_2}]$.

Figure 3(B) also plots the final dimer probability versus $T_{\alpha }$, but this time $\tau$ is held fixed at $\tau =1.5$ and $\mu$ and $\lambda$ are varied instead. The top curve is the same as the second to top curve in panel (A) ($\mu =\lambda =1$). The remaining curves are, in descending order, for $(\mu ,\lambda )= (2,\,2), \;(2,\,1)$, and (4, 2). These curves illustrate several general trends. First, the dimer probability decreases monotonically with increasing $\mu$, reflecting the fact that a less facilitated channel will tend to space out the arrival times of the molecules, making trimer formation more likely. Increasing $\lambda$ tends to have the opposite effect, since reducing the diffusivity of the channel narrows the distribution of arrival times (Eq. (3)), resulting in a less noisy channel. The variance of the inverse Gaussian distribution is $\mu ^3/\lambda$, explaining why $p_F(s_2\vert \tau )$ has a stronger dependence on $\mu$ than on $\lambda$. These curves are well modeled by the same class of fitting function used in Fig. 3(A).

Perhaps the most informative way of quantifying how self-assembly depends upon our model parameters is with a “phase diagram,” where a relevant parameter subspace is divided into regions based upon the most probable structure in each. For our toy system, this phase diagram is fairly simple and is plotted in Fig. 4 as a function of the control parameter $\tau$ and the self-assembly time $T_{\alpha }$. The transport parameters $\mu$ and $\lambda$ are both fixed at unity. The phase boundary, which turns out to be approximately linear ($R^2$-value of ${\approx } 0.997$), was determined by finding, for each value of $\tau$, the critical value of $T_{\alpha }$ for which $p_F(s_2\vert \tau )=1/2$. For large $T_{\alpha }$ and small $\tau$, the shorter average interval between particle emissions and the longer assembly time will make it more likely for the third particle to arrive while the first two are still docking, thereby frustrating trimer formation. In the opposite limit, the time between emissions will be long and assembly will occur swiftly–both circumstances that favor the trimer product.

Fig. 4.

The phase diagram for the toy model when $\mu =\lambda =1$. The phase boundary separating the dimer and trimer favoring regions is approximately linear.

4 Conclusions

While the framework we have devised for quantifying self-assembly in terms of individual molecular interactions is quite general, we have seen even in the simple case of our three-molecule toy model that its computational cost is problematic, especially were one to extend it to the self-assembly of long biopolymers like proteins or microtubules. The set of interaction variables $\{\phi \}$ will necessarily grow linearly with the number of interactions considered, but the real problem is that an integral like that in Eq. (4) will have to be evaluated for every permissible set of values these variables can take. The number of integrations will thus grow exponentially with the number of interactions, rendering even parallelization schemes unfeasible for supramolecular assemblies consisting of more than a handful of subunits.

The most straightforward way to address this problem is to make physically sensible approximations that constrain the hypervolumetric domain of the variables $\{\phi \}$, thereby reducing the number of integrals that must be computed in parallel. In our toy model, for example, we must consider a range of $\varDelta t_1$ and $\varDelta t_2$ values broad enough to allow for $3!=6$ different interaction orders. If we work in the large $\tau$ limit, however, we can assume that the probability of nonconsecutively released particles interacting in reversed order is negligible. This reduces the number of permissible interaction orderings to three (removing the factor of two from the second term on the right of Eq. (6) and deleting the third term entirely) and eliminates the need to consider negative values of $\varDelta t_2$. This is only a modest gain, but if we were to extend our toy model to include tetrameric structures, this approximation scheme would reduce the number of allowable orderings from $4!=24$ to a paltry five.

Our intention moving forward is to begin exploring the impact these sorts of approximation schemes have on both computational time and numerical accuracy in the hopes of ultimately applying the methodology outlined in this paper to systems of actual biological consequence.