1 Introduction

Optimization methods are commonly exploited in the field of multibody dynamics in various aspects, e.g. in the early design stage or in the problems associated with an inverse dynamics task, which is especially important in the robotics field. A broad class of engineering problems involves the determination of input signals which must be supplied to the system [2]. Optimal control methods associated with a direct optimization approach tend to generate a large number of design variables which have to be treated by optimization procedure [1]. The adjoint method allows the computation of the gradient of the performance measure and exhibits a significantly lower computational overhead when compared to other gradient calculation techniques, especially when the number of design variables (or input signals) is large.

In general, the adjoint method requires a solution of a system of differential–algebraic equations (DAEs) backwards in time starting from a prescribed boundary condition in order to obtain a set of adjoint variables which are necessary to determine the gradient [4, 8]. Such an approach is based on continuous cost functional as well as a time integration of equations of motion (EOM). On the other hand, one can derive the discrete system of adjoint equations based on the discretized cost functional and EOM [3, 7]. Therefore, the mathematical models of both dynamic and adjoint systems display certain similar features, which can be exploited to improve numerical efficiency.

On the other hand, the performance of the optimization algorithm may strongly depend on robustness of the formulation of EOM. Herein, Hamilton’s canonical equations of motion are employed to evaluate the dynamic response of a multibody system (MBS). This method possesses many appealing numerical features [5], such as reduced differential index of the resultant DAEs, that ought to be exploited in the development of an efficient and reliable adjoint–based method.

This paper presents an introductory work that demonstrates an effort to develop an adjoint method for the gradient calculation when a multibody system is modeled by using constrained Hamilton’s canonical equations. The primary importance of the paper is to look carefully at the advantages such a connection may provide in the context of efficiency and stability of calculations.

2 Discrete Hamilton’s Equations of Motion

The starting point for the analysis of MBS is a set of Hamilton’s equations of motion, where the system Lagrangian has been modified in order to impose the constraint equations directly at the velocity level:

$$\begin{aligned}&\mathbf {p}^* = \mathbf {M} (\mathbf q) \, \dot{\mathbf {q}} + \varvec{{\Phi }}_{\mathbf {q}}^T \varvec{{\upsigma }} , \end{aligned}$$
(1a)
$$\begin{aligned}&\dot{\mathbf {p}}^* = \mathbf {Q} (\mathbf q, \dot{\mathbf q}, \mathbf u)+\dot{\varvec{{\Phi }}}_{\mathbf {q}}^T\varvec{{\upsigma }} , \end{aligned}$$
(1b)
$$\begin{aligned}&\dot{\varvec{{\Phi }}}(\mathbf {q},\dot{\mathbf {q}}) = \varvec{{\Phi }}_{\mathbf {q}}\, \dot{\mathbf {q}} = \mathbf {0}. \end{aligned}$$
(1c)

Here, \(\mathbf q \in \mathcal {R}^n\) is a vector of generalized coordinates, \(\varvec{{\Phi }}\in \mathcal {R}^m\) indicates a vector of nonlinear holonomic constraints imposed on the system, \(\varvec{{\Phi }}_{\mathbf {q}}\in \mathcal {R}^{m\times n}\) denotes a constraint Jacobian matrix, \(\mathbf Q \in \mathcal {R}^n\) indicates a vector of external forces, \(\mathbf u \in \mathcal {R}^k\) describes input control signals, \(\mathbf M \in \mathcal {R}^{n\times n}\) is a mass matrix, and the quantity \(\varvec{{\upsigma }}\in \mathcal {R}^m\) denotes constraint impulsive forces. The vector of generalized momenta is defined as \(\mathbf p = \mathbf M \dot{\mathbf q}\), whereas Eq. (1) is based on augmented momenta \(\mathbf p^* \in \mathcal {R}^n\) which incorporate impulsive forces distributed along constrained directions indicated by the Jacobian matrix (see Eq. (1a)).

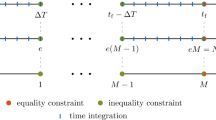
Equation (1) constitutes a set of \(2n+m\) nonlinear DAEs which will be discretized in order to obtain unknown variables, i.e. \(\mathbf p^*_i, \mathbf q_i,\varvec{{\upsigma }}_i\) at all time instances \(i = \{1,2,\cdots N\}\). The trapezoidal method, which is known to be an A-stable integrator, can be employed to tackle a large class of problems arising in MBS dynamics. In the cases of highly stiff problems, this property may be to weak, however, it has been observed to reliably address the solution of DAEs for the systems presented herein. The trapezoidal rule reads as:

$$\begin{aligned} \begin{aligned} \dot{\mathbf q}_i - \frac{2}{\varDelta \, t} \mathbf q_i + \hat{\dot{\mathbf q}}_{i-1}= \mathbf 0 , \quad \hat{\dot{\mathbf q}}_{i-1}= - \frac{2}{\varDelta \, t} \mathbf q_{i-1} - \dot{\mathbf q}_{i-1}, \\ \dot{\mathbf p}^*_i - \frac{2}{\varDelta \, t} \mathbf p^*_i + \hat{\dot{\mathbf p}}_{i-1}= \mathbf 0, \quad \hat{\dot{\mathbf p}}_{i-1}= - \frac{2}{\varDelta \, t} \mathbf p^*_{i-1} - \dot{\mathbf p}^*_{i-1}. \end{aligned} \end{aligned}$$
(2)

This approximation converts the original DAE (1) into a set of nonlinear algebraic equations expressed at \(i^{\text {th}}\) time instance:

$$\begin{aligned} \begin{aligned} - {\mathbf {p}}^*_i + \frac{2}{\varDelta t} {\mathbf {M}}_i {\mathbf {q}}_i + \mathbf {M}_i \hat{\dot{\mathbf q}}_{i-1}+ {\varvec{{\Phi }}}_{\mathbf q_i}^T {\varvec{{\upsigma }}}_i&= \mathbf {0},\\ -\frac{2}{\varDelta t} \mathbf {p}^*_i - \hat{\dot{\mathbf p}}_{i-1}+ \mathbf {Q}_i + \frac{2}{\varDelta t} \big ( {\varvec{{\Phi }}}_{{\mathbf {q}}_i} \mathbf {q}_i \big )^T_{\mathbf {q}_i} {\varvec{{\upsigma }}}_i + \big ({\varvec{{\Phi }}}_{\mathbf q_i} \mathbf {\hat{\dot{\mathbf q}}_{i-1}} \big )^T_{\mathbf q_i} {\varvec{{\upsigma }}}_i&= \mathbf {0} , \\ \frac{2}{\varDelta t} {\varvec{{\Phi }}}_{\mathbf q_i} \mathbf {q}_i + {\varvec{{\Phi }}}_{\mathbf q_i} \hat{\dot{\mathbf q}}_{i-1}&= \mathbf 0 . \end{aligned} \end{aligned}$$
(3)

A combined set of equations (2) and (3) may be expressed succinctly in the following form: \(\mathbf f (\mathbf y_i, \mathbf y_{i-1}, \mathbf u_i) = \mathbf f_i = \mathbf 0\). Given the initial condition \(\mathbf q(0) = \mathbf q, \mathbf p^*(0) = \mathbf p^*_0\), Eq. (3) can be propagated forward in time with the aid of, e.g., Newton method. This approach requires the definition of a tangent matrix to the Eq. (3), i.e. \(\frac{\partial \mathbf f_i}{\partial \mathbf y_i} = \mathbf f^i_{\mathbf y_i}\), where \(\mathbf y_i = [\dot{\mathbf q}^T_i, (\dot{\mathbf p}^*)^T_i, \mathbf q^T_i, (\mathbf p^*)^T_i, \varvec{{\upsigma }}^T_i]^T\). An iterative scheme must be established at every time–step, which will yield an update to the next time instance of unknown variables \(\mathbf y_{i+1}\):

$$\begin{aligned}{}[\, \mathbf f^{\,\,i}_{\mathbf y_i}\, ]^j \varDelta \mathbf y_{i+1}^{j+1} = - [\, \mathbf f_i \,]^j . \end{aligned}$$
(4)

Thus, \(\mathbf y_{i+1}\) may be successively updated as \(\mathbf y_{i+1}^{j+1} = \mathbf y_{i+1}^j = \varDelta \mathbf y_{i+1}^{j+1}\), where j refers to the iterator of Newton–Raphson procedure.

3 Discrete Hamiltonian-Based Adjoint Method

Let us consider an optimal control problem in which the aim is to find a sequence of control inputs \([u_0, u_1 \cdots u_N]\) that minimize the following performance measure:

$$\begin{aligned} J = \sum _{i=0}^{N-1} h_i \big (\mathbf y_i, \mathbf u_i \big ) + S \big (\mathbf y_N \big ), \end{aligned}$$
(5)

where \(h_i\) is a value of discretized cost function at \(i^{\text {th}}\) time–step, and S denotes a terminal cost used to prescribe particular configuration of the state at the final time. Provided that Eq. (3) is fulfilled by all state and control variables, one can premultiply its LHS by a vector of arbitrary adjoint variables \(\mathbf w_i \in \mathcal {R}^{4n+m}\) and add it to Eq. (5) without introducing any quantitative changes:

$$\begin{aligned} \hat{J} = h_0 + \mathbf w_0 \mathbf f_0 + \sum _{i=1}^{N-1} \Big ( h_i \big (\mathbf y_i, \mathbf u_i \big ) + \mathbf w_{i}^T \mathbf f_{i} \Big ) + \mathbf w_{N}^T \mathbf f_{N} + S \big (\mathbf y_N \big ) . \end{aligned}$$
(6)

The variation of Eq. (6) with respect to state variables and control input signals at each time instant reads as:

$$\begin{aligned} \begin{aligned} \delta \hat{J}&= h^0_{\mathbf y_0} \delta \mathbf y_0 + h^0_{\mathbf u_0} \delta \mathbf u_0 + \big ( \mathbf w^T_N \mathbf f^{\,\, N}_{\mathbf y_N} + S_{\mathbf y_N} \big ) \delta \mathbf y_N + \mathbf w^T_N \mathbf f^{\,\, N}_{\mathbf u_N} \delta \mathbf u_N \\&\quad +\sum _{i=1}^{N-1} \Big ( h^i_{\mathbf y_i} \delta \mathbf y_i + h^i_{\mathbf u_i} \delta \mathbf u_i + \mathbf w^T_i \mathbf f^{\,\, i}_{\mathbf y_i} \delta \mathbf y_i + \mathbf w^T_i \mathbf f^{\,\, i}_{\mathbf y_{i-1}} \delta \mathbf y_{i-1} + \mathbf w^T_i \mathbf f^{\,\, i}_{\mathbf u_i} \delta \mathbf u_i \Big ) , \end{aligned} \end{aligned}$$
(7)

where the following abbreviation is used: \(\mathbf a^i_{\mathbf b_j} = \frac{\partial \mathbf a_i}{\partial \mathbf b_j}\) (\(\mathbf a\), \(\mathbf b\) denote a pair of arbitrary vectors). By performing a simple index shift, Eq. (7) can be rewritten in a more favorable form:

$$\begin{aligned} \begin{aligned} \delta \hat{J}&= \big ( h^0_{\mathbf y_0} + \mathbf w^T_1 \mathbf f^{\,\, i}_{\mathbf y0} \big ) \delta \mathbf y_0 + h^0_{\mathbf u_0} \delta \mathbf u_0 + \big ( \mathbf w^T_N \mathbf f^{\,\, N}_{\mathbf y_N} + S_{\mathbf y_N} \big ) \delta \mathbf y_N + \mathbf w^T_N \mathbf f^{\,\, N}_{\mathbf u_N} \delta \mathbf u_N \\&\quad + \sum _{i=1}^{N-1} \Big ( \big ( h^i_{\mathbf y_i} + \mathbf w^T_i \mathbf f^{\,\, i}_{\mathbf y_i} + \mathbf w^T_{i+1} \mathbf f^{\,\, i+1}_{\mathbf y_{i}} \big ) \delta \mathbf y_i + \big ( h^i_{\mathbf u_i} + \mathbf w^T_i \mathbf f^{\,\, i}_{\mathbf u_i} \big ) \delta \mathbf u_i \Big ) . \end{aligned} \end{aligned}$$
(8)

Equation (8) presents a relation between the variation of the performance measure and the variations of all variables expressed at each time instance. Since the adjoint variables are at this point arbitrary, one can equate the expressions staying next to the state variations to zero. This condition uniquely defines all adjoint variables and generates the following sets of algebraic equations:

$$\begin{aligned} \big ( \mathbf f^{\,\, i}_{\mathbf y_i} \big )^T \mathbf w_i = - \big ( h^i_{\mathbf y_i} \big )^T - \big ( \mathbf f^{\,\, i+1}_{\mathbf y_i} \big )^T \mathbf w_{i+1} , \qquad \big ( \mathbf f^{\,\, N}_{\mathbf y_N} \big )^T \mathbf w_N = - \big ( \mathbf S_{\mathbf y_N} \big )^T . \end{aligned}$$
(9)

Jacobi matrices that appear in Eq. (9) have the following explicit form:

$$\begin{aligned} \mathbf f_{\mathbf y_i}^{\,\,i} = \begin{bmatrix} \mathbf {I}&\mathbf {0}&-\gamma \, \mathbf {I}&\mathbf {0}&\mathbf {0}\\ \mathbf {0}&\mathbf {I}&\mathbf {0}&-\gamma \, \mathbf {I}&\mathbf {0}\\ \mathbf {0}&\mathbf {0}&[\,\mathbf f_3^{\,\,i}\,]_{\mathbf q_i}&-\mathbf {I}&\varvec{{\Phi }}_{\mathbf {q}_i}^T \\ \mathbf {0}&\mathbf {0}&[\,\mathbf f_4^{\,\,i}\,]_{\mathbf q_i}&-\gamma \, \mathbf {I}&\dot{\varvec{{\Phi }}}_{\mathbf {q}_i}^T \\ \mathbf {0}&\mathbf {0}&\dot{\varvec{{\Phi }}}_{\mathbf q_i}^i&\mathbf {0}&\mathbf {0}\\ \end{bmatrix} , \quad \mathbf f_{\mathbf y_i}^{\,\,i+1} = \begin{bmatrix} \mathbf {I}&\mathbf {0}&\gamma \, \mathbf {I}&\mathbf {0}&\mathbf {0}\\ \mathbf {0}&\mathbf {I}&\mathbf {0}&\gamma \, \mathbf {I}&\mathbf {0}\\ -\mathbf M_i&\mathbf {0}&-\gamma \, \mathbf M_i&\mathbf {0}&\mathbf {0}\\ [\mathbf f_4^{\,\,i+1}]_{\dot{\mathbf q_i}}&\mathbf {I}&[\mathbf f_4^{\,\,i+1}]_{\mathbf q_i}&\gamma \, \mathbf {I}&\mathbf {0}\\ -\varvec{{\Phi }}_{\mathbf {q}_i}&\mathbf {0}&-\gamma \, \varvec{{\Phi }}_{\mathbf {q}_i}&\mathbf {0}&\mathbf {0}\\ \end{bmatrix} , \end{aligned}$$
(10)

where \(\mathbf I \in \mathcal {R}^{n \times n}\) is the identity matrix, and the abbreviated entries read as:

$$\begin{aligned}&[\,\mathbf f_3^{\,\,i}\,]_{\mathbf q_i} = \gamma \, \mathbf M_i+\left( \varvec{{\Phi }}_{\mathbf {q}}^T \varvec{{\upsigma }}_i \right) _{\mathbf q_i} , \qquad \quad [\,\mathbf f_4^{\,\,i}\,]_{\mathbf q_i} = \mathbf Q^i_{\mathbf q_i} + \gamma \, \mathbf Q^i_{\dot{\mathbf q}_i} + \big [ [\dot{\varvec{{\Phi }}}_{\mathbf q_i}^i]^T \varvec{{\upsigma }}_i \big ]_{\mathbf q_i} ,\\&[\mathbf f_4^{\,\,i+1}]_{\dot{\mathbf q_i}} = -\mathbf S - \mathbf Q^{i}_{\dot{\mathbf q_{i}}}, \qquad \qquad \quad [\mathbf f_4^{\,\,i+1}]_{\mathbf q_i} = -\gamma \, (\mathbf S + \mathbf Q^{i}_{\dot{\mathbf q_{i}}} ) ,\\&\dot{\varvec{{\Phi }}}_{\mathbf q_i}^i = \gamma \, \big (\varvec{{\Phi }}_{\mathbf {q}_i}\mathbf q_i \big )_{\mathbf q_i} + \big (\varvec{{\Phi }}_{\mathbf {q}_i}\hat{\dot{\mathbf q}}_{i-1}\big )_{\mathbf q_i} , \gamma \, = \frac{2}{\varDelta t} = \frac{\partial \dot{\mathbf q}_i}{\partial \mathbf q_i} , \\&\mathbf S = \big [ (\varvec{{\Phi }}_{\mathbf q_{i+1}} \mathbf q_i)^T \varvec{{\upsigma }}_{i+1} \big ]_{\mathbf q_i} = \big [ (\varvec{{\Phi }}_{\mathbf q_{i+1}} \dot{\mathbf q}_i)^T \varvec{{\upsigma }}_{i+1} \big ]_{\dot{\mathbf q}_i} . \end{aligned}$$

The adjoint variables obtained by solving Eq. (9) significantly simplify the expression (8). The gradient of the performance measure (5) can thus be evaluated as follows:

$$\begin{aligned} \nabla J (\mathbf u_i) = \big (h^i_{\mathbf u_i} + \mathbf w_i^T \mathbf f^{\,\, i}_{\mathbf u_i} \big ) \varDelta t , \quad \nabla J(\mathbf u_N) = \mathbf w_N^T \mathbf f^{\,\, N}_{\mathbf u_N} \varDelta t , \end{aligned}$$
(11)

where \(i = \{0, 1, \cdots N-1\}\). Let us note, that this procedure allows solving problems associated with optimal design as well. If we consider \(\mathbf u\) as a vector of static design parameters instead of a control sequence explicitly dependent on time, the formula for a gradient becomes:

$$\begin{aligned} \nabla J (\mathbf u) = h^0_{\mathbf u_0} + \sum _{i=0}^{N-1} \big ( h^i_{\mathbf u_i} + \mathbf w_i^T \mathbf f^{\,\, i}_{\mathbf u_i} \big ) \varDelta t. \end{aligned}$$
(12)

4 Numerical Example

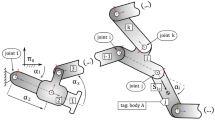
An optimal control problem of an underactuated system is presented as an illustrative example to demonstrate the performance of the developed method [9]. The goal is to identify a control input force \(u = F(t)\) acting on a cart, which allows a swing–up maneuver of a triple pendulum attached to the cart. The layout of the system is presented in Fig. 1. The mass of a cart is \(m_c = 0.8\) kg and its moment of inertia about z axis (perpendicular to the plane of motion) is \(J_c = 0.034\) kg m\(^2\). Three identical bodies are attached sequentially to the cart via revolute joints. The mass of each link is equal to \(m_p = 0.4\) kg and moment of inertia about z axis is \(J_p = 0.083\) kg m\(^2\). Additionally, a linear frictional force is introduced into translational and one of revolute joints, where \(c_{trans} = 0.5 \,\frac{Ns}{m}\) and \(c_{rot} = 0.2 \,\frac{Nsm}{rad}\). Let us note, that in this simple case, friction is included in the EOM in the form of generalized force. The system is initially at rest in a lower equilibrium configuration, i.e. \(\upvarphi _{1} = \upvarphi _{2} = \upvarphi _{3} = -\frac{\pi }{2}\) rad.

The optimization procedure has been supplied with a constant initial sequence of input control variables equal to \(F_0(t) = 10\,N\). Since the trajectory of the links is not provided in any form, the cost function can be reduced to a terminal term from Eq. (5), which reads as: \( J = 0.5 \cdot \big [ (\upvarphi _1 - \upvarphi _{v})^2 + (\upvarphi _2 - \upvarphi _{v})^2 + (\upvarphi _3 - \upvarphi _{v})^2 \big ]_{t_f} , \) where \(\upvarphi _v = \frac{\pi }{2}\) rad can be associated with vertical orientation of each link. The steepest descent method is employed for the optimization, along with a backtracking algorithm as a line–search procedure defining an optimal step size [10]. The gradient obtained with the adjoint method is exploited as a search direction, i.e. the following control inputs are determined as \(\mathbf u_{i+1} = - \alpha _{i+1} \nabla J(\mathbf u_i)\), where \(\alpha _{i+1}\) is a step size obtained via the backtracking procedure. Figure 2 presents four snapshots of the system’s motion (marked with red color) at consequent time–steps. For better readability, initial and final position of the bodies are added as a reference. The cart in the first frame (i.e. when \(t = 1.26\) s) is at its right–most position from which it moves left–wards in the following frames.

Figure 3 depicts a history of iterations of the optimization procedure: blue circles show the value of a cost functional with respect to the number of iterations, whereas red x-shaped markers present first–order optimality \(||\nabla J||_{\inf }\) on a logarithmic scale. The procedure keeps the cost close to zero after 300 iterations. Figure 4 shows the time–histories of position (\(\varvec{{\Phi }}(\mathbf q)\)), velocity (\(\dot{\varvec{{\Phi }}}(\mathbf q, \dot{\mathbf q})\)), and acceleration–level algebraic constraints (\(\ddot{\varvec{{\Phi }}}(\mathbf q, \dot{\mathbf q}, \ddot{\mathbf q})\)). The dynamic response is recorded for the starting iteration. Since velocity–level constraints are explicitly included in the EOM, \(\dot{\varvec{{\Phi }}}\) is very close to zero, i.e. up to \(10^{-14}\). Some constraint violation errors arise at the position level, however, their value generally lies between \(10^{-5}\) and \(10^{-4}\), which does not introduce significant numerical errors. During the optimization process, the shape of the input force acting on the cart is determined. Figure 5 presents the snapshots of the identified force throughout the process: initial, two intermediate ones, and the one obtained at the final iteration.

Fig. 1.
figure 1

Layout of the MBS

Full size image
Fig. 2.
figure 2

Consequent snapshots of the system acting under the identified control input

Full size image
Fig. 3.
figure 3

The progress of the optimization process

Full size image
Fig. 4.
figure 4

Holonomic constraints

Full size image
Fig. 5.
figure 5

Identified force acting on the cart recorded at following iterations

Full size image
Fig. 6.
figure 6

Time variant functions of the gradient calculated with different methods

Full size image

The accuracy of the adjoint method can be compared with a rather reliable, yet remarkably inefficient method of finite differencing. Figure 6 presents a time variant functions of the gradient calculated with both complex finite differences and adjoint method. Both plots are recorded for the initial point of the optimization procedure. The maximum relative error between the gradients, which occurs at \(t=0.52\) s is equal to \(0.5\%\). Let us compare the time required to calculate the gradient from \(t_0 = 0\) s to \(t_f = 2\) s with a constant step size equal to \(\varDelta t = 0.02\) s. Here, a standard PC has been used, which yielded the following execution times: \(T_{adjoint} = 0.35\) s and \(T_{complex} = 150\) s. This significant discrepancy comes from the fact, that the adjoint method solves \(4n+m\) Eq. (9) for all design variables. On the other hand, finite differences method requires to perform a forward solution of dynamic equations (1) for each design parameter, which is by far more time–consuming task compared to the execution of the adjoint method.

5 Conclusions

This paper presents an introductory effort to elaborate systematic methods of efficient gradient calculation for a multibody system. The forward dynamics problem is addressed with an efficient solution strategy based on Hamilton’s canonical equations. A trapezoidal integration rule is incorporated into the equations of motion in order to get its discretized version. Furthermore, the solution of a discrete adjoint system is used to efficiently and reliably compute a gradient vector. A representative optimal control problem is considered in the text, that illustrates an application of the method developed here. The sample test case is an underactuated multi–link pendulum on a cart. Numerical results are compared against the finite differences method. The proposed formulation is amenable to parallelization according to the Hamiltonian based divide and conquer scheme [5, 6]. These areas are of ongoing research for the authors.