Importance of Warping in Beams with Narrow Rectangular Cross-Sections: An Analytical, Numerical and Experimental Flexible Cross-Hinge Case Study

Abstract

This paper reports on the significance of warping deformation on the stability analysis of a flexible cross-hinge mechanism, which consists of two leaf springs with rectangular cross-section. The effect of misalignments in this mechanism is studied analytically, numerically and experimentally. An analytical buckling analysis is carried out to determine the theoretical critical load of a generalized cross-hinge mechanism on the basis of first principles. A geometrically nonlinear beam finite element with a non-uniform torsion description is used to model the leaf springs numerically. The change in natural mode frequencies and stiffness as a function of the misalignment is determined by a multibody program. Measurements from a dedicated experimental set-up confirm that the inclusion of warping effects is crucial, even for narrow rectangular cross-sections: it is found that the effects of warping increase the analytical critical buckling load of the system by 55%.

1 Introduction

In precision manipulation mechanisms, the risk of indeterministic behavior is mitigated by the use flexure joints. Such joints consist of elastically deforming elements, instead of traditional hysteresis-inducing rolling or sliding components. Since the only motion is due to elastic deformation, flexure mechanisms operate without friction, backlash, stick-slip, and wear, resulting in low hysteresis and highly repeatable motion. It also means that the static performance of such mechanisms is characterized by their stiffness properties: in certain directions (typically associated with actuation) low stiffness is desired, whereas especially in load-bearing directions high stiffness is desired. Assemblies of beams with narrow rectangular cross-sections are commonly used to this end.

In pursuit of higher performance (i.e. higher load-bearing stiffness), we are exploring flexure mechanisms that are termed overconstrained. This class of designs is typically avoided altogether because its stiffness properties depend strongly on the correct alignment of components (e.g. due to assembly and manufacturing tolerances). It has been shown that a flexible multibody model can predict this dependency accurately, and actually quantify the mechanism’s limit of operation in terms of the allowable misalignment by means of a buckling analysis [3, 4]. In this paper, we show that the effects of constrained warping have a marked influence on the critical load and therefore the allowable misalignement. An analytical lateral buckling analysis provides the theoretical critical load of the system on the basis of first principles and corroborates the measurements and simulations.

2 Experimental Set-Up

To study the phenomenon, the flexible cross-hinge in Fig. 1 serves as a case study. It consists of two leaf springs (80 mm length) with narrow rectangular cross-sections (30 mm width, 0.35 mm thickness) and a shuttle. The shuttle guides motion with respect to the base about the indicated rotation axis; in the other directions, it constrains motion. The overconstrained nature of this particular design manifests itself as a relatively high stress that occurs due to misalignment displacement $v_0$ (compared to misalignments in the other directions). This stress affects the stiffness properties of the mechanism, therefore its performance, and can even cause bifurcation buckling. The measurement set-up is depicted in Fig. 2.

Fig. 1.

Simplified illustration of the flexible cross-hinge mechanism. The Von Mises stress distribution due to misalignment displacement $v_0$ is indicated.

Fig. 2.

Photograph of the measurement set-up of the cross-hinge mechanism. The guidance stage serves to apply a controllable misalignment to the cross-hinge mechanism. There are several design characteristics for limiting hysteresis and enabling repeatable measurements [4]. The set-up is used for measuring the mechanism’s natural mode frequencies as a function of the misalignment. The natural mode frequencies serve as stiffness measures that are easier to determine experimentally.

3 Analytical Analysis

When the misalignment displacement $v_0$ or force $F_0$ exceeds a critical value, buckling occurs, support stiffness is lost and the mechanism no longer functions. To investigate the effects that warping has on the critical load of the system, an analytical buckling analysis is performed. The analysis follows the same steps and notation as Nijenhuis et al. [4], with the addition of a warping model and a change in solution procedure.

The equilibrium conditions of the system are derived using the potential energy of the system, given by

$$\begin{aligned} \begin{aligned} P_\text {tot} = P_\text {leaf}^\mathrm {l}+ P_\text {leaf}^\mathrm {r}-F_0v^\mathrm {l}(0) +\begin{bmatrix} D_x&D_y&D_z \end{bmatrix} \begin{bmatrix} K_x \\ K_y \\ K_z \end{bmatrix} +\begin{bmatrix} R_\chi&R_\psi&R_\phi \end{bmatrix} \begin{bmatrix} K_\chi \\ K_\psi \\ K_\phi \end{bmatrix}. \end{aligned} \end{aligned}$$

(1)

It consists of strain energy terms, external work $F_0v^\mathrm {l}(0)$ and Lagrange multipliers $D_{x,y,z}$ and $R_{\chi ,\psi ,\phi }$ to account for the kinematic constraints that the shuttle imposes on the leaf spring ends. The multipliers can be interpreted as the forces and moments needed to enforce the kinematic constraints. Superscripts l and r are used to denote the left and right leaf spring. Shuttle elasticity and gravity are ignored. Using beam theory to describe the leaf springs of length L, width w and thickness t, their contribution to $P_\text {tot}$ is given by

$$\begin{aligned} P_\text {leaf} = \frac{1}{2}\int _0^L \left[ S_b \kappa _y^2 + S_t \kappa _z^2 + S_w \left( \kappa _z'\right) ^2 \right] \mathop {}\!\mathrm {d}s +\int _0^L \left( N_u \gamma _x + N_v \gamma _y + N_w \gamma _z + M \kappa _x \right) \mathop {}\!\mathrm {d}s. \end{aligned}$$

(2)

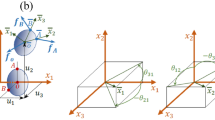
We choose to account for the strain energy only due to deformation modes with relatively low stiffness, i.e. bending in the plane of lowest rigidity (stiffness $S_b$), torsion (stiffness $S_t$) and warping (stiffness $S_w$). The deformation modes of relatively high stiffness are modeled as zero-deformation constraints by means of additional Lagrange multipliers $N_{u,v,w}$ and M for respectively zero transverse shear strain $\gamma _x$ and $\gamma _y$, zero elongation strain $\gamma _z$ and zero bending curvature $\kappa _x$ in the plane of highest rigidity. Figure 3 shows a schematic overview of the system. The deformed leaf spring configuration is described with respect to the initial coordinate frames x, y, z. Resolved in these frames, the position of the elastic lines is given by

$$\begin{aligned} \mathbf {r}(s) = \begin{bmatrix} u(s)&v(s)&s+w(s) \end{bmatrix}. \end{aligned}$$

(3)

Fig. 3.

For treating a wider variety of cross-hinge designs, angle $\alpha$, shuttle length $d_x$ and shuttle width $d_y$ are free parameters in this analysis. Crossing length $b=L-(d_x/2)\csc \alpha$ is positive when the point of intersection lies on the leaf springs; negative when it lies beyond (as depicted). For the demonstrator set-up, $b=L/2$. The position vector and orientation triads are only drawn for the left leaf spring.

Also, the orientation of the orthonormal triad attached to the deformed beam cross-section $[\mathbf m _{x}\; \mathbf m _{y}\; \mathbf m _{z}]$ is described by the rotation

$$\begin{aligned} \begin{aligned} \begin{bmatrix} \mathbf m _{x}&\mathbf m _{y}&\mathbf m _{z} \end{bmatrix}&= \begin{bmatrix} 1&0&0 \\ 0&\cos \phi&-\sin \phi \\ 0&\sin \phi&\cos \phi \end{bmatrix} \begin{bmatrix} \cos \psi&-\sin \psi&0 \\ \sin \psi&\cos \psi&0 \\ 0&0&1 \end{bmatrix} \begin{bmatrix} \cos \chi&0&\sin \chi \\ 0&1&0 \\ -\sin \chi&0&\cos \chi \end{bmatrix} \begin{bmatrix} \mathbf {i}_{x}&\mathbf {i}_{y}&\mathbf {i}_{z} \end{bmatrix} \end{aligned} \end{aligned}$$

(4)

with respect to the undeformed cross-section triad $[\mathbf {i}_{x}\; \mathbf {i}_{y}\; \mathbf {i}_{z}]$. Then, the shuttle constraints for the rotations are given by

$$\begin{aligned} \begin{aligned} K_\chi&= \chi ^\mathrm {l}- \chi ^\mathrm {r}= 0, \\ K_\psi&= \psi ^\mathrm {l}- \psi ^\mathrm {r}\cos 2\alpha +\phi ^\mathrm {r}\sin 2\alpha = 0, \\ K_\phi&= \phi ^\mathrm {l}- \phi ^\mathrm {r}\cos 2\alpha -\psi ^\mathrm {r}\sin 2\alpha = 0, \\ \end{aligned} \end{aligned}$$

(5)

and for the translations by

$$\begin{aligned} \begin{aligned} K_x&= \left( -u^\mathrm {l}+u^\mathrm {r}+ d_y\psi ^\mathrm {l}\right) \cos \alpha + \left( w^\mathrm {l}+w^\mathrm {r}+d_y\phi ^\mathrm {l}\right) \sin \alpha =0, \\ K_y&= -v^\mathrm {l}+v^\mathrm {r}-\left( \psi ^\mathrm {l}+\chi ^\mathrm {l}\phi ^\mathrm {l}\right) d_x\cos \alpha -\left( \phi ^\mathrm {l}-\chi ^\mathrm {l}\psi ^\mathrm {l}\right) d_x\sin \alpha +d_y\left( \phi ^{\mathrm {l}2}+\psi ^{\mathrm {l}2} \right) /2 = 0, \\ K_z&= d_x\chi ^\mathrm {l}+ \left( -w^\mathrm {l}+w^\mathrm {r}-d_y\phi ^\mathrm {l}\right) \cos \alpha - \left( u^\mathrm {l}+u^\mathrm {r}-d_y\psi ^\mathrm {l}\right) \sin \alpha = 0 \end{aligned} \end{aligned}$$

(6)

at $s=L$. Reissner’s relations for the nonlinear beam strains and curvatures energetically dual to the stress resultants are given by [5]

$$\begin{aligned} \begin{aligned} \kappa _x&= \phi ' -\psi '\chi , \\ \kappa _y&= \chi ', \\ \kappa _z&= \psi ', \end{aligned} \qquad \begin{aligned} \gamma _x&= u'-\chi , \\ \gamma _y&= v'+\phi (1+w')-\psi u', \\ \gamma _z&= w', \end{aligned} \end{aligned}$$

(7)

where the prime denotes differentiation with respect to the independent coordinate s. The kinematic boundary conditions, not included in the total potential energy, are given by

$$\begin{aligned} s = 0: \qquad \begin{aligned} u^\mathrm {l}= u^\mathrm {r}= v^\mathrm {r}= w^\mathrm {l}= w^\mathrm {r}= \chi ^\mathrm {l}= \chi ^\mathrm {r}= \psi ^\mathrm {l}= \psi ^\mathrm {r}= \phi ^\mathrm {l}= \phi ^\mathrm {r}= 0 \end{aligned} \end{aligned}$$

(8)

and

$$\begin{aligned} s = 0: \qquad \psi ^{\prime \mathrm {l}} = \psi ^{\prime \mathrm {r}} = \psi ^{\prime \mathrm {l}} = \psi ^{\prime \mathrm {r}} = 0 \end{aligned}$$

(9)

for the constraints on the warping deformation imposed by the mounting fillets at both ends of the leaf springs.

Application of the principle of minimum potential energy yields the equilibrium conditions for the system in terms of the configuration functions and undetermined multipliers. The fundamental solution branch is given by a zero value for all quantities, except for

$$\begin{aligned} \begin{aligned} D_y&= -F_0, \\ R_\phi&= d_x F_0 \cos \alpha \cot 2\alpha , \\ R_\psi&= -d_x F_0 \cos \alpha , \end{aligned} \qquad \begin{aligned} N_v^\mathrm {l}&= - F_0, \\ M^\mathrm {l}&= - F_0 \left( s-b\right) , \end{aligned} \qquad \begin{aligned} N_v^\mathrm {r}&= F_0, \\ M^\mathrm {r}&= F_0 \left( s-b\right) , \end{aligned} \end{aligned}$$

(10)

indicating that load $F_0$ does not cause deformation in the fundamental solution, but only a “reaction” from the multipliers that enforce the idealized zero-deformation constraints. Bifurcation equilibrium conditions are obtained by requiring that the first variation of $P_\text {tot}$ with respect to the fundamental solution vanishes. This means that only the second-order terms of $P_\text {tot}$ need to be taken into account (on the basis of which the nonlinear expressions of Eqs. (5)–(7) were already truncated). The ODEs and natural boundary conditions obtained this way can be solved partially, yielding

$$\begin{aligned} \phi ^\mathrm {l}= \phi ^\mathrm {r}= v^\mathrm {l}= v^\mathrm {r}= w^\mathrm {l}= w^\mathrm {r}= 0. \end{aligned}$$

(11)

The addition of the warping term in $P_\text {leaf}$ leads to coupled variable-coefficient linear ODEs for $\psi ^{\mathrm {l},\mathrm {r}}$ and $\chi ^{\mathrm {l},\mathrm {r}}$ that seem to admit no closed-form solution, unlike the original analysis without a warping model [4]. The remaining boundary conditions, assuming that $0<\alpha <\pi /2$, are

$$\begin{aligned} s=L: \qquad \begin{aligned} \psi ^\mathrm {l}&= \psi ^\mathrm {r}= 0, \\ \chi ^\mathrm {l}&= \chi ^\mathrm {r}, \\ u^\mathrm {l}&= u^\mathrm {r}, \end{aligned} \qquad \begin{aligned} d_x \chi ^\mathrm {l}&= \left( u^\mathrm {l}+u^\mathrm {r}\right) \sin \alpha , \\ S_b \left( \chi ^{\prime \mathrm {l}} + \chi ^{\prime \mathrm {r}} \right)&= \left( b-L \right) \left( N_u^\mathrm {l}+ N_u^\mathrm {r}\right) . \end{aligned} \end{aligned}$$

(12)

To obtain a solution, we reduce the complexity by splitting the solution into a symmetric part, for which $\chi ^\mathrm {l}= - \chi ^\mathrm {r}$, $\psi ^\mathrm {l}= \psi ^\mathrm {r}$, $u^\mathrm {l}= -u^\mathrm {r}$, and an anti-symmetric part, for which $\chi ^\mathrm {l}= \chi ^\mathrm {r}$, $\psi ^\mathrm {l}= -\psi ^\mathrm {r}$, $u^\mathrm {l}= u^\mathrm {r}$. For the symmetric solution, the kinematic boundary conditions and Eq. (12) together become

$$\begin{aligned} \begin{aligned} \psi (0) = \psi (L) = \psi '(0) = \psi '(L) = 0, \quad u(0) = u(L) = u'(0) = u'(L) = 0. \end{aligned} \end{aligned}$$

(13)

An approximate solution can be obtained by choosing a set of shape functions that satisfy the boundary conditions. For the symmetric solution, these can be

$$\begin{aligned} \begin{aligned} \psi (s) = \sum _{k=0}^n g_k \sin \left( \pi s/L \right) \sin \left( k \pi s/L \right) , \quad u(s) = \sum _{k=0}^n h_k \sin \left( \pi s/L \right) \sin \left( k \pi s/L \right) , \end{aligned} \end{aligned}$$

(14)

and $\chi (s) = u'(s)$. Substituting in $P_\text {tot}$ and taking variations now yields a system of 2n linear algebraic equations for the undetermined coefficients $g_k$ and $h_k$, whose determinant has to be zero in order to have nontrivial solutions. The smallest positive root corresponds to the critical load of the system, given by

$$\begin{aligned} F_{0,\text {cr}} = \beta \left( \frac{b}{L},\lambda \right) \frac{\sqrt{S_b S_t}}{L^2}, \qquad \lambda = \sqrt{\frac{S_t L^2}{S_w}} \approx \sqrt{\frac{24}{1+\nu }}\frac{L}{w} , \end{aligned}$$

(15)

where $\beta$ is a dimensionless function of the crossing ratio b/L and the spatial decay rate $\lambda$, which is a measure of the warping stiffness relative to the torsion stiffness and largely dependent on the w/L ratio of the leaf springs. The structure of $F_{0,\text {cr}}$ is similar to the critical load expression in the original analysis without warping, the difference being the dependency of the geometric factor $\beta$ on $\lambda$ as well. Due to the length of the closed-form expression of $\beta$, numeric values of $\beta$ for the symmetric buckling mode are provided in Table 1 for practically relevant values of b / L and $\lambda$.

Table 1. Values of the geometric factor $\beta$ for the symmetric bucking load for $n=15$.

4 Numerical Analysis

For simulation, a geometrically nonlinear beam finite element has been implemented in the software package SPACAR [2]. This element is based on Timoshenko’s bending theory and Reissner’s torsion theory in order to capture non-uniform torsion (in addition to bending, shear and elongation) of thin-walled beams with closed, symmetric cross-sections. The element is formulated in the generalized strain beam framework, in which deformation modes are defined to describe both elastic deformations and rigid-body motion of the element. This formulation has the advantages of the co-rotational formulation, while avoiding interpolation of finite rotations. The inertia properties are described with a consistent and lumped mass formulation; the latter is used to model the warping inertia of the beam cross-section [1].

5 Results and Discussion

The idealized analytical buckling analysis for the mechanism at hand ($b=L/2$) predicts $\beta =34.62$ and a buckling load of 90.63 N, compared to a critical load of 58.25 N in the earlier analysis without warping [4].

In SPACAR, the same idealized conditions can be simulated by excluding the deformation modes of elongation and bending in the plane of highest rigidity, and disabling shear, gravity and shuttle elasticity. Figure 4 (left) shows that the behavior is the same: the critical buckling load of the idealized system increases by 55% from a converged value of 58.60 N to 90.63 N when warping is included in the SPACAR element. A qualitative explanation for the observed behavior is that the warping constraints at the ends of the leaf springs increase the torsional stiffness near the ends, effectively reducing the length over which the leaf spring twists; since the buckling mode exhibits torsion deformation, the buckling load increases.

Fig. 4.

Left: convergence of the critical buckling load. Right: measurement and simulation of the first natural frequency $f_1$.

It is observed that generally the first buckling mode is an anti-symmetric one, in which the shuttle moves and the twist angle of both leaf springs is reversed. The second mode is a symmetric one, in which the shuttle remains stationary, the bending angle of both leaf springs has the same sign and the twist angle is reversed. However, only for the case of the common doubly-symmetric embodiment of the mechanism ($b=L/2$), under the idealized conditions, and with the warping effects included, we see that the anti-symmetric mode stiffens considerably and becomes the second mode. The first mode, which now has multiplicity two, is a symmetric one in which an individual leaf spring buckles and the shuttle remains stationary. For this mode, the analytical buckling load is provided by Eq. (15) and Table 1.

A refined numerical model is obtained by including all flexible deformation modes and the effects due to the leaf spring thickness variations, shuttle elasticity, the guidance stage and gravity. Figure 4 (right) shows the first natural frequency (in a mode that is a rotation about the rotation axis) as a function of the misalignment. With increasing misalignment, the rotation stiffness and the natural frequency decrease, and buckling (mechanism failure) is observed at around 0.11 mm misalignment. The numerical SPACAR results with the effects of warping match well with the measurements (the error in critical misalignment is 5.9%) and ANSYS (with solid elements). Unexpectedly, it also shows that the effects of warping play a significant role: with warping the critical misalignment is 35 $\upmu$m (i.e. 40%) larger.

6 Conclusions

An analytical buckling analysis is presented for generalized overconstrained flexible cross-hinge mechanisms. The critical load matches with simulations from a geometrically nonlinear beam finite element. It is found that the inclusion of warping deformation of beams with narrow rectangular cross-section is crucial. The results are in good agreement with measurements from a demonstrator set-up.