Keywords

1 Introduction

Transform-based image and video compression algorithms are still the preferred choice in many applications [29]. However, there has been a surge in research on alternative approaches in recent years [2, 12, 17, 27]. Especially partial differential equation (PDE)-based methods have proven to be a viable alternative in the context of image compression. To be on a competitive level with state-of-the-art codecs, these methods require sophisticated data optimisation schemes and fast numerical algorithms. The most important task is the choice of a small subset of pixels, often called mask, from which the original image can be accurately reconstructed by solving a PDE.

Especially this data selection problem has proven to be delicate. See [7, 9, 13, 14, 34] for some strategies considered in the past. Most approaches are either very fast but yield suboptimal results or they are relatively slow and return very appropriate data. A thorough optimisation of a whole image sequence is therefore computationally rather demanding and most approaches have resorted to a frame-by-frame consideration. Yet, even such a frame-wise tuning can be expensive, especially for longer videos.

In this work we discuss a simple and fast approach to skip the costly data selection in a certain number of frames. Instead we perform a significantly cheaper data transport along the temporal axis of the sequence. In order to evaluate this idea, we focus on the interplay between reconstruction quality and the accuracy of the transporting vector field. The actual data compression will be the subject of future research.

To give some more details of our approach, we consider an image sequence and compute a highly optimised pixel mask used for a PDE-based reconstruction within the first, single frame. Next, we seek the displacement field between the individual subsequent frames by means of a simple optic flow method. We shift the carefully selected pixels from the first frame according to this flow field and the shifted data is then used for the reconstruction process, in this case PDE-based inpainting. The effects of erroneous or suboptimal shifts of mask pixels on the resulting video reconstruction quality can then be evaluated.

The framework for video compression recently presented in [2] has some technical similarities to our approach. The conceptual difference is that in their work a reconstructed image is shifted via optic flow fields from the first to following frames. In contrast, we use optic flow fields only for the propagation of mask pixel and deal with an inpainting problem in each frame.

Our paper will be structured as follows. We will briefly describe the considered models and methods. Next we describe how they are concatenated in our strategy. Finally, all components are carefully evaluated, where we focus here on quality in terms of reconstruction error. Let us note again that we will not consider the impact on the file compression efficiency, as a detailed analysis of the complete, resulting data compression pipeline would be beyond the scope of this work.

2 Discussion of Considered Models and Methods

The recovery of images, as in a video sequence, by means of interpolation is commonly called inpainting. Since the main issue in our approach is concerned with the selection of data for a corresponding PDE-based inpainting task, it will be useful to elaborate on the problem in some detail. After discussing possible extensions from image to video inpainting, we consider optical flow.

2.1 Image Inpainting with PDEs

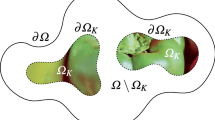
The inpainting problem goes back to the works of Masnou and Morel as well as Bertalmí­o and colleagues [4, 23], although similar problems have been considered in other fields already before. There exist many inpainting techniques, often based on interpolation algorithms, but PDE-based approaches are among the most successful ones, see e.g. [15, 16]. For the latter, strategies based on the Laplacian are often advocated [6, 21, 26, 28]. Mathematically, the simplest model is given by the elliptic mixed boundary value problem

$$\begin{aligned} -\varDelta u = 0\ \text {in}\ \varOmega \setminus \varOmega _{K}, \qquad u = f\ \text {in}\ \partial \varOmega _{K}, \qquad \partial _{n} u = 0\ \text {in}\ \partial \varOmega \setminus {}\partial \varOmega _{K}, \end{aligned}$$
(1)

Here, f represents known image data in a region \(\varOmega _{K}\subset \varOmega \) (resp. on the boundary \(\partial \varOmega _{K}\)) of the whole image domain \(\varOmega \). Further, \(\partial _{n} u\) denotes the derivative in outer normal direction. In an image compression context the image f is known on its whole domain \(\varOmega \) and one would like to identify the smallest set \(\varOmega _{K}\) that yields a good reconstruction when solving (1).

While solving (1) numerically is a rather straightforward task, finding an optimal subset \(\varOmega _{K}\) is much more challenging. Mainberger et al. [22] consider a combinatorial strategy while Belhachmi and colleagues [3] approach the topic from the analytic side. Recently [18], the “hard” boundary conditions in (1) have been replaced by softer weighting schemes. If we denote the weighting function by \(c:\varOmega \rightarrow \mathbb {R}\), then (1) becomes:

(2)

In the case where c is the indicator function of \(\varOmega _K\), (2) coincides with the PDE in (1). Whenever \(c(x)=1\), we require \(u(x)-f(x)=0\) and \(c(x)=0\) implies \(-\varDelta u(x) = 0\).

Optimising a weighting function c which maps to \(\mathbb {R}\) is notably simpler than solving a combinatorial optimisation problem when the mask c maps to \(\{0,1\}\). As the optimal set \(\varOmega _{K}\) is given by the support of the function c the benefit of the formulation (2) is that one may adopt ideas from sparse signal processing to find such a good mask. To this end, Hoeltgen et al. [18] following optimal control formulation:

(3)

Equation (3) can be solved by an iterative linearisation of the PDE in terms of (u, c), followed by a primal-dual optimisation strategy such as [10] for the occurring convex problem with linear constraints. As reported in [18], a few hundred linearisations need to be performed to obtain a good solution. This also implies that an equal amount of convex optimisation problems need to be solved. Even if highly efficient solvers are used for the latter convex optimisation, the run time will still be considerable. An alternative approach for solving (3) was also presented in [24].

Besides optimising \(\varOmega _{K}\) (resp. c), it is also possible to optimise the Dirichlet boundary data in such a way that the global error is minimal. If M(c) denotes the linear solution operator with mask c that yields the solution of (2), then we can write this tonal optimisation as

(4)

This idea has originally been presented in [22]. In [19] it is shown that there exists a dependence between non-binary optimal c (i.e. mapping to \(\mathbb {R}\) instead of \(\{0,1\}\)) and optimal tonal values g. Efficient algorithms for solving (4) can be found in [19, 22]. These algorithms are faster than solving (3), yet their run times still range from a few seconds to a minute.

2.2 Extension from Images to Videos

The mentioned strategies have so far been applied to grey-value or colour images almost exclusively. Yet extensions to video sequences would be rather straightforward. The simplest strategy would be to consider a frame-by-frame strategy. In (3) one could also extend the Laplacian into the temporal direction to compute an optimal mask in space-time. This would reduce the temporal redundancy (assuming that the content of subsequent frames does not change much) in the mask c compared to a frame-wise approach. Unfortunately, the latter strategy is prohibitively expensive. A one second long video sequence in 4K resolution (\(3860 \times 2160\) pixels) with a framerate of 60 Hz would require analysing approximately 500 million pixels. A frame-by-frame optimisation would be more memory efficient, since the whole sequence does not need to be loaded at once, but it would still require solving 60 expensive optimisation problems.

There exists an alternative approach which is commonly used in modern video compression codecs such as MPEG, see [30] for a general overview on the concepts and ideas. Instead of computing mask points for each frame, we compute a displacement field and shift mask points from one frame to the next.

2.3 Optical Flow

For the sake of simplicity we opt for the method of Horn and Schunck [20]. Given an image sequence f(x, y, t), where x and y are the spatial dimensions and t the temporal dimension, this method computes a displacement field (u(x, y), v(x, y)) that maps the frame at time t onto the frame at time \(t+1\) by minimising the energy functional

(5)

where \(f_{x}\), \(f_{y}\), and \(f_{t}\) denote the partial derivatives of f with respect to x, y, and t and where \(\varOmega \subset \mathbb {R}^{2}\) denotes the image domain. The model of Horn and Schunck is very popular and highly efficient numerical schemes exist that are capable of solving (5) in real-time (30 frames per second), see [8]. Obviously, replacing already a single computation of c with the computation of a displacement field (u, v) will save a significant amount of time. If the movements in the image sequence are small and smooth enough, it is very likely, that several masks c can be replaced by a flow field, thus saving even more run time.

3 Combining Optimal Masks with Flow Data

Given an image sequence f, we compute a sparse inpainting mask for the first frame with the method from [18]. According to the results in [19], we threshold the mask c and set all non-zero values to 1. Next, we compute the displacement field between all subsequent frames in the sequence by solving (5) for each pair of consecutive frames. The obtained flow fields (u, v) are rounded point-wise to their nearest integers to assert that they point exactly onto a grid point. Then, the mask points from the first frame are simply moved according to the displacement field. If the displacement points outside of the image or if it points onto a position where a mask point is already located, then we drop the current mask point. Since we are considering sparse sets of mask points, the probability of these events is rather low such that hardly any data gets lost over the course of action. Once the mask has been set for each frame, we perform a tonal optimisation of the data as discussed in [19]. The reconstruction can then simply be done by solving (2) for each frame. The complete procedure is also detailed in Algorithm 1.

figure a

Instead of rounding the flow field vectors, one could also follow the idea to perform a forward warping [25] and spread a single mask point on all neighbouring mask points. With this strategy, flow fields that point to the same location would simply add up the mask values. Even though this appears as a mathematically clean approach, our experiments showed that the smearing of the mask values caused strong blurring effects in the reconstructions and lead to overall worse results.

The data that needs to be stored for the reconstruction consists of the mask point positions in the first frame, the flow fields that move the mask points along the image sequence (resp. the mask positions in the subsequent frames), and the corresponding tonal optimised pixel values. We emphasise that it is not necessary to store the whole displacement field but only at the locations of a mask point in each frame. Thus, the memory requirements for the storage remain the same as when optimising the mask in each frame. Yet, we are considerably faster. We also remark that the considered strategy is rather generic. One may exchange the mask selection algorithm and the optic flow computation with any other method that yields similar data.

4 Experimental Evaluation

To evaluate the proposed approach, we give further details on our experimental setup, including a rough comparison of runtimes for the different stages of Algorithm 1.

We discuss the influence of the quality of the flow fields at hand of an example. By comparing our approach to compression with fixed mask points, we derive some clues for typical use case scenarios. Then we proceed by evaluating the proposed method for a number of image sequences.

4.1 Methods Considered

As already mentioned, we compute the inpainting masks with the algorithm from [18] and use the LSQR-based algorithm from [19] for tonal optimisation. In terms of quality these methods are among the best performing ones for Laplace reconstruction. However, alternative solvers such as presented in [11, 22] may be used as well.

For a reasonable comparison of simple optical flow methods we have resorted to the builtin Matlab implementation of the Horn and Schunck method [32] and a more sophisticated implementation available from [31]. The latter implementation additionally includes a coarse-to-fine warping strategy. Evaluations on the Yosemite sequence have shown that the latter is usually twice as accurate (see Fig. 1) as the builtin Matlab function, but it also exhibits slightly larger run times. However, the computation of an accurate displacement field is still significantly faster than a thorough optimisation of the mask point locations.

All methods have been implemented in Matlab. On a desktop computer with an Intel Xeon E5 CPU with 6 cores clocked at 1.60 GHz and 16 GB of memory the average run time of the Matlab optic flow implementation (10000 iterations at most) on the \(512\times {}512\times {}10\) “Toy Vehicle” sequence from [1] was 41 s for each flow field between two frames. The implementation from [31] (8 coarse-to-fine levels with 10 warping steps at most) took 50 s. The tonal optimisation (360 iterations at most) took on average 32 s per frame. The optimal control based mask optimisation (1500 linearisation and 3000 primal dual iterations at most) required on average 6–30 s per linearisation and usually all 1500 linearisations are carried out. A complete optimisation takes therefore about 8 hours per frame. The large variations in the run times of the single linearisations stem from the fact that the sparser the mask becomes the more ill-posed the optimisation problem becomes and the more iterations are needed to achieve the desired accuracy. All in all, the mask optimisation is at least 600 times slower than the optic flow computation or the tonal optimisation.

4.2 Evaluation

We evaluate the proposed Algorithm 1 on several image sequences. First we consider the Yosemite sequence with clouds, available from [5]. Since the ground truth of the displacement field is completely known we can also analyse the impact of the quality of the flow on the reconstruction. Further, we evaluate the image sequences from the USC-SIPI Image Database [1]. The database contains four sequences of different length with varying image characteristics. For the latter sequences, no ground truth displacement field is known. As a such we can only report the reconstruction error in terms of squared error (MSE) and structural similarity index (SSIM) [33].

4.3 Influence of the Optical Flow

In Table 1 we present the evaluation of our approach on the Yosemite sequence for different choices of parameters of the mask optimisation algorithm and the corresponding reconstruction. In all these experiments we set \(\mu \) to 1.25 (see [18] for a definition of this parameter) and \(\varepsilon \) to \(10^{-9}\) in the mask optimisation algorithm. The regularisation weight in (5) was always optimised by means of a line search strategy.

Fig. 1.
figure 1

Angular errors (in degree) and endpoint errors (in pixel width) in the optic flow field of the Yosemite sequence in-between frame i and \(i+1\) for the considered methods. The solid line corresponds to the implementation [32] and the dashed line to the implementation [31]. The regularisation weight was optimised for each pair of frames to minimise the angular error. The method from [31] is roughly twice as accurate as [32] but exhibits slightly higher run times.

Full size image

The first column of the table lists the parameter \(\lambda \) which is responsible for the mask density and the second column contains the corresponding mask density in the first frame. The last five columns list the average reconstruction error over all 15 frames when (i) using an optimised mask obtained from the optimal control framework explained in [18] in all the frames, (ii) the optimised mask from the first frame shifted in accordance with the ground truth displacement field, (iii) the mask from the first frame shifted in accordance with the computed displacement fields for both considered implementations of the Horn and Schunck model, (iv) the mask from the first frame used for all subsequent frames (i.e. using a zero flow field), and (v) the mask from the first frame shifted by a random flow field within the same numerical range between each pair of frames as the ground truth.

Table 1. Evaluation of the Yosemite sequence. The density specifies the percentage of non-zero mask pixels in the first frame. The errors in the Horn & Schunck column correspond (in order) to the implementation from [31], and the builtin Matlab function [32]. The second-to-last column sets the flow field in every pixel to 0. The last column shows the error when using a random flow field in the same numerical range as the ground truth. The bottom part of the table represents the same experiments but without tonal optimisation in the reconstruction. The results show that on average, zero flow is almost as good as the methods where a computed flow field is used. These methods outperform zero flow especially in the first frames, cf. Fig. 2.
Full size table

All reconstructions in the upper half of the table have been done according to Algorithm 1. The lower half exhibits the same experiment but without the tonal optimisation in step 6 of Algorithm 1. Instead the original image data at the mask locations were used.

Table 2. Evaluations of the MSE and SSIM on Image Sequences from the USC-SIPI Image Database [1]. An optimal mask is computed on the first frame and shifted according to the computed optic flow. The error for the “Toy Vehicle” sequence is not monotonically increasing due to strong occlusions in certain frames.
Full size table

As expected, a higher mask density yields a smaller error in the reconstruction in all cases. Interestingly, we observe that computed flow fields are accurate enough to outperform in many cases the ground truth flow (rounded to the nearest grid point). The solution of the Horn and Schunck model in (5) involves the Laplacian and is a smooth flow field. We conjecture that, compared to the ground truth flow, this solution is more compatible with our choice for the inpainting procedure, which is also based on the Laplacian. The investigation of this possible synergy will require a more dedicated analysis in the future. When considering the plots in Fig. 2, one sees that there is a clear benefit to using computed flow fields in the first 7 or 8 frames of the sequence, when comparing to a flow field that is zero everywhere. Afterwards the iterative shifting of the masks has accumulated too many errors to outperform a zero flow. This suggests that the usage of a flow field is mostly beneficial for a short time prediction of the mask. Let us also note that the impact of the quality of the computed optical flow is visible over a shorter period within the first 5 frames.

Table 1 also shows that tonal optimisation has the expected beneficial influence. The tonal optimisation causes a global decrease in the error by as much as a factor 2, however it cannot compensate errors in the flow field.

4.4 Evaluation of the Reconstruction Error

Overall, the error evolution, as observed in the Yosemite sequence, is rather steady and predictable, even though such a behaviour can only be expected in well behaved sequences. The “Toy Vehicle” sequence from [1] exhibits strong occlusions and non-monotonic behaviour of the error, see Table 2. Nevertheless, the behaviour of the error evolution could be used to automatically detect frames after which a full mask optimisation becomes again necessary.

Fig. 2.
figure 2

Reconstruction error for the Yosemite sequence in each frame using a mask with density \(5.5\%\) shifted by different flow fields. The average angular error over all frames of the method from [31] is 8.59 and 5.27 if measured at mask points only. For the method from [32], the corresponding errors are 19.72 and 15.74. The error in the reconstruction is hardly influenced by the quality of the optic flow. The dashed line indicates the error in the reconstruction from an optimal mask.

Full size image

Figure 3 presents an optimal mask for the last frame of the Yosemite sequence as well as the shifted mask. The corresponding reconstructions are also depicted. Fine details are lost with the reconstruction from the shifted mask. However, the overall structure of the scene remains preserved. We remark that the bright spots are due to our choice of the inpainting operator, see also [14].

Fig. 3.
figure 3

(a) and (d): Inpainting masks (5.5% density) with (b) and (e): magnified details and (c) and (f): corresponding reconstructions for frame 15 of the Yosemite sequence. Black pixels indicate mask pixels, grey regions are to be inpainted. Top: optimal mask, Bottom: shifted mask.

Full size image

Finally, Tab. 2 contains further evaluations of the MSE as well as the SSIM for the image sequences from [1]. Both measures show a similar behaviour. Denser masks have higher a SSIM (resp. lower MSE), and the SSIM decreases (resp. MSE increases) with the number of considered frames. The error evolution is usually monotone. However, if occlusions occur, then important mask pixels may be badly positioned or even completely absent. In that case notable fluctuations in the error will occur. This is especially visible in the “Toy Vehicle” sequence where the maximal error is not the error in the last frame.

5 Summary and Conclusion

Our work shows that it is possible to replace the expensive frame-wise computation of optimal inpainting data with the simple computation of a displacement field. Since run times to compute the latter are almost negligible when compared to the former, we gain a significant increase in performance. Our experiments demonstrate that simple and fast optic flow methods are sufficient for the task at hand, yet one may spend higher attention to movement of object boundaries.

In addition, the loss in accuracy along the temporal axis can easily be predicted. We may decide automatically when it becomes necessary to recompute an optimal mask while traversing the individual frames. We conjecture that the presented insights are certainly helpful in the future development of PDE-based video compression techniques.