Keywords

1 Introduction

The performance characteristics of the product as a whole and its durability depend on the accuracy and quality of manufacture of individual parts and assemblies. However, in the course of processing, under the action of the components of the cutting force, elements of the technological system are displaced from the initial (unloaded) state, thereby causing the appearance of machining error [1]. This is especially evident in the turning of non-rigid shafts. Due to the low rigidity of the blanks, the magnitude of this type of error in the turning of them reaches 80–90% of the total machining error [2]. These operations are preliminary, and their result, due to the effect of technological heredity, substantially predetermines the quality of the subsequent finishing treatment. The formulas adopted in manufacturing engineering for calculating the errors of this type have relatively low convergence with experimental data [3], because they are simplified and do not take into account the peculiarities of the course of the treatment process. This circumstance causes the appearance of an error in the technological process at the design stage of the technological process, in particular in assigning allowance for machining for subsequent finishing operations.

2 Elastic Strains of the Technological System Elements Under the Turning of Non-rigid Shafts Based Between the Centers

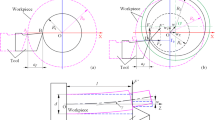
Consider the mechanism of the formation this type of machining error under the turning a smooth non-rigid shaft. This type of mounting is widespread, because provides the highest accuracy and for its implementation requires minimal time investment compared with other bonding technique. Figure 1 shows basing scheme and distribution scheme of forces acting in the process. In the above scheme, the centrifugal inertia force is not taken into account, because the effect of which on the amount of elastic strains under the turning a smooth shaft is insignificant [4]. The shaft-based between centers is represented a beam and freely supported by its ends. The tangential component of the cutting force PZ causes the appearance of bearing pressures RZH and RZR, acting on the head and rear centers, respectively. In addition, the weight of the shaft Q is perceived by the centers and also affects to the magnitude of reactions RZH and RZR. The radial component of the cutting force PY causes the appearance of bearing pressures RYH and RYR, acting on the center in the horizontal plane perpendicular to the axis of the lathe. In addition, the moment in the horizontal plane, caused by the action of the axial component of the force PX applied at a distance of half the diameter of the workpiece from the centerline, also affects to the magnitude of reactions RYH and RYR. The very force PX is entirely perceived by the head center, thereby unloading the rear center. Therefore, in order to avoid a weakening of the rear center, he is informed about the preliminary tightening of FT equal to the value of PX.

Fig. 1
figure 1

Basing scheme and distribution scheme of forces acting in the process of turning

Full size image

Consider separately the effect of strains of each of the elements of the technological system on the accuracy of machined surface. It should be noted that elastic strains of the system, primarily due to the effect of the radial component of the cutting force PY and partly action of the axial component of the cutting force PX. As for the strains under the action of the tangential component of cutting force PZ, their influence on the accuracy of machining is small, and it can be neglected [2].

2.1 Strains of the System Under the Action of Radial Component of the Cutting Force PY

In considering the bending of the shaft axis under the action of the components of cutting forces in turning, the machine units we will assume absolutely rigid. Then, the magnitude of the bending of the shaft y1i under the action of the radial component of the cutting force can be determined according to the energy method:

$$y_{1i} = \int\limits_{0}^{x} {\frac{{M_{{P_{Y} {\text{I}}}} \cdot M_{{ 1 {\text{I}}}} }}{{E \cdot I_{1} }}{\text{d}}x + \int\limits_{x}^{l} {\frac{{M_{{P_{Y} {\text{II}}}} \cdot M_{{ 1 {\text{II}}}} }}{{E \cdot I_{2} }}{\text{d}}x} ;}$$
(1)

where

  • MPYI, MPYII—bending moment from the radial component of the cutting force PY on the treated and treated area, respectively;

  • M1I, M1II—bending moment from a unit force on the treated and treated area, respectively;

  • I1, I2—moment of inertia of cross section of the finished and treated stages, respectively.

Based on the design scheme shown in Fig. 1, and after the transformations, Expression (1) takes the form:

$$y_{1i} = \frac{{P_{Y} \cdot x^{3} \cdot (l - x)^{2} }}{{3 \cdot E \cdot I_{1} \cdot l^{2} }} + \frac{{P_{Y} }}{{E \cdot I_{2} }}\left[ {\left( {\frac{{l^{3} - x^{3} }}{3}} \right) \cdot \left( {\frac{x}{l}} \right)^{2} - \left( {l^{2} - x^{2} } \right) \cdot \frac{{x^{2} }}{l} + \left( {l - x} \right) \cdot x^{2} } \right];$$
(2)

However, in practice, for the calculation of the shaft strains instead of Expression (2) is used a simplified calculation formula which does not take into account the changing shaft stiffness due to the change in its cross section during turning. It is wrong. Calculations showed that the difference in determining the amount of deflection by using the simplified formula adopted in manufacturing engineering, with the calculation by using the refined formula (2) reaches 50% compared. Such a ratio often occurs in practice while turning workpieces with a diameter of less than 40 mm with a cutting depth of 0.25 d1.

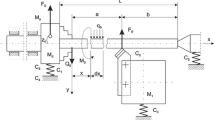
Consider the displacement of centers. In this case, we while considered the shaft absolutely rigid and the caliper is unyielding. Under the action of the force PY in the process of machining, the centers of the lathe are elastically pressed, and after the removal of the load, they return to their initial position (Fig. 2). So, in the initial position of the cutter, the head center is not under load and stay at rest (yH = 0), while the rear center under the action of the force PY will move to the maximum value (yR = max).

Fig. 2
figure 2

Displacement of the centers of the lathe under the action of the radial component of the cutting force PY

Full size image

As the cutter moves to the headstock, displacement of rear center depresses to zero and displacement the head center increasing and reaches its maximum at the extreme left position of the cutter. The curve A1aB1 in Fig. 2 expresses the distorted shaft profile. The magnitude of the error y2i can be found analytically based on the similarity of triangles Aicb and AidBi:

$$y_{2i} = \left( {1 - \frac{x}{l}} \right) \cdot y_{Ri} + \frac{x}{l} \cdot y_{Hi} ;$$
(3)

Since the strain of stocks is directly proportional to the loads, the equation of shaft cross-sectional line can be written in the form:

$$y_{2i} = P_{Y} \cdot \left[ {\left( {1 - \frac{x}{l}} \right)^{2} \cdot \varepsilon_{R} + \left( {\frac{x}{l}} \right)^{2} \cdot \varepsilon_{H} } \right];$$
(4)

where

  • ɛH, ɛR—flexibility of the headstock and tailstock, respectively.

As for the stain of the support, the operating experience of lathe showed that the flexibility of the support ɛS remains almost constant over the entire length of the treatment, conditional upon it properly assembled and in good condition. Its release under the action of force PY is constant and equal to:

$$y_{3i} = P_{Y} \cdot \varepsilon_{S} ;$$
(5)

2.2 Strains of the System Under the Action of Axial Component of the Cutting Force PX

Applied at a distance d/2 from the axis of rotation, the axial component of the cutting force PX creates a torque MX, under the influence of which bearing pressure P′R and P′H occur. It acting, respectively, on the tailstock and headstock of the lathe in opposite directions:

$$P^{\prime}_{R} = P^{\prime}_{H} = P_{X} \cdot \frac{d}{l};$$
(6)

Under the action of a bending moment MX, the shaft axis is bent through an angle θ, as a result of which longitudinal deformation of the shaft axis y4i occurs, as shown in Fig. 3a. Equation bending moment at the section x for this case has the form:

Fig. 3
figure 3

a Bending of the shaft axis under the action of moment MX; b Displacement of the line of centers under the action of moment MX

Full size image
$$M = P^{\prime}_{R} \cdot x - M_{X} = P_{X} \cdot \frac{d}{2 \cdot l} \cdot x - P_{X} \cdot \frac{d}{2};$$
(7)

Equation of the elastic line for this case has the form:

$$\begin{aligned} \theta (x) & = \theta_{0} + \frac{{P_{X} \cdot d \cdot x^{2} }}{{2 \cdot E \cdot I_{1} \cdot l}} - \frac{{P_{X} \cdot d \cdot x}}{{2 \cdot E \cdot I_{1} }}; \\ y_{4i} & = y(x) = \theta_{0} \cdot x + \frac{{P_{X} \cdot d \cdot x^{3} }}{{6 \cdot E \cdot I_{1} \cdot l}} - \frac{{P_{X} \cdot d \cdot x^{2} }}{{4 \cdot E \cdot I_{1} }}; \\ \end{aligned}$$
(8)

where θ0—initial angle of rotation of the shaft.

To determine the integration constant θ0, we use the boundary conditions. At the points corresponding to x = 0 and x = l, the diameters of the shaft are not distorted, then:

$$\theta_{0} = \frac{{P_{X} \cdot d \cdot l}}{{12 \cdot E \cdot I_{1} }};$$
(9)

Thus, the magnitude of the strain of the shaft axis, caused by the action of the moment MX, can be determined by the following expression:

$$y_{4i} = \frac{{P_{X} \cdot d \cdot l \cdot x}}{{12 \cdot E \cdot I_{1} }} \cdot \left( {2 \cdot \frac{{x^{2} }}{{l^{2} }} - 3\frac{x}{l} + 1} \right);$$
(10)

However, calculations show that the bending of the shaft axis caused by the action of the moment MX can be significant only when turning very thin shafts with a diameter of up to 20 mm and a ratio of length to diameter over 15. In this case, the bending of the axis from the action of the radial component of the force PY turns out to be so large that the bending of the shaft axis caused by the action of the moment MX can be neglected.

Since both stocks have unequal flexibility, they are displaced on different values y′R and y′H in opposite directions under the action of the bearing pressure P′R and P′i. As a result, the shaft rotates in a horizontal plane passing through a line of centers, as shown in Fig. 3b. If we assume that the shaft is absolutely rigid, then the offset position of the axis A1B1 will remain unchanged throughout the length of the turning. In this case, the diametrical dimensions of the shaft will change by the amount of double displacement of the axis y5i, which can be determined based on the similarity of triangles AA2B and B1cd:

$$y_{5i} = \left( {1 - \frac{x}{l}} \right) \cdot y^{\prime}_{R} - \frac{x}{l} \cdot y^{\prime}_{H} ;$$
(11)

Since the strain of stocks is directly proportional to the loads and unchanged during processing, Eq. (11) can be written as:

$$y_{5i} = P_{X} \cdot \frac{d}{2 \cdot l} \cdot \left[ {\left( {1 - \frac{x}{l}} \right) \cdot \varepsilon_{R} - \left( {\frac{x}{l}} \right) \cdot \varepsilon_{H} } \right];$$
(12)

However, according to the calculations, the magnitude of the displacement of the centerline under the action of the moment MX is insignificant in comparison with the total flexibility of the system, which is why this type of error can be neglected.

Also, under the action of the force PX, the cutter is pressed, bent and turned; however, these deformations are so small that they practically do not affect the accuracy of the diametrical dimensions of the machined shaft and can be neglected.

3 Experimental Procedure

The final formula for calculating the machining error ΔΣ caused by the elastic strains of the technological system elements under the turning of non-rigid shafts-based between the centers will take the form:

$$\Delta_{\varSigma } = 2 \cdot \sum {y_{ji} = } P_{y} \cdot \left\{ \begin{aligned} \frac{{x^{3} \cdot (l - x)^{2} }}{{3 \cdot E \cdot I_{1} \cdot l^{2} }} + \frac{1}{{E \cdot I_{2} }}\left[ {\left( {\frac{{l^{3} - x^{3} }}{3}} \right) \cdot \left( {\frac{x}{l}} \right)^{2} - \left( {l^{2} - x^{2} } \right) \cdot \frac{{x^{2} }}{l} + \left( {l - x} \right) \cdot x^{2} } \right] \hfill \\ + \left[ {\left( {1 - \frac{x}{l}} \right)^{2} \cdot \varepsilon_{R} + \left( {\frac{x}{l}} \right)^{2} \cdot \varepsilon_{H} } \right] + \varepsilon_{S} \hfill \\ \end{aligned} \right\};$$
(13)

Table 1 presents the experimental data on the study of machining error ΔΣ obtained by turning a shaft with a diameter of 24.8 mm and length of 325 mm from steel 45 on a lathe model 16A20F3 CNC with a T15K6 cutting plate with the following cutting conditions: feed −0.25 mm/rev, depth of cut −0.6 mm, and cutting speed −46.3 m per min [5]. Table 1 also presents the data obtained by calculating the machining error by the refined formula (13) and by the traditional formula given in the source [6].

Table 1 Experimental data and the results of the calculation of machining error for theoretical dependencies
Full size table

A significant discrepancy between the calculated data obtained in the calculation using the refined formula (13) and the experimental data at the beginning of the turning process may indicate that the turning was carried out without sufficient preliminary pressing of the rear center (sliding of the center). The discrepancy in the data at the end of turning process is due to significant wear of the metal-cutting tool during treatment.

4 Conclusion

The analysis of the data showed that the proposed refined mathematical model for calculating the machining error due to the strains of the technological system elements has a higher convergence of results with experimental data in comparison with traditional mathematical models adopted in mechanical manufacturing engineering. Application of this mathematical model will improve the reliability of technology at the design stage of the technological process, in particular in assigning allowance for machining for subsequent finishing operations. In addition, the resulting refined model can be used in control algorithms for adaptive control systems, which will improve the accuracy of their operation.