Keywords

1 Introduction

Several ionic models are available to describe the evolution of the electrical potential across cardiac cell membranes. These models usually read as a system of coupled highly nonlinear differential equations with many adjustable parameters. The adjustment of parameters becomes increasingly important to be able to personalize these models using medical data (see for instance [10, 11]), to compare models with each other in the best possible way or to represent the more complex dynamical behavior of cardiac cells such as restitution properties. It is not easy to study the combined effect of varying the parameters and the literature is usually not too explicit on the way the parameters are adjusted in ionic models.

Parameter adjustment is possible with simpler ionic models using asymptotic formula connecting the parameters with the phase durations [6, 11, 12]. Few attempts have been made to address the adjustment of the ionic model parameters using fully nonlinear models. We are aware of the recent paper [2] where a genetic algorithm was used to build a cell-specific cardiac electrophysiology model and [5] where simulated annealing is used to compare two ionic models. Genetic algorithms were also used to adjust conductances in nonlinear models [13], then a larger set of parameters in [3]. Direct recording of action potentials (AP) or membrane resistance were used to build least-square functions. In [13], AP recorded at various frequencies were included in the least-square function to eventually match restitution properties.

In [7], we introduced numerical methods to optimally adjust the parameters in ionic models. Our method is based on the numerical solution of an optimal control problem with a least-square objective function to fit the main features of the cardiac AP, e.g. the action potential duration (APD), the depolarization time (DT), recovery time (RT), etc. We then provided a second function to fit the trans-membrane potential predicted by the model to experimental recording on a single cell. The goal of the current paper is to show that this methodology naturally leads to parameter identification to match restitution properties in fully nonlinear ionic models directly from simple potential recordings in a cell or heart at multiple frequencies. No assumption will be made on the amplitude of the recorded potential (a limitation of indirect measurement techniques), consequently scaling factors for the data will have to be identified together with the model parameters.

We will illustrate the efficiency of the method for the Mitchell-Schaeffer model [6], which is a simple two variables ionic model with a limited set of parameters. Our methodology is not limited to this model. Numerical results are presented, in particular model fitting to experimental AP measurements obtained through an optical fluorescence imaging technique.

2 Mathematical Models

2.1 Mitchell-Schaeffer Model

As one particular example where the proposed parameter identification technique can be applied, we consider the Mitchell-Schaeffer (MS) two-variable model [6]. This model describes the dynamics of the trans-membrane potential u in the myocardium and a gating variable v representing in a lumped way the opening and closing of ionic channels controlling the passage of ions across the cell membranes. Here we consider the 0D model for a single cell (no space dependence of the variables u and v).

The dependent variables \(u=u(t)\) and \(v=v(t)\), \(t>0\), are solutions of:

$$\begin{aligned} \frac{du}{dt} = f(u,v) + I_{stim}(t),\quad \text {with} \quad f(u,v)=\frac{1}{\tau _{in}}vu^{2}(1-u) - \frac{1}{\tau _{out}}u, \end{aligned}$$
(1)
$$\begin{aligned} \frac{dv}{dt}= g(u,v),\quad \text {with} \quad g(u,v)={\left\{ \begin{array}{ll} \frac{1-v}{\tau _{open}}, \quad \text { if}\quad u< u_{gate}, \\ \\ \frac{-v}{\tau _{close}},\quad \text { if}\quad u\ge u_{gate}. \end{array}\right. } \end{aligned}$$
(2)

The trans-membrane current f(u, v) is the sum of the gated inward current \(vu^{2}(1-u)/\tau _{in}\) with time scale \(\tau _{in}\) that tends to depolarize the cardiac cell and the ungated current \(-u/\tau _{out}\) that tends to repolarize the cardiac cell with time scale \(\tau _{out}\). Finally, \(I_{stim}\) represent an external current produced by a stimulation electrode. The dynamics of the gating variable v depends on the threshold potential \(u_{gate}\) for the initiation of an AP, and on two time constants, \(\tau _{open}\) and \(\tau _{close}\), respectively controlling the opening and closing of the gate. We set \(\tau = [\tau _{in}, \tau _{out}, \tau _{open}, \tau _{close}]\) to simplify notations. The functions f and g depend on the parameter \(\tau \). Equations (1)–(2) require initial conditions \(u(0)=u_0\) and \(v(0)=v_0\), where \(u_0,v_0\in [0,1]\) are given. In the MS model, the variables u and v are non-dimensional, while the time t is in ms. Consequently, the parameters \(\tau \) are in ms, and the source terms f and g are in ms\(^{-1}\).

Since the model needs to be periodically stimulated in order to account for restitution properties, \(I_{stim}\) can then be written as

$$\begin{aligned} I_{stim}(t)={\left\{ \begin{array}{ll} A&{} \text {if } t\in [n\cdot BCL,n\cdot BCL+\varDelta t],\ n\in \mathbb {N} \\ 0&{} \text {otherwise } , \end{array}\right. } \end{aligned}$$
(3)

where BCL, or Basic Cycle Length, is the delay between stimulations, \(\varDelta t\) is the duration of the stimulations and A is their amplitude. As stated in [6], the amplitude A depends on the model parameters and indirectly on BCL:

$$\begin{aligned} A=\frac{1}{\varDelta t}\left( \frac{1}{2}-\sqrt{\frac{1}{4}-\frac{\tau _{in}}{\tau _{out} v^*}}\ \right) \cdot (1+\beta ) \end{aligned}$$
(4)

where \(v^*\) is the value of v at the time of stimulation, \(\beta >0\) is a small “safety factor” set to guarantee depolarization.

2.2 Optimal Control Problem

We introduce a control problem to fit in the least-square (LS) sense the trans-membrane potential \(u=u(t)\) from the model to a recorded potential \(\tilde{u}=\tilde{u}(t)\), \(t\in [0,T]\), measured experimentally, normalized in a specific way and rescaled using a scaling factor \(s\in (0,1)\).

Define \(\tilde{J}=\tilde{J}(\tau ,s)\)

$$\begin{aligned} \tilde{J}(\tau ,s) = \frac{\int _{0}^{T}\mid u(t,\tau ) - s\,\tilde{u}(t)\mid ^{2}\, dt}{\int _{0}^{T}\mid s\,\tilde{u}(t)\mid ^{2}\, dt}, \end{aligned}$$

where u and v are solution of (1)–(2) with parameters \(\tau \) and \(I_{stim}\) is adjusted to match the BCL of \(\tilde{u}\). For the solution of the MS model to reach a stable cyclical response from beat to beat, we disregard the first five AP in the evaluation of the cost function \(\tilde{J}\). The parameter \(u_{gate}\) is intentionally left out from the parameter identification as a senstivity analysis showed that \(u_{gate}\) has little impact on the phase durations or the shape of the AP [8].

Now consider multiple different \(\tilde{u}_i\), \(i=1,\ldots ,N\), obtained by stimulating the same heart or cardiac cell at different frequencies and find \((\tau ^*,S^*)\) minimizing

$$\begin{aligned} J(\tau ,S)=\sum _{i=1}^N \tilde{J}(\tau ,s_i) \end{aligned}$$
(5)

where \(S=(s_1,\ldots ,s_N)\) are the scaling factors for each \(\tilde{u}_i\). The connection between the parameter \(\tau \) and the objective function J is occurring through the dependance of the solutions (u, v) on the parameters \(\tau \).

3 Numerical Methods

The equations (1)–(2) are solved using the function ode45 in Octave, which implements an explicit Dormand-Prince method of order 4.

The function g is discontinuous in u, which leads to a lack of regularity of the solution (u, v) of (1)–(2) and consequently of the function \(J=J(\tau ,S)\). The derivatives of J with respect to \(\tau \) may not be well defined. Work done in [7] showed that numerical derivatives do not converge when the increments in \(\tau \) are reduced. To avoid the computation of the sensitivities and the gradient of J with respect to \(\tau \), we use non-differentiable optimization methods [1]. The Compass Search method described in Algorithm 1 is taken from [4]. This method can be changed in a few ways to improve performance, but the principle behind the method is maintained for all modified versions.

figure a

The algorithm repeats the process of constructing D and moving x, if possible, as long as the stopping criteria are not met. Options for stopping criteria include \(f(x)\le ftol\) for a chosen tolerance ftol on the value of the cost function, \(\delta \le \delta tol\) for a chosen tolerance \(\delta tol\) on the step-size, and maximal numbers of iterations and function evaluations.

The optimization methods used introduce a sensitivity to the initial guess of the parameters and scaling factors. If convergence is reached but the value of the least-square function J is not small for the final iterate, the minimum is likely to be local only and new initial guesses must be attempted in the hope of getting a better fit. We used our experience with the fitted model as well as trial and error to find good initial guesses.

4 Data Acquisition

For parameterization of mathematical models, AP waves were recorded using voltage-based optical fluorescence imaging, as described in [9]. The fluorescence dye (di4-ANEPPS) and uncoupler to block contraction (2, 3 BDM) were injected into the coronary circulation of a healthy explanted swine heart perfused by a Langendorff system. The optical dye was excited with green light (\(\sim \)530 nm) while the emitted epicardial signals were filtered (>610 nm) and captured by a high-speed CCD camera (MICAM02, BrainVision Inc. Japan) at 256 frames/second (Fig. 1). The field of view was 184\(\,\times \,\)124 pixels (12\(\,\times \,\)10 cm), yielding an \(\sim \)0.7 mm spatial resolution. We stimulated the heart at several frequencies to study the restitution properties (see Table 1 below). The relative change in fluorescence signal intensity (\(\varDelta F/F\)) recorded at each pixel, gives directly the AP waves. For model fitting, we used the AP waves recorded at one pixel selected from an area in the left ventricle (LV) where tissue was homogeneously illuminated, and also both fluorescence signal and tissue perfusion were homogeneous.

5 Numerical Results

5.1 Preparation of the Experimental Data

The potential measured with fluorescence imaging are recorded as signal intensity, consequently these must be normalized between 0 and 1 before fitting with the MS model. We worked directly on the raw data. In order to normalize the data, averaged extrema must be calculated. The average values are considered, since taking the absolute minimum or maximum of a set of noisy values would not make sense when trying to normalize the recorded potential. The average minimum was found by taking the average of the values during a single diastolic interval. Since the data is very noisy, determining which values were to be considered to be in the diastolic interval presented some challenges, so this was done manually. A representative diastolic interval was identified by looking at the graph of raw data and noting the approximate times at which the diastolic interval starts and ends. A similar logic was used when finding the averaged maximum. The maximum was taken manually to be approximately the value at which each potential peaks. Once the average extrema are found, the data is normalized, by subtracting the minimum and dividing by the amplitude, to obtain a normalized potential \(\tilde{u}_i\) between 0 and 1. Also, when considering the problem of matching the MS model to the data, it is convenient for the data to start with an upstroke, so the first part of most of the data sets is ignored (data acquisition does not always start in sync with the stimulation, it can start mid heartbeat). Finally, the aforementioned scaling \(s_i \tilde{u}\) further adjusts the data so that the peaks of the potential have the same values as the peaks in the model. This is required since the peak trans-membrane potential u predicted by the MS model gets smaller as BCL is reduced (the usual mechanism for restitution).

Fig. 1.
figure 1

(a) Snapshot of the optical experiment to record epicardial AP wave propagation using a fast CCD camera (C), where the pig heart (H) was stimulated via an electrode (E). (b) Examples of waves recorded at one pixel in the heart without the uncoupler (top) as well as after the uncoupler (bottom) was injected. Note that the inverse of the relative loss of fluorescence signal \(\varDelta F/F\) (arbitrary units) gives the AP. The waves were displayed with BV-Ana software (BrainVision, Japan). (Color figure online)

Full size image

5.2 Single Pacing Frequency

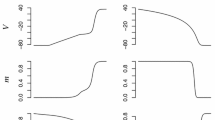
To validate our approach, we verify that our method is efficient at fitting data sets individually (i.e N = 1 in (5)). For each of the cases given in Table 1 (presented in order of increasing frequencies), we pace the MS model according to (3)–(4) with \((u_0,v_0)=(0,1)\), \(\varDelta t=2\) ms, \(\beta =0.25\) and BCL calculated from column 2 of Table 1. Figure 2 shows the measured potential and the trans-membrane potential from the fitted MS model for dataset 5. The potential predicted by the model matches the noisy data very well, which is confirmed by the small value of the least-square function J in Table 1. The fit is good for all datasets, with datasets 3 and 4 showing a slightly larger deviation. This shows that the parameter identification method is capable of identifying parameters \(\tau \) simultaneously with a scaling factor.

Table 1. Statistics of single dataset fitting
Full size table
Fig. 2.
figure 2

Result of fitting dataset 5 individually

Full size image
Table 2. Statistics of multiple datasets fitting
Full size table
Fig. 3.
figure 3

Best (left) and average-quality (right) fitting of multiple datasets

Full size image

5.3 Multiple Pacing Frequency

We next illustrate how problem (5) is capable of adjusting parameters for restitution properties. We use different combinations of three datasets among six, as given in Table 2. The stimulation current and initial conditions for the MS model are set as in Sect. 5.2. Figure 3 shows the experimental and fitted potentials for combinations that give the best and an average-quality fit, respectively. This is confirmed by the values of J in Table 2. We note that a comparison of single and multiple dataset fitting can be made by dividing the values of J by the number N of datasets used. As expected, multiple dataset fitting is more difficult.

The value \(v^*\) of the gating variable at pacing time and the maximal potential reached for each AP predicted by the MS model decrease with increasing frequency. This is easily seen for case 6, which has the largest frequency, by comparing the amplitude of the potential with the other cases on Fig. 3. Restitution is thus well represented by the model, at least qualitatively and to some extent quantitatively. When the quality of fit deteriorates, the MS model still predicts decreasing \(v^*\) and maximal potential, only with a small mismatch of the APD for either low or high frequencies. We should recall that the optical measurements are taken at a specific location on a heart, not on an isolated cell. This may explain the difficulties at matching a cell ionic model uniformly across all frequencies.

6 Conclusions and Perspectives

We provided a new framework for fitting electrophysiology model parameters based on control theory in order to adjust the dynamic response of the model. The only required data is indirect measurement of the potential (e.g. obtained through fluorescence imaging) for N pacing frequencies. As opposed to direct measures (e.g. obtained through clamping), the scale of our data had to be fitted simultaneously with the model parameters. The control problem is solved by a non-differentiable optimization method, hence differentiability of the ionic model is not required and complex dynamic response functions can be included in the cost function (e.g. restitution curve). The compass search method used is a simple alternative to genetic methods, requiring a reasonable number of function evaluations (200 to 500) as opposed to \(10^4\) for genetic methods [13]. The least-square function (5) gave a good fit of the trans-membrane potential predicted by the model to the potential recorded over time for N frequencies. However, the fit for this latter is as good as a given ionic model can represent the data. The applicability to more complex models will have to be investigated. We know from previous work [7] that models with 8–10 parameters can be identified for non-dynamic response (e.g. phase durations of a single AP). We are convinced that such models will be identifiable in the dynamic case with our new method.