On Tseitin Formulas, Read-Once Branching Programs and Treewidth

Abstract

We show that any nondeterministic read-once branching program that decides a satisfiable Tseitin formula based on an $n\times n$ grid graph has size at least $2^{\varOmega (n)}$. Then using the Excluded Grid Theorem by Robertson and Seymour we show that for arbitrary graph G(V, E) any nondeterministic read-once branching program that computes a satisfiable Tseitin formula based on G has size at least $2^{\varOmega (\mathrm {tw}(G)^\delta )}$ for all $\delta <1/36$, where $\mathrm {tw}(G)$ is the treewidth of G (for planar graphs and some other classes of graphs the statement holds for $\delta =1$). We also show an upper bound of $O(|E| 2^{\mathrm {pw}(G)})$, where $\mathrm {pw}(G)$ is the pathwidth of G.

We apply the mentioned results to the analysis of the complexity of derivations in the proof system $\mathrm {OBDD}(\wedge , \mathrm {reordering})$ and show that any $\mathrm {OBDD}(\wedge , \mathrm {reordering})$-refutation of an unsatisfiable Tseitin formula based on a graph G has size at least $2^{\varOmega (\mathrm {tw}(G)^\delta )}$.

The research was supported by Russian Science Foundation (project 16-11-10123).

1 Introduction

This paper continues the study of representation of satisfiable Tseitin formulas by read-once branching programs.

A Tseitin formula $\mathrm {TS}_{G,c}$ [20] is defined for every undirected graph G(V, E) and labelling function $c: V\rightarrow \{0,1\}$. We introduce a propositional variable for every edge of G. The Tseitin formula $\mathrm {TS}_{G,c}$ represents a linear system over the field $\mathrm{GF}(2)$ that for every vertex $v\in V$ states that the sum of all edges adjacent to v equals c(v). It is well known that a Tseitin formula is satisfiable if and only if the sum of values of the labeling function for all vertices in every connected component is even [21].

In 2017 Itsykson et al. [13] showed that any OBDD representing satisfiable Tseitin formulas based on d-regular expanders on n vertices has size at least $2^{\varOmega (n)}$. Then Glinskih and Itsykson [9] extended this lower bound to nondeterministic read-once branching programs ($1{\text {-}}\mathrm{NBP}$).

In this paper we consider an $n\times n$ grid and study the complexity of representation of Tseitin formulas based on it by read-once branching programs. In Theorem 2 we prove that any $1{\text {-}}\mathrm{NBP}$ computing a satisfiable Tseitin formula based on an $n\times n$ grid has size $2^{\varOmega (n)}$. Although an $n \times n$ grid graph has some edge-expansion properties, we could not prove the lower bound based only on these properties; our proof requires careful analysis and we use the geometric properties of the grid.

As an important corollary we establish a connection between the complexity of $1{\text {-}}\mathrm{NBP}$ representation of a satisfiable Tseitin formula and the treewidth of the underlying graph. The treewidth is one of the most important structural measures of a graph and it is one of the main parametrizations for computational graph problems. Theorem 3 states that any $1{\text {-}}\mathrm{NBP}$ computing a satisfiable Tseitin formula $\mathrm {TS}_{G,c}$ has size at least $2^{\varOmega (\mathrm {tw}(G)^{\delta })}$ for all $\delta <1/36$, where $\mathrm {tw}(G)$ denotes the treewidth of the graph G. The proof is based on the Excluded Grid Theorem by Robertson and Seymour [19]: there is a function g such that if a graph G has treewidth at least g(t), then G contains a grid of size $t \times t$ as a minor. Recent results of Chekuri and Chuzhoy [4] and [5] give polynomial upper bound on the function g. Hence we know that every graph G has a $t\times t$ grid as a minor, where $t=\varOmega (\mathrm {tw}(G)^\delta )$ for all $\delta <1/36$. For several classes of graphs it is possible to improve the value of $\delta$, for example, for planar graphs $\delta =1$ [11, 18]. Thus Theorem 3 is followed by Lemma 8 stating that if H is a minor of G, then for every S and for every $1{\text {-}}\mathrm{NBP}$ of size S that computes a satisfiable Tseitin formula $\mathrm {TS}_{G,c}$ there is an $1{\text {-}}\mathrm{NBP}$ that computes a satisfiable Tseitin formula $\mathrm {TS}_{H,c'}$ of size at most S. This lemma is proved separately for every operation: an edge deletion, a vertex deletion and an edge contraction. We use the non-determinism in the case of an edge contraction: we replace nodes labelled with contracted edges by guessing nodes.

In Theorem 4 we show that for every satisfiable Tseitin formula based on a graph G(V, E) has an $\mathrm {OBDD}$ of size $O(|E| 2^{\mathrm {pw}(G)})$, where $\mathrm {pw}(G)$ is the pathwidth of G (note that the pathwidth differs from the treewidth by at most a logarithmic factor: $\mathrm {tw}(G)\le \mathrm {pw}(G)\le O(\mathrm {tw}(G) \log |V|)$). Since the pathwidth of an $n\times n$ grid is O(n), our upper and lower bounds for grids match up to a constant in the exponent.

There are several known approaches to defining the treewidth of CNF formulas. Ferrara, Pan and Vardi [7] considered a graph on variables of a CNF formula where two variables are connected iff they share a common clause. They proved that if a graph associated with CNF formula has the treewidth t, then the formula has an $\mathrm {OBDD}$ of size $n^{O(t)}$ (it is very similar to Theorem 4 but it uses another notion of treewidth). Razgon [17] showed that this bound is tight and there is a family of CNF formulas with the treewidth at most k that requires $1{\text {-}}\mathrm{NBP}$ of size $n^{\varOmega (k)}$. In the case of a Tseitin formula $\mathrm {TS}_{G,c}$, the associated graph is the edge-graph of G, where the vertices are the edges of G and two edges are connected iff they are incident to the same vertex of G. For example, if G is a star on $n+1$ vertices (a star is a tree and, hence, it has the treewidth 1), then the edge-graph is the complete graph $K_{n-1}$ and it has the treewidth $n-2$.

Applications to Proof Complexity. The interest of the study of Tseitin formulas comes from the propositional proof complexity; unsatisfiable Tseitin formulas are one of the basic examples of hard formulas for many proof systems.

The study of representations of satisfiable Tseitin formulas by read-once branching program was motivated by the study of proof systems based on OBDDs introduced by Atserias, Kolaitis and Vardi [2]. Itsykson et al. [13] studied the proof system $\mathrm {OBDD}(\wedge , \mathrm {reordering})$; a proof of unsatisfiability of a CNF formula $\varphi$ in this proof system is a sequence of OBDDs: $D_1, D_2, \dots , D_s$ such that $D_s$ is a constant false $\mathrm {OBDD}$ and for all $i\in [s]$, $D_i$ either represents a clause of $\varphi$, or represents the conjunction of $D_k\wedge D_\ell$, where $k, \ell <i$ and $D_i, D_k$ and $D_\ell$ use the same order, or represents the same function as $D_{\ell }$ but using another order, where $\ell <i$. The paper [13] gives an exponential lower bound on size of $\mathrm {OBDD}(\wedge , \mathrm {reordering})$-refutations of unsatisfiable Tseitin formulas based on constant degree expanders. The lower bound proof is organized as follows: for any refutation of Tseitin formula $\mathrm {TS}_{G,c}$ of size S it is possible to construct an $\mathrm {OBDD}$ of size at most $S^2$ representing a satisfiable Tseitin formula $\mathrm {TS}_{G',c'}$, where $G'$ is a graph obtained from G by the deletion of several edges. Thus it is sufficient to prove lower bound on the size of $\mathrm {OBDD}$ representation of $\mathrm {TS}_{G',c'}$. We adapt this approach and show in Theorem 6 that our results imply that any $\mathrm {OBDD}(\wedge , \mathrm {reordering})$-refutation of an unsatisfiable Tseitin formula $\mathrm {TS}_{G,c}$ has size at least $2^{\varOmega (\mathrm {tw}(G)^\delta )}$, where $\delta$ is a constant as above. In particular we get a lower bound $2^{\varOmega (n)}$ on the complexity of $\mathrm {OBDD}(\wedge , \mathrm {reordering})$-refutations of Tseitin formulas based on the $n\times n$ grid.

The recent paper by Buss et al. [3] shows that this proof system cannot be polynomially simulated by Resolution and even by Cutting Planes. The paper shows that any Resolution proof of Tseitin formula based on the complete graph on $\log n$ vertices $K_{\log n}$ has size at least $2^{\varOmega (\log ^2 n)}$, while it has an $\mathrm {OBDD}(\wedge , \mathrm {reordering})$-refutation of polynomial size. It is well known that the size of the shortest regular Resolution proof of any unsatisfiable CNF formula $\phi$ equals the size of the minimal read-once branching program for the following search problem $\mathrm {Search}_\phi$: given an assignment of variables of $\phi$, find a clause that is refuted by this assignment [15, 16]. Our upper bound implies that satisfiable $\mathrm {TS}_{K_{\log n},c}$ can be computed by an $\mathrm {OBDD}$ of size poly(n). Thus we have that computing of $\mathrm {Search}_{\mathrm {TS}_{K_{\log n},c}}$ for an unsatisfiable $\mathrm {TS}_{K_{\log n},c}$ is superpolynomially harder than computing of a satisfiable $\mathrm {TS}_{K_{\log n},c'}$ for read-once branching programs.

Tseitin formulas based on the grid graphs were studied in proof complexity. The first superpolynomial lower bound for regular resolution was proved for grid graphs in 1968 by Tseitin [20]. In 1987 Urquhart proved a lower bound for Tseitin formulas based on expanders in unrestricted Resolution [21] but tight lower bounds for grids were proved by Dantchev and Riis only in 2001 [6]. In the recent paper [12] Hastad proved lower bound on Bounded depth Frege refutations for Tseitin formulas based on $n \times n$ grid graphs that implies that polynomial size Frege proofs of such formulas should use formulas with almost logarithmic depth.

The treewidth was also studied in the context of resolution refutations of Tseitin formulas. Alekhnovich and Razborov [1] considered a hypergraph that corresponds to every CNF formula, where variables are vertices and clauses as sets of variables form hyperedges. For Tseitin formulas the branch-width of this hypergraph is up to a constant factor equal to the Resolution width [1]. For constant degree graphs the treewidth is equal to the branch-width of the hypergraph up to a multiplicative constant. Galesi, Talebanfard and Torán in the recent paper [8] consider cop-robber games on graphs that is very similar to games characterising the treewidth, they used such games in an analysis of the complexity parameters of resolution refutations of Tseitin formulas.

Proofs omitted due to space constraints can be found in [10].

2 Preliminaries

Branching Programs. A deterministic branching program (BP) is a form of representation of Boolean functions. A Boolean function $f(x_1, x_2, \dots , x_n)$ is represented by a directed acyclic graph with exactly one source and two sinks. All nodes except sinks are labeled with a variable; every internal node has exactly two outgoing edges: one is labeled with 1 and the other is labeled with 0. One of the sinks is labeled with 1 and the other is labeled with 0. The value of the function for given values of variables is evaluated as follows: we start a path from the source such that for every node on its path we go along the edge that is labeled with the value of the corresponding variable. This path will end in a sink. The label of this sink is the value of the function.

A nondeterministic branching program (NBP) differs from a deterministic in the way that we also allow guessing nodes that are unlabeled and have two outgoing unlabeled edges. So nondeterministic branching program may have three types of nodes: guessing nodes, nodes labeled with a variable (we call them just labeled nodes) and two sinks; the source is either a guessing node or a labeled node. The result of a function represented by a nondeterministic branching program for given values of variables equals 1, if there exists at least one path from the source to the sink labeled with 1 such that for every node labeled with a variable on its path we go along an edge that is labeled with the value of the corresponding variable (for guessing nodes we are allowed to choose any of two outgoing edges). Note that deterministic branching programs constitute a special case of nondeterministic branching programs.

A deterministic or nondeterministic branching program is (syntactic) read-k (k-BP or k-NBP) if every path from the source to a sink contains at most k occurrences of each variable.

Let $\pi$ be a permutation of the set $\{1, \dots , n \}$ (an order). A $\pi$-ordered binary decision diagram is a 1-BP such that on every path from the source to a sink variable $x_{\pi (i)}$ can not appear before $x_{\pi (j)}$ if $i > j$. An ordered binary decision diagram ($\mathrm {OBDD}$) is a $\pi$-ordered binary decision diagram for some $\pi$.

Lemma 1

([22]). Assume that Boolean functions $f_1$ and $f_2$ have $\pi$-ordered OBDDs of sizes $k_1$ and $k_2$ respectively, then (1) $f_1 \wedge f_2$ has a $\pi$-ordered OBDD of size at most $k_1 k_2$; (2) for any partial substitution $\rho$, $f_1|_{\rho }$ has a $\pi$-ordered OBDD of size at most $k_1$.

Tseitin Formulas. Let G(V, E) be an undirected graph without loops but possibly with multiple edges, $c:V \rightarrow \{0,1\}$ be a labeling function that matches every vertex with a Boolean value. We associate every edge $e\in E$ with a propositional variable $x_e$. A Tseitin formula $\mathrm {TS}_{G,c}$ based on a graph G and a labeling function c is the conjunction of the following conditions: for every vertex v the sum of variables $x_e$ for all edges e that are incident to v equals c(v) modulo 2. More formally: $\bigwedge \limits _{v \in V}\left( {\sum \limits _{e \text{ is } \text{ incident } \text{ to } v}{x_{e}}}=c(v) \bmod {2}\right)$.

Usually, Tseitin formulas are written in the CNF. If the maximal degree of a graph is upper bounded by a constant d, then a sum modulo 2 can be written as a d-CNF of size at most $2^d$, hence the size of CNF representation of $\mathrm {TS}_{G,c}$ is at most $O(2^d n)$.

We will use the following criterion of the satisfiability of Tseitin formulas:

Lemma 2

([21]). A Tseitin formula $\mathrm {TS}_{G,c}$ is satisfiable if and only if for every connected component of the graph G the sum of values of the function c for all of the vertices is even. I.e., for every connected component U the following holds: $\sum \limits _{v \in U}{c(v)} = 0 \bmod 2$.

Remark 1

Note that a substitution of a value to a variable $x_e:=\alpha$ transforms Tseitin formula $\mathrm {TS}_{G,c}$ to a Tseitin formula $\mathrm {TS}_{G',c'}$, where graph $G'$ is obtained from the graph G by deleting the edge e, $c'$ equals c in every vertex except two vertices that are incident to edge e. On these two vertices the values of c and $c'$ differ by $\alpha$.

For a graph G(V, E) let $k_G(l)$ be the maximal number of connected components that can be obtained from G by the deletion of l edges. The following lower bound on the size of $1{\text {-}}\mathrm{NBP}$ for satisfiable Tseitin formula is known:

Lemma 3

([9], Corollary 20). For every connected graph G(V, E) and arbitrary $1\le l\le |E|$ any $1{\text {-}}\mathrm{NBP}$ evaluating a satisfiable Tseitin formula $\mathrm {TS}_{G,c}$ has size at least $2^{|V|-k_G(l)-k_G(|E|-l)+1}$.

Proof

(sketch). If a graph H(U, F) consists of k connected components, then a satisfiable Tseitin formula $\mathrm {TS}_{H,f}$ has exactly $2^{|F|-|U|+k}$ satisfying assignments ([9], Lemma 2). For every l we estimate the number of nodes of an $1{\text {-}}\mathrm{NBP}$ for $\mathrm {TS}_{G,c}$ on the level l. The graph G is connected, hence $\mathrm {TS}_{G,c}$ has exactly $2^{|E|-|V|+1}$ satisfying assignments. For every satisfying assignment of $\mathrm {TS}_{G,c}$ we consider an accepting path of the $1{\text {-}}\mathrm{NBP}$ corresponding to it. We consider the beginnings of these paths of length l. The number of accepting paths with the same beginning of length l is at most $2^{|E|-l-|V|+k_{G}(|E|-l)}$ (it is an upper bound on the number of satisfying assignments for Tseitin formulas on subgraph of G with $|E|-l$ edges). Thus, the number of different beginnings of length l of the accepting paths is at least $2^{l-k_{G}(|E|-l)+1}$. The number of different beginnings of length l of accepting paths that go through a fixed vertex on the level l is at most $2^{l-|V|+k_{G}(l)}$ (it is an upper bound on the number of satisfying assignments for Tseitin formulas on subgraph of G with l edges). Finally, the number of vertices on the l-th level is at least $2^{|V|-k_G(l)-k_G(|E|-l)+1}$.    $\square$

Lemma 4

Let G be an undirected graph, c and $c'$ be such that Tseitin formulas $\mathrm {TS}_{G,c}$ and $\mathrm {TS}_{G,c'}$ are satisfiable. Then sizes of minimum-size $1{\text {-}}\mathrm{NBP}$s ($1\text{- }\mathrm{BP}$s and $\mathrm {OBDD}$s) for $\mathrm {TS}_{G,c}$ and $\mathrm {TS}_{G,c'}$ are equal.

Treewidth, Pathwidth and Minors. $A~tree~decomposition$ of an undirected graph G(V, E) is a tree $T=(V_T, E_T)$ such that every vertex $u\in V_T$ corresponds to a set $X_u\subseteq V$ and it satisfies the following properties: 1. The union of $X_u$ for $u\in V_T$ equals V. 2. For every edge $(a,b)\in E$ there exists $u \in V_T$ such that $a, b \in X_u$. 3. If a vertex $a \in V$ is in the sets $X_u$ and $X_v$ for some $u,v\in V_T$, then it is also in $X_w$ for all w on the path between u and v in T.

If a tree T is a path, then this representation is a $path~decomposition$. $The~width~of~a~tree~decomposition$ is the maximum $|X_u|$ for $u\in V_T$ minus one. $A~treewidth$ of a graph G is the minimal value of the width among all tree decompositions of the graph G. We denote it as $\mathrm {tw}(G)$. $The~pathwidth$ of a graph G is the minimal value of the width among all path decompositions of a graph G. We denote it as $\mathrm {pw}(G)$.

Lemma 5

([14]). For every graph G on n vertices $\mathrm {pw}(G)=O(\log (n) \cdot \mathrm {tw}(G))$.

$A~minor$ of an undirected graph G is a graph that can be obtained from a graph G by a sequence of edge contractions, edge deletions and vertex deletions.

Theorem 1

([5]). For every constant $\delta < 1/36$ every graph G contains a $t\times t$ grid as a minor, where $t=\varOmega (\mathrm {tw}(G)^\delta )$.

3 Lower Bound for Grids

In this section we prove the following Theorem.

Theorem 2

Let $T_n$ be an $n \times n$ grid graph. Then if a Tseitin formula $\mathrm {TS}_{T_n,c}$ is satisfiable, then every $1{\text {-}}\mathrm{NBP}$ that computes $\mathrm {TS}_{T_n,c}$ has size at least $2^{\varOmega (n)}$.

Proof

$T_n$ contains $(n+1)^2$ vertices and $2n(n+1)$ edges. In order to prove this theorem we use Lemma 3 for $l=n(n+1)$ (so l is the half of the number of edges). So we have to prove that if we delete half of the edges of $T_n$, then the resulting graph will have at most $\frac{(n+1)^2}{2} - \varepsilon \cdot n$ connected components for some constant $\varepsilon >0$. Hence, by Lemma 3, every $1{\text {-}}\mathrm{NBP}$ for $\mathrm {TS}_{T_n,c}$ has size at least $2^{2\varepsilon n+1}$.

We call a subgraph of $T_n$ optimal if it contains l edges and has the maximal number of connected components. The plan of the proof is the following. At first we show that there exists an optimal subgraph H that has one connected component that contains all edges and all other connected components are isolated vertices. Then we estimate the number of connected components of H.

Lemma 6

There is an optimal subgraph of $T_n$ that has exactly one connected component with at least two vertices.

Proof

Consider all optimal subgraphs of $T_n$. Choose among them a subgraph H that contains a connected component M with the maximal number of edges. If M contains all edges of H, then the lemma is proved. Further we assume that not all edges are in M.

Consider the properties of the chosen graph H.

• 1. All the edges of the grid $T_n$ between vertices of M are in M. Indeed, otherwise we can delete an edge from another connected component and add it to M. After this operation the number of connected components does not decrease, but the number of edges in M is strictly increased. This is a contradiction since M has the maximal number of edges among all the optimal subgraphs.

• 2. Every connected component, except M, is edge-biconnected (i.e. it is impossible to increase the number of connected components by the deletion of an edge from it). Indeed, assume that for some connected component except M it is possible to delete an edge from it such that the number of connected component increases. Then we delete this edge and add an edge of the grid that connects M with a vertex out of M. In this case the number of connected components is not changed but the number of edges in the maximal component would be increased. This is a contradiction.

• 3. There is no vertex v of $T_n$ such that it is not in M but there are at least two edges between v and vertices of M in $T_n$. Proof by contradiction, assume that such a vertex exists. Consider a connected component K that differs from M and has edges. Consider a set of the lowest vertices in K and let u be the leftmost vertex among them. There are no edges to the left or down from the vertex u in the graph H. Since the connected component K has edges, there is at least one edge that is incident to u. By the previous property, K is edge-biconnected, hence, u has precisely two incident edges. Let us delete the two edges incident to u from K and add two edges that connect the vertex v and M. The number of connected components doesn’t decrease, but the number of edges in the maximal component increases. This is a contradiction.

• 4. Every $1 \times 1$ square of the grid $T_n$ contains 0, 1 or 4 edges from M. A $1\times 1$ square cannot contain exactly 3 edges because it contradicts the property 1. Let an $1\times 1$ square contains exactly 2 edges from M. If these are two incident edges then we get a contradiction with the property 3 or the property 1. If these are two opposite edges, then we get a contradiction with the property 1.

• 5. For every $u,v\in M$, the minimal rectangle of the grid that contains both u and v (with all interior edges) is a subgraph of M (one of the sides of the rectangle could be of zero length, in that case it’s just a line of the grid). It can be easily shown by the induction on the length of the shortest path between u and v using the property 4.

• 6. M is a rectangle of the grid with all edges of this rectangle. Consider the maximal rectangle of the grid that is fully contained (with all edges) in M. If there are vertices in M that are not in this rectangle, then we could increase this rectangle using the property 5.

So M is a rectangle of the grid. We say that M can be moved one step to the left (right, down or up) if all left (right, down or up) neighbours of the left (right, down or up) border of M are isolated vertices in H. Such a move doesn’t change the number of connected components and the number of edges in them. Consider some connected component K that differs from M and contains edges. We move M one step closer to K in the way of decreasing the distance between them while it is possible. By the distance we understand the minimal $L_1$-distance between two vertices from M and K. After some step it is not possible anymore; it means that one of the borders of M (w.l.o.g. it is the upper border) has upper neighbours from connected components that consist of more than one vertex.

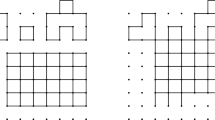
Let M be a rectangle $x\times y$, where x, y are non-negative integers. That means that every horizontal line of M contains $x+1$ vertices. Assume that among upper neighbours of the upper border of M there are m vertices that are in some connected component that consists of more than one vertex. Let these m vertices be in k connected components. Assume that there are r edges of the graph H between $x+1$ upper neighbours of M (see an example on the left part of Fig. 1). Since every edge between upper neighbours of M decreases the number of connected components, the following inequality holds $k\le m-r$. Obviously, $r\le x$.

Fig. 1.

Example: $x=6, y=4, r=3, k=3, m=7$

Fig. 2.

Spines

Consider the following modification of the graph H: we move the rectangle M one step up and add edges down from r vertices on the bottom border of M (see example on the right part of Fig. 1). The number of edges after this transformation is not changed since r edges overlapped and we added r edges. Now we estimate the number of connected components. On the bottom border we add $(x+1)-r$ new connected components. On the upper border $(x+1)-m+k$ connected components disappeared (were merged to one). Finally, the number of connected components increased by $m-k-r$, that is at least zero since $k\le m-r$. But the number of edges in the maximal connected component increases, this contradicts the choice of the graph H. So we get a contradiction with the assumption that there are more than one connected components with at least one edge.    $\square$

So we may assume that there is an optimal graph H that has one connected component M with at least two vertices and t isolated vertices. Notice that M is not necessary a rectangle now (in Lemma 6 we only show that it has to be a rectangle under the assumption that the statement of the lemma is wrong). We are going to estimate $k_{T_n}(l)=t+1$ from the above.

For every connected component K we define a set of spines that go out of it. We assume that $T_n$ is a part of the infinite grid. An edge e of the infinite grid is a spine of K if it connects a vertex u from K with a vertex out of K and u is the right or bottom endpoint of e (see Fig. 2). Note that spines can go outside of the square $T_n$ if u is on the upper or left border of $T_n$. If a component is an isolated vertex, then it has exactly two spines.

The same edge cannot be a spine for two different connected components since we choose only the edges that go up or to the left from the component. Let h be the total number of all spines for all of the connected components of H. Every spine is either an edge of the square $T_n$ that is not in H or is among $2(n+1)$ edges that go outside the square $T_n$. Hence, $2(n+1)+n(n+1)\ge h$.

Let X be the number of spines of the connected component M, then we get that $h=2t+X$. Using the previous inequality we estimate t as follows: $t\le (n+1)(n+2)/2-X/2=(n+1)^2/2+ (n+1-X)/2$. Hence, we need to show that $X\ge (1+\epsilon )n$ for some constant $\epsilon$.

Consider the minimal grid rectangle that contains M. Assume it has size $(a-1)\times (b-1)$, where a, b are natural numbers. Then there are spines of M in every of a vertical lines and in every of b horizontal lines. Then we get that $X\ge a+b \ge 2 \sqrt{ab}$. On the other hand, the component M contains exactly $n(n+1)$ edges, they need to be embedded into a rectangle $(a-1)\times (b-1)$ that contains $a(b-1)+b(a-1)$ edges. Then we can estimate $2ab>a(b-1)+b(a-1)\ge n (n+1)$ and we get $X\ge \sqrt{2n(n+1)}>\sqrt{2} n$.

Using the upper bound on t, the number of connected components can be estimated as: $k_{T_n}(l)=t+1\le (n+1)^2/2 -(\sqrt{2}-1)n+\frac{3}{2}$. Then by Lemma 3, every $1{\text {-}}\mathrm{NBP}$ for a satisfiable Tseitin formula $\mathrm {TS}_{T_n,c}$ has size at least $2^{2(\sqrt{2}-1)n-2}$.    $\square$

4 Treewidth

The main goal of this section is to prove the following theorem.

Theorem 3

Let $\mathrm {TS}_{G,c}$ be a satisfiable Tseitin formula. Then every $1{\text {-}}\mathrm{NBP}$ for $\mathrm {TS}_{G,c}$ has size at least $2^{\varOmega \left( \mathrm {tw}(G)^{\delta }\right) }$ for all $\delta <1/36$.

Lemma 7

Let D be a $1{\text {-}}\mathrm{NBP}$ computing a Boolean function $f:\{0,1\}^n\rightarrow \{0,1\}$. If we change every node in D labeled with the variable $x_1$ by a guessing node and remove all labels of all its outgoing edges, then we obtain a valid $1{\text {-}}\mathrm{NBP}$ that computes $\exists x_1 f(x_1, x_2,\dots , x_n)$.

Lemma 8

Let H be a minor of an undirected graph G and Tseitin formulas $\mathrm {TS}_{G,c}$ and $Ts_{H,c'}$ be satisfiable. Then for every S and every $1{\text {-}}\mathrm{NBP}$ of size S that computes $\mathrm {TS}_{G,c}$, there is a $1{\text {-}}\mathrm{NBP}$ that computes $\mathrm {TS}_{H,c'}$ of size at most S.

Proof

It suffices to prove the statement of the lemma for the case when H is obtained from G by the application of one operation. Let us consider all types of operations separately.

• 1. H is obtained from G by the deletion of an edge e. Let $\sigma$ be a satisfying assignment of $\mathrm {TS}_{G,c}$. We apply the partial assignment $x_e:=\sigma (x_e)$ to $\mathrm {TS}_{G,c}$ and get the satisfiable formula $\mathrm {TS}_{H,c''}$. It is well known that the application of a substitution does not increase size of the $1{\text {-}}\mathrm{NBP}$. By Lemma 4, sizes of the minimal $1{\text {-}}\mathrm{NBP}$s for $\mathrm {TS}_{H,c''}$ and $\mathrm {TS}_{H,c'}$ are equal.

• 2. H is obtained from G by the deletion of a vertex v. Since all the variables of Tseitin formulas are associated with edges, this case can be considered as a sequence of edge deletions.

• 3. A graph $H(V_H, E_H)$ is obtained from a graph G(V, E) by the contraction of an edge $e=(u,v)$. Let us define a labeling function $c'':V_H\rightarrow \{0,1\}$ as follows: for all the vertices that differ from the joined vertex $\{u,v\}$ it has the same value as in the labeling function c and $c''(\{u,v\})=c(u)+c(v)\bmod 2$. By the construction, every connected component U of H corresponds to a connected component $U'$ of G with the same sum of the labeling functions: $\sum _{w\in U}c''(w)=\sum _{w\in U'} c(w) \bmod 2$. Hence, by Lemma 2, $\mathrm {TS}_{H,c''}$ is satisfiable.

   $\square$

Lemma 9

Formulas $\mathrm {TS}_{H, c''}$ and $\exists x_e \mathrm {TS}_{G,c}$ define the same function.

By Lemma 7, the minimal size of a $1{\text {-}}\mathrm{NBP}$ for $\exists x_e \mathrm {TS}_{G,c}$ (that is by Lemma 9 equivalent to $\mathrm {TS}_{H,c''}$) is at most the minimal size of a $1{\text {-}}\mathrm{NBP}$ for $\mathrm {TS}_{G,c}$. By Lemma 4, minimal sizes of $1{\text {-}}\mathrm{NBP}$s for $\mathrm {TS}_{H,c''}$ and for $\mathrm {TS}_{H,c'}$ are equal.    $\square$

Proof

(Proof of Theorem 3).

By Theorem 1, the graph G contains a $t \times t$ grid graph as a minor, where $t=\varOmega (\mathrm {tw}(G)^{\delta })$. The theorem follows from Theorem 2 and Lemma 8.    $\square$

We also obtain an upper bound:

Theorem 4

Every satisfiable Tseitin formula $\mathrm {TS}_{G,c}$ can be represented as $\mathrm {OBDD}$ of size $|E| 2^{\mathrm {pw}(G)+1}+2$.

Corollary 1

Any satisfiable Tseitin formula based on a graph G(V, E) can be represented as $\mathrm {OBDD}$ of size $O(|E| |V|^{O(\mathrm {tw}(G))})$.

Proof

Follows from Theorem 4 and Lemma 5.    $\square$

5 Lower Bound in the Proof System $\mathrm {OBDD}(\wedge , \mathrm {reordering})$

In this section we show that any refutation of an unsatisfiable Tseitin formula $\mathrm {TS}_{G,c}$ in the proof system $\mathrm {OBDD}(\wedge , \mathrm {reordering})$ has size at least $2^{\varOmega \left( tw(G)^\delta \right) }$ for all $\delta <1/36$.

If F is a formula in CNF, we say that a sequence $D_1, D_2, \dots , D_t$ of $\mathrm {OBDD}$s is an $\mathrm {OBDD}(\wedge , \mathrm {reordering})$-refutation of F if $D_t$ is an $\mathrm {OBDD}$ that represents the constant false function, and for all $1 \le i \le t$, $D_i$ is an $\mathrm {OBDD}$ that represents a clause of F or can be obtained from the previous $D_j$’s by one of the following inference rules: (conjunction or join) $D_i$ is an $\mathrm {OBDD}$ with order $\pi$, that represents $D_k \wedge D_l$ for $1 \le l, k < i$, where $D_k, D_l$ have the same order $\pi$; (reordering) $D_i$ is an $\mathrm {OBDD}$ that is equivalent to an $\mathrm {OBDD}$ $D_j$ with $j < i$ (note that $D_i$ and $D_j$ may have different orders).

We say that a graph H is t-good if H is connected and every $\mathrm {OBDD}$-representation of any satisfiable Tseitin formula $\mathrm {TS}_{H,c}$ has size at least t. The following theorem can be proved using ideas from [13]:

Theorem 5

(cf. [13]). Let G(V, E) be a connected graph and degrees of all vertices of G be bounded by a constant. Assume that the graph G has the following properties: (1) if we delete any vertex from G, we get a t-good graph; (2) for every two vertices u and v of G there is a path p between them such that if we delete all vertices from p, we get a t-good graph. And if we delete from G vertices u and v and the edges of the path p, we also get a connected graph.

Then any $\mathrm {OBDD}(\wedge , \mathrm {reordering})$-refutation of an unsatisfiable Tseitin formula $\mathrm {TS}_{G,c}$ has size at least $\varOmega (\sqrt{t})$.

Proof

(sketch). We consider the last step of the $\mathrm {OBDD}(\wedge , \mathrm {reordering})$-refutation: the conjunction of $\mathrm {OBDD}$s $F_1$ and $F_2$ is the identically false function but both $F_1$ and $F_2$ are satisfiable. Both $F_1$ and $F_2$ are conjunctions of several clauses of $\mathrm {TS}_{G, c}$.

Since G remains connected after removing of any single vertex, $F_1$ and $F_2$ together contain all clauses of $\mathrm {TS}_{G, c}$. Assume that there are two nonadjacent vertices u and v such that $F_1$ does not contain a clause $C_u$ that corresponds to the vertex u and $F_2$ does not contain a clause $C_v$ that corresponds to v (if this assumption is false, the proof is rather straightforward). We consider two partial substitutions $\rho _1$ and $\rho _2$ that are both defined on the edges adjacent to u and v and on the edges of the path p between u and v. The substitutions $\rho _1$ and $\rho _2$ assign opposite values to edges of the path p and are consistent on all other edges. The substitution $\rho _1$ satisfies $C_v$ and refutes $C_u$ and $\rho _2$ satisfies $C_u$ and refutes $C_v$.

By the construction $F_1|_{\rho _1} \wedge F_2|_{\rho _2}$ is almost a satisfiable Tseitin formula based on the graph that is obtained from G by deletion of the vertices u and v and all edges from the path p. However, it is also possible that this formula does not contain some clauses for the vertices from p. Thus we make additional partial substitution $\tau$ that substitute values from a satisfying assignment for all remaining edges for vertices from p. $(F_1|_{\rho _1} \wedge F_2|_{\rho _2})|_{\tau }$ is satisfiable Tseitin formula based on the graph that is obtained from G by deletion of all vertices from the path p. The size of an $\mathrm {OBDD}$ representation of such a formula is at least t by the condition of the theorem. Hence by Lemma 1 we get that either $F_1$ or $F_2$ has size at least $\varOmega (\sqrt{t})$ in the given order.    $\square$

Theorem 5 is used in the proof of the main result of this section:

Theorem 6

Let G be a connected graph and $\mathrm {TS}_{G,c}$ be an unsatisfiable formula. Then every $\mathrm {OBDD}(\wedge , \mathrm {reordering})$-refutation of $\mathrm {TS}_{G,c}$ has size at least $2^{\varOmega \left( \mathrm {tw}(G)^\delta \right) }$ for all $\delta <1/36$.