1 Introduction

Interaction of deformation and temperature fields was started from [1, 2] as a coupled thermoelasticity theory. These basic results were generalized in [3,4,5]. To solve coupled thermoelastic problems, different methods was developed since then, both analytical [4, 5] and numerical [6]. In [6], a finite element scheme was developed to solve a coupled thermoelasticity problem. Further investigations on coupled elasticity also heavily used the finite element method, for example [7,8,9,10,11]. Analytical methods for these problems have not gained such wide development as numerical. Intermediate results on analytical methods was summarized in [12].

Starting from [13,14,15,16,17,18], uncoupled thermoelasticity problems were considered accounting for friction , frictional heating and abrasive wear of the coating. Due to large number of parameters in the sliding thermoelastic contact problems [15,16,17,18,19], one-dimensional quasi-static problems were mostly considered. Solutions of uncoupled problems in [15,16,17,18,19] were constructed by the Laplace integral transform in the form of functional series over poles of integrands of contour integrals of the inverse Laplace transform. This method of the uncoupled thermoelastic problems solutions allowed one to obtain parametric boundaries of sliding contact thermoelastic instability and to investigate properties of the obtained solutions. In [20,21,22] a new directions were developed for the model of sliding of two elastic bodies against each other accounting for friction , frictional heating and wear , based on the virtual energy principle and main laws of thermodynamics. To solve problems based on this model, the finite element method is adopted [22].

The present works addresses effect of the dimensionless parameter of thermal and elastic fields coupling on the main parameters of sliding contact and on the thermoelastic instability occurrence.

2 Statement of the Coupled Problem of Wear

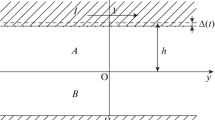
To investigate the effect of thermoelastic coupling on the occurrence of thermoelastic instability in sliding contact problems, the contact problem of coupled thermoelasticity on sliding with a constant velocity V of a rigid heat-insulated half-plane I \(\left( {h \le x < \infty } \right)\) over the upper \((x = h)\) surface of an elastic thermal-conducting coating of thickness h \(\left( {0 \le x \le h} \right)\), is considered. The lower surface of the coating is rigidly coupled to a non-deformable non-heat-conducting substrate in the form of a half-plane II \(\left( {\infty < x < 0} \right)\). Sliding of the half-plane I along the surface of the elastic coating takes into account Coulomb friction and abrasive wear of the coating surface [15,16,17,18,19]. The heat flux generated at the contact due to friction is directed into the coating. From the initial time moment, the half-plane I moving along the axis y deforms the surface \((x = h)\) of the elastic coating, moving in the direction opposite to the x-axis, according to the law \(\Delta (t)\). Until the initial moment, the coating was at rest, and its temperature was equal to \(T_{0}\).

The formulation of the problem assumes that the distributions of temperature, stresses and displacements in the coating do not depend on the choice of the horizontal coordinate along the y-axis parallel to the direction of the half-plane I sliding , and are functions of only the coordinate x and time t [15,16,17,18,19]. The displacements and temperature in the coating are governed by quasi-static coupled thermoelasticity equations [23]:

$$\frac{{\partial^{2} u}}{{\partial x^{2} }} = \frac{1 + v}{1 - v}\upalpha\frac{\partial T}{\partial x},\quad \frac{{\partial^{2} w}}{{\partial x^{2} }} = 0,\quad 0 \le x \le h,\quad t > 0$$
(29.1)
$$\frac{{\partial^{2} T}}{{\partial x^{2} }} - \frac{1}{\upkappa}\frac{\partial T}{\partial t} =\upalpha\frac{{3\uplambda + 2\upmu}}{K}T_{0} \frac{{\partial^{2} u}}{\partial x\partial t}\quad 0 \le x \le h,\quad t > 0$$
(29.2)

where \(T(x,t)\) is the temperature distribution in the coating, \(u(x,t)\), \(w(x,t)\) are the vertical and horizontal displacements in the coating, α is a coefficient of linear expansion of coating material, \(\upkappa\) is a coefficient of thermal diffusivity, \(\uplambda\), \(\upmu\) are Lamé coefficients, K is a coefficient of thermal conductivity, \(T_{0}\) is the initial temperature in the coating.

The boundary conditions of the problem for the differential equations (29.1) and (29.2) are:

  • mechanical \((t > 0)\)

$$x = h\quad u(h,t) = - \Delta (t) + u_{w} (t)$$
(29.3)
$$\upsigma_{xy} (h,t) = - f\upsigma_{xx} (h,t)$$
(29.4)
$$x = 0\quad u(0,t) = 0$$
(29.5)
$$w(0,t) = 0$$
(29.6)

  • temperature \((t > 0)\)

$$x = h\quad K\frac{\partial T(h,t)}{\partial x} = Q(t)$$
(29.7)
$$x = 0\quad K\frac{\partial T(0,t)}{\partial x} = k\left( {T(0,t) - T_{0} } \right)$$
(29.8)

where f is a coefficient of friction , k is a coefficient of heat transfer, \(u_{w} (t)\) is the half-plane I displacement due to the wear of the coating, \(Q(t) = fV( -\upsigma_{xx} (h,t))\) is the heat generated by friction at the contact interface [24]; \(\upsigma_{xx} =\upsigma_{xx} (x,t)\), \(\upsigma_{xy} =\upsigma_{xy} (x,t)\) are the normal and tangential stresses in the coating, defined by a form of the Hooke’s law:

$$\upsigma_{xx} = \left( {\uplambda + 2\upmu} \right)\frac{\partial u}{\partial x} - \left( {3\uplambda + 2\upmu} \right)\upalpha\left( {T - T_{0} } \right),\quad\upsigma_{xy} =\upmu\frac{\partial w}{\partial x}$$
(29.9)

Further, the abrasive wear model [25] is used, according to which the amount of wear is

$$u_{w} (t) = - fVK^{*} \int\limits_{0}^{t} {\upsigma_{xx} (h,\uptau) \text{d}\uptau} \quad t > 0$$
(29.10)

where \(K^{*}\) is a coefficient of proportionality between the work of friction al forces and the amount of material removed from the contact . In addition, according to (29.7), it is assumed that all the heat at the contact is formed due to friction .

The initial conditions for displacement in the coating are zero:

$$u(x,0) = w(x,0) = 0$$
(29.11)

while initial temperature is set to \(T_{0}\):

$$T(x,0) = T_{0}$$
(29.12)

Thus, the solution of the formulated problem is reduced to solution the system of differential equations (29.1) and (29.2) with the boundary (29.3)–(29.8) and initial conditions (29.11) and (29.12). It should be noted that the vertical displacements \(u(x,t)\), normal stresses \(\upsigma_{xx} (x,t)\) and temperature T(x, t) in the coating are determined independently from the horizontal displacements w(x, t), while latter are determined from (29.1), (29.4) and (29.6) through \(\upsigma_{xx} (x,t)\).

3 Exact Solution of the Problem

The solution of the coupled contact thermoelasticity problem given in Sect. 29.2 is constructed using the Laplace integral transformation [27]:

$$u^{L} (x,p) = \int\limits_{0}^{\infty } {u(x,t)e^{ - pt} {\text{d}}t} ,\quad u(x,t) = \frac{1}{{2\uppi\,i}}\int\limits_{ - i\infty + c}^{i\infty + c} {u^{L} (x,p)e^{pt} {\text{d}}p} ,\quad \text{Re} \;p < c,\;\;c > 0$$
(29.13)

The index L in (29.13) denotes the transform of the Laplace transformation.

The Laplace transformation (29.13) is applied to the differential equations (29.1) and (29.2) taking into account the initial conditions (29.11) and (29.12) and the existence conditions for the Laplace integrals (29.13) [27]. As a result, a system of ordinary differential equations is obtained with respect to the transforms \(u^{L} (x,p)\) and \(T^{L} (x,p)\):

$$\frac{{{\text{d}}^{2} u^{L} }}{{{\text{d}}x^{2} }} = \frac{1 + v}{1 - v}\upalpha\frac{{{\text{d}}T^{L} }}{{{\text{d}}x}},\quad 0 \le x \le h$$
(29.14)
$$\frac{{{\text{d}}^{2} T^{L} }}{{{\text{d}}x^{2} }} - \frac{p}{\upkappa}T^{L} - \frac{1}{\upkappa}T_{0} = \frac{{2\upmu(1 + v)}}{1 - 2v}\frac{\upalpha}{K}T_{0} p\frac{{{\text{d}}u^{L} }}{{{\text{d}}x}},\quad 0 \le x \le h$$
(29.15)

Differentiating (29.15) and substituting the second derivative of \(u^{L} (x,p)\) from (29.14) into the resulting relation, the following differential equation is obtained with respect to \(T^{L} (x,p)\):

$$\frac{\text{d}}{{{\text{d}}x}}\left( {\frac{{{\text{d}}^{2} T^{L} }}{{{\text{d}}x^{2} }} - \frac{{\upbeta^{2} }}{\upkappa}pT^{L} } \right) = 0\quad 0 \le x \le h$$
(29.16)
$$\upbeta^{2} = 1 + \hat{T},\quad \hat{T} = \frac{{2\upmu(1 + v)^{2} }}{(1 - v)(1 - 2v)}\frac{{\upkappa \upalpha ^{2} }}{K}T_{0}$$

The general solution of the differential equation (29.16) has the form:

$$T^{L} (x,p) = A_{1} + A_{2} \,{\text{sh}}\left( {\sqrt {\frac{p}{\upkappa}}\upbeta\,x} \right) + A_{3} \,{\text{ch}}\left( {\sqrt {\frac{p}{\upkappa}}\upbeta\,x} \right)$$
(29.17)

in which \(A_{1}\), \(A_{2}\), \(A_{3}\) are arbitrary constants.

Substituting \(T^{L} (x,p)\) from (29.17) into (29.14), an inhomogeneous differential equation with respect to \(u^{L} (x,p)\) is obtained. Its double integration gives the general solution:

$$u^{L} (x,p) = \frac{1 + v}{1 - v}\upalpha\frac{1}{{\sqrt {\frac{p}{\upkappa}}\upbeta}}\left( {A_{2} \,{\text{ch}}\left( {\sqrt {\frac{p}{\upkappa}}\upbeta\,x} \right) + A_{3} \,{\text{sh}}\left( {\sqrt {\frac{p}{\upkappa}}\upbeta\,x} \right)} \right) + A_{4} x + A_{5}$$
(29.18)

where \(A_{2}\), \(A_{3}\) are from (29.17), \(A_{4}\), \(A_{5}\) are new unknown values depending on p.

Substituting (29.17) and (29.18) into (29.15), a dependence between \(A_{1}\) and \(A_{4}\) is found:

$$A_{1} = \frac{{T_{0} }}{p} - \frac{1 - v}{1 + v}\frac{{\hat{T}}}{\upalpha}A_{4}$$
(29.19)

Replacing \(A_{1}\) by \(A_{4}\) in (29.17) according to (29.19), the general solution for \(T^{L} (x,p)\) from (29.14), (29.15) is obtained as

$$T^{L} (x,p) = \frac{{T_{0} }}{p} + A_{2} \,{\text{sh}}\left( {\sqrt {\frac{p}{\upkappa}}\upbeta\,x} \right) + A_{3} \,{\text{ch}}\left( {\sqrt {\frac{p}{\upkappa}}\upbeta\,x} \right) - \frac{1 - v}{1 + v}\frac{{\hat{T}}}{\upalpha}A_{4}$$
(29.20)

Thus, \(u^{L} (x,p)\) from (29.18) and \(T^{L} (x,p)\) from (29.20) with constants A2–A5 are general solutions of the system (29.14) and (29.15), and the constants A2–A5 are found from the boundary conditions (29.3), (29.5), (29.7) and (29.8), after applying the integral Laplace transform to them:

  • mechanical

$$x = h\quad u^{L} (h,p) = - \Delta^{L} (p) + u_{w}^{L} (p)$$
(29.21)
$$x = 0\quad u^{L} (x,p) = 0$$
(29.22)

  • temperature

$$x = h\quad K\frac{{dT^{L} (h,p)}}{dx} = - fV\upsigma_{xx}^{L} (h,p)$$
(29.23)
$$x = 0\quad K\frac{{dT^{L} (0,p)}}{dx} = k\left( {T^{L} (0,p) - \frac{{T_{0} }}{p}} \right)$$
(29.24)

in which \(u_{w}^{L} (p) = - fVK^{*} \frac{{\upsigma_{xx}^{L} (h,p)}}{p}\)

$$\upsigma_{xx}^{L} (x,p) = \frac{{2\upmu(1 - v)}}{1 - 2v}\frac{{du^{L} (x,p)}}{dx} - \frac{{2\upmu(1 + v)}}{1 - 2v}\upalpha\left( {T^{L} (x,p) - \frac{{T_{0} }}{p}} \right)$$
(29.25)

Substituting (29.18) and (29.20) into the boundary conditions (29.22) and (29.24) gives relations for \(A_{4}\) and \(A_{5}\) which, after being itself substituted to (29.18) and (29.20), allow us to obtain \(u^{L} (x,p)\) and \(T^{L} (x,p)\) in the new form, depending only on \(A_{2}\) and \(A_{3}\):

$$\begin{aligned} u^{L} (x,p) & = \frac{1 + v}{1 - v}\frac{{\upalpha\,h}}{{\sqrt {\frac{p}{\upkappa}}\upbeta\,h}}\left( {A_{2} \left( {{\text{ch}}\sqrt {\frac{p}{\upkappa}}\upbeta\,x - 1} \right) + A_{3} \,{\text{sh}}\sqrt {\frac{p}{\upkappa}}\upbeta\,x} \right) \\ & \quad - \frac{1 + v}{1 - v}\frac{\alpha }{{\hat{T}{\text{Bi}}}}\left( {\sqrt {\frac{p}{\upkappa}}\upbeta\,hA_{2} - {\text{Bi}}A_{3} } \right)x \\ \end{aligned}$$
(29.26)
$$T^{L} (x,p) = A_{2} \frac{1}{\text{Bi}}\left( {\sqrt {\frac{p}{\upkappa}}\upbeta\,h + {\text{Bi}}\,{\text{sh}}\sqrt {\frac{p}{\upkappa}}\upbeta\,x} \right) + A_{3} \left( {{\text{ch}}\sqrt {\frac{p}{\upkappa}}\upbeta\,x - 1} \right) + \frac{{T_{0} }}{p}$$
(29.27)

The constants \(A_{2}\) and \(A_{3}\) are determined by substituting (29.26) and (29.27) into the boundary conditions (29.21) and (29.23), after which a system of linear algebraic equations is formed with respect to \(A_{2}\) and \(A_{3}\):

$$\sum\limits_{j = 1}^{2} {a_{ij} A_{j + 1} } = b_{i} \quad i = 1,2$$
(29.28)

where \(b_{i}\), \(a_{ij}\) \(i,j = 1,2\) are calculated from the formulas:

$$a_{11} = \sqrt z \left( {\hat{T}{\text{Bi }}\left( {{\text{ch}}\sqrt z - 1} \right) - z - \hat{V}k_{w}\upbeta^{2} } \right),\quad a_{12} = {\text{Bi}}\left( {\hat{T}h\sqrt z \,{\text{sh}}\,\sqrt z + z + \hat{V}k_{w}\upbeta^{2} } \right)$$
$$a_{21} = \sqrt z \left( {\hat{T}{\text{Bi}}\,{\text{ch}}\sqrt z - \hat{V}\upbeta^{2} } \right),\quad a_{22} = {\text{Bi}}\left( {\hat{T}\sqrt z \,{\text{ch}}\,\sqrt z + \hat{V}\upbeta^{2} } \right)$$
$$b_{1} = - \frac{1 - v}{1 + v}\frac{{\hat{T}{\text{Bi}}}}{{\upalpha\,h}}z\Delta^{L} (p),\quad b_{2} = 0$$
$$z = \frac{p}{\upkappa}\upbeta^{2} h^{2} ,\quad \hat{V} = \frac{{fV\upalpha}}{K}\frac{{2\upmu(1 + v)h}}{1 - 2v},\quad k_{w} = \frac{1 - v}{1 + v}\frac{{KK^{*} }}{{\upalpha \upkappa }}\upbeta^{2} ,\quad {\text{Bi}} = \frac{kh}{K}$$
(29.29)

By solving the equation system (29.28) with respect to the constants \(A_{2}\), \(A_{3}\), and substituting them into (29.25)–(29.27), the Laplace images of temperature, displacements and stresses are obtained (not given here).

After inversion of the resulting images: \(T^{L} (x,p)\), \(u^{L} (x,p)\), \(\upsigma_{xx}^{L} (x,p)\), with the help of the inverse Laplace transform (29.13), it is convenient to write down the considered problem solution \(T(x,t)\), \(u(x,t)\), \(\upsigma_{xx} (x,t)\) in the form of convolutions:

$$T(x,t) - T_{0} = \frac{1 - v}{1 + v}\frac{1}{{\upalpha\,h}}\int\limits_{0}^{t} {\Delta (\uptau)f_{T}^{0} (x,t -\uptau)d\uptau} ,\quad 0 \le x \le h,\quad t > 0$$
(29.30)
$$f_{T}^{0} (x,t) = \frac{1}{{2\uppi\,i}}\int\limits_{\Gamma } {\frac{{N_{T}^{0} (x,z)}}{{t_{\upkappa} R(z)}}e^{{z\tilde{t}}} {\text{d}}z} ,\quad \tilde{t} = \frac{t}{{t_{\upkappa} }},\quad t_{\upkappa} = \frac{{h^{2} }}{\upkappa}$$
(29.31)
$$N_{T}^{0} (x,z) = \hat{V}\upbeta^{2} \sqrt z \left( {{\text{Bi}}\,{\text{sh}}\sqrt z \frac{x}{h} + \sqrt z \,{\text{ch}}\,\sqrt z \frac{x}{h}} \right) + \hat{T}z\left( {r(z) - {\text{Bi}}\,{\text{ch}}\,\sqrt z \frac{h - x}{h}} \right)$$
(29.31)
$$R(z) = zr(z) - \hat{V}\upbeta^{2} \left( {\left( {1 - k_{w} } \right)r(z) - {\text{Bi}}} \right) + \hat{T}{\text{Bi}}\sqrt z \,{\text{sh}}\,\sqrt z$$
(29.32)
$$r(z) = {\text{Bi}}\,{\text{ch}}\,\sqrt z + \sqrt z \,{\text{sh}}\,\sqrt z$$
$$u(x,t) = - \int\limits_{0}^{t} {\Delta (\uptau)f_{u}^{0} (x,t -\uptau){\text{d}}\uptau} ,\quad 0 \le x \le h,\quad t > 0$$
(29.33)
$$f_{u}^{0} (x,t) = \frac{1}{{2\uppi\,i}}\int\limits_{\Gamma } {\frac{{N_{u}^{0} (x,z)}}{{t_{\upkappa} R(z)}}e^{{z\tilde{t}}} {\text{d}}z} ,\quad \tilde{t} = \frac{t}{{t_{\upkappa} }}$$
(29.34)
$$\begin{aligned} N_{u}^{0} (x,z) & = zr(z)\frac{x}{h} - \hat{V}\upbeta^{2} \left( {{\text{Bi}}\,{\text{ch}}\,\sqrt z \frac{x}{h} + \sqrt z \,{\text{sh}}\,\sqrt z \frac{x}{h} - {\text{Bi}}} \right) \\ & \quad - \hat{T}{\text{Bi}}\sqrt z \left( {{\text{sh}}\,\sqrt z \frac{h - x}{h} - {\text{sh}}\,\sqrt z } \right) \\ \end{aligned}$$
(29.35)
$$\upsigma_{xx} (x,t) = - \frac{{2\upmu(1 - v)}}{(1 - 2v)h}\int\limits_{0}^{t} {\Delta (\uptau)f_{\upsigma}^{0} (x,t -\uptau){\text{d}}\uptau} ,\quad 0 \le x \le h,\quad t > 0$$
(29.36)
$$f_{\upsigma}^{0} (x,t) = \frac{1}{{2\uppi\,i}}\int\limits_{\Gamma } {\frac{{N_{\upsigma}^{0} (x,z)}}{{t_{\upkappa} R(z)}}{\text{e}}^{{z\tilde{t}}} {\text{d}}z} ,\quad \tilde{t} = \frac{t}{{t_{\upkappa} }}$$
(29.37)
$$N_{\upsigma}^{0} (x,z) = (1 + \hat{T})zr(z),$$
(29.38)

where the integration contour \(\Gamma = \left\{ {z: - i\infty + {\text{d}}t_{\upkappa} , + i\infty + {\text{d}}t_{\upkappa} } \right\}\) represents a straight line in the complex plane of the variable of integration z parallel to the imaginary axis and spaced from it by an amount \({\text{d}}t_{\upkappa}\) that is selected so that the integration contour passes to the right of all isolated singular points of the integrands.

The wear \(u_{w} (t)\) calculation formula can be obtained from (29.3):

$$u_{w} (t) = k_{w} \hat{V}\upbeta^{2} \int\limits_{0}^{t} {\Delta (\uptau)f_{w}^{0} (x,t -\uptau){\text{d}}\uptau} ,\quad t > 0$$
(29.39)
$$f_{w}^{0} (x,t) = \frac{1}{{2\uppi\,i}}\int\limits_{\Gamma } {\frac{{N_{w}^{0} (x,z)}}{{t_{\upkappa} R(z)}}e^{{z\tilde{t}}} {\text{d}}z} ,\quad \tilde{t} = \frac{t}{{t_{\upkappa} }}$$
(29.40)

where \(N_{w}^{0} (z) = r(z)\), and \(r(z)\) is from (29.32).

The obtained formulas for \(T(x,t)\), \(u(x,t)\), \(\upsigma_{xx} (x,t)\), \(u_{w} (t)\) contain contour quadratures (29.30), (29.34), (29.37) and (29.40). In the complex plane of the integration variable z, the integrands of the contour quadratures (29.30), (29.34), (29.37) and (29.40) are meromorphic functions that contain a countable set of poles. Along the axis of integration, when \(|z| \to \infty\) and \(\arg z =\uppi/2\), the integrands in (29.30), (29.34), (29.37) and (29.40) behave as follows:

$$N_{T}^{0} (x,z)R^{ - 1} (z) = \hat{T} + O\left( {z^{ - 1/2} } \right),\quad 0 < x < h$$
$$N_{u}^{0} (x,z)R^{ - 1} (z) = \frac{x}{h} + O\left( {z^{ - 1/2} } \right),\quad 0 < x < h$$
(29.41)
$$N_{\upsigma}^{0} (x,z)R^{ - 1} (z) = 1 + \hat{T} + O\left( {z^{ - 1/2} } \right),\quad 0 < x < h$$
$$N_{w}^{0} (z)R^{ - 1} (z) = O\left( {z^{ - 1} } \right).$$

The asymptotics (29.41) show that the quadratures (29.30), (29.34) and (29.37) do not exist in the common sense, but are understood as generalized [26]. To calculate the quadratures in (29.30), (29.34) and (29.37), regularization of the integrands at infinity (when \(|z| \to \infty\)) is performed with the estimates (29.41) taken into account. As a result, the quadratures are represented as a superposition of the regular part of the generalized component and the quadrature existing in the common sense:

$$T(x,t) - T_{0} = \frac{1 - v}{1 + v}\frac{1}{{\upalpha\,h}}\left( {\hat{T}\Delta (t) + \int\limits_{0}^{t} {\Delta (\uptau)f_{T} (x,t -\uptau){\text{d}}\uptau} } \right),\quad 0 \le x \le h,\;t > 0$$
(29.42)
$$f_{T} (x,t) = \frac{1}{{2\uppi\,i}}\int\limits_{\Gamma } {\frac{{N_{T} (x,z)}}{{t_{\upkappa} R(z)}}{\text{e}}^{{z\tilde{t}}} {\text{d}}z} ,\quad N_{T} (x,z) = N_{T}^{0} (x,z) - \hat{T}R(z)$$
(29.43)
$$u(x,t) = - \Delta (t)\frac{x}{h} - \int\limits_{0}^{t} {\Delta (\uptau)f_{u} (x,t -\uptau){\text{d}}\uptau} ,\quad 0 \le x \le h,\;t > 0$$
(29.44)
$$f_{u} (x,t) = \frac{1}{{2\uppi\,i}}\int\limits_{\Gamma } {\frac{{N_{u} (x,z)}}{{t_{\upkappa} R(z)}}{\text{e}}^{{z\tilde{t}}} {\text{d}}z} ,\quad N_{u} (x,z) = N_{u}^{0} (x,z) - \frac{x}{h}R(z)$$
(29.45)
$$\upsigma_{xx} (x,t) = - \frac{{2\upmu(1 - v)}}{(1 - 2v)h}\left( {(1 + \hat{T})\Delta (t) - \int\limits_{0}^{t} {\Delta (\uptau)f_{\upsigma} (x,t -\uptau){\text{d}}\uptau} } \right),\quad 0 \le x \le h,t > 0$$
(29.46)
$$f_{\upsigma} (x,t) = \frac{1}{{2\uppi\,i}}\int\limits_{\Gamma } {\frac{{N_{\upsigma} (x,z)}}{{t_{\upkappa} R(z)}}{\text{e}}^{{z\tilde{t}}} {\text{d}}z} ,\quad N_{\upsigma} (x,z) = N_{\upsigma}^{0} (x,z) - (1 + \hat{T})R(z)$$
(29.47)

where \(N_{T}^{0} (x,z)\), \(N_{u}^{0} (x,z)\), \(N_{\upsigma}^{0} (x,z)\), \(R(z)\) are from the formulas (29.31), (29.35), (29.38) and (29.32).

To calculate the integrals in (29.43), (29.45) and (29.47), in which the integrand functions are meromorphic and decreasing at infinity along the axis of integration, according to estimates:

$$N_{a} (x,z)R^{ - 1} (z) = O\left( {z^{ - 1/2} } \right)\quad |z| \to \infty ,\quad 0 \le x \le h,\quad a = T,u,\upsigma$$
(29.48)

the methods of the theory of functions of a complex variable [28] can be used. When implementing these methods, it becomes necessary to determine the poles of the integrands in (29.43), (29.45) and (29.47) in the complex plane of the integration variable.

4 Poles of Integrands

The poles of the integrands in (29.43), (29.45) and (29.47) coincide with the zeros \(R(z)\) of (29.32) except for those zeros that are removable singular points of the integrands. To determine the zeros \(R(z)\) in the complex plane \(z =\upxi + i\upeta\), the equation is solved:

$$R(z) = zr(z) - \hat{V}\upbeta^{2} \left( {\left( {1 - k_{w} } \right)r(z) - {\text{Bi}}} \right) + \hat{T}{\text{Bi}}\sqrt z \,{\text{sh}}\,\sqrt z = 0$$
(29.49)

where \(\upbeta^{2}\), \({\text{Bi}}\), \(\hat{T}\), \(\hat{V}\), \(k_{w}\) are from (29.29), \(r(z)\) is from (29.32).

In (29.49), the zeros \(R(z)\) depend on four dimensionless parameters of the problem \(\hat{V}\), \(k_{w}\), \(\hat{T}\),\({\text{Bi}}\), since the fifth parameter \(\upbeta^{2}\) is expressed in terms of \(\hat{T}\) in (29.29). Using the approach of [19, 29, 30], we will investigate the behavior of the zeros from (29.49) for fixed \(k_{w}\), \(\hat{T}\), \({\text{Bi}}\) and variable parameter \(\hat{V}\), which varies from 0 to \(\infty\). Assuming \(\hat{V} = 0\) and \({\text{Bi}} = 0\) in (29.49), we obtain a simplified equation to determine the zero approximations \(\upzeta_{k}^{0} =\upzeta_{k} (0)\), \(k = 0,1,2, \ldots\) of the roots \(\upzeta_{k} \left( {\hat{V}} \right)\) \(k = 0,1,2, \ldots\) of (29.49). It was found that all zero approximations of zeros \(R(z)\) from (29.49) are located on the negative part of the real axis or at zero. Nevertheless, when changing \(\hat{V}\) from 0 to \(\infty\) for fixed \(k_{w}\), \(Bi\), \(\hat{T}\), the first two poles \(\upzeta_{0}\) and \(\upzeta_{1}\) can be located: I—on the negative part of the real axis (at \(0 < \hat{V} < \hat{V}_{\text{I}}\)); II—in the left half-plane \((\hat{V}_{\text{II}} < \hat{V} < \hat{V}_{\text{III}} )\); III—in the right half-plane \((\hat{V}_{\text{II}} < \hat{V} < \hat{V}_{\text{III}} )\); IV—on the positive part of the real axis \((\hat{V}_{\text{III}} < \hat{V} < \infty )\). Figure 29.1 shows the trajectories of the poles \(\upzeta_{0} \left( {\hat{V}} \right)\) and \(\upzeta_{1} \left( {\hat{V}} \right)\) with change of \(\hat{V}\) from 0 to \(\infty\). The closed points indicate the location of the poles \(\upzeta_{0} \left( {\hat{V}} \right)\) and \(\upzeta_{1} \left( {\hat{V}} \right)\) at \(\hat{V} = 0\), while open ones correspond to \(\hat{V} \to \infty\). The crossed-out square marks the point of the trajectory, with the passage of which with the increasing of \(\hat{V}\) the real poles \(\upzeta_{0} \left( {\hat{V}} \right)\) and \(\upzeta_{1} \left( {\hat{V}} \right)\) become a pair of complex conjugate poles, and vice versa.

Fig. 29.1
figure 1

Location of R(z) (29.49) zeros \(\upzeta_{0}\), \(\upzeta_{1}\) in the upper part of the complex plane z and their movement when \(\hat{V}\) increases from 0 to ∞ (lower part is symmetrical), when \({\text{Bi}} = 1\) is fixed for three values of \(\hat{T} = 0\) (solid lines); 0.01 (dashed lines); 0.02 (dash-dotted lines) and different \(k_{w} = 0.5\) (set of curves 1), 0.9 (2), 1.0 (3), 1.35 (4), 5.0 (5)

Full size image

It should be noted that even a small change in the coefficient \(k_{w}\), containing the ratio of the dimensional parameters \(K^{*}\) and \(\upalpha\), regulating respectively the wear and thermal expansion of the strip, leads to significant changes in the trajectories of \(\upzeta_{0} \left( {\hat{V}} \right)\) and \(\upzeta_{1} \left( {\hat{V}} \right)\) and, to a lesser extent, of the others \(\upzeta_{k} \left( {\hat{V}} \right)\) \(k = 2,3,4, \ldots\). When wear prevails (Fig. 29.1, curves 5, 6), then \(\upzeta_{0}\), \(\zeta_{1}\) and even more \(\upzeta_{k}\) \(k = 2,3,4, \ldots\) at \(k_{w} > 1\) are in regions I, II. The prevalence of the expansion of the strip from the incoming heat over wear \(0 < k_{w} < 1\) (curves 1–4) leads to the fact that \(\upzeta_{0}\) and \(\upzeta_{1}\) go to the right half-plane to the regions III, IV (Fig. 29.1).

Note than when a neighboring pair of poles is located in the complex plane, they are complex conjugant, i.e. \(\upzeta_{1} = \overline{{\upzeta_{0} }}\) and \(\upzeta_{0} = \overline{{\upzeta_{1} }}\) in regions II, III.

It is important that, in contrast to quasi-static problems with friction and heat generation from friction , but without wear , when the poles \(\upzeta_{0}\) and \(\upzeta_{1}\) at \(\hat{V} \in \left[ {0,\infty } \right)\) always remained on the real axis and did not come out into the complex plane [31], in the corresponding problems, which take into account wear , friction and heat release from friction , the poles \(\upzeta_{0}\) and \(\upzeta_{1}\) move into the complex plane at \(\hat{V} \in \left( {\hat{V}_{\text{I}} ,\hat{V}_{\text{II}} } \right)\).

5 Formulas for the Exact Solution of the Problem

Let the poles of the integrands \(\upzeta_{k}\) \(k = 0,1,2, \ldots\) in (29.43), (29.45) and (29.47) are known. The calculation of the quadratures in (29.43), (29.45) and (29.47) in this case is reduced to calculating the sum of the residues at the poles of the integrands. Assuming that the poles \(\upzeta_{k}\), \(k = 0,1,2, \ldots\) are simple, we obtain the following formulas for calculating the quadratures (29.43), (29.45) and (29.47):

$$\frac{1}{{2\uppi\,i}}\int\limits_{\Gamma } {\frac{{N_{a} (x,z)}}{{t_{\upkappa} R(z)}}{\text{e}}^{{z\tilde{t}}} {\text{d}}z} = \sum\limits_{k = 0}^{\infty } {B_{a} \left( {x,\upzeta_{k} } \right){\text{e}}^{{\upzeta_{k} \tilde{t}}} } ,\quad \tilde{t} = \frac{t}{{t_{\upkappa} }}$$
(29.50)
$$B_{a} (x,z) = \frac{{N_{a} (x,z)}}{{t_{\upkappa} R^{\prime } (z)}}$$
(29.51)

where \(R^{\prime } (z)\) is derivative of \(R(z)\). Replacing index a in (29.50) and (29.51) with T, u, \(\upsigma\) gives the formula for computing integral in (29.43), (29.45) and (29.47), respectively. If \(\upzeta_{k}\) and \(\upzeta_{k + 1}\), \(k = 0,1,2, \ldots\) represent a complex conjugate pair \(\upzeta_{k + 1} = \overline{{\upzeta_{k} }}\), \(k = 0,1,2, \ldots\), then

$$B_{a} (x,z){\text{e}}^{{z\tilde{t}}} = 2\text{Re} \frac{{N_{a} (x,z)}}{{t_{\upkappa} R^{\prime } (z)}}{\text{e}}^{{z\tilde{t}}}$$
(29.52)

and the summation in (29.50) can be carried out over even numbers \(k = 2n\), \(n = 0,1,2, \ldots\) for complex conjugates \(\upzeta_{k}\), \(k = 0,1,2, \ldots\). Taking into account (29.42)–(29.47) and (29.51), integration formula is obtained as

$$f_{a} (x,t) = \frac{1}{{2\uppi\,i}}\int\limits_{\Gamma } {\frac{{N_{a} (x,z)}}{{t_{\upkappa} R(z)}}{\text{e}}^{{z\tilde{t}}} {\text{d}}z} = \sum\limits_{k = 0}^{\infty } {B_{a} \left( {x,\upzeta_{k} } \right){\text{e}}^{{\upzeta_{k} \tilde{t}}} } ,\quad a = T,u,\upsigma$$
(29.53)

The solutions of the problem are written in the following series:

$$T(x,t) - T_{0} = \frac{1 - v}{1 + v}\frac{1}{{\upalpha\,h}}\left( {\hat{T}\Delta (t) + \sum\limits_{k = 0}^{\infty } {B_{T} \left( {x,\upzeta_{k} } \right)D\left( {\upzeta_{k} ,t} \right)} } \right),\quad 0 \le x \le h,\quad t > 0$$
(29.54)
$$u(x,t) = - \frac{x}{h}\Delta (t) + \sum\limits_{k = 0}^{\infty } {B_{u} \left( {x,\upzeta_{k} } \right)D\left( {\upzeta_{k} ,t} \right)} ,\quad 0 \le x \le h,\quad t > 0$$
(29.55)
$$\upsigma_{xx} (x,t) = - \frac{{2\upmu(1 - v)}}{(1 - 2v)h}\left( {(1 + \hat{T})\Delta (t) - \sum\limits_{k = 0}^{\infty } {B_{\upsigma} \left( {x,\upzeta_{k} } \right)D\left( {\upzeta_{k} ,t} \right)} } \right),\quad 0 \le x \le h,\quad t > 0$$
(29.56)

where \(B_{a} (x,z)\) are calculated according formulas (29.51) or (29.52), \(D(z,t)\) uses the formula:

$$D(z,t) = \int\limits_{0}^{t} {\Delta (\uptau)\exp \left( {z(t -\uptau)/t_{\upkappa} } \right){\text{d}}\uptau} \quad t > 0$$
(29.57)

After calculation of \(f_{w}^{0} (t)\) in (29.40) by using the formula:

$$f_{w}^{0} (x,t) = \frac{1}{{2\uppi\,i}}\int\limits_{\Gamma } {\frac{{N_{w} (z)}}{{t_{\upkappa} R(z)}}{\text{e}}^{{z\tilde{t}}} {\text{d}}z} = \sum\limits_{k = 0}^{\infty } {B_{w} \left( {\upzeta_{k} } \right){\text{e}}^{{\upzeta_{k} \tilde{t}}} } ,\quad B_{w} = \frac{{N_{w} (z)}}{{t_{\upkappa} R^{\prime } (z)}}$$
(29.58)

and substituting it in (29.39), the expression is obtained for calculating the wear \(u_{w} (t)\) of the coating material on the contact :

$$u_{w} (t) = \sum\limits_{k = 0}^{\infty } {B_{w} \left( {\upzeta_{k} } \right)D(\upzeta_{k} ,t)} ,\quad t > 0$$
(29.59)

The horizontal displacements \(w(x,t)\) are determined from (29.1), (29.4) and (29.6) and after integration in (29.1), the following formula is obtained:

$$w(x,t) = - f\upmu^{ - 1}\upsigma_{xx} (h,t)x,\quad 0 \le x \le h,\quad t > 0$$
(29.60)

6 Analysis of the Problem Solution: Domains of Stable and Unstable Solutions

Investigation of the solutions of the problem \(T(x,t)\), \(u(x,t)\), \(\upsigma_{xx} (x,t)\), represented by formulas (29.54)–(29.56), shows that if \(\text{Re} \left( {\upzeta_{k} } \right) < 0\) \(k = 0,1,2, \ldots\) the solutions of the problem are stable and tend to a stationary state with increasing time t. If at least one \(\upzeta_{k}\), \(k = 0,1,2, \ldots\) has \(\text{Re} \left( {\upzeta_{k} } \right) > 0\), then the amplitude of the solution increases indefinitely at \(t \to \infty\) and is oscillating with frequency \(\text{Im} \left( {\upzeta_{k} } \right) \ne 0\), which indicates the instability of the solution of the problem. If we assume that the law of penetration \(\Delta (t)\) is a bounded function:

$$m < \Delta (t) < M\quad m,M > 0,\quad 0 < t < \infty$$

then for the integral (29.57), the following estimate takes place:

$$\left| {D\left( {\upzeta_{k} ,t} \right)} \right| \ge m\left| {\frac{{1 - {\text{e}}^{{\upzeta_{k} \tilde{t}}} }}{{\upzeta_{k} }}} \right|,\quad {\text{when}}\quad \text{Re} \left( {\upzeta_{k} } \right) > 0,\quad k = 0,1,2, \ldots ,\quad t = \frac{t}{{t_{\upkappa} }}$$

In the complex z-plane, the pole trajectories \(\upzeta_{k} \left( {\hat{V}} \right)\), \(k = 0,1,2, \ldots\), \(\hat{V} \in \left[ {0,\infty } \right)\) in the left half-plane represent stable solutions \(\left( {\text{Re} \left( {\upzeta_{k} } \right) < 0} \right)\), and the regions I and II themselves are called the regions of stable solutions. Regions III and IV in the right half-plane \(\left( {\text{Re} \left( {\upzeta_{k} } \right) > 0\,k = 0,1} \right)\) are regions of unstable solutions of the problem, since in region III the limits \(\mathop {\lim }\limits_{t \to \infty } T(h,t)\) and \(\mathop {\lim }\limits_{t \to \infty }\upsigma_{xx} (h,t)\) do not exist because of \(\text{Im} \left( {\upzeta_{k} } \right) \ne 0\) \(k = 0,1\), and in region IV \(\mathop {\lim }\limits_{t \to \infty } T(h,t) = \mathop {\lim }\limits_{t \to \infty }\upsigma(h,t) = \infty\), since \(\text{Im} \left( {\upzeta_{k} } \right) = 0\) \(k = 0,1\).

Parametric boundaries of stable and unstable solutions of the problem in the space of dimensionless parameters \(\hat{V}\), \(k_{w}\), \({\text{Bi}}\), \(\hat{T}\) present theoretical and practical interest. Figure 29.2 shows the domains of stable I, II and unstable III, IV solutions on the \((\hat{V},k_{w} )\) plane for different values of Bi and \(\hat{T}\). The analysis of the graphs in Fig. 29.2 shows the significant influence of the parameters \(\hat{V}\), \(k_{w}\), Bi on the change in the boundaries of regions I–IV. When \(k_{w} \to 0\) for Bi = 1 and Bi = 100, the boundaries of regions I–IV converge on the axis \(\hat{V}\) to a point \(\hat{V} = 2{\text{Bi}}/\left( {2 + {\text{Bi}}} \right)\) that does not depend on \(\hat{T}\). This means that thermomechanical coupling in heat equation have no effect on stability in the considered case but without wear .

Fig. 29.2
figure 2

Boundaries of stable (I, II) and unstable (III, IV) solution domains at a Bi = 1, b Bi = 10, c Bi = 100 \(({\text{Bi}} \to \infty )\); different values of \(\hat{T}\) are represented by solid lines \((\hat{T} = 0)\), dotted lines \((\hat{T} = 0.1)\), and dash-dotted lines \((\hat{T} = 0.5)\); unstable solution domains are shaded

Full size image

It is worth to note that dimensionless thermomechanical coupling coefficient \(\hat{T}\) does not significantly affect the stable (II) and unstable (III) solutions domains boundary, except narrow range of dimensionless wear rates \(k_{w} \in \left[ {1,1.14} \right]\) (at Bi = 100). At \(k_{w} = 1.120\), change of \(\hat{T}\) from 0 to 0.5 leads to 1.5 times change in critical dimensionless speed \(\hat{V}_{*}\) (from 33.532 to 51.143); at \(k_{w} = 1.222\) to 1.7 times change (from 35.164 to 60.065). At \(k_{w} = 1.124\) and \(\hat{T} = 0\) there is critical value of \(\hat{V}_{*} = 37.051\), whereas for all \(k_{w} \ge 1.124\) at \(\hat{T} = 0.05\) there are no unstable solution domain, and thermoelastic stability is kept in all dimensionless speed range.

7 Asymptotic and Numerical Analysis of the Obtained Solutions

It is necessary to determine the effect of dimensionless coupling parameter \(\hat{T}\) and other parameters on behavior of obtained solutions. For this purpose, the asymptotic analysis of the solutions \(T(x,t)\), \(u(x,t)\), \(\upsigma_{xx} (x,t)\), \(u_{w} (t)\) for small values of t was performed. The separated principal terms \(T(x,t) - T_{0}\) in (29.42), \(u(x,t)\) in (29.44), \(\upsigma_{xx} (x,t)\) in (29.46), taking into account the convolution integral formula, allow us to obtain following asymptotic relations:

$$T(x,t) - T_{0} = \frac{1 - \nu }{1 + \nu }\frac{{\hat{T}}}{\upalpha} \cdot \frac{\Delta (t)}{h} + O\left( {t^{3/2} \Delta (t)} \right),\quad t \to 0$$
(29.61)
$$u(x,t) = - x\frac{\Delta (t)}{h} + O\left( {t^{3/2} \Delta (t)} \right),\quad t \to 0$$
(29.62)
$$\upsigma_{xx} (x,t) = - \frac{{2\upmu(1 - \nu )}}{1 - 2\nu }(1 + \hat{T})\frac{\Delta (t)}{h} + O\left( {t^{3/2} \Delta (t)} \right),\quad t \to 0$$
(29.63)

Note that at differentiation of \(u(x,t)\) in (29.62) according to x and t, rate of deformation on the contact (when \(x = h\)) is written as

$${\dot{\upvarepsilon}}_{xx} = \frac{{\partial^{2} u}}{\partial x\partial t} = - \frac{{\dot{\Delta }(t)}}{h} + O\left( {t^{3/2} \Delta (t)} \right),\quad t \to 0$$
(29.64)

Differentiation of the relations (29.61) and (29.63) on t shows that the rate of temperature \(\dot{T}(x,t)\) and contact stresses \(\dot{p}(t) = - {\dot{\upsigma}}_{xx} (x,t)\) at small values of t is proportional to the rate of deformation \({\dot{\upvarepsilon}}_{xx}\), and coefficients:

$$- \frac{1 - \nu }{1 + \nu }\frac{{\hat{T}}}{{\upalpha\,h}}\;{\text{and}}\; - \frac{{2\upmu(1 - \nu )}}{(1 - 2\nu )h}\left( {1 + \hat{T}} \right)$$

indicate decreasing of temperature and contact stresses, respectively, with increasing of coupling parameter. These relations also show effect of the other parameters of the problem contained in them. Rate of wear \(\dot{u}_{w} (t)\) on the contact is deduced from (29.39) and (29.40) by separating principal term in (29.40) and subsequent differentiating the result, and its final form is given by

$$\dot{u}_{w} (t) = k_{w} \hat{V}\upbeta^{2} \frac{\upkappa}{h} \cdot \frac{{\dot{\Delta }(t)}}{h} + O\left( {t\Delta (t)} \right)\quad t \to 0$$
(29.65)

where ratio between \(\dot{u}_{w} (t)\) and \({\dot{\upvarepsilon}}_{xx}\) depends on \(\hat{T}\) and other parameters of the problem.

Numerical analysis of the solutions of the considered coating wear problem is carried out by the formulas (29.54), (29.56) and (29.59). Suppose that the maximum level of penetration of the rigid half-plane I into an elastic coating is given by \(\Delta_{0}\), and its penetration law \(\Delta (t)\), consisting of the active and the passive penetration phase, is described by the formulas:

$$\Delta (t) = \Delta_{0} \left\{ {\begin{array}{*{20}l} { - 1 + {\text{e}}^{{\upvarepsilon\,t}} } \hfill \\ 1 \hfill \\ \end{array} } \right.\quad \begin{array}{*{20}c} {0 < t < t_{\upvarepsilon} } \\ {t_{\upvarepsilon} < t < \infty } \\ \end{array}$$
(29.66)

where \(t_{\upvarepsilon} =\upvarepsilon^{ - 1} \ln 2\) is the active penetration duration, \(\upvarepsilon\) is the penetration law parameter.

The nature of the loss of stability of solutions \(T(h,t)\), \(u_{w} (t)\), \(\upsigma_{xx} (h,t)\) of the uncoupled problem of sliding contact thermoelasticity depending on the parameters of the problem \(\hat{V}\), \(k_{w}\), \({\text{Bi}}\) was described in detail in [15, 19, 29, 30]. Here we study the effect of the parameters V (m/s), \(K^{*}\) (m2/N), \(T_{0}\) (K) of the considered coupled thermoelastic sliding friction al wear contact problem on the main contact parameters: temperature \(T(h,t)\) from (29.54), contact stresses \(p(t) = -\upsigma_{xx} (h,t)\) from (29.56) that arise and develop in time on the contact interface between the rigid half-plane I and the coating, wear of the coating \(u_{w} (t)\) from (29.59), and wear rate of the coating \(\dot{u}_{w} (t)\) from (29.59). The material of the coating is aluminum alloy with the following thermomechanical characteristics: μ = 24.8 GPa, ν = 0.34, κ = 88.1 × 10−6 m2/s, α = 22.9 × 10−6 1/К, K = 209.3 W/(m K), f = 0.47, h = 25 mm, \(\Delta_{0} = 0.01h = 0.25\,{\text{mm}}\). Wear of the coating surface ends at t = tw, when the contact stresses turn to zero: \(p(t_{w} ) = -\upsigma_{xx} (h,t_{w} ) = 0\). The time tw is called the coating wear time.

The effect of the wear coefficient \(K^{*}\) and the initial temperature \(T_{0}\) on the solutions of the problem under consideration is illustrated in Figs. 29.3, 29.4, 29.5 and 29.6, which show the graphs \(T_{*} (h,t) = T(h,t) - T_{0}\), \(p(t)\), \(u_{w} (t)\), \(\dot{u}_{w} (t)\), respectively for the following task parameters: V = 3.22 mm/s \((\hat{V} = 0.86085)\), \({\text{Bi}} = 11.9446\). V = 3.22 mm/s \((\hat{V} = 0.86085)\), \({\text{Bi}} = 11.9446\). The graphs denoted by 1 are constructed at \(K^{*} = 7.5 \cdot 10^{ - 12} {\text{m}}^{2} /{\text{N}}\) (kw = 0.3833); those denoted by 2 are constructed at \(K^{*} = 1.5 \cdot 10^{ - 11} {\text{m}}^{2} /{\text{N}}\) (kw = 0.7665); those denoted by 3 correspond to \(K^{*} = 2.25 \cdot 10^{ - 11} {\text{m}}^{2} /{\text{N}}\) (kw = 1.1498). The solid lines in Figs. 29.3, 29.4, 29.5 and 29.6 represent the graphs of the solution of the present coupled thermoelastic problem at \(T_{0}\) = 0 К \((\hat{T} = 0)\), which coincide with the graphs for the solution of the corresponding uncoupled problem; the dashed line shows the solution graphs at \(T_{0}\) = 300 К \((\hat{T} = 0.0279)\), the dash-dotted line shows the solution graphs at \(T_{0}\) = 525 К \((\hat{T} = 0.0489)\).

Fig. 29.3
figure 3

Temperature \(T(h,t)\) at the contact interface

Full size image
Fig. 29.4
figure 4

Contact pressure \(p(t) = -\upsigma_{xx} (h,t)\)

Full size image
Fig. 29.5
figure 5

Wear amount \(u_{w} (t)\)

Full size image
Fig. 29.6
figure 6

Wear rate \(\dot{u}_{w} (t)\)

Full size image

From Figs. 29.3, 29.4 and 29.5, it follows that the values of \(p(t)\) and \(T_{*} (h,t)\) decrease with increasing of wear coefficient \(K^{*}\) and initial temperature \(T_{0}\) (curves 3), while wear is accelerating.

8 Conclusion

An analysis of the exact solution of the coupled quasi-static thermoelasticity problem of wear by a rigid body of an elastic coating on a sliding thermofriction al contact makes it possible to draw the following conclusions:

  1. (i)

    the boundary between the region of stable (I, II) and unstable (III, IV) solutions of the problem remains unchanged for any values of the thermomechanical coupling parameter;

  2. (ii)

    the eigenvalues of the problem essentially depend on the thermomechanical coupling parameter of the problem;

  3. (iii)

    an increase in the thermomechanical coupling parameter of the problem, as well as an increase in the wear coefficient, leads to a decrease in both the temperature and the stresses at the contact .

The obtained solutions of the coupled quasi-static problem of wear allow one to solve inverse problems. These problems are devoted to control the parameters of a sliding contact due to a special selection of the law of penetration of a rigid body into an elastic coating, as well as monitoring problems of sliding contact parameters using buried sensors. The sensor readings then can be recalculated to contact parameter values using the obtained formulas.