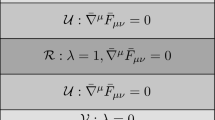Background Independence in a Background Dependent RG

Abstract

In Sect. 1.3.2 we underlined the importance of background independence in quantum gravity and motivated going beyond the single field approximation to instead work within bi-metric truncations in which separate dependence on the background field is retained. In this chapter we investigate background independence within the context of conformally reduced gravity.

3.1 Introduction

In Sect. 1.3.2 we underlined the importance of background independence in quantum gravity and motivated going beyond the single field approximation to instead work within bi-metric truncations in which separate dependence on the background field is retained. Recall that using bi-metric truncations requires imposing a modified split Ward identity (msWI) to ensure that background independence is recovered in the limit the cutoff k is removed, $k \rightarrow 0$. We also remarked in Sect. 1.3.2 that fixed points can be forbidden by the very msWIs that are enforcing background independence, an unsettling conclusion from the research reported in [1]. In this chapter we present the research of [2] in which we uncover the underlying reasons for fixed points being forbidden within the derivative expansion and polynomial truncations of conformally reduced gravity, extending the work of [1].

In the conformally truncated gravity model investigated in [1], fixed points are forbidden generically when the anomalous dimension $\eta$ is non-vanishing. This can however be avoided by a careful choice of parametrisation f (setting it to be a power of the background field $\chi$ determined by its scaling dimension [1]). On the other hand, it was shown in [1] that the situation is saved in all cases, at least in the conformally reduced gravity model, by the existence of an alternative background independent description of the flow. This involves in particular a background independent notion of RG scale, $\hat{k}$. This background independent description exists at a deeper underlying level since in terms of these background independent variables, the RG fixed points and corresponding flows always exist, and are manifestly independent of the choice of parametrisation $f(\chi )$.

After approximating the exact RG flow equations and msWIs to second order in the derivative expansion (as will be reviewed later), the crucial technical insight was to notice that, just as in the scalar field theory model [3], the msWIs and RG flow equations can be combined into linear partial differential equations. It is the solution of the latter equations by the method of characteristics, that uncovers the background independent variables. And it is by comparing the description in these variables with the equivalent description in the original variables, that we see that fixed points in the original variables are in general forbidden by background independence.

However, in order to facilitate combining the RG flow equations and msWIs when the anomalous dimension $\eta \ne 0$, the authors of [1] were led to a particular form of cutoff profile $R_k$, namely a power-law cutoff profile. In the research presented in this chapter we will show that in fact this cutoff profile plays a role that is much deeper than the convenience of a mathematical trick. It in fact provides a condition that, if obeyed, means that the flow and msWI are compatible. Recall from Sect. 1.3.2, that compatibility is achieved if solutions to the flow equation also satisfy the msWI. The notion of compatibility is of great importance as without it fixed points are forbidden to exist, as we will see in the ensuing sections. As already argued in 1.3.2, at the exact level the msWIs are guaranteed to be compatible with the exact RG flow equation, but this will typically not be the case once approximated.¹ We will see that in the $O(\partial ^2)$ derivative expansion approximation derived in reference [1], the msWI and flow equations are in fact compatible if and only if either the cutoff profile is power law,² or we have the special case that $\eta =0$.³

The structure of this chapter is then as follows. In Sect. 3.2 we quickly review the results we need from [1] and their context. In Sect. 3.3 we provide a proof of compatibility at the exact level and investigate compatibility in the $O(\partial ^2)$ derivative expansion along with deriving the requirements needed in order to achieve it. If the msWIs are not compatible with the flow equations within the derivative expansion, it does not immediately follow that there are no simultaneous solutions to the system of equations. However, as we argue in Sect. 3.3, the equations are overconstrained and it is for this reason that it is hopeless to expect any solutions for the non-compatible case. We verify this using the LPA in Sect. 3.4 (see also 3.5). We also see in Sect. 3.4 that when the LPA equations are compatible they can indeed be combined to give a background independent description of the flow; however, even when compatibility is achieved with power-law cutoff, we understand why the msWI can still forbid fixed points for general parameterisation f and $\eta \ne 0$. Finally, in Sect. 3.5, we consider how these issues become visible in polynomial truncations and without resorting to the trick of combining the flow and msWI equations. It is instructive to do so since it seems likely that this is the only way we could investigate these issues using the exact non-perturbative flow equations. We verify very straightforwardly that generically there can be no fixed points as the equations over-constrain the solutions if the truncation is taken to a sufficiently high order.

3.2 Conformally Reduced Gravity at Order Derivative-Squared

In this section we give a quick review of the results we need and their context from reference [1]. Recall that we arrive at conformally reduced gravity (in Euclidean signature) by writing:

$$\begin{aligned} \tilde{g}_{\mu \nu } = f(\tilde{\phi }) \hat{g}_{\mu \nu }= f(\chi +\tilde{\varphi })\hat{g}_{\mu \nu } \qquad \text {and} \qquad \bar{g}_{\mu \nu } = f(\chi )\hat{g}_{\mu \nu }. \end{aligned}$$

(3.2.1)

The metric $\tilde{g}_{\mu \nu }$ is restricted to an overall conformal factor $f(\tilde{\phi })$ times a reference metric which in fact we set to flat: $\hat{g}_{\mu \nu }=\delta _{\mu \nu }$. Following the background field method, we split the total conformal factor field $\tilde{\phi }(x)$ into a background conformal factor field $\chi (x)$ and fluctuation conformal factor field $\tilde{\varphi }(x)$. It is then the latter that is integrated over. Similarly, we parametrise the background metric $\bar{g}_{\mu \nu }$ in terms of the background conformal factor field $\chi$.

Examples of parametrisations used previously in the literature include $f(\phi ) = \exp (2\phi )$ [13] and $f(\phi )=\phi ^2$ [14, 15]. However we leave the choice of parametrisation unspecified. It is important to note however that f cannot depend on k since it is introduced at the bare level and has no relation to the infrared cutoff (moreover if f depended on k, the flow equation (3.2.2) would no longer hold). Later we will change to dimensionless variables using k and in these variables it can be forced to depend on k (see Sects. 3.3.5 and 3.4.1).

By keeping only the conformal factor of the metric, diffeomorphism invariance is destroyed. Therefore gauge fixing and ghosts are not required in this setup. A remnant diffeomorphism is preserved however, a multiplicative rescaling, which constrains appearances of the background field.

Introducing the classical fluctuation field $\varphi = \langle \tilde{\varphi }\rangle$ and total classical field $\phi = \langle \tilde{\phi }\rangle = \chi + \varphi$, the effective action satisfies the flow equation

$$\begin{aligned} \partial _t \Gamma _k[\varphi ,\chi ] = \frac{1}{2}\mathrm {Tr}\left[ \frac{1}{\sqrt{\bar{g}}\sqrt{\bar{g}}}\frac{\delta ^2\Gamma _k}{\delta \varphi \delta \varphi }+ R_k[\chi ]\right] ^{-1} \partial _t R_k[\chi ]. \end{aligned}$$

(3.2.2)

Note that here we are using the same notation for the effective action as in Chap. 1. We have also introduced RG time

$$\begin{aligned} t=\ln (k/\mu ), \end{aligned}$$

(3.2.3)

with $\mu$ being a fixed reference scale, which can be thought of as being the usual arbitrary finite physical mass-scale. Recall from Sect. 1.3.1 that in the context of the background field method the cutoff operator $R_k$ itself depends on the background field $\chi$ as it becomes a function of the covariant Laplacian of the background metric $R_k\left( -\bar{\nabla }^2\right)$. We see that again, now in the context of conformally reduced gravity, that the effective action possesses a separate dependence on the background field, enforced through the cutoff.

By specialising to a background metric ${\bar{g}}_{\mu \nu }$ that is slowly varying, so that space-time derivatives of it can be neglected, we effectively terminate at the level of the LPA for the background conformal factor $\chi$. For the classical fluctuating conformal factor $\varphi$ however, $\mathcal {O}(\partial ^2)$ in the derivative expansion approximation is fully implemented, making no other approximation. The effective action in its most general form at this level of truncation is thus given by

$$\begin{aligned} \Gamma _k[\varphi , \chi ] = \int d^dx \sqrt{\bar{g}} \left( -\frac{1}{2}K(\varphi ,\chi ) \bar{g}^{\mu \nu }\partial _{\mu }\varphi \partial _{\nu }\varphi + V(\varphi ,\chi ) \right) . \end{aligned}$$

(3.2.4)

The msWI originates from the observation that the introduction of the cutoff action into the functional integral violates split symmetry:

$$\begin{aligned} \tilde{\varphi }(x) \mapsto \tilde{\varphi }(x) + \varepsilon (x) \qquad \text {and}\qquad \chi (x) \mapsto \chi (x) -\varepsilon (x), \end{aligned}$$

(3.2.5)

under which the bare action is invariant.⁴ It is the breaking of this symmetry that signals background independence has been lost, both at the level of the functional integral and at the level of the effective action. The msWI encodes the extent to which the effective action violates split symmetry⁵:

$$\begin{aligned} \frac{1}{\sqrt{\bar{g}}}\left( \frac{\delta \Gamma _k}{\delta \chi }-\frac{\delta \Gamma _k}{\delta \varphi }\right) \! =\frac{1}{2}\mathrm {Tr}\left[ \frac{1}{\sqrt{\bar{g}}\sqrt{\bar{g}}}\frac{\delta ^2\Gamma _k}{\delta \varphi \delta \varphi }+ R_k[\chi ]\right] ^{\!-1}\! \frac{1}{\sqrt{\bar{g}}} \left\{ \frac{\delta R_k[\chi ] }{\delta \chi }+\frac{d}{2}\,\partial _\chi \! \ln \! f \,R_k[\chi ]\right\} . \end{aligned}$$

(3.2.6)

Exact background independence would be realised if the right-hand side of the msWI was zero, implying that the effective action is only a functional of the total field $\phi = \chi + \varphi$. The presence of the cutoff operator however causes the right-hand side to be non-vanishing in general. It is only in the limit $k\rightarrow 0$ (again whilst holding unscaled momenta and fields fixed) that the cutoff operator drops out and background independence can be restored exactly. We now see how imposing the msWI in addition to the flow equation (3.2.2) automatically ensures exact background independence in the limit $k\rightarrow 0$. The observation we further explore in the work presented in this chapter is that restricting flows to satisfy (3.2.6) then has consequences for RG properties, in particular fixed point behaviour, that follow from (3.2.2).

Computing the flow equation and msWI in the derivative expansion (3.2.4) results in flow equations and modified split Ward identities,⁶ for the potential V:

$$\begin{aligned} \partial _t V(\varphi ,\chi )&= f(\chi )^{-\frac{d}{2}}\int dp\, p^{d-1} Q_p\dot{R}_p,\end{aligned}$$

(3.2.7)

$$\begin{aligned} \partial _\chi V - \partial _\varphi V +\frac{d}{2}\partial _\chi \text {ln} f V&= f(\chi )^{-\frac{d}{2}}\int dp\, p^{d-1} Q_p\left( \partial _\chi R_p + \frac{d}{2}\partial _\chi \text {ln} f R_p\right) , \end{aligned}$$

(3.2.8)

and for K:

$$\begin{aligned} f^{-1}\partial _t K(\varphi ,\chi )&= 2 f^{-\frac{d}{2}}\int dp\,p^{d-1} P_p(\varphi ,\chi )\dot{R}_p,\end{aligned}$$

(3.2.9)

$$\begin{aligned} f^{-1}\!\left( \partial _\chi K- \partial _\varphi K + \frac{d-2}{2}\partial _\chi \text {ln}fK\right)&\!= 2 f^{-\frac{d}{2}}\!\!\int dp\,p^{d-1} P_p(\varphi ,\chi ) \left( \partial _{\chi }R_p + \frac{d}{2}\partial _\chi \text {ln} f R_p\right) . \end{aligned}$$

(3.2.10)

The p subscripts denote the momentum dependence of $Q_p, P_p$ and the cutoff $R_p$ and as usual RG time derivatives are denoted also by a dot on top. $Q_p$ is defined as

$$\begin{aligned} Q_p=\left( \partial ^2_\varphi V - p^2\frac{K}{f} + R_p \right) ^{-1}. \end{aligned}$$

(3.2.11)

and $P_p$ is given by

$$\begin{aligned} P_p=&-\frac{1}{2}\frac{\partial _\varphi K}{f}Q_p^2 +\frac{\partial _\varphi K}{f}\left( 2\partial _\varphi ^3 V - \frac{2d+1}{d}\frac{\partial _{\varphi }K}{f}p^2\right) Q_p^3\nonumber \\&-\left[ \left\{ \frac{4+d}{d}\frac{\partial _\varphi K}{f}p^2 - \partial ^3_\varphi V\right\} \left( \partial _{p^2}R_p - \frac{K}{f}\right) +\frac{2}{d}p^2\partial ^2_{p^2} R_p\left( \frac{\partial _\varphi K}{f} - \partial _\varphi ^3V\right) \right] \nonumber \\&\quad \times \left( \partial _\varphi ^3 V - \frac{\partial _\varphi K}{f}p^2\right) Q_p^4\nonumber \\&-\frac{4}{d}p^2\left( \partial _{p^2}R_p-\frac{K}{f}\right) ^2 \left( \partial _\varphi ^3 V - \frac{\partial _\varphi K}{f} p^2\right) ^2 Q_p^5. \end{aligned}$$

(3.2.12)

3.3 Compatibility of the msWI With the Flow Equation

Compatibility of the msWI with the flow equation can be phrased in the following way. Write the msWI in the form $\mathcal {W}=0$ and assume that this holds at some scale k. Computing $\dot{\mathcal {W}}$ by using the flow equation, we say that the msWI is compatible if $\dot{\mathcal {W}}=0$ then follows at scale k without further constraints.

In the first part of this section we rederive the flow equation and msWI for conformally reduced gravity but organised in a different way from reference [1] so as to make the next derivation more transparent. We then prove that they are compatible with one another. As previously emphasized, this is naturally to be expected since both are derived from the same partition function. For completeness we include it here in order to fully understand the issues once we consider derivative expansions. (For a proof of the exact case in a more general context see reference [16].) In the second part we study the notion of compatibility for conformally reduced gravity in the truncation (3.2.4). Asking for compatibility in the derivative expansion is actually non-trivial. We derive the requirements necessary to achieve it.

3.3.1 Compatibility at the Exact Level

The proof of compatibility of the un-truncated system consists of demonstrating that the RG time derivative of the msWI is proportional to the msWI itself [17, 18]. In analogy with references [17, 18], we expect to find that this RG time derivative is, more specifically, proportional to a second functional derivative with respect to $\varphi$ acting on the msWI and it is with this in mind that we proceed (see also reference[16]).

We begin by considering the following Euclidean functional integral over the fluctuation field $\tilde{\varphi }$

$$\begin{aligned} \text {e}^{W_k}=\int \!\mathcal {D}\tilde{\varphi }\, \text {exp}\left( -S[\chi +\tilde{\varphi }]-\Delta S_k[\tilde{\varphi },\bar{g}] + S_{\text {src}}[\tilde{\varphi },\bar{g}]\right) . \end{aligned}$$

(3.3.1)

This integral is regulated in the UV (as it must be), however we leave this regularisation implicit in what follows. Compatibility can be shown most easily by presenting both the flow equation and the msWI as matrix expressions. Thus we begin by rewriting the source term using matrix notation, introduced in Chap. 1:

$$\begin{aligned} S_\mathrm{src}[\tilde{\varphi },\bar{g}]=\int \!d^d x\sqrt{\bar{g}(x)}\,\tilde{\varphi }(x) J(x)\equiv \tilde{\varphi }_xT_{xy}J_y\equiv \tilde{\varphi }\cdot T\cdot J, \end{aligned}$$

(3.3.2)

where $T_{xy}\equiv T(x,y)\equiv \sqrt{\bar{g}(x)}\delta (x-y)$. Similarly, we write the cutoff action as

$$\begin{aligned} \Delta S_k[\tilde{\varphi }, \bar{g}]=\frac{1}{2}\int \!d^d x\sqrt{\bar{g}(x)}\,\tilde{\varphi }(x)R_k[\bar{g}]\tilde{\varphi }(x) \equiv \frac{1}{2}\tilde{\varphi }_x r_{xy} \tilde{\varphi }_{y}\equiv \frac{1}{2}\,\tilde{\varphi }\cdot r \cdot \tilde{\varphi }, \end{aligned}$$

(3.3.3)

where

$$\begin{aligned} r_{xy}\equiv r(x,y)\equiv \sqrt{\bar{g}(x)}\sqrt{\bar{g}(y)}R_{k}(x,y), \end{aligned}$$

(3.3.4)

and where the cutoff operator and its kernel are related according to

$$\begin{aligned} R_k(x,y) = R_{k,x}\frac{\delta (x-y)}{\sqrt{\bar{g}(y)}}. \end{aligned}$$

(3.3.5)

We refrain from putting a k subscript on $r_{xy}$ to avoid clutter with indices, but note that it still has k-dependence. Also note that now the factors of $\sqrt{\bar{g}}$ are no longer part of the integration; this is to enable all $\chi$-dependent quantities to be easily accounted for when acting with $\delta /\delta \chi$ later on.

With these definitions in place, the RG time derivative of (3.3.1) gives

$$\begin{aligned} \dot{W}_k=-\frac{1}{2}\dot{r}_{xy} \langle \tilde{\varphi }_x \tilde{\varphi }_y \rangle . \end{aligned}$$

(3.3.6)

In the usual way, we take the Legendre transform of $W_k$:

$$\begin{aligned} \tilde{\Gamma }_{k}=J\cdot T \cdot \varphi - W_k \quad \text {with} \quad T\cdot \varphi =\frac{\delta W_k}{\delta J} \end{aligned}$$

(3.3.7)

and from this we define the effective average action

$$\begin{aligned} \Gamma _k[\varphi ,\bar{g}]=\tilde{\Gamma }_k[\varphi ,\bar{g}]-\Delta S_k[\varphi ,\bar{g}]. \end{aligned}$$

(3.3.8)

From (3.3.7), it also follows that

$$\begin{aligned} \langle \tilde{\varphi }_x \tilde{\varphi }_y \rangle = \left( \frac{\delta ^{2}\tilde{\Gamma }_k}{\delta \varphi _x \delta \varphi _y}\right) ^{\!-1}+\,\varphi _x \varphi _y. \end{aligned}$$

(3.3.9)

Finally substituting (3.3.7) and (3.3.9) into (3.3.6), together with (3.3.8), we obtain the flow equation for the effective average action

$$\begin{aligned} \dot{\Gamma }_k=\frac{1}{2}\text {Tr}\left[ \left( \frac{\delta ^{2}\Gamma _k}{\delta \varphi \delta \varphi } +r\right) ^{\!-1}\dot{r}\right] \equiv \frac{1}{2}\text {Tr}\,\Delta \, \dot{r}, \end{aligned}$$

(3.3.10)

where

$$\begin{aligned} \Delta _{xy}\equiv \left( \frac{\delta ^{2}\Gamma _k}{\delta \varphi _x \delta \varphi _y}+r_{xy}\right) ^{-1}. \end{aligned}$$

(3.3.11)

The msWI is derived by applying the split symmetry transformations (3.2.5), with infinitesimal $\varepsilon (x)$, to the functional integral (3.3.1). Applying these shifts we obtain

$$\begin{aligned} -\frac{\delta W_k}{\delta \chi }\cdot \varepsilon =\langle \varepsilon \cdot T\cdot J- \tilde{\varphi }\cdot \left( \frac{\delta T}{\delta \chi }\cdot \varepsilon \right) \cdot J - \varepsilon \cdot r\cdot \tilde{\varphi }+\frac{1}{2}\tilde{\varphi }\cdot \left( \frac{\delta r}{\delta \chi }\cdot \varepsilon \right) \cdot \tilde{\varphi }\rangle . \end{aligned}$$

(3.3.12)

Under these same shifts, the Legendre transformation (3.3.7) gives

$$\begin{aligned} \frac{\delta W_k}{\delta \chi }\cdot \varepsilon = J\cdot \left( \frac{\delta T}{\delta \chi }\cdot \varepsilon \right) \cdot \varphi - \frac{\delta \tilde{\Gamma }_k}{\delta \chi }\cdot \varepsilon . \end{aligned}$$

(3.3.13)

Substituting the above relation into (3.3.12) together with (3.3.8), we obtain the msWI:

$$\begin{aligned} \frac{\delta \Gamma _k}{\delta \chi _\omega }-\frac{\delta \Gamma _k}{\delta \varphi _\omega }= \frac{1}{2}\,\Delta _{xy}\,\frac{\delta r_{yx}}{\delta \chi _\omega }, \end{aligned}$$

(3.3.14)

where we have used the fact that the identity must hold for arbitrary $\varepsilon (\omega )$. Note that in deriving (3.3.14) the contribution of the source term to the separate background field dependence of $\Gamma _k[\varphi ,\chi ]$ drops out.

The equations just derived, (3.3.10) and (3.3.14), appear at first sight to be in conflict with (3.2.2) and (3.2.6) respectively. In particular factors of $\sqrt{\bar{g}}$ are apparently missing. This is because the $\sqrt{\bar{g}}$ factors are absorbed in a different definition of the inverse kernel. Indeed the inverse kernel (3.3.11) now satisfies

$$\begin{aligned} \left( \frac{\delta ^{2}\Gamma _k}{\delta \varphi _x \delta \varphi _y}+r_{xy}\right) \Delta _{yz} =\delta _{xz} \end{aligned}$$

(3.3.15)

without a $\sqrt{\bar{g}}(y)$ included in the integration over y.

Now that we have derived the flow equation and msWI written in a convenient notation, we are ready to prove that they are compatible. We begin by defining

$$\begin{aligned} \mathcal {W}_\omega \equiv \frac{\delta \Gamma _k}{\delta \chi _\omega }-\frac{\delta \Gamma _k}{\delta \varphi _\omega } -\frac{1}{2}\Delta _{xy}\frac{\delta r_{yx}}{\delta \chi _\omega } =0. \end{aligned}$$

(3.3.16)

Taking the RG time derivative of $\mathcal {W_\omega }$ then gives

$$\begin{aligned} \mathcal {\dot{W}}_\omega = \frac{\delta \dot{\Gamma }_k}{\delta \chi _\omega } -\frac{\delta \dot{\Gamma }_k}{\delta \varphi _\omega }+ \frac{1}{2}\left[ \Delta \left( \frac{\delta ^{2}\dot{\Gamma }_k}{\delta \varphi \delta \varphi } +\dot{r}\right) \Delta \right] _{\!xy}\frac{\delta r_{yx}}{\delta \chi _\omega } -\frac{1}{2}\Delta _{xy}\frac{\delta \dot{r}_{yx}}{\delta \chi _\omega } \end{aligned}$$

(3.3.17)

and upon substituting the flow equation (3.3.10) into the right-hand side, we have

$$\begin{aligned} \mathcal {\dot{W}}_{\omega }=&-\frac{1}{2}\Delta _{xz} \frac{\delta ^{3}\Gamma _k}{\delta \varphi _{z}\delta \varphi _{z'}\delta \chi _{\omega }}\Delta _{z'y}\dot{r}_{yx} + \frac{1}{2}\Delta _{xz}\frac{\delta ^{3}\Gamma _k}{\delta \varphi _{z} \varphi _{z'}\varphi _\omega }\Delta _{z'y}\dot{r}_{yx} \nonumber \\&\quad +\frac{1}{4}\Delta _{xz}\left( \frac{\delta ^{2}}{\delta \varphi _{z}\delta \varphi _{z'}}\Delta _{uu'}\right) \dot{r}_{u'u}\Delta _{z'y}\frac{\delta r_{yx}}{\delta \chi _{\omega }}\nonumber \\ =&-\frac{1}{2}(\Delta \dot{r} \Delta )_{zz'}\frac{\delta ^{2}}{\delta \varphi _{z'}\delta \varphi _{z}} \left( \frac{\delta \Gamma }{\delta \chi _\omega }-\frac{\delta \Gamma }{\delta \varphi _\omega }\right) +\frac{1}{4}\left( \frac{\delta ^{2}}{\delta \varphi _{z}\delta \varphi _{z'}}\Delta _{uu'}\right) \dot{r}_{u'u}\,\Delta _{z'y}\frac{\delta r_{yx}}{\delta \chi _{\omega }}\Delta _{xz}. \end{aligned}$$

(3.3.18)

The first term in the last equality is in the form we want: a differential operator acting on (part of) $\mathcal {W_\omega }$. We now expand out the second term with the aim of also putting it into the desired form. For the sake of neatness let us define

$$\begin{aligned} \Gamma _{x_1...x_n}\equiv \frac{\delta ^n\Gamma _k}{\delta \varphi _{x_1}...\delta \varphi _{x_n}}. \end{aligned}$$

(3.3.19)

Expanding out the second term then gives

$$\begin{aligned} \!\!\left( \! \frac{\delta ^2}{\delta \varphi _z\delta \varphi _{z'}}\Delta _{uu'}\!\right) \! \dot{r}_{u'u}\,\Delta _{z'y}\frac{\delta r_{yx}}{\delta \chi _\omega }\Delta _{xz} \! =\!\Delta _{xz}&\bigg (\! \Delta _{uv}\Gamma _{zvs}\Delta _{sv'}\Gamma _{z'v's'}\Delta _{s'u'} \! +\! \Delta _{uv'}\Gamma _{v's'z'}\Delta _{s'v}\Gamma _{zvs}\Delta _{su'}\nonumber \\&\qquad -\Delta _{uv'}\Gamma _{v's'zz'}\Delta _{s'u'}\bigg ) \dot{r}_{u'u}\Delta _{z'y}\frac{\delta r_{yx}}{\delta \chi _\omega }. \end{aligned}$$

(3.3.20)

Upon exchanging factors of $\Delta$ and relabelling indices, we find

$$\begin{aligned} \left( \frac{\delta ^2}{\delta \varphi _{z}\delta \varphi _{z'}}\Delta _{uu'}\right) \dot{r}_{u'u}\left( \Delta _{z'y}\frac{\delta r_{yx}}{\delta \chi _{\omega }}\Delta _{xz}\right) = (\Delta \dot{r}\Delta )_{s'v'}\frac{\delta ^2}{\delta \varphi _{v'}\delta \varphi _{s'}} \Delta _{xy}\frac{\delta r_{yx}}{\delta \chi _{\omega }}, \end{aligned}$$

(3.3.21)

which now has the structure we require. Thus we have shown that the RG time derivative of the msWI can be written as

$$\begin{aligned} \mathcal {\dot{W}}_{\omega }=-\frac{1}{2}\text {Tr} \left( \Delta \dot{r}\Delta \frac{\delta ^2}{\delta \varphi \delta \varphi }\right) \mathcal {W}_{\omega }, \end{aligned}$$

(3.3.22)

i.e. that it is proportional to the msWI itself. If $\Gamma _{k}$ satisfies $\mathcal {W_\omega }$ at some initial scale $k_0$, and satisfies the flow equation there, it thus follows without further restriction that $\mathcal {\dot{W}_\omega }|_{k_{0}}=0$ since it is proportional to $\mathcal {W_\omega }$. Thus the msWI is compatible with the flow equation. If $\Gamma _{k}$ continues to evolve according to the flow equation, it then follows that $\mathcal {W_\omega }$ and thus $\mathcal {\dot{W}_\omega }$ will be zero for all k.

3.3.2 Compatibility Versus Derivative Expansion

Recalling from (3.3.11) that $\Delta$ is an infrared regulated full propagator, we see from (3.3.20) that the identity (3.3.21) can be understood diagrammatically in terms of two-loop diagrams as sketched in Fig. 3.1. The symmetry of these diagrams means that nothing changes if we exchange $\dot{r}\leftrightarrow \delta r/\delta \chi$. This exchange immediately leads to the identity (3.3.21).

Fig. 3.1

The two-loop diagrams in (3.3.20). Their symmetry immediately implies the identity (3.3.21). Momentum flow is indicated in the case where the fluctuation field $\varphi$ is then set to zero.

This identity breaks down in general in the derivative expansion. If the Ward identity is approximated by a derivative expansion, the full propagator in the one-loop term in (3.3.16) is also expanded in a derivative expansion. This full propagator has loop momentum q say, and is then expanded in powers of momenta carried by the external fluctuation field $\varphi (p)$, i.e. by the external legs. The RG time derivative of the Ward identity yields the RG time derivative of such vertices, as can be seen from the $\delta ^2\dot{\Gamma }_k/\delta \varphi ^2$ term in (3.3.17). This latter term has two internal legs given by the explicit functional derivatives, carrying the loop momentum q and joining full internal propagators $\Delta$, and any number of external legs contained in the vertices of $\dot{\Gamma }_k$. Substituting the flow equation (3.3.10) then gives in particular the last term in eqn. (3.3.18) in which two of these external legs are now joined to form a loop connected via $\dot{r}$. However it is momenta external to this new loop which are Taylor expanded in the derivative expansion of the flow equation (see also [10, 11]). This is illustrated in the diagram displayed in fig. 3.1. In particular when the remaining external fluctuation field dependence is removed by setting $\varphi =0$, we have exactly the momentum dependence displayed in the figure. We see that a derivative expansion of the Ward identity involves Taylor expanding in small p, while integrating over q. However a derivative expansion of the flow equation involves Taylor expanding in small q, and integrating over p instead. Thus the symmetry between the two loops is broken and the identity (3.3.21) no longer follows.

On the other hand we see that if $\dot{r}$ and $\delta r/\delta \chi$ have the same momentum dependence then the identity (3.3.21) is restored because it is no longer possible to distinguish the two loops. Returning the placement of $\sqrt{\bar{g}}$ from (3.3.4) to the integration measure, this in fact would give us the relation (3.3.40) that is necessary and sufficient for compatibility of the Ward identities within the derivative expansion, and which we will now derive directly within the derivative expansion.

3.3.3 Compatibility at Order Derivative-Squared

We now proceed to compute the flow of the msWI for the system truncated at $\mathcal {O}(\partial ^2)$ as described in Sect. 3.2, and investigate directly under which circumstances it vanishes. Let us start by writing the flow equations and msWIs for both V and K in the following form so that we can study both cases simultaneously:

$$\begin{aligned} \dot{A}(\varphi ,\chi )&= \int _p B_p\dot{R}_p,\end{aligned}$$

(3.3.23)

$$\begin{aligned} \mathcal {W}^{(A)}&=\bar{\partial }A - \gamma A + \int _p B_p(\partial _\chi R_p + \gamma R_p)=0, \end{aligned}$$

(3.3.24)

where A is either V or K/f such that $B_p$ is either $Q_p$ or $2 P_p$ respectively. Here we have also introduced the shorthand notation

$$\begin{aligned} \int _p \equiv f(\chi )^{-\frac{d}{2}}\int dp \,p^{d-1},\qquad \gamma \equiv \frac{d}{2}\partial _\chi \text {ln}f,\qquad \mathrm{and}\qquad \bar{\partial }\equiv \partial _\varphi - \partial _\chi . \end{aligned}$$

(3.3.25)

It will also be useful to have to hand the following relations:

$$\begin{aligned} \left( \bar{\partial }+ \partial _t - \gamma \right) V&= \mathcal W^{(V)} + \int _q Q_q (\dot{R}_q - \partial _{\chi } R_q - \gamma R_q), \end{aligned}$$

(3.3.26)

$$\begin{aligned} \left( \bar{\partial }+ \partial _t - \gamma \right) \frac{K}{f}&= \mathcal W^{(K)} + 2 \int _q P_q (\dot{R}_q - \partial _{\chi } R_q - \gamma R_q), \end{aligned}$$

(3.3.27)

$$\begin{aligned} \left( \bar{\partial }+ \partial _t + n \gamma \right) Q_p^n&= -n \, \, Q_p^{n+1} \int _q (\partial _{\varphi }^2 Q_q - 2 \, p^2 P_q)(\dot{R}_q - \partial _{\chi } R_q - \gamma R_q)\nonumber \\&\qquad -n \, Q_p^{n+1} (\dot{R}_p - \partial _{\chi } R_p - \gamma R_p) -n \, Q_p^{n+1} (\partial _{\varphi }^2 \mathcal W^{(V)} - p^2 \mathcal W^{(K)}). \end{aligned}$$

(3.3.28)

The first two relations are derived by subtracting the msWI from the flow equation for V and K/f respectively. The last relation is then derived by using the first two relations above together with the definition of $Q_p$ given in (3.2.11).

We begin by taking the RG time derivative of (3.3.24). Substituting in the flow equation for $\dot{A}$, and remembering the power of $f(\chi )$ hidden in the integral over p, this gives

$$\begin{aligned} \dot{ \mathcal W } ^ {(A)} = \int _p \dot{R}_p \left( \bar{\partial }+ \partial _t + \gamma \right) B_p - \int _p \dot{B}_p \left( \dot{R}_p - \partial _{\chi } R_p - \gamma R_p \right) . \end{aligned}$$

(3.3.29)

In order to proceed we have to assume a particular form of $B_p$ so that we can compute the result of the linear operators under the integral acting on it. A general term in $P_p$ takes the form

$$\begin{aligned} \tilde{B}_p = \left( \partial _{\varphi }^i V \right) ^ a \left( \partial _{\varphi }^j \frac{K}{f} \right) ^ b \left( \partial _{p^2}^k R_p \right) ^ c \left( p^2\right) ^l Q_p^e , \end{aligned}$$

(3.3.30)

where a, b, c, e, i, j,  k (not to be confused with the cutoff scale), and l are non-negative integers. From the structure of the terms in $P_p$ one can read off the following sum rule for the exponents:

$$\begin{aligned} a+b+c = e-1 . \end{aligned}$$

(3.3.31)

Notice that the case $B_p = Q_p$ for the potential is also included, since $a=b=c=l=0$ and $e=1$ also satisfies the sum rule. Taking the term under the first integral of (3.3.29), we find

$$\begin{aligned} \left( \bar{\partial }+ \partial _t + \gamma \right) \tilde{B}_p&= \bigg [a \left( \partial _{\varphi }^i V \right) ^ {-1} \partial _{\varphi }^i \left( \bar{\partial }+ \partial _t \right) V + b \left( \partial _{\varphi }^j \frac{K}{f} \right) ^ {-1} \partial _{\varphi }^j \left( \bar{\partial }+ \partial _t \right) \frac{K}{f} \nonumber \\&\quad + c \left( \partial _{p^2}^k R_p \right) ^ {-1} \partial _{p^2}^k \left( - \partial _{\chi } + \partial _t \right) R_p + e \, Q_p^{-1} \left( \bar{\partial }+ \partial _t \right) Q_p+ \gamma \bigg ] \tilde{B}_p. \end{aligned}$$

(3.3.32)

Substituting equations (3.3.26)–(3.3.28) into the above expression and using the sum rule, we obtain

$$\begin{aligned} \left( \bar{\partial }+ \partial _t + \gamma \right) \! \tilde{B}_p&\!=\!\! \bigg [a \left( \partial _{\varphi }^i V \right) ^ {-1} \partial _{\varphi }^i \left( \mathcal W^{(V)} + \int _q Q_q \bar{R}_q \right) \nonumber \\&\!\quad + b \left( \partial _{\varphi }^j \frac{K}{f} \right) ^ {-1} \partial _{\varphi }^j \left( \mathcal W^{(K)} + 2 \int _q P_q \bar{R}_q \right) + c \left( \partial _{p^2}^k R_p \right) ^ {-1} \partial _{p^2}^k \bar{R}_p \nonumber \\&\!\quad - e\, Q_p\! \int _q\!\! \left( \partial _{\varphi }^2 Q_q - 2 p^2 P_q \right) \!\bar{R}_q - e\, Q_p \bar{R}_p - e\, Q_p \left( \partial _{\varphi }^2 \mathcal W^{(V)}\! - p^2 \mathcal W^{(K)} \right) \! \bar{R}_q\bigg ] \tilde{B}_p \end{aligned}$$

(3.3.33)

where we have introduced the shorthand notation

$$\begin{aligned} \bar{R}_p = \dot{R}_p - \partial _\chi R_p - \gamma R_p. \end{aligned}$$

(3.3.34)

Turning our attention now to the second integral of (3.3.29) we take the RG time derivative of $\tilde{B}_p$ and again substitute in the flow equations for V and K/f. This gives

$$\begin{aligned} \dot{ \tilde{B} }_p&= \bigg [ a \left( \partial _{\varphi }^i V \right) ^ {-1} \partial _{\varphi }^i \int _q Q_q \dot{R}_q + b \left( \partial _{\varphi }^j \frac{K}{f} \right) ^ {-1} \partial _{\varphi }^j \int _q 2 P_q \dot{R}_q \nonumber \\&\quad + c \left( \partial _{p^2}^k R_p \right) ^ {-1} \partial _{p^2}^k \dot{R}_p - e \, Q_p \int _q \left( \partial _{\varphi }^2 Q_q - 2 p^2 P_q \right) \dot{R}_q - e \, Q_p \dot{R}_q\bigg ] \tilde{B}_p. \end{aligned}$$

(3.3.35)

Inserting (3.3.33) and (3.3.35) into (3.3.29) we obtain

$$\begin{aligned} \mathcal {\dot{W}}^{(A)}\!&=\! \sum _{\tilde{B}_p} \Bigg \{a \int _{p,q} \tilde{B}_p ( \partial _{\varphi }^i V ) ^ {-1} \partial _{\varphi }^i \bigg ( \dot{R}_p \mathcal {W}^{(V)} +Q_q [ \dot{R} , \partial _{\chi } R + \gamma R ]_{qp} \bigg ) \nonumber \\&\quad + b \int _{p,q} \tilde{B}_p \left( \partial _{\varphi }^j \frac{K}{f} \right) ^ {-1} \partial _{\varphi }^j \bigg ( \dot{R}_p \mathcal {W}^{(K)} + 2 P_q [ \dot{R} , \partial _{\chi } R + \gamma R ]_{qp} \bigg ) \\&\quad + c \int _p \tilde{B}_p \left( \partial _{p^2}^k R_p \right) ^ {-1} \left( \left( \partial _\chi R_p + \gamma R_p\right) \partial _{p^2}^k \dot{R}_p - \dot{R}_p \partial _{p^2}^k \left( \partial _\chi R_p + \gamma R_p\right) \right) \nonumber \\&\quad -\! e \!\int _p \!\tilde{B}_p Q_p \dot{R}_p \bigg ( \partial ^2_{\varphi } \mathcal {W}^{(V)}\!\! - p^2 \mathcal {W}^{(K)}\! \bigg )\!- e\!\! \int _{p,q}\!\!\tilde{B}_p Q_p \bigg ( \partial _{\varphi }^2 Q_q\!\! - 2 p^2 P_q\! \bigg ) [ \dot{R} , \partial _{\chi } R + \gamma R ]_{qp}\!\Bigg \}\nonumber \end{aligned}$$

(3.3.36)

where we have introduced the commutator-like construct $[A,B]_{qp} = A_q B_p - B_qA_p$.

When $A = V$ the above expression simplifies considerably to

$$\begin{aligned} \mathcal {\dot{W}}^{(V)}=- \int _p Q^2_p \dot{R}_p\, \bigg ( \partial ^2_{\varphi } \mathcal {W}^{(V)} - p^2 \mathcal {W}^{(K)} \bigg ) - \int _{p,q} Q^2_p\, \bigg ( \partial _{\varphi }^2 Q_q - 2 p^2 P_q \bigg ) [ \dot{R} , \partial _{\chi } R + \gamma R ]_{qp}, \end{aligned}$$

(3.3.37)

which we see contains only terms that contain either the Ward identities or the ‘commutator’ $[ \dot{R} , \partial _{\chi } R + \gamma R ]_{qp}$. On the other hand for the flow of the K/f msWI, the terms do not collect, so that it remains separately dependent on the individual $\tilde{B}_p$. However each term either contains the Ward identities themselves, the ‘commutator’ $[ \dot{R} , \partial _{\chi } R + \gamma R ]_{qp}$, or the additional commutator-like structures:

$$\begin{aligned} \left( \partial _\chi R_p + \gamma R_p\right) \partial _{p^2}^k \dot{R}_p - \dot{R}_p \partial _{p^2}^k \left( \partial _\chi R_p + \gamma R_p\right) . \end{aligned}$$

(3.3.38)

These appear in the third line of (3.3.36), and the integer k takes values 1 and 2. For a general cutoff $R_p$, these two additional commutator terms neither vanish nor combine with other terms of the flow.

If $[ \dot{R} , \partial _{\chi } R + \gamma R ]_{qp}$ vanishes, the flow (3.3.37) of the V msWI is automatically satisfied providing that both the K and V msWI are also satisfied. In this case we have by rearrangement that

$$\begin{aligned} \left( \partial _\chi R_p + \gamma R_p \right) /\dot{R}_p = \left( \partial _\chi R_q + \gamma R_q \right) /\dot{R}_q, \end{aligned}$$

(3.3.39)

which means that the ratio is independent of momentum. Equivalently

$$\begin{aligned} \partial _\chi R_p + \gamma R_p = F(\chi ,t) \,\dot{R}_p, \end{aligned}$$

(3.3.40)

where F can be a function of $\chi$ and t but not of p. However it is straightforward to see that (3.3.40) also forces the additional commutators (3.3.38) to vanish.

We have therefore shown that all the commutator-like terms vanish if and only if $\dot{R}_p$ and $\partial _{\chi } R_p + \gamma R_p$ have the same dependence on p, with the consequence that both the $\mathcal {\dot{W}}^{(A)}$ vanish, if the Ward identities $\mathcal {W}^{(A)}$ themselves vanish. Since for general choices of the functions, the vanishing of the ‘commutators’ is surely necessary to achieve $\mathcal {\dot{W}}^{(A)}=0$ without further restriction, we have thus shown that the condition (3.3.40) is necessary and sufficient to ensure compatibility, as defined at the beginning of this section.

3.3.4 Incompatibility Implies no Solutions

However even if the commutators do not vanish, and thus the Ward identities are incompatible with the flow equations, a priori there could still be a non-empty restricted set of solutions that both satisfy the flow equations and Ward identities. In this case the equations are satisfied not by the vanishing of the commutators themselves, but by the fact that for the given solutions the sum of all these terms vanish after performing the integration over momenta. Therefore, as well as obeying the flow equations and the msWIs $\mathcal {W}^{(A)}=0$, the solutions must also separately obey two further conditions, namely the vanishing of the right-hand sides of (3.3.36). In the language of Dirac’s classification of constraints [19, 20], the $\mathcal {W}^{(A)}=0$ provide the primary constraints. We have shown that if the ‘commutators’ do not vanish, then the solutions are subject also to non-trivial secondary constraints $\mathcal {\dot{W}}^{(A)}=0$. Given the involved form of $\mathcal {\dot{W}}^{(K)}$ in particular, we can be sure that the procedure does not close and that actually there is then an infinite tower of secondary constraints, $\partial ^n_t \,\mathcal {W}^{(A)}=0,\;\forall \,n>0$, all of which must be satisfied. It would therefore seem inevitable that there are in fact no non-trivial solutions in this case. We will confirm this by example in Sect. 3.4.2. We conclude that the vanishing of the ‘commutators’, and hence condition (3.3.40), is both necessary and sufficient for there to be any solutions to the flows and Ward identities in the derivative expansion approximation outlined in Sect. 3.2.

The condition (3.3.40) was already used in reference [1], where however it was introduced as a mathematical trick to help solve the coupled system of flow equations and msWI. As we recall below, it implies either that $\eta =0$ or $R_p$ is of power-law form. We now see that the requirement for $\dot{R}_p$ and $\partial _{\chi } R_p + \gamma R_p$ to have the same dependence on p, goes much deeper: the flow equations (3.2.7) and (3.2.9), and the Ward identities (3.2.8) and (3.2.10), are incompatible without this constraint, and incompatibility forces there to be no solutions to the combined system.

3.3.5 Required Form of the Cutoff Profile

Note that $R_p$ must take a form that respects the scaling dimensions. Introducing dimensionless variables for use in the next section and later on, we can make these scaling dimensions explicit by employing the RG scale k. We denote the new dimensionless quantities with a bar. We have

$$\begin{aligned} \varphi = k^{\eta /2}\bar{\varphi }, \qquad \chi = k^{\eta /2}\bar{\chi }, \qquad f(\chi ) = k^{d_f}\bar{f}(\chi ),\nonumber \\ V(\varphi ,\chi ) = k^{d_V}\bar{V}(\bar{\varphi },\bar{\chi }), \qquad K(\varphi , \chi ) = k^{d_R- 2 + d_f} \bar{K}(\bar{\varphi },\bar{\chi }), \end{aligned}$$

(3.3.41)

where

$$\begin{aligned} d_V = d(1-d_f/2)\qquad \mathrm{and}\qquad d_R = d_V - \eta , \end{aligned}$$

(3.3.42)

and thus from (3.3.3) and (3.2.1), we have by dimensions that $R_p$ must take the form

$$\begin{aligned} R(p^2/f)= - k^{d_R} \,r\left( \frac{p^2}{k^{2-d_f}f}\right) = - k^{d_R} \,r(\hat{p}^2), \end{aligned}$$

(3.3.43)

where r is a dimensionless cutoff profile of a dimensionless argument,⁷ and we have introduced the dimensionless momentum magnitude $\hat{p} = p\sqrt{k^{d_f-2}/f}$.

If $\dot{R}_p$ and $\partial _{\chi } R_p + \gamma R_p$ have the same dependence on p, i.e. satisfy (3.3.40), then either $\eta =0$ or $R_p$ is of power-law form [1]. To see this, note that from (3.3.43) and (3.3.25) we have

$$\begin{aligned} \gamma {\dot{R}}_p = d_V \left[ \partial _\chi R_p+\gamma R_p\right] -\eta \gamma R_p. \end{aligned}$$

(3.3.44)

Thus (choosing $F=\gamma /d_V$) we see that (3.3.40) is satisfied if $\eta =0$, without further restriction on R. However if $\eta \ne 0$, then (3.3.44) together with (3.3.40) implies

$$\begin{aligned} f \frac{\partial R_p}{\partial f} = \frac{d}{2}\left( \frac{\eta F}{ d_VF- \gamma } - 1\right) R_p, \end{aligned}$$

(3.3.45)

and thus from (3.3.43)

$$\begin{aligned} \hat{p} \frac{d}{d\hat{p}} r(\hat{p}^2) = -d\left( \frac{\eta F}{ d_VF- \gamma } - 1\right) r(\hat{p}^2). \end{aligned}$$

(3.3.46)

Since the term in brackets does not depend on p, we see that this is only possible if in fact the term in brackets is a constant. Setting this constant to be 2n / d for some constant n, we thus also deduce that $r\propto \hat{p}^{-2n}$.

An example of a cutoff that does not satisfy (3.3.40) if $\eta \ne 0$, and thus leads to incompatible msWIs in this case, is the optimised cutoff [7, 8]:

$$\begin{aligned} r(\hat{p}^2) = (1-\hat{p}^2)\theta (1-\hat{p}^2). \end{aligned}$$

(3.3.47)

It is straight-forward to confirm that this does not satisfy (3.3.40) if $\eta \ne 0$. Using (3.3.43) and (3.3.44) we find

$$\begin{aligned} \dot{R}_p \propto d_V \left[ \frac{2}{d}\,\theta (1-\hat{p}^2) + (1-\hat{p}^2)\theta (1-\hat{p}^2)\right] - \eta \, (1-\hat{p}^2)\theta (1-\hat{p}^2). \end{aligned}$$

(3.3.48)

In order for (3.3.47) to satisfy (3.3.40), the right-hand side must be proportional to $\partial _\chi R_p+\gamma R_p$ i.e. to the term in square brackets. This is only true if $\eta =0$.

3.4 LPA Equations

We will now use the Local Potential Approximation to further investigate the restriction imposed by the msWI on the RG flow equation, in terms of general solutions and also on the existence of k-fixed points (i.e. RG fixed points with respect to variations in k). We start with a very clear example where the msWI forbids the existence of k-fixed points.

Then using the concrete example of the optimised cutoff we show explicitly that compatibility forces $\eta =0$ for non-power-law cutoffs. Setting $\eta =0$ we will see that background independent variables exist, in other words they exist whenever the msWI is compatible with the flow. We will also see that such $\hat{k}$-fixed points⁸ coincide with the k-fixed points. The background independent variables allow us to solve for the fixed points explicitly, uncovering a line of fixed points, consistent with the findings for power-law cutoff [12].

3.4.1 Demonstration of Background Independence Forbidding Fixed Points in General

We use the change to dimensionless variables (3.3.41) and (3.3.43). In the LPA we discard the flow and Ward identity for K, and set $\bar{K}=1$. The result, for a general cutoff profile $r(\hat{p}^2)$, is:

$$\begin{aligned} \partial _t \bar{V} + d_V \bar{V} - \frac{\eta }{2} \, \bar{\varphi }\, \frac{\partial \bar{V}}{\partial \bar{\varphi }} - \frac{\eta }{2} \, \bar{\chi }\, \frac{\partial \bar{V}}{\partial \bar{\chi }}&= \int _0^{\infty } d\hat{p} \, \hat{p}^{d-1} \, \frac{d_R\, r - \frac{d_V}{d} \, \hat{p} \, r'}{\hat{p}^2 + r - \partial ^2_{\bar{\varphi }}\bar{V}},\end{aligned}$$

(3.4.1)

$$\begin{aligned} \frac{\partial \bar{V}}{\partial \bar{\chi }} - \frac{\partial \bar{V}}{\partial \bar{\varphi }} + \bar{\gamma }\, \bar{V}&= \bar{\gamma }\int _0^{\infty } d\hat{p} \, \hat{p}^{d-1} \, \frac{r - \frac{1}{d} \, \hat{p} \, r'}{\hat{p}^2 + r - \partial ^2_{\bar{\varphi }}\bar{V}}, \end{aligned}$$

(3.4.2)

where $r'$ means $dr(\hat{p}^2)/d\hat{p}$ and from the change to dimensionless variables we find:

$$\begin{aligned} \bar{\gamma } = \frac{d}{2}\frac{\partial }{\partial \bar{\chi }}\ln \bar{f}\left( \mathrm{e}^{\eta t/2}\mu ^{\eta /2}\bar{\chi }\right) . \end{aligned}$$

(3.4.3)

Note that since f cannot depend on t (see the discussion in Sect. 3.2), once we go to dimensionless (i.e. scaled) variables, $\bar{f}$ is in general forced to depend on t if $\chi$ has non-vanishing scaling dimension $\eta$. At the (k-)fixed point we must have $\partial _t \bar{V} = 0$. We see at once why fixed points are generically forbidden by the msWI: the fixed point potential $\bar{V}$ would have to be independent of t, but through (3.4.2) and (3.4.3) this is impossible in general since $\bar{V}$ is forced to be dependent on explicit t-dependence in $\bar{f}$ through the Ward identity. This is true even in the case of power-law cutoff profile⁹ which as we have seen allows (3.4.2) to be compatible with the flow (3.4.1).

At first sight an escape from this problem is simply to set f to be power law. Indeed setting $f\propto \chi ^{\rho }$ for some constant $\rho$, (3.4.3) implies

$$\begin{aligned} \bar{\gamma } = \frac{d}{2} \frac{\rho }{\bar{\chi }}, \end{aligned}$$

(3.4.4)

and thus (3.4.2) no longer has explicit t dependence. Recall that for power-law cutoff profiles r, it was indeed found that k-fixed points for $\bar{V}$ are allowed if f is chosen to be of power law form [1].¹⁰ However we have seen in Sect. 3.3.5 that any other cutoff profile does not allow the Ward identity to be compatible with the flow unless $\eta =0$. We argued in Sect. 3.3.4 that incompatibility overconstrains the equations leading to no solutions. In the next subsection, Sect. 3.4.2, we will confirm this explicitly, choosing as a concrete example the optimised cutoff profile and space-time dimension $d=4$.

On the other hand, if we set $\eta =0$ then the msWI (3.4.2) is compatible with the flow (3.4.1), for any parametrisation f. Apparently k-fixed points are also now allowed without further restriction, since again (3.4.3) loses its explicit t dependence. Opting once more for optimised cutoff profile and $d=4$, we will see in Sect. 3.4.3 that indeed they are allowed and furthermore they coincide with fixed points in a background independent description that we also uncover.

3.4.2 Confirmation of No Solutions if the msWI is Incompatible With the Flow

Specialising to the optimised cutoff and (for simplicity) the most interesting case of spacetime dimension $d=4$, the equations read

$$\begin{aligned} \partial _t\bar{V}+ d_V \bar{V} - \frac{\eta }{2} \bar{\varphi }\, \partial _{\bar{\varphi }}\bar{V} -\frac{\eta }{2} \bar{\chi }\, \partial _{\bar{\chi }}\bar{V}&= \left( \frac{d_R}{6} + \frac{\eta }{12} \right) \frac{1}{1 - \partial ^2_{\bar{\varphi }}\bar{V}},\end{aligned}$$

(3.4.5)

$$\begin{aligned} \partial _{\bar{\chi }}\bar{V} - \partial _{\bar{\varphi }}\bar{V} + \bar{\gamma } \bar{V}&= \frac{\bar{\gamma }}{6} \frac{1}{1 - \partial ^2_{\bar{\varphi }}\bar{V}}. \end{aligned}$$

(3.4.6)

Choosing power law f and thus eliminating explicit dependence on t, cf. (3.4.4), apparently these equations can work together. Combining them by eliminating their right-hand sides, we get

$$\begin{aligned} 2\partial _t\bar{V}+\eta \bar{V}-\left( \eta \bar{\varphi }-\alpha \bar{\chi }\right) \partial _{\bar{\varphi }}\bar{V}-(\eta +\alpha )\bar{\chi }\partial _{\bar{\chi }} \bar{V}=0, \end{aligned}$$

(3.4.7)

where we have introduced the constant $\alpha = (d_R+\eta /2)/\rho$. This equation can be solved by the method of characteristics (see e.g. the appendix in reference [1]). Parametrising the characteristic curves with t, they are generated by the following equations:

$$\begin{aligned} \frac{d\bar{V}}{dt} = -\frac{\eta }{2}\bar{V},\quad \frac{d\bar{\chi }}{dt}=-\frac{\alpha +\eta }{2}\bar{\chi },\quad \frac{d\bar{\varphi }}{dt}=\frac{\alpha \bar{\chi }-\eta \bar{\varphi }}{2}. \end{aligned}$$

(3.4.8)

Solving the second equation before the third, it is straightforward to find the curves:

$$\begin{aligned} \bar{V}= \hat{V}\mathrm{e}^{-\eta t/2},\quad \bar{\chi }= \hat{\chi }\, \mathrm{e}^{-(\eta +\alpha )t/2},\quad \bar{\varphi }+\bar{\chi }= \hat{\phi }\, \mathrm{e}^{-\eta t/2}, \end{aligned}$$

(3.4.9)

in terms of initial data $\hat{V},\hat{\phi },\hat{\chi }$. Thus the solution to (3.4.7) can be written as

$$\begin{aligned} \bar{V}=\mathrm{e}^{-\eta t/2}\, \hat{V}(\hat{\phi },\hat{\chi }) =\mathrm{e}^{-\eta t/2} \,\hat{V}\left( \mathrm{e}^{\eta t/2}[\bar{\varphi }+\bar{\chi }],\mathrm{e}^{(\eta +\alpha )t/2}\bar{\chi }\right) , \end{aligned}$$

(3.4.10)

as can be verified directly. Plugging this into either (3.4.5) or (3.4.6) gives the same equation, which in terms of the hatted variables reads

$$\begin{aligned} \hat{\chi }\partial _{\hat{\chi }}\hat{V}+2\rho \hat{V}= \frac{\rho }{3}\frac{1}{\mathrm{e}^{-\frac{\eta }{2} t} \,-\partial ^2_{\hat{\phi }}\hat{V}}. \end{aligned}$$

(3.4.11)

Since $\hat{V}(\hat{\phi },\hat{\chi })$ is independent of t, we see there are no solutions unless $\eta =0$. We saw in Sect. 3.3.5 that this was also the necessary and sufficient condition for compatibility in this case.

3.4.3 Background Independence at Vanishing Anomalous Dimension

We now set $\eta =0$. As recalled in Sect. 3.3.5, the msWI is now compatible with the flow, and furthermore from (3.4.3) the explicit t dependence has dropped out. For power-law cutoff profiles we found that k-fixed points exist and coincide with background independent $\hat{k}$-fixed points for any form of f with any dimension $d_f$ [1]. We will see that for non-power law cutoff that the same is true. (Again we choose optimised cutoff and $d=4$ as an explicit example.) We will uncover consistent background independent variables for which the full line of fixed points is visible [12].

Since $\eta =0$, in the equations (3.4.5) and (3.4.6), we also have $d_R=d_V=2(2-d_f)$ and $\bar{\gamma }=2\partial _{\bar{\chi }}\ln \bar{f}(\bar{\chi })$. Note that from (3.3.43), $d_f=2$ is excluded otherwise the IR cutoff no longer depends on k. Also note that since $\eta =0$ we can drop the bars on $\chi$ and $\varphi$. Combining the equations into a linear partial differential equation we get

$$\begin{aligned} \partial _t\bar{V}+\frac{2-d_f}{\partial _{\chi }\ln \bar{f}}\left( \partial _{\varphi }\bar{V}-\partial _{\chi }\bar{V}\right) =0, \end{aligned}$$

(3.4.12)

whose characteristic curves satisfy

$$\begin{aligned} \frac{d\chi }{dt}=\frac{d_f-2}{\partial _{\chi }\ln \bar{f}},\quad \frac{d\varphi }{dt}=\frac{2-d_f}{\partial _{\chi }\ln \bar{f}},\quad \frac{d\bar{V}}{dt}=0. \end{aligned}$$

(3.4.13)

Solving the first equation gives:

$$\begin{aligned} \hat{t}= t+\frac{\ln \bar{f}}{2-d_f}, \end{aligned}$$

(3.4.14)

where the integration constant $\hat{t}$ is thus the background independent definition of RG time (see the appendix to reference [1]). Exponentiating,

$$\begin{aligned} \hat{k}= k \left\{ \bar{f}(\chi )\right\} ^{\frac{1}{2-d_f}} = k^{2\frac{1-d_f}{2-d_f}} \left\{ f(\chi )\right\} ^{\frac{1}{2-d_f}}, \end{aligned}$$

(3.4.15)

where the second equality follows from (3.3.41). The sum of the first two equations in (3.4.13) tells us that $\phi =\varphi +\chi$ is an integration constant for the characteristics, and finally the last equation says that $\bar{V}$ is also constant for characteristics. Thus we learn that the change to background independent variables is achieved by writing

$$\begin{aligned} \bar{V}= \hat{V}(\phi ,\hat{t}\,). \end{aligned}$$

(3.4.16)

It is straightforward to verify that this solves (3.4.12). Substituting into either (3.4.5) or (3.4.6) gives the same flow equation:

$$\begin{aligned} \partial _{\hat{t}}\hat{V}+d_V\hat{V}= \frac{d_V}{6}\frac{1}{1-\partial ^2_\phi \hat{V}^{ {H^H}}}, \end{aligned}$$

(3.4.17)

which is indeed now background independent, i.e. independent of $\chi$, and indeed independent of parametrisation f. There remains a dependence on the dimension of f through $d_V = 2(2-d_f)$ although this disappears for $\hat{k}$-fixed points, and can be removed entirely by a rescaling $\hat{t}\mapsto \hat{t}\, d_V$ which however changes the dimension of $\hat{k}$ to $d_V$.

We also see from (3.4.14) and (3.4.16) that

$$\begin{aligned} \partial _t \bar{V}= \partial _{\hat{t}} \hat{V}, \end{aligned}$$

(3.4.18)

and thus fixed points in k coincide with the background independent fixed points.

Finally, the fixed points are readily found from (3.4.17) similarly to references [5, 12] by recognising that

$$\begin{aligned} \frac{d^2\hat{V}}{d\phi ^2} = 1-\frac{1}{6\hat{V}} \end{aligned}$$

(3.4.19)

is equivalent to Newton’s equation for acceleration with respect to ‘time’ $\phi$ of a particle of unit mass at ‘position’ $\hat{V}$ in a potential $U=-\hat{V}+ (\ln \hat{V})/6$. In this way it can be verified that there is a line of fixed points ending at the Gaussian fixed point, which is here $\hat{V}=1/6$. The appearance of this line of fixed points is a consequence of the conformal factor problem, discussed in Sect. 1.4 of Chap. 1, and is in agreement with the findings for power-law cutoff in reference [12] in which the problem has been addressed.

3.5 Polynomial Truncations

The analysis so far has used properties of conformally truncated gravity and the derivative expansion approximation method. In order to gain insight about what might happen at the non-perturbative level, and in full quantum gravity, we will consider how the issues would become visible in polynomial truncations.

The generic case treated in Sect. 3.4.1 will be just as clear in the sense that truncations of the Ward identity will still force the effective potential (effective action in general) to be t-dependent if the dimensionless parametrisation (3.4.3) is similarly forced to be t-dependent. In general therefore, if the way the metric is parametrised forces the parametrisation to become t-dependent, we can expect that background independence excludes the possibility of fixed points, at least with respect to t.

Consider next the situation treated in Sect. 3.4.2. Expanding the dimensionless potential and the equations in a double power series in the fluctuation and the background field, we write:

$$\begin{aligned} \bar{V}(\bar{\varphi },\bar{\chi }) = \sum _{n,m=0}^{\infty } a_{nm} \bar{\varphi }^n \bar{\chi }^m. \end{aligned}$$

(3.5.1)

Substituting (3.4.4) into (3.4.6) and multiplying through by $\bar{\chi }$, we can read off from this and (3.4.5) the zeroth level equations:

$$\begin{aligned} d_V a_{00} = \left( \frac{d_R}{6} + \frac{\eta }{12} \right) \frac{1}{1 - 2a_{20}},\qquad 2\rho \, a_{00} = \frac{\rho }{3} \frac{1}{1 - 2a_{20}}. \end{aligned}$$

(3.5.2)

Since $\rho$ cannot vanish and $a_{20}$ cannot diverge, combining these equations gives $d_V = d_R+\eta /2$ which from (3.3.42) implies $\eta =0$. Thus we recover already from the zeroth order level that fixed points are excluded unless $\eta =0$. (Of course the real reason, namely that the equations are incompatible, and the full consequence that there are no t-dependent solutions either, is maybe not so easy to see this way.)

3.5.1 Counting Argument

We remarked the Introduction that generically the solutions become over-constrained if we consider a sufficiently high truncation. We now proceed to make a careful count of the coefficients appearing in the equations and estimate the level at which this happens.

We concentrate on fixed point solutions to the LPA system (3.4.1), (3.4.2) and (3.4.3) where either $\eta =0$ or we choose power-law f, so that explicit t dependence does not already rule out such solutions. We introduce the short-hand notation $\bar{V} ^{(n,m)}=\partial _{\bar{\varphi }}^n \partial _{\bar{\chi }}^m \bar{V}(\bar{\varphi },\bar{\chi })$. To obtain the system at order r we have to plug the expansion of the potential (3.5.1) into both the fixed point equation and msWI, act on them with operators $\frac{\partial ^{i+j}}{\partial \bar{\varphi }^i \, \partial \bar{\chi }^j}$ such that $i+j=r$, before finally setting the fields to zero. In particular, for any fixed value $r_{\star }$ we have $2 \, (r_{\star }+1)$ equations and hence up to order r there are

$$\begin{aligned} n_{\text {eqn}}(r) = \sum _{i=0}^{r} 2\,(i+1) = r^2 + 3r + 2 \end{aligned}$$

(3.5.3)

equations.

To count the coefficients appearing in these $n_{\text {eqn}}(r)$ equations let us start with the left-hand sides. First note that

$$\begin{aligned} \bar{V}^{(i,j)} \bigg |_{\bar{\varphi }= \bar{\chi }= 0} \propto a_{ij}. \end{aligned}$$

(3.5.4)

That is, for any fixed pair (i, j) the left-hand side of (3.4.2) will contain the coefficients $a_{ij}$, $a_{i+1,j}$ and $a_{i,j+1}$, whereas the left-hand side of (3.4.1) will only contain $a_{ij}$. Up to some fixed order r there will be thus coefficients $a_{ij}$ where i and j run from 0 to $r+1$ and $i+j \leqslant r+1$

Fig. 3.2

Coefficients of the potential appearing on the left sides of the equations

$$\begin{aligned} \bigg \lbrace a_{00}, a_{01}, \ldots , a_{0,r+1}, a_{10}, \ldots , a_{1,r}, \ldots , a_{2,r-1}, \ldots , a_{r+1,0} \bigg \rbrace , \end{aligned}$$

(3.5.5)

(cf. figure 3.2). This adds up to the following number of coefficients

$$\begin{aligned} n_{\text {lhs}}(r) = \sum _{i=1}^{r+2} \, i = \frac{1}{2} \, r^2 + \frac{5}{2} \, r + 3. \end{aligned}$$

(3.5.6)

Including the coefficients on the right-hand sides, we have to be careful not to double count any coefficients that have already been taken account of on the left-hand sides. Let us suppose we have fixed the cutoff and let us assume that for the moment $\bar{\gamma } =$ const. Then all additional coefficients on the right-hand sides come from the expansion of the propagator

$$\begin{aligned} \frac{\partial ^{i+j}}{\partial \bar{\varphi }^i \, \partial \bar{\chi }^j} \, \left( \frac{1}{1 - \bar{V}^{(2,0)}} \right) \bigg |_{\bar{\varphi }= \bar{\chi }= 0} = \frac{\partial ^{j}}{\partial \bar{\chi }^j} \left[ \frac{\partial ^{i-1}}{\partial \bar{\varphi }^{i-1}} \left( \frac{\bar{V}^{(3,0)}}{(1 - \bar{V}^{(2,0)})^2} \right) \right] \bigg |_{\bar{\varphi }= \bar{\chi }= 0}\, . \end{aligned}$$

(3.5.7)

Since we can always arrange the $\bar{\varphi }$–derivatives to act first, the expression in the square brackets will involve terms $\bar{V}^{(2,0)} \cdots \, \bar{V}^{(i+2,0)}$. Using (3.5.4), we see that the expression given in (3.5.7) will then include terms

$$\begin{aligned} \bigg \lbrace a_{20}, a_{21}, \ldots , a_{2i}, a_{30}, \ldots , a_{3i}, \ldots , a_{i+2,0}, \ldots , a_{i+2,j} \bigg \rbrace . \end{aligned}$$

(3.5.8)

Up to any fixed order r, i and j can take values between 0 and r such that $i+j = r$, and in total we will have the following coefficients on the right-hand sides

$$\begin{aligned} \bigg \lbrace a_{20}, \ldots , a_{2,r}, a_{30}, \ldots , a_{3,r-1}, \ldots , a_{4,r-2}, \ldots , a_{r+2,0} \bigg \rbrace , \end{aligned}$$

(3.5.9)

(cf. figure 3.3). Most of these coefficients have however already been accounted for on the left-hand sides cf. (3.5.5). The only ones not yet counted are

Fig. 3.3

Coefficients of the potential appearing in the expansion of the propagator

Fig. 3.4

All the coefficients of the potential appearing on both sides of the equations

$$\begin{aligned} \bigg \lbrace a_{2,r}, a_{3,r-1}, a_{4,r-2}, \ldots , a_{r+2,0} \bigg \rbrace , \end{aligned}$$

(3.5.10)

(cf. figure 3.4) which precisely add up to a further $r+1$ coefficients. We also must include another two coefficients, namely $\eta$ and $d_f$. Finally, since $\gamma$ is in general some function of $\chi$ it is easy to see that

$$\begin{aligned} \frac{d^r}{d \bar{\chi }^r} \, \bar{\gamma } \propto \frac{d^r}{d \bar{\chi }^r} \, \left( \frac{f'}{f}\right) \subseteq \bigg \lbrace f, f', \ldots , f^{(r+1)} \bigg \rbrace , \end{aligned}$$

(3.5.11)

which gives us an additional $(r+2)$ coefficients from the Taylor expansion of f. The total number of coefficients from both left and right-hand sides is then given by

$$\begin{aligned} n_{\text {coeff}}(r) = n_{\text {lhs}} + (r+1) + (r+2) + 2 = \frac{1}{2} \, r^2 + \frac{9}{2} \, r + 8. \end{aligned}$$

(3.5.12)

From (3.5.3) we see that for large r the number of equations $\sim$ $r^2$, while from (3.5.12) the number of coefficients only $\sim$ $r^2/2$. There are therefore asymptotically twice as many equations as coefficients, as already discussed in the Introduction. Equating the number of equations and coefficients yields the positive solution

$$\begin{aligned} r = 5.3. \end{aligned}$$

(3.5.13)

Therefore the number of equations exceeds the number of coefficients for the first time at order $r=6$. If there is to be a conflict between the existence of (k-)fixed points and background independence generically we would expect this to become evident at about this level. Equally, if there is no conflict between background independence and the existence of (k-)fixed points then from this level onwards some equations become redundant (i.e. they provide constraints that are automatically satisfied once the other equations are obeyed). In the limit $r\rightarrow \infty$ fully half of the equations must become redundant if (k-)fixed points are to be consistent with background independence.

3.6 Conclusions

If we construct the non-perturbative flow equation for quantum gravity by introducing a cutoff defined through a background metric then independence from this artificial metric can only be achieved if the appropriate modified split Ward identity is obeyed. However even if it is obeyed, background independence is guaranteed only in the limit $k\rightarrow 0$. RG properties on the other hand are defined at intermediate scales k. There is therefore the potential for conflict in this formulation between RG notions such as fixed points, and the requirement of background independence. Examples of such conflicts were uncovered in reference [1].

In this paper we have further investigated these issues. Our findings, together with those of reference [1], are summarised in table 3.1.¹¹ The first question that needs to be addressed is whether the msWI, $\mathcal {W}=0$, is compatible with the exact RG flow equation, i.e. such that $\dot{\mathcal {W}}=0$ then follows. At the exact level, compatibility is guaranteed since they are both identities derived from the partition function (see also Sect. 3.3.1). Within the derivative expansion approximation of conformally reduced gravity considered in reference [1] (reviewed in Sect. 3.2), we have shown in Sects. 3.3.3 and 3.3.5, that this compatibility follows if and only if either $\eta =0$ or the cutoff profile is power law. In Sect. 3.3.2, we saw precisely why the derivative expansion breaks compatibility in general and why these special cases restore it. We argued in Sect. 3.3.4 that if the equations are incompatible they are overconstrained since there are then an infinite number of secondary constraints, and thus not even t-dependent solutions can exist. We confirmed this latter conclusion by example in Sect. 3.4.2 in the LPA. In Sect. 3.5, we also saw that the fixed point equations and Ward identities together generically overconstrain the system when expanded in terms of vertices beyond the six-point level.

Table 3.1 RG properties of the derivative expansion for conformally reduced gravity, when the msWI is also satisfied. The results depend on whether the conformal factor develops an anomalous dimension $\eta$, on the choice of cutoff profile r, and on how the metric is parametrised via f. Depending also on its dimension $d_f$, f can contain a massive parameter, and thus run with k when written in dimensionless terms, as listed in the table. $\widehat{\mathrm{FP}}$ indicates that a background independent description exists, while (

) FP indicates that k-fixed points are (not) allowed; the (in)equality shows how these relate to the $\hat{k}$-fixed points

Even if the equations are compatible, the msWI can still forbid fixed points. In Sect. 3.4.1 the reason was laid out particularly clearly. The Ward identity

$$\begin{aligned} \frac{\partial \bar{V}}{\partial \bar{\chi }} - \frac{\partial \bar{V}}{\partial \bar{\varphi }} + \bar{\gamma }\, \bar{V} = \bar{\gamma }\int _0^{\infty } d\hat{p} \, \hat{p}^{d-1} \, \frac{r - \frac{1}{d} \, \hat{p} \, r'}{\hat{p}^2 + r - \partial ^2_{\bar{\varphi }}\bar{V}} \end{aligned}$$

(3.6.1)

(which is compatible for power-law r), forces the effective potential $\bar{V}$ to depend on t through

$$\begin{aligned} \bar{\gamma } = \frac{d}{2}\frac{\partial }{\partial \bar{\chi }}\ln \bar{f}\left( \mathrm{e}^{\eta t/2}\mu ^{\eta /2}\bar{\chi }\right) , \end{aligned}$$

(3.6.2)

whenever this dimensionless combination is similarly forced to be t-dependent. For example we see that fixed points with respect to k are forbidden for exponential parametrisations $f(\phi )= \exp (\phi )$ if the field grows a non-zero anomalous dimension. It is clear that the reasons for this conflict are general and not tied to the derivative expansion of the conformally truncated model per se. Therefore this issue could provide important constraints for example on the exponential parametrisations recently advocated in the literature [21,22,23,24,25,26,27,28,29].

In Sect. 3.5 we considered how these issues arise in polynomials truncations. We saw that the problem is that if the fixed point equations and msWI equations are truly independent, then they will over-constrain the solutions if carried to a sufficiently high order truncation. Indeed, expanding in powers of the fluctuation field $\varphi$ to the mth level and background field $\chi$ to the nth level, we get one fixed point equation for each (m, n)-point vertex and one msWI equation per vertex. Even though each of these equations is open (depending on yet higher-point vertices) we saw that since there are two equations for every vertex, at sufficiently high order truncation there are more equations than vertices (indeed eventually double the number) and thus either the equations become highly redundant or the vertices are constrained to the point where there are no solutions. This analysis strongly suggests that the full non-perturbative Ward identities would lead to important constraints on RG properties.

For full quantum gravity, such conflict between k-fixed points and background independence may also show up clearly in a vertex expansion, as discussed in 3.5, or generically it may not become visible until the six-point level. However for full quantum gravity, if we are to follow the standard procedure, we must also fix the gauge. The original msWI, which formally expresses background independence before gauge fixing, will no longer be compatible with the flow equation. Instead we must use the appropriate version which has contributions from the background dependence of the gauge fixing and ghost terms as well as from cutoff terms for the ghost action itself. However background independence is then only restored in the limit $k\rightarrow 0$ after going “on-shell” (assuming such an appropriate property can be defined). This last step is required to recover quantities that are independent of the gauge fixing. If we are to continue with a flow equation for a Legendre effective action [30, 31] then to get around this obstruction, the Vilkovisky-DeWitt covariant effective action seems called for [16, 32,33,34], with the msWI replaced by the corresponding modified Nielsen identities where the role of the background field is played by the “base point” [35].

Returning to the present study, it seems surely significant that whenever the msWI equations are actually compatible with the flow equations, it is possible to combine them and thus uncover background independent variables, including a background independent notion of scale, $\hat{k}$. These are not only independent of $\chi$ but also independent of the parametrisation f. Of course such an underlying description has only been shown in this $\mathcal {O}(\partial ^2)$ approximation and in conformally truncated gravity, and one might doubt that this happy circumstance could be generalised to full quantum gravity, and not only for the reasons outlined above. However we also saw in Sect. 3.5.1 that if modified Ward identities are to be compatible with the flow equations then in terms of vertices, the information they contain becomes highly redundant at sufficiently high order (the six-point level in our case). This in itself suggests the existence of a simpler description. Finally, a formulation for non-perturbative RG has recently been proposed where computations can be made without ever introducing a background metric (or gauge fixing) [36].