Keywords

36.1 Introduction

In recent years, the number of aged buildings suffering from natural disasters has shown an increasing trend. This increasing trend has stimulated a rapid development of the state-of-the-art devices for vibration control. The application of such devices requires the reliable information of structural damping ratio, which is a commonly used physical parameter to characterize the energy dissipation of structural dynamic response. However, the actual structural damping ratio for existing and new-designed buildings subject to earthquake and wind loading is difficult to be precisely quantified because of its complicated mechanism, which has become a troublesome issue in optimizing structural designs [1].

Unlike characterizing the structural stiffness and mass properties, which can be intuitively evaluated from the material and geometric features, quantifying the structural damping ratio is much more complicated. Currently, the structural damping ratio of civil structures is usually obtained by experimental/field tests, which measure the responses of structures to different excitations [2], such as shake tables, wind loadings, environment loadings, or strong earthquakes [3]. Among these experiments, the shake table test uses excessively idealized models, therefore it cannot exactly represent real structures.

Since the 1970s, a large number of dynamic response records of real civil structures have been collected for the analysis of structural damping ratios. The influences of construction materials, structure dimensions, foundation types, vibration orientations, vibration amplitudes, excitation types, non-structural components, etc. on the structural damping ratio have been studied. These studies resulted in the currently recommended design values of structural damping ratios in building design provisions of different countries. For example, in the United States, the structural damping ratio of steel and RC (reinforced concrete) structures can be calculated as an inverse proportion to the structural height [4]. In China, the structural damping ratio is given as a few fixed numbers for several cases, such as 0.05 for normal case, 0.04 for steel structures less than 50 m, 0.03 and 0.02 for structures less and higher than 200 m, respectively, 0.05 for plastic analysis of earthquake [5], 0.04 for concrete high-rise buildings under multiple earthquakes, 0.02 for wind vibration of high-rise buildings, and 0.01–0.02 for mixed structures [6].

Even though the above studies and design provisions have involved many influence factors for structural damping ratios. There are still many concerns such as: (1) the mechanism of damping energy dissipation in real structure remains unclear. Limited research has been conducted in this field. Wyatt [7] and Davenport [8] proposed Stiction and Stick-Slip theories, respectively, to explain the damping energy dissipation mechanism, which depicted a close relationship between the deformation of structural members and the damping energy dissipation. Based on these theories, Spence and Kareem [9] proposed a joint-probability amplitude-dependent damping model, which considered the viscous damping in structural materials and the Coulomb friction damping between components for the low-amplitude motion. (2) The tested structural damping ratios showed high dispersion. The relative errors for the estimated damping ratios are more than 50 times higher than that for the estimated frequencies [10]. (3) The structural damping ratio is very sensitive to identification methods. Previous studies have proved that the reliability of the half-power bandwidth method, a widely used method in early studies, is low. Therefore, the modal analysis and system identification method have been widely adopted in recent years.

Apparently, the study of structural damping ratio is still far from comprehensive and satisfactory. This research explores deep understandings on the structural damping features of different RC structures under actual ground motion excitations. The field response data of several RC structures collected by the CESMD are analyzed. An empirical formula for the equivalent structural damping ratio of RC structures is proposed statistically for practical use, which including the three common types of RC structures (the RC frame structures, the RC shear wall structures, and the RC frame-shear wall structures).

36.2 Parameter Identification

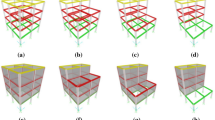
In this section, the theoretical analysis procedure of this study is introduced. Figure 36.1 showed the analytical model of a multi-story building under ground motion v b(t).

Fig. 36.1
figure 1

A shear-type building under ground motion: (a) model of the building; equilibriums of (b) the first floor, (c) the i th floor and (d) the top floor

Full size image

This model made the following assumptions:

  1. 1.

    The number of modes contributing to responses is no more than the number of sensors.

  2. 2.

    No external loading is applied to the building in addition to the ground motion.

  3. 3.

    The damping forces are linear combinations of the absolute velocity of each floor and the relative velocity between adjacent floors.

The equilibrium of each floor (Fig. 36.1b–d) yields equation (36.1a, 36.1b, 36.1c: from top to bottom):

$$ \left\{\begin{array}{l}-{m}_1{\ddot{v}}_1^{\left(\mathrm{m}\right)}-{c}_1^{\left(\mathrm{m}\right)}{\dot{v}}_1^{\left(\mathrm{m}\right)}+{k}_1\left[{v}^{\left(\mathrm{b}\right)}-{v}_1^{\left(\mathrm{m}\right)}\right]+{c}_1^{\left(\mathrm{s}\right)}\left[{\dot{v}}^{\left(\mathrm{b}\right)}-{\dot{v}}_1^{\left(\mathrm{m}\right)}\right]+{k}_2\left[{v}_2^{\left(\mathrm{m}\right)}-{v}_1^{\left(\mathrm{m}\right)}\right]+{c}_2^{\left(\mathrm{s}\right)}\left[{\dot{v}}_2^{\left(\mathrm{m}\right)}-{\dot{v}}_1^{\left(\mathrm{m}\right)}\right]=0\kern0.5em \\[4pt] {}-{m}_j{\ddot{v}}_j^{\left(\mathrm{m}\right)}-{c}_j^{\left(\mathrm{m}\right)}{\dot{v}}_j^{\left(\mathrm{m}\right)}+{k}_j\left[{v}_{j-1}^{\left(\mathrm{m}\right)}-{v}_j^{\left(\mathrm{m}\right)}\right]+{c}_j^{\left(\mathrm{s}\right)}\left[{\dot{v}}_{j-1}^{\left(\mathrm{m}\right)}-{\dot{v}}_j^{\left(\mathrm{m}\right)}\right]+{k}_{j+1}\left[{v}_{j+1}^{\left(\mathrm{m}\right)}-{v}_j^{\left(\mathrm{m}\right)}\right]+{c}_{j+1}^{\left(\mathrm{s}\right)}\left[{\dot{v}}_{j+1}^{\left(\mathrm{m}\right)}-{\dot{v}}_j^{\left(\mathrm{m}\right)}\right]=0\\[4pt] {}-{m}_n{\ddot{v}}_n^{\left(\mathrm{m}\right)}-{c}_n^{\left(\mathrm{m}\right)}{\dot{v}}_n^{\left(\mathrm{m}\right)}+{k}_n\left[{v}_{n-1}^{\left(\mathrm{m}\right)}-{v}_n^{\left(\mathrm{m}\right)}\right]+{c}_n^{\left(\mathrm{s}\right)}\left[{\dot{v}}_{n-1}^{\left(\mathrm{m}\right)}-{\dot{v}}_n^{\left(\mathrm{m}\right)}\right]=0\end{array}\right. $$
(36.1)

Physical interpretations of each notation in Eq. (36.1) are described in Fig. 36.1b–d. Equation (36.1) represents the motion of the building floors. The unique solution of Eq. (36.1) implies that the equation has an inhomogeneous form. Dividing Eq. (36.1a) by m 1 and moving \( {\ddot{v}}_1^{\left(\mathrm{m}\right)} \) to the right-hand side of the equation yields:

$$ -\frac{c_1^{\left(\mathrm{m}\right)}}{m_1}{\dot{v}}_1^{\left(\mathrm{m}\right)}+\frac{k_1}{m_1}\left[{v}^{\left(\mathrm{b}\right)}-{v}_1^{\left(\mathrm{m}\right)}\right]+\frac{c_1^{\left(\mathrm{s}\right)}}{m_1}\left[{\dot{v}}^{\left(\mathrm{b}\right)}-{\dot{v}}_1^{\left(\mathrm{m}\right)}\right]+\frac{k_2}{m_1}\left[{v}_2^{\left(\mathrm{m}\right)}-{v}_1^{\left(\mathrm{m}\right)}\right]+\frac{c_2^{\left(\mathrm{s}\right)}}{m_1}\left[{\dot{v}}_2^{\left(\mathrm{m}\right)}-{\dot{v}}_1^{\left(\mathrm{m}\right)}\right]={\ddot{v}}_1^{\left(\mathrm{m}\right)} $$
(36.2)

The unknown coefficients in Eq. (36.2) can be calculated by the Least Square Method as:

$$ {\overline{\mathbf{C}}}^{(1)}={\left\{{\overline{c}}_1^{\left(\mathrm{m}\right)}/{m}_1\kern0.5em {\overline{k}}_1/{m}_1\kern0.5em {\overline{c}}_1^{\left(\mathrm{s}\right)}/{m}_1\kern0.5em {\overline{k}}_2/{m}_1\kern0.5em {\overline{c}}_2^{\left(\mathrm{s}\right)}/{m}_1\right\}}^{\mathrm{T}} $$
(36.3)

Dividing Eq. (36.1b) by m 1 on both sides yields its inhomogeneous form, Eq. (36.4), for j = 2, 3, ···, n−1:

$$ -\frac{m_j}{m_1}{\ddot{v}}_j^{\left(\mathrm{m}\right)}-\frac{v_j^{\left(\mathrm{m}\right)}}{m_1}{\dot{v}}_j^{\left(\mathrm{m}\right)}+\frac{k_{j+1}}{m_1}\left[{v}_{j+1}^{\left(\mathrm{m}\right)}-{v}_j^{\left(\mathrm{m}\right)}\right]+\frac{c_{j+1}^{\left(\mathrm{s}\right)}}{m_1}\left[{\dot{v}}_{j+1}^{\left(\mathrm{m}\right)}-{\dot{v}}_j^{\left(\mathrm{m}\right)}\right]=-\frac{k_j}{m_1}\left[{v}_{j-1}^{\left(\mathrm{m}\right)}-{v}_j^{\left(\mathrm{m}\right)}\right]-\frac{c_j^{\left(\mathrm{s}\right)}}{m_1}\left[{\dot{v}}_{j-1}^{\left(\mathrm{m}\right)}-{\dot{v}}_j^{\left(\mathrm{m}\right)}\right] $$
(36.4)

By substituting the calculated values of parameters \( {\overline{k}}_2/{m}_1 \) and \( {\overline{c}}_2^{\left(\mathrm{s}\right)}/{m}_1 \) from Eq. (36.2) into the right-hand side of Eq. (36.4) for j = 2, the remaining parameters in Eq. (36.4) can be calculated iteratively until j = n − 1. For the jth floor, the unknown coefficients, by the Least Square Method, are:

$$ {\overline{\mathbf{C}}}^{(j)}={\left\{\begin{array}{cccc}-{\overline{m}}_j/{m}_1& -{\overline{c}}_j^{\left(\mathrm{m}\right)}/{m}_1& {\overline{k}}_{j+1}/{m}_1& {\overline{c}}_{j+1}^{\left(\mathrm{s}\right)}/{m}_1\end{array}\right\}}^{\mathrm{T}} $$
(36.5)

For the top floor (j = n), dividing both sides of Eq. (36.1c) by m 1 yields:

$$ -\frac{m_n}{m_1}{\ddot{v}}_n^{\left(\mathrm{m}\right)}-\frac{v_n^{\left(\mathrm{m}\right)}}{m_1}{\dot{v}}_n^{\left(\mathrm{m}\right)}==-\frac{k_n}{m_1}\left[{v}_{j-1}^{\left(\mathrm{m}\right)}-{v}_j^{\left(\mathrm{m}\right)}\right]-\frac{c_n^{\left(\mathrm{s}\right)}}{m_1}\left[{\dot{v}}_{n-1}^{\left(\mathrm{m}\right)}-{\dot{v}}_n^{\left(\mathrm{m}\right)}\right] $$
(36.6)

The parameters \( {\overline{k}}_n/{m}_1 \) and \( {\overline{c}}_n^{\left(\mathrm{s}\right)}/{m}_1 \) can be calculated by substituting Eq. (36.4) for j = n − 1 into the right-hand side of Eq. (36.6). The unknown coefficients in Eq. (36.6), by the Least Square Method, are:

$$ {\overline{\mathbf{C}}}^{(n)}={\left\{\begin{array}{cc}-{\overline{m}}_n/{m}_1& -{\overline{c}}_n^{\left(\mathrm{m}\right)}/{m}_1\end{array}\right\}}^{\mathrm{T}} $$
(36.7)

Using Eq. (36.3), Eq. (36.5) and Eq. (36.7), all the unknown physical parameters of the building model in Fig. 36.1 can be obtained. Then, the normalized mass matrix M, damping matrix C, and stiffness matrix K of the model can be reconstructed as:

$$ \overline{\mathbf{M}}=m_1\mathbf{M} = m_1\left[\begin{array}{cccc}{m}_1&\ &\ &\ \\ {}\ & {\overline{m}}_2&\ &\ \\ {}\ &\ & \ddots &\ \\ {}\ &\ &\ & {\overline{m}}_n\end{array}\right] $$
(36.8)
$$ \overline{\mathbf{C}}=m_1\mathbf{C}=m_1\left[\begin{array}{ccccc}{\overline{c}}_1^{\left(\mathrm{s}\right)}+{\overline{c}}_2^{\left(\mathrm{s}\right)}& -{\overline{c}}_2^{\left(\mathrm{s}\right)}& 0& \cdots & 0\\ {}-{\overline{c}}_2^{\left(\mathrm{s}\right)}& {\overline{c}}_2^{\left(\mathrm{s}\right)}+{\overline{c}}_3^{\left(\mathrm{s}\right)}& -{\overline{c}}_3^{\left(\mathrm{s}\right)}&\ & \vdots \\ {}0& \ddots & \ddots & \ddots & 0\ \\ {}\vdots &\ & -{\overline{c}}_{n-1}^{\left(\mathrm{s}\right)}& {\overline{c}}_{n-1}^{\left(\mathrm{s}\right)}+{\overline{c}}_n^{\left(\mathrm{s}\right)}& -{\overline{c}}_n^{\left(\mathrm{s}\right)}\\ {}0& \cdots & 0& -{\overline{c}}_n^{\left(\mathrm{s}\right)}& {\overline{c}}_n^{\left(\mathrm{s}\right)}\end{array}\right]+m_1\left[\begin{array}{cccc}{\overline{c}}_1^{\left(\mathrm{m}\right)}&\ &\ &\ \\ {}\ & {\overline{c}}_2^{\left(\mathrm{m}\right)}&\ &\ \\ {}\ &\ & \ddots &\ \\ {}\ &\ &\ & {\overline{c}}_n^{\left(\mathrm{m}\right)}\end{array}\right] $$
(36.9)
$$ \overline{\mathbf{K}}=m_1\mathbf{K}=m_1\left[\begin{array}{ccccc}{k}_1+{k}_2& -{k}_2& 0& \cdots & 0\\ {}-{k}_2& {k}_2+{k}_3& -{k}_3&\ & \vdots \\ {}0& \ddots & \ddots & \ddots & 0\ \\ {}\vdots &\ & -{k}_{n-1}& {k}_{n-1}+{k}_n& -{k}_{n-1}\\ {}0& \cdots & 0& -{k}_{n-1}& {k}_n\end{array}\right] $$
(36.10)

The free vibration of the building model can then be expressed using these reconstructed matrices as Eq. (36.11):

$$ \vspace*{-3pt}\mathbf{M}\ddot{\mathbf{X}}+\mathbf{C}\dot{\mathbf{X}}+\mathbf{KX}=0\vspace*{-3pt} $$
(36.11)

Usually, the reconstructed damping matrix is not proportional, i.e. C ≠ αM + βK. In order to solve for the modal parameters, a state-space form of Eq. (36.11) is constructed as:

$$ \mathbf{P}\dot{\mathbf{U}}+\mathbf{QU}=0 $$
(36.12)

where \( \mathbf{P}=\left[\begin{array}{cc}\mathbf{C}& \mathbf{M}\\ {}\mathbf{M}& 0\end{array}\right]\in {\mathrm{\mathbb{R}}}^{2n\times 2n} \), \( \mathbf{Q}=\left[\begin{array}{cc}\mathbf{K}& 0\\ {}0& -\mathbf{M}\end{array}\right]\in {\mathrm{\mathbb{R}}}^{2n\times 2n} \), \( \mathbf{U}=\left[\begin{array}{c}\mathbf{X}\\ {}\dot{\mathbf{X}}\end{array}\right]\in {\mathrm{\mathbb{R}}}^{2n\times 1} \)

Assuming that the solution of Eq. (36.12) is in the form of U = λΦ, then Eq. (36.11) is written as:

$$ \vspace*{-3pt}\mathbf{P}\boldsymbol{\Phi } =-\lambda \mathbf{Q}\boldsymbol{\Phi}\vspace*{-3pt} $$
(36.13)

The eigenvalue of Eq. (36.13) can be solved as:

$$ {\lambda}_j=-{\xi}_j{\omega}_j\pm i{\omega}_j\sqrt{1-{\xi}_j^2},\kern0.5em \left(j=1,2,\cdots, n\right) $$

where ω j is the undamped circular frequency of the j th mode, and the structural damping ratio can be calculated as:

$$ {\overline{\xi}}_j=\frac{\left|\operatorname{Re}\left({\lambda}_j\right)\right|}{\left|{\lambda}_j\right|} $$
(36.14)

The eigenvector of Eq. (36.13) is:

$$ {\boldsymbol{\Phi}}_j={\left\{\begin{array}{cc}{\lambda}_j{\boldsymbol{\upvarphi}}_j& {\boldsymbol{\upvarphi}}_j\end{array}\right\}}^{\mathrm{T}}\in {\mathrm{\mathbb{C}}}^{2n\times 1} $$
(36.15)

where φ j ∈ ℂn × 1 represents the j th complex mode.

36.3 Case Example

In this section, a typical case example is illustrated for the modal analysis method introduced in Sect. 36.2. This case example analyzed a 10-story shear wall structure (CSMIP station No. 24385) as shown in Fig. 36.2. Precast concrete shear walls are the main transverse resistance system of the structure. The dynamic responses of the building to earthquakes are measured by accelerometers. The tag numbers and locations of these accelerometers are shown in Fig. 36.2. Earthquake records for 4.4 Mw Encino Earthquake, on 17th March 2014 measured by accelerometers No.10, No.11, No.12, and No.16 were selected for this study. No.16 accelerometer measured the excitation signal (Fig. 36.3a) and the other three measured the responses of the building (Fig. 36.3b–d).

Fig. 36.2
figure 2

Location of the accelerometers [11]

Full size image
Fig. 36.3
figure 3

The measured acceleration responses: (a) the first floor; (b) the fourth floor; (c) the eighth floor; (d) the top floor

Full size image

By integrating the measured acceleration responses in a frequency domain, velocity and displacement responses of the building were obtained as shown in Figs. 36.4 and 36.5, respectively. During this integrating process, the components of the acceleration responses below 0.16 Hz frequency, which is much lower than the natural frequency of the building, were filtered out in order to eliminate trend effects.

Fig. 36.4
figure 4

The velocity responses obtained by the frequency-domain integral: (a) the first floor; (b) the fourth floor; (c) the eighth floor; (d) the top floor

Full size image
Fig. 36.5
figure 5

The displacement responses obtained by the frequency-domain integral: (a) the first floor; (b) the fourth floor; (c) the eighth floor; (d) the top floor

Full size image

By applying these acceleration, velocity, displacement responses to the analysis procedure described in Sect. 36.2, the modal parameters of the building (frequency, modes, damping) were identified. While analyzing, each time-domain signal was divided into several sub-signals based on different time windows to study the time-varying effect on the damping behavior with different PGAs (Peak Ground Accelerations). Special attention needs to be paid on two issues when defining the length of the time window function: (1) the length of the time window function should be as short as possible in order to reveal the time-varying effect with a high resolution, (2) the length of the time window should yield t d ≥ 20/f 1 (where f 1 is the fundamental frequency of the structure) in order to ensure that the characteristics of the fundamental mode can be captured. Therefore, the length of the time window as t d = 10 s was used, which includes approximately 2000 sampling points. Table 36.1 and Fig. 36.6 showed the analysis results of natural frequencies, damping ratios, and mode shapes of the building for one example sub-signal (20~30 s) with PGA of 0.512 m/s2.

Table 36.1 The mode frequencies and damping ratios
Full size table
Fig. 36.6
figure 6

The identified mode shapes: (a) the first mode; (b) the second mode; (c) the third mode

Full size image

Each sub-signal can result in a pair of damping ratio and PGA data. With a large group of response records on a variety of buildings, the relationship between the structural damping ratio and PGA can be revealed statistically. The procedure is introduced as follows.

36.4 Statistical Investigation of Damping Ratio

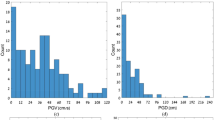
Based on analyses of a variety of buildings under various earthquakes, an empirical relationship between the first mode structural damping ratio and the PGA for RC structures was revealed statistically. In order to obtain a reasonable statistic relationship, a large database of dynamic response records on different buildings under different earthquakes is required. Therefore, this study selected 258 dynamic response records on 45 RC structures from the CESMD data center. Among the 258 records, 162 are on shear-wall structures (25), 30 are on moment-frame structures (7), and 66 are on moment-frame plus shear-wall structures (14). Figure 36.7 showed the height histogram of the selected buildings. All these selected buildings belong to low to medium height buildings. Because of this, the variation trend of the structural damping ratio corresponding to different building heights cannot be obtained in this study. Therefore, this study focused on the relationship between the structural damping ratio and the PGA for RC buildings with relatively similar height.

Fig. 36.7
figure 7

Height distribution histogram for of RC buildings

Full size image

Figure 36.8 showed the identified results of the structural damping ratio vs. PGA. The blue, red, and black dots in the figure represent the shear wall structures, the frame-shear wall structures, and the frame structures, respectively. As shown, the dots for PGA less than 0.01g are randomly distributed. The possible reasons are: (1) the building dynamic responses for these dots are weak and significantly polluted by noises before earthquake arrives, and (2) the accelerometers used in this study are designed for measuring high-amplitude responses which have wide measurement range but coarse resolution. These accelerometers are unable to capture weak dynamic responses precisely and result in unacceptable errors in the calculated damping ratios. Therefore, the data dots in Fig. 36.8 with PGA less than 0.0015 m/s2 were filtered out in this study. Besides, because this paper is just a starting point for this damping ratio study, statistical analyses based on different structure types are not demonstrated here. Only the relationship between the structural damping ratio and PGA for generalized RC structures are reported in this paper.

Fig. 36.8
figure 8

The estimated damping ratios in terms of different PGA values

Full size image

To obtain a regression curve for the damping ratio vs. PGA relationship, this study selected the exponential function, based on existing literature and constant experiments, which can be written as:

$$ \upxi ={c}_1-{c}_2{e}^{\frac{- PGA}{c_3}} $$
(36.16)

The fitting error of the regression curve was defined as square root sum square of all errors. By minimizing the fitting error, the parameters c 1, c 2, c 3 in Eq. (36.16) were calculated as 6.05, 2.65, 0.023, respectively. The green curve in Fig. 36.8 represents the regression results. Based on Fig. 36.8, it can be concluded that the damping ratio of RC structures increases with respect to PGA increases when the PGA value is small, and it yields a constant value (6.05%) when the PGA value reaches approximately 0.1 g. This result is very different from the fixed values recommended in current RC building design provisions.

36.5 Conclusion

This research explored deeper understandings on the structural damping features of different RC structures under actual ground motion excitations. A time-domain Least Square Method was developed and applied for estimating the physical parameters of RC structures, which allows identifying the structure’s modal parameters by reconstructing the normalized stiffness and mass matrices. The developed method requires few sampling points, which allows studying the time-vary effect of damping behavior by shortening the window function.

As a case study, this research analyzed an extensive large number of real building dynamic response records. A reliable statistical relationship between the equivalent damping ratio and the peak ground motions (PGA) was validated. An empirical statistic curve describing the structural damping ratio of RC buildings with respect to PGA was proposed based on nonlinear regression analyses.

The proposed empirical results can be applied not only in a post-earthquake assessment of building structures, but also in a dynamic analysis for structural seismic design. However, the study of structural damping behavior is far from comprehensive and satisfactory. The improvement of damping models and the refinement of statistical analyses will be the future focus.