Combustion Stability Analysis

Abstract

Cyclic combustion stability is an important factor that impacts the overall engine performance. Large cycle-to-cycle variations undermine combustion stability, and it brings serious problems such as engine roughness, efficiency loss, higher emissions, compromised power, etc. Thus, investigation of combustion stability is necessary during engine development and calibration process to achieve desired stable operating condition through appropriate control strategy. The manifestation and origin of combustion variability are discussed in this chapter along with the characterization of combustion variability in terms of partial burn and misfire regimes. To analyze the engine combustion stability, traditional statistical measures of cyclic variability such as coefficient of variation (COV), frequency distribution, and histograms, lowest normalized value, autocorrelation, and cross-correlation are discussed. The conventional statistical analysis assumes that each measurement is an independent, random event. Typically, the coefficient of variation in mean effective pressure is used as measure of combustion stability. Chaotic time series analysis methods such as Poincare sectioning, mutual information, data symbolization, symbol sequence histograms, time irreversibility, modified Shannon entropy, and return maps are discussed for analyzing cycle-resolved combustion data series obtained from different engine operating conditions and combustion modes. Studies demonstrated that cyclic combustion variability has at least some nonlinear deterministic structure depending on engine operating conditions and combustion modes. Nonlinear dynamics methods such as recurrence plot and its quantification, multifractal analysis, 0–1 test, and wavelets are described for engine combustion stability analysis. It is demonstrated that the engine combustion process has different levels of complexity depending on the engine operating conditions as well as fuel.

8.1 Combustion Stability in Reciprocating Engines

Emission legislation and automotive market demands have been a constant driving force for significant increases in vehicle fuel economy to reduce petroleum use and CO₂ emissions. Achieving this goal while also continuing to reduce emissions of traditional pollutants is a significant challenge. Increasing fuel conversion efficiency while maintaining emissions performance is a necessary component of any solution. An approach which has gained widespread adoption in the market is the combination of engine downsizing with gasoline direct injection (GDI) and turbocharging utilized to maintain high torque output [1]. Another potential approach for future powertrain is advanced low-temperature combustion (LTC) modes that meet the requirement of higher engine efficiency and lower emissions [2]. Stability and combustion control are potential roadblocks to the most efficient implementation of many advanced combustion concepts due to higher cyclic combustion variability.

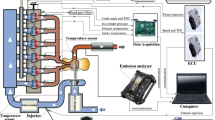
The cylinder pressure measurement for consecutive engine cycles depicts significant variations on a cycle-to-cycle basis (Fig. 8.1). Figure 8.1a shows the variation in cylinder pressure with increasing amount of EGR (higher throttle opening angle) in a homogeneous charge compression ignition (HCCI) engine [3]. In HCCI engine, autoignition of well-mixed charge occurs in the combustion chamber. Increasing exhaust gas recirculation (EGR) changes (increases) the specific heat of charge, which lowers down the combustion temperature. Thus, autoignition reaction rate decreases in the cylinder, and combustion phasing is retarded. The combustion variability increases with retarded combustion phasing [2]. Increasing the EGR reaches to a point where cycle-to-cycle variations in the combustion process are very high, and engine operation becomes rough and unstable and unburned hydrocarbons increase rapidly. The engine operating condition at which this phenomenon occurs defines the stable operating limit of the engine. Figure 8.1a depicts that some of the engine cycles misfire or partially burn for highest EGR operating condition. Similarly, variations in the cylinder pressure can be observed in spark ignition (SI) engines (Fig. 8.1b). Significant variations in the cylinder processes (flow and ignition characteristics) lead to the significant variation in the combustion process because the pressure development is uniquely defined with the combustion process. The cycle-to-cycle variations in the combustion process are the result of cyclic variations of mixture motion in the combustion chamber at the time of spark, the variations in air-fuel ratio in each cycle (due to variations in the amounts of air or fuel or both), and cyclic variations in the mixing of fresh mixture and residual gases in the combustion chamber particularly in the vicinity of spark plug [5].

Fig. 8.1

(a) Variations in the cylinder pressure curve of 64 consecutive cycles for different EGR operation (varied by a throttle angle; Θ_D) in an HCCI engine [3] and (b) cylinder pressure for 100 consecutive engine cycle in an SI engine [4]

Analysis of cycle-to-cycle variations in the SI engine combustion is more important because engine operation is limited by extreme cyclic variations. Additionally, the optimum spark timing is set for the average cycle. Thus, combustion cycle faster than average cycle has effectively over-advanced spark timing, and cycles slower than average cycles have retarded spark timings. The advanced or retarded spark timings lead to a loss of power and efficiency [5]. Due to the spark timing set for the average cycle, the faster cycles are more likely to have knocking tendency, and the slower cycles are likely to be partial burn or misfire cycles. The slowest cycle actually defines the lean operating limit of the engine and also the maximum EGR tolerance of the engine.

Figure 8.2 illustrates the stable and unstable engine operating region and the edge of combustion stability. The stable combustion is characterized by acceptable cyclic variations in the combustion process. During engine operation in the lean and highly diluted mixture (with air or EGR) or at lower loads and engine speeds (such as under idle conditions), the cyclic variation increases and engine operation shifts to transition regime (partial burn), and in extreme conditions misfire can occur (Fig. 8.2). In the transition period, the cyclic variations in the combustion process (COV_IMEP) are very high, and the engine efficiency decreases rapidly. Unintended excursions to the unstable operating region may result in misfires and very strong “rebound” events which could damage the engine and/or catalyst system [7]. Thus, to avoid unintended excursions, practically engines need to operate well away from the edge of stability. Cyclic combustion variations are governed by stochastic (in-cylinder variations) and deterministic (cycle-to-cycle coupling) processes, and deterministic mechanisms act as a nonlinear amplifier to stochastic variations. Cyclic combustion variation can also amplify the cylinder-to-cylinder imbalances [7]. Thus, improved understanding of instability mechanism is required for better control of the engine.

Fig. 8.2

Stable and unstable engine operating regions (adapted from [6, 7])

Combustion stability is one of the main parameters on which researchers are keenly interested in improving the drivability, fuel economy, and emissions. Combustion stability (cyclic variations) can be quantified in terms of standard deviation of indicated mean effective pressure (SD_IMEP) , the coefficient of variation of IMEP (COV_IMEP) , lowest normalized value (LNV), and standard deviation and coefficient of variation of speed [8]. Figure 8.3 illustrates the cycle-to-cycle combustion variations in HCCI engine during stable and unstable operations.

Fig. 8.3

Illustration of (a) stable and (b) unstable engine operation in HCCI combustion [3]

Figure 8.3a shows that the stable operation of HCCI engine has small cyclic combustion variation (COV_IMEP = 3.56%) at average combustion phasing (CA₅₀) of 13.4 °CA after TDC. In the stable operating condition, cyclic variations of the mass and temperature of each gas content at intake valve closing (IVC) (m_air, m_fuel, m_EEGR, m_REGR, T_air, T_fuel, T_EEGR, T_REGR) and the T_IVC are also small. The EEGR denotes external exhaust gas recirculation, and REGR denotes rebreathed exhaust gas recirculation. Cyclic combustion variations for the stable operation are equally distributed to values higher and lower than the average (Fig. 8.3a). In contrast, a much larger spread around the average value in m_air, m_EEGR, m_REGR, T_REGR, and the resulting T_IVC is exhibited by several cycles during unstable engine operation (Fig. 8.3b). The unstable engine operation has larger variations in combustion as depicted by IMEP and CA₅₀ in Fig. 8.3b. Some of the cycles partially burn in the unstable engine operating region as illustrated in Fig. 8.2. The partial burn cycles can be observed in unstable engine operation in Fig. 8.3b. The partial burn and misfire cycles are discussed in Sect. 8.2. The manifestation of combustion variability and sources of combustion variability are discussed in the next subsections.

8.1.1 Manifestation of Combustion Variability

Cycle-to-cycle combustion variability phenomenon is significant during engine operation typically at low load and speed conditions (particularly idle conditions), high EGR operation, and highly diluted mixture. The two consecutive engine combustion cycles are not exactly same similar to human fingerprints. There exist cycle-to-cycle and cylinder-to-cylinder variations in developed torque along with fluctuations in the engine speed.

The signs of combustion variability in automotive engines are summarized as engine roughness, compromised torque/power, higher engine emissions, loss in engine efficiency, lower fuel economy, lower knock resistance, compromised dilution tolerance, compromised spark/injection timing (injection point diesel), and cyclic variations in torque and engine speed [9]. The significant cyclic variations in the developed engine torque directly affect the drivability of the vehicle. Therefore, minimization of cyclic combustion variations is essential for stable engine operation along with optimal engine performance in terms of emissions and fuel economy.

Combustion variability influences the engine performance at all operating conditions. Idle instability typically is governed by variations in fuel flow and exhaust residuals. Part-load combustion variability is driven by fuel flow variations and EGR. Wide open throttle (WOT) combustion instability is typically dictated by variations in airflow [9]. The summarized general negative impacts of the cycle-to-cycle variations in the combustion process on engine performance are presented in Fig. 8.4. The cyclic variations in the combustion duration result in a condition where the combustion process in some of the cycles is faster while in others is slower than average cycle. The combustion variations are associated with losses in terms of power and thermodynamic efficiency and fluctuations in the amount of work done. The faster combustion cycles (than optimized) will have higher peak pressure and the tendency of knocking. Thus, these cycles impose the lower limit for the allowed fuel octane number and the upper limit for the engine compression ratio, which compromises the thermodynamic efficiency. In the slow combustion cycles (than optimized), the combustion may not be completed before exhaust valve opening (EVO) timing, which leads to a high unburned hydrocarbon (HC) emissions as well as high fuel consumption. This effect is significantly observed in with diluted mixtures (either with EGR, with lean mixtures, or under throttled conditions) [11]. The cyclic combustion variations also lead to the engine speed and torque fluctuations which affect the overall engine performance characteristics, such as the engine brake power and its specific fuel consumption. The speed and torque fluctuations also result in poor drivability of the vehicle for some kinds of transmissions, such as lockup torque converters and manual transmissions [12]. The cyclic variations also partially contribute to engine noise due to variations in cylinder pressure [10,11,12]. Thus, reduction in cyclic variations in combustion may also help in mitigating the engine noise. Periodic oscillations in engine speed of a port fuel-injected (PFI) SI engine at idle conditions are also found to be affected by combustion perturbations [10, 11]. Considering the negative impacts of cyclic combustion variations, it is important to determine the sources of variability and quantify (characterize) the combustion variation. The origin of combustion variability in reciprocating engines is discussed in the next subsection.

Fig. 8.4

Effect of cyclic variations in the combustion process on engine performance (adapted from [10])

8.1.2 Sources of Cyclic Combustion Variability

The cycle-to-cycle combustion variations are evident from the beginning of the combustion process (Fig. 8.1). Variations in burning rate are also apparent throughout the combustion process. Combustion variability may be caused by various factors including cyclic variations in gas motion in the cylinder during combustion; variations in the amount of fuel, air, and residual gases inducted in every engine cycle; gas charge motion and composition at the location and time of spark; mixing homogeneity; fuel preparation (targeting, droplet size, swirl, cone angle); disproportionate dilution (by EGR or air); long combustion duration because of poor combustion system hardware design; and low ignition energy or a small spark plug gap [9]. Origins of cyclic combustion variations can be divided into two groups: (1) prior-cycle effects (residual gas, etc., results of misfire and partial burn, wall temperature) and (2) same-cycle effects (in-cylinder flow, etc., results of random variations) [13]. Both prior-cycle and same-cycle effects are always present in reciprocating engines. However, one effect may dominate depending on engine operating conditions. The relative contribution of each process to overall cyclic combustion variability is not known and may be different for different engines depending on fuel injection system, engine geometry, and operating conditions. The specific reasons for cyclic combustion variations depend on the charge preparation process and combustion mode. The sources of cyclic variation in spark ignition and compression ignition engines are discussed in the next two subsections.

8.1.2.1 Causes of Cyclic Combustion Variations in SI Engines

Cyclic variations in the combustion process are generated due to the variations in mixture motion within the combustion chamber; variations in the amounts of air and fuel fed to the cylinder; variations in the mixing of fresh mixture and residual gases, particularly in the vicinity of the spark plug, which determine mixing, stratification, convection of spark kernel away from the electrodes, and heat loss from the kernel to the electrodes; etc. [13]. It is proposed to divide all the sources of cyclic combustion variation in SI engine into the four categories, namely, (1) mixture composition, (2) spark and spark plug, (3) in-cylinder mixture motion, and (4) engine operating factors/conditions [11, 12, 14]. Figure 8.5 presents the summary of all the major factors influencing the cycle-to-cycle variations in spark ignition engine. These factors affect the different stages of combustion depending on their characteristics. In spark ignition engine, the combustion process can be divided into four main stages, namely, (1) sparking and flame initiation, (2) initial flame kernel development, (3) turbulent flame propagation (main combustion stage), and (4) flame termination [11]. Each of these stages of SI engine combustion may be influenced by a different set of dominating factors, while each preceding stage affects the subsequent ones. The last stage (flame termination) does not affect noticeably the cyclic combustion variations.

Fig. 8.5

Summary of factors influencing the cyclic combustion variation in spark ignition engine (adapted from [11, 12, 14])

There are several known factor responsible for creating cyclic combustion variation in SI engine including turbulent nature of the in-cylinder flow, mixture spatial inhomogeneity, fluctuations in the mean flow vector at the spark gap, etc. (Fig. 8.5). Other factors, such as spark plug orientation, electrode shape, overall equivalence ratio, etc., though do not generate cyclic combustion variation but influence their intensity [10]. The complexity of the phenomenon of cyclic combustion variations is illustrated in Fig. 8.6. Solid lines in the figure represent the ways of the influence of the factors which contribute to cyclic variation generation, and dashed lines show the influence of the factors which only affect the extent of cyclic variations. Figure 8.6 shows how several factors affect the cyclic variations in the SI engine combustion through different mechanism and stages of the combustion development. For example, mixture spatial inhomogeneity causes cyclic variations in “first eddy burnt” composition and thereby affects the initial flame kernel development stage. Besides that, some of the factors are strongly interrelated [10]. The other observation is one group of factors such as overall equivalence ratio, spark plug location, or fuel type do not cause cyclic combustion variation themselves but affect the extent of cyclic variation generated by other factors. Thus, understanding of the contribution of a particular factor in cyclic variation and its mechanism of influence at a particular stage of combustion is important.

Fig. 8.6

Mechanisms of the influence of the various factors involved in cyclic combustion variations in SI engine performance (adapted from [10])

Mixture composition-related factors include the type of fuel, the overall equivalence ratio (Φ) of the mixture and its cyclic variations, the overall fraction of diluents and its cyclic variation, and the mixture equivalence ratio and diluent spatial inhomogeneity. The fuel type affects the cyclic combustion variation through laminar burning velocity, which significantly affects the initial flame kernel development [11]. Two major characteristics of the fuel type affecting the cyclic combustion variations are (1) magnitude of the maximum flame speed and (2) the equivalence ratio at which it occurs [12]. It was found that fuel with very high laminar burning velocity show closely repeated cycles (less cyclic variations) and the flame remained centered at the spark gap [15]. Fuels having higher laminar flame velocity leads to the higher burning rate, which results in relatively lower the cyclic combustion variations. One more parameter by which one fuel can differ from another is its heating value. This parameter can influence the burning rate through the expansion rate of the flame and adiabatic flame temperature [11]. The overall equivalence ratio of the mixture and its cyclic variations affect the combustion variations through the laminar burning speed, which is highest in stoichiometric or slightly enriched mixtures. Thus, any deviation from the engine operation at a stoichiometric ratio leads to a decrease in the laminar burning velocity with a consequent increase in the ignition delay time and the level of cyclic combustion variations [11, 12]. The overall fraction of diluents and its cyclic variations reduces charge flammability and the laminar burning rate. The amount of diluents can be varied by different methods including throttle opening variation, skipping ignition in cycles, variation of the extent of EGR, and the introduction of inert additives [12]. It is observed that higher dilution reduces the burning rate which leads to higher cyclic combustion variations. Mixture and diluent spatial inhomogeneity are created due to imperfect mixing of charge components which includes air, fuel, and residual gases (internal or external EGR). The spatial inhomogeneity in the charge leads to the cyclic variations in local equivalence ratio and the diluent quantity in the vicinity of the spark electrode gap which consequently leads to cyclic variations in the initial flame kernel development stage [11, 14].

Design of spark plug and the spark discharge characteristics are the dominant parameters in the initial flame kernel development. The evolution of cylinder pressure in the combustion chamber is strongly related with the initial flame kernel development stage, and thus, spark plug design and its characteristics strongly affect the engine performance [16, 17]. Spark and spark plug-related factors include spark timing, spark discharge characteristics, spark plug design (electrode gap and shape), and spark plug number and location. All the spark-related parameters affect the early stage of flame development. In the later stage of combustion process, both the location of the spark plug and their number play a significant role [11]. Minimum cyclic variations in combustion and pressure development generally take place at maximum brake torque (MBT) spark timing. The dependence of cyclic variations on the spark timing is affected by overall mixture strength and location of spark plug. The more prominent cyclic variations are observed for leaner mixtures or the large spark plug offset from the center of the combustion chamber. The spark discharge process also has an important influence on flame initiation. The initial flame development plays an important role in cyclic variations. The quicker (fast) the flame kernel reaches a certain critical size, the lower cyclic variations are observed. Enhanced ignition increases the early flame development rates and thus results in lower cyclic variations. The ignition system should be redesigned so that most of the electrical energy is dissipated in the breakdown phase. This would ensure that energy is transferred to the gas most efficiently and produce sharp temperature gradients and the right plasma geometry to enhance the initial flame speed [18]. Spark duration and spark energy are two characteristics that are typically used to characterize spark discharge. Generally, these two are strongly coupled with each other, and varying spark duration causes changes in the total spark energy. It is suggested that one of the methods of reducing cyclic variations is by increasing the energy of the conventional spark [17]. This implies that the spark energy has an effect on cyclic combustion variations. The design of spark plug can affect the cyclic combustion variations through several mechanisms. The number of spark plug electrode and their shape govern the flame contact area fraction, which controls the heat losses into the body. The electrode shape and number also influence the flow field characteristics within the spark gap [19]. More favorable kernel heat balance is expected from thin and/or sharply pointed electrodes. However, thin/sharply pointed electrodes are subjected to relatively stronger erosion and therefore have less durability. Additionally, the surface temperature of a thin or sharply pointed electrode will be higher. This creates a danger of preignition at high engine load operations. Spark gap affects the breakdown voltage and energy. Higher voltage is required for breakdown at larger spark gap. Additionally, the spark plug gap also affects the energy loss from the flame kernel to the electrodes by heat transfer. Increasing the spark gap leads to the larger ratio between flame kernel volume and “wetted” electrode surface area. Thus, the electrode gap of spark plug affects the flame initiation and the stage of flame kernel growth. Typically, the spark gap is required to be larger than the flame quenching distance.

Mixture motion and turbulence are the causes deemed most responsible for the cyclic variations in combustion and the subsequent pressure development. In-cylinder measurements of flow are difficult to obtain so that the role of turbulence and mixture motion in cyclic behavior of combustion has been largely inferred from the nature of the physical changes made to the engine. This evidence, although largely circumstantial, appears strong enough to single flow variations as being instrumental in determining the character of the combustion from cycle-to-cycle. Turbulence in the cylinder accelerates the combustion by increasing flame front area and improving heat and mass transport between the burned and unburned parts of the charge, which tend to decrease cyclic variations. On the other hand, turbulence leads to fluctuation in the magnitude and direction of the charge velocity due to random flow pattern in the spark gap vicinity which results in cyclic variations in early flame kernel development [11].

Factors related to the mixture motion are (1) mean flow velocity vector in the spark gap vicinity and its cyclic variations, (2) spark plug orientation with respect to the mean flow velocity vector, (3) turbulence intensity and scales, and (4) overall in-cylinder flow pattern. In the very early stage of sparking and flame initiation, the mean flow velocity near the spark plug lengthens the discharge channel and increases the electrical energy deposited into the flame kernel in the breakdown phase. Later, in the initial flame kernel development stage, mean flow velocity can convect flame kernel away from the electrodes which lower down the heat loss [20]. This convection toward the electrodes of a spark plug or combustion chamber walls is undesirable. The early flame kernel convection affects both ignition delay time and flame kernel radius at the particular crank position. The cyclic variation in the mean flow can lead to random convection which transports the kernel to different locations around the spark plug. The flame propagation in a particular cycle depends on the initial position of the early flame kernel center [11]. Gas dynamics conditions in the early flame kernel growth stage are influenced by local flow field around the electrodes which is governed by mean flow direction and location of the spark plug in the combustion chamber. Several types of flow pattern can be achieved in the combustion chamber of the reciprocating engine. The engine design parameters (such as the shape of the combustion chamber and induction ports, and the type and configuration of inlet valves) govern the actual flow in the cylinder. The instantaneous flow also depends on the crank angle position (piston position) and the engine operating conditions. Swirl, squish, and tumble are the three main macrostructures found in the in-cylinder flow. Early flame development was more affected than the main combustion period when swirl was present in the combustion chamber. It was found that cyclic variations reduced by 30% at part load with volumetric efficiency of 72% by swirl due to increase in burning rate [21]. Tumble flow generates turbulence in the combustion chamber more effectively than does swirl flow. Swirling flow reduces the cycle-by-cycle variability of the mean velocity in the combustion chamber, which tends to be generated by tumble motion [22].

Ambient conditions (such as intake temperature, coolant temperature, cold start, etc.) and engine operating conditions (such as injection timings, engine speed, load etc.) also significantly affect the cyclic variations. Increasing the inlet air temperature improves the evaporation of fuel droplets and compensates for the reduction of charge temperature because of the latent heat effect of fuel. It is demonstrated that cyclic variations (COV_IMEP) have optimal values in the inlet temperature range of 60–70 °C [23]. Engine operating factors such as engine speed also affect the cyclic variations as it influences the turbulence intensity. Injection characteristics such as fuel spray patterns at the pressurized conditions affect the combustion stability [24].

The physical factors leading to cyclic combustion variability are summarized in Fig. 8.7. Cycle-to-cycle combustion variability in spark ignition engines limits the use of lean mixtures, the amount of recycled exhaust the engine will tolerate, and lower idle speeds because of increased emissions and poor engine stability.

Fig. 8.7

Summary of physical factors leading to cyclic combustion variability in SI engine (adapted from [25, 26])

Causes of cyclic combustion variations can be categorized into two groups: prior-cycle effects (residual gas, etc., results of misfire and partial burn, engine thermal state, EGR) and same-cycle effects (in-cylinder flow, etc., results of random variations) [13]. Prior-cycle effects are mainly due to residual gas in the cylinder and thermal state of the engine. The residual gases from the previous cycle alter the burning rates of burning and may even cause an engine misfire. The residual gases consist of exhaust gases remained in the clearance volume of cylinder (internal) and gases returned by backflow during the valve overlap period. Additionally, external exhaust gas recirculation (EGR) through intake manifold also leads to prior-cycle effect. Mass flow analysis of gases suggests that the major portion of residual gases are contributed by the gases that remained in the clearance volume of cylinder. The gases remained in the clearance volume are dependent on valve profile, flow coefficients, and engine speed. Additionally, the gases exchanged during valve overlap are governed by the gas dynamics in the manifold [27]. The pressure fluctuations during valve overlap can result in variations in the fresh air-fuel mixture and backflow of exhaust gases. This leads to variations in residual gases in the cylinder which affect the succeeding combustion event [28]. The amount of residual gases are influenced by several factors including the pressure difference across the valves, valve characteristic, pressure, engine speed, and the gas dynamics during valve overlap [29].

The same-cycle effects leading to cyclic variations are mainly governed by variation in the flow of the air-fuel mixture as well as the quality of mixture which is also partially based on the type of fuel injection system used in the engine. The port fuel injection (PFI) as well as direct injection (DI) is typically used in commercial vehicles using spark ignition engines. The fuel-air mixture changes by the way gases flow through inlet manifold during transportation to the cylinder, particularly in PFI engines. Therefore, the charge in the cylinder can vary in different cycles, which leads to combustion variability. Physical study of the mixture preparation in PFI engines showed that fuel puddles are located on the valves, downstream in the intake port near the valve, upstream near the injector, and on the cylinder wall [30]. These puddles of fuels lead to cyclic variations in the air-fuel mixture. Fuel properties affect the puddles of fuels due to the difference in evaporation characteristics [31]. Thus, different fuels will have a different level of variability in fuel-air mixture. In PFI engines, fuel transportation process significantly depends on the timing and duration of the fuel injector pulse. In some systems, the fuel spray is targeted on the back of the intake valve, and fuel is injected in fully closed valve conditions or partially open conditions. Thus, the backflow of hot residual gas leads to the vaporization of liquid fuel off the valve and wall. The fuel can be drawn into the cylinder as a liquid drop in some cases although the engine is running under fully warm conditions [5]. Fuel transportation mechanism in the intake manifold can be understood regarding impingement regimes of fuel. The impingement regimes are divided into different categories: (1) stick, (2) spread, (3) rebound, (4) rebound with a breakup, (5) boiling-induced with breakup, (6) breakup, and (7) splash [32]. These regimes are influenced by different fuel parameters (droplet velocity, size, temperature, the angle of wall hitting, and fuel properties) and manifold wall parameters (temperature, surface roughness, and remaining fuel droplets). These effects significantly influence the air-fuel ratio before the start of combustion.

Additional factors such as turbulence intensity and scale, mean flow velocity at spark plug, air-fuel ratio, variations in spark discharge characteristics (breakdown energy, timing, type of spark plug, and spark orientation), variations in mass of charge, leakage through valves, and crevice effects also influence the cyclic combustion variation in spark ignition engine [13].

8.1.2.2 Causes of Cyclic Combustion Variations in CI Engines

Conventionally in compression ignition (CI) engines, the diesel fuel ignites spontaneously following the injection event. The combustion and fuel injection often overlap with a very short ignition delay period in conventional CI diesel engines. Therefore, diesel engines offer superior combustion stability characterized by the low cyclic combustion variations [33]. Diesel engine usually exhibits lower significant cyclic combustion variations because non-premixed combustion dominates the overall combustion process, which is mainly governed by fuel-air mixing [34]. The fuel-air mixing is governed by fuel injection system, which is the highly repeatable system. Thus, there exists only a very small amount of time where combustion is uncoupled with the injection or uncontrolled combustion that results in significantly lower cyclic variations in comparison to homogeneous spark ignition engine. Modern high-speed diesel engines are equipped with multiple pilot injections potential with an objective of reducing the main injection ignition delay. The reduction in ignition delay leads to mainly diffusion-dominated combustion in a modern diesel engine. Cyclic variations in background turbulence (swirl, etc.) are minimal, and will not affect the diesel combustion rate significantly because the intensity of background turbulence is several times lower than the injection-generated turbulence [34].

However, cyclic combustion variability can also occur in CI engine mainly due to instabilities in the fuel injection system or prolonged ignition delay. Cyclic variations in a diesel engine are observed due to variations in injection timing between cycles because of rotary fuel pump used for fuel injection [35]. Recent studies also demonstrated the cyclic combustion variations in diesel engine due to the variations in the fuel path [36, 37]. Study showed that cyclic variations in the fuel injection pressure (at a command pressure of 1000 bar) are between 1 and 9% which results in variations in the needle lift that leads to variations in fuel delivery up to 23%. The variations in the fuel delivery are correlated with the corresponding cyclic variations in the IMEP and instantaneous angular velocity of the engine [36]. Cycle-to-cycle variations demonstrate very fast dynamics. Among all the controlled inputs available in diesel engines, the injector pulse or current profile, typically defined by start of injection (SOI), fuel ratio, dwell time, etc., has the most immediate dynamic effect on the combustion process [37].

In addition to instabilities of the fuel injection system, prolonged ignition delay contributes to increase in cycle-to-cycle combustion variations. It is demonstrated that the cyclic variations in the cylinder pressure cannot be fully explained by variations in the fuel injection [38]. Prolonged ignition delay conditions created by varying intake temperature, pressure (engine load), and fuel injection timings show higher cyclic combustion variation in diesel engine [34]. Ignition characteristics of fuel also affect the cyclic variations, and lower cetane number (CN) fuels exhibit larger cyclic combustion variations. Cold start studies in diesel engines show that colder in-cylinder conditions are resulting into a longer ignition delay period that leads to larger cyclic variations [39]. Diesel cold starting is influenced by many design and operating parameters, which affect the air temperature and pressure near the end of the compression stroke. Such parameters include the ambient temperature, cranking speed, injection parameters, and fuel properties particularly cetane number and volatility. Combustion instability during the cold start of diesel engines is influenced by several factors, most important of which are the ambient temperature, injection timing, and the instantaneous engine speed during the cycle [40]. Combustion instability was found to increase with the drop in temperature. Cycle-to-cycle analysis suggested that the number of misfiring cycles increases with the drop in ambient temperature. The cause of misfiring was found to be a mismatch between the injection parameters and the instantaneous engine speed at the time of misfiring. Combustion instability can be reduced if fast injection timing controls are developed. Ideally, the injection timing should be adjusted to suit the conditions in each cylinder, which requires fast response fuel injection controls. [40]. It is found that the cycle-to-cycle stability of IMEP is generally improved by using triple- or quad-pilots over single and possible twin pilots [41]. Additionally, increasing the glow plug temperature always improves stability, even when the best fuel injection strategy is used. The number of pilot injections is more important than the total pilot quantity. Total pilot quantity has been observed to have an influence which can produce a deterioration or improvement in stability, and the direction of change may depend on the number of pilot injections [41].

In well-mixed (homogeneous) charge compression ignition (HCCI) engine, the cyclic combustion variation is typically lower than conventional spark ignition (SI) engine, but it can be high in some of the operating conditions due to no direct control on ignition timings [2]. Ignition timing in HCCI engines is sensitive to inlet air temperature, equivalence ratio, residual gases/EGR, cylinder wall temperature, compression ratio, and chemical kinetics of fuel-air mixture. The HCCI combustion in the engine cylinder is achieved using different strategies for autoignition of charge. Typically, cyclic combustion variations and cylinder-to-cylinder variations in HCCI engines depend on combustion phasing and strategies employed to control the combustion [2, 42, 43]. Several factors affect the HCCI combustion, and the level of cyclic combustion variations is governed by variations in several factors including (1) equivalence ratio, (2) inlet air temperature and pressure, (3) mixture inhomogeneity (thermal and composition stratifications), (4) amount of EGR (external or internal), (5) coolant and lubricating oil temperatures, (6) intensity of intake charge motion and bulk turbulence, (7) fuel-air mixing and charge preparation strategies, and (8) combustion completeness in the previous engine cycle [43]. Several strategies (such as inlet air preheating, variable compression ratio (VCR), exhaust recompression, exhaust reinduction, employing multi-fuel and multiple injection strategies) can be used to control/minimize the cyclic variations in HCCI engine [44].

In HCCI engine, four major contributing sources of cyclic combustion variations are identified, namely, (1) mixture composition stratification, (2) thermal stratification, (3) cycle-to-cycle variations in fuel-air ratio, and (4) cycle-to-cycle variations in diluents (residual gases and/or EGR) [45]. Spatial mixture composition inhomogeneity occurs in the cylinder due to inadequate mixing of air, fuel, and residual/recirculated burned gas from the previous cycle. Homogeneity of charge is affected by fuel injection strategy used for fuel-air mixture preparation [2]. Cyclic variations in charge composition homogeneity (stratification) lead to the cyclic combustion variations. Temperature stratification is created by heat transfer from surfaces (piston, valves, and cylinder head) having different temperatures and from the insufficient mixing of air, fuel, and residual gas [46]. The inhomogeneous heat release from the low-temperature heat release (cool flame chemistry) can also contribute to the temperature stratification in the combustion chamber [47]. Delayed combustion phasing significantly enhanced the thermal stratification in the combustion chamber because of longer time available for developing the stratification [48]. Cyclic variations in the residual gas temperature can generate the cyclic thermal stratification in the cylinder that results in cyclic combustion variations in HCCI engine [2, 49]. Cyclic variations in the mean equivalence ratio of the charge can occur in PFI engine [50], which is typically used for fuel injection in HCCI engine. Cyclic variations in equivalence ratio can also be generated by variations in gas exchange process as well as incomplete evaporation of fuel droplets. The cyclic variations in mean equivalence ratio lead to cyclic combustion variations in HCCI engine.

The HCCI combustion phasing is typically controlled by internal (trapped residuals) as well as external cooled EGR. Due to the incomplete mixing of EGR, thermal stratification in the cylinder can be created. The level of dilution by EGR affects the HCCI combustion, and thus, cycle-to-cycle variations in the amount and composition of diluents result in cycle-to-cycle variations in combustion. Both chemical and thermal effects are responsible for cyclic combustion variation in HCCI engine when EGR is used for dilution [3].

Figure 8.8 illustrates the unstable HCCI engine operation using EGR. The number of cycles presented is zoomed version of Fig. 8.3b. It can be noticed from Fig. 8.8d that a partial burn cycle is often followed by another partial burn cycle due to a lower temperature at intake valve closing (T_IVC) which is the result of the lower temperature of rebreathed EGR. The lower temperature leads to delayed combustion phasing, which increases the possibility of a second partial burn cycle with further lower IMEP [3]. Figure 8.8d also shows the variations of IMEP do not well matched with the variations of CA₅₀ (particularly for the partial burn cycles). Additionally, immediate cycle after an excessive partial burn cycle (the lowest IMEP cycle with number 38 and 52) improves the IMEP toward the average value at substantially lower T_IVC and highly retarded CA₅₀ timings. Engine cycles number 39 and 53 (Fig. 8.8d) have maximum IMEP at the highly retarded CA₅₀ instead of the lowest T_IVC. The recovery of IMEP just after misfire cycle cannot be described by thermal effects of the charge, and it suggests a chemical state of charge is responsible (chemical enhancement of autoignition) [3]. The low-temperature heat release is maximum for excessive partial burn cycle (Fig. 8.8c). It is suggested that trace species produced during low-temperature heat release period are recirculated in the next cycle, which is responsible for the sufficient enhancement of autoignition of charge. Therefore, cycle-to-cycle variations in the EGR can lead to cycle-to-cycle variations in combustion process through chemical effects also.

Fig. 8.8

(a) Mass of in-cylinder air, external exhaust gas recirculation (EEGR), and rebreathed exhaust gas recirculation (REGR) at IVC; (b) temperature of REGR and averaged charge temperature (T_IVC) at IVC: (c) fueling rate, total heat release, and low-temperature heat release; (d) CA₅₀ and IMEP as a function of consecutive cycles of #32–#58 for the unstable HCCI operation [3]

The low-temperature combustion (LTC) engines have higher sensitivity to cyclic variations input parameters than conventional diesel combustion. The LTC engines show higher cyclic variations than conventional diesel engines [2]. Figure 8.9 shows the normalized contribution to cyclic variations in output parameters (IMEP, CA₅₀, gross indicated efficiency (GIE), and peak pressure rise rate (PPRR)) by several input parameters in HCCI and reactivity controlled compression ignition (RCCI) engines. The considered input parameters are temperature and pressure at intake valve closing (T_ivc, P_ivc), PFI fuel mass (PFI_FuelMass), EGR, cylinder surface temperature (Cyl_Temp), and direct injected fuel mass (CR_FuelMass) in case of RCCI combustion. Individual contributions of every input parameter are calculated by the response surface model (RSM) by uncertainty propagation technique [51]. The major contribution in cyclic variations of the output parameters is from four sources: PFI mass, DI mass, trapped gas temperature, and EGR% (Fig. 8.9). The P_ivc has an only minor influence to the variation in RCCI combustion, but it is a significantly contributing factor in cycle-to-cycle variation HCCI engine [51]. The combustion phasing (CA₅₀) is mainly affected by T_IVC, P_IVC, EGR%, and cylinder surface temperature in the HCCI engine. The PFI fuel mass has a minimal effect on CA₅₀ even though it has a very strong effect on IMEP and PPRR (Fig. 8.9a). The cyclic variations in CA₅₀ are mainly influenced by T_IVC, direct injection fuel mass, and EGR% in RCCI combustion (Fig. 8.9b). The accurate and consistent fuel delivery systems are crucial to minimizing the cyclic variations in LTC engines. Additionally, management of the temperature and EGR sensitivity is required to take the full advantages of TLC engines [51].

Fig. 8.9

Effect of several input parameters on the cyclic variations in output parameters (IMEP, CA₅₀, GIE, and PRRR) in (a) HCCI and (b) RCCI engines [51]

8.2 Characterization of Cyclic Combustion Variations

The problem of cycle-to-cycle variations in engine operation is fundamentally a problem of variation in combustion from one cycle to the next. The cyclic variations can be characterized by the variations in the different combustion parameters. Increase in cyclic variations eventually leads to deterioration of combustion stability to unacceptable levels, which results in partial burning on some cycles, and in the extreme, misfires or weak burn cycles occur that produce no work output. In this section, indicators of cyclic variations and recognition of partial burn and misfire cycles are discussed.

8.2.1 Indicators of Cyclic Combustion Variations

Various parameters used as measures of combustion variability can be classified into four main categories [5, 52]: (1) parameters related to characteristics of engine cylinder pressure, (2) parameters related to characteristics of engine combustion, (3) parameters related to characteristics of flame front, and (4) parameters related to the concentration of engine exhaust gas.

The use of pressure-related parameters for cyclic variation analysis appears to be a natural choice because these parameters can easily be measured using a pressure transducer that can be usually integrated with the spark plug unit (SI engine) or glow plug unit (CI engine). The technique of using pressure-related characteristics provides a link between the flame propagation process and the thermodynamics of the SI engine cycle. Among the major pressure-related variables include (1) maximum pressure (P_max), (2) crank angle position corresponding to the maximum cylinder pressure $\left({\theta }_{{\mathit{P}}_{\max }}\right)$, (3) maximum pressure rise rate ((dP/dθ)_max), (4) crank angle position corresponding to the maximum rate of pressure rise (θ(dP/dθ)_max), and (5) variations in the indicated mean effective pressure (IMEP).

The maximum cylinder pressure is the most widely characteristic variable for cyclic combustion variability because of the relative ease with which it is measured. The crank angle position of the maximum cylinder pressure $\left({\theta }_{{\mathit{P}}_{\max }}\right)$ is also a useful index for determining cyclic variability. Cyclic variations in P_max respond to variations in the combustion phasing which is introduced by fluctuations in the initial part of combustion. It also responds to cyclic variations in peak burn rate and in fueling level or airflow (charging). This behavior suggests that care must be taken while relating variations in P_max to variation in the flame propagation process. The maximum pressure is typically higher with higher burn rates and vice versa. Using the location of peak pressure $\left({\theta }_{{\mathit{P}}_{\max }}\right)$ as a measure of phasing of cyclic variation analysis is similar to using peak pressures. The relationship between the maximum in-cylinder pressure (P_max) and the crank angle at which it occurs (CAP_max) is shown in Fig. 8.10. The figure shows that the P_max reduces and the corresponding crank position for the P_max first retards and then advances with the increase of excess air ratio at a specified hydrogen enrichment (Fig. 8.10). This phenomenon illustrates that the effect of piston motion on the P_max is getting pronounced at extremely lean conditions due to the further prolonged combustion duration [53]. It is also found that the relationship between P_max and ${\theta }_{{\mathit{P}}_{\max }}$ is approximately linear for fast burn in the entire range, while for the slow burn case this linearity prevails only up to a certain retard. For further retarding, there is a “hook-back” region, which corresponds to a very late phasing of combustion, when the effect of expansion due to the piston movement becomes an important factor [5, 11].

Fig. 8.10

Variation in maximum cylinder pressure and its corresponding crank angle position at the various levels of hydrogen enrichments $\left({\alpha}_{{\mathrm{H}}_2}\right)$ at 1400 rpm in a gasoline engine [53]

The maximum pressure rise rate can be used for variation analysis as close to TDC position the piston movement is not significant and maximum pressure rise occurs close to constant volume condition. In this case, the maximum pressure rise rate would be expected to be related to burning rate and hence to flame speed. A combination of maximum pressure rise rate and its crank position in the cycle can provide some discrimination between burning rate variations and initiation period variations in much the same way that peak pressure and its location in the cycle correspond to a unique burn rate and phasing variations. The interpretation is more complex, however, and requires accurate estimation of the maximum pressure rise rate ((dP/dθ)_max) despite an inherent sensitivity to noise in the pressure data. Another measure of cyclic variability is the variation in the work output in each cycle or the variability in the IMEP. The coefficient of variation in IMEP (COV_IMEP) is a widely used parameter for determination of combustion stability. Figure 8.11 illustrates the variations in COV_IMEP with ignition timing at different excess air ratios and throttle positions (TP) in a spark ignition engine. The figure shows that COV_IMEP decreases firstly and then increases with the retard of ignition timing, and thus, the ignition timing should be set at the optimum timing with the lowest cyclic variations [54]. Figure 8.11 also demonstrates that COV_IMEP generally increases with the increase of excess air ratio due to the slower flame propagation speed caused by increased level of dilution mixture in-cylinder.

Fig. 8.11

The variations in COV_IMEP with ignition timing at different excess air ratios and throttle positions (TP) [54]

Practically, the combustion-related parameters are derived from the measured pressure data by using thermodynamic heat release model. The following are the methods used to quantify cycle-to-cycle variations based on the combustion characteristics: (a) maximum rate of heat release, (dQ/dθ)_max, (b) total heat release rate, (c) combustion duration, (d) ignition delay, (e) time period in crank angle degrees from ignition to the point where a certain mass fraction is burned, and (f) maximum rate of mass burning or maximum rate of change of mass burnt fraction in the cylinder [5]. Combustion-related parameters, such as the ignition delay, the combustion duration, the total heat release, and the crank angle period from ignition to a certain heat release fraction (typically 10 and 50%), are frequently used. Ignition delay is a good parameter to indicate the extent of cyclic combustion variations in initial stages of combustion, and it is commonly accepted that both its mean value and its variance to a great extent determine the cyclic variations [11].

Typically, flame front-related parameters such as (1) flame front position, smoothed flame front area, or flame entrained volume at a specific crank angle, (2) crank angle lapse between flame front arrival and two pre-specified different locations in the cylinder, and (3) displacement of the flame kernel center from the spark gap at different crank angles are used for the analysis of cyclic variations. In exhaust gas-related parameters, generally the concentration of different components in the exhaust gases is used for the analysis [11].

8.2.2 Recognition of Partial Burn and Misfire Cycles

In reciprocating engines, terms such as misfire and partial burn are used to indicate an absence of combustion or weak combustion in the cylinder. Typically, engine operation with diluted mixture leads to the increase in the duration of all the stages of the combustion process, and in some of the engine cycles, there is no time to complete the combustion within the cylinder. Further increasing the mixture dilution may lead to a situation when the mixture never ignites and misfiring cycles occur [55]. A cylinder misfire occurs when the injected fuel mass (diesel engines) or the air-fuel mixture (port or direct injection gasoline engines) does not ignite, or it burns incompletely. Misfire events can occur due to several reasons such as a fault in the spark ignition or fuel injection control system, defective fuel injection and air intake systems, insufficient ignition energy, bad fuel quality, excessive EGR, low temperature, etc. [9, 56]. Besides the irregular engine running, further consequences of regular misfires are long-term increases mainly in hydrocarbon (HC) and carbon monoxide (CO) emissions. Sustained misfiring can also damage the catalytic converter in the exhaust system [57]. Misfire can also lead to a sudden engine speed decrease. Misfire cycles are undesirable since it can lead to speed and torque fluctuations [58]. The misfire detection is one of the most important aspects of onboard diagnostics (OBD). The diagnostic system must be able to detect a single misfire and also to determine the specific cylinder in which the misfire event has occurred. An alert must be generated whenever the rate of misfire exceeds a particular threshold (corresponding either to excessive catalyst temperature or increased HC emissions) [56]. Thus, partial burn and misfire can be detected by the cylinder pressure signal, and several methods are proposed for different combustion modes [59,60,61,62].

Typically, two types of constraints (misfire limit and cyclic variability limits) can be defined as combustion stability limits [2]. For a particular engine speed and fuel, the HCCI engine operation is limited by three boundaries: misfire, partial burn, and knock limit. Maximum achievable load in HCCI combustion is limited by misfire operating conditions. Figure 8.12 illustrates the normal burn, partial burn, and misfire cycles in unstable operating conditions of an HCCI engine. The figure shows that at cyclic combustion variations are very high at unstable operating conditions.

Fig. 8.12

Measured cylinder pressure and IMEP variations at an unstable operating condition in an HCCI engine for 300 consecutive cycles [63]

Figure 8.13 illustrates the three regions, normal, partial burn, and misfire, in the HCCI engine. The figure shows that the IMEP and heat release in misfiring cycles are far below the well-burning cycle and heat release of the misfire cycle is less than 50% compared to a well-burning cycle [59]. Typically, when IMEP of a cycle is negative, then that particular operating cycle is considered a misfire cycle [60]. A cycle is defined as a partial burn cycle if its total heat release is reduced by 10% or more compared to a well-burning cycle [61]. A study defined partial burn and misfire operating condition in an HCCI engine based on the estimation of partial burn cycles [64]. An operating condition is defined as a partial burn operating condition if more than 20% of the cycles are partial burn cycles (heat release is reduced more than 10% from the previous cycle). Misfire operating condition is considered with more than 30% partial burn cycles at a particular engine operating condition. The COV_IMEP is typically used to define the partial burn or misfire conditions. A method combined the COV_IMEP and heat release method to determine the partial burn operating conditions. It is found that all the operating conditions with COV_IMEP more than 6% and higher than 14% partial burn cycles can be defined as the partial burn operating conditions [62].

Fig. 8.13

Percentage of heat release as a function of IMEP for 120 consecutive cycles in HCCI engine [59]

It was concluded that the operating conditions have a lower risk of misfire where the coefficient of variation (COV) of IMEP is below 3.5% in HCCI engine [2]. The value of IMEP is low at lower engine loads near idle operating conditions. In such low IMEP conditions, the stable operating limit is defined in terms of the standard deviation (STD) of IMEP instead of COV of IMEP, and the typical limit is 15 kPa of IMEP for stable combustion [65]. Another stable HCCI operating criteria is developed as the operating conditions where the standard deviation of IMEP is below 2% which correspond to the occurrence of less than one percent (<1%) partial burn cycles [61]. Figure 8.14 illustrates the stable operating criteria for stable HCCI combustion using isooctane and PRF80 fuel. The figure shows that the latest acceptable CA₅₀ is 373 °CA for isooctane HCCI operation. A high frequency of partial burn cycles occurs for CA₅₀ beyond 373 °CA. In contrast, the PRF80 fuel can tolerate more retarded combustion phasing (Fig. 8.14) while maintaining stable combustion due to low-temperature heat release (two-stage heat release fuel) [61].

Fig. 8.14

Standard deviation of IMEP with combustion phasing in HCCI engine [61]

Similarly, in SI engines, the leaner engine operation (dilution by air, residual, or EGR) leads to an increase in flame development period and the duration of rapid combustion phase along with higher cyclic combustion variations. Leaning of the mixture can eventually lead to a condition where the engine becomes rough and unstable with the rapid increase in unburned hydrocarbon emission. These engine operating conditions are defined as a stable engine operating limit [5]. Leaner mixture operations slow down the combustion process, and it may happen that time is not sufficient for consuming the full charge by flame propagation before the exhaust valve opening. This condition is considered as partial burn. With the increase of EGR, slow burn, then partial burn, and then misfire cycles occur in SI engine. The combustion is able to complete in slow burn cycles (typically after 80° aTDC), and IMEP is low (between 85 and 46% of average value). The IMEP value is less than 46% of average IMEP in partial burn cycles [66]. Typically, misfire operating cycle has negative IMEP value. However, these values can be updated based on the current acceptable limits. A more recent study used the occurrence of partial burning cycles as burning cycle producing less than 70% of the mean IMEP output, and it starts to be significant once the COV_IMEP exceeds about 8% [67]. Further increase of COV_IMEP after 8% leads to an increase in partial burn frequency with a reasonably linear variation and with a weak dependence on engine speed and load. Misfire cycles are considered as cycles producing less than 5% of the mean IMEP output, and it starts to occur at COV_IMEP values of around 20%. Thus, characterization of partial burn and misfire is important for better engine performance. Several methods are used in published literature for misfire recognition including cylinder pressure sensor signal, crankshaft angular speed, ionization current or breakdown voltage, and temperature and oxygen concentration.

In modern engines, sometimes rare partial burn and misfire conditions occur at robust operating conditions also. Figure 8.15 illustrates the rare random partial burn and misfire cycle in a spray-guided spark-ignited direct injection SI engine with well-burned cycles comparable to those at spark timing (ST) at 31° bTDC. To investigate the causes of the partial burn and misfire, the spatial equivalence ratio and charge velocity near the spark plug are investigated along with spark energy and spark duration. Figure 8.16 shows the variations of spatial-average equivalence ratio and velocity and range of spark duration and spark energy during well-burned, misfire, and partial burn cycles in spray-guided direct injection SI engine. The values for occurrence of partial burn and misfire are highlighted.

Fig. 8.15

Random partial burn and misfire in spray-guided direct injection SI engine [60]

Fig. 8.16

(a) Spatial-average equivalence ratio and velocity and (b) range of spark duration and spark energy during well-burned, misfire, and partial burn cycles in spray-guided direct injection SI engine [60]

Figure 8.16a illustrates that there exists a very large cyclic variation of equivalence ratio and velocity near the spark plug at the beginning of the discharge that produces well-burning cycles. Additionally, the partial burn and misfires occur within the range of equivalence ratio and velocity for well-burned cycles but are heavily biased toward lean mixture and low velocities (less than 8 m/s). However, these metrics are not sufficient by themselves to recognize the causes of partial burn and misfire because these errant cycles occur in the same range of well-burning cycles [60]. Figure 8.16b shows that partial burn and misfires are somewhat biased toward the low-energy, short duration discharge (below the line).

Traditionally, partial burn and misfire detection are conducted by measuring the in-cylinder pressure signal analysis and calculating IMEP. The other methods based on cylinder pressure measurement are developed for determination of misfire and partial burns [55, 59, 68, 69]. The pressure angular ratio (ratio of pressure at two symmetric points before and after TDC) is used for the identification of partial burning and misfire events [55]. When the pressure angular ratio (P(θ)/P(−θ)) is greater than a pre-defined value, a partial burning event occurs and when less than unity for misfire event. This method is able to determine the misfire event more reliably than partial burn conditions. Skewness and kurtosis of in-cylinder pressure data are found to have a desirable correlation with maximum heat release rate and IMEP, and thus, it can be used for misfire detection in HCCI engine [69]. For misfire detection, the values of skewness and kurtosis are compared with the data of normal burn cycles.

Artificial neural networks (ANN) have been used for the detection of misfires in SI and HCCI engines [59, 70]. Misfiring is directly related to the maximum heat release rate in the cylinder [71]. The cylinder pressure values at different crank angle positions (0°, 5°, 10°, 15°, 20° after TDC) well correlated with the maximum heat release rate (MHRR) as illustrated in Fig. 8.17. The pressure values at crank positions 0°, 5°, 10°, 15°, and 20° aTDC are designated as P0, P5, P10, P15, and P20.

Fig. 8.17

Cylinder pressure at different crank angle positions, (a) 0°, (b) 5°, (c) 10°, (d) 15°, (e) 20° after TDC, as a function of the maximum heat release rate in HCCI engine [59]

Figure 8.17 shows that the regression line fits in the center of the data points for P10, P15, and P20 with a good correlation coefficient (R² > 0.97). For cylinder pressure at 5CAD after TDC (P5), the R² is less than the value of P10, P15, and P20, but for pressure at TDC position (P0), a scattering of the points is far from the regression line (Fig 8.17a). The in-cylinder pressure variation at the TDC position has significant variations (scatter in the data), and it is less sensitive to the variations of the maximum heat release rate [59]. The pressure values at these points are used as input of ANN model used for determination of misfire in HCCI engine. This model is able to well differentiate between the normal burn cycles and misfire cycles.

Understanding the dynamics of cyclic combustion variation particularly in partial burn and misfire regime helps in designing effective control of the engine. A comprehensive ignition timing metric is required for effective control of the engine, and that metric should be applicable over a wide range of engine operating conditions particularly in partial burn operating conditions [2]. An additional requirement of metric for engine control is that it needs to be computationally less expensive such as $\left({\theta }_{{\mathit{P}}_{\max }}\right)$. Two combustion timing parameters ${\theta}_{P_{\mathrm{max}}}\kern0.5em \mathrm{and}\kern0.5em {\mathrm{CA}}_{50}$ are compared for determination of accurate and robust HCCI combustion timing over a wide range of operating conditions (329 different engine operating conditions including both normal and partial burn) [72]. Figure 8.18 illustrates the cyclic variations of ${\theta }_{{\mathit{P}}_{\max }}$ and CA₅₀ in HCCI combustion in the particular operating condition. The figure depicts that the cyclic variation of ${\theta }_{{\mathit{P}}_{\max }}$ is higher than CA₅₀ that indicates a higher sensitivity of ${\theta }_{{\mathit{P}}_{\max }}$. Particularly, the ${\theta }_{{\mathit{P}}_{\max }}$ is able to register a cycle of early ignition timing with misfire occurs (cycle 44) which is not registered using CA₅₀ (Fig. 8.18). This observation is further validated, and ${\theta }_{{\mathit{P}}_{\max }}$ is found to be a good ignition timing criteria to differentiate between normal and misfire operation in HCCI engine [72, 73]. When the standard deviation of CA₅₀ is greater than 2 CAD, the combustion phasing (CA₅₀) is found to be a poor measure of cyclic variations.

Fig. 8.18

The variation of ${\theta }_{{\mathit{P}}_{\max }}$ and CA₅₀ in a HCCI engine operating at PRF0, 1000 rpm, T_i = 100 °C, ϕ = 0.57, EGR = 0%, T_coolant = 75 °C (adapted from [72, 73] Courtesy of Ahmad Ghazimirsaied)

8.3 Combustion Stability Analysis by Statistical Methods

Several factors (chemical (gas composition), mixing, turbulence, and spark discharge-related) affect the cyclic combustion variation in engines (Sect. 8.1.2). Measured cylinder pressure data and subsequently calculated combustion parameters for a large number of consecutive engine cycles are used for analysis of combustion stability. Based on measured cylinder pressure data, several indicators are used for characterization of combustion stability such as peak pressure, IMEP, crank angle of peak pressure, and maximum heat release rate, different combustion phasing parameters, etc. Traditionally, statistical distributions of these indicators are used as measures of combustion stability or cyclic combustion variability. Typically, the statistical methods treat the indicators as independent random variables, which ignore the possible temporal correlations in the data. The most common methods to quantify cycle-to-cycle and cylinder-to-cylinder variability include the standard deviation (σ) of IMEP and the standard deviation of engine speed. Several statistical parameters generally used for quantification of cyclic and cylinder-to-cylinder variations are coefficient of variation (COV) of IMEP, lowest normalized value (LNV) of IMEP, root mean square (RMS) of the ΔIMEP, and IMEP imbalance [9]. These parameters can be defined using the following equations:

$$ \mathrm{Standard}\kern0.17em \mathrm{Deviation}\kern0.17em \mathrm{of}\kern0.17em \mathrm{IMEP}\left({\sigma}_{\mathrm{IMEP}}\right)=\sqrt{\frac{1}{N-1}\sum \limits_{i=1}^N\left({\mathrm{IMEP}}_i-\overline{\mathrm{IMEP}}\right)} $$

(8.1)

where i is the sample of interest and N is the number of the samples. The mean of IMEP is calculated by Eq. (8.2):

$$ \overline{\mathrm{IMEP}}=\sum \limits_{i=1}^N\frac{{\mathrm{IMEP}}_i}{N} $$

(8.2)

The COV of IMEP (COV_IMEP) is estimated using Eq. (8.3):

$$ \mathrm{COV}\;\mathrm{of}\kern0.17em \mathrm{IMEP}=\frac{\sigma_{\mathrm{IMEP}}}{\overline{\mathrm{IMEP}}}\times 100 $$

(8.3)

For any combustion parameter, the COV can be calculated using Eq. (8.4):

$$ \mathrm{COV}(x)=\frac{\sigma }{\overline{x}}\times 100\% $$

(8.4)

$$ \overline{x}=\sum \limits_{i=1}^n\frac{x_i}{n};\kern1em \mathrm{and}\kern1em \sigma =\sqrt{\sum \limits_{i=1}^n\frac{{\left({x}_i-\overline{x}\right)}^2}{\left(n-1\right)}} $$

(8.5)

The lowest normalized value (LNV) of IMEP is calculated by normalizing the lowest IMEP value in a data set by the mean IMEP value as shown in Eq. (8.6) [9]:

$$ \mathrm{LNV}=\frac{{\mathrm{IMEP}}_{\mathrm{min}}}{\overline{\mathrm{IMEP}}} $$

(8.6)

A measure of cylinder-to-cylinder variations is defined by IMEP imbalance, which is defined as Eq. (8.7). The IMEP imbalance is calculated by subtracting the average IMEP in the weakest cylinder from the average IMEP in the strongest cylinder and then normalizing by the mean IMEP [9]:

$$ {\mathrm{IMEP}}_{\mathrm{imbalance}}=\frac{{\overline{\mathrm{IMEP}}}_{\mathrm{max}}-{\overline{\mathrm{IMEP}}}_{\mathrm{min}}}{{\overline{\mathrm{IMEP}}}_{\mathrm{engine}}} $$

(8.7)

The root mean square (RMS) of the ΔIMEP (i.e., the difference between highest and lowest IMEP reading in the cylinders) characterizes the difference in work performed in each cylinder event (in the firing order) and calculated by Eq. (8.8) [9]:

$$ \mathrm{RMS}\;\mathrm{of}\kern0.17em \Delta \mathrm{IMEP}=\sqrt{\frac{{\Delta \mathrm{IMEP}}^2}{n_{\mathrm{c}}\cdot x-1}} $$

(8.8)

where n_c is the number of cylinders and x is the number of cycles.

Commonly used statistical analysis of different combustion and performance parameters are discussed in the following subsections.

8.3.1 Time Series Analysis

The cyclic variation data series of different combustion parameters are calculated from measured cylinder pressure over a large number of consecutive engine cycles. The different types of pattern can be observed by simply plotting the data series with respect to cycle number. Figure 8.19 depicts the three different types of pattern in cycle-to-cycle variations of IMEP P_max and start of combustion (SOC) in an HCCI engine. The figure clearly illustrates that the cyclic combustion variations are not always an unstructured random event. Figure 8.19a illustrates the normal variation pattern, which does not follow a definite pattern and frequently occurs in the engine [45]. A periodic pattern fluctuating within two limits in combustion data series can appear (Fig. 8.19b), which can possibly due to fluctuation in equivalence ratio [45]. Figure 8.19c illustrates another type of pattern with several weak/misfired ignitions and some strong ignitions, and this engine operating condition has very large cyclic combustion variations. The weak/misfire cycles are sometimes followed by a strong cycle, and the values of peak pressure and IMEP are very low in weak/misfire cycles. The larger cyclic variations during these (weak/misfire pattern and periodic pattern) operating conditions need to be eliminated by engine control. However, for the normal cyclic variation pattern, the amplitude of the variation needs to be minimized to improve the engine stability.

Fig. 8.19

Cycle-to-cycle variation patterns of IMEP, P_max, and SOC in HCCI combustion for (a) normal variation (φ = 0.40, T_i = 121 °C, ON = 20, P_i = 119 kPa, 800 rpm); (b) periodic variation (φ = 0.36, T_i = 133 °C, ON = 20, P_i = 125 kPa, 1003 rpm); (c) variations with weak (misfire) cycles (φ = 0.42, T_i = 116 °C, ON = 40, P_i = 124 kPa, 907 rpm) [45]

Further analysis of time data series of different combustion parameter reveals important information regarding combustion characteristics. Variation in one parameter can be analyzed with respect to another parameter. Figure 8.20 depicts the variation of maximum pressure (P_max) with a crank angle corresponding to maximum pressure (CA(P_max)), which is also sometimes referred as Matekunas diagrams [52]. The large eddy simulation (LES) and experimental results are compared for the stable and two unstable conditions (created by dilution by residual and dilution by air to produce lean mixture). The experimental results are colored by their probability of reaching their instantaneous values [74]. Three zones are identified by Matekunas in their study [52] which include (1) a linear zone where P_max and CA(P_max) vary linearly for fast burning cycles, (2) a hook-back area where P_max varies much more than CA(P_max), and (3) a return zone with only small variations of P_max. Figure 8.20 illustrates that the stable engine operation occurs in the linear zone in P_max versus CAP_max plot. In the unstable engine operating conditions, the clear deviation from the linear region is observed for both the conditions (Fig. 8.20a, b).

Fig. 8.20

Variation of maximum pressure with crank angle position corresponding to maximum pressure in (a) unstable operating conditions by dilution with nitrogen, (b) unstable operating condition using lean mixture (reducing Φ), and (c) stable operating condition [74]

The cyclic variations in stable and unstable operating condition can be explained in terms of the variations in flame initiation, flame development, and flame propagation stage of combustion. The variation in these stages of combustion leads to the cyclic variations in pressure- and corresponding combustion-related parameters.

Figure 8.21 illustrates the cyclic variations by depicting the flame surface variations at 35 crank angle degrees after ignition in six consecutive engine cycles for an unstable lean operating condition. The flame surface is visualized using an iso-surface of the reaction rate (50 mol m³ s⁻¹) colored by the velocity (blue, 0 m/s; red, 20 m/s). The cylinder pressure trace for respective cycles is also presented to differentiate between slow and fast burning cycles. Figure 8.21 shows typically faster propagation toward the exhaust side (negative x-direction) as a result of the tumbling flow. The cycle number 15 occupies a small volume of the cylinder and is very elongated toward the exhaust side. Another cycle (number 16) shows a more isotropic shape , which is also the fastest combustion cycle [74]. The trend variations in cylinder pressure follow the trend in the flame surface (area and velocity).

Fig. 8.21

Flame surface visualization using an iso-surface of the reaction rate (50 mol m³ s⁻¹) colored by the velocity (blue, 0 m/s; red, 20 m/s) at 35 crank angle degrees after ignition for six consecutive cycles in an unstable lean operating condition [74]

8.3.2 Frequency Distribution and Histograms

Data series of combustion parameters are typically characterized with both univariate statistics and linear temporal analysis. In the traditional statistical analysis, each measurement is assumed to be independent random events, and probability density function (PDF) of these events is characterized [75]. Typically, characteristics of PDF include skewness, kurtosis, LNV, and COV. However, these statistical parameters do not consider the temporal pattern in the data series, which might be present in the data series obtained from engine combustion.

Histogram is a graphical presentation of a time series showing the frequencies of different values in the data. Histograms typically reveal a qualitative assessment of the underlying distribution of the data series. Figure 8.22 shows the histograms of heat release data for different equivalence ratio in an SI engine. The distributions in the histogram have either a Gaussian or non-Gaussian shape. Figure 8.22 illustrates that the cyclic variations closely follow a Gaussian distribution for engine operation at the near-stoichiometric fuel-air ratio. Normally distributed data typically indicates a strong presence of independent random sources in the data [75]. It can be reasonably presumed that nearly normal distribution at stoichiometric conditions means the cyclic variations are stochastic in nature at these operating conditions. This would be possible according to the central limit theorem if the cyclic combustion variations are the result of a large number of different independent effects leading to a Gaussian distribution [76].

Fig. 8.22

Histograms of heat release data for different equivalence ratios (a) Φ=0.91, (b) Φ=0.83, (c) Φ=0.77, (d) Φ=0.67, (e) Φ=0.63, (f) Φ=0.59, (g) Φ=0.53 in an SI engine [76]

Relatively larger cyclic variations are observed as the fuel-air mixture becomes leaner than stoichiometric, and histogram significantly deviated from Gaussian distribution (Fig. 8.22). The non-Gaussian distribution is asymmetric with a peaked maximum and broad tail [76]. Further leaning of the charge (ϕ < 0.67), the variations in heat release data tends to move back toward Gaussian distribution but with substantial asymmetry (Fig. 8.22g). Non-Gaussian distribution of the data indicates that there are not many dominant independent random sources in the data [75].

Three statistical parameters, namely, standard deviation (σ), skewness (S), and kurtosis (K), are used for quantitative estimation of the data distribution with respect to normal distribution [76, 77]. The standard deviation is a measure of the data spread about the mean of the distribution. Skewness quantifies the asymmetry of the data distribution about the mean and is defined as third moment about the mean of data distribution (Eq. 8.10). Variance (σ²) is defined as the second moment about the mean (Eq. 8.9), and it also basically depicts the spread of distribution about the mean. Kurtosis characterizes the shape of distribution (flatness) around the mean with respect to normal distribution and defined by the fourth moment about the mean (Eq. 8.11).

$$ {\sigma}^2=\frac{\sum \limits_{i=1}^N{\left({x}_i-\overline{x}\right)}^2}{N} $$

(8.9)

$$ S=\frac{\sum \limits_{i=1}^N{\left({x}_i-\overline{x}\right)}^3}{\left(N-1\right)\cdot {\sigma}^3} $$

(8.10)

$$ K=\frac{\sum \limits_{i=1}^N{\left({x}_i-\overline{x}\right)}^4}{\left(N-1\right)\cdot {\sigma}^4} $$

(8.11)

The values of skewness and kurtosis are usually zero for normally distributed data. Skewness values can be positive and negative. A positive value of skewness suggests the existence of right asymmetric tails longer than the left tail which means data distribution has the frequency bias above the mean value. The negative value of skewness shows the reverse trend. Kurtosis is a measure of whether the data is peaked (leptokurtic or super-Gaussian distribution) (K > 3) or flat (platykurtic or sub-Gaussian distribution) (K < 3) relative to a normal distribution [77]. Figure 8.22 shows the largest kurtosis and lowest skewness values at ϕ = 0.67.

The probability distribution functions (PDF) can be further characterized by fitting the different probability distribution models in the experimental data [78, 79]. Figures 8.23 and 8.24 show the best fit probability distribution models for IMEP and combustion duration in RCCI and HCCI engines, respectively. The goodness of fit is analyzed using Kolmogorov-Smirnov test. Figure 8.23 shows that IMEP variations in RCCI engine are relatively close to a normal distribution (with certain deviation) at near TDC diesel injection timings, and deviation from normal distribution that increases at advanced diesel injection timings. Methanol/diesel RCCI combustion has a relatively more significant deviation from normal distribution than gasoline/diesel RCCI combustion. Among all distributions fitted to the experimental data, generalized extreme value (GEV) and Johnson SB distribution cover the entire range of distribution shapes observed in IMEP ensemble at different RCCI operating conditions.

Fig. 8.23

The PDF plots for IMEP in gasoline/diesel RCCI and methanol/diesel RCCI operation at advanced diesel injection timings

Fig. 8.24

The PDF plots for combustion duration in an HCCI engine for misfire and normal operating conditions [78]

The GEV distribution provides a continuous range of shapes by combining three simpler distributions (Gumbel, Frechet, and Weibull) into a single form. The probability density function for this model is based on three main parameters including a location parameter (mean), a scale parameter (standard deviation), and a shape parameter:

$$ P(x)=\left\{\begin{array}{l}\frac{1}{\sigma }\ \exp \left[-{\left[1-k\frac{\left(x-\mu \right)}{\sigma}\right]}^{\frac{1}{k}}\right]\ \left[{\left[1-k\frac{\left(x-\mu \right)}{\sigma}\right]}^{\frac{1}{\left(k-1\right)}}\right],\kern1em k\ne 0\\ {}\frac{1}{\sigma }\ \exp \left[-\exp \left(\frac{\mu -x}{\sigma}\right)\right]\exp\ \left(\frac{\mu -x}{\sigma}\right),\kern6em k=0\ \end{array}\right. $$

(8.12)

where σ is the scale parameter, μ is the location parameter, and k is the shape parameter. This distribution can be used to model the cyclic variation in RCCI engine.

Similarly, GEV distribution is also the best fitting distribution in the range of distribution shapes in HCCI combustion duration data series at different HCCI operating conditions (Fig. 8.24) [78].

In case of large data set, plotting of cumulative percentage occurrence of the coefficient of variations with a certain parameter can reveal some useful global information regarding the cyclic variability. Figure 8.25 illustrates the cumulative percentage of occurrence for COV_IMEP for a different range of CA₁₀ (crank angle position corresponding to 10% heat release) and COV of combustion duration for different combustion duration for 273 engine operating conditions in an HCCI engine by varying fuel, engine speed, inlet temperature, and air-fuel ratio. The occurrence percentage is calculated by counting the number of engine operating conditions out of all the test conditions with a particular interval of CA₁₀, or combustion duration has the same range of cyclic variations.

Fig. 8.25

Cumulative occurrence for (a) COV_IMEP for different CA₁₀ positions and (b) COV of combustion duration for different CA_90–10 [78]

Figure 8.25a depicts that advanced CA₁₀ operating conditions have lower cyclic variations in IMEP in comparison to the retarded CA₁₀ positions. This observation is confirmed by the fact that 80% operating conditions having CA₁₀ in the range of −5.5 and − 2 CAD show the COV_IMEP less than 3.5% and 60% operating conditions with CA₁₀ in the range of −2 and 2.5 CAD show COV_IMEP lower than 3.5% (Fig. 8.25a). The COV_IMEP less than 3.5% is considered as an acceptable range. Similarly, Fig. 8.25b shows the cumulative occurrence for COV of combustion duration, and shorter combustion duration seems to have lower cyclic variations in combustion duration. The longer combustion duration is the lowest curve showing lower cumulative occurrences at a particular variation (Fig. 8.25b).

8.3.3 Normal Distribution Analysis

To describe the patterns of cycle-to-cycle variations in reciprocating engines, the data series combustion parameters (IMEP, combustion phasing, combustion duration, etc.) using a large number of consecutive engine cycles are calculated and further analyzed. This ensemble of combustion parameters shows different types of distribution shapes depending on engine operating conditions. Knowledge of the distributions provides valuable information to be able to find high cyclic variability regions of engines. The time series of any combustion parameter at a particular engine operating condition can be used to form a probability distribution. For statistical analysis, the normal distribution is the most commonly used probability distribution function. The normal probability plot is a good graphical tool to test whether or not a data series follows a normal distribution. Experimental data points are plotted against a theoretical normal distribution. The data series have normal distribution that closely follow the theoretical normal distribution line, and the level of departures from normality is judged by how far the points vary from the straight line [2, 80]. Figure 8.26 shows the normal probability plots of IMEP for gasoline/diesel RCCI and methanol/diesel RCCI operation at very advanced diesel injection timings. A large deviation from the normal distribution is found for the very advanced diesel injection timings for both gasoline and methanol RCCI (Fig. 8.26). However, relatively close to a normal distribution is observed for close to TDC diesel injection timings [79].

Fig. 8.26

Normal probability plots of IMEP for gasoline/diesel RCCI and methanol/diesel RCCI operation at very advanced diesel injection timings. (a) RCCI-GD-single diesel injection—60 CAD bTDC. (b) RCCI-MD-single diesel injection—40 CAD bTDC

Similarly, Fig. 8.27 depicts the normal probability graphs for combustion duration time series at normal stable, misfire, and knocking conditions in an HCCI engine. A large deviation from the normal distribution is observed in combustion duration distribution during knocking (RI = 12.9 MW/m²) and misfire range (COV_IMEP = 12.55%) operating conditions in HCCI engine (Fig. 8.27). During knocking operating condition, a stretched C-shape distribution and in misfire operating condition a V-shape distribution of combustion duration are observed. However, in the stable HCCI engine operating condition, close to a normal distribution is found (Fig. 8.27c). As discussed in Sect. 8.3.2, the normal distribution conditions may have a strong presence of independent random sources in the data. Thus, cyclic variations are stochastic in nature. The deviation from the normal distribution depicts dependency of sources in the data, or some deterministic pattern is present in the data. Thus, HCCI operation in misfire or knocking condition or RCCI combustion with advanced diesel injection timings (Figs. 8.26 and 8.27) has some dependent sources of variation, and not many dominant independent random sources in the data.

Fig. 8.27

Normal probability plots using time series of burn duration (a) normal stable, (b) misfire, and (c) knocking engine operating conditions in the HCCI combustion [78]

8.3.4 Coefficient of Variability and Standard Deviation

Standard deviation and coefficient of variability (COV) are statistical parameters used for analysis of combustion variability, and their values are calculated using Eqs. (8.4) and (8.5). Typically, the standard deviation and COV of IMEP are used as a measure of the statistical instability of combustion. It was demonstrated that the COV_IMEP values greater than 10% in SI engine leads to drivability issues [5] and more stringent values are suggested for idle operating conditions [81]. However, the acceptable COV_IMEP for advanced premixed combustion mode is typically 3.5% [2]. The COV and standard deviation of IMEP are measures of the roughness or unsteadiness of engine combustion [81]. The fast burn engine cycles typically have acceptable levels of COV and standard deviation of IMEP. Burning rate depends on the several engine operating parameters such as equivalence ratio, turbulences, overall flow pattern, etc.

Figure 8.28 demonstrates the effect of flow field (high and low tumble) on the COV_IMEP, dilution limit, heat release, and fuel economy of SI engine. The improvement of fuel consumption is constrained at excessive dilution by reducing the laminar burning speed, which finally reaches to a dilution limit where flame propagation fails. Cylinder flow structures (such as tumble) are used to intensify the turbulence intensity and enhance the flame propagation. Figure 8.28 shows that the high tumble has stable combustion (lower COV_IMEP) and improves the fuel economy. High tumble flow increases the dilution limit in comparison to low tumble by stabilizing the combustion. However, further increase of dilution may lead to misfire in some of the cycles (Fig. 8.28).

Fig. 8.28

The effect of tumble flow on heat release, combustion stability, and fuel economy [82]

Typically, the COV of maximum pressure (P_max) and IMEP is used to characterize the cyclic variations in the combustion. Figure 8.29 shows the ${\mathrm{COV}}_{{\mathit{P}}_{\max }}$ and COV_IMEP with excess air ratio at different hydrogen enrichment fractions. The figure shows that the variations of ${\mathrm{COV}}_{{\mathit{P}}_{\max }}$ and COV_IMEP with excess air ratio have different trends.

Fig. 8.29

The variation of (a) ${\mathrm{COV}}_{{\mathit{P}}_{\max }}$ and (b) COV_IMEP with excess air ratio for different hydrogen enrichment $\left({\alpha}_{{\mathrm{H}}_2}\right)$ at 1400 rpm and a MAP of 61.5 kPa in SI engine [53]

The ${\mathrm{COV}}_{{\mathit{P}}_{\max }}$ first increases with excess air ratio and reaches to a peak and then starts decreasing at particular hydrogen enrichment condition. However, the COV_IMEP always increases with excess air ratio (Fig. 8.29). This interesting trend can be explained by the fact that the COV_IMEP is affected by the entire combustion process and ${\mathrm{COV}}_{{\mathit{P}}_{\max }}$ is only symbolized by the maximum cylinder pressure. The combustion rate decreases with an increase in excess air ratio, and prolonged combustion duration increases the cyclic combustion variations. Thus, COV_IMEP distinctly increases with leaner mixtures. Comparatively, the maximum cylinder pressure is influenced by both combustion and piston motion [53]. Due to different trends in variations of ${\mathrm{COV}}_{{\mathit{P}}_{\max }}$ and COV_IMEP, the combustion stability limits should be decided carefully looking at the operating conditions.

The values of COV for the stable operating condition can also depend on a parameter selected for the analysis. Figure 8.30 illustrates the variations of COV for four different combustion parameters (P_max, IMEP, mass fraction burning rate (MFBR), and combustion duration (Δα_c)) in SI engine at 1500 rpm. The figure clearly illustrates that the COV values of all the parameters increase with leaner mixture. The trend of ${\mathrm{COV}}_{{\mathit{P}}_{\max }}$ is different from Fig. 8.29 due to the selected range of equivalence ratio of engine operation for the study. The COV of the mass fraction burning rate (MFBR) is calculated for 50% mass fraction burned, and it has the highest cyclic variation relative to other three parameters. The mass fraction burning rate is related to the combustion velocity, and it is calculated by Eq. (8.13) [83]:

$$ \mathrm{MFBR}\left(\alpha \right)=\frac{d\left(\mathrm{MFB}\left(\alpha \right)\right)}{d\alpha}=\frac{{\dot{m}}_{\mathrm{b}}}{m\cdot \omega }=\frac{\rho_{\mathrm{u}}\left(\alpha \right){A}_{\mathrm{f}}\left(\alpha \right)}{m\cdot \omega }{S}_{\mathrm{c}}\left(\alpha \right) $$

(8.13)

where ρ_u is the unburned density, A_f is the flame front surface, S_c is the turbulent combustion velocity, m is the total mass, and ω is the engine speed.

Fig. 8.30

The variations of COV with equivalence ratios for different combustion parameters in SI engine [83]

Using Eq. (8.13), the turbulent fluctuation of the combustion speed (S_c) can be determined from the variations in MFBR. Figure 8.31 illustrates the variations in the standard deviation in MFBR at different engine speed and equivalence ratio. The figure illustrates that the equivalence ratio has almost no effect (very weak dependence) on the variation of MFBR, but significant differences with variation in engine speed for a particular mass fraction burned value. The variation in MFBR is a function of mass fraction burned (MBF), and it reaches to maxima in the range of 30–60% of MFB of the charge (Fig. 8.31).

Fig. 8.31

Variations in the standard deviation of MFBR with mass fraction burned for different engine speeds and equivalence ratio [83]

The standard deviation of MFB is also dependent on the ignition system. Figure 8.32 shows the variations in combustion phasing (5% MFB position) with transistor coil ignition (TCI), advanced spark ignition (ASI), and corona ignition with combustion duration (the difference between 5 and 50% MBF). The main difference between conventional TCI and ASI system is that ASI has longer applicable spark duration and it can provide sufficient current level for the longer duration [84]. The ASI system has relatively higher dilution tolerance than a conventional system. The TCI and ASI systems become unstable for the longer main duration at 12 °CA and 14 °CA, respectively. However, with corona ignition system, stable region lasts for even more longer duration, and almost no scattering is observed in combustion phasing (Fig. 8.32). Thus, the ignition system also has the significant effect on the combustion of spark ignition, and it can be effectively observed by statistical parameters.

Fig. 8.32

Variations in combustion phasing with transistor coil ignition (TCI), advanced spark ignition (ASI), and corona ignition with combustion duration [84]

The cyclic variations in IMEP also depend on the combustion phasing (CA₅₀) and combustion duration (CA_90–10). Important trend can be extracted by observing simultaneously. Figure 8.33 illustrates the variations of COV_IMEP as a function of combustion phasing and combustion duration in a HCCI engine employing gasoline and ethanol. Both fuels have higher cyclic variations of IMEP for longer combustion duration and late combustion phasing (Fig. 8.33). The contour lines represent the constant variation lines. Contour lines of COV_IMEP are almost horizontally inclined for ethanol, which suggest that cyclic variation in IMEP has more dependency on combustion duration than combustion phasing (Fig. 8.33). However, in case of gasoline HCCI combustion, the variation depends on both combustion phasing and duration.

Fig. 8.33

The COV_IMEP as a function of combustion phasing and combustion duration in an HCCI engine using gasoline and ethanol [78]

In modern direct injection spark ignition, the injection and ignition timings, engine load and speed, compression ratio, and injector configuration significantly affect cyclic combustion variations. Since the COV_IMEP characterizes the engine roughness, it can be used to optimize the injection and ignition timings. Figure 8.34 shows the variation of COV with injection timing and spark timing in a direct injection SI engine using methanol at 1200 rpm. The figure depicts that the COV value is minimum in the middle of the map (at an injection timing of 37° bTDC and an ignition timing of 17° bTDC) and the COV increases with deviation in the ignition or injecting timing corresponding to the minimum value. This is possibly due to the fact that the mixture distribution in the cylinder is ideal and the flame propagation is the fastest at an injection timing of 37° bTDC and an ignition timing of 17° bTDC [85].

Fig. 8.34

The map of ${\mathrm{COV}}_{{\mathit{P}}_{\max }}$ in a direct injection SI engine using methanol at full load and 1200 rpm [85]

Combustion stability can be quantified in terms of variation in engine speed. Weak combustion events are considered to be one of the primary causes for poor combustion stability. Severe weak combustion events can lead to misfire, in which there will be no work done by the piston. This will act as an impulse load to the structure of the vehicle which starts to vibrate on its natural frequency giving an unpleasant feeling to passengers and the driver [8]. Figure 8.35 illustrates the variation of idle engine speed with ignition timing and air-fuel ratio. The ignition timing is varied from 0° (TDC) up to an advance of 16° bTDC. Higher idle speed shows higher engine stability with variation in both ignition timing and an air-fuel ratio (Fig. 8.35). Fluctuations in speed are higher at lower idle engine speed. Ignition timing close to TDC and air-fuel ratio close to stoichiometric are found to be more stable. Advancing the ignition timing leads to misfire and, thus, increases in COV of idle speed [8].

Fig. 8.35

Variation of COV of engine speed with ignition timing and air-fuel ratio for different idle speed (adapted from [8])

8.3.5 Lowest Normalized Value

The lowest normalized value (LNV) is defined as the lowest single IMEP in the total cycles divided by the mean IMEP (Eq. 8.6). LNV can predict the misfire or partial burning tendency of the engine. The concept of LNV in judging the combustion stability found that the minimum permissible value of LNV is around 75% [81]. To achieve acceptable levels of LNV, typically “fast burn” engines are required. The LNV is of great importance for transient engine operation because it reveals better the driver feeling during acceleration. In transient engine operation, increased tolerance of the mixture in the combustion chamber can be witnessed because the gas exchange flow varies from stationary conditions. Temperature and pressure relevant to the gas exchange are away from their equilibrium state. This can lead to EGR rate overshoots; nevertheless a continuous evolution of the torque is expected [86]. Typically the LNV value should drop below 80%. Figure 8.36 shows the typical variations of LNV and COV with an increase in EGR at different ignition energy and ignition system. The TCI (transistor coil ignition) is still dominating ignition system of a passenger car in spite of the tremendous variety of ignition concepts and their competition. Figure 8.36 compares the TCI system with DCO (dual coil offset) and CEI (controlled electronic ignition) systems at a different spark energy. The CEI and DCO systems facilitate shifting the combustion stability limit by around ΔEGR = 5% applying a COV limit of 5%, but benefit vanishes compared to the 80 mJ case if the full engine COV limit of 3% is selected (Fig. 8.36).

Fig. 8.36

Variation of COV and LNV with external EGR in a SI engine at 1500 rpm [86]

8.3.6 Autocorrelation and Cross-Correlation

Statistical parameters such as skewness, kurtosis, LNV, and COV do not consider the temporal variation in the data. The autocorrelation and power spectrum functions can reveal temporal structure effectively in linear systems, but the complete description is not revealed when underlying dynamics are inherently nonlinear [75]. The autocorrelation is defined as the amount of linear correlation a time series has with itself. Serial coupling between elements of a data series is quantified by the autocorrelation function (ACF), which can be calculated by Eq. (8.14):

$$ \mathrm{ACF}\left(\tau \right)=\left(\sum \limits_{i=1}^{N-\tau}\left({x}_i-\overline{x}\right)\left({x}_{i+\tau }-\overline{x}\right)\right)\cdot {\left(\sum \limits_{i=1}^N{\left({x}_i-\overline{x}\right)}^2\right)}^{-1} $$

(8.14)

where τ is lag and N is the number of elements in the data series.

Non-zero values of autocorrelation suggest the degree of serial coupling in time. Some important features of a time series (e.g., power spectrum, stationarity, or decorrelation time) can be extracted by the autocorrelation function. The autocorrelation function is analogous to the power spectrum, which can be employed to observe oscillations in a time series [75]. According to the Wiener-Khinchin theorem, the power spectrum of a data series can be obtained by applying the Fourier transform to the autocorrelation function [87]. When autocorrelation of a data series exponentially decays toward zero as the lag approaches infinity, the data series is most likely to be stationary. A system or process is said to be stationary if its statistical and dynamical properties remain constant over time. A nonstationary or periodic time series has a non-zero autocorrelation value at very large lag times [75, 88]. The decorrelation time is defined as the first zero crossing (or minimum in the case of a nonstationary time series) of the autocorrelation function [75, 89]. Especially this feature of the autocorrelation function is helpful in highlighting the “memory” effect between cycles of combustion data.

Figure 8.37 shows the autocorrelation of heat release data series while transitioning from stable combustion to increased levels of internal EGR. An element in a time series will correlate perfectly with itself, and thus, the correlation coefficient at lag zero is one (Fig. 8.37). Figure 8.37 shows the persistent anticorrelated oscillations start developing between successive cycles when EGR is increased from the point of stable combustion. This oscillating trend depicts a clearly deterministic “memory” between cycles [90]. The anticorrelation occurs due to the small variation in the degree of dilution of the inlet charge by residual gases from prior cycles. This dilution by residual can lead to either better or worse SI in the following cycles. Additionally, other factors such as pressure fluctuations in the intake and exhaust manifolds in the injection system can also contribute to the correlation of heat release.

Fig. 8.37

Autocorrelation of heat release data series while transitioning from (a) stable combustion to (b) and (c) increased levels of internal EGR [90]

Figure 8.38 shows the autocorrelation in the IMEP data series at different engine speeds in a diesel engine. The figure shows that the autocorrelation reduces at a different rate depending on the engine speed. The IMEP data series has a relatively low and high degree of autocorrelation between adjacent and near-adjacent data at 1200 rpm and 2000 rpm, respectively. The autocorrelation undergoes fast modulation at the intermediate speed of 1600 rpm (Fig. 8.38). The slow decay of the autocorrelation curve suggests the presence of nonstationarity in the IMEP data [91].

Fig. 8.38

Autocorrelations in the IMEP for different engine speeds in a diesel engine [91]

The cross-correlation function reveals information very similar to the autocorrelation function but between two data series. Cross-correlation is used to quantify the temporal coupling between two variables instead of one which is used in autocorrelation. The cross-correlation can be calculated using Eq. (8.15) [75]:

$$ \mathrm{CCF}\left(\tau \right)=\left(\sum \limits_{i=1}^{N-\tau}\left({x}_i-\overline{x}\right)\left({y}_{i+\tau }-\overline{y}\right)\right)\cdot {\left(\sum \limits_{i=1}^N\left({x}_i-\overline{x}\right)\left({y}_i-\overline{y}\right)\right)}^{-1} $$

(8.15)

where CCF (τ) is the cross-correlation function at lag τ, $\overline{x}$ and $\overline{y}$ is the average of the first and second data series, and N is the number of samples in the data series.

8.3.7 Principal Component Analysis

To further analyze the combustion variations and possible sources, statistical methods such as principal component analysis, factor analysis, and independent component analysis are typically used [37, 92]. The principal component analysis uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components. Assuming X is a dataset with the row is the variable, the column is the observations. Its transpose X^T is an n × m matrix. The singular value decomposition of X defined in Eq. (8.16) is a principal component analysis of these variables:

$$ X=W\Sigma {V}^{\mathrm{T}} $$

(8.16)

where W is an n × m matrix of eigenvectors of the covariance matrix XX^T; the nonnegative real entries on the diagonal of matrix ∑ are the eigenvalues; and V is an n × n matrix of eigenvectors of X^TX. Each eigenvector represents a variation pattern in X. The ratio of its eigenvalue over the sum of all eigenvalues gives the important information of this variation pattern [37].

Independent component analysis (ICA) is applied to cycle-resolved images of luminosity in SI engine combustion [92]. The independent components related to the underlying phenomena of the combustion process are identified using ICA. The components (and corresponding coefficients) are used to characterize the morphological evolution of the luminous combustion during a particular cycle and over a number of cycles. The three components identified from the images are representative of ignition and radial-like flame propagation (first component) and erratic luminous combustion (second and third component) occurring subsequently [92].

8.4 Combustion Stability Analysis Using Wavelets

Cyclic combustion variations are typically quantified by using statistical and chaotic methods [78, 93,94,95,96]. These methods are used for determination of variation patterns and their possible correlation as well as deterministic contents. Conventional statistical approaches normally use the coefficient of variation (COV) to measure the cycle-to-cycle variations in combustion parameters such as IMEP, peak cylinder pressure (P_max), heat release, etc. The key limitation of traditional statistical approaches is that they only provide the temporal variations present in the data series. Traditional statistical methods are unable to consider the spectral characteristics (frequency domain) of the data. Typically, the frequency content of the data is analyzed using Fourier transform. Constituting frequencies of the signal is revealed (and calculated) by the Fourier transform. Inverse Fourier transform is typically applied to back convert the signal from frequency domain to the time domain. Using Fourier transform, measured signal can be represented in terms of sine and cosine functions. Information regarding the frequency content of a signal is generated by Fourier transform. However, Fourier transform is unable to provide the information on variation of frequency with time if the frequency content of the signal is changing with time. Fourier transform of a transient or rapidly varying signal can provide the information regarding the frequencies present in the signal, but it cannot reveal any facts about the time of appearance of these frequencies as well as the duration of occurrences of frequencies [97]. Fourier analysis is sufficient if the signal to be analyzed is stationary and if the time period is accurately known. However, Fourier analysis may not be appropriate if the signal has nonstationary characteristics such as drifts and frequency trends [98]. To overcome the disadvantages of Fourier transform, short time Fourier transform (STFT) or windowed Fourier transform (WFT) is proposed to get the information on the frequencies present in the signal at different time locations. The STFT or WFT divides the original signal into smaller segment signal of equal time length, which subsequently apply the Fourier transform on each smaller segments of original signal. For each shorter segment, Fourier spectrum is calculated and presented as a function of time [99]. The sampling of signals may produce leakages, which are also denoted as aliases. Sampling (for creating segments for STFT) may lead to aliasing, which makes different signals to become indistinguishable. The STFT uses a fixed window size leading to fixed frequency and the time resolution, which results in poor temporal or spectral resolution. Aliasing of low- and high-frequency constituents, which does not occur in the frequency range of window, may lead to inaccuracies [100]. The fixed size of the window is the main drawback of STFT.

The wavelet transform is introduced to overcome the difficulties of Fourier transform. Fourier transform does not represent the abrupt changes and functions are not localized in space and time. This limits their applications for signals with slowly changing and transient fluctuating trends. Wavelet analysis eliminates the difficulties related to STFT by using adaptive usage of long windows for retrieving low-frequency information and short windows for high-frequency information. The ability to perform the flexible localized analysis is one of the main features of the wavelet transform. Wavelet analysis is successfully used in characterizing the cyclic combustion variations in reciprocating engines [79, 101,102,103]. Wavelets are used to determine the amplitude as well as periodicities of cycle-to-cycle variations in combustion engines because wavelet transform offers good spectral and temporal resolution.

A wavelet function is defined as rapidly decaying small oscillation or wave. A function with zero mean and finite energy can be characterized as a wavelet, and the admissibility condition of a function ψ(t) to be considered as the wavelet is shown in Eq. (8.17):

$$ {\int}_{-\infty}^{\infty}\psi (t) dt=0;\kern1em \mathrm{and}\kern1em {\int}_{-\infty}^{\infty }{\left|\psi (t)\right|}^2 dt<\infty $$

(8.17)

Wavelet transform is fundamentally an integral transform. The basis functions which are localized in both frequency as well as time domains are used in wavelet transform. It decomposes the original signal into frequency bands (or scales) at various resolutions by scaling the basis functions. The original signal is projected on a set of basis functions called mother wavelets [104]. The scale and translation parameters make the difference between various wavelet functions. Originally, Morlet thought the wavelets as a family of functions generated from translations and dilations of a single function (known as mother wavelet) [105]. Daughter wavelet in terms of mother wavelet is presented by Eq. (8.18) [104]:

$$ {\psi}_{a,b}(t)=\frac{1}{\sqrt{\left|a\right|}}\ \psi \left(\frac{t-b}{a}\right),\kern1em a,b\in R,\kern1em a\ne 0 $$

(8.18)

where ψ(t) is the mother wavelet with unit energy, ψ_a,b (t) is daughter wavelet created by mother wavelet (ψ(t)) by scaling and translating, and parameters “a” and “b” are the scaling (or dilation) and translating factors, respectively. Compressed or compacted version of the mother wavelet is created when |a| > 1, while enlarged or widened version of the mother wavelet is created when scaling factor is less than one (|a| < 1). Stretched wavelet or small scales are used for slowly changing signal, and compressed wavelet is used for abrupt changes in signal. The translating parameter “b” governs the time location of the wavelet, and wavelet is shifted depending upon the sign of translating parameter. The shifting of the function on the real axis is termed as translating the function. The factor $\frac{1}{\sqrt{\left|a\right|}}$ is used, so that the function ψ_{a, b}(t) has the same energy for all scale “a.” Wavelets can vary their time width by varying the scale “a,” which means wavelets are adaptive of their frequencies. Scaling parameter allows the wavelets to fine-tune the width at higher frequencies in the signal and increase the width while focusing on smaller frequencies, similar to a zoom lens [99]. Wavelet transform can have combinations of time-frequency representations with different resolutions of the same signal. Thus, wavelet transform is preferably used over Fourier transform.

The continuous wavelet transform (CWT) with respect to a wavelet ψ(t) is given by Eq. (8.19) [99]:

$$ \mathrm{CWT}\left(a,b\right)=\frac{1}{\sqrt{\left|a\right|}}{\int}_{-\infty}^{\infty }x(t){\psi}^{\ast}\left(\frac{t-b}{a}\right),\kern1em a,b\in R,\kern1em a\ne 0 $$

(8.19)

where x(t) is continuous signal, ψ(t) is a mother wavelet with unit energy, and ψ^∗ indicates its conjugate. Equation (8.19) can be rewritten in terms of a daughter wavelet as in Eq. (8.20):

$$ \mathrm{CWT}\left(a,b\right)={\int}_{-\infty}^{\infty }x(t){\psi}_{a,b}^{\ast }(t)\kern0.75em $$

(8.20)

Practical applications such as cyclic variations in engines involve a discrete time series signal. Continuous wavelet transform (CWT) [106] on a discrete time series x_n is represented in Eq. (8.21):

$$ {\mathrm{CWT}}_n(s)={\left(\frac{\delta t}{a}\right)}^{\frac{1}{2}}\ \sum \limits_{n^{\prime }=0}^{N-1}{x}_{n^{\prime }}{\psi}^{\ast}\left[\frac{\left({n}^{\prime }-n\right)\delta t}{a}\right] $$

(8.21)

where ${x}_{n^{\prime }}$ is the discrete time series, “a” is the scaling parameter, ψ(t) is the wavelet function, ψ^∗ is its conjugate, and “n” is the localized time index. From Eq. (8.21) “N” different signals are achieved that are combined using convolution to get a single continuous wavelet transform [100]. To approximate the continuous wavelet transform, the convolution (8.21) should be done “N” times for each scale, where “N” is the number of points in the time series. “N” simultaneous convolutions performed using discrete Fourier transform in Fourier space [100]. The discrete Fourier transform is used on the time series ${x}_{n^{\prime }}$ which is shown in Eq. (8.22):

$$ {\widehat{x}}_k=\frac{1}{N}\sum \limits_{n=0}^{N-1}{x}_n{\mathrm{e}}^{-2\pi ikn/N} $$

(8.22)

where k ranges from 0, 1, 2, …, N − 1. Using Eq. (8.22), Eq. (8.21) can be represented as Eq. (8.23):

$$ {\mathrm{CWT}}_n(a)={\left(\frac{\delta t}{a}\right)}^{\frac{1}{2}}\ \sum \limits_{k=0}^{N-1}{\widehat{x}}_k{\widehat{\psi}}^{\ast}\left(s{\omega}_k\right){\mathrm{e}}^{i{\omega}_k n\delta t} $$

(8.23)

where the angular frequency ω_k is given by Eq. (8.24) [100]:

$$ {\omega}_k=\left\{\begin{array}{cc}\frac{2\pi k}{N\delta t}\ & k\le \frac{N}{2}\\ {}-\frac{2\pi k}{N\delta t}& k>\frac{N}{2}\end{array}\right. $$

(8.24)

The CWT at all the n time indices can be calculated using Eqs. (8.22)–(8.24).

Mexican hat wavelet and the Morlet wavelet more often used continuous wavelets. The mathematical representation of the Morlet wavelet [100, 102] is represented in Eq. (8.25):

$$ \psi \left(\eta \right)={\pi}^{-1/4}{\mathrm{e}}^{i{\omega}_0\eta }{\mathrm{e}}^{-{\eta}^2/2} $$

(8.25)

where ω₀ is chosen as 6 to satisfy the admissibility condition and π^−1/4 is a normalizing factor. The chosen value of ω₀ allows to obtain good time and frequency localization, and in this case Fourier period and the scale are equal. Similar value of ω₀ was also chosen for yielding good results in reference [102].

The wavelet power spectrum (WPS) reveals the information about the fluctuations of variances at different scales or frequencies. The magnitude of signal energy at a particular scale “a” and certain position “n” is computed by the squared modulus of CWT. This is denoted as WPS and is also presented as scalogram. The WPS is normalized by dividing with σ² such that the power relative to white noise is achieved. The WPS is calculated by Eq. (8.26):

$$ \mathrm{WPS}={\left|{\mathrm{CWT}}_n(a)\right|}^2 $$

(8.26)

The normalized WPS is depicted in Eq. (8.27):

$$ {\mathrm{WPS}}_n=\frac{{\left|{\mathrm{CWT}}_n(a)\right|}^2}{\sigma^2} $$

(8.27)

where σ is the standard deviation. The continuous wavelet transform is typically a complex function (real and imaginary part), and thus, modulus would actually mean the amplitude of continuous wavelet transform. The WPS depends on the time and scale (frequency) represented by a surface. The contours of the surface can be plotted on a plane to obtain a time scale representation of WPS. Through WPS important information can be obtained such as events with higher variances and the frequency of their occurrences and the duration of time for which they persist. This information can be used to modify and control the system. The wavelet power spectrum is the distribution of energy within the data, so by observing the WPS regions of large power can be identified, which will provide a better understanding as to the features that are important in the signal. As wavelet has a changing window size in comparison to that of a fast Fourier transform, the variations in frequency of occurrence can be visualized in a WPS. The WPS is contour plot, which has the cycles number (data series) on the x-axis and the Fourier period on the y-axis, and the intensity of the variations in the data series represented in the contour plot. The stronger color in the contour plot indicates a higher variation of the parameter (Fig. 8.39). The period (on y-axis) at which the higher variation occurs, indicates the frequency of stronger variations and the x-axis shows the occurrence of these stronger variations. The color bar in the figures is the logarithm (base 2) of the WPS. For example, a value of −4 on the color scale bar indicates that the WPS is 2^(−4) = 1/16. Similarly, if the value is +4, it indicates the WPS of 16.

Fig. 8.39

WPS and GWS of THR at compression ratios (a) 16, (b) 17, and (c) 18, respectively, at no load conditions

Typically, measured data is discrete and finite length time series. In this particular case, time series of combustion parameters such as IMEP, P_max, ${\theta }_{{\mathit{P}}_{\max }}$, etc. of finite number of cycles are typically used for wavelet analysis. The finite length time series can lead to errors at the start and end of the wavelet power spectrum due to the assumption of cyclic data by Fourier transform. To overcome this issue, the original signal is padded with zeroes at the end of the data series, and these are eliminated after applying wavelet transform. The data series is padded with zeroes to create the total length of data series equal to next nth power of 2, which speed up the Fourier transform and limit the edge effects [100]. Zero padding introduces some discontinuities, and it leads to a decrease in amplitude at the edges. The edge effects become important in cone of influence (COI) region. The COI is characterized as the e-folding time for autocorrelation of wavelet power spectrum at every scale [100]. The e-folding time is considered in such that the magnitude of wavelet power decreases by a factor e⁻² at the edges where discontinuities are present. Therefore, the region inside the COI is considered for wavelet analysis and the outside region is not used for extracting information about time series [100].

Global wavelet spectrum (GWS) is the time average of the WPS and calculated by Eq. (8.28):

$$ \mathrm{GWS}={W}_{\mathrm{s}}=\frac{1}{N}\sum \limits_{n=1}^N{\left|{\mathrm{CWT}}_n(a)\right|}^2 $$

(8.28)

The global wavelet spectrum is represented by W_s. The peak locations in the global wavelet spectrum give an indication about the dominant periodicities in the time data series.

Figure 8.39 shows the time scale representation of the wavelet power spectrum of THR at no load conditions for three different compression ratios 16, 17, and 18. The thick contour lines represent the 5% significance level below which denotes the cone of influence (COI). The COI is the region where edge effects become important and the region inside the COI is considered for analysis and the region outside COI is ignored from analysis.

Figure 8.39a shows that the strongest intensity of variance occurs in the periodic band 221–625 cycles along the COI during 690–1665 cycles. Other weaker bands are 128–315 and 39–157 spanning in the ranges of 545–920 and 1440–1800 cycles, respectively. The presence of strong periodic band over a large number of cycles indicates a high cyclic variability in the no load condition at compression ratio (CR) 16. With the increase in the compression ratio (from 16 to 17), the maximum GWS power decreases from 5250 to 1930, which indicates a decrease in cyclic variations. The period at which maximum GWS power is obtained also shifts from 512 to 16 with an increase in compression ratio (Fig. 8.39), which suggests that frequency of variation also increases with compression ratio. Figure 8.39b shows the WPS and GWS of CR 17, and the strongest intensity bands are found in the period 14–20 cycles in cycles ranging from 50 to 410, 570 to 880, 925 to 955, 1020 to 1070, 1180 to 1550, and 1655 to 1880. As the CR increased to 18, the cycle-to-cycle variations shift to higher period indicating the cyclic variations are occurring with lower frequencies. The WPS of THR at CR 18 is depicted in Fig. 8.39c. The strongest intensity band is observed in the 10–16 periodic band intermittently in 161–347, 453–731, 909–987, 1057–1122, 1230–1319, and 1391–1631 cycles. The GWS indicates a power of 1025 which is lower than the previous cases and symbolizes a decrease in the cycle-to-cycle variations with an increase in compression ratio at no load condition. With the increase in compression ratios, combustion temperature increases, which results in better combustion stability (lower cyclic variations). With the increase in compression ratio, combustion temperature increases along with advanced combustion phasing. The sensitivity of combustion variation decreases at advanced combustion phasing (near TDC) due to high temperature and slow piston speed. Higher combustion temperature in particular combustion cycle leads to higher residual temperature and wall temperature, which affects the next consecutive cycles.

Figure 8.40 shows the time scale representation of the wavelet power spectrum of P_max at no load conditions for different compression ratios. For CR 16, the strongest intensity periodic band 128–625 period occurs in the cycle range of 433–1834 adjacent to the COI, and other weaker periods are observed in the period 32–64 for the cycles ranging in between 467–692, 815–1035, and 1801–1886, respectively (Fig. 8.40a). Maximum GWS power of 4.89 at the period around 350 is shown by GWS in Fig. 8.40a. For an increase in CR to 17, the bands with the highest power are scattered over the entire WPS (Fig. 8.40b). Few of the strong intensity bands are observed in the periods 55–78, 55–96, 96–156, and 156–315 cycles ranging from 1316 to 1420, 826 to 952, 212 to 419, and 1085 to 1631 cycles, respectively. A GWS power of 1 (at period 256) is observed in this case (CR 17), which indicates lower cycle-to-cycle variations, in comparison to 16 compression ratio. Figure 8.40c indicates that the maximum GWS power further decreases to 0.75 (at period 128) for CR 18, which implies that cycle-to-cycle variations have been further diminished. The period at which maximum GWS occurs also decreases with an increase in compression ratio, and a similar trend is observed for THR. Very few strong intensity bands are observed and occur in the period of 46–64, 55–110, and 256–312 cycles and stretch in between 85–215, 1305–1720, and 1327–1536 cycles, respectively, at compression ratio 18.

Fig. 8.40

WPS and GWS of P_max at compression ratios (a) 16, (b) 17, and (c) 18, respectively, at no load conditions

The WPS and GWS of IMEP for various diesel start of injection (SOI) timings for gasoline/diesel RCCI operation is illustrated in Fig. 8.41. In the WPS, the horizontal axis depicts the number of cycles (time scale), and the vertical axis shows the periodicity (frequency scale) of the time series. In the GWS, the peaks of the power depict the prevailing periodicities in the time series. The areas above this COI are only significant and considered in the analysis. Figure 8.41 reveals that variations in IMEP occur at multiple time scales in RCCI engines. Figure 8.41a illustrates the WPS and GWS of IMEP for diesel SOI timing at 10 CAD bTDC for gasoline/diesel RCCI operation. The figure depicted that periodic band of the 4–8 period having higher variations in the cycle ranging from 48 to 68 and 398 to 422 (red color patches represent the higher cyclic variations). Similarly, a periodic band of the 8–16 period has higher variations between the cycles ranging from 70 to 84, 121 to 142, 271 to 284, and 732 to 747. A periodic band of 128–256 period shows higher variations during the cycles 538–660. The periodic band with strong intensity (dark red color) reveals higher variations.

Fig. 8.41

WPS and GWS of IMEP for various diesel SOI timings for gasoline/diesel RCCI operation. (a) WPS of IMEP; Diesel SOI—10 CAD bTDC. (b) WPS of IMEP; Diesel SOI—30 CAD bTDC. (c) WPS of IMEP; Diesel SOI—50 CAD bTDC. (d) WPS of IMEP; Diesel SOI—60 CAD bTDC

Figure 8.41b shows the WPS and GWS of IMEP for diesel SOI timing at 30 CAD bTDC. The figure shows that a periodic band of the 4–16 period with moderate intensity is observed intermittently throughout the cycles. Peak power in the GWS with advanced injection timing, i.e., 30 CAD bTDC (Fig. 8.41b), in comparison to diesel SOI timing at 10 CAD bTDC (Fig. 8.41a) is slightly higher, which indicates higher cyclic variations. Higher cyclic variations are mainly due to lower mean combustion temperature and retarded combustion phasing with advanced diesel injection timing. Further advancing in diesel injection timing from 30 CAD bTDC to 50 CAD bTDC, the peak of the GWS increases which depicts higher cyclic variations. Additionally, the band of period 4–16 with strong intensity of variance observed in the cycle ranging from 24 to 57, 213 to 263, 418 to 486, 563 to 662, 695 to 738, and 829 to 863. Periodicity with strong intensity throughout the combustion cycles reveals to higher cyclic variations. Similarly, Fig. 8.41d shows the periodic band with strong intensity of period 8–16 occurs in the cycles between 13–70, 122–162, 630–686, and 743–765. The peak power in the GWS is also increased for diesel SOI timing at 60 CAD bTDC. It is interesting to note that in the condition of 50 CAD bTDC and 60 CAD bTDC, a significant portion of the spectrogram is empty (white), which means these frequencies are not present. This may be due to misfires (very high cyclic variations or poor combustion efficiency) occurring intermittently throughout the combustion cycles [79]. It is very interesting to note that (Fig. 8.41) the period at which the peak GWS power obtained for conventional dual fuel combustion (retarded combustion timing condition) is shifting from 256 period to 8–16 periodic band for gasoline/diesel RCCI operation. This indicates that the frequency of variations increases with advanced diesel injection timing. In conventional dual fuel operation, combustion initiates with diesel pilot injection, which means the variations in the start of combustion is possible due to the variation in injection parameters. In modern CRDI system, the variations are very minimal at constant demand/setting. Hence, in conventional dual combustion operation, the variations are mainly due to long-term effect (such as wall temperature), which leads to higher period band (lower-frequency) variations. However, in premixed RCCI combustion (advanced DI timings), even combustion initiation is controlled by local equivalence ratio, reactivity, and temperature, where cyclic variations are very likely, which leads to higher-frequency variations. In premixed case, the variations in local equivalence ratio, reactivity, and temperature depends on various conditions such as flow conditions, evaporation of diesel, mixing of droplets and distribution of droplets, etc. even at constant DI timings.

WPS and GWS of IMEP for multiple diesel injections in gasoline/diesel RCCI operation are presented in Fig. 8.42. By keeping pilot diesel injection timing constant at 55 CAD bTDC, main diesel injection timing is swept from 10 to 50 CAD bTDC. Figure 8.42a shows the WPS and GWS of IMEP for diesel main injection timing 10 CAD bTDC. WPS depicts that the strong intensity periodic band of 16–32 and 32–64 period occurs in the cycles ranging from 665 to 708, 722 to 747, and 692 to 734, respectively. The WPS and GWS of IMEP for diesel main injection timing 30 CAD bTDC are illustrated in Fig. 8.42b. The WPS indicates that periodic band with strong intensity of 16–32 and 32–64 period occurring in the cycles ranging from 450 to 575 and 754 to 786, respectively. It is interesting to note that for the same diesel injection timing (i.e., after 30 CAD bTDC) of single and double injection strategy, double injection strategy has a lower peak for GWS. This depicts that double diesel injection has lower cyclic variations in comparison to single injection strategy, which is also confirmed by statistical technique [79]. Similarly, a strong intensity periodic band of 32–64 period occurs in the cycle ranging from 600 to 698 (Fig. 8.42c). For same diesel injection timing of 50 CAD bTDC, double diesel injections have a lower peak of GWS in comparison to single injection strategy. Figures 8.41 and 8.42 also show that in the case of a single diesel injection strategy, the cyclic variations are mainly concentrated in the periodic band of 8–16 (for advanced DI timing), while in the case of double injection strategy, the cyclic variations are distributed in the different periodic bands. This indicates that frequency of variation is higher for single diesel injection strategy in comparison to double injection strategy. In double injection strategy, the fuel injected by pilot injection at very early timings mixes with gasoline mixture and creates partial reactivity stratification, but combustion initiation is mainly triggered by the main injection. Thus, periods of variations will be higher, but periods decrease with advanced main injection timings (Fig. 8.42) because of mainly premixed combustion.

Fig. 8.42

WPS and GWS of IMEP for various main diesel SOI timings for gasoline/diesel RCCI operation. (a) WPS of IMEP; Main DI—10 CAD bTDC. (b) WPS of IMEP; Main DI—30 CAD bTDC. (c) WPS of IMEP; Main DI—50 CAD bTDC

8.5 Nonlinear and Chaotic Analysis of Combustion Stability

The nonlinear dynamics in the combustion variations can be revealed through nonlinear analysis. Traditional statistical methods are not able to provide the information regarding the temporal variations. The autocorrelation and Fourier transform can provide the linear temporal correlations. However, nonlinear factors can govern the combustion variation dynamics in the reciprocating engines. Thus, nonlinear time series analysis methods such as return maps, Poincare sectioning, mutual information, modified Shannon entropy, data symbolization, etc. can provide additional information/features which are not revealed by traditional measures. Table 8.1 compares the linear and nonlinear signal processing methods [107].

Table 8.1 Comparative analysis of linear and nonlinear signal processing [107]

Nonlinear analysis techniques are used to detect the information linked to temporal correlations, and it is used to discern prior-cycle effects. Nonlinear analysis methods for combustion stability analysis in reciprocating engines are discussed in the following subsections.

8.5.1 Phase Space Reconstruction

The phase space (or state space) of a dynamical system is a mathematical space with orthogonal coordinate directions representing each of the variables needed to specify the instantaneous state of the system [108]. Several approaches in nonlinear data analysis fundamentally start with the construction of a phase space portrait of the considered system. Phase space of a dynamical system is defined as a finite-dimension vector space Rⁿ, and a state is specified by a vector x ∈ Rⁿ [109]. A point in phase space diagram represents a completely defined state of the system [87]. Thus, the time series of the system occurs as an orbit or trajectory in the phase space representing the time evolution, the dynamics, of the system. The shape of the trajectory of points in the phase space provides guidance regarding the characteristics of the dynamical system such as periodic or chaotic systems. Chaos has a structure in phase space [107].

In systems like reciprocating engines, a time series of measured in-cylinder pressure or calculated combustion parameters on crank angle basis or cycle-to-cycle basis is available for analysis. The observed time series needs to be converted into state vectors for phase space reconstruction. The conversion into state vectors is typically done by time delay embedding, derivative coordinates, or principal component analysis [109]. A d-dimensional system is possible to be reconstructed in a m-dimensional phase space by using time delays and m ≥ 2d + 1 for an adequate reconstruction [110]. Time delay embedding comprises of creating a state space trajectory matrix X from the measured time series x by the time delay (τ) coordinates as shown in Eq. (8.29):

$$ \left\{\begin{array}{l}{X}_1=x(t),\\ {}{X}_2=x\left(t+\tau \right),\\ {}\vdots \\ {}{X}_m=x\left(t+\left(m-1\right)\tau \right).\end{array}\right. $$

(8.29)

Alternatively, derivative coordinates can be used for phase space reconstruction (Eq. 8.30). The derivative coordinates have the advantage of their clear physical meaning [109]:

$$ \left\{\begin{array}{l}{X}_1=x(t),\\ {}{X}_2=\frac{dx(t)}{dt},\\ {}\vdots \\ {}{X}_m=\frac{d^{m-1}x(t)}{dt^{m-1}}.\end{array}\right. $$

(8.30)

Figure 8.43 shows the phase spaces generated using measured cylinder pressure data of 100 cycles for different equivalence ratios (Φ = 0.781, 0.677, 0.595, 0.588, and 0, respectively) in a spark ignition engine. Phase spaces are created using derivative coordinates as shown in Eq. (8.31):

$$ \left\{\begin{array}{c}X=p\left(\varphi \right),\\ {}Y=\frac{d p\left(\varphi \right)}{d\varphi},\\ {}Z=\frac{d^2p\left(\varphi \right)}{d{\varphi}^2}.\end{array}\right. $$

(8.31)

Fig. 8.43

Phase spaces reconstructed using measured pressure time series at different equivalence ratio [109]. (a) Case A1. (b) Case A2. (c) Case A3. (d) Case A4. (e) Case A5

Figure 8.43a depicts that the part of the phase space diagram shows very small variations of different trajectory cycles and close to the peak pressure position, with an obvious divergence between each cycle. Figure 8.43a, b shows well-developed combustion at the point of peak pressure because the trajectories disperse adequately at that point. However, the well dispersion part in projection plans is pushed to the area after the point of peak pressure (Fig. 8.43c, d). With the decrease in equivalence ratio, both the beginning and the end of combustion phase are delayed. Figure 8.43a–d shows that, although the curves in phase space diagram show obvious cyclic variations, these curves are rather well confined in the phase space and well organized. Therefore, cylinder pressure evolution could be possibly governed by a dynamics with deterministic components [109]. Poincaré section can be used to reduce the dimension of the phase space and reveal a structure, which can further identify the patterns of the dynamical behavior of time series.

Two of the most important parameters are time lag (τ) and embedding dimension (m) in the process of phase space reconstruction. Figure 8.44 shows the effect of time delay on the phase space portrait of cylinder pressure of a spark ignition engine. The normalized in-cylinder pressure time series is used to avoid the influence of pressure units. In case of too short time delay, the coordinates P(i) and P(i + τ) will not be independent enough, which means not enough time will have evolved for the dynamical system to have explored enough of its state space to generate the new information about that state space. In case of too large time delay, any connection between the measurements P(i) and P(i + τ) is numerically equivalent to being random with respect to each other because chaotic systems are intrinsically unstable [107].

Fig. 8.44

Phase space portrait of normalized cylinder pressure for time lag of (a) τ = 1, (b) τ = 48, and (c) τ = 92 in SI engine operated at stoichiometric mixture [111]

The simple way to determine the time delays is the autocorrelation function method, and it is commonly used although a linear method [87, 111]. This method is relatively simple for calculation (Eq. 8.32), and it can be used as the phase space reconstruction is not so sensitive to time delay [111]:

$$ C\left(\tau \right)=\frac{\sum \left[{P}^{\prime}\left(i+\tau \right){P}^{\prime }(i)\right]}{N} $$

(8.32)

The optimal time lag (τ) value is chosen when the value of the autocorrelation function (C(τ)) decreases to C(0)/e. It was found that the value of autocorrelation function decreases to C(0)/e and zero at 48 and 92, respectively (Fig. 8.44). The figure shows that the attractor of the combustion process is fully unfolded when time delay τ = 48, and thus, the optimal τ value can be determined at which C(τ) = C(0)/e [111].

An alternative method of time lag determination is the average mutual information (AMI) [112]. However, AMI needs a larger scale of calculations. The time lag at which the first minimum of mutual information occurs can be considered as time lag for phase space construction [107]. Mutual information is an analysis tool based on information theory that measures univariate temporal coupling (i.e., the predictability in a signal). Mutual information-based method for detecting temporal relationships is more powerful than autocorrelation because it is equally sensitive to linear and nonlinear structure [75].

The mutual information between two time series at time delay τ in bits can be calculated by Eq. (8.33):

$$ \mathrm{MI}\left(\tau \right)=\sum \limits_{x_i=1}^N\sum \limits_{x_j=1}^Np\left({x}_i,{x}_j\right)\mathrm{lo}{\mathrm{g}}_2p\left({x}_i,{x}_j\right)-\sum \limits_{x_i=1}^Np\left({x}_i\right)\mathrm{lo}{\mathrm{g}}_2p\left({x}_i\right)-\sum \limits_{x_j=1}^Np\left({x}_j\right)\mathrm{lo}{\mathrm{g}}_2p\left({x}_j\right) $$

(8.33)

where x_i is the time series value at time t, x_j is the time series value at time t + τ, p(x_i) is the individual probability density for x_i, p(x_j) is the individual probability density for x_j, and p(x_i, x_j) is the joint probability density for x_i and x_j. The probability functions can be calculated by binning the data and constructing histograms [75].

One of the most common methods to determine the value of the embedding dimension (m) is the false nearest neighbors (FNN) [113]. The m value is selected as the embedding dimension at which the percentage of FNN decreases to approximately 0%. The FNN can be calculated as shown in Eq. (8.34):

$$ {f}_m(i)={\left[\frac{R_{m+1}^2(i)-{R}_m^2(i)}{R_m^2(i)}\right]}^{1/2}=\frac{\left|{p}^{\prime}\left(i+ mn\right)-{p}^{\prime \mathrm{MM}}\left(i+ mn\right)\right|}{R_m\left(\mathrm{i}\right)} $$

(8.34)

where p′(i) is the normalized time series of pressure data, n is equal to τ/t, t is the sampling time interval, p′^MM(i) is the nearest neighbor of p′(i), and R_m(i) represents the distance between p′(i) and p′^MM(i) when the embedding dimension is m [111].

8.5.2 Poincaré Section

To determine the structure in the attractor, the Poincare section is used to reduce the dimension of the phase space. This method reduces one dimension of the phase space portrait. An invertible map can be constructed on the section by following the trajectory of the flow. The iterates of the map are given by the points where the trajectory intersects the section in a specified direction [109]. It is easier to analyze the distribution of these points because the Poincaré section has a lower dimension. Figure 8.45 shows the Poincare section of phase spaces shown in Fig. 8.43. Poincaré section reduces the dimension of the earlier phase space (Fig. 8.43) to a two-dimensional representation, which can be used to identify patterns of the dynamical behavior. Poincaré sections defined by Eq. (8.35) are shown in Fig. 8.45:

$$ {\sum}_{XZ}=\left\{\left(X,Y\right)\left.\in {\Re}^2\right|Y=0,Z\le 0\right\}. $$

(8.35)

Fig. 8.45

Poincare sections in corresponding phase spaces in Fig. 8.43 for case1-case5 [109]

Figure 8.45a shows that the combustion strongly dominates the cylinder pressure development and a straight band of points with inverse ratio indicating linear deterministic characteristics in the Poincaré section. The Poincaré section reveals a bifurcation structure (Fig. 8.45b), in which a short branch appears at the upside of the main band. This structure suggests an unstable trend of combustion [109]. A more obvious bifurcation occurs with a decrease in equivalence ratio, which suggests that the domination of deterministic components to the cylinder pressure development is weakened further (Fig. 8.45c). Further reduction in equivalence ratio, the Poincaré section displays a more erratic structure with high levels of dynamic noise indicating stronger stochastic characteristics (Fig. 8.45d) [109].

8.5.3 Return Maps

Most commonly used phase spaces are return maps, which have embedding dimension of two and delay time selected to one. Return map provides a simple way to study the interactions between consecutive events. In reciprocating engines, the return maps can be used to determine the inherent deterministic interaction between combustion cycles qualitatively [2, 114]. Consecutive engine cycles are not interrelated in random time series of combustion events, and the return map shows an unstructured cloud of data points collected around a fixed point. The return map reveals more structures such as dispersed data points about a diagonal line when the deterministic coupling between combustion cycle exists [90]. In return maps, pairs of consecutive data series values of combustion parameters (cycle i versus cycle i + 1) are plots with each other (Fig. 8.46). Data point of each cycle relates to the next successive cycle through the general statistical picture of the whole cycles interrelation using return map plots [71].

Fig. 8.46

Return map of ${\theta }_{{\mathit{P}}_{\max }}$ for different octane numbers (ON) in HCCI combustion for 3000 consecutive engine cycles [71]

Figures 8.46 and 8.47 show the return maps ${\theta }_{{\mathit{P}}_{\max }}$ and heat release for HCCI combustion using primary reference fuel (PRF) where octane number (ON) varies from 3 to 7. Return maps for octane number three (ON = 3) show an unstructured cluster of circular data collected around a fixed point (Figs. 8.46a and 8.47a), indicating stochastic variations in the combustion cycle. The combustion is relatively stable with octane number three as relatively lower dispersion. Further increasing the octane number, the fixed concentrated points (as with ON = 3) start to destabilize in certain directions of the return map, and the highest levels of destabilization occur for ON 6 and 7 (Figs. 8.46 and 8.47). The data points scattered over diagonal line. The structured patterns of return map can be attributed to the deterministic coupling between consecutive cycles [71]. The functional form (Eq. 8.36) at cycle (i) using previous cycles can be used to characterize the dynamics of a combustion parameter (e.g., ${\theta }_{{\mathit{P}}_{\max }}$):

$$ {\theta}_{P_{\mathrm{max}}}(i)=f\left({\theta}_{P_{\mathrm{max}}}\left(i-1\right),{\theta}_{P_{\mathrm{max}}}\left(i-2\right),\dots, {\theta}_{P_{\mathrm{max}}}\left(i-\left(L-1\right)\right)\right) $$

(8.36)

Fig. 8.47

Return map of heat release for different octane numbers (ON) in HCCI combustion for 3000 consecutive engine cycles [71]

Chaotic methods like return maps and symbol sequence techniques (see Sect. 8.5.4) are used to estimate the approximate function f and value of L. A random time data series having an unstructured cluster of data points on return map tends to produce a high-dimensional function f [90]. Thus, the return maps of ON 5–7 (Fig. 8.46) suggest a relatively low value of L. Additionally, Fig. 8.46 indicates that the function f is a nonlinear function [71]. Pattern in the return map is also dependent on the combustion parameters (Figs. 8.46 and 8.47) in the unstable combustion zone. Combustion parameters such as P_max, IMEP, combustion duration, combustion phasing, etc. can also be used for generating a return map for combustion stability analysis.

Typically, low-temperature combustion (LTC) engines have intrinsically high sensitivity for small fluctuations in the engine running conditions. Thus, the control system is required which should be able to satisfactorily respond to such disturbances on cycle-to-cycle basis [2]. Figure 8.48 shows the complex dynamics of heat release using return maps during SI to HCCI combustion mode transition. The differences in combustion modes can be observed from the heat release return maps (Fig. 8.48). Data points are collected in a small unstructured cluster of around a fixed point in SI combustion (Fig. 8.48a) which shows the nominal flame propagation heat release [90].

Fig. 8.48

Heat release return maps during the transition from (a) stable SI combustion to (e) HCCI operation using increased levels of internal EGR [90]

In typical port fuel-injected SI combustion, data is slightly dispersed on the return map indicating the stochastic or high-dimensional component (Fig. 8.48a). With the increase in internal EGR during the transition, the cyclic variations increases, and data points on return map scatter in particular directions (Fig. 8.48b), which indicates unstable manifolds in low-dimensional phase space [90, 107]. The level of destabilization reaches to a maximum with a further increase in EGR (Fig. 8.48c), and combustion again starts to become more stable (Fig. 8.48d). Finally, in HCCI combustion mode, combustion is stabilized, and scatters in return map is eliminated with concentrating the data points around a fixed point (Fig. 8.48e).

Figure 8.49 shows the return map of combustion phasing (CA₅₀) at different relative air-fuel ratio (λ) in an HCCI engine. For lean combustion (λ = 2.8), return map of combustion phasing shows a circular cloud indicating stochastic component. For rich combustion (λ = 2.3), the return map of the combustion phasing distribution shows flat distribution along the diagonal line. In this case, it is difficult to find correlation as skewed distributions can also produce dispersed data leading to complication in the return map analysis [2]. Generation of return map using normalized value (or quantile values) can solve this issue of visualization on the return map. The dataset of N values can be converted into another data set of N quantile values by replacing the lowest data value to 1/N, next lowest to 2/N, such that the maximum data value is assigned a value of 1 (N/N = 1). However, it is essential to ensure that the sequence of data is not disturbed. During this process, all the data points are converted into values between 0 and 1. In this process, highly skewed distribution is converted to a uniform distribution of data points evenly distributed between 0 and 1 [115]. Thus, an uncorrelated data will show a uniform density of data points on the return map using quantile values, and correlated data have nonuniform (higher and lower) densities of data points on the map [115]. Return maps using quantile values of combustion phasing for the lean and rich condition is shown in the right of Fig. 8.49. The figure shows that the leaner mixture has a relatively uniform distribution of data points and richer mixture has uneven distribution in the density. The nonuniform densities of data points indicate a deterministic dependency on the previous combustion cycles [2].

Fig. 8.49

Return maps for combustion phasing with a lag of one cycle for different λ in HCCI engine

8.5.4 Symbol Sequence Statistics

Symbol sequence statistics method is very useful for time series data analysis, which can provide important insight into the behavior of different combustion parameters of reciprocating engines. Deterministic and stochastic behaviors can be identified with this approach. The presence of determinism in combustion parameters indicates that intelligent control of the system can extend the limits of engine operation over a wide range [2]. The deterministic information can be effectively used by controllers, and small variations in control input parameters/actuators can shift back the engine to stable operating conditions [116]. Control of cyclic variations in HCCI engine is demonstrated using symbol-statistics predictive approach [71]. Symbol generation process and histogram analysis are discussed in the following subsections.

8.5.4.1 Symbolization

Symbolization of combustion data of the engine can be very advantageous and effective to analyze the pattern when data contains measurement noise and/or has measurement errors. For correctly selected partition number, symbolization can also correctly estimate the deterministic effect of the previous cycle or inherent structure in the time series. A dynamic noise appears if the number of partition is higher. Symbolization of data can also act as a data compression methodology, which leads to relatively faster data processing during data acquisition. These characteristics of symbolization make it an effective tool for real-time control and onboard diagnostics of the engine [117, 118].

Symbolization of data converts it into a series of data with symbols. Figure 8.50 illustrates the process of symbolization of data using the binary partition. The times series data first divides the data into two equiprobable partitions in such a way that both the partitions contain the same number of data points. The data above the partition line is assigned a symbol “1,” and below is assigned symbol “0” (Fig. 8.50). This data conversion results in a series of binary symbols. After data conversion into symbols, the frequency of occurrence of particular sequence length (3 in Fig. 8.50) is computed. The total number of possible sequences “N_seq” is dependent on the number of partition (n_part) or number of symbols and selected symbol sequence length “L.” The total number of possible sequences can be calculated by Eq. (8.37):

$$ {N}_{\mathrm{seq}}={\left({n}_{\mathrm{part}}\right)}^L $$

(8.37)

Fig. 8.50

Illustration of symbol generation process and presenting a symbol sequence histogram [117]. (a) Data series. (b) Symbol-sequence histogram

For three sequence length in the binary partition (Fig. 8.50), six (2³) sequences are possible that can be presented in a binary or decimal format (as shown in Fig. 8.50). To generate a histogram, the number of occurrences of every sequence is counted and presented as bar as illustrated in Fig. 8.50b.

Figure 8.51 further illustrates the symbolization of 1000 combustion phasing (CA₅₀) data using the binary partition. Binary partition is the simplest partition, where data is divided into two equiprobable partitions using the median of the data. The combustion phasing values below the median are assigned symbol “0” and above the median “1.” More than two partitions can also be possible leading to a different number/symbol system (e.g., 0, 1, 2, 3, 4, 5, 6, and 7 for n_part = 8). The sequence of symbols depicts important information regarding the combustion dynamics. The relative frequency corresponding to each possible sequence number is shown in Fig. 8.51 for sequence length of six. Sixty-four possible numbers (2⁶) are represented in the decimal format on the x-axis of Fig. 8.51b. In this method, the relative frequency of truly random data is equal due to an equal number of values in each partition. All histogram bins will be equally probable within the uncertainty due to the finite data set. Therefore, significant deviation from equiprobability (for truly random data) indicates the deterministic structure or time correlation in the data [118]. The baseline frequency F_b for purely random data can be calculated using Eq. (8.38) [116]:

$$ {F}_{\mathrm{b}}={\left(\frac{1}{n_{\mathrm{part}}}\right)}^L $$

(8.38)

Fig. 8.51

(a) Symbolization of combustion phasing, (b) relative frequency of symbols using sequence length of six

This baseline frequency for the combustion phasing data in Fig. 8.51b is represented by the thick red line. Therefore, the sequences appearing as peaks rising above the red line (F_b) corresponds to repeating deterministic events on the histogram plot (Fig. 8.51b). However, selection of appropriate sequence length and partition is essential for accurate analysis using symbolization method.

8.5.4.2 Modified Shannon Entropy

Shannon entropy is a statistic derived from information theory that measures the degree of predictability in a time series, and it is useful for detecting dynamic patterns [75]. The optimal sequence length for creating a symbol sequence histogram can be computed using a modified form of Shannon entropy. A modified form of Shannon entropy is used to quantify the deviation of symbol statistics from randomness [116, 119]. Modified Shannon entropy value “1” indicates a purely random data series and for values less than “1” suggests a correlation between sequential points. The modified Shannon entropy (H_s) can be calculated by Eq. (8.39):

$$ {H}_{\mathrm{s}}=\frac{1}{\log\;{n}_{\mathrm{s}\mathrm{eq}}}\sum \limits_k{p}_k\;\log\;{p}_k $$

(8.39)

where p_k is the probability with which sequence “k” occurs and n_seq is a total number of sequence with non-zero probability.

Figure 8.52 shows the variation of modified Shannon entropy with symbol sequence length for different octane numbers in HCCI engine (conditions shown in Fig. 8.46). In this calculation, the octal partition is used. The value of modified Shannon entropy varies as the sequence length, and it is found minimum at a sequence length of 3. Thus, it can be assumed that it is an optimal sequence length for this partition and combustion parameter. Another method based on joint probability distribution to predict the next cycle occurrence using previous cycle information is used to determine the optimal sequence length [71]. The joint probability histograms provide the maximum likelihood probability of the next cycle based on the occurrence of previous cycles. Then, based on a comparison of the one-cycle ahead predictions for different values of L, an optimal value of L can be determined.

Fig. 8.52

The variation of modified Shannon entropy with symbol sequence length for different octane numbers in HCCI engine [71]

The optimal combination of a number of partition and sequence length is required in symbol sequence method for effective control strategy. To determine the optimal combination of number of partition and sequence length, a matrix of values for both ranging 2–10 is calculated as shown in Fig. 8.53. The figure shows that for binary partition the optimal sequence length (minimum Shannon entropy) seems to be 8 or 9 for all the test condition. For 6–8 number of partitions, the optimal sequence length seems to be 3 where Shannon entropy is minimum. Figure 8.53 shows that the optimal combination of a number of partition and sequence length depends on the engine operating conditions [120].

Fig. 8.53

Variation of modified Shannon entropy with sequence length and number of partition at (a) λ = 2.0, (b) λ = 2.2, (c) λ = 2.4, and (d) λ = 2.6 in a HCCI engine [120]

8.5.4.3 Symbol Sequence Histograms

The symbol sequence histogram is used to find the sequence with a higher frequency above the baseline frequency for purely random data. The highest frequency provides the most repeated pattern in the data series. Figure 8.54 shows the symbol sequence histogram for combustion duration and IMEP data series at different relative air-fuel ratio using octal partition and sequence length 3. Sequence having higher relative frequency than baseline frequency shows the determinism in the data series. Figure 8.85a shows that frequency of sequence number increases more as the engine is operated at the richer mixture. The relative frequency at richer mixture is highest for the richest mixture (λ = 2.0) in case of combustion duration data series. However, with IMEP data series, the number of sequence numbers having a higher frequency than baseline are higher for leanest mixture operation (λ = 2.6), indicating a higher number of deterministic patterns. Thus, two combustion parameters combustion duration and IMEP behave differently for the determination of deterministic patterns. Therefore, it is important to select a right number of partitions and sequence length for a particular combustion parameter [120].

Fig. 8.54

Symbol sequence histograms of (a) combustion duration (b) IMEP for different λ using octal partition and sequence length 3 [120]

Figure 8.55 shows the symbol sequence histograms of combustion phasing for different λ in HCCI engine at 1800 rpm using octal partition and sequence length 3. The figure shows that the richest mixture has a higher number of sequences above baseline frequency indicating more deterministic patterns. The sequence codes that occur more frequently with higher frequency are 0, 8, 16, 64, 128, 276, and 511. These numbers when converted from decimal to octal number corresponds to sequence 0–0–0, 0–1–0, 0–2–0, 1–0–0, 2–0–0, 4–2–4, and 7–7–7. The two sequences 0–0–0 and 7–7–7 represent the steady behavior of combustion timing. Other patterns indicate that advanced-to-retard and retard-to-advanced timing combustion events are dominant.

Fig. 8.55

Symbol sequence histograms of combustion phasing for different λ at 1800 rpm using octal partition and sequence length 3

8.5.4.4 Time Irreversibility

Time irreversibility is defined such that a qualitative or quantitative description of a time series is indistinguishable from a time-reversed version of itself [75]. Qualitatively time irreversibility can be depicted from the return map, which shows symmetry about diagonal for reversible data and significant bias for irreversible data. Nonstationarity in the data increases the possibility of observing time irreversibility.

Time irreversibility can be quantified using symbol sequence histograms because the relative frequencies will shift when the data series is used in backward time. There should be no significant variation in the histogram for the backward time series if the data measures are time symmetric. To compare forward- and reverse-time histograms, a quantified statistic can be defined by Eq. (8.40) [75, 121]:

$$ {T}_{\mathrm{irr}}=\sqrt{\sum \limits_i{\left(F-R\right)}^2} $$

(8.40)

where “i” is indexed over all possible sequence codes . F and R are the symbol sequence histogram frequencies for the forward- and reverse-time analyses, respectively. The magnitude of T_irr quantifies the level of time irreversibility.

8.5.5 Recurrence Plot and Its Quantification

Recurrence plot (RP) method is first introduced by Eckmann et al. [122] in 1987 to visualize the time-dependent behavior of the dynamics of systems, which were used later for the identification of nonlinear systems with various possible behaviors [123,124,125,126]. A recurrence plot is a useful tool to visualize recurrences of phase space trajectories, and it provides a qualitative description of the dynamics of a time series. The recurrence plot efficiently visualizes recurrences mathematically expressed by matrix given by Eq. (8.41) [123, 127]:

$$ {R}_{i,j}^{m,\epsilon }=\varTheta \left(\epsilon -\left\Vert {\boldsymbol{X}}_{\boldsymbol{i}}-{\boldsymbol{X}}_{\boldsymbol{j}}\right\Vert \right),\kern1em i,j=1,\dots, N $$

(8.41)

where N is the number of measured points X_i, ε is a threshold distance, Θ (٠) the Heaviside function (i.e., Θ (x) =0, if x < 0, and Θ (x) =1 otherwise), and ||٠|| is a norm. For the analysis of combustion cycles of reciprocating engines, X_i can be heat release, combustion phasing, or IMEP based time series data. The phase space vectors for one-dimensional cycle-based time series observations can be reconstructed by using time delay method, X_i = (x_i, x_i+τ, …, x_{i + (m−1)τ}), where τ is the time delay and m is the embedding dimension [110]. The dimension m can be determined using the method of false nearest neighbors [125]. Since R_i,i = 1 (i = 1, …, N) by definition, the recurrence plot has a black main diagonal line, the line of identity (LOI), with angle of π/4 [127]. It is possible to classify the dynamics of the system by its characteristic patterns showing diagonal, vertical, or horizontal structure of lines using recurrence plot method [126, 128]. This method (applied to time series) is capable of distinguishing chaotic and stochastic behavior [126]. A pattern for a stochastic system is based on uniform distribution of points in the recurrence plot, while a chaotic system possesses structure of lines with finite lengths. On the other hand, in a case of the intermittent motion [129], a vertical stripe structure is expected [121,122,123,124,125,126,127,128,129,130,131]. In recurrence plot, the abrupt changes in dynamics and extreme events are characterized by white areas or bands, and oscillating systems have diagonally oriented or periodic recurrent structures (i.e., diagonal lines or checkerboard patterns) [91].

Figure 8.56 shows the recurrence plot for IMEP at different engine speeds of 1000, 1200, 1400, 1600, 1800, and 2000 rpm, respectively, in a diesel engine. Figure 8.56a, c–e shows several vertical lines identifying the presence of intermittency in the IMEP time series. A series of lines with unit slope parallel to the main diagonal line is observed at engine speed of 1200 rpm (Fig. 8.56b), which indicate a more regular oscillatory behavior [91]. Interestingly, the recurrence plot has a checkerboard structure indicating a regular oscillatory behavior also at the maximum speed of 2000 rpm (Fig. 8.56f) similar to Fig. 8.56b.

Fig. 8.56

Recurrence plots of the IMEP for different engine speeds (n = (a) 1000, (b) 1200, (c) 1400, (d) 1600, (e) 1800, and (f) 2000 rpm) in a diesel engine [91]

Recurrence quantification analysis (RQA) provides measures of complexity quantifying structures in a recurrence plot [123]. The first measure of RQA is the recurrence rate (RR) or percent of recurrences given by Eq. (8.42), which counts the black dots in the recurrence plot [127]. It is a measure of the density of recurrence points:

$$ \mathrm{RR}\left(\epsilon \right)=\frac{1}{N^2}\sum \limits_{i,j=1}^N{R}_{i,j}^{m,\epsilon } $$

(8.42)

RQA can be used to identify vertical or diagonal lines through the maximal lengths L_max and V_max for diagonal and vertical lines, respectively, given by Eqs. (8.43) and (8.44) [123]:

$$ {L}_{\mathrm{max}}=\max \left(\left\{{l}_i;\kern0.5em i=1,\dots, {N}_l\right\}\right) $$

(8.43)

$$ {V}_{\mathrm{max}}=\max \left(\left\{{v}_i;\kern0.5em i=1,\dots, {N}_v\right\}\right) $$

(8.44)

RQA also enables to perform probability p(l) or p(v) distribution analysis of lines according to their length l or v (for diagonal and vertical lines). Practically they are calculated by Eq. (8.45) [126, 127]:

$$ p(x)=\frac{P^{\epsilon }(x)}{\sum_{x={x}_{\mathrm{min}}}^N{P}^{\epsilon }(x)} $$

(8.45)

where x = l or v depending on diagonal or vertical structures in the specific recurrence diagram and P^ε (x) is probability for a given threshold value ε.

The measures of entropy refer to the Shannon entropy of the frequency distribution along the diagonal and vertical line length given by Eqs. (8.46) and (8.47) and reflect the complexity of the deterministic structure in the system [123, 126, 127]. The larger value indicates more complex deterministic structure.

$$ {L}_{\mathrm{ENTR}}=-\sum \limits_{l={l}_{\mathrm{min}}}^Np(l)\mathrm{lnp}(l) $$

(8.46)

$$ {V}_{\mathrm{ENTR}}=-\sum \limits_{v={v}_{\mathrm{min}}}^Np(v)\mathrm{lnp}(v) $$

(8.47)

Other measures of RQA like determinism (DET) are given by Eq. (8.48), calculated using probabilities. Determinism (DET) is the measure of the predictability of the examined time series that gives the ratio of recurrent points formed in diagonals to all recurrent points. It can be noted that in a periodic system, all points would be included in the lines [123].

$$ \mathrm{DET}=\frac{\sum_{l={l}_{\mathrm{min}}}^N{lP}^{\epsilon }(l)}{\sum_{i,j=1}^N{R}_{i,j}^{m,\varepsilon }} $$

(8.48)

Laminarity (LAM) is a similar measure which corresponds to points formed in vertical lines, given by Eq. (8.49). This measure is telling about dynamics behind sampling point changes. For small point-to-point changes, the consecutive points form a vertical line [123]. It indicates the extent of laminar phases or intermittency in the time series [91].

$$ \mathrm{LAM}=\frac{\sum_{v={v}_{\mathrm{min}}}^N{vP}^{\epsilon }(v)}{\sum_{v=1}^N{vP}^{\epsilon }(v)} $$

(8.49)

Trapping time (TT) is given by Eq. (8.50) calculated using probabilities:

$$ \mathrm{TT}=\frac{\sum_{v={v}_{\mathrm{min}}}^N{vP}^{\epsilon }(v)}{\sum_{v={v}_{\mathrm{min}}}^N{P}^{\epsilon }(v)} $$

(8.50)

Trapping time (TT) refers the average length of vertical lines measuring the time scale (in terms of sampling intervals) of these small changes in the examined time history [123]. This parameter describes how long the system remains in a specific laminar phase.

Figure 8.57 shows the different RQA parameters with engine speed for a recurrence plot shown in Fig. 8.56. The figure shows that L_ENTR is largest at 1800 rpm engine speed indicating higher structural complexity [91]. Additionally, at this speed (1800 rpm), the parameters LAM and TT have their minimum values, while DET shows its minimum value at 2000 rpm. The small value of DET indicates low predictability, whereas the small values of LAM and TT, respectively, indicate a dominance of large fluctuations and a short duration of time spent in a laminar phase in the intermittent dynamics [91].

Fig. 8.57

Variations of (a) DET and LAM, (b) L_ENTR and V_ENTR, and (c) TT with engine speed, for the same value of RR = 0.2 [91]

8.5.6 0–1 Test

The 0–1 test is proposed for investigation of the dynamical system and tests whether the system is regular or chaotic [132,133,134]. In comparison to conventional methods, the advantages of 0–1 test are as follows: (1) it can be applied to any deterministic dynamical system directly and universally, (2) this method does not require the phase space reconstruction, (3) this method requires relatively less computational effort, and (4) the output is intuitive with only one value, approximately equal to 0 or 1, based on whether the system is regular or chaotic [135]. The errors due to the selection of embedding dimensions and time lag are eliminated in this method because it does not require the phase space construction.

Combustion instability is typically analyzed using measured cylinder pressure. The measured cylinder pressure time series P(j) is converted into new coordinates (u(n), v(n)) by Eq. (8.51) [135]:

$$ u(n)=\sum \limits_{j=1}^nP(j)\cos (jc)\kern1em \mathrm{and}\kern1em v(n)=\sum \limits_{j=1}^nP(j)\sin (jc) $$

(8.51)

where c in range (0, π) is a random frequency and n = 1, 2, 3… .

The form of coordinates is changed to reduce the effect of potential resonance caused by the choice of c frequency. Suitable choice of c is crucial in the application of 0–1 test. Normalized pressure values are used to remove the effect of pressure units. The final coordinates used for combustion analysis is computed using Eq. (8.52) [135]:

$$ u(n)=\sum \limits_{j=1}^n{P}^{\prime }(j)\cos \left(\psi (j)\right)\kern1em \mathrm{and}\kern1em v(n)=\sum \limits_{j=1}^n{P}^{\prime }(j)\sin \left(\psi (j)\right) $$

(8.52)

$$ \psi (j)= jc+\sum \limits_{h=1}^jP(h)\kern1em \mathrm{and}\kern1em {P}^{\prime }(j)=\frac{P(j)-{P}_{\mathrm{mean}}}{\sigma_{\mathrm{P}}} $$

(8.53)

where P_mean is the mean value of the pressure time series and σ_P is the standard deviation of pressure time series.

Quantitative characterization of function in Eq. (8.52) is performed by the mean square displacement (MSD), which is calculated by Eq. (8.54) in the new (u, v) plane:

$$ \mathrm{MSD}(n)=\underset{N\to \infty }{\lim}\frac{1}{N-n}\sum \limits_{j=1}^N\left\{{\left[u\left(j+n\right)-u(j)\right]}^2+{\left[v\left(j+n\right)-v(j)\right]}^2\right\} $$

(8.54)

Distribution characteristics of MSD characterized the regular and chaotic time series. The MSD is bounded in time for regular time series, while it grows linearly with time for chaotic time series. The dynamics of the time series can be further characterized by computing the asymptotic growth rate K_c, which can be calculated by Eq. (8.55):

$$ {K}_c=\frac{\operatorname{cov}\left(n,\mathrm{MSD}(n)\right)}{\sqrt{\mathrm{Var}(n)\mathrm{Var}\left(\mathrm{MSD}(n)\right)}} $$

(8.55)

where cov(n, MSD(n)) is the covariance of two different time series and var(n) is the cov(n, n). Averaging the K_c values on c in (0, π), the final 0–1 test result K is calculated. The K values provide the quantitative information regarding the dynamics of the process. The K value is close to 0 for regular time series, while it approaches to 1 for chaotic time series. Typically, K ≥ 0.7–0.8 is considered as the chaotic regions [133, 135,136,137].

Figure 8.58 shows the cylinder pressure time series (u, v) planes at c = 2.5 for motoring and different fuel injection timings in natural gas SI engine . Figures 8.59 and 8.60 show the corresponding MSD versus n (at various c values) and K_c (asymptotic growth rate) versus c. In the motoring engine operating conditions (Fig. 8.58a), the pressure time series shows the bounded behavior indicating a regular time series. However, the cylinder pressure time series at different injection timings (Fig. 8.58b–h) show unbounded Brownian (random) behavior in u–v plane. Similarly, all the MSDs for different injection timings (Fig. 8.59b–h) show an approximately linear increase (unbounded) with n for various c values. The MSD values show bounded behavior for motoring condition (Fig. 8.59a), indicating regular behavior. The K_c values for different injection timings (Fig. 8.60b–h) show close to 1 for all the cases with a certain level of fluctuations. The observations from Figs. 8.58 to 8.60 clearly indicate that the combustion process of this engine is a chaotic dynamical system [135]. In motoring engine operation, the K value is 0.077, which clearly indicates that this process is regular. It can be further observed that K value first increase and then decreases with increasing injection timings and has larger K values for 45–60 °CA injection timing after intake TDC . The larger K values indicate the stronger chaotic behavior at those particular fuel injection timings.

Fig. 8.58

The (u, v) planes of cylinder pressure time series for motoring condition (a) and different injection timings (b) 0 °CA, (c) 15 °CA, (d) 30 °CA, (e) 45 °CA, (f) 60 °CA, (g) 75 °CA, and (h) 90 °CA, respectively, after intake TDC in SI engine [135]

Fig. 8.59

The variation of MSD (n) with n for different injection timings in SI engine. The cases (a)–(h) are defined in Fig. 8.58 [135]

Fig. 8.60

The value of K_c for different values of c for different injection timings in an SI engine. The cases (a)–(h) are defined in Fig. 8.58 [135]

8.5.7 Multifractal Analysis

The multifractal analysis provides a method to analyze the signals having nonlinear power-law behavior that depends on higher-order moments and scale. Multifractals are used to explain the dynamics of complex processes exhibiting multiple time scales in addition to a range of oscillation amplitudes [76]. A monofractal process is self-similar in such a way that its dynamics can be fully explained by one power-law time-scaling exponent (such as Hurst exponent) and its complexity can be described by single fractal dimension. The multifractal process needs a spectrum of scaling exponents to fully describe the complex dynamics, and it can be considered as locally self-similar. One method to explain such multifractal spectrum is to use Hölder exponent [76, 138]. The singularity spectrum (f(α)) is created by calculating the average relative contribution of the different possible Hölder exponents over the observation window (i.e., the overall time series). The broadness of the singularity spectrum is one measure of the complexity of the process [76]. Engine combustion process is analyzed using multifractals based on cylinder pressure measurement [76, 139,140,141].

Figure 8.61 shows the multifractal spectrum at different engine operating conditions in SI engine. Figure 8.61a illustrates the method to determine the coefficient of the multifractal spectrum. Calculated exponential distribution f(α) (red points) is found using multifractal analysis, and then it is interpolated with a polynomial trend line. Two main characteristics of multifractal spectrum are typically used for analysis. First is the value of the Hölder exponent, α = α₀, at the peak of f(α), and second is the broadness, Δα, that is defined as the distance between the (extrapolated) points of intersection of the spectral curve with the α-axis [76, 141]. The parameter, α₀, signifies the most dominant fractal exponent in the data series, and it shows the correlation or degree of persistence in the data series. Persistent or positively correlated process has α₀ > 0.5, and anti-persistent or negatively correlated process has α₀ < 0.5. The two cases, α₀ = 0.5 and α₀ = 0, represent a Brownian random walk and Gaussian random process, respectively. The Gaussian process is considered as the series of random numbers, while the Brownian walk is characterized by random steps. The broadness of a singularity spectrum (Δα) reflects the range of possible fractal exponents. Therefore, the complexity of the process is characterized by the distribution of α, and Δα provides a measure of multifractality or complexity in the data [76, 141]. A large value of Δα shows a richer multifractal structure, whereas a small value approaches a monofractal limit. Figure 8.61b depicts that as the fuel-air mixture becomes leaner (decrease in ϕ), the broadness (Δα) first increases to reach a maximum at ϕ = 0.67, and further leaning of charge decreases the broadness. This observation suggests the highest degree of multifractal complexity in heat release time series when the engine is operated at ϕ = 0.67.

Fig. 8.61

(a) Illustration of method for determination of coefficients of multifractal spectrum using IMEP time series [141] and (b) multifractal spectrum at different equivalence ratio ϕ = 0.91, 0.83, 0.77, 0.67, 0.63, 0.59, and 0.53 using heat release time series [76]

Figure 8.62 shows the variation of α₀ and Δα (obtained by multifractal analysis) at different engine operating conditions with hydrogen enrichment. The engine operating conditions at which experiments are conducted are shown in the right of Fig. 8.62. The optimal conditions are indicated by a full line on the left-hand side of Fig. 8.62. Engine operating points 8 and 10–12 have higher Δα (broadness) with higher peaks, which suggests the IMEP time series is characterized by higher cycle-to-cycle interactions [141]. It means the IMEP oscillations depend on the IMEP in the previous cycle when the engine is fueled with hydrogen at an engine load of 85 kPa (Fig. 8.62). The highest value of α₀ indicates the lowest negative correlations in the anti-persistent walk. The most expected value of α₀ is below 0.2 and a range of critical Δα below 0.7 for the IMEP time series. Figure 8.62 clearly indicates that there is no change in the combustion process with hydrogen addition at low engine load (operating points 1–4). Thus, in summary, the multifractal analysis provides the quantitative information of the combustion process using persistence and complexity measures. This information can be used in the design of effective engine control strategy [141].

Fig. 8.62

Result of multifractal analysis of IMEP data series with the most expected exponent α₀ and a range of critical exponents Δα (right) with measurement points (left) [141]

8.6 Steps to Improve Combustion Stability

Combustion stability in reciprocating engines can be analyzed using statistical methods or chaotic methods using measured cylinder pressure data. The quantitative measures are defined to determine the levels of the cyclic combustion variability. After characterizing the cyclic combustion variations, the methods can be suggested to improve the combustion stability and control strategy of engine to minimize the cyclic variations. Generally, the combustion stability in reciprocating engines improve with (1) higher engine load and speed, (2) higher compression ratio, (3) lower valve overlap, (4) higher energy of ignition system, (5) higher temperatures, and (6) lower humidity [9]. Typically, combustion stability improves with parameters, which tends to increase the combustion rate of the engines, and faster combustion has typically lower cyclic variations. Therefore, the cylinder pressure-based combustion stability methods can help to see the effect of design changes on the combustion stability. The engine operating parameters and combustion mode can be tuned for lower cyclic variability by combustion stability analysis using cylinder pressure measurement.

Discussion/Investigation Questions

• 1. Why measurement and characterization of cycle-to-cycle variations are important in internal combustion engines? Discuss the reason for cycle-to-cycle variations in SI, CI, and LTC (HCCI, RCCI, etc.) modes of engine operation.

• 2. Define the combustion stability in a reciprocating internal combustion engine. Discuss how cyclic combustion variability manifests in the engine performance.

• 3. Discuss the mechanism on how mixture composition (a type of fuel, overall equivalence ratio, and an overall fraction of diluents) affects the cycle-to-cycle variations (CCV) in SI engine. Describe the stage of combustion (sparking and flame initiation, initial flame kernel development, and turbulent flame propagation) most affected by each parameter. Explain how each parameter can be adjusted to minimize the CCV in SI engine.

• 4. Explain why cycle-to-cycle variations in conventional diesel engines are relatively lower than the conventional spark ignition engines.

• 5. Discuss the mechanism on how spark characteristics (spark plug gap vicinity, electrode shape, spark plugs number, and location) affects the cycle-to-cycle variations (CCV) in SI engine. Describe the stage of combustion (sparking and flame initiation, initial flame kernel development, and turbulent flame propagation) most affected by each parameter. Explain how each parameter can be adjusted to minimize the CCV in SI engine. Discuss the advantage in terms of cyclic variations gained by advanced ignition systems such as laser ignition.

• 6. Discuss the mechanism on how in-cylinder mixture motion (mean flow vector at the spark plug gap vicinity, overall in-cylinder flow pattern, turbulence intensity, and scale) affects the cycle-to-cycle variations (CCV) in SI engine. Describe the stage of combustion most affected by each parameter and also explain how each parameter can be adjusted to minimize the CCV in SI engine. Suggest the engine design changes for minimization of cyclic combustion variability.

• 7. Discuss the reasons why low-temperature combustion modes (HCCI, RCCI, etc.) typically have relatively higher cyclic combustion variations than conventional diesel engines.

• 8. Discuss the effect of cyclic variations in equivalence ratio (ϕ), diluents, mean flow vector, spark discharge characteristics, and in-cylinder charging on cycle-to-cycle combustion variations in SI engine. Comment on the combustion stage which is most affected by the variations in each parameter.

• 9. Discuss the prior-cycle effects and same-cycle effects contributing to the cyclic combustion variations in homogeneous spark ignition engines and compression ignition engines.

• 10. Describe the sources of cyclic combustion variability in homogeneous and heterogeneous charge compression ignition engines.

• 11. Describe why fast burn operating conditions typically have lower cycle-to-cycle variations in reciprocating engines.

• 12. Explain the different indices based on in-cylinder pressure and heat release used for characterization of the combustion stability in reciprocating internal combustion engines. Discuss the significance of each parameter with respect to information revealed by each parameter.

• 13. Write the causes of partial burn and misfire cycles in reciprocating internal combustion engines.

• 14. How can you determine partial burn operation or misfire in SI and HCCI engine using in-cylinder pressure-based measurement methods?

• 15. Discuss the difference between statistical and nonlinear dynamics approach of combustion stability analysis. Write the advantages of both the approaches of cyclic variation analysis.

• 16. Define skewness and kurtosis of a data series, and discuss the significance of these statistical parameters with respect to the kind of information revealed. Discuss the different methods that can be used to test whether an engine data series has Gaussian or non-Gaussian distribution.

• 17. Define the coefficient of variation and lowest normalized value of IMEP data for a large number of engine cycles. Discuss the information revealed by COV_IMEP and LNV parameter at particular engine operating conditions.

• 18. Discuss the advantages of wavelet transform over Fourier transform. Write the typical applications of continuous wavelet transform and discrete wavelet transform. Explain how wavelets can be used for characterization of cycle-to-cycle variations under different engine operating conditions.

• 19. Discuss the differences between linear and nonlinear signal processing methods. Describe the additional features of engine cyclic combustion variations which can be extracted from the nonlinear analysis that are not available in the traditional statistical analysis.

• 20. Describe the methods to find the optimal embedding dimension and the time lag during phase space reconstruction. Describe the information depicted by phase space reconstruction, Poincare section, and return map.

• 21. Discuss the patterns by which return maps can reveal deterministic or stochastic component in the variation. Discuss the significance of quantile return map with normalized value.

• 22. Explain the methods that can be used to determine whether cyclic variations are random or deterministic in nature. Why this information is important for the engine designer and how these methods can be used to improve engine performance?

• 23. Explain the advantages of data symbolization. Discuss the methods to find the optimal sequence length and number of partition in symbol sequence analysis. Write the major issues with an inappropriate number of partition in the data.

• 24. Discuss the steps that can be taken during engine design and calibration to improve the combustion stability in SI, CI, and HCCI engines. Describe the effects of fuel on the combustion stability of engine and suggest fuel characteristics/properties for improving the combustion stability.