Online Learning of Weighted Relational Rules for Complex Event Recognition

Abstract

Systems for symbolic complex event recognition detect occurrences of events in time using a set of event definitions in the form of logical rules. The Event Calculus is a temporal logic that has been used as a basis in event recognition applications, providing among others, connections to techniques for learning such rules from data. We advance the state-of-the-art by combining an existing online algorithm for learning crisp relational structure with an online method for weight learning in Markov Logic Networks (MLN). The result is an algorithm that learns complex event patterns in the form of Event Calculus theories in the MLN semantics. We evaluate our approach on a challenging real-world application for activity recognition and show that it outperforms both its crisp predecessor and competing online MLN learners in terms of predictive performance, at the price of a small increase in training time. Code related to this paper is available at: https://github.com/nkatzz/OLED.

1 Introduction

Complex event recognition systems [7] process sequences of simple events, such as sensor data, and recognize complex events of interest, i.e. events that satisfy some temporal pattern. Systems for symbolic event recognition [3] typically use a knowledge base of first-order rules to represent complex event patterns. Learning such patterns from data is highly desirable, since their manual development is usually a difficult and error-prone task. The Event Calculus (EC) [23] is a temporal logical formalism that has been used as a basis in event recognition applications [2], providing among others, direct connections to machine learning, via Inductive Logic Programming (ILP) [8] and Statistical Relational Learning (SRL) [9].

Event recognition applications typically deal with noisy data streams [1]. Algorithms that learn from such streams are required to work in an online fashion, building a model with a single pass over the input [14]. Although a number of online relational learners have been proposed [12, 18, 31], learning theories in the EC is a challenging task that most relational learners, including the aforementioned ones, cannot fully undertake [19, 28]. As a result, two online algorithms have been proposed, both capable of learning complex event patterns in the form of EC theories, from relational data streams. The first, OLED (Online Learning of Event Definitions) [21], adapts the Hoeffding bound-based [16] framework of [10] for online decision tree learning to an ILP setting. The second algorithm, (Online Structure Learning with Background Knowledge Axiomatization) [27], builds on the method of [18] for learning structure and weights in Markov Logic Networks (MLN) [29], towards online learning of EC theories in the MLN semantics.

Both these algorithms have shortcomings. OLED is a crisp learner, therefore its performance could be improved via SRL techniques that combine logic with probability. On the other hand, uses an efficient online weight learning technique, based on the AdaGrad algorithm [13], but its structure learning component is sub-optimal: It tends to generate large sets of rules, many of which are of low heuristic value with a marginal contribution to the quality of the learned model. The maintenance cost of such large rule sets during learning results in poor efficiency, with no clear gain in the predictive accuracy, while it also negatively affects model interpretability.

In this work we present a new algorithm that attempts to combine the best of these two learners: OLED’s structure learning strategy, which is more conservative than ’s and typically explores much smaller rule sets, with ’s weight learning technique. We show that the resulting algorithm outperforms both its predecessors in terms of predictive performance, at the price of a tolerable increase in training time. We empirically validate our approach on a benchmark dataset of activity recognition.

2 Related Work

Machine learning techniques for event recognition are attracting attention in the Complex Event Processing community [26]. However, existing approaches are relatively ad-hoc and they have several limitations [19], including limited support for background knowledge utilization and uncertainty handling. In contrast, we adopt an event recognition framework that allows access to well-established (statistical) relational learning techniques [8, 9], which can overcome such limitations. Moreover, using the EC allows for efficient event recognition via dedicated reasoners, such as RTEC [2].

However, learning with the EC is challenging for most ILP and SRL algorithms. A main reason for that is the non-monotonicity of the Negation as Failure operator that the EC uses for commonsense reasoning, which makes the divide-and-conquer-based search of most ILP algorithms inappropriate [19, 20, 28]. Non-monotonic ILP algorithms can handle the task [5, 28], but they scale poorly, as they learn whole theories from the entirety of the training data, while improvements to such algorithms that allow some form of incremental processing to enhance efficiency [4, 24] cannot handle data arriving over time. Contrary to such approaches, OLED, the ILP algorithm we build upon, scales adequately and learns online [21].

A line of related work tries to “upgrade” non-monotonic ILP learners to an SRL setting, via weight learning techniques with probabilistic semantics [6, 11]. However, the resulting algorithms suffer from the same limitations, related to scalability, as their crisp predecessors. In the field of Markov Logic Networks (MLN), which is the SRL framework we adopt, is the sole algorithm capable of learning structure and weights for EC theories.

Online learning settings, as the one we assume in this work, are under-explored both in ILP and in SRL. A few ILP approaches have been proposed. In [12] the authors propose an online algorithm, which generates a rule from each misclassified example in a stream, aiming to construct a theory that accounts for all the examples in the stream. In [31] the authors propose an online learner based on Aleph¹ and Winnow [25]. The algorithm maintains a set of rules, corresponding to Winnow’s features. Rules are weighted and are used for the classification of incoming examples, via the weighted majority of individual rule verdicts for each example, while their weights are updated via Winnow’s mistake-driven weight update scheme. New rules are greedily generated by Aleph from misclassified examples. A similar approach is put forth by OSL [18], an online learner for MLN, which builds upon to allow for learning with the EC. OSL greedily generates new rules to account for misclassified examples that stream in, and then relies on weight learning to identify which of these rules are relevant. Common to these online learners is that they tend to generate unnecessarily large rule sets, which are hard to maintain. This is precisely the issue that we address in this work.

Table 1. (a), (b) The basic predicates and the domain-independent axioms of EC. (c) Example data from activity recognition. For example, at time point 1 person with $id_1$ is walking, her (X, Y) coordinates are (201, 454) and her direction is $270^{\circ }$. The annotation for the same time point states that persons with $id_1$ and $id_2$ are not moving together, in contrast to the annotation for time point 2. (d) An example of two domain-specific axioms in the EC. E.g. the first clause dictates that moving together between two persons X and Y is initiated at time T if both X and Y are walking at time T, their euclidean distance is less than 25 pixel positions and their difference in direction is less than $45^{\circ }$. The second clause dictates that moving together between X and Y is terminated at time T if one of them is standing still at time T (exhibits an inactive behavior) and their euclidean distance at T is greater that 30.

3 Background

We assume a first-order language, where predicates, terms, atoms, literals (possibly negated atoms), rules (clauses) and theories (collections of rules) are defined as in [9], while not denotes Negation as Failure. A rule is represented by $\alpha \leftarrow \delta _1,\ldots ,\delta _n$, where $\alpha$ is an atom, (the head of the rule), and $\delta _1,\ldots ,\delta _n$ is a conjunction of literals (the body of the rule). A term is ground if it contains no variables. We follow [9] and adopt a Prolog-style syntax. Therefore, predicates and ground terms in logical expressions start with a lower-case letter, while variable terms start with a capital letter.

The Event Calculus (EC) [23] is a temporal logic for reasoning about events and their effects. Its ontology consists of time points (integer numbers); fluents, i.e. properties that have different values in time; and events, i.e. occurrences in time that may alter fluents’ values. The axioms of the EC incorporate the commonsense law of inertia, according to which fluents persist over time, unless they are affected by an event. We use a simplified version of the EC that has been shown to suffice for event recognition [2]. The basic predicates and its domain-independent axioms are presented in Table 1(a) and (b) respectively. Axiom (1) in Table 1(b) states that a fluent F holds at time T if it has been initiated at the previous time point, while Axiom (2) states that F continues to hold unless it is terminated. Definitions for initiatedAt/2 and terminatedAt/2 predicates are given in an application-specific manner by a set of domain-specific axioms.

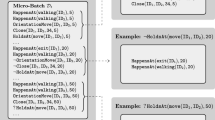
As a running example we use the task of activity recognition, as defined in the CAVIAR project². The CAVIAR dataset consists of 28 videos of actors performing a set of activities. Manual annotation (performed by the CAVIAR team) provides ground truth for two activity types. The first type corresponds to simple events and consists of the activities of a person at a certain video frame/time point, such as walking, or standing still. The second activity type corresponds to complex events and consists of activities that involve more than one person, e.g. two people meeting each other, or moving together. The goal is to recognize complex events as combinations of simple events and additional contextual knowledge, such as a person’s direction and position.

Table 1(c) presents some example CAVIAR data, consisting of a narrative of simple events in terms of happensAt/2, expressing people’s short-term activities, and context properties in terms of holdsAt/2, denoting people’ coordinates and direction. Table 1(c) also shows the annotation of complex events (long-term activities) for each time-point in the narrative. Negated complex events’ annotation is obtained via the closed-world assumption (although both positive and negated annotation atoms are presented in Table 1(c), to avoid confusion). Table 1(d) presents two domain-specific axioms in the EC.

The learning task we address in this work is to learn definitions of complex events, in the form of domain-specific axioms in the EC, i.e. initiation and termination conditions of complex events, as in Table 1(d). The training data consists of a set of Herbrand interpretations, i.e. sets of narrative atoms, annotated by complex event instances, as in Table 1(c). Given such a training set $\mathcal {I}$ and some background knowledge B, the goal is to find a theory H that accounts for as many positive and as few negative examples as possible, throughout $\mathcal {I}$. Given an interpretation $I\in \mathcal {I}$, a positive (resp. negative) example is a complex event atom $\alpha \in I$ (resp. $\alpha \notin I$). We assume an online learning setting, in the sense that a learning algorithm is allowed only a single-pass over $\mathcal {I}$.

3.1 Online Learning of Markov Logic Networks with

[27] builds on the OSL [18] algorithm for online learning of Markov Logic Networks (MLN). An MLN is a set of weighted first-order logic rules. Along with a set of domain constants, it defines a ground Markov network containing one feature for each grounding of a rule in the MLN, with the corresponding weight. Learning an MLN consists of learning its structure (the rules in the MLN) and their weights.

works by constantly updating the rules in an MLN in the face of new interpretations that stream-in, by adding new rules and updating the weights of existing ones. At time t, OSL receives an interpretation $I_t$ and uses its current hypothesis, $H_t$, to “make a prediction”, i.e. to infer the truth values of query atoms, given the evidence atoms in $I_t$. In the learning problem that we address in this work, query atoms are instances of initiatedAt/2 and terminatedAt/2 predicates, the “target” predicates defining complex events, while evidence atoms are instances of predicates that declare simple events’ occurrences, or other contextual knowledge, like happensAt/2 and $distLessThan /4$ respectively (see also Table 1(c)).

To infer the query atoms’ truth values given the interpretation $I_t$, uses Maximum Aposteriori (MAP) inference [18], which amounts to finding the truth assignment to the query atoms that maximizes the sum of the weights of $H_t$’s rules satisfied by $I_t$. This is a weighted MAX-SAT problem, whose solution efficiently approximates using LP-relaxed Integer Linear Programming, as in [17]. The inferred truth values of the query atoms, resulting from MAP inference may differ from the true ones, dictated by the annotation in $I_t$. The mistakes may be either False Negatives (FNs) or False Positives (FPs). Since FNs are query atoms which are not entailed by an existing rule in the inferred interpretation, in the next step constructs a set of new rules as a remedy. To this end, represents the current interpretation $I_t$ as a hypergraph with the constants of $I_t$ as the nodes and each true ground atom $\delta$ in $I_t$ as a hyperedge connecting the nodes (constants) that appear as $\delta$’s arguments. Each inferred FN query atom $\alpha$ is used as a “seed” to generate new rules, by finding all paths in the hypergraph, up to a user-defined maximum length, that connect $\alpha$’s constants. Each such path consists of hyperedges, corresponding to a conjunction of true ground atoms connected by their arguments. The path is turned into a rule with this conjunction in the body and the seed FN atom in the head, and a lifted version of this rule is obtained by variabilizing the ground arguments. By construction, each such rule logically entails the seed FN atom it was generated from.

This technique of relational pathfinding may generate a large number of rules from each inferred FN query atom, and many of these rules are not useful. Thus, relies on $L_1$-regularized weight learning, which in the long run, pushes the weights of non-useful rules to zero. Weight learning is also ’s way to handle FP query atoms in the inferred state, which are due to erroneously satisfied rules in the current theory $H_t$. These rules are penalized by reducing their weights. uses an AdaGrad-based [13] weight learning technique, which supports $L_1$-regularization.

AdaGrad is a subgradient-based method for online convex optimization, i.e. at each step it updates a feature vector, based on the subgradient of a convex loss function of the features. Seeing the rules in an MLN theory $H = \{r_1,\ldots ,r_n\}$ as the feature vector that needs to be optimized, the authors in [18] use a simple variant of the hinge-loss as a loss function, whose subgradient is the vector $-\langle \varDelta g_1,\ldots \varDelta g_n\rangle$, where $\varDelta g_i$ denotes the difference between the true groundings of the i-th rule in the actual true state and the MAP-inferred state respectively. Based on this difference, AdaGrad updates the weight $w_i^{t}$ of the i-th rule in the theory at time t by:

$$\begin{aligned} w_i^{t+1} = sign(w_i^{t} - \frac{\eta }{C_i^t}\varDelta g_i^t) \ max\{0, |w_i^t - \frac{\eta }{C_t^i}\varDelta g_i^t| - \lambda \frac{\eta }{C_t^i} \} \end{aligned}$$

(1)

where t-superscripts in terms denote the respective values at time t, $\eta$ is a learning rate parameter, $\lambda$ is a regularization parameter and $C_i^t = \delta + \sqrt{\sum _{j=1}^{t}(\varDelta g_i^j)^2}$ is a term that expresses the rule’s quality so far, as reflected by the accumulated sum of $\varDelta g_i$’s, amounting to the i-th rule’s past mistakes (plus a $\delta \ge 0$ to avoid division by zero in $\eta /C_i^t$). The $C_i^t$ term gives an adaptive flavour to the algorithm, since the magnitude of a weight update via the term $|w_i^t - \frac{\eta }{C_t^i}\varDelta g_i^t|$ in Eq. (1), is affected by the rule’s previous history, in addition to its current mistakes, expressed by $\varDelta g_i^t$. The regularization term in Eq. (1), $\lambda \frac{\eta }{C_t^i}$, is the amount by which the i-th rule’s weight is discounted when $\varDelta g_i^t = 0$. This is to eventually push to zero the weights of irrelevant rules, which have very few, or even no groundings in the training interpretations.

In contrast to its predecessor, OSL, uses specialized techniques for pruning large parts of the hypergraph structure to enhance efficiency when learning with the EC. However, its rule generation technique remains an important bottleneck. Repeatedly searching for paths in the hypergraph structure is expensive in its own right, but it also tends to blindly generate large sets of rules, which, in turn, increases the cost of MAP inference during learning.

4 Learning Weighted Rules with WoLED

Aiming to improve the efficiency of online learning with the EC in MLN, we propose WoLED (Weighted Online Learning of Event Definitions), an extension of the OLED crisp online ILP learner [21], to an MLN setting. OLED draws inspiration from the VFDT (Very Fast Decision Trees) algorithm [10], whose online strategy is based on the Hoeffding bound [16]. Given a random variable X with range in [0, 1] and an observed mean $\overline{X}$ of its values after n independent observations, the Hoeffding Bound states that, with probability $1 - \delta$, the true mean $\hat{X}$ of the variable lies in an interval $(\overline{X} - \epsilon , \overline{X} + \epsilon )$, where $\epsilon = \sqrt{\frac{ln(1/\delta )}{2n}}$.

OLED learns a rule r with a hill-climbing process, where literals are gradually added to r’s body yielding specializations of r of progressively higher quality, which is assessed by some scoring function G, based on the positive and negative examples that a rule entails. This strategy is common in ILP, where at each specialization step (addition of a literal), a number of candidate specializations of the parent rule are evaluated on the entire training set and the best one is selected. OLED adapts this strategy to an online setting, using the Hoeffding bound, as follows: Assume that after having evaluated r and a number of its candidate specializations on n examples, $r_1$ is r’s specialization with the highest mean G-score $\overline{G}$ and $r_2$ is the second-best one, i.e. $\varDelta \overline{G} = \overline{G}(r_1)-\overline{G}(r_2) > 0$. Then by the Hoeffding bound we have that for the true mean of the scores’ difference $\varDelta \hat{G}$ it holds that $\varDelta \hat{G} > \varDelta \overline{G} - \epsilon \text {, with probability } 1 - \delta$, where $\epsilon = \sqrt{\frac{ln(1/\delta )}{2n}}$. Hence, if $\varDelta \overline{G} > \epsilon$, then $\varDelta \hat{G} > 0$, implying that $r_1$ is indeed the best specialization, with probability $1 - \delta$. In order to decide which specialization to select, it thus suffices to evaluate the specializations on examples from the stream until $\varDelta \overline{G} > \epsilon$. Each of these examples is processed once, thus giving rise to a single-pass rule learning strategy.

Positive (resp. negative) examples in this setting are true (resp. false) instances of target predicates, which are present in (resp. generated via the closed-world assumption from) the incoming training interpretations. Such instances correspond to query atoms in an MLN setting (see Sect. 3.1), therefore we henceforth refer to positive and negative examples as true and false query atoms respectively.

The literals used for specialization are drawn from a bottom rule [8], denoted by $\bot$, a most-constrained rule that entails a single true query atom. A bottom rule is usually too restrictive to be used for classification and its purpose is to define a space of potentially good rules, consisting of those that $\theta$-subsume $\bot$. OLED moves through this search space in a top-down fashion, starting from an empty-bodied rule $head(\bot ) \leftarrow true$ and considering at each time specializations that result by the addition of a fixed number of literals from $\bot$ to the body of a parent rule (the default is one literal).

4.1 WoLED

Our approach is based on combining OLED’s rule learning technique with ’s weight learning strategy. Contrary to ’s approach, where once a rule is generated, its structure remains fixed and the only way to improve its quality is by tuning its weight, WoLED progressively learns both the structure of a rule and its weight, by jointly optimizing them together. To this end, a rule is gradually specialized via the online hill-climbing strategy described earlier, while constantly updating the weight of each such specialization. Given a rule r and a set of r’s specializations $S_r$, WoLED learns weights for r and each $r' \in S_r$, and uses Hoeffding tests to identify over time, a rule $r_{1} \in S_r$ of higher quality, as assessed by a combination of $r_{1}$’s structure and weight. Once that happens, r is replaced by $r_1$ and the process continues for as long as new specializations of $r_1$ improve its quality. To learn weights, WoLED replaces OLED’s crisp logical inference with MAP inference and uses ’s mistake-driven weight learning technique described in Sect. 3.1, which updates a rule’s weight based on the query atoms that the rule misclassifies in the MAP-inferred state.

WoLED’s high-level strategy is illustrated in Fig. 1. At each point in time WoLED maintains a theory $H_t = \{r_1, \ldots , r_n\}$, and for each rule $r_i$, a set of current specializations $\{r_i^{1}, \ldots , r_i^{n}\}$ and an associated bottom rule $\bot _{r_i}$. At time t, WoLED receives the t-th training interpretation $I_t$ and it subsequently goes through a five-step process. In the first step it performs MAP inference on $I_t$, using the current theory $H_t$ and the background knowledge. The MAP-inferred interpretation is checked for FN query atoms. If such an atom $\alpha$ exists, meaning that no existing rule in $H_t$ entails it, WoLED proceeds to a “theory expansion” step, where it starts growing a new rule $r_{i+1}$ to account for that. This amounts to using the FN atom $\alpha$ as a“seed” to generate a bottom rule $\bot _{r_{i+1}}$ and adding to H the empty-bodied rule $head(\bot _{r_{i+1}} ) \leftarrow true$. From that point on this rule is gradually specialized using literals from $\bot _{r_{i+1}}$. The generation of $\bot _{r_{i+1}}$ is guided by a set of mode declarations [8] (see Fig. 1), a form of language bias specifying the signatures of literals that are allowed to be placed in the head or the body of a rule, in addition to the types of their arguments (e.g. time, or id in the declarations of Fig. 1) and whether they correspond to variables or constants (indicated respectively by “+” and “$\#$” in the declarations of Fig. 1).

Fig. 1.

Illustration of WoLED’s high-level strategy.

After a potential theory expansion a weight update step follows, where the weights of each rule $r\in H_t$ and the weights of each one of its current specializations are updated, based on their mistakes on the MAP-inferred state generated previously. A Hoeffding test for each rule $r\in H_t$ follows, and if a test succeeds for some rule r, it is “expanded”, i.e. r’s structure and weight are replaced by the ones of its best-scoring specialization, $r_1$. The final step is responsible for pruning the current theory, i.e. removing low-quality rules. The current version of the weighted theory is output and the training loop continues (see Fig. 1).

We next go into some details of WoLED’s functionality, using the pseudocode in Algorithm 1. The input to Algorithm 1 consists of the background knowledge, a rule-scoring function G, based on the true positive (TP), false positive (FP) and false negative (FN) examples entailed by a rule, AdaGrad’s parameters $\eta , \delta _a, \lambda$, discussed in Sect. 3.1, the confidence parameter for the Hoeffding test $\delta _h$ and a set of mode declarations. Additionally, a minimum G-score value for acceptable rules, a “warm-up” parameter $N_{min}$ and a“specialization depth” parameter d, to be explained shortly.

The MAP-inferred state is generated in lines 2–3 of Algorithm 1, using the active fragment of the theory. The latter consists of those rules in the theory that have been evaluated on at least $N_{min}$ examples (line 2), where $N_{min}$ is the input “warm-up” parameter. This is to avoid using rules which are too premature and useless for inference, such as an empty-bodied rule that has just been created.

In lines 4–8 of Algorithm 1, new rules are generated for each FN atom in the MAP-inferred state, as described earlier. In addition to its corresponding bottom rule to draw literals for specialization, each rule is also equipped with a number of counters, which accumulate the TP, FP and FN instances entailed by the rule over time, to use for calculating its G-score; and an accumulator, denoted by $Subgradients (r)$, which is meant to store the history (sum) of the rule’s mistakes throughout the learning process (see the term $C_i^t$ in Eq. (1)). As explained in Sect. 3.1, a rule’s mistakes w.r.t. each incoming interpretation is a coordinate in the the subgradient vector of AdaGrad’s loss function (hence the name “$Subgradients (r)$” for their accumulator) and they affect the magnitude of a rule’s weight update. Therefore, $Subgradients (r)$ is used for updating r’s weight with AdaGrad.

Updating the weights of each rule $r\in H$, as well as the weights of r’s candidate specializations follows, in lines 9–13 of Algorithm 1 (r’s specializations are denoted by $\rho _d(r)$ (line 10), where d is the specialization depth parameter mentioned earlier, controlling the “depth” of allowed specializations, which are considered at each time). The weight-update process is presented in Algorithm 2. It uses AdaGrad’s strategy discussed in Sect. 3.1. The difference between r’s true groundings in the true state and the MAP-inferred one is first calculated (line 2), it’s square is added to r’s $Subgradients$ accumulator (line 3 – see the $C_i^t$ term in Eq. (1), Sect. 3.1) and then r’s weight is updated (line 5). Algorithm 2 is also responsible for updating the $TP, FP, FN$ counters for a rule r, which are used to calculate its G-score.

The Hoeffding test follows to decide if a rule should be specialized (lines 14–18, Algorithm 1). A rule is specialized either if the test succeeds ($\varDelta \bar{G} > \epsilon$), or if a tie-breaking condition is met ($\varDelta \bar{G}< \epsilon < \tau$), where $\tau$ is a threshold set to the mean value of $\epsilon$ observed so far. Also, to ensure that no rule r is replaced by a specialization of lower quality, we demand that $\bar{G}(r_1) > \bar{G}(r)$, where $r_1$ is r’s best-scoring specialization indicated by the Hoeffding test.

The final step is responsible for removing rules of low quality (lines 19–21, Algorithm 1). A rule is removed if it remains unchanged (is not specialized) for a significantly large period of time, set to the average number of $\mathcal {O}(\frac{1}{\epsilon ^2}ln\frac{1}{\delta _h})$ examples for which the Hoeffding test has succeeded so far, and there is enough confidence, via an additional Hoeffding test, that its mean G-score is lower than a minimum acceptable G-score $Score_{min}$.

5 Experimental Evaluation

We present an experimental evaluation of WoLED on CAVIAR, a benchmark dataset for activity recognition (see Sect. 3 for CAVIAR’s description). All experiments were conducted on Debian Linux machine with a 3.6 GHz processor and 16 GB of RAM. The code and the data to reproduce the experiments are available online³. WoLED is implemented in Scala, using the Clingo answer set solver⁴ for grounding and the lpsolve⁵ Linear Programming solver for probabilistic MAP-inference, on top of the LoMRF⁶ platform, an implementation of MLN. The version to which we compare in these experiments also relies on lpsolve, but uses LoMRF’s custom grounder.

5.1 Comparison with Related Online and Batch Learners

In our first experiment we compare WoLED with (i) and OSL [18], discussed in Sect. 3.1; (ii) The crisp version of OLED; (iii) $\mathsf {EC_{crisp}}$, a hand-crafted set of crisp rules for CAVIAR; (iv) $\mathsf {MaxMargin}$, an MLN consisting of $\mathsf {EC_{crisp}}$’s rules, with weights optimized by the the Max-Margin weight learning method of [17]; (v) XHAIL, a batch, crisp ILP learner using a combination of inductive and adbuctive logic programming. The rules used by $\mathsf {EC_{crisp}}$ and $\mathsf {MaxMargin}$ may be found in [30].

$\mathsf {MaxMargin}$ was selected because it was shown to achieve good results on CAVIAR [30], while XHAIL was selected because it is one of the few existing ILP algorithms capable of learning theories in the EC.

A fragment of the CAVIAR dataset has been used in previous work to evaluate and $\mathsf {MaxMargin}$’s performance [27, 30]. To compare to these approaches we therefore used this fragment in our first experiment. The target complex events in this dataset are related to two persons meeting each other or moving together and the training data consist of the parts of CAVIAR where these complex events occur. The fragment dataset contains a total of 25,738 training interpretations. The results with OLED were achieved using a significance parameter $\delta _h = 10^{-2}$ for the Hoeffding test, a rule pruning threshold $Score_{min}$ (see also Algorithm 1) of 0.8 for meeting and 0.7 for moving and a warm-up parameter of $N_{min} = 1000$ examples. WoLED also used this parameter configuration, in addition to $\eta = 1.0, \lambda = 0.01, \delta _{\alpha } = 1.0$ for weight learning with AdaGrad. These parameters were reported in [27] and were also used with /OSL.

The results were obtained using 10-fold cross validation and are presented in Table 2(a) in the form of precision, recall and $f_1$-score. These statistics were micro-averaged over the instances of recognized complex events from each fold. Table 2(a) also presents average training times per fold for all approaches except $\mathsf {EC_{crisp}}$, where there is no training involved, average theory sizes for OLED, , and XHAIL, as well as the fixed theory size of $\mathsf {EC_{crisp}}$ and $\mathsf {MaxMargin}$. The reported theory sizes are in the form of total number of literals in a theory. The online methods were allowed only a single-pass over the training data.

WoLED achieves the best $F_1$-score for meeting and the second-best $F_1$-score for moving, right after the batch weight optimizer $\mathsf {MaxMargin}$. This is a notable result. Moreover, this gain in predictive accuracy comes with a tolerable decrease in efficiency of approximately half a minute, as compared to OLED’s training times, which are the best among all learners. This extra overhead in training time for WoLED is due to the cost of the probabilistic MAP-inference, which replaces OLED’s crisp logical inference to allow for weight optimization. Regarding theory sizes, WoLED outputs hypotheses comparable in size with the hand-crafted knowledge base, and much more compressed as opposed to . This is another notable result. XHAIL learns the most compressed hypotheses, since it is a batch learner, which also explains its increased training times. $\mathsf {MaxMargin}$, also has high training times, paying the price of batch (weight) optimization.

Table 2. Experimental results on (a) the CAVIAR fragment of [30] (top) and (b) the complete CAVIAR dataset (bottom).

Fig. 2.

Online holdout evaluation on CAVIAR.

OSL was unable to process the dataset within 25 h, at which time training was terminated. The reasons for that are related to it being unable to take advantage of the background knowledge, thus it is practically unable to learn with the Event Calculus [27]. overcomes OSL’s difficulties, but learns unnecessarily large theories, which differ in size by several orders of magnitude from all others learners’. In turn, this affects ’s training times, which are also increased. In contrast, WoLED achieves improved predictive accuracy and compressed theories with minimal training overhead.

Figure 2 presents the holdout evaluation [15] for the online learners compared in this experiment. Holdout evaluation consists of assessing the quality of an online learner on a holdout test set, at regular time intervals during learning, thus obtaining a learning curve of its performance over time. Figure 2 presents average $F_1$-scores, obtained by performing holdout evaluation on each fold of the tenfold cross-validation process: at each fold, each learner’s theory is evaluated on the fold’s test set every 1000 time points and the $F_1$-scores from each evaluation point are averaged over all ten folds.

WoLED and OLED have an adequate performance, with relatively smooth learning curves, while they eventually converge to stable theories of acceptable performance. Moreover, WoLED outperforms both OLED and in most of the evaluation process.

In contrast to the online behaviour of WoLED and OLED, ’s performance exhibits abrupt fluctuations. For moving in particular, ’s average $F_1$-score reaches its peak (0.87) after processing data from approximately 10,000 time points, and then it drops significantly until the final average $F_1$-score value of 0.69 reported in Table 2. This behavior may be attributed to ’s rule generation strategy. Contrary to WoLED, which uses Hoeffding tests to select rules with significant heuristic value, greedily adds new rules to the current theory, so as to locally improve its performance, without taking into account the new rules’ quality on larger portions of the data. Overall, this results in poor online performance, since rules with no quality guarantees on the training set may be responsible for a large number of mistakes on unseen data, by e.g. fitting the noise in the training data. relies solely on weight learning to minimize the weights of low-quality rules in the long run. However, ’s holdout evaluation indicates that in principle this requires larger training sets, since, at least in the case of moving, ’s theories exhibit no sign of convergence. On the other hand, ’s increased training times reported in Table 2, due to the ever-increasing cost of maintaining unnecessarily large theories, indicate that training on larger datasets is impractical.

5.2 Evaluation on Larger Data Volumes

In this section we evaluate WoLED on larger data volumes, starting with the entire CAVIAR dataset, which consists of 282,067 interpretations, in contrast to 25,738 interpretations in the CAVIAR fragment. Due to the increased training times of , XHAIL and MaxMargin, we did not experiment with these algorithms. The target complex events were meeting and moving as previously. The additional training data (i.e. those not contained in the CAVIAR fragment) were negative instances for both complex events (recall that the parts of CAVIAR where meeting and moving occur were already contained in the CAVIAR fragment). This way, the dataset used in this experiment is much more imbalanced than the one used in the previous experiment. The parameter configuration for the two learners was as reported in Sect. 5.1. The results were obtained via tenfold cross-validation and are presented in Table 2(b).

Fig. 3.

Evaluation on larger data volumes for the moving complex event.

The average $F_1$-score for both algorithms is decreased, as compared to the previous experiment, due to the increased number of false positives, caused by the large number of additional negative instances. WoLED significantly outperforms OLED for both complex events, at the price of a tolerable increase in training times.

To test our approach further we used larger datasets generated from CAVIAR in two different settings. In the first setting, to which we henceforth refer as CAVIAR-1, we generated datasets by sequentially appending copies of the original CAVIAR dataset, incrementing the time-stamps in each copy. Therefore, training with datasets in the CAVIAR-1 setting amounts to re-iterating over the original dataset a number of times. In the second setting, to which we refer as CAVIAR-2, datasets were also obtained from copies of CAVIAR, but this time the time-stamps in the data were left intact and each copy differed from the others in the constants referring to the tracked entities (persons, objects) that appear in simple and complex events. In each copy of the dataset, the coordinates of each entity p differ by a fixed offset from the coordinates of the entity of the original dataset that p mirrors. The copies were “merged”, grouping together by time-stamp the data from each copy. Therefore, the number of constants in each training interpretation in datasets of the CAVIAR-2 setting is multiplied by the number of copies used to generate the dataset. We performed experiments on datasets obtained from 2, 5, 8 and 10 CAVIAR copies for both settings. The target concept was moving and on each dataset we used tenfold cross-validation to measure $F_1$-scores and training times.

The results are presented in Fig. 3. $F_1$-scores improve with larger data volumes for both learners, slightly more so with the datasets in the CAVIAR-2 setting, while WoLED achieves better $F_1$-scores than OLED thanks to weight learning. Training times increase slowly with the data size in the “easier” CAVIAR-1 setting, where both learners require 8–10 minutes on average to learn from the largest dataset in this setting. In contrast, training times increase abruptly in the harder CAVIAR-2 setting, where learning from the largest dataset requires more than 2.5 h on average for both learners. This is due to the additional domain constants in the datasets of the CAVIAR-2 setting, which result in exponentially larger ground theories.

6 Conclusions and Future Work

We presented an algorithm for online learning of event definitions in the form of Event Calculus theories in the MLN semantics. We extended an online ILP algorithm to a statistical relational learning setting via online weight optimization. We evaluated our approach on an activity recognition application, showing that it outperforms both its crisp predecessor and competing algorithms for online learning in MLN. There are several directions for further work. We plan to improve scalability using parallel/distributed learning, along the lines of [22]. We also plan to evaluate different algorithms for online weight optimization and develop methodologies for online hyper-parameter adaptation.